Model Updating Using Measurements from Sensors Installed in Arbitrary Positions and Directions
Abstract
:1. Introduction
2. Materials and Methods
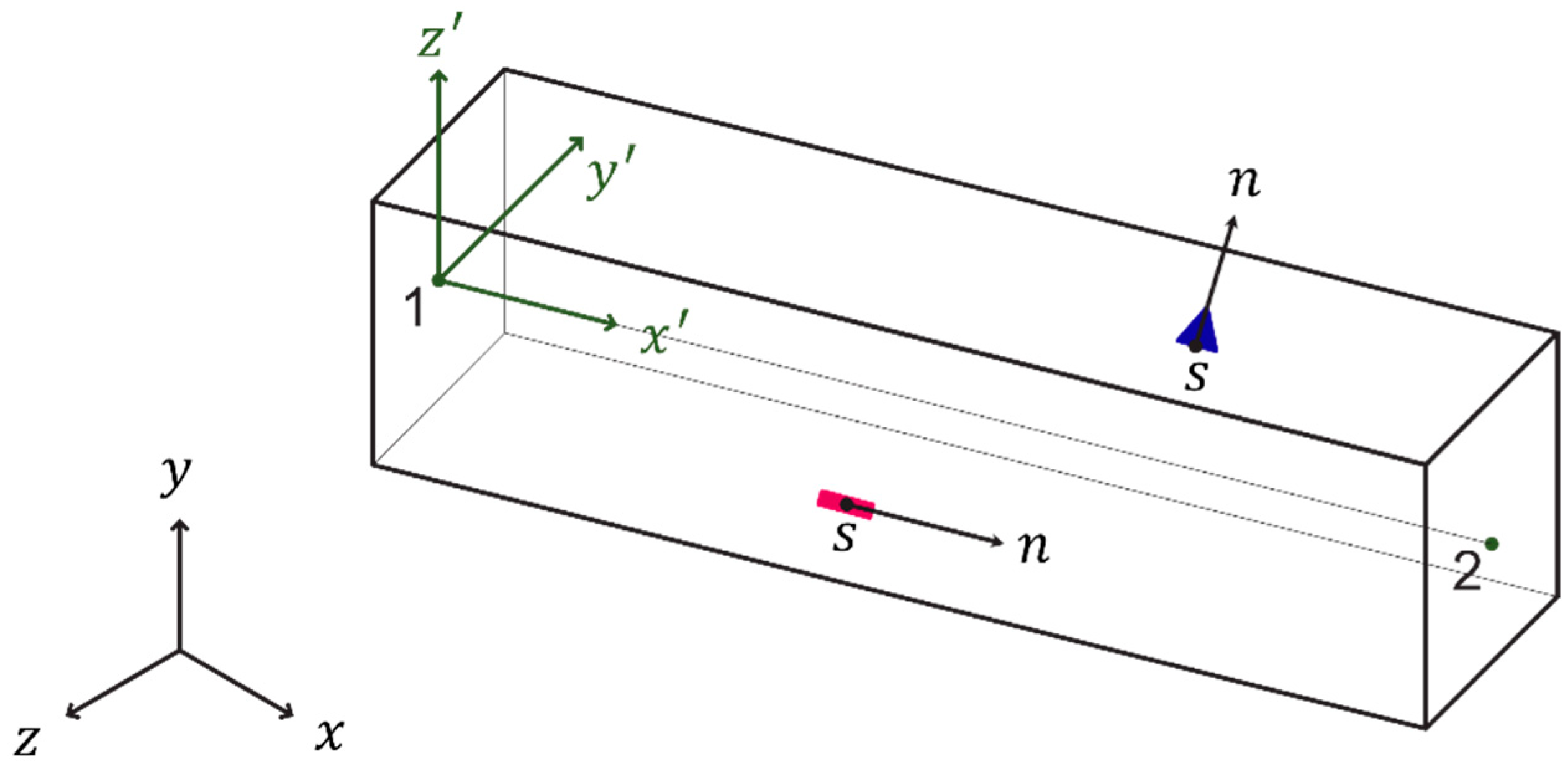
2.1. Measurement–Model Link
2.1.1. The Case Where the Displacement, Velocity, and Acceleration are Measured
2.1.2. The Case Where the Strain is Measured
2.2. Model Updating
2.2.1. Eigenvalue Residual
2.2.2. Mode Shape Residual
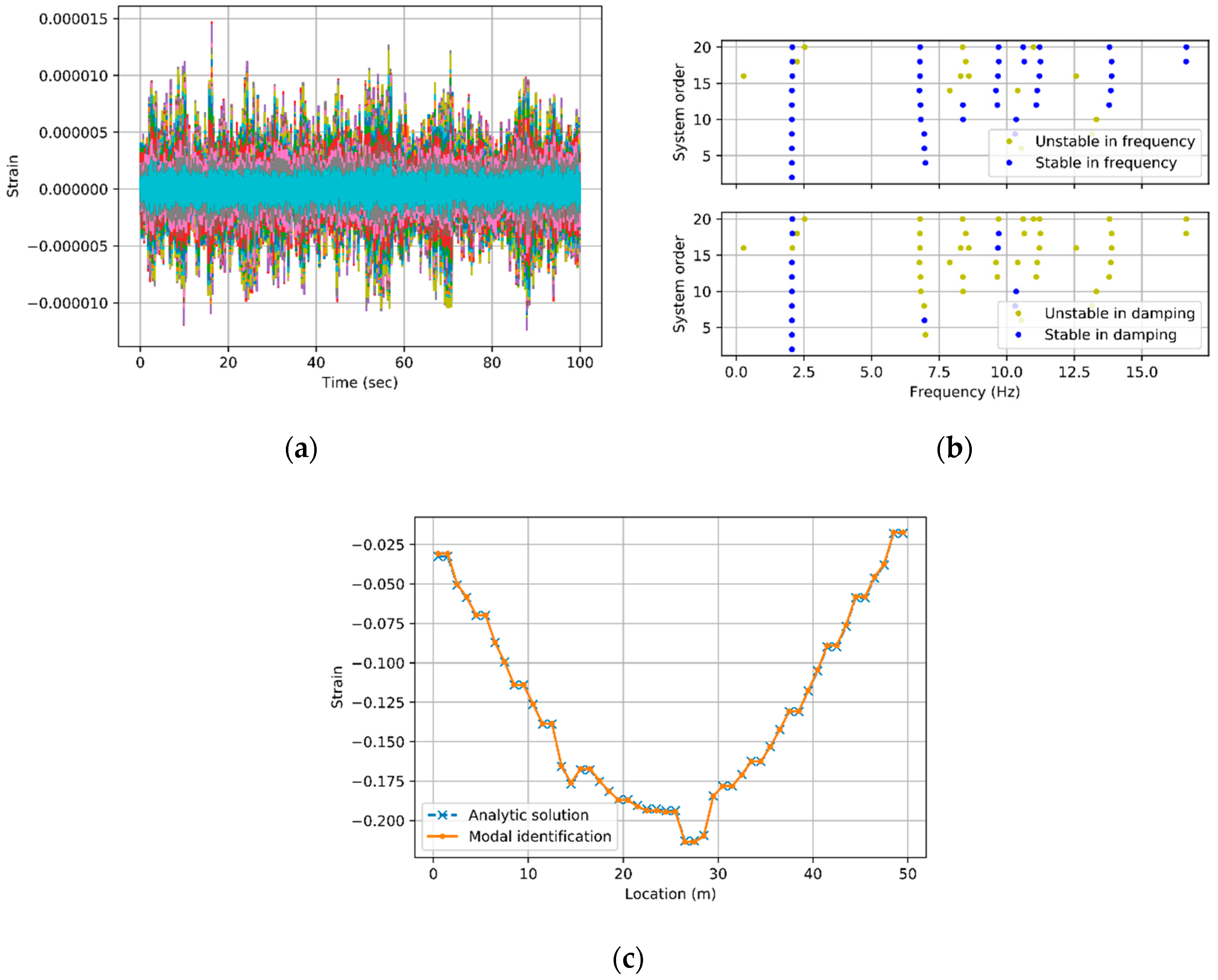
3. Numerical Example
3.1. Modal Identification
3.2. Construction of Transform Matrices
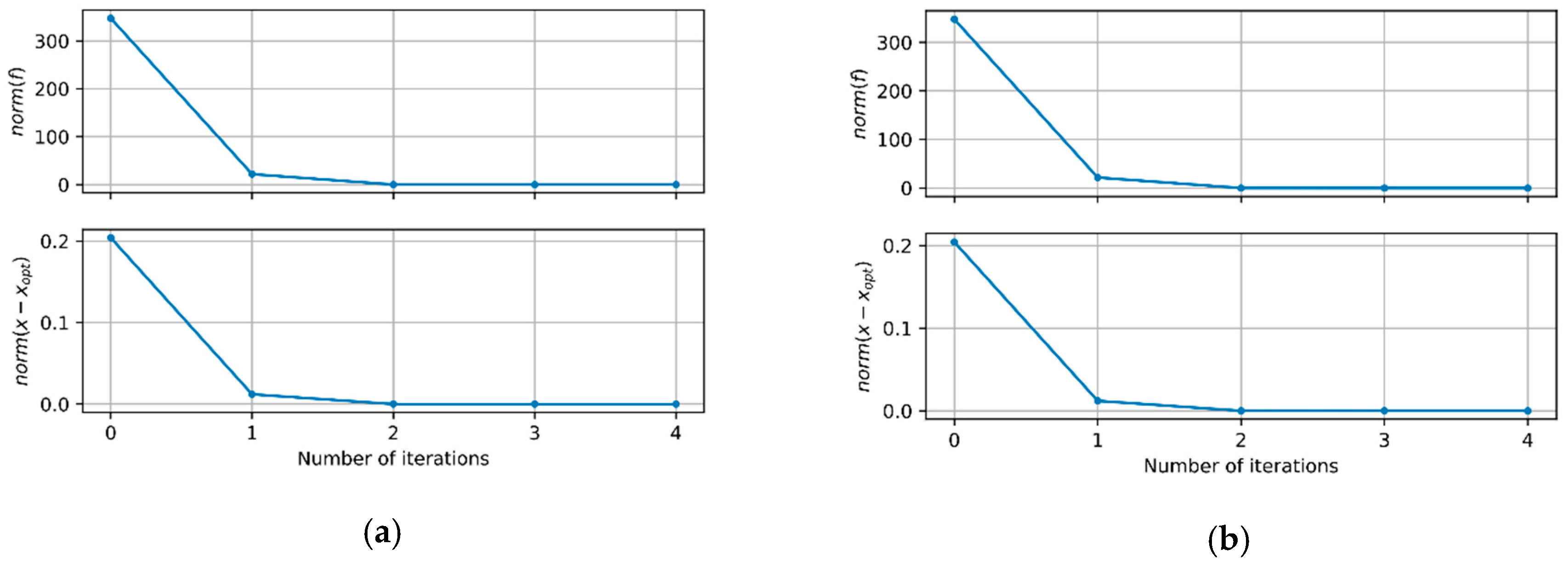
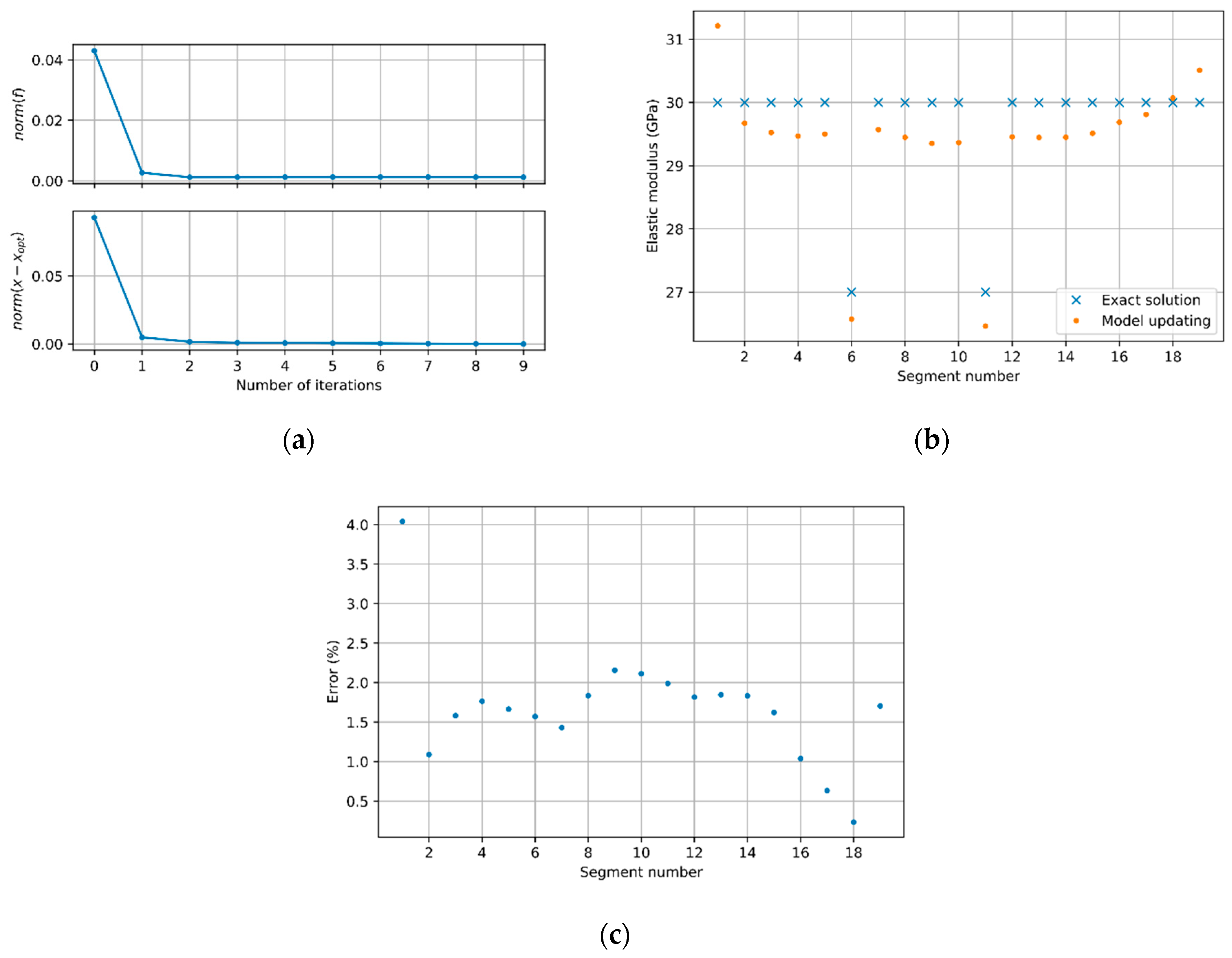
3.3. Model Updating
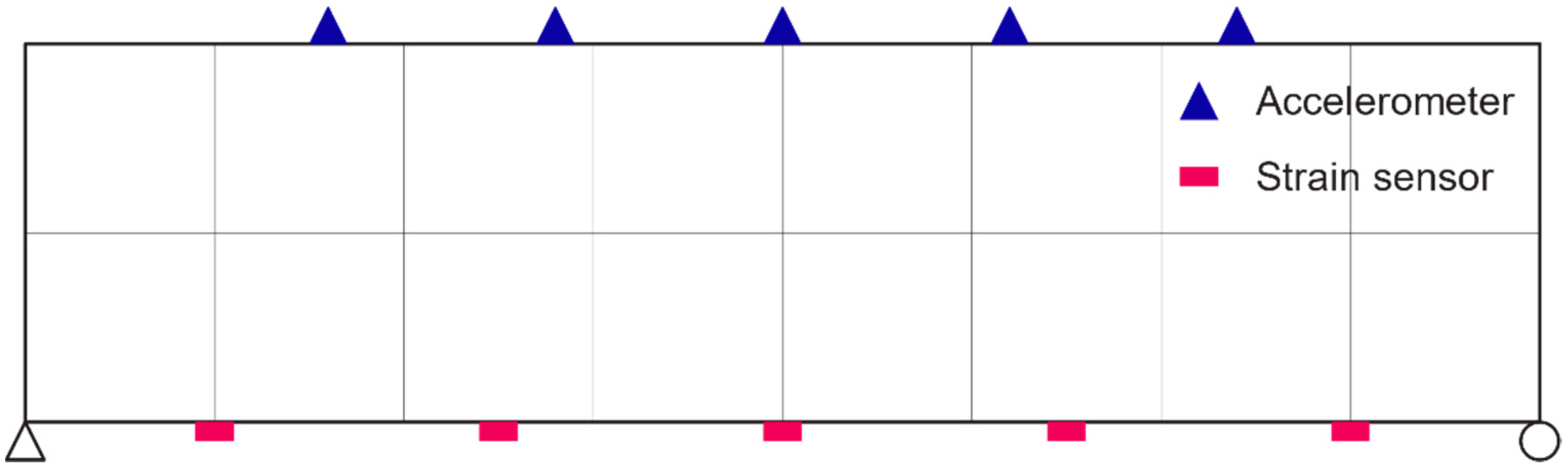
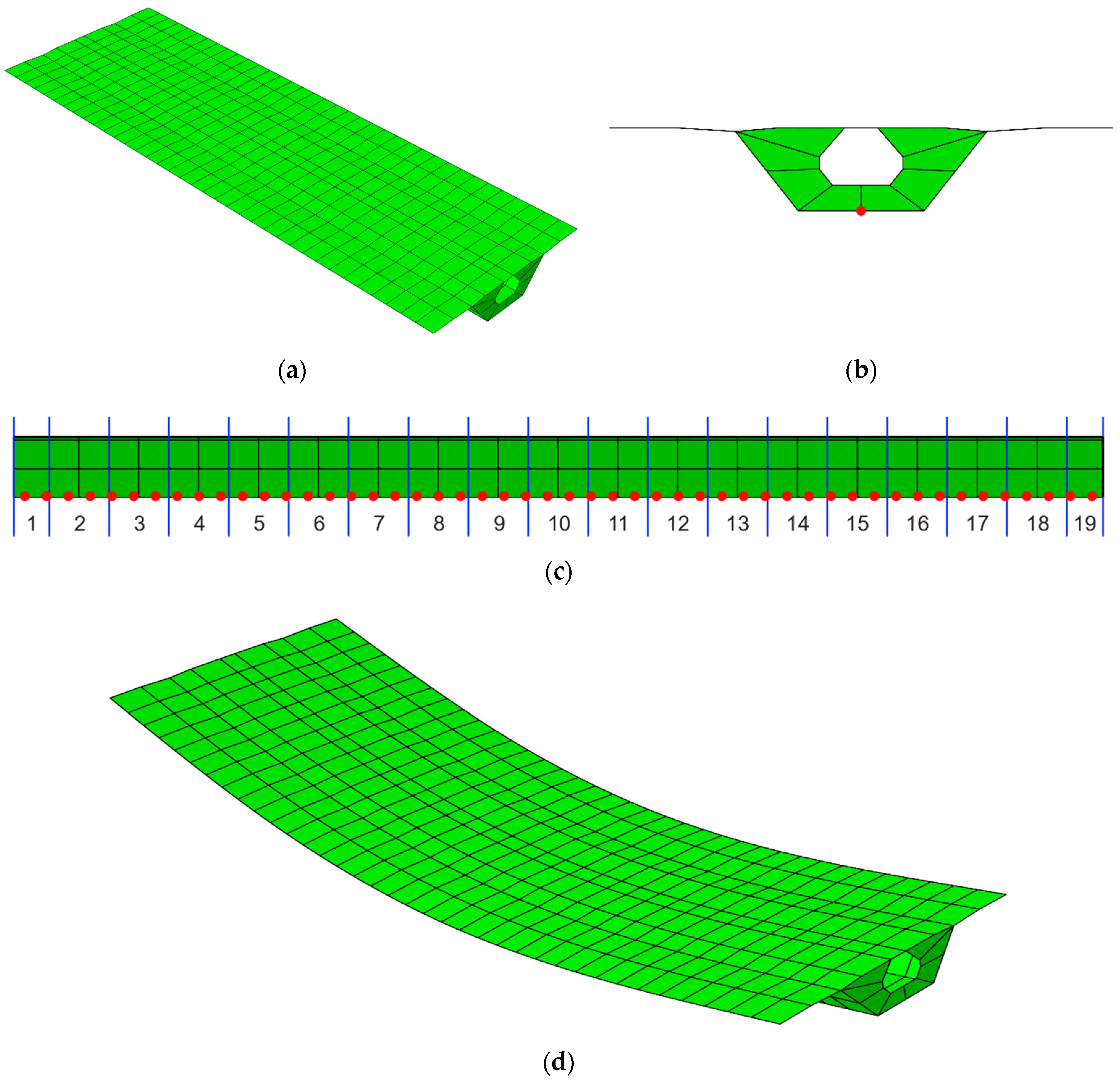
4. Numerical Application to Bridge
4.1. Without Uncertainties
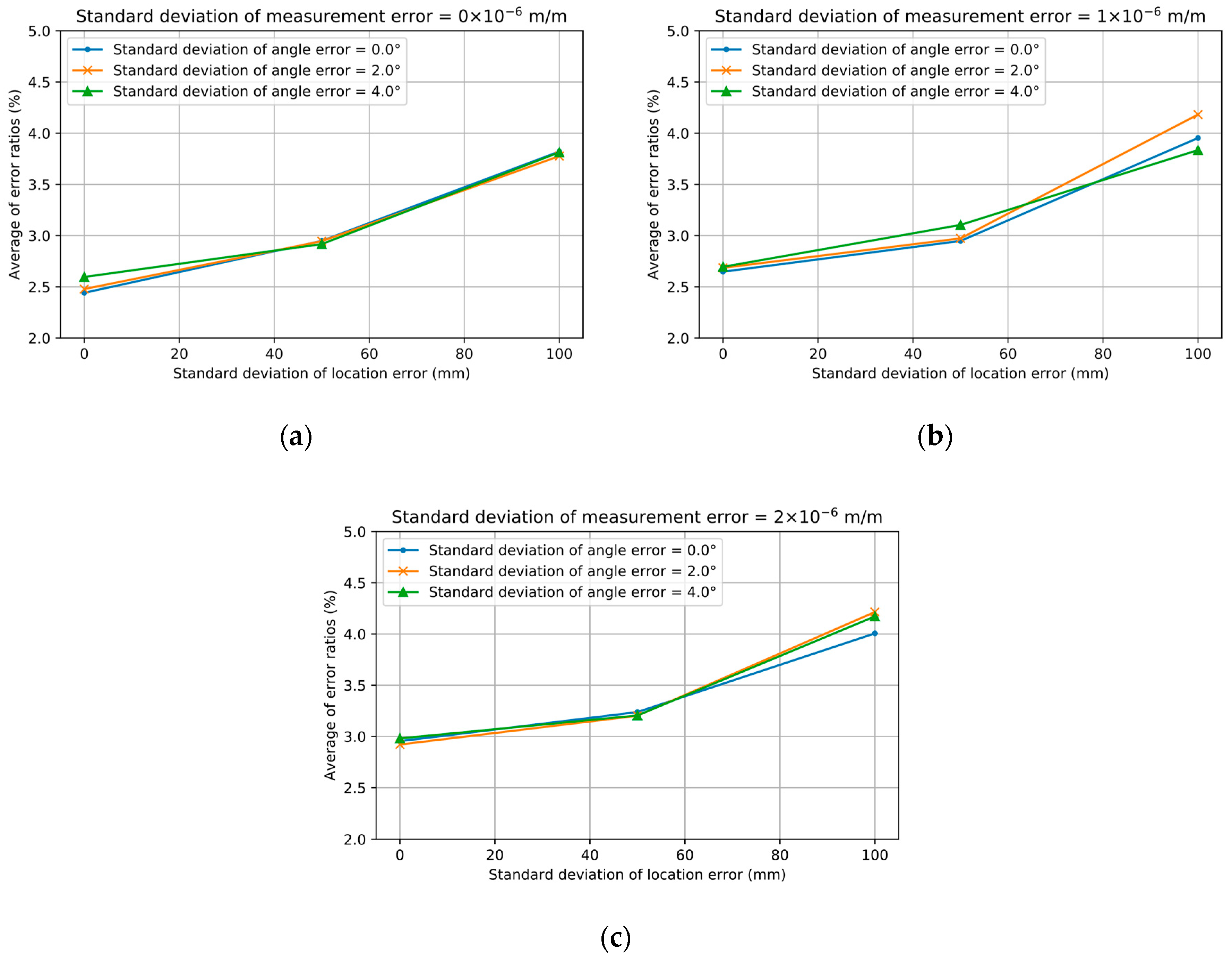
4.2. With Uncertainties
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Two-Dimensional Euler–Bernoulli Beam Element

References
- Brincker, R.; Zhang, L.; Andersen, P. In Modal identification from ambient responses using frequency domain decomposition. In Proceedings of the 18th International Modal Analysis Conference (IMAC), San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- Juang, J.-N.; Pappa, R.S. An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Qin, S.J. An overview of subspace identification. Comput. Chem. Eng. 2006, 30, 1502–1513. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace identification for linear systems: Theory—Implementation—Applications; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Friswell, M.I. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Yuen, K.V. Bayesian Methods for Structural Dynamics and Civil Engineering. John Wiley & Sons: Singapore, 2010. [Google Scholar]
- Katafygiotis, L.S.; Beck, J.L. Updating models and their uncertainties. Ii: Model identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Mares, C.; Mottershead, J.; Friswell, M. Stochastic model updating: Part 1—Theory and simulated example. Mech. Syst. Signal Process. 2006, 20, 1674–1695. [Google Scholar] [CrossRef]
- Sanayei, M.; Saletnik, M.J. Parameter estimation of structures from static strain measurements. I: Formulation. J. Struct. Eng. 1996, 122, 555–562. [Google Scholar] [CrossRef]
- Esfandiari, A.; Sanayei, M.; Bakhtiari-Nejad, F.; Rahai, A. Finite element model updating using frequency response function of incomplete strain data. AIAA J. 2010, 48, 1420–1433. [Google Scholar] [CrossRef]
- Allemang, R.J. The modal assurance criterion–twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Fox, R.; Kapoor, M. Rates of change of eigenvalues and eigenvectors. AIAA J. 1968, 6, 2426–2429. [Google Scholar] [CrossRef]
- Nelson, R.B. Simplified calculation of eigenvector derivatives. AIAA J. 1976, 14, 1201–1205. [Google Scholar]
- Kim, S.T.; Park, Y.; Park, S.Y.; Cho, K.; Cho, J.R. A sensor-type pc strand with an embedded fbg sensor for monitoring prestress forces. Sensors 2015, 15, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Kim, S.; Cho, J.R.; Park, Y.H. Estimation of tendon force distribution in prestressed concrete girders using smart strand. Appl. Sci. 2017, 7, 1319. [Google Scholar] [CrossRef]
- Kim, G.H.; Park, S.M.; Park, C.H.; Jang, H.; Kim, C.S.; Lee, H.D. Real-time quasi-distributed fiber optic sensor based on resonance frequency mapping. Sci. Rep. 2019, 9, 3921. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, K.; Park, Y.-H.; Cho, J.-R. Model Updating Using Measurements from Sensors Installed in Arbitrary Positions and Directions. Appl. Sci. 2019, 9, 4309. https://doi.org/10.3390/app9204309
Cho K, Park Y-H, Cho J-R. Model Updating Using Measurements from Sensors Installed in Arbitrary Positions and Directions. Applied Sciences. 2019; 9(20):4309. https://doi.org/10.3390/app9204309
Chicago/Turabian StyleCho, Keunhee, Young-Hwan Park, and Jeong-Rae Cho. 2019. "Model Updating Using Measurements from Sensors Installed in Arbitrary Positions and Directions" Applied Sciences 9, no. 20: 4309. https://doi.org/10.3390/app9204309
APA StyleCho, K., Park, Y.-H., & Cho, J.-R. (2019). Model Updating Using Measurements from Sensors Installed in Arbitrary Positions and Directions. Applied Sciences, 9(20), 4309. https://doi.org/10.3390/app9204309




