1. Introduction
As a structural material of buildings or infrastructure, stainless steel has important characteristics such as corrosion resistance, durability, fire resistance, and aesthetics compared to carbon steel. Therefore, the use of stainless steel as nonstructural members of interior and exterior materials, as well as structural members of buildings at home and abroad, has been increasing recently. Structural design specifications for cold-formed stainless steel were established in the United States (American Society of Civil Engineers, ASCE) [
1], Europe (Eurocode 3, EC 3 part 1–4) [
2], Japan (Stainless Steel Building Association of Japan, SSBA) [
3], and Australia/New Zealand (AS/NZS 4673) [
4]. However, in Korea, stainless steel has not been designated as a structural steel material in the Korean Building Code (KBC) up to now [
5]. Moreover, the structural design standards for stainless steel structural members are not yet available. In Korea, recently, many researchers have performed studies on structural behaviors, such as fracture mode and ultimate strength of bolted and welded connections of thin-walled (cold-formed) stainless steel plates through experimental and analytical methods [
6,
7,
8,
9].
Since ferritic stainless steel among various types of stainless steels does not contain smaller amounts of alloying elements such as molybdenum, nickel, titanium, and niobium, the material cost is lower than austenitic and duplex stainless steels, and its demand for use as interior and exterior materials and structural materials of general buildings, which are not harshly corrosive environments such as coastal areas and chemical plants, is increasing [
10]. Additionally, it usually possesses better deep drawability and resistance to stress corrosion cracking. However, ferritic stainless steel has lower ductility than austenitic stainless steel and contains a large amount of carbon (C), which causes embrittlement (brittle fracture) of the heat affected zone (HAZ) and poor weldability than austenitic stainless steel. Ferritic stainless steels are hardened by cold working and not hardened (strengthened) by quenching, and develop minimum hardness and maximum ductility, impact toughness, and corrosion resistance in the annealed and quenched condition [
11].
With the development of welding technology for ferritic stainless steel, recently, all of the ferritic types are considered weldable with the majority of the welding processes except for the free machining grade (AISI 430F, which contains high sulphur content). ASCE specifies that Type 430 stainless steel shall not be used for welded connections due to deterioration of corrosion resistance and toughness. Thus far, there have been few studies on the structural behaviors of ferritic stainless steel welded connections.
As a series of the block shear strength estimation for stainless steel welded connection, experimental and analytical studies have been performed on the structural behavior of the base metal and weld metal fracture of welded connections made of austenitic stainless steel STS304 (ASTM 304 type) [
12] and STS304L (ASTM 304L type) [
13]. The predicted block shear strength according to the current design equations of KBC, AISC, and EC3. Moreover, the proposed equations of previous studies on carbon steel welded connections by Topkaya [
14] and Oosterhof and Driver [
15] were compared with the experimental and analytical results. However, these research projects did not include the consideration of welded connections with ferritic stainless steel, which has different material properties such as yield stress, tensile strength, yield ratio, elongation, etc. [
16]. Teh and Deierlein have studied block shear behavior of bolted connections and proposed the block shear equation considering a limiting shear tearout stress of 0.6
Fu on each effective shear area and shear failure plane to be midway between the gross and the net shear planes [
17].
Studies on buckling behaviors and web crippling design of ferritic stainless steel structural members have been carried out by Bock et al. [
18], Zhao et al. [
19] and Yousefi et al. [
20]. Kim [
21] performed an experimental study on the ferritic stainless steel (STS430) welded connection with base metal block shear fracture and evaluated the ultimate strength depending on the length of the weld line according to loading direction. It was found that the current design equations for carbon steel welded connections did not consider the shear lag effect, stress triaxiality effect, and stress distribution factor in the critical fracture section for ferritic stainless steel welded connection.
This study examines the stress and strain distribution of welded connections based on the previous experimental results of ferritic stainless steel (STS430) fillet-welded connections with base metal block shear fracture and develops a finite element analysis model to predict the ultimate strength of welded connection with the base metal block shear fracture. Additional analysis on the weld length on the welding direction without further testing to compare and review the fracture mode and strength according to the variables was also performed. In addition, this study considered the applicability of the design formula by comparing the ultimate block shear strength of the analysis results with the predicted strength according to the current design equations and the equations proposed by Topkaya [
14], Oosterhof and Driver [
15], and Lee et al. [
13]. The current design equations such as KBC/AISC and EC3 and the equations proposed by Oosterhof and Driver were conservative to predict the base metal block shear strength of ferritic stainless steel. Although proposed equations by Topkaya and Lee et al. for carbon steel and austenitic stainless steel provided more accurate ultimate strengths, it is required that tensile stress and shear stress factors in the block shear path to reflect the characteristics of ferritic stainless steel material properties. Finally, a modified block shear strength equation considering the effects of the stress triaxiality on ultimate strength, stress distribution at the critical block shear section of ultimate state and weld length of the ferritic stainless steel welded connection was proposed.
2. Overview of Previous Experimental Studies
A total of seven specimens of ferritic stainless steel (STS430) welded connections with base metal fracture were tested by Kim [
21] and this chapter summarizes the test results.
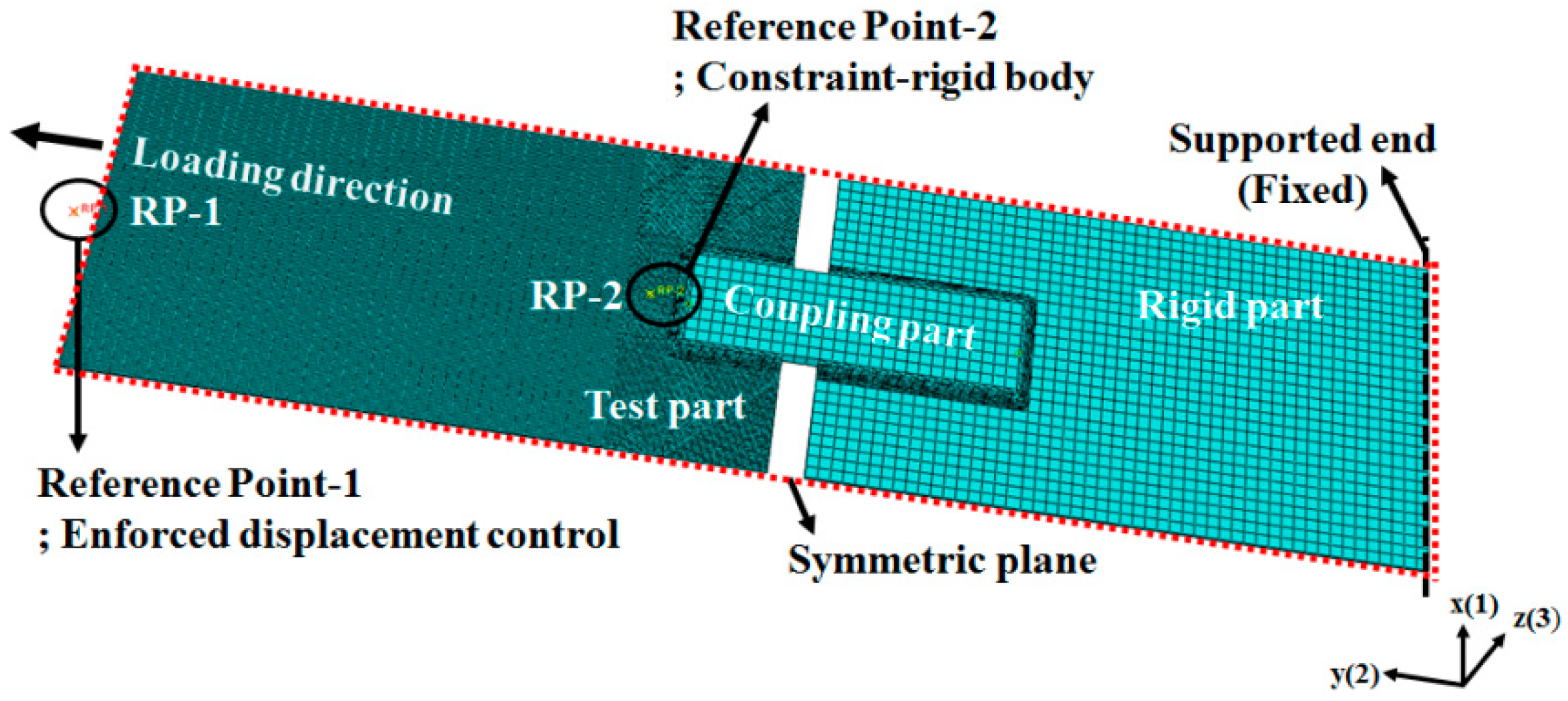
Table 1 includes the names of the specimens and the test results according to the combination of the weld length (
L) in the loading direction and the weld length (
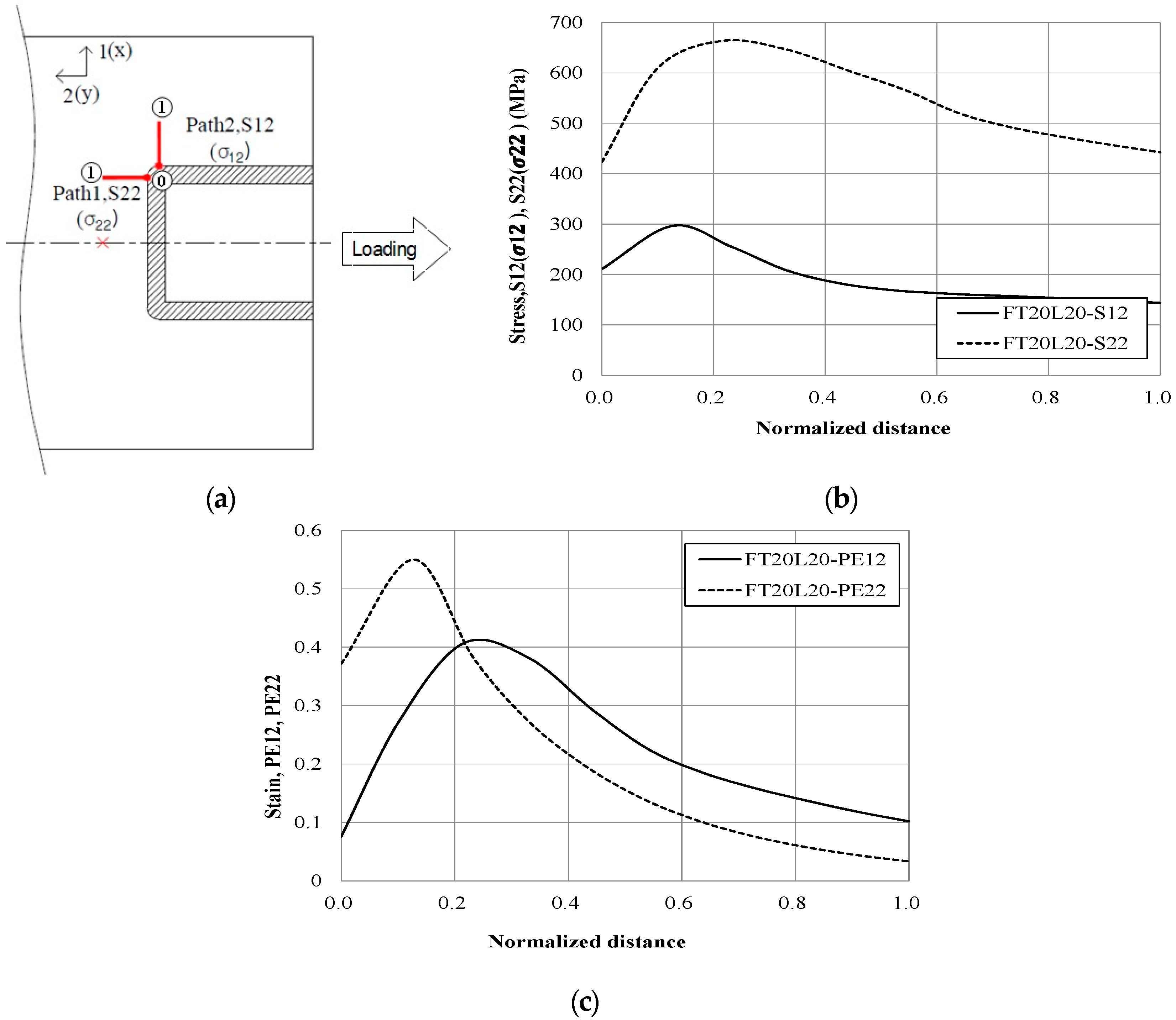
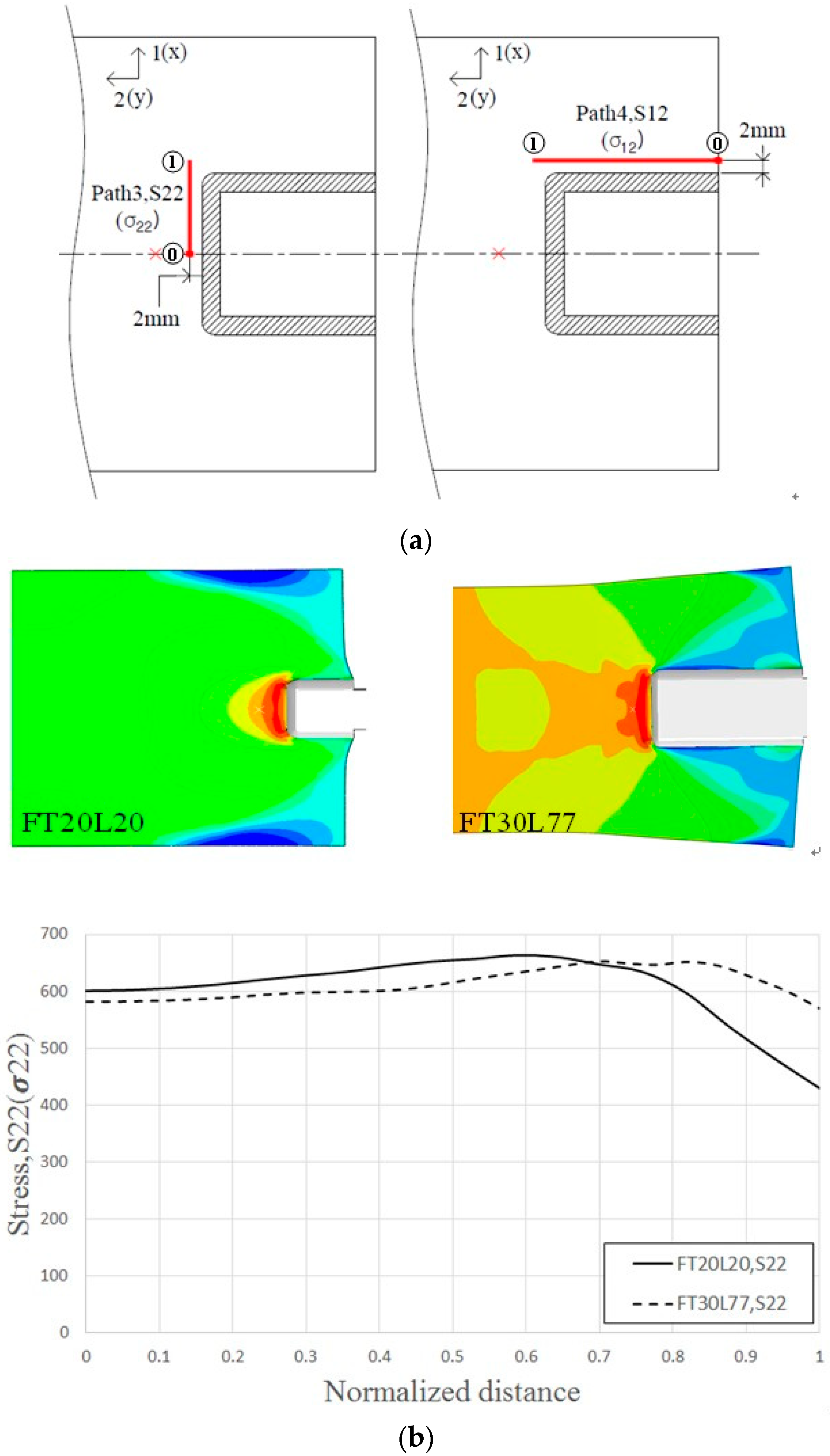
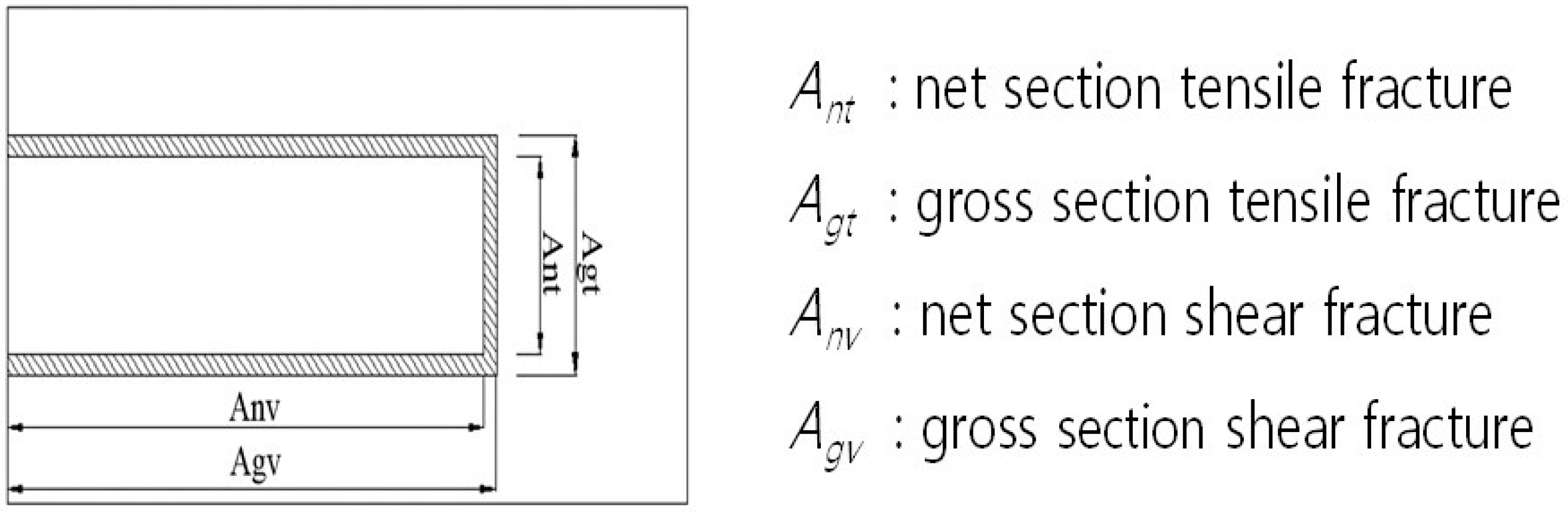
T) perpendicular to the loading direction. The test specimens were composed of three parts (test part, coupling part, and clamping part). Test and clamping parts were chosen with 3.0 mm thick plane plates and coupling part was machined with 6.0 mm thick plane plate. Two plates of test part and clamping part were joined to Arc weld with 3.0 mm weld size (
) on both sides of coupling part (refer to the Figure 4a of the reference [
21]). In order to evaluate the difference of structural behaviors according to the weld length and welding direction of the STS 430 welded connection, the specimens were produced by combining the weld lengths in the loading direction and perpendicular to the applied load as the main variables. Post weld heat treatment (PWHT) for Arc welded specimens after arc welding was not performed additionally and they were air cooled. Electrode for Arc welding of ferritic stainless steel (STS430) plates was chosen as E430-16 (minimum specified strength of
Fxx = 480 MPa) with the diameter of 3.2 mm specified in KS D 7014 (corresponds to E430-16 in AWS A5.4).
Three tensile coupons were tested to determine material properties of nominal 3.0 mm thick ferritic stainless steel (STS430) plate in accordance with KS B 0802 (Method of tensile test for metallic materials, corresponds to ISO 6892). The average plate thickness (
te) is 2.93 mm, elastic modulus (
E) was 179.50 GPa, the yield stress (
) was 259.93 MPa, the tensile strength (
) was 412.87 MPa, the yield ratio (
) was 62.93%, the ultimate strain at tensile stress was 0.36 mm/mm, and the elongation (
EL) at failure was 42.28% [
21]. Material test for the heat affected zone (HAZ) of welded connection with 3.0 mm thick ferritic stainless steel plate was not conducted in the previous study. Based on the previous test results, the fracture modes and the load-displacement curves of the representative specimens at the end of the experiment are shown in
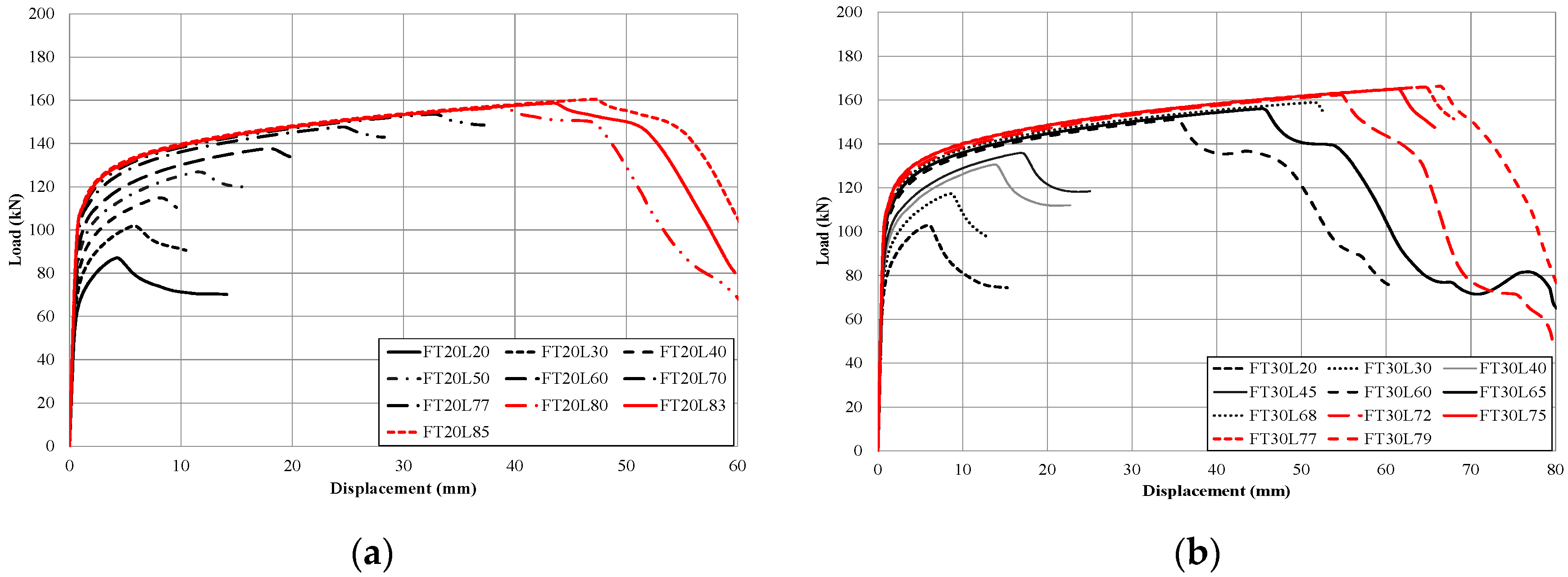
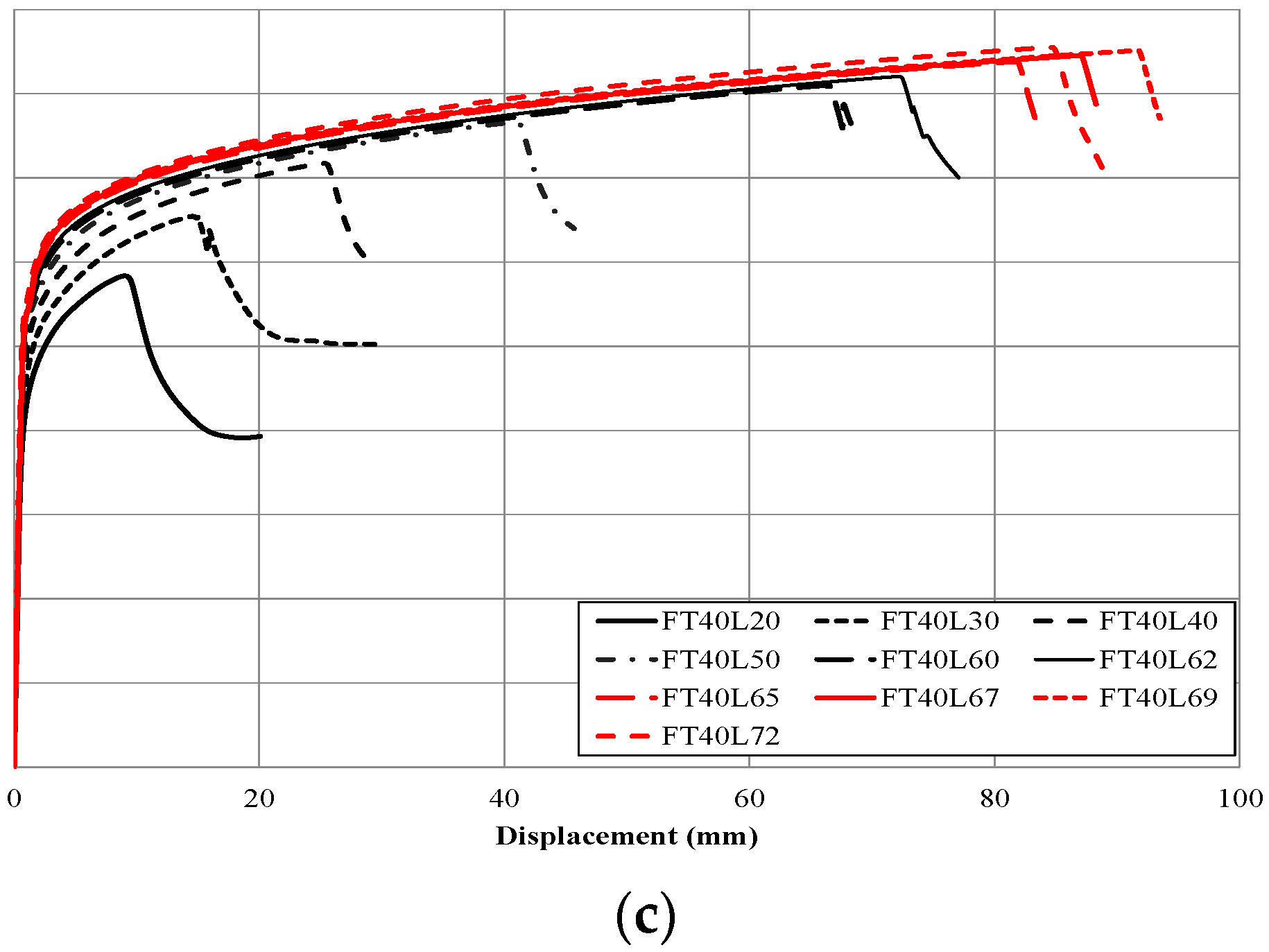
Figure 1 and
Figure 2, respectively. As shown in
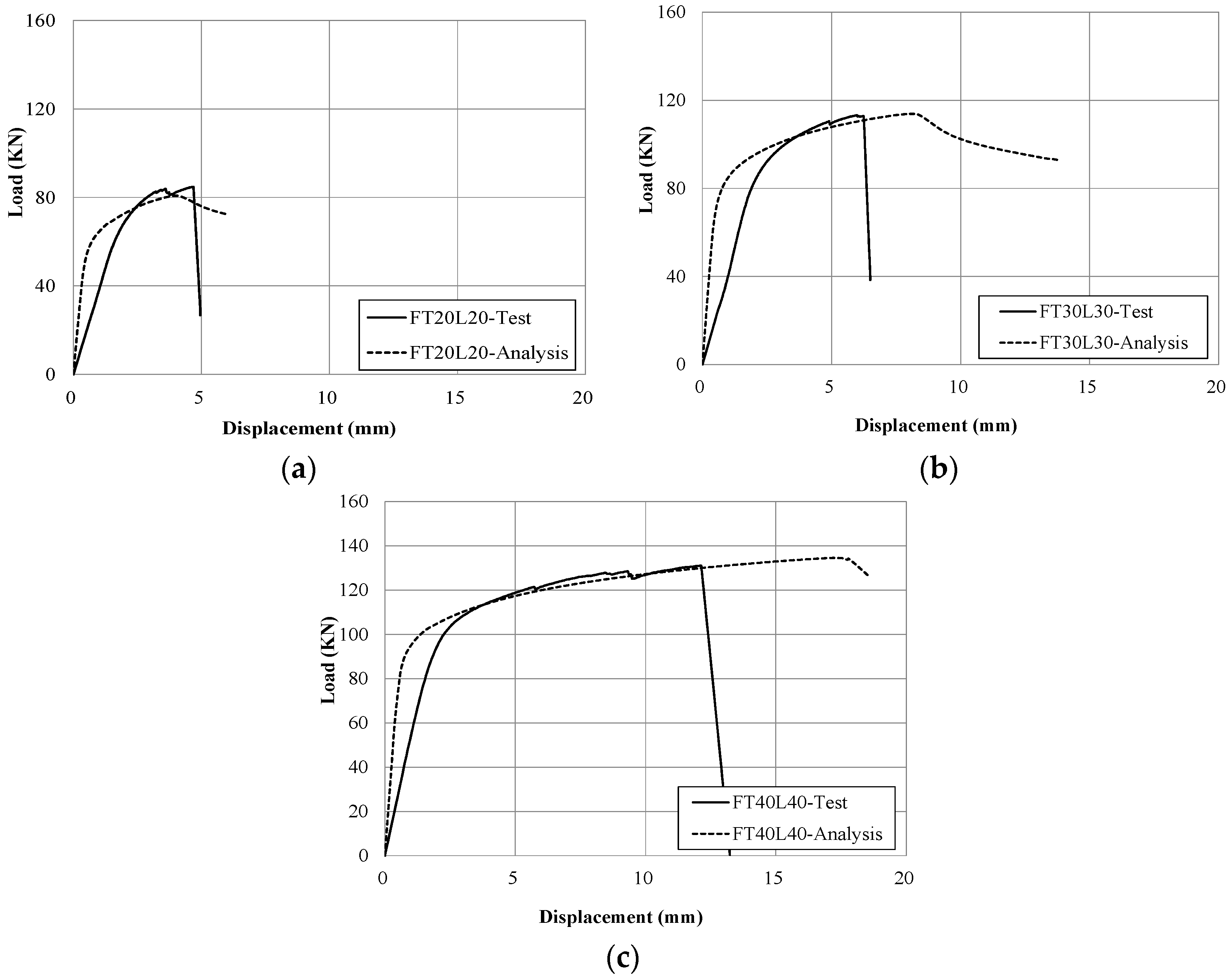
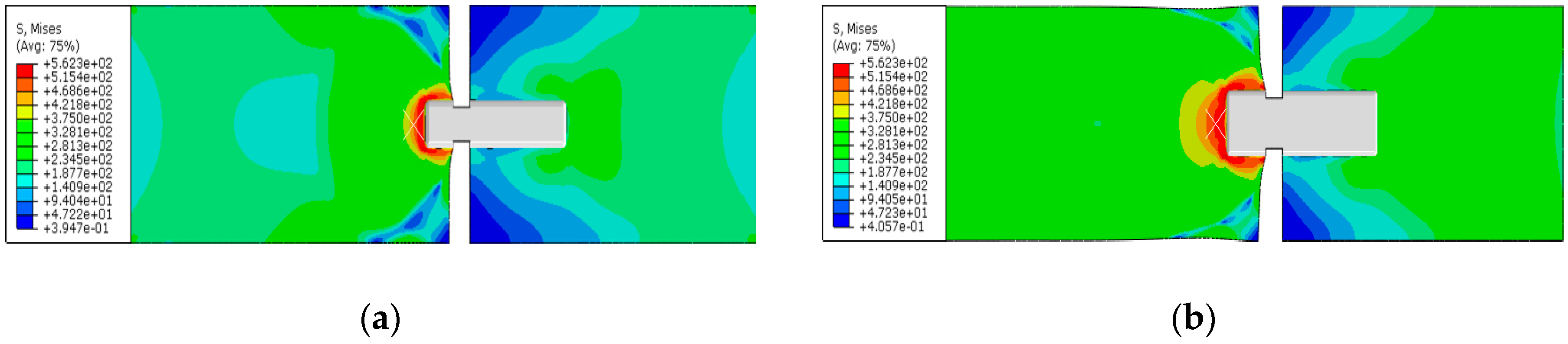
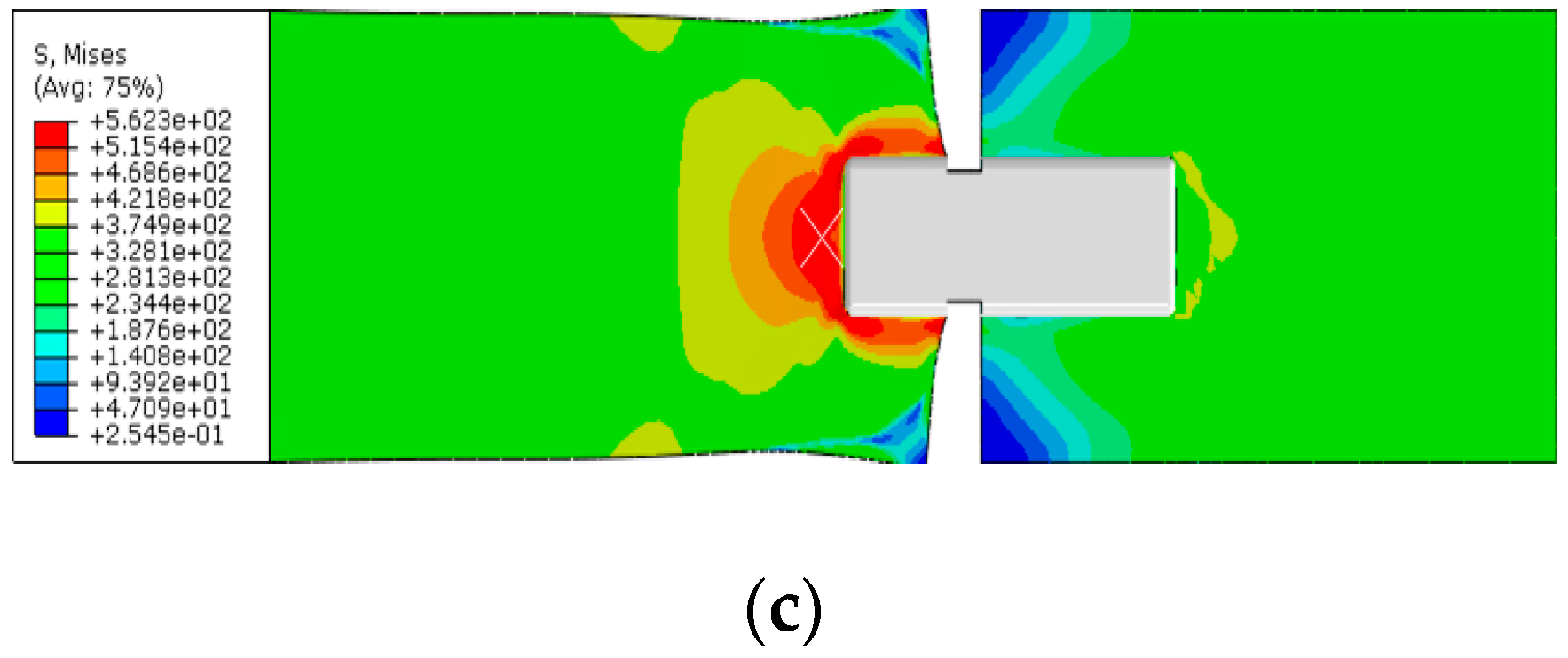
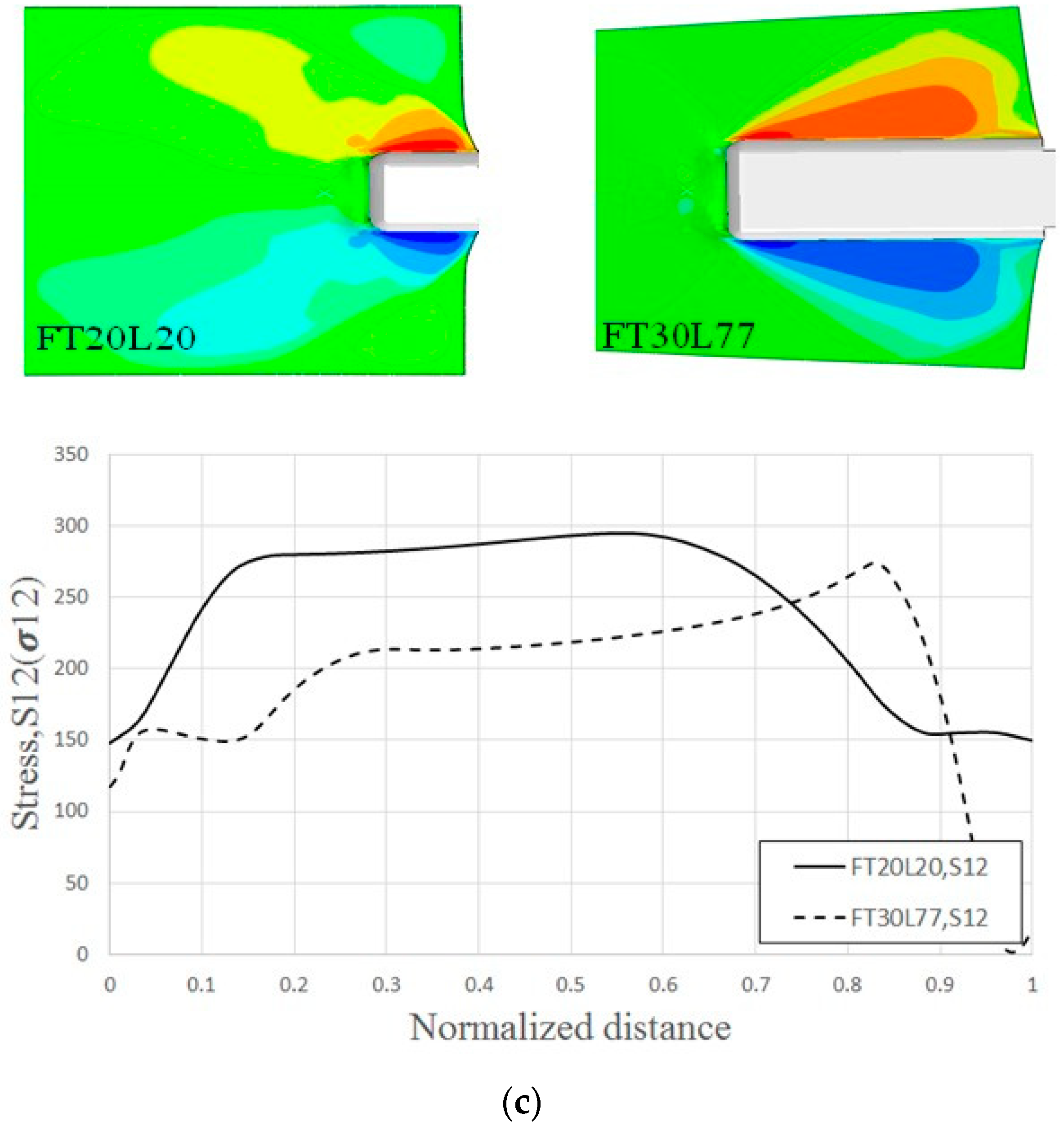
Figure 1, the block shear fracture, which is a combination of a tensile fracture in the perpendicular direction to the load and a shear fracture in the loading direction, occurred in the base metal near the toe of the weld metal, rather than in the weld metal. As shown in the load-displacement curves of
Figure 2, it was found that stress was concentrated on the welding end point of shear plane and shear yielding or shear crack started at the point. As a result, temporary strength drop on the curves of the specimens were observed due to the shear yielding or shear fracture of both ends (welding end point) in the loading direction. However, the shear yielding or shear fracture did not contribute to the determination of ultimate strength. Finally, tensile fractures in the direction perpendicular to the load occurred as the enforced displacement increased, and determined the ultimate strength. In the existing experimental study of ferritic stainless steel (STS430), welded connections with base metal block shear fracture [
21] and block shear strengths were investigated according to weld lengths and welding methods and were compared with those calculated by current design equations.
5. Conclusions
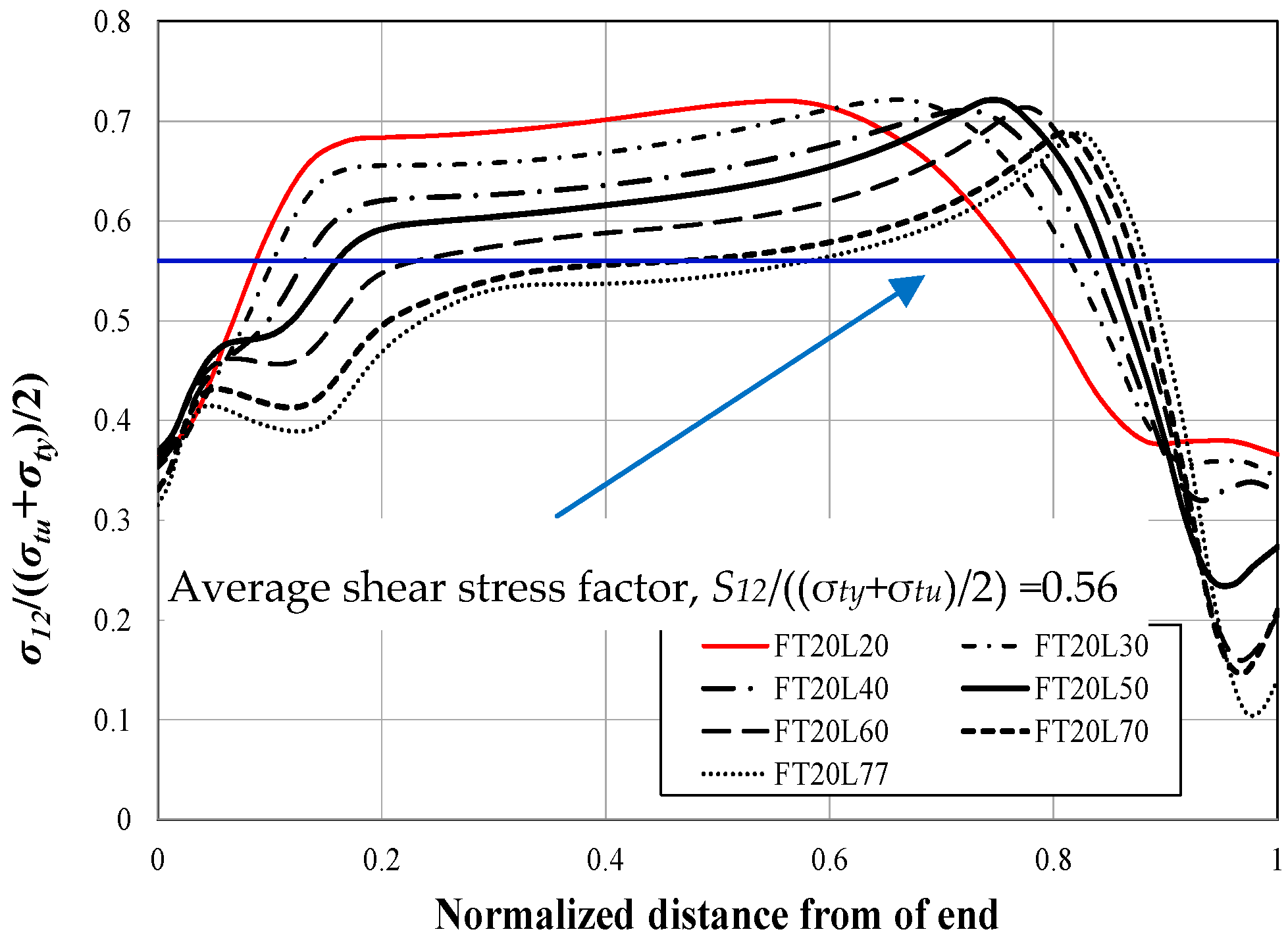
A finite element analysis model based on the previous experimental study results of ferritic stainless steel (STS430) fillet-welded connections with base metal block shear fracture was developed. In addition, the stress distribution in the critical section of the welded connection through additional parametric analysis by using the weld lengths in the direction of the load and perpendicular to the load was examined, and the predicted strengths by the analysis results, current design equations, and equations proposed by other researchers were compared. The design equations of KBC2016, AISC2016, and EC3 underestimated the block shear strength of the welded connections because they do not fully consider the stress triaxiality effect on the ultimate strength of welded connection. Moreover, Topkaya’s equation, based on the results of research of carbon steel welded connections, showed the closest evaluation of the block shear fracture strength. Since the material properties of ferritic stainless steel are different from those of carbon steel; therefore, the tensile stress factor was modified from 1.25 to 1.36 by examining the critical section and stress distribution at the point of ultimate strength in the welded connection from the analysis results and the shear stress factor was also modified by the average value of the tensile strength and yield stress of the STS430 material. As a result, it is found that the prediction accuracy of the ferritic stainless steel (STS430) welded connection with base metal block shear fracture strength by the proposed equation was improved.