Labeled Multi-Bernoulli Filter Joint Detection and Tracking of Radar Targets
Abstract
:1. Introduction
2. Backgound
2.1. LMB RFS
2.2. The Observation Model and Likelihood Function of Radar
2.3. Multi-Target Bayes Filter
3. The S-LMB-GOM Filter
3.1. Prediction
3.2. Update
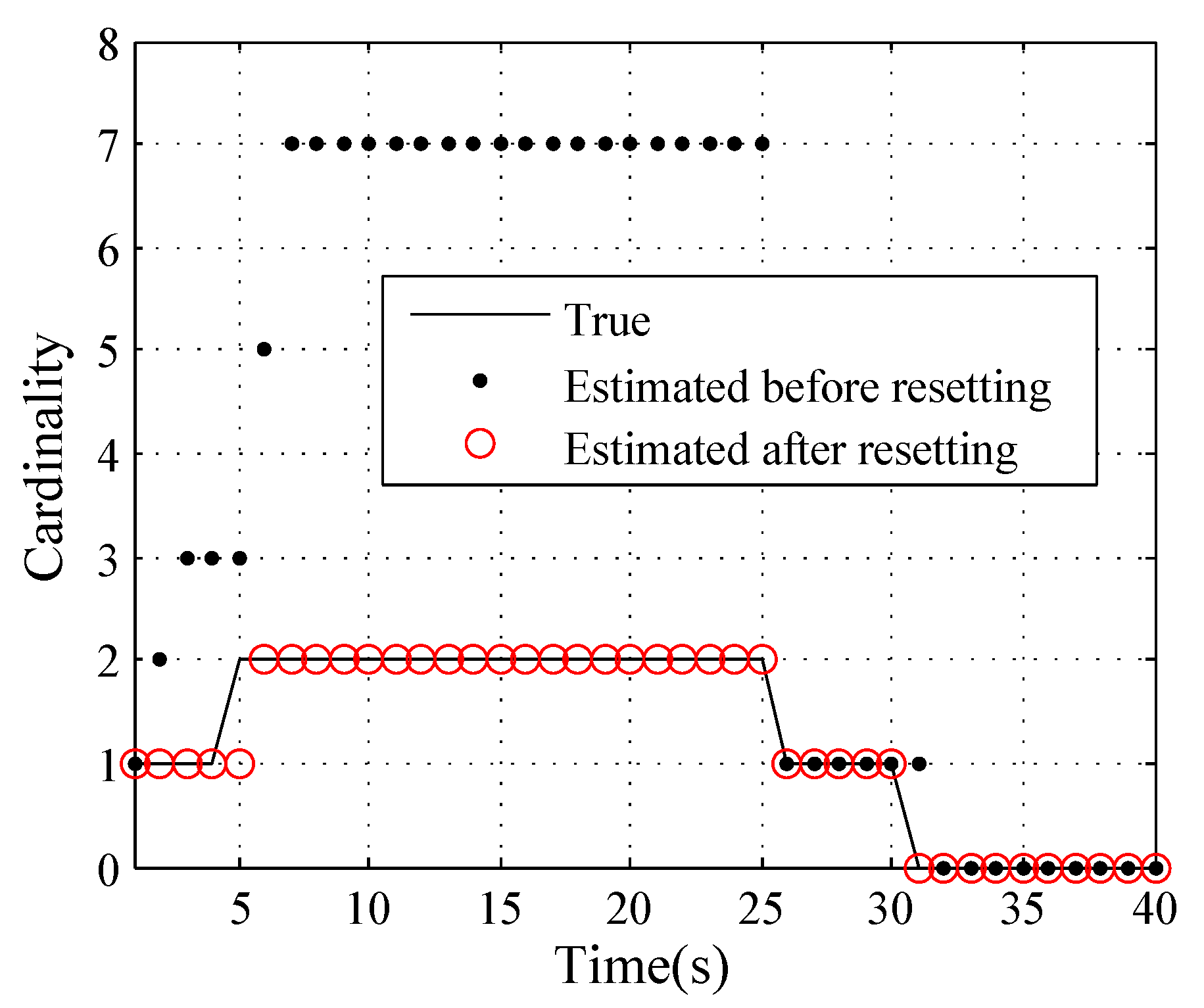
3.3. A Method to Overcome the Cardinality Estimate Bias
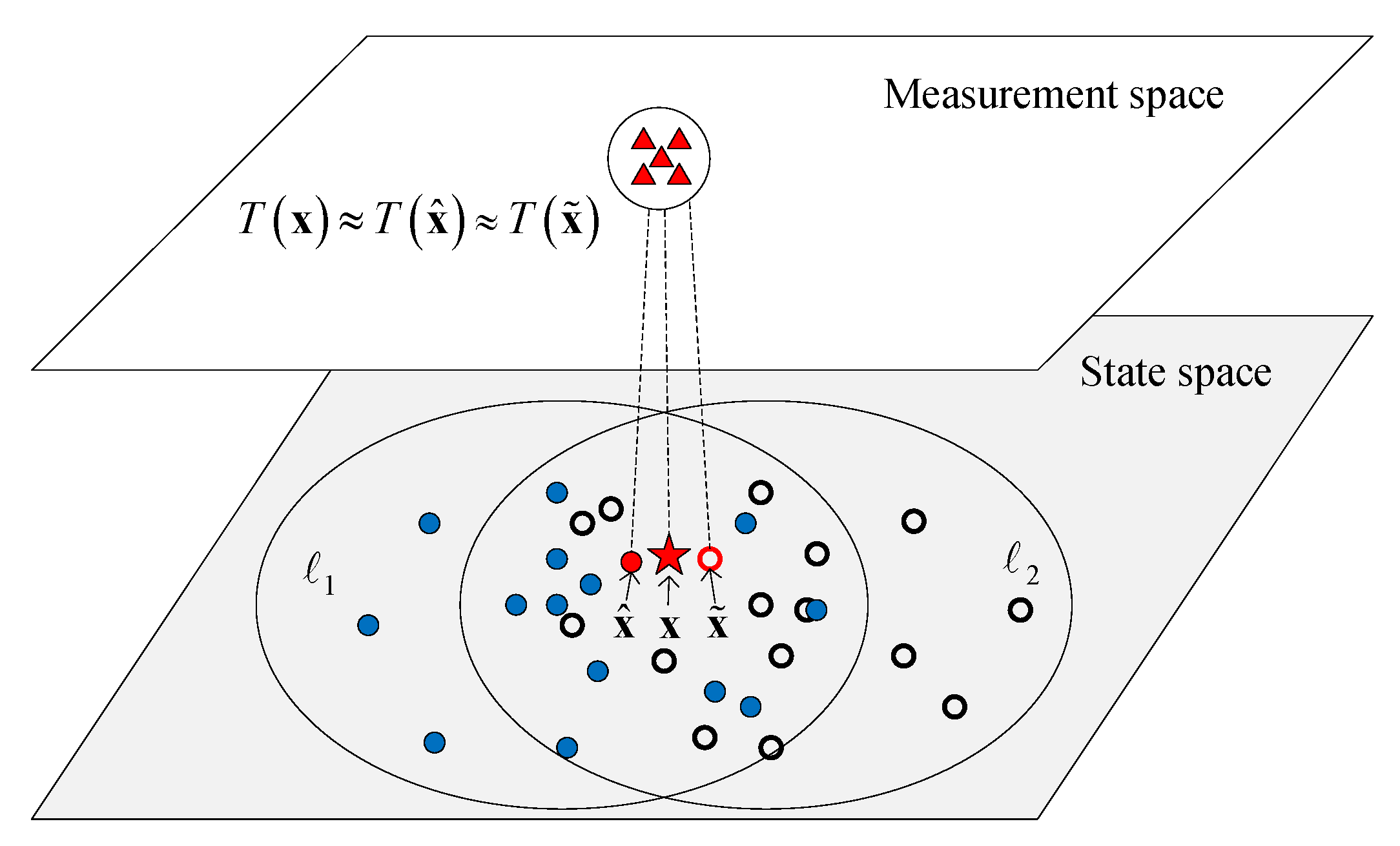
3.3.1. The Reason of the Bias
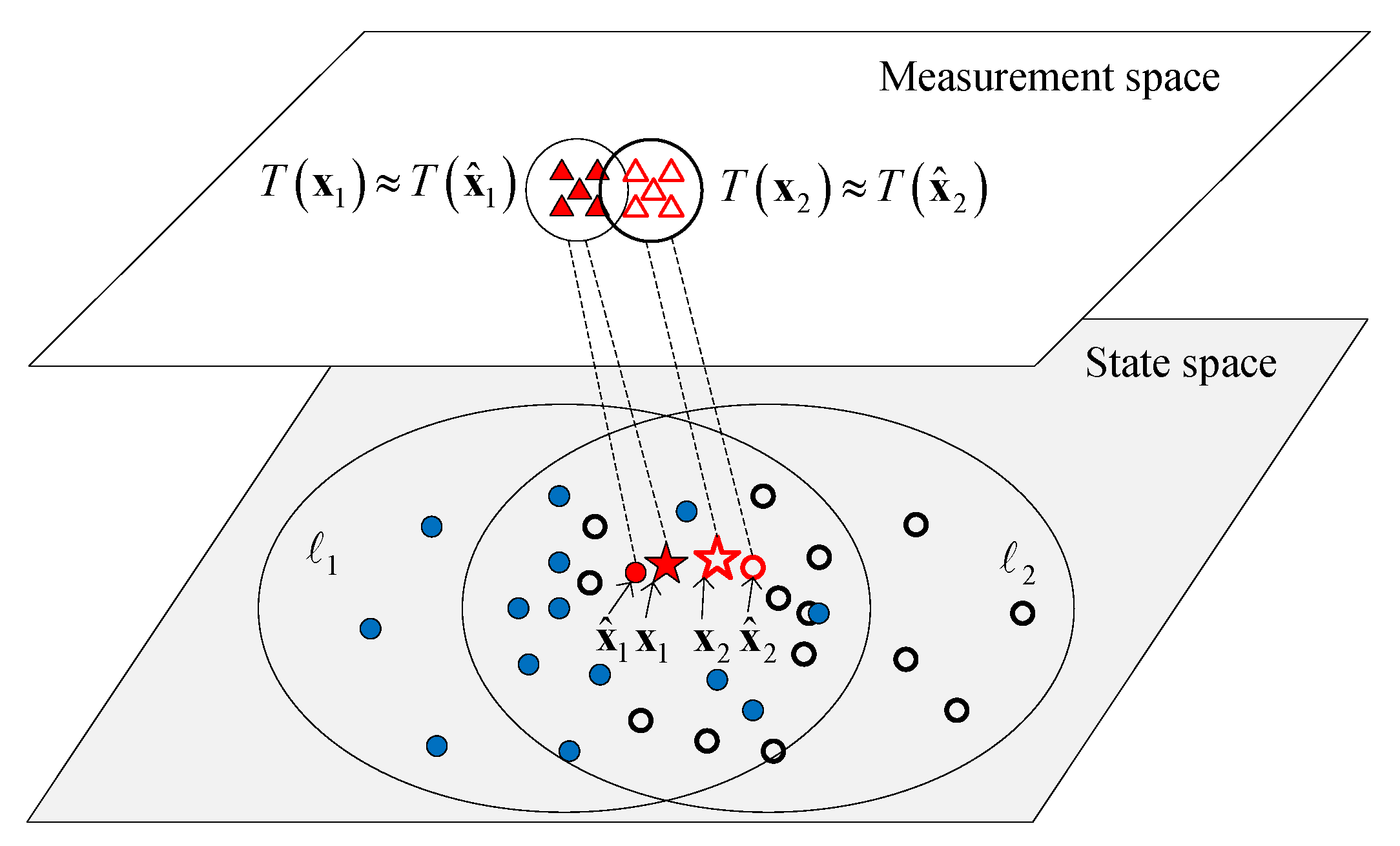
3.3.2. The One-to-One Correspondence Method
| Algorithm 1 One-to-one correspondence method |
1. Descending sort: . 2: Update in order of to get and . If (compute-likelihood()). . reset-noise. end |
3.3.3. The Analysis and Performance of the Proposed Method
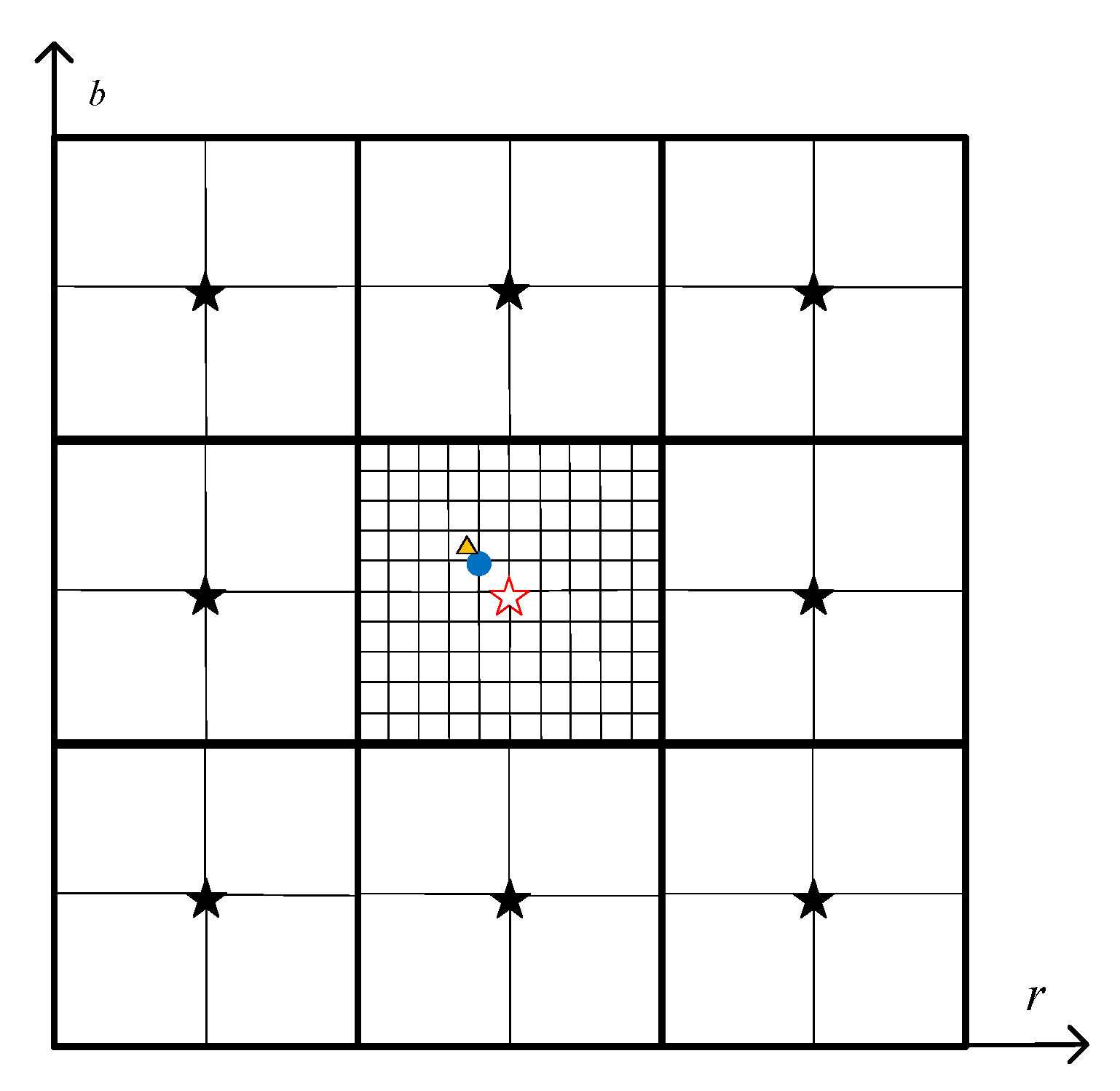
3.4. The Property Analysis and the Set of the Point Spread Function
3.5. An Approximate Method for Calculating Point Spread Function
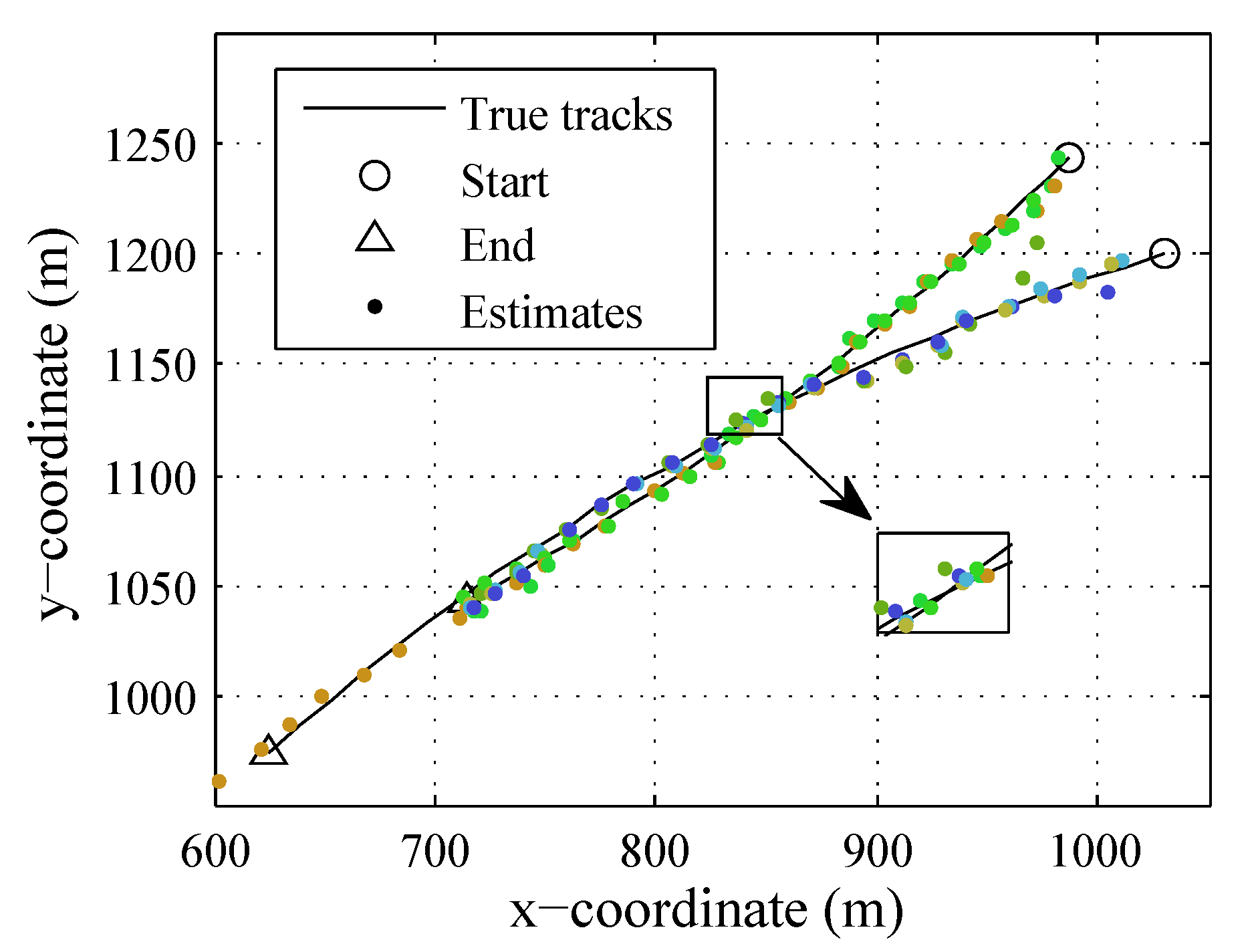
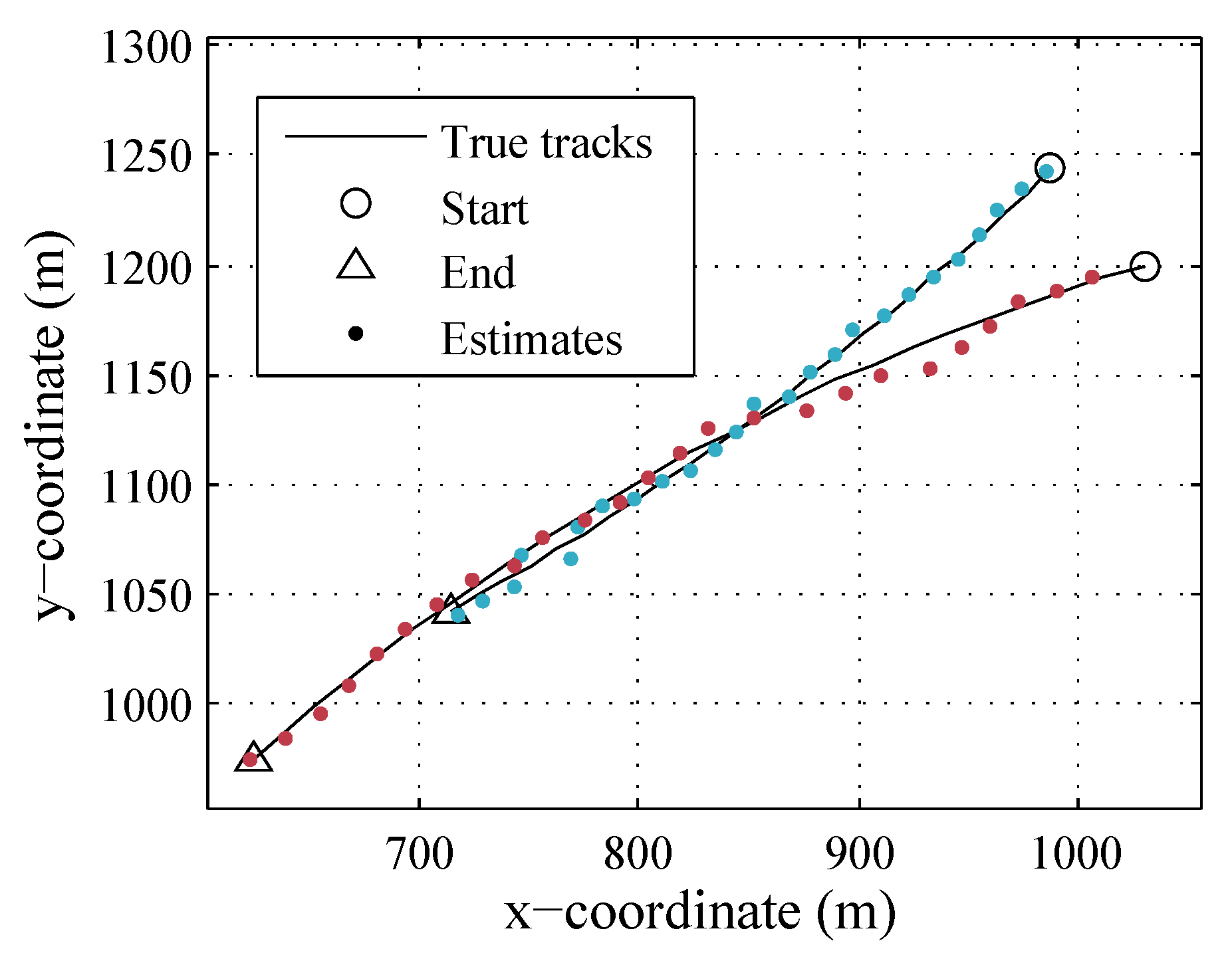
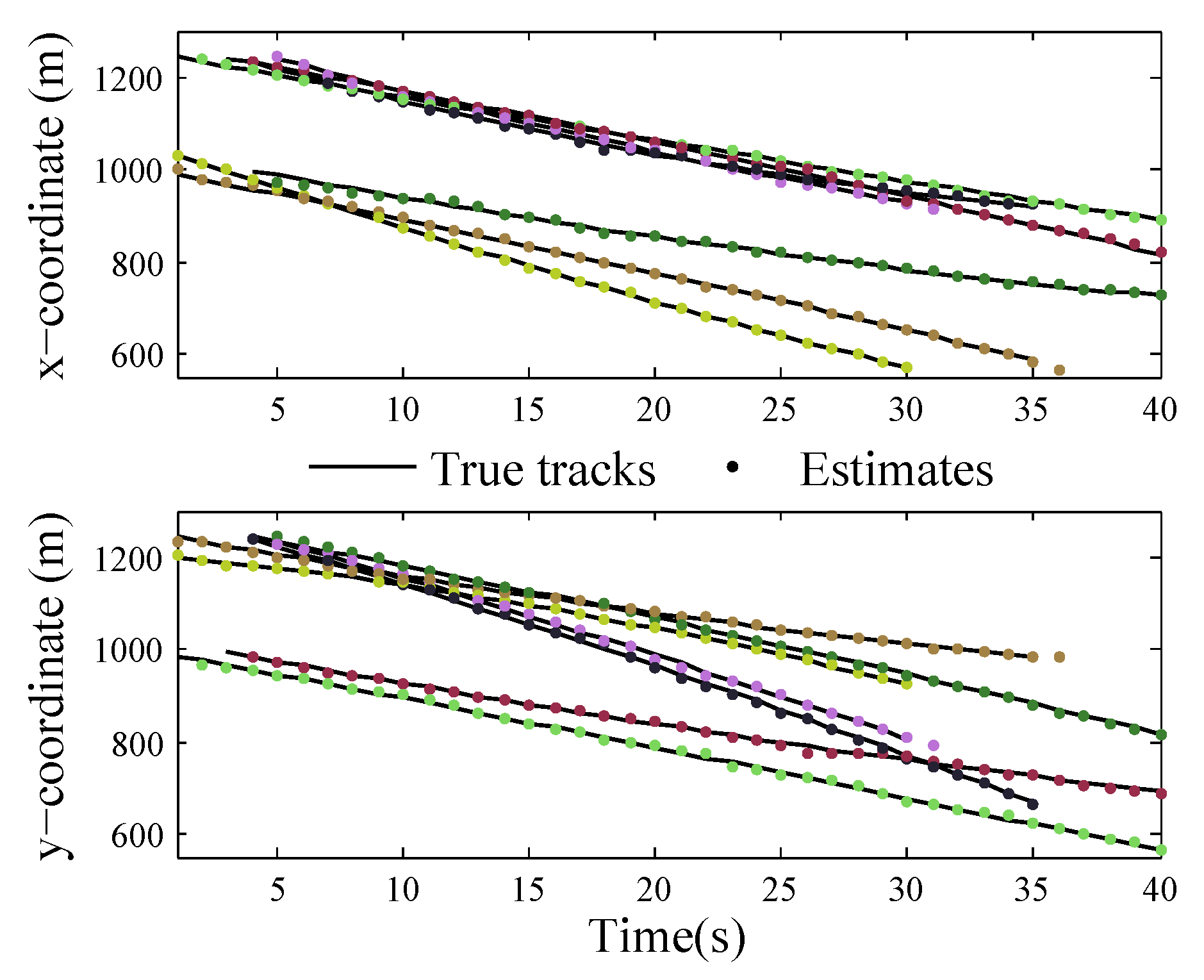
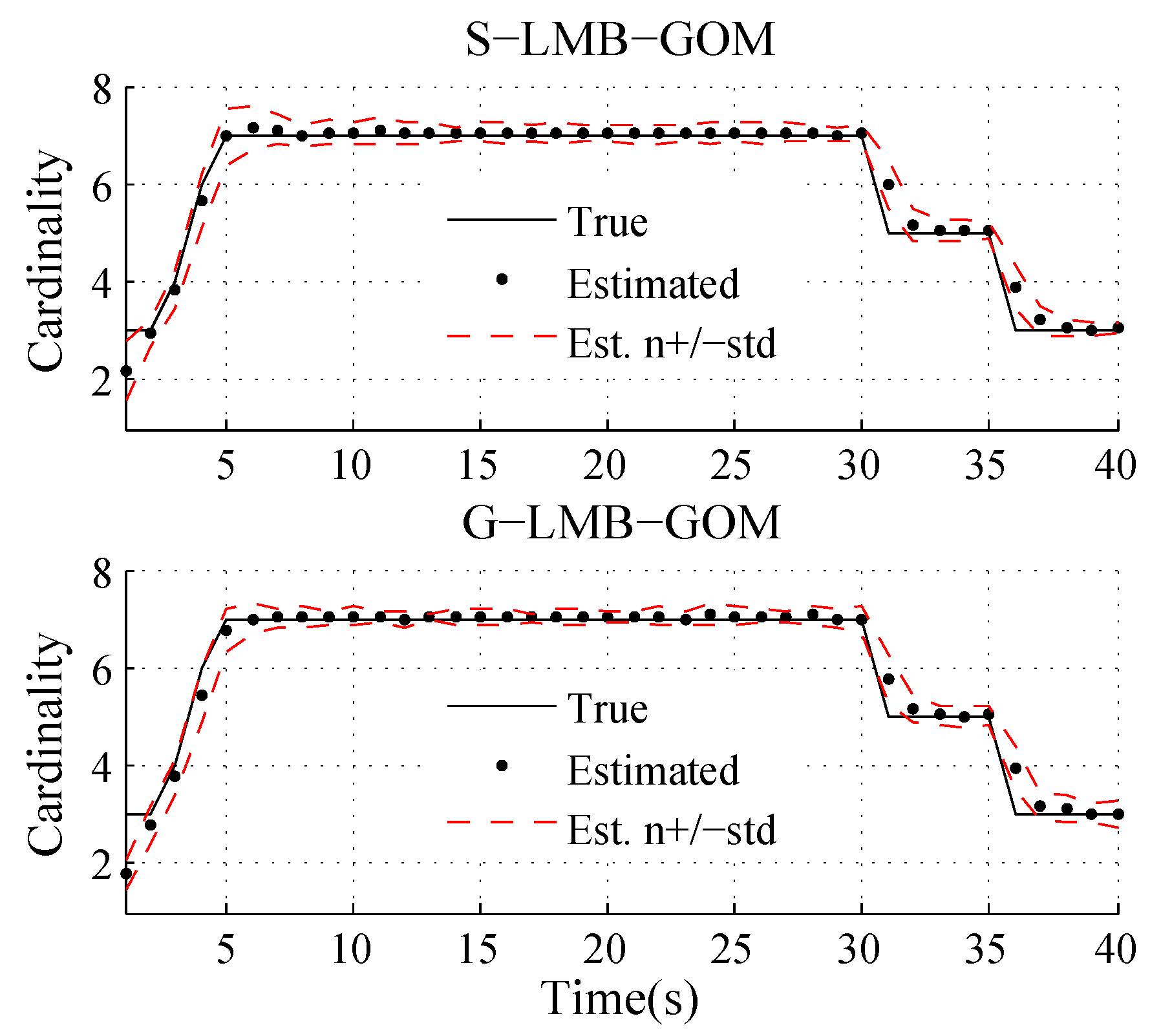
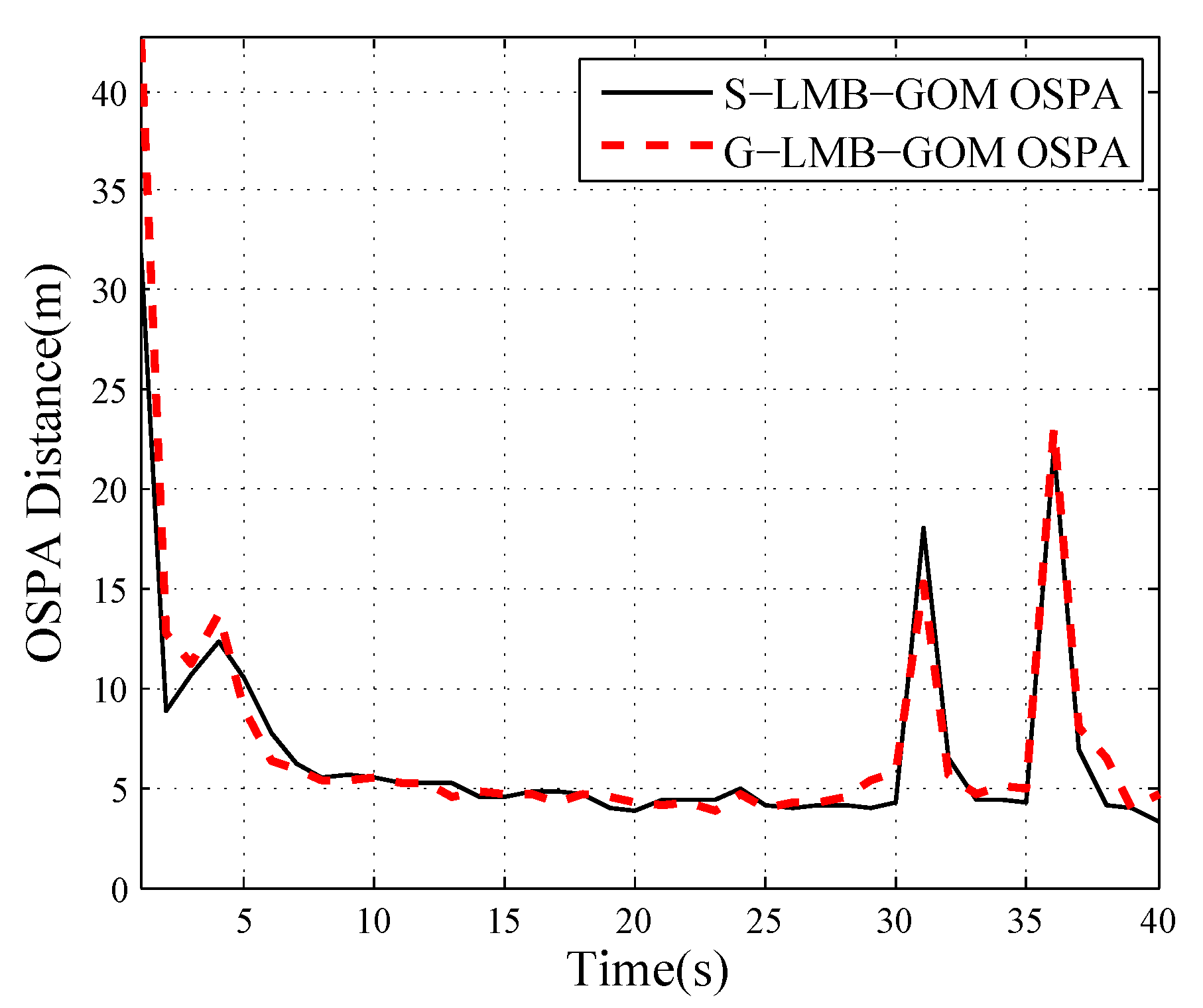
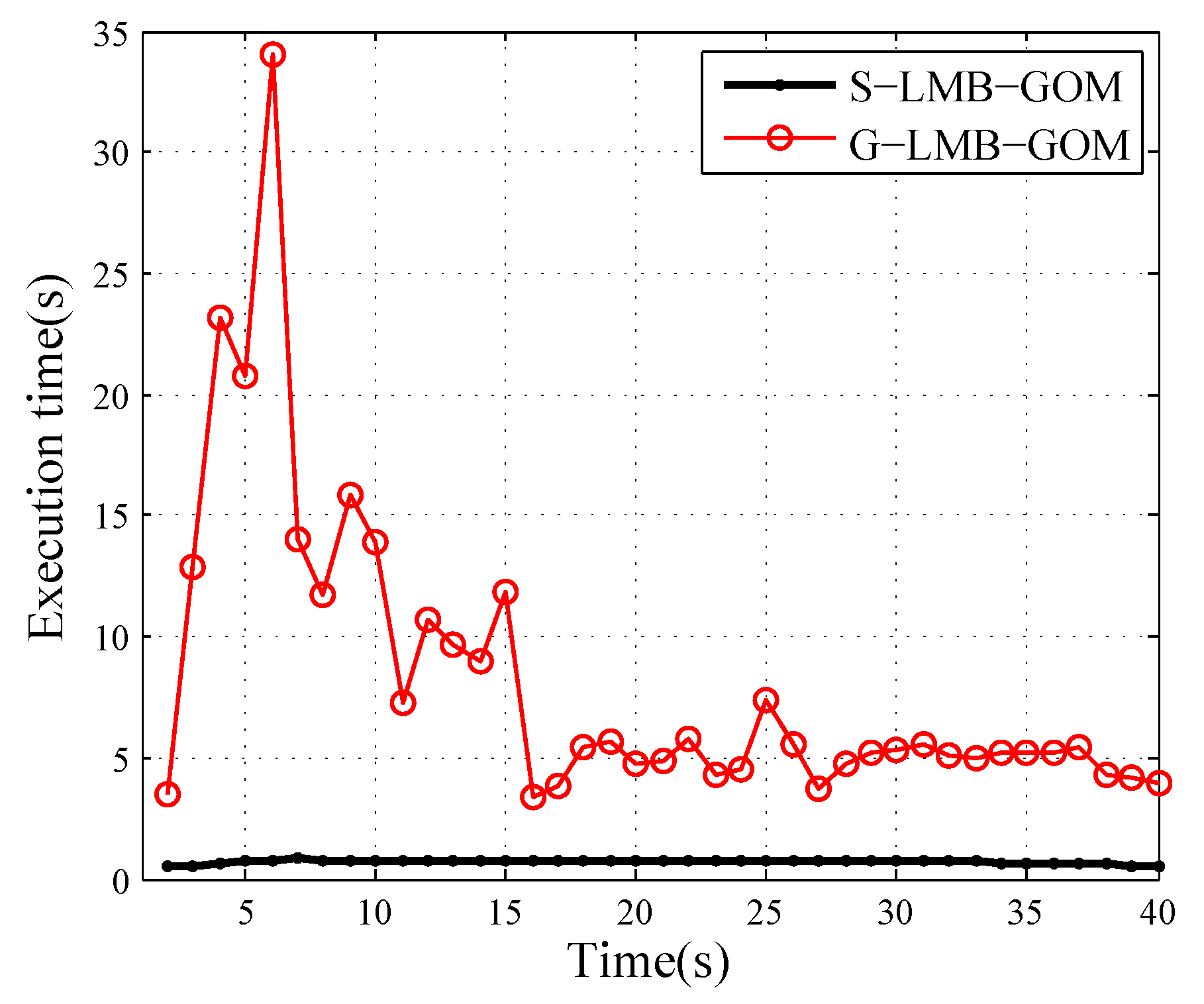
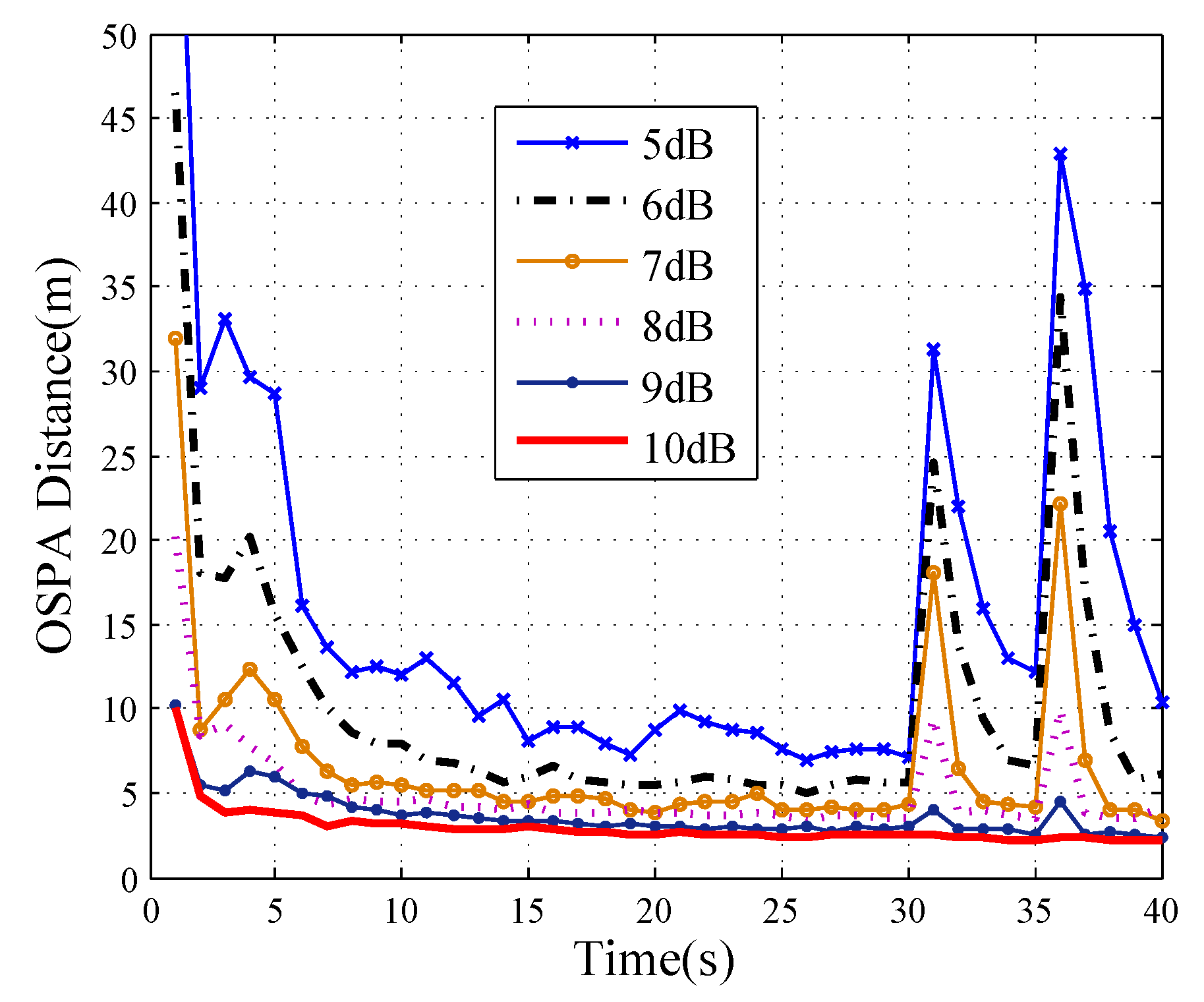
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meyer, F.; Kropfreiter, T.; Williams, J.L.; Lau, R.; Hlawatsch, F.; Braca, P.; Win, M.Z. Message Passing Algorithms for Scalable Multitarget Tracking. Proc. IEEE 2018, 106, 221–259. [Google Scholar] [CrossRef]
- Meyer, F.; Win, M.Z. Joint Navigation and Multitarget Tracking in Networks. In Proceedings of the IEEE International Conference on Communications Workshops, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Mahler, R.P.S. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: Norwood, MA, USA, 2007. [Google Scholar]
- Li, T.; Su, J.; Liu, W.; Corchado, J.M. Approximate Gaussian conjugacy: Recursive parametric filtering under nonlinearity, multimodality, uncertainty, and constraint, and beyond. Front. Inf. Technol. Electron. Eng. 2017, 18, 1913–1939. [Google Scholar] [CrossRef]
- Mahler, R.P.S. “Statistics 103” for Multitarget Tracking. Sensors 2019, 19, 202. [Google Scholar] [CrossRef] [PubMed]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2004, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R.P.S. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2008, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Vo, B.T.; Vo, B.N. Labeled Random Finite Sets and Multi-Object Conjugate Priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef] [Green Version]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Mahler, R.P.S. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T.; Suter, D. Visual tracking of numerous targets via multi-Bernoulli filtering of image data. Pattern Recognit. 2012, 45, 3625–3635. [Google Scholar] [CrossRef]
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T. Visual Tracking in Background Subtracted Image Sequences via Multi-Bernoulli Filtering. IEEE Trans. Signal Process. 2013, 61, 392–397. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M.; Mahler, R. Computationally-Tractable Approximate PHD and CPHD Filters for Superpositional Sensors. IEEE J. Sel. Top. Signal Process. 2013, 7, 410–420. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M. Particle Filter Implementation of the Multi-Bernoulli Filter for Superpositional Sensors. In Proceedings of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 15–18 December 2013; pp. 368–371. [Google Scholar]
- Mahler, R.P.S. A Fast Labeled Multi-Bernoulli Filter for Superpositional Sensors. In Proceedings of the SPIE, Orlando, FL, USA, 27 April 2018. [Google Scholar]
- Beard, M.; Vo, B.T.; Vo, B.N. Bayesian Multi-Target Tracking with Merged Measurements Using Labelled Random Finite Sets. IEEE Trans. Signal Process. 2015, 63, 1433–1447. [Google Scholar] [CrossRef]
- Lundquist, C.; Granstrom, K.; Orguner, U. An Extended Target CPHD Filter and a Gamma Gaussian Inverse Wishart Implementation. IEEE J. Sel. Top. Signal Process. 2013, 7, 472–483. [Google Scholar] [CrossRef] [Green Version]
- Papi, F.; Vo, B.N.; Vo, B.T.; Fantacci, C.; Beard, M. Generalized Labeled Multi-Bernoulli Approximation of Multi-Object Densities. IEEE Trans. Signal Process. 2015, 63, 5487–5497. [Google Scholar] [CrossRef]
- Boers, Y.; Driessen, J.N. Multitarget particle filter track before detect application. Radar Sonar Navig. IEE Proc. 2004, 151, 351–357. [Google Scholar] [CrossRef] [Green Version]
- Boers, Y.; Driessen, H.; Torstensson, J.; Trieb, M. Track-before-detect algorithm for tracking extended targets. Radar Sonar Navig. IEE Proc. 2006, 153, 345–351. [Google Scholar] [CrossRef] [Green Version]
- Habtemariam, B.K.; Tharmarasa, R.; Kirubarajan, T. PHD filter based track-before-detect for MIMO radars. Signal Process. 2012, 92, 667–678. [Google Scholar] [CrossRef]
- Papi, F.; Kyovtorov, V.; Giuliani, R.; Oliveri, F.; Tarchi, D. Bernoulli Filter for Track-Before-Detect using MIMO Radar. IEEE Signal Process. Lett. 2014, 21, 1145–1149. [Google Scholar] [CrossRef]
- Papi, F.; Du, Y.K. A Particle Multi-Target Tracker for Superpositional Measurements Using Labeled Random Finite Sets. IEEE Trans. Signal Process. 2015, 63, 4348–4358. [Google Scholar] [CrossRef]
- Li, S.; Yi, W.; Hoseinnezhad, R.; Wang, B.; Kong, L. Multiobject Tracking for Generic Observation Model Using Labeled Random Finite Sets. IEEE Trans. Signal Process. 2018, 66, 368–383. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.; Suter, D. Joint Detection and Estimation of Multiple Objects From Image Observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Rathnayake, T.; Gostar, A.K.; Hoseinnezhad, R. Labeled Multi-Bernoulli Track-before-Detect for Multi-Target Tracking in Video. In Proceedings of the International Conference on Information Fusion, Washington, DC, USA, 2–5 July 2015; pp. 1353–1358. [Google Scholar]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Li, T.; Chen, H.; Sun, S.; Corchado, J.M. Joint Smoothing and Tracking Based on Continuous-Time Target Trajectory Function Fitting. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1476–1483. [Google Scholar] [CrossRef]
- Li, T. Single-Road-Constrained Positioning Based on Deterministic Trajectory Geometry. IEEE Comm. Lett. 2019, 23, 80–83. [Google Scholar] [CrossRef]
- Rutten, M.G.; Gordon, N.J.; Maskell, S. Recursive track-before-detect with target amplitude fluctuations. Radar Sonar Navig. IEE Proc. 2005, 152, 345–352. [Google Scholar] [CrossRef]
- Xia, S.Z.; Liu, H.W. Bayesian track-before-detect algorithm with target amplitude fluctuation based on expectation-maximisation estimation. IET Radar Sonar Navig. 2012, 6, 719–728. [Google Scholar] [CrossRef]

| Cell Number k | When | When |
|---|---|---|
| 1 | 0.0635 | 0.0436 |
| 3 | 0.6882 | 0.5794 |
| 5 | 0.9728 | 0.9432 |
| 7 | 0.9992 | 0.9973 |
| 9 | 0.999991 | 0.999951 |
| Parameter | Symbol | Value |
|---|---|---|
| Signal-to-Noise Ratio | SNR | 7 dB |
| Mean of 1st birth track | ||
| Mean of 2st birth track | ||
| Mean of 3st birth track | ||
| Mean of 4st birth track | ||
| Variances of all birth tracks | Q | |
| Range Resolution | R | 5 m |
| Azimuth Resolution | B | rad |
| Doppler Resolution | D | 1 m/s |
| Time Sampling Interval | 1 s |
| Method | Localization | Cardinality | Total |
|---|---|---|---|
| Component (m) | Component (m) | OSPA (m) | |
| S-LMB | 4.1 | 2.95 | 7.05 |
| G-LMB | 4.48 | 2.81 | 7.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Fan, H.; Xiao, H. Labeled Multi-Bernoulli Filter Joint Detection and Tracking of Radar Targets. Appl. Sci. 2019, 9, 4187. https://doi.org/10.3390/app9194187
Liu R, Fan H, Xiao H. Labeled Multi-Bernoulli Filter Joint Detection and Tracking of Radar Targets. Applied Sciences. 2019; 9(19):4187. https://doi.org/10.3390/app9194187
Chicago/Turabian StyleLiu, Rang, Hongqi Fan, and Huaitie Xiao. 2019. "Labeled Multi-Bernoulli Filter Joint Detection and Tracking of Radar Targets" Applied Sciences 9, no. 19: 4187. https://doi.org/10.3390/app9194187
APA StyleLiu, R., Fan, H., & Xiao, H. (2019). Labeled Multi-Bernoulli Filter Joint Detection and Tracking of Radar Targets. Applied Sciences, 9(19), 4187. https://doi.org/10.3390/app9194187





