Which Local Search Operator Works Best for the Open-Loop TSP?
Abstract
1. Introduction
2. Local Search
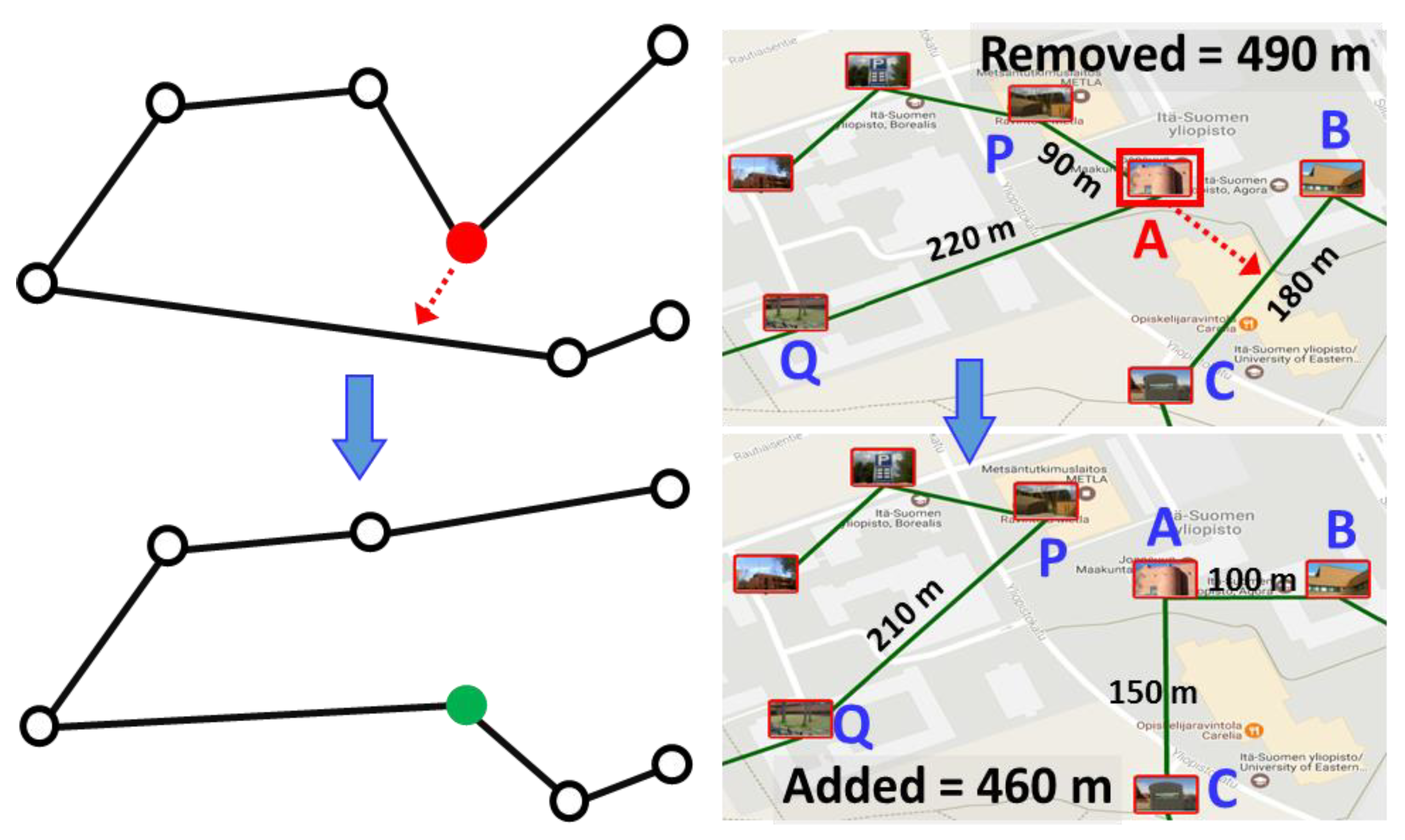
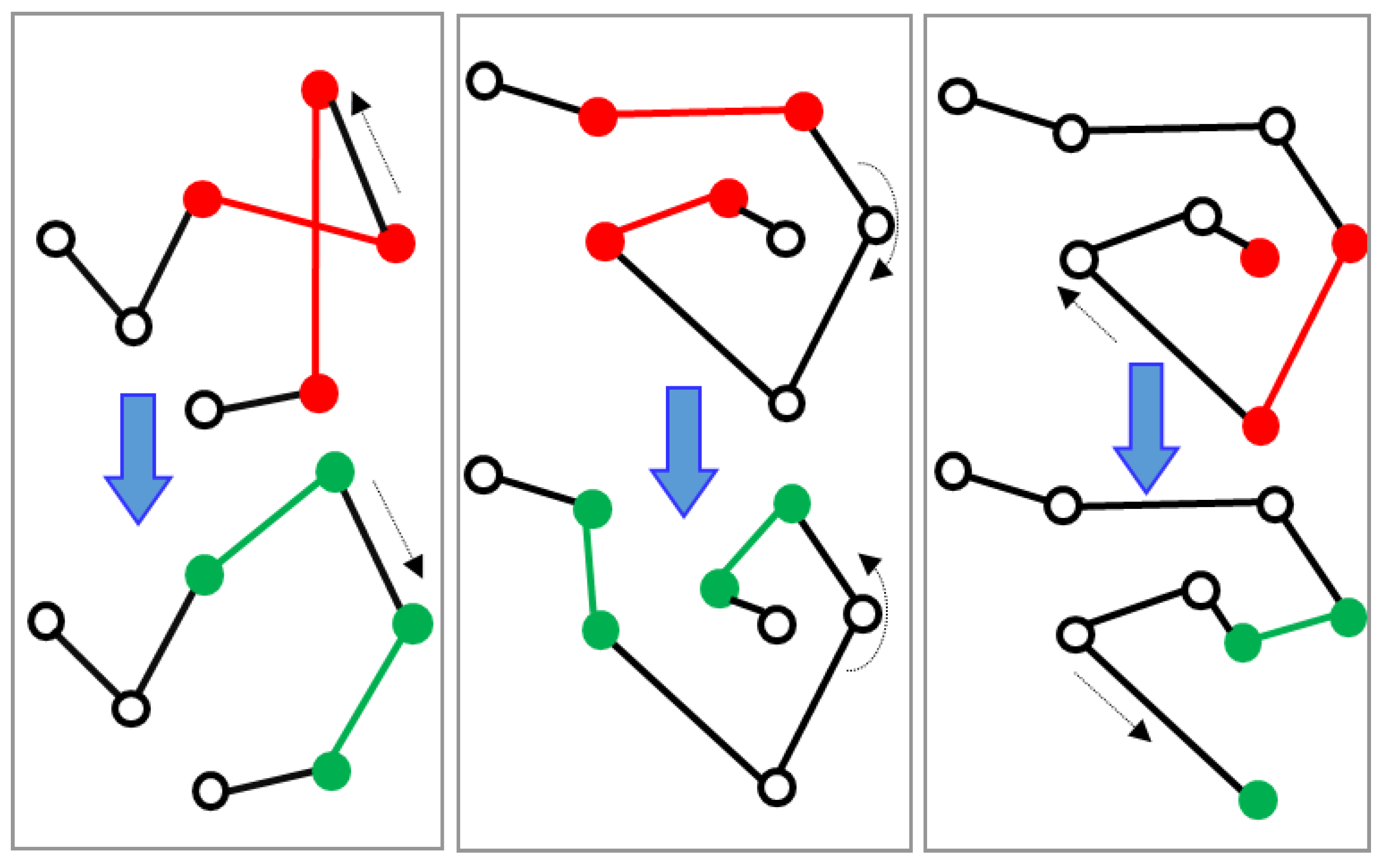
2.1. Relocate
2.2. Two-Optimization (2-opt)
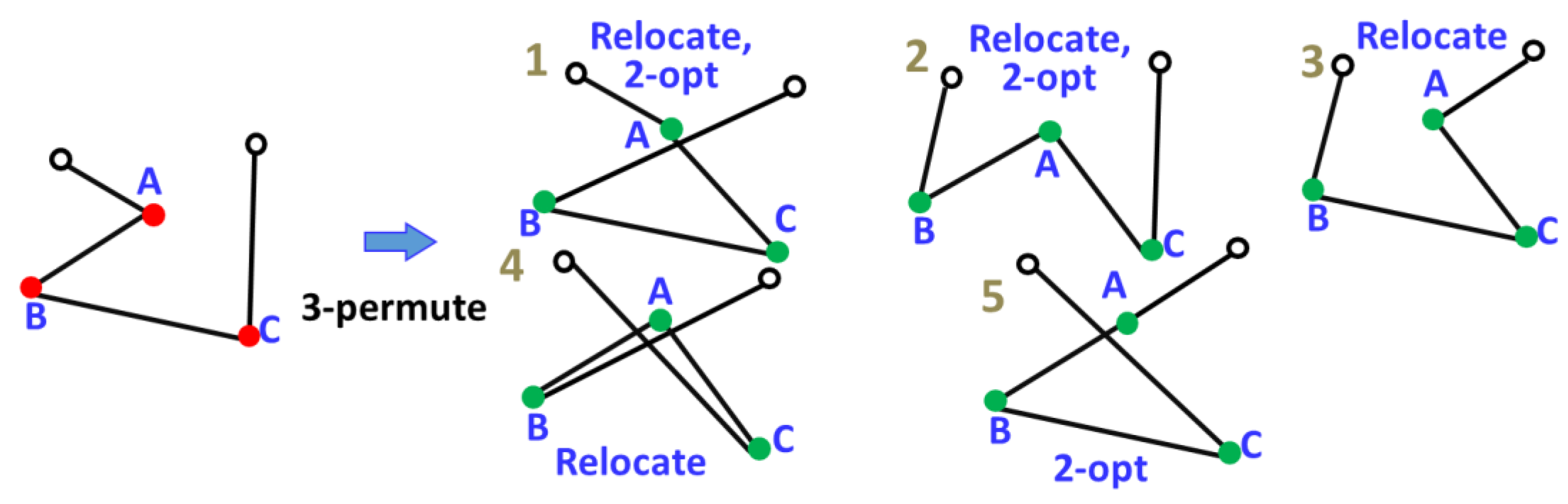
2.3. Three-Node Permutation (3-permute)
2.4. Link Swap
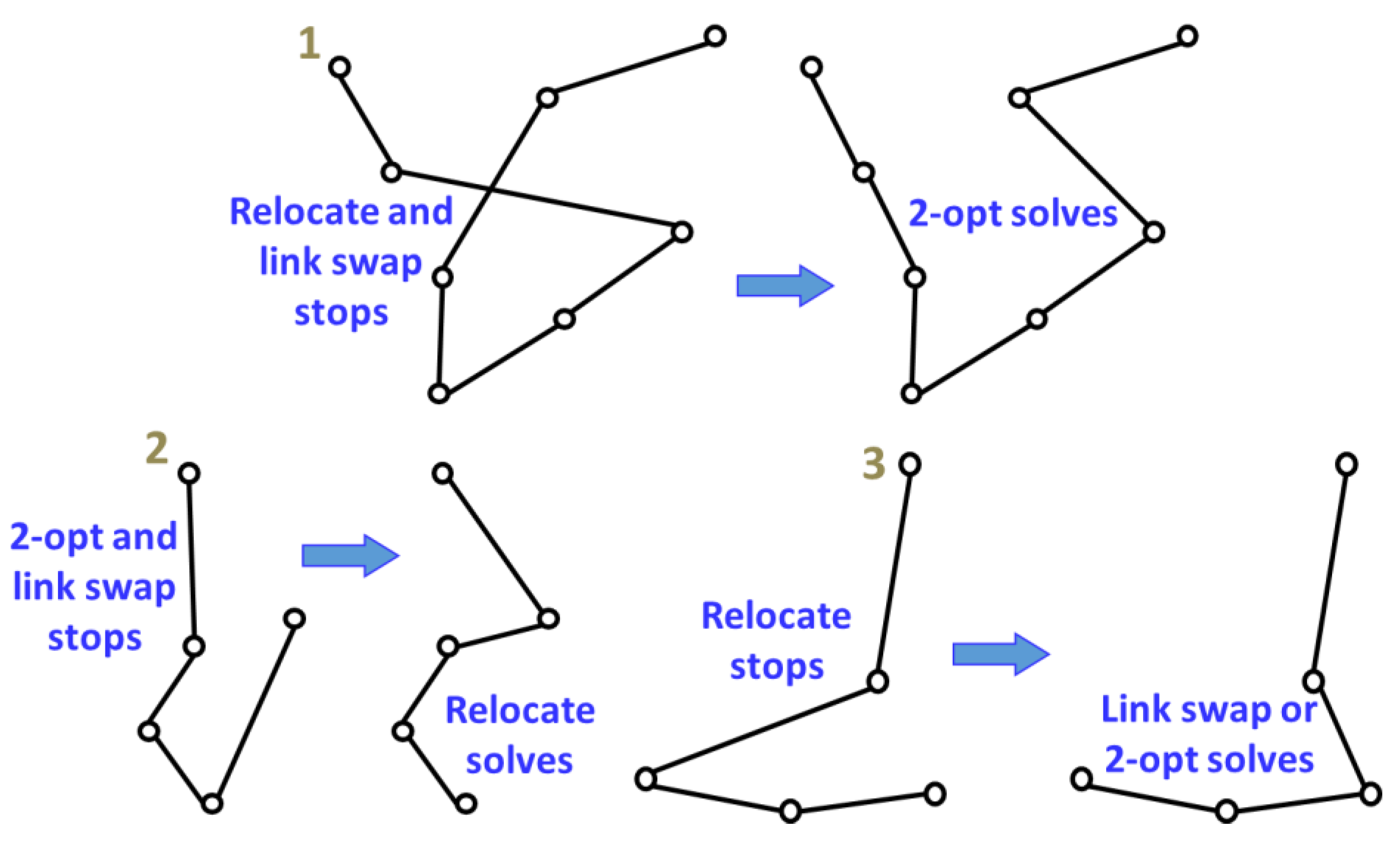
2.5. The Uniqueness of the Operators
3. Performance of a Single Operator
3.1. Initial Solution
- Random
- Heuristic (greedy)
| Algorithm 1: Finding the heuristic initial path |
| HeuristicPath () InitialPath ← infinity FOR node ← 1 TO N DO NewPath ← GreedyPath ( node ) IF Length ( NewPath ) < Length ( InitialPath ) THEN InitialPath ← NewPath RETURN InitialPath |
| GreedyPath ( startNode ) NewPath [1] ← startNode FOR i ← 2 TO N DO NewPath [i] ← Nearest node from startNode startNode ← NewPath [i] RETURN NewPath |
3.2. Search Strategy
- Best improvement
- First improvement
- Random search
| Algorithm 2: Finding the improved tour by all the operators for different search strategies |
| LocalSearch ( InitialPath, OperationType ) Path ← InitialPath SWITCH SearchType CASE RANDOM FOR i ← 1 TO Iterations DO NewPath ← NewRandomSolution ( Path, OperationType ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath CASE FIRST Path ← NewFirstSolution ( Path ) CASE BEST Path ← NewBestSolution ( Path ) RETURN Path NewRandomSolution ( Path, OperationType ) SWITCH OperationType CASE RELOCATE Target ← Random ( 1, N ) Destination ← Random ( 1, N ) NewPath ← relocate ( Path, Target, Destination ) CASE 2OPT FirstLink ← Random ( 1, N ) SecondLink ← Random ( 1, N ) NewPath ← 2Opt ( Path, FirstLink, SecondLink ) CASE LINKSWAP Link ← Random ( 1, N ) NewPath ← linkSwap ( Path, Link ) RETURN NewPath NewFirstSolution ( Path, OperationType ) FOR i ← 1 TO N DO FOR j ← 1 TO N DO SWITCH OperationType CASE RELOCATE NewPath ← relocate ( Path, i, j ) CASE 2OPT NewPath ← 2Opt ( Path, i, j ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath RETURN Path IF OperationType = LINKSWAP NewPath ← linkSwap ( Path, i ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath RETURN Path NewBestSolution ( Path, OperationType ) FOR i ← 1 TO N DO FOR j ← 1 TO N DO SWITCH OperationType CASE RELOCATE NewPath ← relocate ( Path, i, j ) CASE 2OPT NewPath ← 2Opt ( Path, i, j ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath IF OperationType = LINKSWAP NewPath ← linkSwap ( Path, i ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath RETURN Path |
3.3. Results With A Single Operator
- Gap (%)
- Instances solved (%)
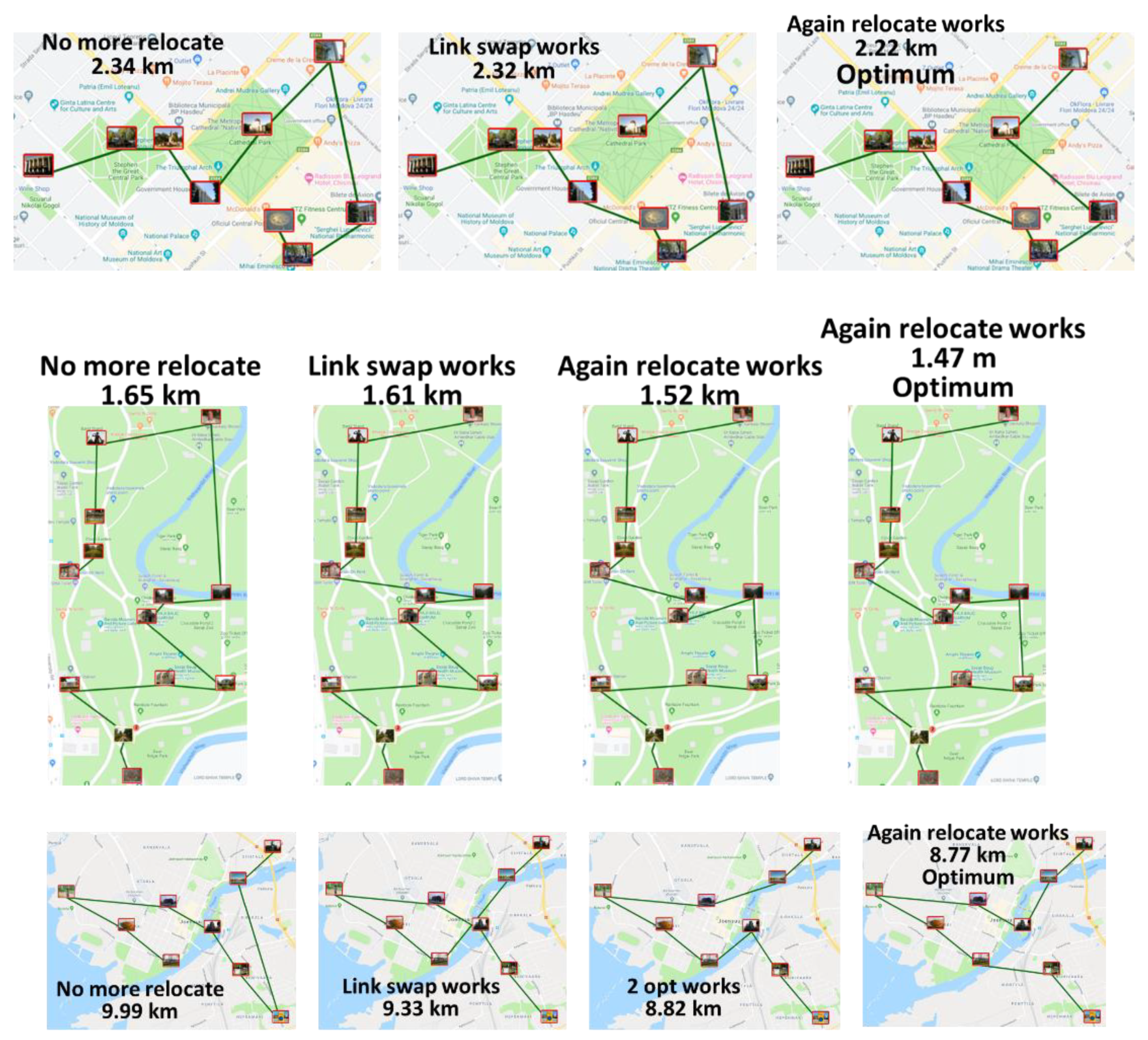
3.4. Combining the Operators
| Algorithm 3: Finding a solution by mixing local search operators |
| RandomMixing ( NumberOfIteration, Path ) FOR i ← 1 TO NumberOfIteration DO operation ← Random ( NodeSwap, 2opt, LinkSwap ) NewPath ← NewRandomSolution ( Path, operation ) IF Length ( NewPath ) < Length ( Path ) THEN Path ← NewPath RETURN Path |
4. Analysis of Repeated Random Mixed Local Search
4.1. Effect of the repetitions
4.2. Processing Time
4.3. Parameter Values
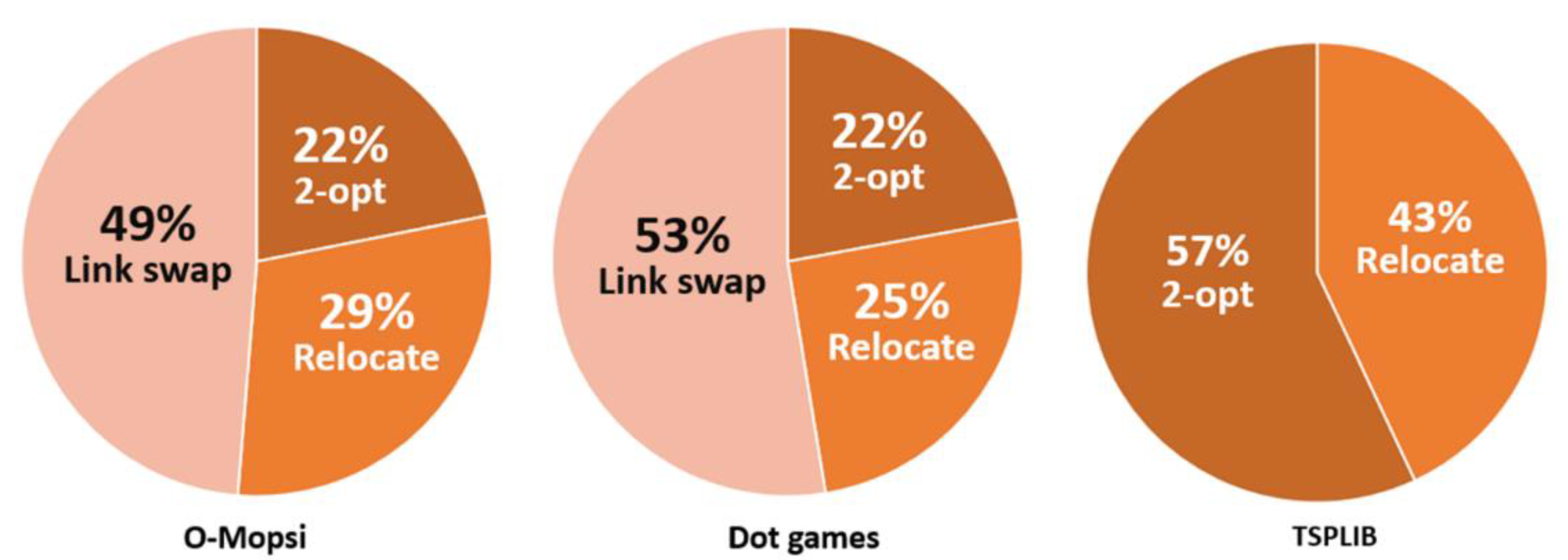
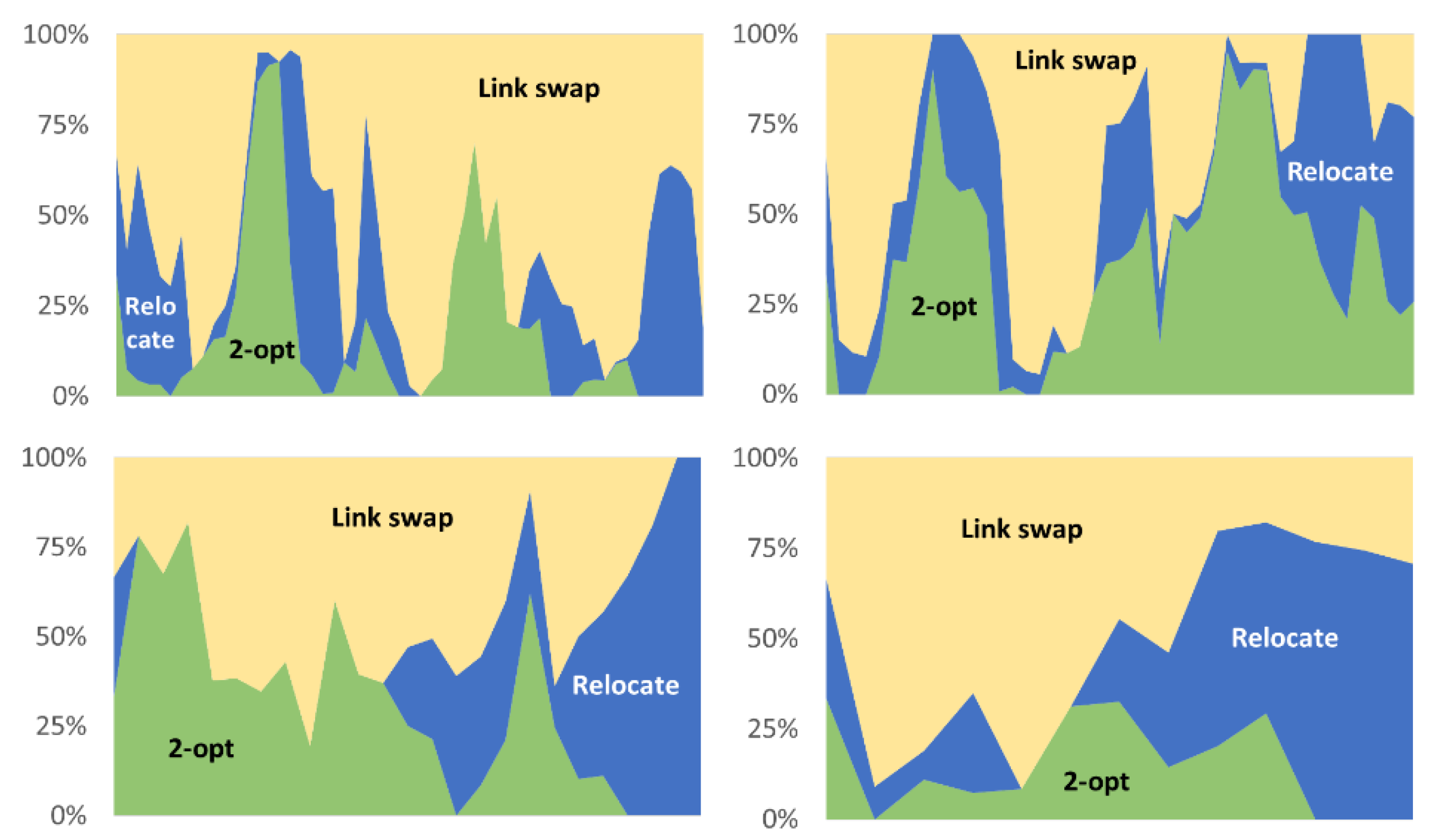
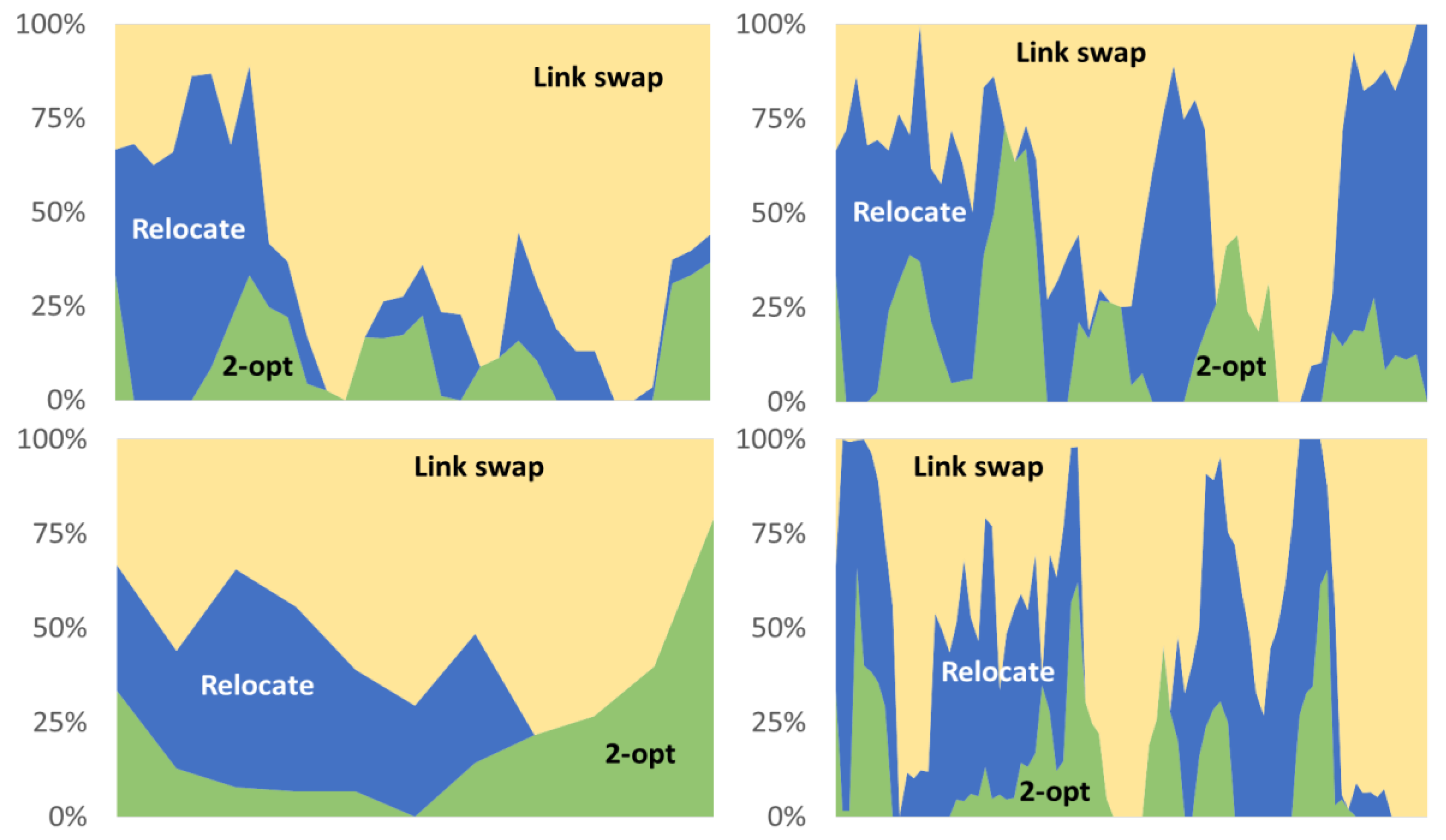
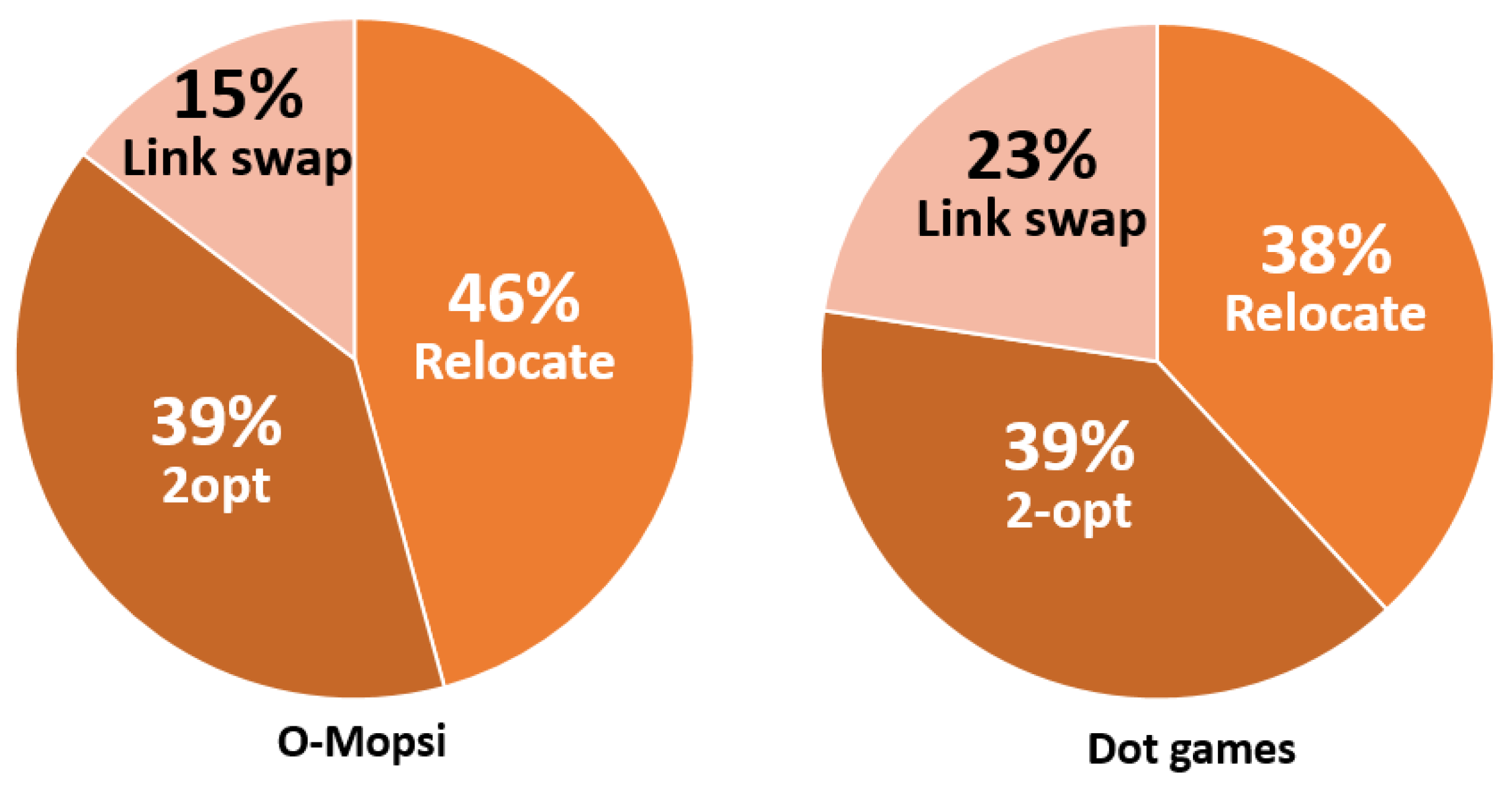
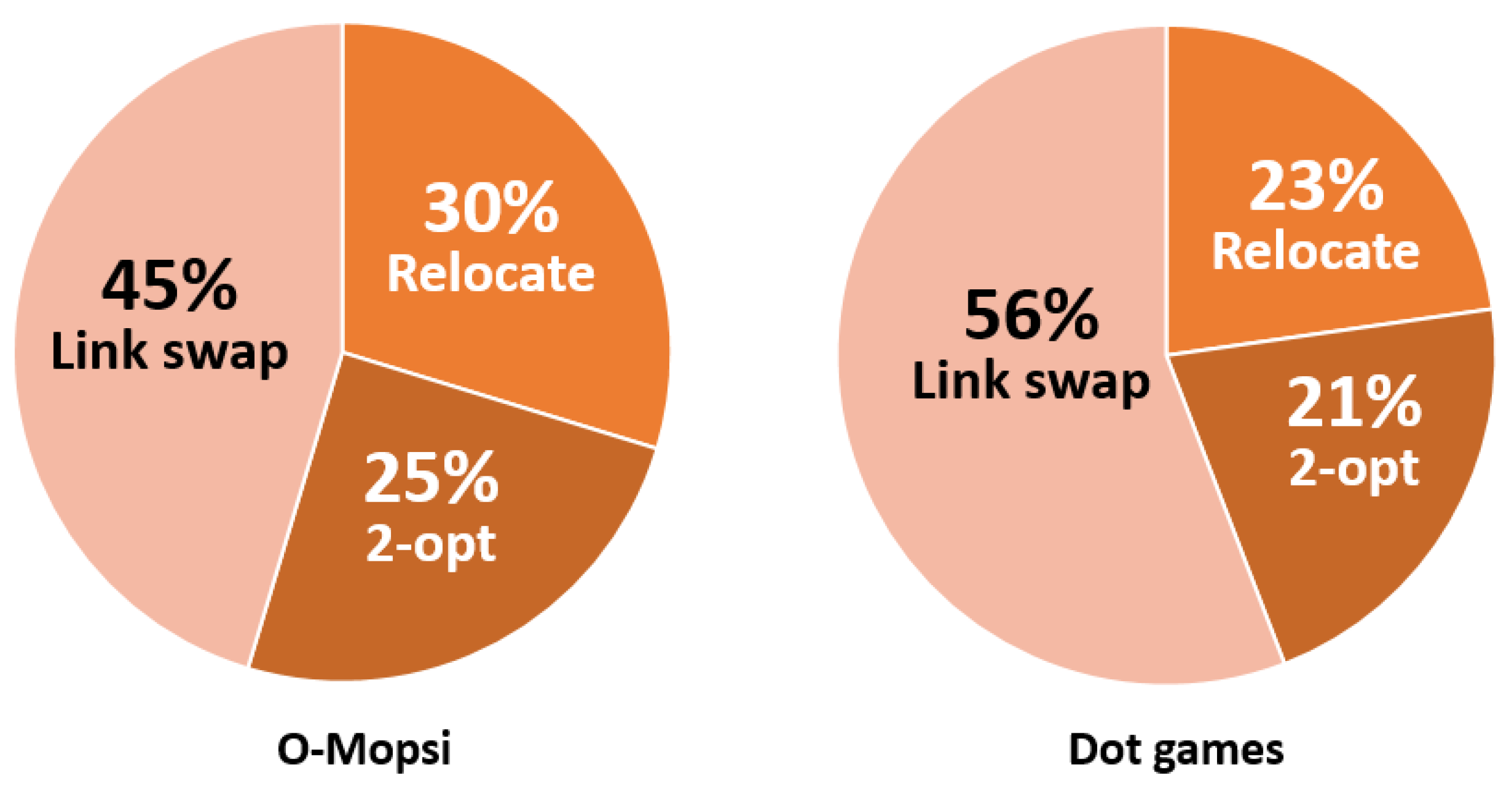
4.4. The Productivity of the Operators
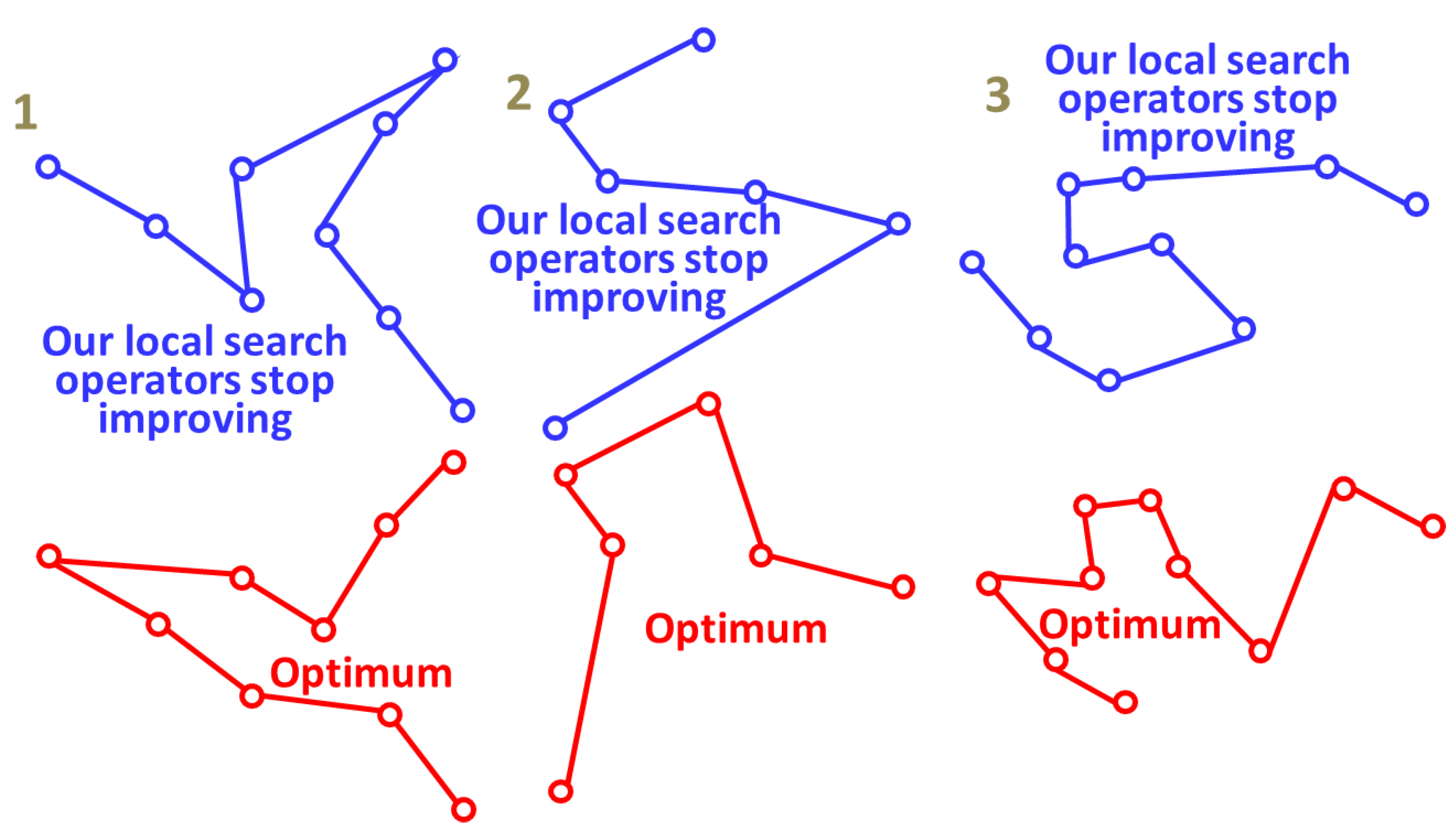
5. Stochastic Variants
6. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of Np-Completeness; W.H. Freeman & Co.: New York, NY, USA, 1979; ISBN 0716710455. [Google Scholar]
- Papadimitriou, C.H. The Euclidean travelling salesman problem is NP-complete. Theor. Comput. Sci. 1977, 4, 237–244. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R.; Sengupta, L. O-Mopsi: Mobile Orienteering Game for Sightseeing, Exercising, and Education. ACM Trans. Multimed. Comput. Commun. Appl. 2017, 13, 56. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Souffriau, W.; Van Oudheusden, D. The orienteering problem: A survey. Eur. J. Oper. Res. 2011, 209, 1–10. [Google Scholar] [CrossRef]
- Chieng, H.H.; Wahid, N. A Performance Comparison of Genetic Algorithm’s Mutation Operators in n-Cities Open Loop Travelling Salesman Problem. In Recent Advances on Soft Computing and Data Mining. Advances in Intelligent Systems and Computing; Herawan, T., Ghazali, R., Deris, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 287. [Google Scholar]
- Gavalas, D.; Konstantopoulos, C.; Mastakas, K.; Pantziou, G. A survey on algorithmic approaches for solving tourist trip design problems. J. Heuristics 2014, 20, 291–328. [Google Scholar] [CrossRef]
- Golden, B.L.; Levy, L.; Vohra, R. The Orienteering Problem. Nav. Res. Logist. 1987, 34, 307–318. [Google Scholar] [CrossRef]
- Perez, D.; Togelius, J.; Samothrakis, S.; Rohlfshagen, P.; Lucas, S.M. Automated Map Generation for the Physical Traveling Salesman Problem. IEEE Trans. Evol. Comput. 2014, 18, 708–720. [Google Scholar] [CrossRef]
- Sengupta, L.; Mariescu-Istodor, R.; Fränti, P. Planning your route: Where to start? Comput. Brain Behav. 2018, 1, 252–265. [Google Scholar] [CrossRef]
- Sengupta, L.; Fränti, P. Predicting difficulty of TSP instances using MST. In Proceedings of the IEEE International Conference on Industrial Informatics (INDIN), Helsinki, Finland, June 2019; pp. 848–852. [Google Scholar]
- Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. Solution of a Large Scale Traveling Salesman Problem; Technical Report P-510; RAND Corporation: Santa Monica, CA, USA, 1954. [Google Scholar]
- Held, M.; Karp, R.M. The traveling salesman problem and minimum spanning trees: Part II. Math. Program. 1971, 1, 6–25. [Google Scholar] [CrossRef]
- Padberg, M.; Rinaldi, G. A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems. SIAM Rev. 1991, 33, 60–100. [Google Scholar] [CrossRef]
- Grötschel, M.; Holland, O. Solution of large-scale symmetric travelling salesman problems. Math. Program. 1991, 51, 141–202. [Google Scholar] [CrossRef]
- Applegate, D.; Bixby, R.; Chvatal, V. On the solution of traveling salesman problems. Documenta Mathematica Journal der Deutschen Mathematiker-Vereinigung. Int. Congr. Math. 1988, Extra Volume III, 645–656. [Google Scholar]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Applegate, D.L.; Bixby, R.E.; Chvatal, V.; Cook, W.J. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Johnson, D.S.; Papadimitriou, C.H.; Yannakakis, M. How easy is local search? J. Comput. Syst. Sci. 1988, 37, 79–100. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Christofides, N. Worst-Case Analysis of a New Heuristic for the Travelling Salesman Problem (Technical Report388); Graduate School of Industrial Administration, Carnegie Mellon University: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Johnson, D.S.; McGeoch, L.A. The traveling salesman problem: A case study in local optimization. Local Search Comb. Optim. 1997, 1, 215–310. [Google Scholar]
- Croes, G.A. A Method for Solving Traveling-Salesman Problems. Oper. Res. 1958, 6, 791–812. [Google Scholar] [CrossRef]
- Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Rego, C.; Glover, F. Local search and metaheuristics. In The Traveling Salesman Problem and Its Variations; Springer: Boston, MA, USA, 2007; pp. 309–368. [Google Scholar]
- Okano, H.; Misono, S.; Iwano, K. New TSP construction heuristics and their relationships to the 2-opt. J. Heuristics 1999, 5, 71–88. [Google Scholar] [CrossRef]
- Johnson, D.S.; McGeoch, L.A. Experimental analysis of heuristics for the STSP. In The Traveling Salesman Problem and Its Variations; Springer: Boston, MA, USA, 2007; pp. 369–443. [Google Scholar]
- Aarts, E.; Aarts, E.H.; Lenstra, J.K. (Eds.) Local Search in Combinatorial Optimization; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Jünger, M.; Reinelt, G.; Rinaldi, G. The traveling salesman problem. Handb. Oper. Res. Manag. Sci. 1995, 7, 225–330. [Google Scholar]
- Laporte, G. A concise guide to the traveling salesman problem. J. Oper. Res. Soc. 2010, 61, 35–40. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Ergun Ö Orlin, J.B.; Punnen, A.P. A survey of very large-scale neighborhood search techniques. Discret. Appl. Math. 2002, 123, 75–102. [Google Scholar] [CrossRef]
- Rego, C.; Gamboa, D.; Glover, F.; Osterman, C. Traveling salesman problem heuristics: Leading methods, implementations and latest advances. Eur. J. Oper. Res. 2011, 211, 427–441. [Google Scholar] [CrossRef]
- Matai, R.; Singh, S.; Mittal, M.L. Traveling salesman problem: An overview of applications, formulations, and solution approaches. In Traveling Salesman Problem, Theory and Applications; IntechOpen: London, UK, 2010. [Google Scholar]
- Laporte, G. The vehicle routing problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 345–358. [Google Scholar] [CrossRef]
- Vidal TCrainic, T.G.; Gendreau, M.; Prins, C. Heuristics for multi-attribute vehicle routing problems: A survey and synthesis. Eur. J. Oper. Res. 2013, 231, 1–21. [Google Scholar] [CrossRef]
- Gendreau, M.; Hertz, A.; Laporte, G. New insertion and postoptimization procedures for the traveling salesman problem. Oper. Res. 1992, 40, 1086–1094. [Google Scholar] [CrossRef]
- Mersmann, O.; Bischl, B.; Bossek, J.; Trautmann, H.; Wagner, M.; Neumann, F. Local Search and the Traveling Salesman Problem: A Feature-Based Characterization of Problem Hardness. In Lecture Notes in Computer Science, Proceedings of the Learning and Intelligent Optimization, Paris, France, 16–20 January 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7219, p. 7219. [Google Scholar]
- Helsgaun, K. An effective implementation of the Lin–Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Pan, Y.; Xia, Y. Solving TSP by dismantling cross paths. In Proceedings of the IEEE International Conference on Orange Technologies, Xian, China, 20–23 September 2014; pp. 121–124. [Google Scholar]
- Martí, R. Multi-start methods. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 355–368. [Google Scholar]
- O’Neil, M.A.; Burtscher, M. Rethinking the parallelization of random-restart hill climbing: A case study in optimizing a 2-opt TSP solver for GPU execution. In Proceedings of the 8th Workshop on General Purpose Processing using GPUs, San Francisco, CA, USA, 7 February 2015; pp. 99–108. [Google Scholar]
- Al-Adwan, A.; Sharieh, A.; Mahafzah, B.A. Parallel heuristic local search algorithm on OTIS hyper hexa-cell and OTIS mesh of trees optoelectronic architectures. Appl. Intell. 2019, 49, 661–688. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Chen, Z. A local search based restart evolutionary algorithm for finding triple product property triples. Appl. Intell. 2018, 48, 2894–2911. [Google Scholar] [CrossRef]
- Lawler, E.L.; Lenstra, J.K.; Rinnooy Kan AH, G.; Shmoys, D.B. The Traveling Salesman Problem; A Guided Tour of Combinatorial Optimization; Publisher Wiley: Chichester, UK, 1985. [Google Scholar]
- Reinelt, G. A traveling salesman problem library. INFORMS J. Comput. 1991, 3, 376–384. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search-Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Charon, I.; Hurdy, O. Application of the noising method to the travelling salesman problem. Eur. J. Oper. Res. 2000, 125, 266–277. [Google Scholar] [CrossRef]
- Chen, S.M.; Chien, C.Y. Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques. Expert Syst. Appl. 2011, 38, 14439–14450. [Google Scholar] [CrossRef]
- Ezugwu, A.E.S.; Adewumi, A.O.; Frîncu, M.E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem. Expert Syst. Appl. 2017, 77, 189–210. [Google Scholar] [CrossRef]
- Geng, X.; Chen, Z.; Yang, W.; Shi, D.; Zhao, K. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Appl. Soft Comput. 2011, 11, 3680–3689. [Google Scholar] [CrossRef]
- Albayrak, M.; Allahverdi, N. Development a new mutation operator to solve the Traveling Salesman Problem by aid of Genetic Algorithms. Expert Syst. Appl. 2011, 38, 1313–1320. [Google Scholar] [CrossRef]
- Nagata, Y.; Soler, D. A new genetic algorithm for the asymmetric traveling salesman problem. Expert Syst. Appl. 2012, 39, 8947–8953. [Google Scholar] [CrossRef]
- Singh, S.; Lodhi, E.A. Study of variation in TSP using genetic algorithm and its operator comparison. Int. J. Soft Comput. Eng. 2013, 3, 264–267. [Google Scholar]
- Vashisht, V.; Choudhury, T. Open loop travelling salesman problem using genetic algorithm. Int. J. Innov. Res. Comput. Commun. Eng. 2013, 1, 112–116. [Google Scholar]
- Quintero-Araujo, C.L.; Gruler, A.; Juan, A.A.; Armas, J.; Ramalhinho, H. Using simheuristics to promote horizontal collaboration in stochastic city logistics. Prog. Artif. Intell. 2017, 6, 275. [Google Scholar] [CrossRef]
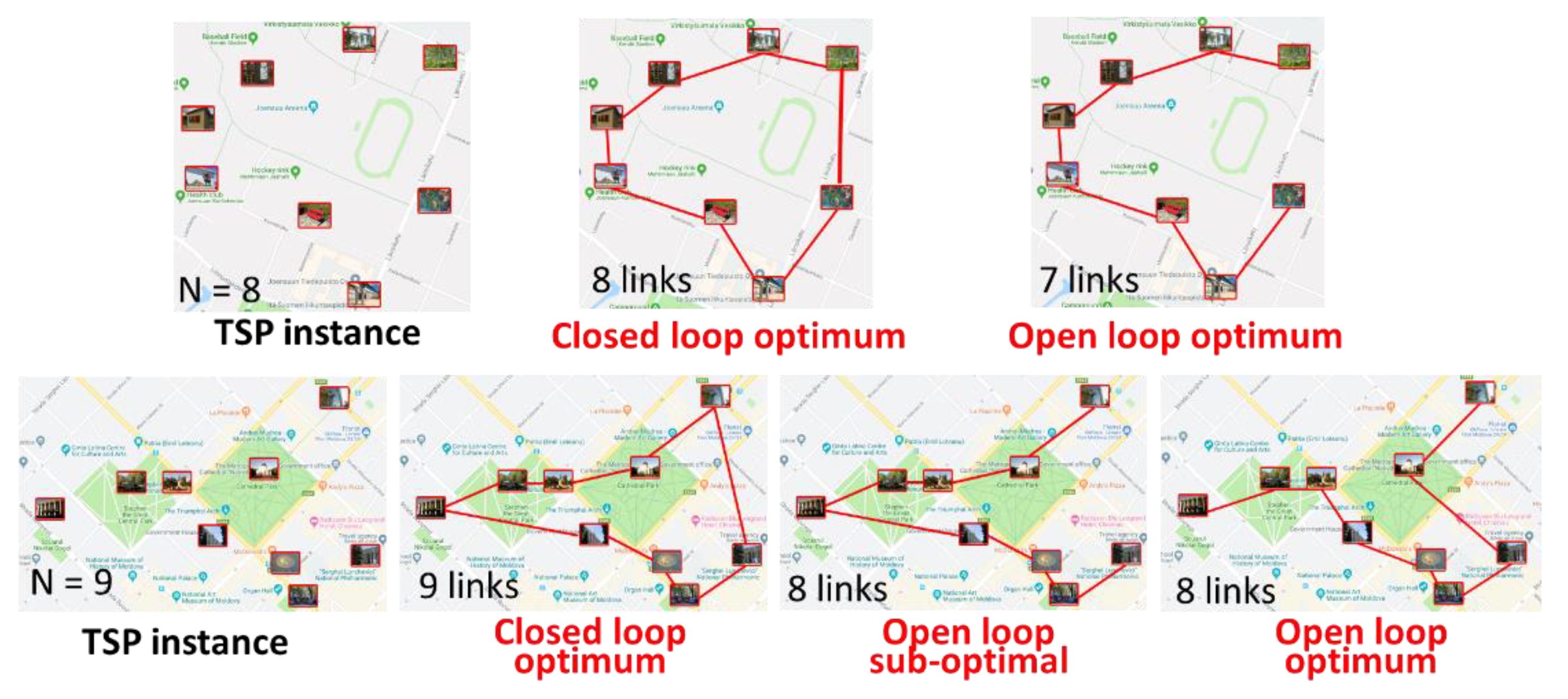
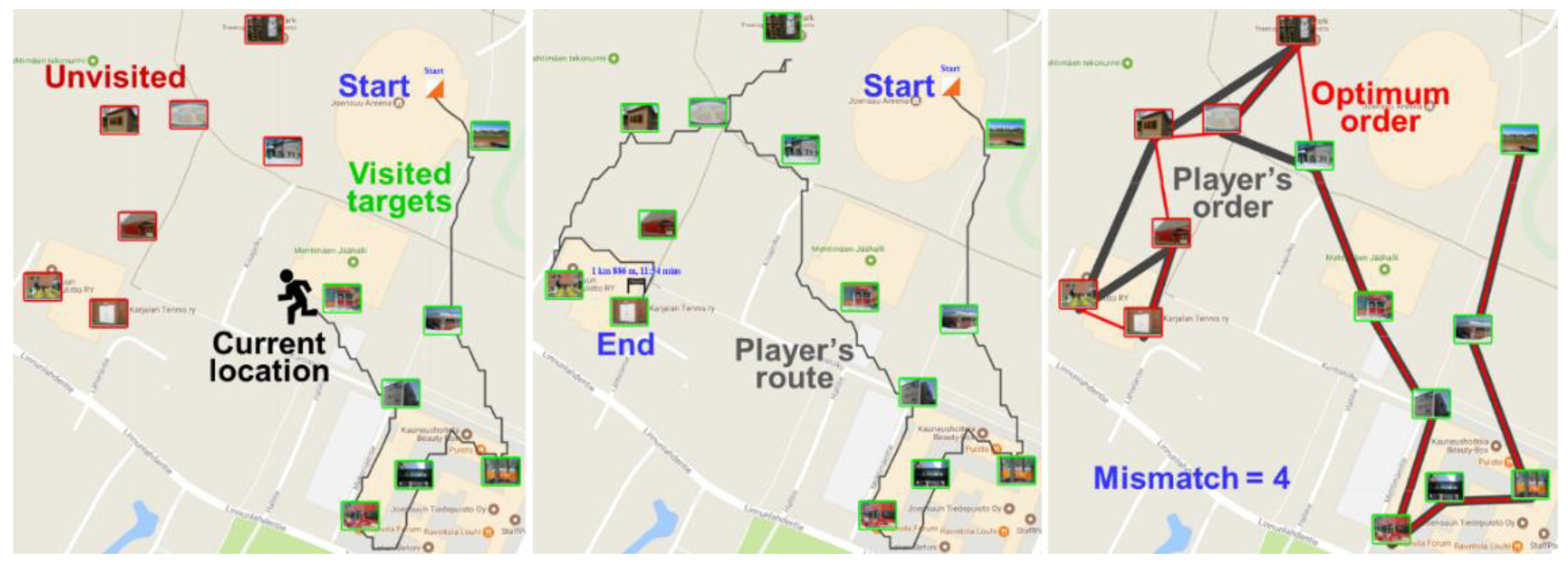
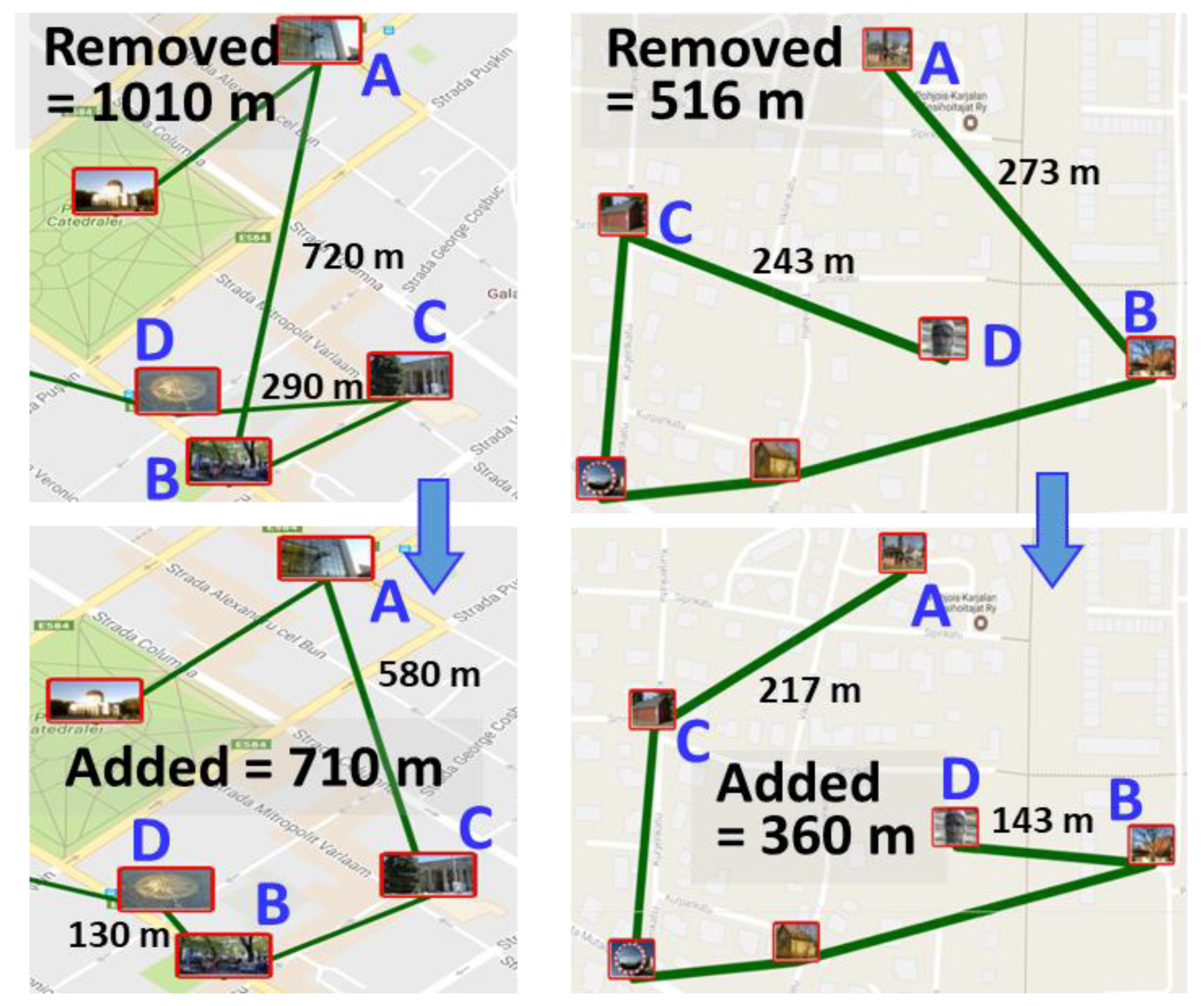
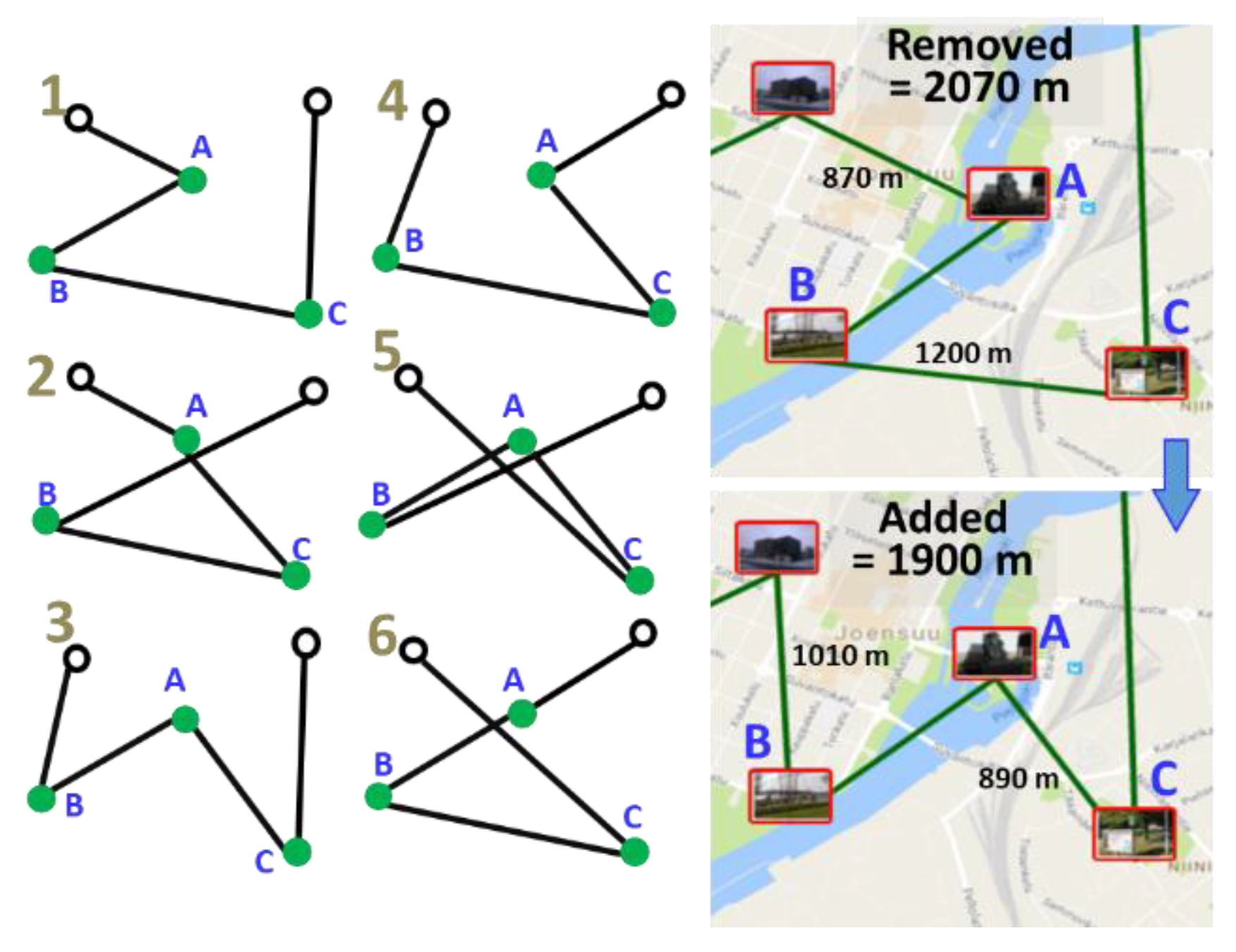
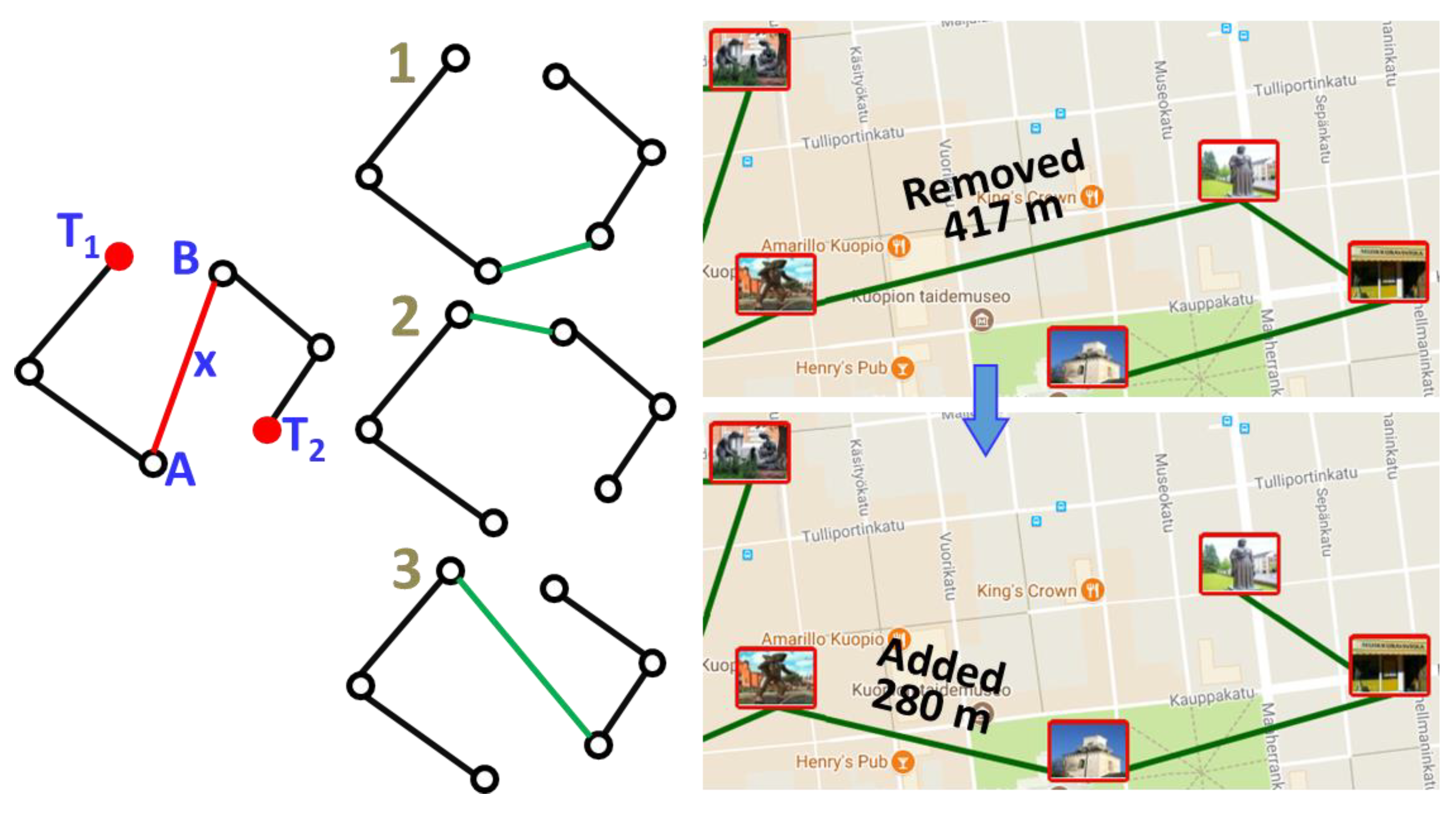
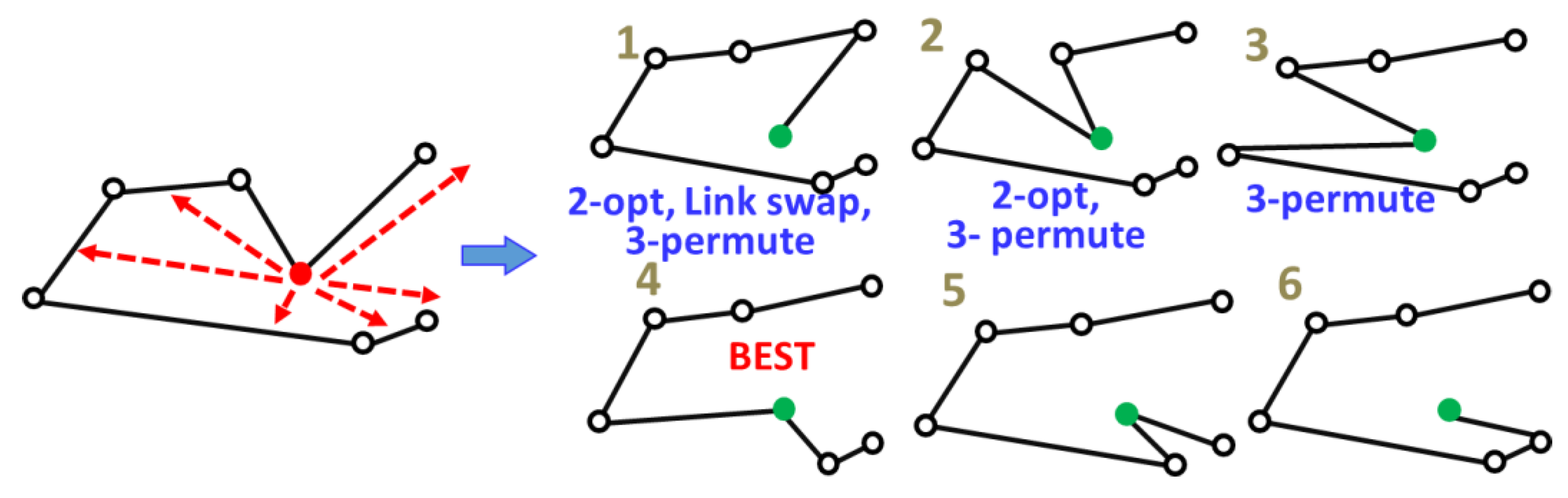


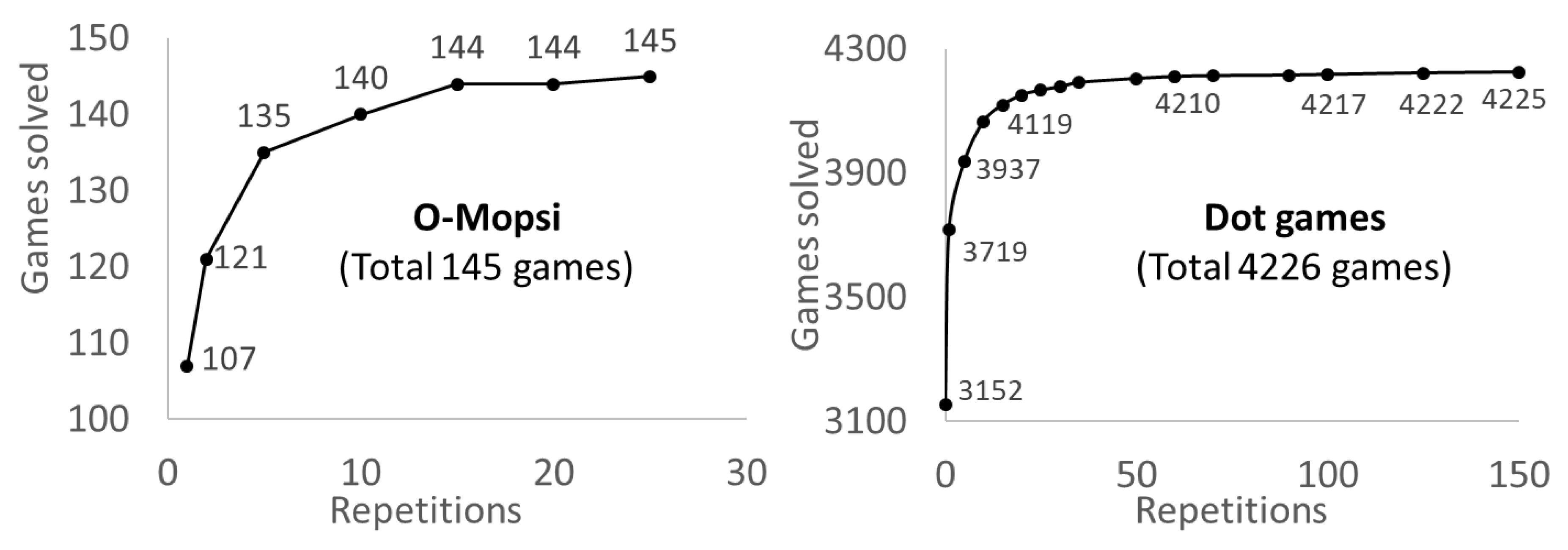
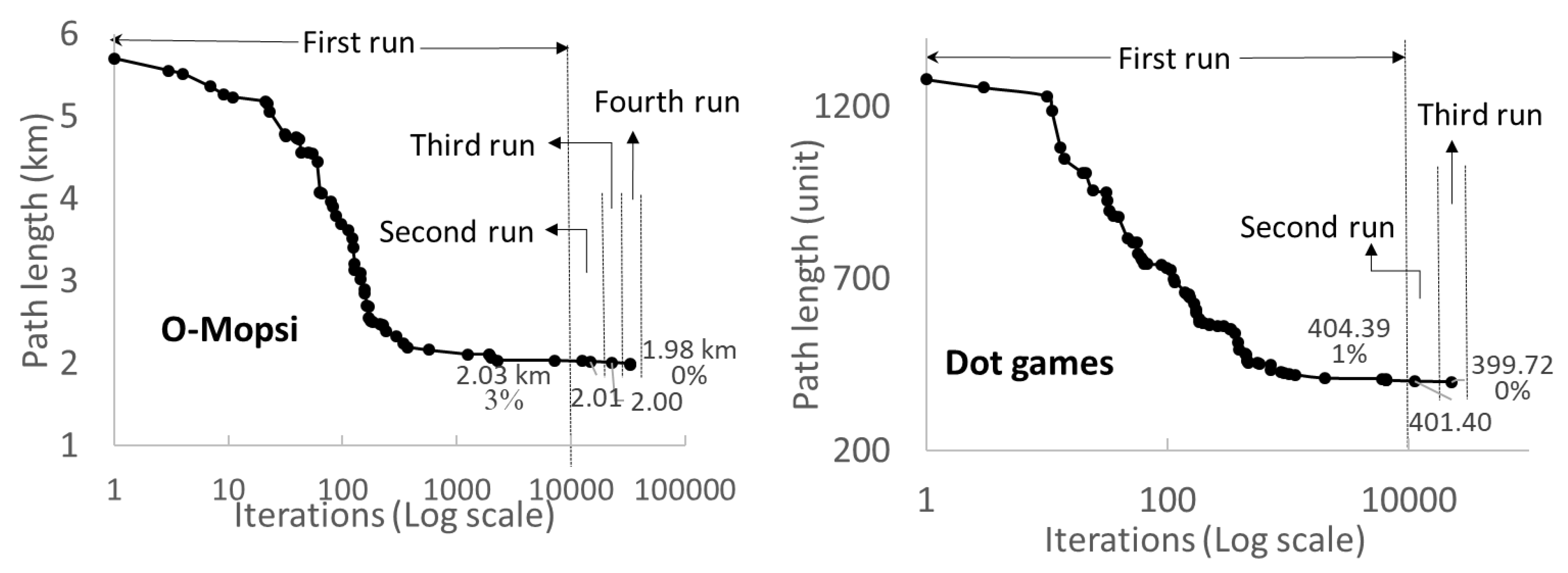
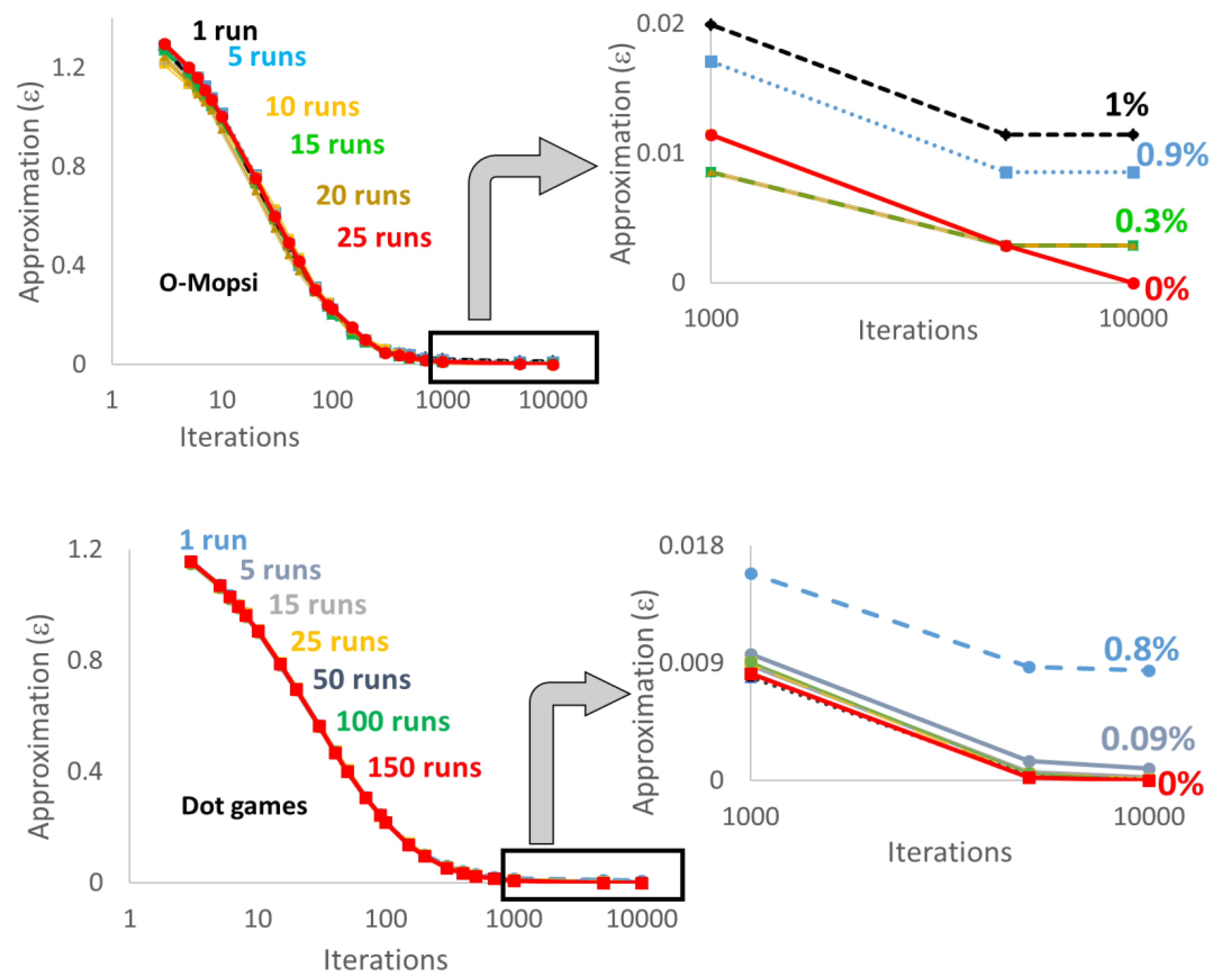




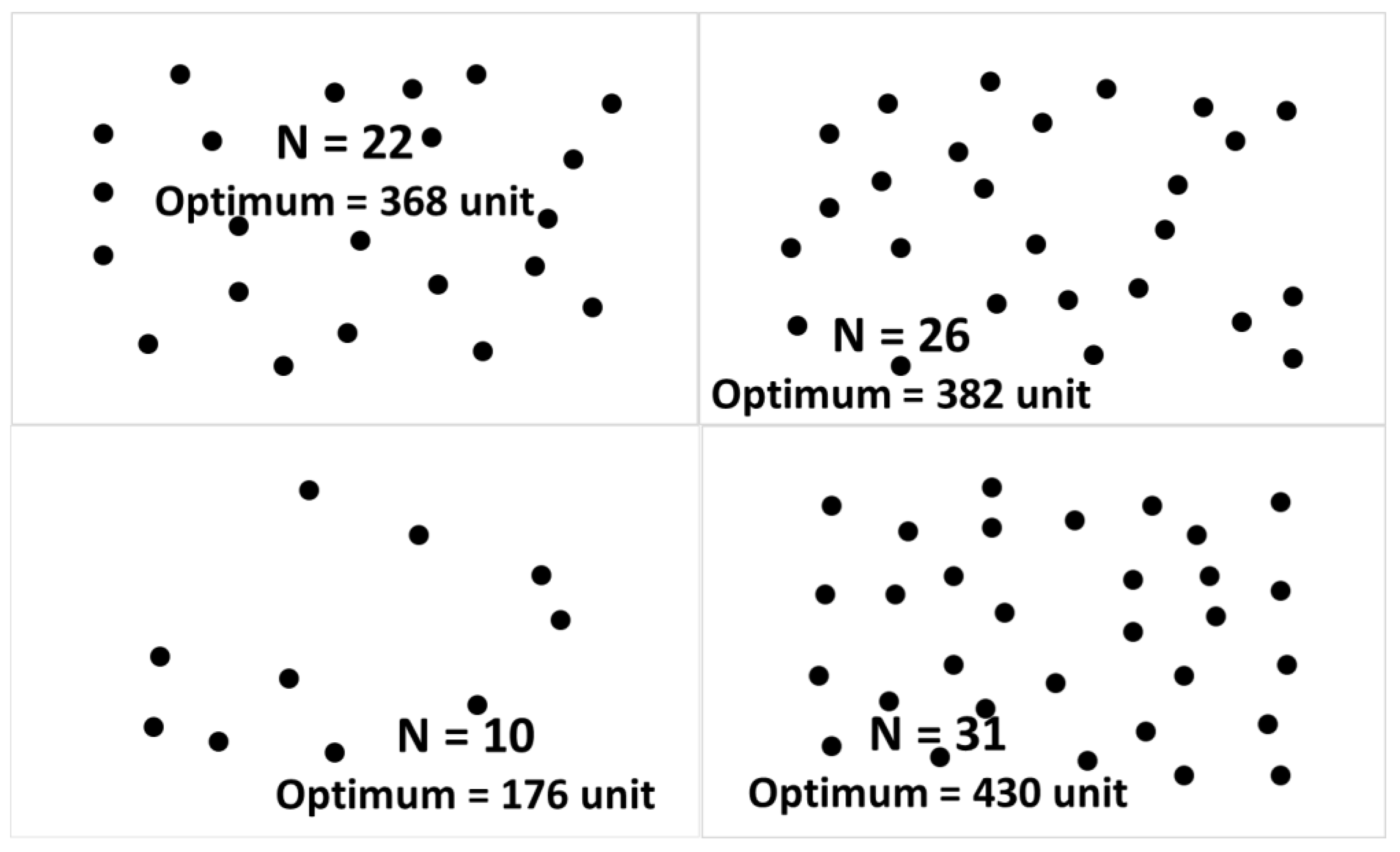
| Dataset: | Type: | Distance: | Instances: | Sizes: |
|---|---|---|---|---|
| O-Mopsi 1 | Open loop | Haversine | 145 | 4-27 |
| Dots 1 | Open loop | Euclidean | 4226 | 4-31 |
| Single Operator | Double Operators | Mix of Three | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Initialization | Random | Heuristic | Repeated (25 times) | Repeated (25 times) Second Operator: | Repeated (25 times) | ||||
| Relocate | 2-opt | Link swap | Subseq-uent | Mixed | |||||
| First | 7% (30%) | 1.0% (70%) | - | - | - | - | - | - | |
| Reloc-ate | Best | 6% (34%) | 0.9% (72%) | - | - | - | - | - | - |
| Random | 6% (34%) | 0.9% (71%) | 0.18% (90%) | - | 0.007% (98%) | 0.032% (97%) | 0.010% (98%) | 0.005%(99.7%) | |
| 2-opt | First | 2% (54%) | 1.0% (70%) | - | - | - | - | - | - |
| Best | 2% (57%) | 0.8% (73%) | - | - | - | - | - | - | |
| Random | 2% (52%) | 0.8% (73%) | 0.02% (97%) | 0.009% (98%) | - | 0.018% (97%) | 0.005% (99%) | 0.005% (99.7%) | |
| Link swap | Best | 44% (5%) | 2.9 (59%) | - | - | - | - | - | - |
| Random | 11% (31%) | 3.0 (58%) | 1.00% (77%) | 0.019% (98%) | 0.010% (97%) | - | 0.006% (99%) | 0.005% (99.7%) | |
| Single Run | 25 Repeats | |
|---|---|---|
| O–Mopsi | 0.8 ms | 16 ms |
| Dots | 0.7 ms | 16 ms |
| Repeated (25 times) | |||
|---|---|---|---|
| Gap (avg.) | Not Solved | ||
| O–Mopsi | Random mixed local search | 0% | 0 |
| Tabu search | 0% | 0 | |
| Simulated annealing (SA) | 0% | 0 | |
| Dots | Random mixed local search | 0.001% | 1 |
| Tabu search | 0.0003% | 3 | |
| SA | 0.007% | 10 | |
| Results | Random mix | Tabu | SA | |||
|---|---|---|---|---|---|---|
| Gap | Time | Gap | Time | Gap | Time | |
| O–Mopsi | 0% | <1 s | 0% | 1.3 s | 0 % | <1 s |
| Dots | 0.001% | <1 s | 0.0003% | 1.3 s | 0.007% | <1 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sengupta, L.; Mariescu-Istodor, R.; Fränti, P. Which Local Search Operator Works Best for the Open-Loop TSP? Appl. Sci. 2019, 9, 3985. https://doi.org/10.3390/app9193985
Sengupta L, Mariescu-Istodor R, Fränti P. Which Local Search Operator Works Best for the Open-Loop TSP? Applied Sciences. 2019; 9(19):3985. https://doi.org/10.3390/app9193985
Chicago/Turabian StyleSengupta, Lahari, Radu Mariescu-Istodor, and Pasi Fränti. 2019. "Which Local Search Operator Works Best for the Open-Loop TSP?" Applied Sciences 9, no. 19: 3985. https://doi.org/10.3390/app9193985
APA StyleSengupta, L., Mariescu-Istodor, R., & Fränti, P. (2019). Which Local Search Operator Works Best for the Open-Loop TSP? Applied Sciences, 9(19), 3985. https://doi.org/10.3390/app9193985







