Ground-State and Thermodynamical Properties of Uranium Mononitride from Anharmonic First-Principles Theory
Abstract
1. Introduction
2. Computational Methods
2.1. Electronic Structure Method
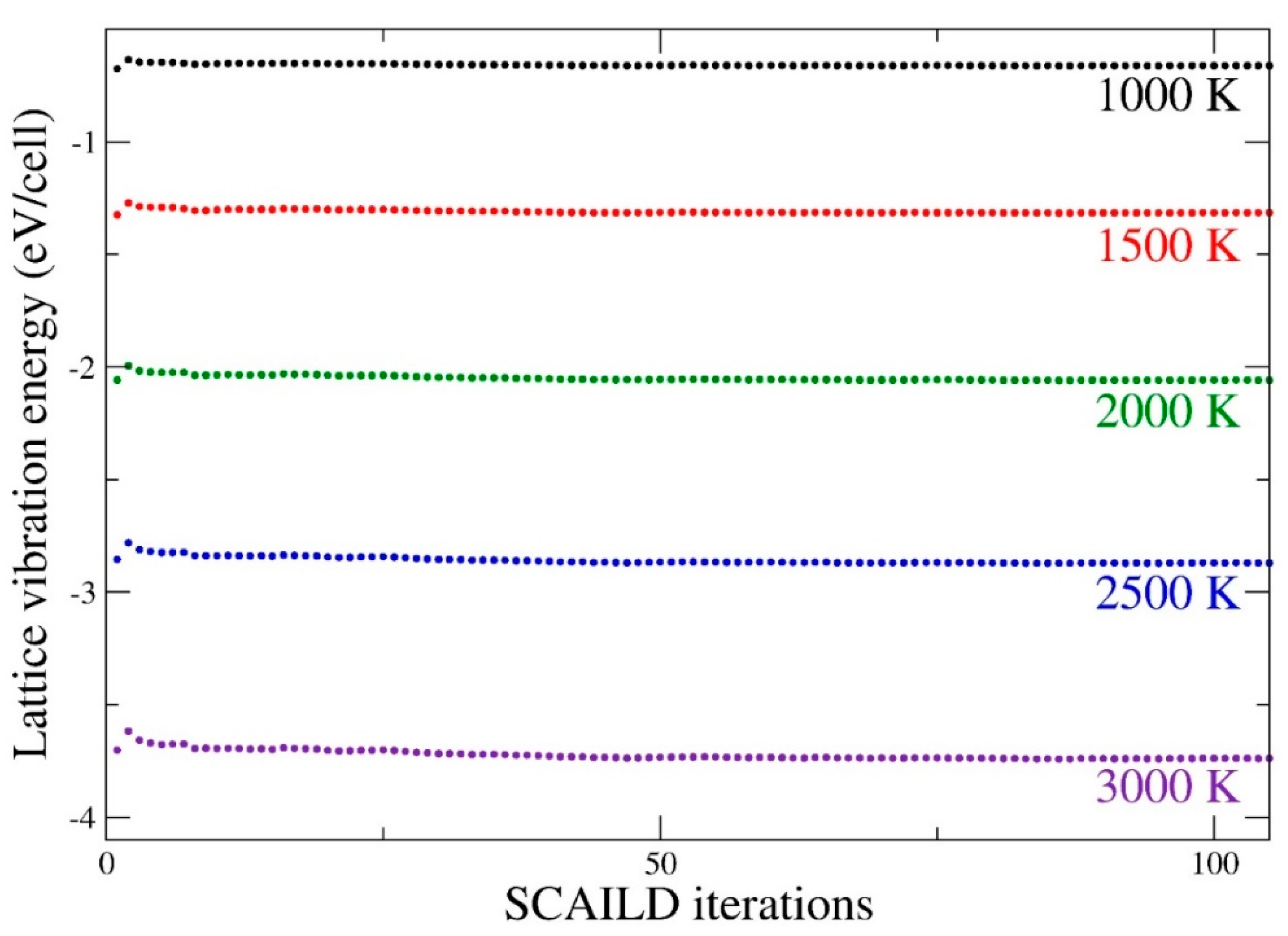
2.2. Self-Consistent Ab Initio Lattice Dynamics Method (SCAILD)
2.3. CALPHAD Method
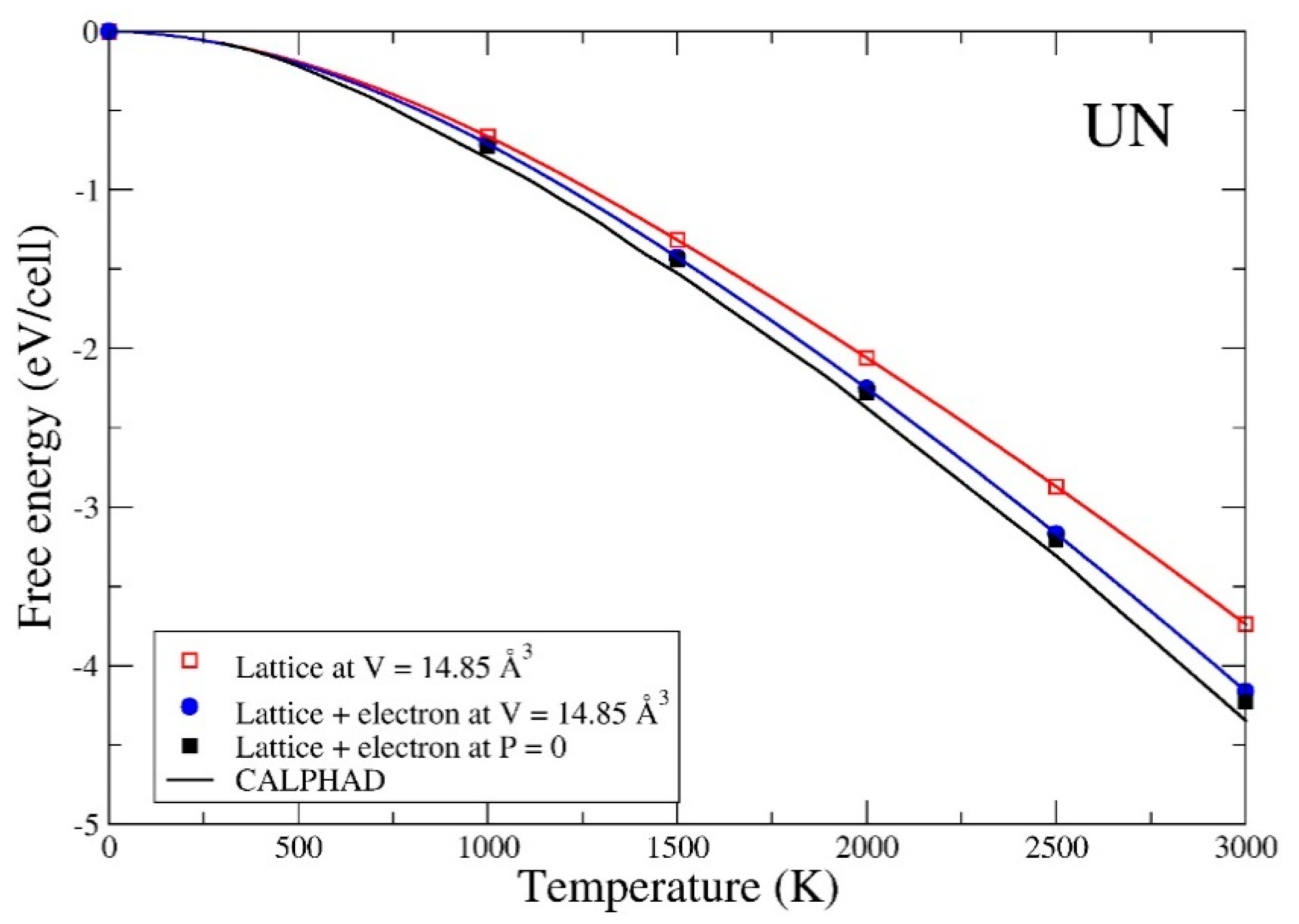
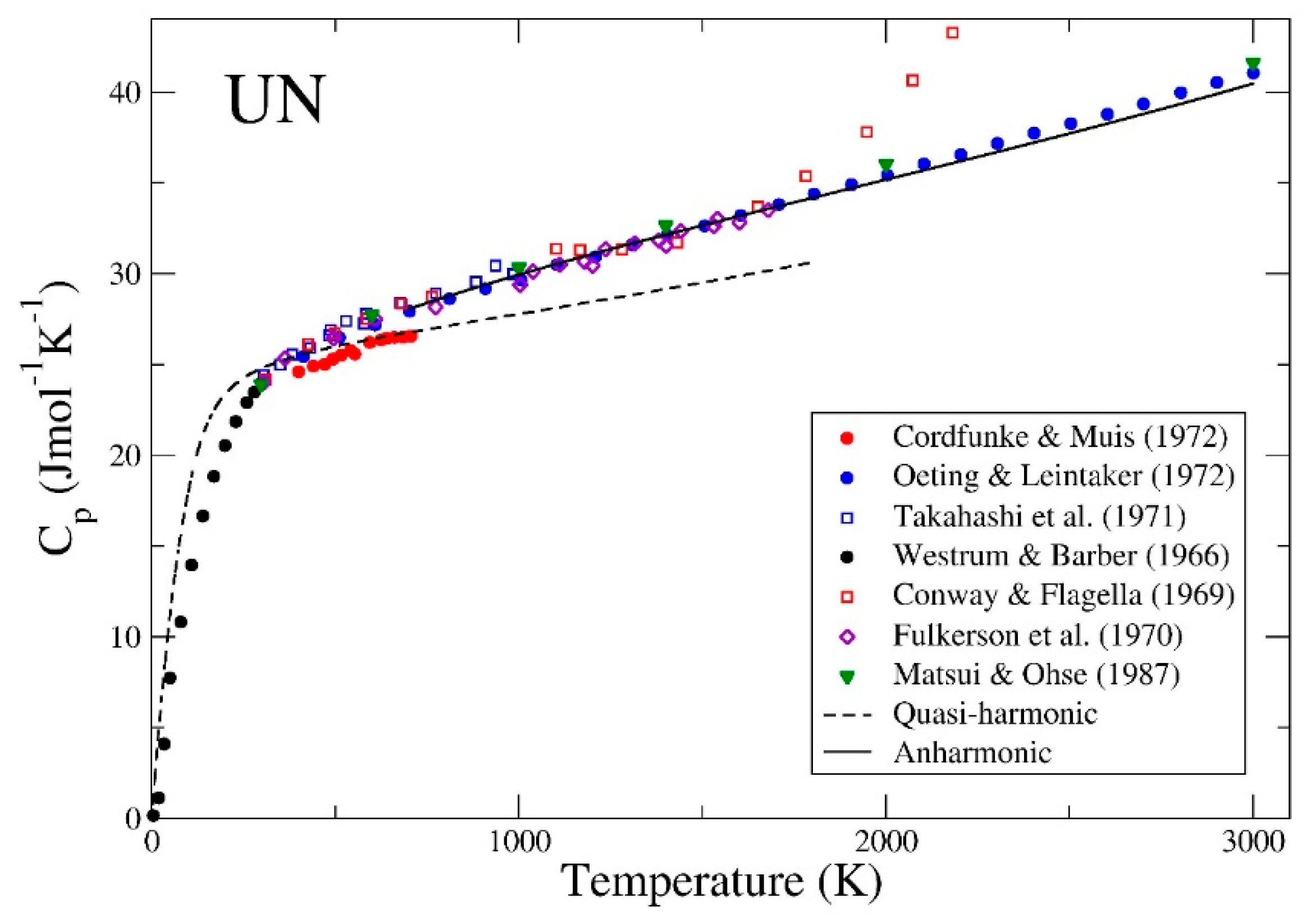
3. Results
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kempter, C.P.; Elliott, R.O. Thermal expansion of <UN>, <UO2>, <UO2•ThO2>, and <ThO2>. J. Chem. Phys. 1959, 30, 1524–1526. [Google Scholar] [CrossRef]
- Speidel, E.O.; Keller, D.J. Fabrication and Properties of Hot-Pressed Uranium Mononitride; BMI-1633; Battelle Memorial Institute: Columbus, OH, USA, 1963. [Google Scholar] [CrossRef]
- Curry, N.A. An investigation of the magnetic structure of uranium nitride by neutron diffraction. Proc. Phys. Soc. 1965, 86, 1193–1198. [Google Scholar] [CrossRef]
- Westrum, E.G.; Barber, C.M. Uranium mononitride: Heat capacity and thermodynamic properties from 5 to 350 K. J. Chem. Phys. 1966, 45, 635–638. [Google Scholar] [CrossRef]
- Councell, J.F.; Dell, R.M.; Martin, J.F. Thermodynamic properties of uranium compounds. Part 2.—Low-temperature heat capacity and entropy of three uranium nitrides. Trans. Faraday Soc. 1966, 62, 1736–1747. [Google Scholar] [CrossRef]
- Padel, A.; De Novion, C.H. Constantes elastiques des carbides, nitrides et oxydes d’uranium ed de plutonium. J. Nucl. Mater. 1969, 33, 40–51. [Google Scholar] [CrossRef]
- Conway, J.B.; Flagella, P.N. Physical and Mechanical Properties of Reactor Materials; GEMP-1012; General Electric Company: Cincinnati, OH, USA, 1969. [Google Scholar]
- Fulkerson, W.; Kollie, T.G.; Weawer, S.C.; Moore, J.P.; Williams, R.K. Plutonium 1970 and other Actinides Part I and II. In Proceedings of the 4th International Conference on Plutonium and Other Actinides (AIME), Santa Fe, NM, USA, 5–9 October 1970. [Google Scholar]
- Affortit, C. Chaleur specifique de UC et UN. J. Nucl. Mater. 1970, 34, 105–107. [Google Scholar] [CrossRef]
- Akhachinskii, V.V.; Bashlykov, S.N. Thermodynamics of the uranium-carbon, uranium-nitrogen, and plutonium-carbon systems. Atom. Enegriya 1970, 29, 1211–1219. [Google Scholar] [CrossRef]
- Benz, R.; Balog, G.; Baca, B.H. U-UO2-UN2 phase diagram. High Temp. Sci. 1994, 2, 405–406. [Google Scholar] [CrossRef]
- Takahashi, Y.; Murabayashi, M.; Akimoto, Y.; Mukaibo, T. Uranium mononitride: Heat capacity and thermal conductivity from 298 to 1000 K. J. Nucl. Mater. 1971, 38, 303–308. [Google Scholar] [CrossRef]
- Cordfunke, E.H.P.; Muis, R.P. The heat capacity of uranium mononitride. J. Nucl. Mater. 1972, 42, 233–234. [Google Scholar] [CrossRef]
- Guinan, M.; Cline, C.F. Elastic properties of uranium mononitride at 298 K. J. Nucl. Mater. 1972, 43, 205–206. [Google Scholar] [CrossRef]
- Oeting, F.L.; Leitnaker, J.M. The chemical thermodynamic properties of nuclear materials I. uranium mononitride. J. Chem. Thermodyn. 1972, 4, 199–211. [Google Scholar] [CrossRef]
- Muromura, T.; Tagawa, H. Lattice parameter of uranium mononitride. J. Nucl. Mater. 1979, 79, 264–266. [Google Scholar] [CrossRef]
- Benedict, U. Study of actinide metals and actinide compounds under high pressures. J. Less Common Met. 1984, 100, 153–170. [Google Scholar] [CrossRef]
- Jackman, J.A.; Holden, T.M.; Buyers, W.J.L.; De Villiers Du Plessis, P.; Vogt, O.; Genossar, J. Systematic study of the lattice dynamics of the uranium rocksalt-structure compounds. Phys. Rev. B 1986, 33, 7144–7153. [Google Scholar] [CrossRef]
- Matsui, T.; Ohse, R.W. Thermodynamic properties of uranium nitride, plutonium, nitride and uranium-plutonium mixed nitride. High Temp. High Press. 1987, 18, 1–17. [Google Scholar]
- Krikorian, O.H. Thermal expansivity correlations for refractory materials with the NaCl-type structure. High Temp. High Press. 1988, 20, 169–175. [Google Scholar]
- Staun Olsen, J.; Gerward, L.; Benedict, U.; Dabos, S.; Itié, J.-P.; Vogt, O. Bulk moduli and high-pressure phases of the uranium rocksalt structure compounds: II. The monopnictides. High Press. Res. 1989, 1, 253–266. [Google Scholar] [CrossRef]
- Hayes, S.L.; Thomas, J.K.; Peddicord, K.L. Material property correlations for uranium mononitride: I. Physical properties. J. Nucl. Mater. 1990, 171, 262–318. [Google Scholar] [CrossRef]
- Benedict, U. Comparative aspects of the high-pressure behaviour of lanthanide and actinide compounds. J. Alloys Compd. 1995, 223, 216–225. [Google Scholar] [CrossRef]
- Wang, W.E.; Olander, D.R. Thermodynamics of gas dissolution in liquid metals with extensive solubility; the U(L)-N, Zr(L)-O, and Th(L)-O systems. J. Alloys Compd. 1995, 228, 31–36. [Google Scholar] [CrossRef]
- Le Bihan, T.; Idiri, M.; Heathman, S. New investigation of pressure-induced rhombohedral distortion of uranium nitride. J. Alloys Compd. 2003, 358, 120–125. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Masayoshi, U. Thermal and mechanical properties of uranium nitride prepared by SPS technique. J. Mater. Sci. 2008, 43, 6429–6434. [Google Scholar] [CrossRef]
- Aczel, A.A.; Granroth, G.E.; MacDougall, G.J.; Buyers, W.J.L.; Abernathy, D.L.; Samolyuk, G.D.; Sticks, G.M.; Nagler, S.E. Quantum oscillations of nitrogen atoms in uranium nitride. Nat. Commun. 2012, 3, 1124. [Google Scholar] [CrossRef] [PubMed]
- King, D.M.; Tuna, F.; McInnes, E.J.L.; McMaster, J.; Lewis, W.; Blake, A.J.; Liddle, S.T. Synthesis and structure of a terminal uranium nitride complex. Science 2012, 337, 717–720. [Google Scholar] [CrossRef] [PubMed]
- Baranov, V.G.; Tenishev, A.V.; Kuzmin, R.S.; Pokrovskiy, S.A.; Mikhachik, V.V.; Astafyev, V.A.; Taubin, M.L.; Solntseva, E.S. Thermal stability investigation technique for uranium nitride. Ann. Nucl. Energy 2016, 87, 784–792. [Google Scholar] [CrossRef]
- Brooks, M.S.S. Electronic structure of NaCl-type compound of the light actinides. III. The actinide nitride series. J. Phys. F Met. Phys. 1984, 14, 857–871. [Google Scholar] [CrossRef]
- Chavalier, P.-Y.; Fisher, E.; Cheynet, B. Thermodynamic modelling of the N-U system. J. Nucl. Mater. 2000, 280, 136–150. [Google Scholar] [CrossRef]
- Kurosaki, K.; Yano, K.; Yamada, K.; Uno, M.; Yamanaka, S. A molecular dynamics study of the heat capacity of uranium mononitride. J. Alloys Compd. 2000, 297, 1–4. [Google Scholar] [CrossRef]
- Freyss, M.; Sato, I. Ab initio study of uranium and plutonium carbides and nitrides. In Recent Advances in Actinide Science; Alvarez, R., Bryan, N.D., May, I., Eds.; RSC Publishing: Cambridge, UK, 2005; pp. 430–432. [Google Scholar]
- Weck, P.F.; Kim, E.; Balakrishnan, N.; Poineau, F.; Yeamans, C.B.; Czerwinski, K.R. First-principles study of single-crystal uranium mono- and dinitride. Chem. Phys. Lett. 2007, 443, 82–86. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Losev, M.V.; Panin, A.I.; Mosyagin, N.S.; Titov, A.V. Electronic structure of crystalline uranium nitride: LCAO DFT calculations. Phys. Stat. Sol. (b) 2008, 245, 114–122. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Panin, A.I.; Bandura, A.V.; Losev, M.V. Electronic structure of crystalline uranium nitrides UN, U2N3 and UN2: LCAO calculations with the basis set optimization. J. Phys. Conf. Ser. 2008, 117, 012015. [Google Scholar] [CrossRef]
- Petit, L.; Svane, A.; Szotek, Z.; Temmerman, W.M.; Stocks, G.M. Ground-state electronic structure of actinide monocarbides and mononitrides. Phys. Rev. B 2009, 80, 045124. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, B.-T.; Li, R.-W.; Shi, H.; Zhang, P. Structural, electronic, and thermodynamic properties of UN: Systematic density functional calculations. J. Nucl. Mater. 2010, 406, 218–222. [Google Scholar] [CrossRef]
- Modak, P.; Verma, A.K. First-principles investigation of electronic, vibrational, elastic, and structural properties of ThN and UN up to 100 GPa. Phys. Rev. B 2011, 84, 024108. [Google Scholar] [CrossRef]
- Baranov, V.G.; Devyatko, Y.N.; Tenishev, A.V.; Khlunov, A.V.; Khomyakov, O.V. A physical model for evaluating uranium nitride specific heat. J. Nucl. Mater. 2013, 443, 248–251. [Google Scholar] [CrossRef]
- Su, Q.; Deng, H.; Ao, B.; Xiao, S.; Li, X.; Chen, P.; Hu, W. First-principles study of the interaction of nitrogen atom with α-uranium: From surface absorption to bulk diffusion. J. Appl. Phys. 2014, 115, 164902. [Google Scholar] [CrossRef]
- Claisse, A.; Klipfel, M.; Lindbom, N.; Freyss, M.; Olsson, P. GGA+U study of uranium mononitride: A comparison of the U-ramping and occupation matrix scheme and incorporation energies of fission products. J. Nucl. Mater. 2016, 478, 119–124. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, J.-H.; Pu, C.; Song, Y. Prediction of stable ground-state uranium nitrides at ambient and high pressures. arXiv 2018, arXiv:1804.00095v1. [Google Scholar]
- Streit, M.; Franz, I. Nitrides as a nuclear fuel option. J. Eur. Ceram. Soc. 2005, 25, 2687–2692. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams with Special Reference to Refractory Metals; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Saunders, N.; Miodownik, A. CALPHAD Calculation of Phase Diagrams: A Comprehensive Guide; Pergamon materials series; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lukas, H.; Fries, S.; Sundman, B. Computational Thermodynamics: The CALPHAD Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. Entropy driven stabilization of energetically unstable crystal structures explained from first principles theory. Phys. Rev. Lett. 2008, 100, 095901. [Google Scholar] [CrossRef] [PubMed]
- Söderlind, P.; Grabowski, B.; Yang, L.; Landa, A.; Björkman, T.; Souvatzis, P.; Eriksson, O. High-temperature stabilization of γ-uranium from relativistic first-principles theory. Phys. Rev. B 2012, 85, 060301. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Söderlind, P.; Eriksson, O.; Johansson, B.; Wills, J.M. Electronic properties of f-electron metals using the generalized gradient approximation. Phys. Rev. B 1994, 50, 7291–7294. [Google Scholar] [CrossRef] [PubMed]
- Söderlind, P.; Gonis, A. Assessing a solids-biased density-gradient functional for actinide metals. Phys. Rev. B 2010, 82, 033102. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations for solids. Science 2016, 351, aad3000(1)–aad3000(7). [Google Scholar] [CrossRef]
- Wills, J.M.; Alouani, M.; Andersson, P.; Delin, A.; Eriksson, O.; Grechnyev, O. Full-Potential Electronic Structure Method; Springer Series in Solid-State Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 167. [Google Scholar]
- Nordström, L.; Wills, J.M.; Andersson, P.H.; Söderlind, P.; Eriksson, O. Spin-orbit coupling in the actinide elements: A critical evaluation of theoretical equilibrium volumes. Phys. Rev. B 2000, 63, 035103. [Google Scholar] [CrossRef]
- Eriksson, O.; Brooks, M.S.S.; Johansson, B. Orbital polarization in narrow-band systems: Application to volume collapses in light lanthanides. Phys. Rev. B 1990, 41, 7311–7314. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Sadigh, B. Density-functional theory for plutonium. Adv. Phys. 2019, 68, 1–47. [Google Scholar] [CrossRef]
- Vinet, P.; Ferrante, J.; Smith, J.R.; Rose, J.H. Universal equation of state for solids. J. Phys. C Solid State Phys. 1986, 19, L467–L473. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. The self-consistent ab initio lattice dynamical method. Comput. Mat. Sci. 2009, 44, 888–894. [Google Scholar] [CrossRef]
- Bajaj, S.; Landa, A.; Söderlind, P.; Turchi, P.E.A.; Arroyave, R. The U-Ti system: Strengths and weaknesses of the CALPHAD method. J. Nucl. Mater. 2011, 419, 177–185. [Google Scholar] [CrossRef]
- Perron, A.; Turchi, P.E.A.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F.; Kurata, M. Thermodynamic re-assessment of the Pu-U system and its application to the ternary Pu-U-Ga system. J. Nucl. Mater. 2014, 454, 81–95. [Google Scholar] [CrossRef]
- Perron, A.; Turchi, P.E.A.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F. The Pu-U-Am system: An ab initio informed CALPHAD thermodynamic study. J. Nucl. Mater. 2015, 458, 425–441. [Google Scholar] [CrossRef]
- Besmann, T.H.; Shin, D.; Lindemer, T.B. Uranium nitride as LWR TRISO fuel: Thermodynamic modeling of U-C-N. J. Nucl. Mater. 2012, 427, 162–168. [Google Scholar] [CrossRef]
- Söderlind, P. First-principles elastic and structural properties of uranium metal. Phys. Rev. B 2002, 66, 085113. [Google Scholar] [CrossRef]
- Sedmidubský, D.; Konings, R.J.M.; Novák, P. Calculation of enthalpies of formation of actinide nitrides. J. Nucl. Mater. 2005, 344, 40–44. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Crystal Structures; John Wiley & Sons: New York, NY, USA, 1963; Volume I. [Google Scholar]
- Mei, Z.-G.; Stan, M.; Pichler, B. First-principles study of structural, elastic, vibrational, and thermodynamic properties of UN. J. Nucl. Mater. 2013, 440, 63–69. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Abbasi-Pérez, D. Gibbs2: A new version of the quasi-harmonic model code. II Models for solid thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Equation of state and thermodynamics of solids using empirical corrections in the quasi-harmonic approximation. Phys. Rev. B 2011, 84, 184103. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Treatment of first-principles data for predictive quasiharmonic thermodynamics of solids: The case of MgO. Phys. Rev. B 2011, 84, 024109. [Google Scholar] [CrossRef]
- Buyers, W.J.L.; Murray, A.F.; Holden, T.M.; Svensson, E.C.; DuPlessis, P.D.V.; Lander, G.H.; Vogt, O. Spin and phonon excitations in actinide systems. Physica 1980, 102B, 291–298. [Google Scholar] [CrossRef]
| Method | V (Å3) | B (GPa) | B’ | ΔE (mRy/at) | ΔE (kJ/mol) | M (μB) | ΔfH (mRy/at) | ΔfH (kJ/mol) |
|---|---|---|---|---|---|---|---|---|
| DFT-FM | 14.85 | 182 | 5.2 | 0 | 0 | 0.78 (1.56) | −226.6 | −297.5 |
| DFT-AF | 14.85 | 183 | 5.0 | 1.5 | 1.97 | 0.78 | n/a | n/a |
| DFT-NM | 14.75 | 232 | 2.0 | 2.3 | 3.02 | 0 | n/a | n/a |
| Expt | 14.62 | 191–206 | 6.3 | n/a | n/a | 0.75 | −223.6 | −293.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Söderlind, P.; Landa, A.; Perron, A.; Sadigh, B.; Heo, T.W. Ground-State and Thermodynamical Properties of Uranium Mononitride from Anharmonic First-Principles Theory. Appl. Sci. 2019, 9, 3914. https://doi.org/10.3390/app9183914
Söderlind P, Landa A, Perron A, Sadigh B, Heo TW. Ground-State and Thermodynamical Properties of Uranium Mononitride from Anharmonic First-Principles Theory. Applied Sciences. 2019; 9(18):3914. https://doi.org/10.3390/app9183914
Chicago/Turabian StyleSöderlind, Per, Alexander Landa, Aurélien Perron, Babak Sadigh, and Tae Wook Heo. 2019. "Ground-State and Thermodynamical Properties of Uranium Mononitride from Anharmonic First-Principles Theory" Applied Sciences 9, no. 18: 3914. https://doi.org/10.3390/app9183914
APA StyleSöderlind, P., Landa, A., Perron, A., Sadigh, B., & Heo, T. W. (2019). Ground-State and Thermodynamical Properties of Uranium Mononitride from Anharmonic First-Principles Theory. Applied Sciences, 9(18), 3914. https://doi.org/10.3390/app9183914







