Texture Segmentation: An Objective Comparison between Five Traditional Algorithms and a Deep-Learning U-Net Architecture
Abstract
1. Introduction
2. Materials and Methods
2.1. Texture Composite Images
2.2. Training Data
2.3. Traditional Texture Segmentation Algorithms
2.4. U-Net Configuration
2.5. Misclassification
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Bigun, J. Multidimensional Orientation Estimation with Applications to Texture Analysis and Optical Flow. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 775–790. [Google Scholar] [CrossRef]
- Bovik, A.C.; Clark, M.; Geisler, W.S. Multichannel Texture Analysis Using Localized Spatial Filters. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 55–73. [Google Scholar] [CrossRef]
- Cross, G.R.; Jain, A.K. Markov Random Field Texture Models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 5, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M. Statistical and Structural Approaches to Texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Tamura, H.; Mori, S.; Yamawaki, T. Texture Features Corresponding to Visual Perception. IEEE Trans. Syst. Man Cybern. 1978, 8, 460–473. [Google Scholar] [CrossRef]
- Tuceryan, M.; Jain, A.K. Texture Analysis. In Handbook of Pattern Recognition and Computer Vision, 2nd ed.; Chen, C.H., Pau, L.F., Wang, P.S.P., Eds.; World Scientific Publishing: Singapore, 1998; pp. 207–248. [Google Scholar]
- Reyes-Aldasoro, C.C.; Bhalerao, A. The Bhattacharyya Space for Feature Selection and Its Application to Texture Segmentation. Pattern Recognit. 2006, 39, 812–826. [Google Scholar] [CrossRef]
- Bouman, C.; Liu, B. Multiple Resolution Segmentation of Textured Images. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 99–113. [Google Scholar] [CrossRef]
- Jain, A.K.; Farrokhnia, F. Unsupervised Texture Segmentation using Gabor Filters. Pattern Recognit. 1991, 24, 1167–1186. [Google Scholar] [CrossRef]
- Kadyrov, A.; Talepbour, A.; Petrou, M. Texture Classification with Thousand of Features. In Proceedings of the 13th British Machine Vision Conference (BMVC), Cardiff, UK, 2–5 September 2002; pp. 656–665. [Google Scholar]
- Kervrann, C.; Heitz, F. A Markov Random Field Model-based Approach to Unsupervised Texture Segmentation using Local and Global Spatial Statistics. IEEE Trans. Image Process. 1995, 4, 856–862. [Google Scholar] [CrossRef]
- Unser, M. Texture Classification and Segmentation Using Wavelet Frames. IEEE Trans. Image Process. 1995, 4, 1549–1560. [Google Scholar] [CrossRef] [PubMed]
- Weszka, J.; Dyer, C.; Rosenfeld, A. A Comparative Study of Texture Measures for Terrain Classification. IEEE Trans. Syst. Man Cybern. 1976, 6, 269–285. [Google Scholar] [CrossRef]
- Tai, C.; Baba-Kishi, K. Microtexture Studies of PST and PZT Ceramics and PZT Thin Film by Electron Backscatter Diffraction Patterns. Text. Microstruct. 2002, 35, 71–86. [Google Scholar] [CrossRef]
- Carrillat, A.; Randen, T.; Snneland, L.; Elvebakk, G. Seismic Stratigraphic Mapping of Carbonate Mounds using 3D Texture Attributes. In Proceedings of the 64th EAGE Conference & Exhibition, Florence, Italy, 27–30 May 2002. [Google Scholar]
- Randen, T.; Monsen, E.; Abrahamsen, A.; Hansen, J.O.; Schlaf, J.; Snneland, L. Three-dimensional Texture Attributes for Seismic Data Analysis. In Proceedings of the 70th SEG Annual Meeting, Calgary, AB, Canada, 6–11 August 2000. [Google Scholar]
- Thybo, A.K.; Martens, M. Analysis of Sensory Assessors in Texture Profiling of Potatoes by Multivariate Modelling. Food Qual. Prefer. 2000, 11, 283–288. [Google Scholar] [CrossRef]
- Létal, J.; Jirák, D.; Šuderlová, L.; Hájek, M. MRI ‘Texture’ Analysis of MR Images of Apples during Ripening and Storage. LWT Food Sci. Technol. 2003, 36, 719–727. [Google Scholar] [CrossRef]
- Lizarraga-Morales, R.A.; Sanchez-Yanez, R.E.; Baeza-Serrato, R. Defect Detection on Patterned Fabrics using Texture Periodicity and the Coordinated Clusters Representation. Text. Res. J. 2017, 87, 1869–1882. [Google Scholar] [CrossRef]
- Bianconi, F.; González, E.; Fernández, A.; Saetta, S.A. Automatic Classification of Granite Tiles through Colour and Texture Features. Expert Syst. Appl. 2012, 39, 11212–11218. [Google Scholar] [CrossRef]
- Kovalev, V.A.; Petrou, M.; Bondar, Y.S. Texture Anisotropy in 3D Images. IEEE Trans. Image Process. 1999, 8, 346–360. [Google Scholar] [CrossRef]
- Reyes-Aldasoro, C.C.; Bhalerao, A. Volumetric Texture Description and Discriminant Feature Selection for MRI. In Proceedings of the Information Processing in Medical Imaging, Ambleside, UK, 20–25 July 2003; Taylor, C., Noble, A., Eds.; pp. 282–293. [Google Scholar]
- Lerski, R.; Straughan, K.; Schad, L.R.; Boyce, D.; Bluml, S.; Zuna, I. MR Image Texture Analysis—An Approach to tissue Characterization. Magn. Resonance Imaging 1993, 11, 873–887. [Google Scholar] [CrossRef]
- Schad, L.R.; Bluml, S.; Zuna, I. MR Tissue Characterization of Intracranial Tumors by means of Texture Analysis. Magn. Resonance Imaging 1993, 11, 889–896. [Google Scholar] [CrossRef]
- Reyes Aldasoro, C.C.; Bhalerao, A. Volumetric Texture Segmentation by Discriminant Feature Selection and Multiresolution Classification. IEEE Trans. Med. Imaging 2007, 26, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Shen, D. Automated Segmentation of 3D US Prostate Images Using Statistical Texture-Based Matching Method. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI), Montréal, QC, Canada, 15–18 November 2003; pp. 688–696. [Google Scholar]
- Xie, J.; Jiang, Y.; tat Tsui, H. Segmentation of Kidney from Ultrasound Images based on Texture and Shape Priors. IEEE Trans. Med. Imaging 2005, 24, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, E.A.; Reinhardt, J.M.; Sonka, M.; Simon, B.A.; Guo, J.; Saba, O.; Chon, D.; Samrah, S.; Shikata, H.; Tschirren, J.; et al. Characterization of the Interstitial Lung Diseases via Density-Based and Texture-Based Analysis of Computed Tomography Images of Lung Structure and Function. Acad. Radiol. 2003, 10, 1104–1118. [Google Scholar] [CrossRef]
- Segovia-Martínez, M.; Petrou, M.; Kovalev, V.A.; Perner, P. Quantifying Level of Brain Atrophy Using Texture Anisotropy in CT Data. In Proceedings of the Medical Image Understanding and Analysis, Oxford, UK, 19–20 July 1999; pp. 173–176. [Google Scholar]
- Ganeshan, B.; Goh, V.; Mandeville, H.C.; Ng, Q.S.; Hoskin, P.J.; Miles, K.A. Non–Small Cell Lung Cancer: Histopathologic Correlates for Texture Parameters at CT. Radiology 2013, 266, 326–336. [Google Scholar] [CrossRef] [PubMed]
- Sabino, D.M.U.; da Fontoura Costa, L.; Gil Rizzatti, E.; Antonio Zago, M. A Texture Approach to Leukocyte Recognition. Real-Time Imaging 2004, 10, 205–216. [Google Scholar] [CrossRef]
- Wang, X.; He, W.; Metaxas, D.; Mathew, R.; White, E. Cell Segmentation and Tracking using Texture-Adaptive Snakes. In Proceedings of the 2007 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Washington, DC, USA, 12–16 April 2007; pp. 101–104. [Google Scholar] [CrossRef]
- Kather, J.N.; Weis, C.A.; Bianconi, F.; Melchers, S.M.; Schad, L.R.; Gaiser, T.; Marx, A.; Zollner, F. Multi-class Texture Analysis in Colorectal Cancer Histology. Sci. Rep. 2016, 6, 27988. [Google Scholar] [CrossRef] [PubMed]
- Dunn, D.; Higgins, W.; Wakeley, J. Texture Segmentation using 2-D Gabor Elementary Functions. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 130–149. [Google Scholar] [CrossRef]
- Bigun, J.; du Buf, J.M.H. N-Folded Symmetries by Complex Moments in Gabor Space and Their Application to Unsupervised Texture Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 80–87. [Google Scholar] [CrossRef]
- Bianconi, F.; Fernández, A. Evaluation of the Effects of Gabor Filter Parameters on Texture Classification. Pattern Recognit. 2007, 40, 3325–3335. [Google Scholar] [CrossRef]
- Rajpoot, N.M. Texture Classification Using Discriminant Wavelet Packet Subbands. In Proceedings of the 45th IEEE Midwest Symposium on Circuits and Systems (MWSCAS 2002), Tulsa, OK, USA, 4–7 August 2002. [Google Scholar]
- Chang, T.; Kuo, C.C.J. Texture Analysis and Classification with Tree-Structured Wavelet Transform. IEEE Trans. Image Process. 1993, 2, 429–441. [Google Scholar] [CrossRef]
- Chellapa, R.; Jain, A. Markov Random Fields; Academic Press: Boston, MA, USA, 1993. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems—Volume 1 (NIPS’12), Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates Inc.: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Berlin, Germany, 2014; pp. 818–833. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Whelan, P.F. Chapter 4—Deep Learning in Texture Analysis and Its Application to Tissue Image Classification. In Biomedical Texture Analysis; Depeursinge, A., Al-Kadi, O.S., Mitchell, J.R., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 95–129. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Berlin, Germany, 2015; Volume 9350, pp. 234–241. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Jansson, A.; Humphrey, E.J.; Montecchio, N.; Bittner, R.M.; Kumar, A.; Weyde, T. Singing Voice Separation with Deep U-Net Convolutional Networks. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017. [Google Scholar]
- Dong, H.; Yang, G.; Liu, F.; Mo, Y.; Guo, Y. Automatic Brain Tumor Detection and Segmentation Using U-Net Based Fully Convolutional Networks. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; Valdés Hernández, M., González-Castro, V., Eds.; Springer International Publishing: Berlin, Germany, 2017; Volume 723, pp. 506–517. [Google Scholar]
- Falk, T.; Mai, D.; Bensch, R.; Çiçek, Ö.; Abdulkadir, A.; Marrakchi, Y.; Böhm, A.; Deubner, J.; Jäckel, Z.; Seiwald, K.; et al. U-Net: Deep Learning for Cell Counting, Detection, and Morphometry. Nat. Methods 2019, 16, 67. [Google Scholar] [CrossRef] [PubMed]
- Malpica, N.; Ortuño, J.E.; Santos, A. A Multichannel Watershed-based Algorithm for Supervised Texture Segmentation. Pattern Recognit. Lett. 2003, 24, 1545–1554. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A Comparative Study of Texture Measures with Classification based on Feature Distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
- Ojala, T.; Valkealahti, K.; Oja, E.; Pietikäinen, M. Texture Discrimination with Multidimensional Distributions of Signed Gray Level Differences. Pattern Recognit. 2001, 34, 727–739. [Google Scholar] [CrossRef]
- Randen, T.; Husøy, J.H. Filtering for Texture Classification: A Comparative Study. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 291–310. [Google Scholar] [CrossRef]
- Randen, T.; Husøy, J.H. Texture Segmentation using Filters with Optimized Energy Separation. IEEE Trans. Image Process. 1999, 8, 571–582. [Google Scholar] [CrossRef]
- Brodatz, P. Textures: A Photographic Album for Artists and Designers; Dover: New York, NY, USA, 1996. [Google Scholar]
- Yamada, R.; Ide, H.; Yudistira, N.; Kurita, T. Texture Segmentation using Siamese Network and Hierarchical Region Merging. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2735–2740. [Google Scholar] [CrossRef]
- Petrou, M.; Garcia-Sevilla, P. Image Processing: Dealing with Texture; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Reyes-Aldasoro, C.C.; Bhalerao, A.H. Volumetric Texture Analysis in Biomedical Imaging. In Biomedical Diagnostics and Clinical Technologies: Applying High-Performance Cluster and Grid Computing; Pereira, M., Freire, M., Eds.; IGI Global: Hershey, PA, USA, 2011; pp. 200–248. [Google Scholar]
- Mirmehdi, M.; Xie, X.; Suri, J. Handbook of Texture Analysis; Imperial College Press: London, UK, 2009. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Gabor, D. Theory of Communication. J. IEE 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Knutsson, H.; Granlund, G.H. Texture Analysis Using Two-Dimensional Quadrature Filters. In Proceedings of the IEEE Computer Society Workshop on Computer Architecture for Pattern Analysis and Image Database Management—CAPAIDM, Pasadena, CA, USA, 12–14 October 1983; pp. 206–213. [Google Scholar]
- Randen, T.; Husy, J.H. Multichannel filtering for image texture segmentation. Opt. Eng. 1994, 33, 2617–2625. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Verhoeven, J.; Miller, N.R.; Daems, L.; Reyes-Aldasoro, C.C. Visualisation and Analysis of Speech Production with Electropalatography. J. Imaging 2019, 5, 40. [Google Scholar] [CrossRef]


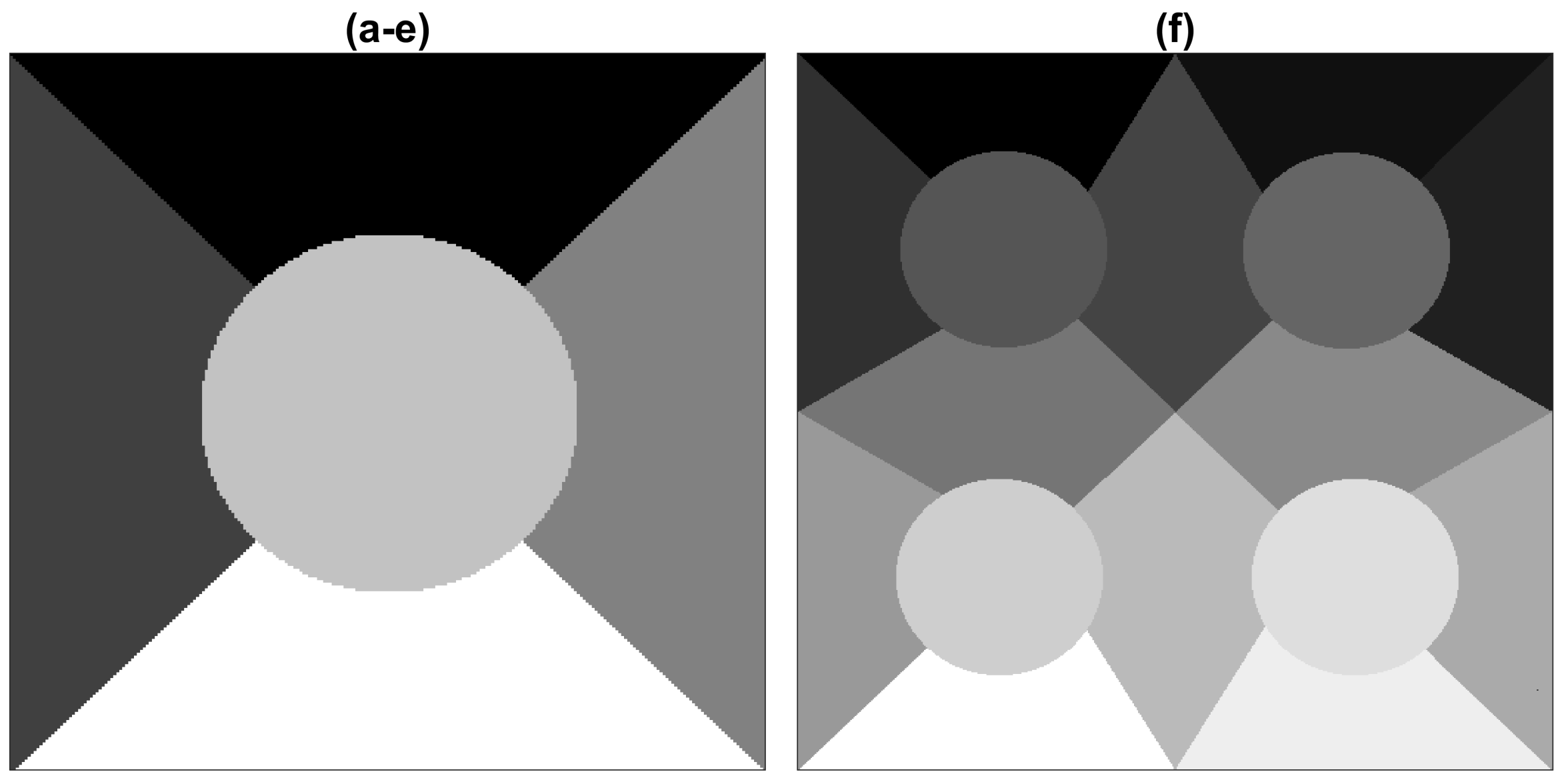




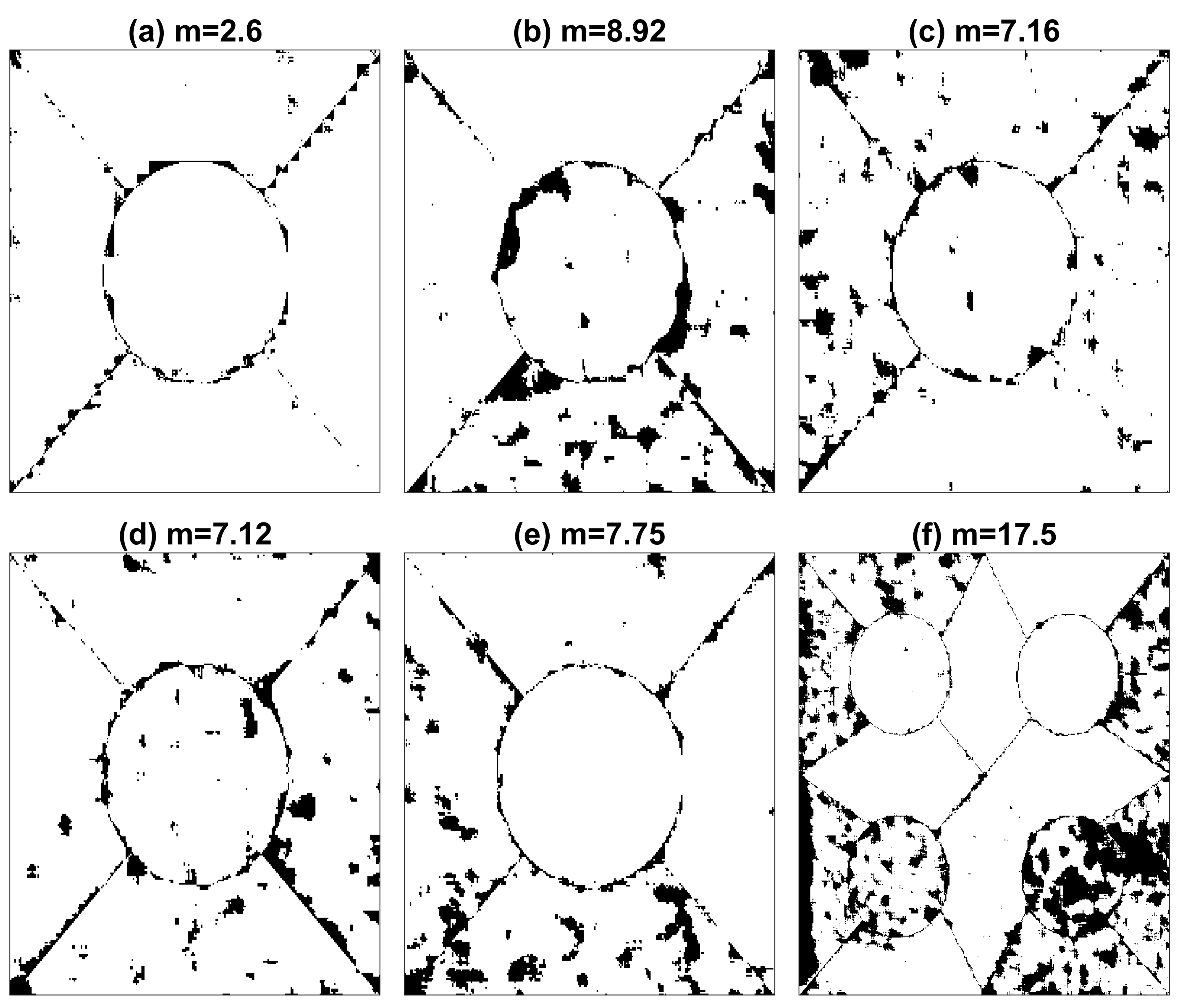
| Method | Figures | |||||||
|---|---|---|---|---|---|---|---|---|
| Layers | Optimisation Algorithm | Epochs | a | b | c | d | e | f |
| 15 | sgdm | 10 | 6.8 | 21.5 | 40.8 | 31.2 | 27.2 | 20.9 |
| 20 | sgdm | 10 | 33.0 | 59.0 | 74.3 | 79.1 | 77.3 | 41.9 |
| 20 | sgdm | 10 | 71.9 | 62.9 | 74.3 | 78.8 | 72.1 | 39.0 |
| 15 | Adam | 10 | 3.2 | 10.4 | 7.9 | 7.1 | 17.8 | 19.3 |
| 20 | Adam | 10 | 7.4 | 15.5 | 46.5 | 25.0 | 45.1 | 94.2 |
| 20 | Adam | 10 | 6.4 | 15.5 | 36.0 | 21.1 | 26.7 | 32.9 |
| 15 | RMSprop | 10 | 5.1 | 8.9 | 14.0 | 18.3 | 12.1 | 17.6 |
| 20 | RMSprop | 10 | 5.3 | 42.4 | 45.3 | 59.9 | 56.2 | 27.7 |
| 20 | RMSprop | 10 | 20.2 | 37.4 | 47.0 | 43.7 | 44.2 | 26.1 |
| 15 | sgdm | 20 | 3.8 | 23.1 | 17.5 | 15.9 | 14.1 | 19.8 |
| 20 | sgdm | 20 | 27.3 | 60.5 | 74.8 | 69.3 | 73.9 | 27.4 |
| 20 | sgdm | 20 | 23.8 | 51.0 | 63.6 | 66.8 | 56.5 | 26.7 |
| 15 | Adam | 20 | 3.7 | 11.6 | 7.5 | 7.4 | 9.5 | 71.7 |
| 20 | Adam | 20 | 6.1 | 13.3 | 28.7 | 18.5 | 40.8 | 32.2 |
| 20 | Adam | 20 | 5.6 | 17.9 | 27.4 | 22.5 | 39.3 | 94.0 |
| 15 | RMSprop | 20 | 3.8 | 11.7 | 14.5 | 19.2 | 11.7 | 17.9 |
| 20 | RMSprop | 20 | 6.1 | 42.2 | 54.7 | 47.5 | 42.6 | 22.3 |
| 20 | RMSprop | 20 | 19.1 | 30.3 | 44.7 | 51.7 | 37.1 | 26.9 |
| 15 | sgdm | 50 | 3.2 | 15.3 | 9.2 | 7.7 | 13.8 | 19.6 |
| 20 | sgdm | 50 | 18.2 | 32.2 | 60.3 | 42.8 | 30.2 | 28.9 |
| 20 | sgdm | 50 | 9.4 | 55.2 | 56.0 | 16.0 | 32.4 | 32.4 |
| 15 | Adam | 50 | 3.4 | 10.4 | 9.8 | 9.9 | 39.1 | 22.6 |
| 20 | Adam | 50 | 8.3 | 80.3 | 19.8 | 82.3 | 79.6 | 34.8 |
| 20 | Adam | 50 | 7.2 | 9.6 | 41.4 | 10.0 | 27.6 | 23.6 |
| 15 | RMSprop | 50 | 3.4 | 18.7 | 10.0 | 8.3 | 11.2 | 17.5 |
| 20 | RMSprop | 50 | 5.6 | 33.2 | 25.7 | 34.8 | 34.4 | 22.4 |
| 20 | RMSprop | 50 | 5.4 | 22.8 | 45.3 | 20.0 | 34.7 | 29.2 |
| 15 | sgdm | 100 | 3.9 | 10.6 | 7.9 | 7.7 | 7.7 | 21.4 |
| 20 | sgdm | 100 | 9.6 | 22.1 | 39.4 | 39.7 | 30.3 | 23.8 |
| 20 | sgdm | 100 | 13.7 | 17.1 | 52.8 | 26.3 | 37.1 | 30.5 |
| 15 | Adam | 100 | 2.7 | 16.6 | 80.3 | 7.2 | 18.2 | 21.9 |
| 20 | Adam | 100 | 2.6 | 38.9 | 79.9 | 80.1 | 31.1 | 25.7 |
| 20 | Adam | 100 | 3.4 | 80.0 | 79.7 | 80.9 | 80.3 | 28.6 |
| 15 | RMSprop | 100 | 4.8 | 11.2 | 7.2 | 8.1 | 9.5 | 18.1 |
| 20 | RMSprop | 100 | 7.1 | 66.0 | 46.0 | 28.6 | 30.9 | 24.0 |
| 20 | RMSprop | 100 | 5.6 | 29.5 | 26.9 | 18.5 | 29.3 | 22.9 |
| Max | 71.9 | 80.3 | 80.3 | 82.3 | 80.3 | 94.1 | ||
| Mean | 10.4 | 30.7 | 39.4 | 33.7 | 35.6 | 30.7 | ||
| Min | 2.6 | 8.9 | 7.2 | 7.1 | 7.7 | 17.5 | ||
| Method | Figures | ||||||
|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | Average | |
| Co-occurrence [5] | 9.9 | 27.0 | 26.1 | 51.1 | 35.7 | 49.6 | 33.23 |
| Best in Randen [55] | 7.2 | 18.9 | 20.6 | 16.8 | 17.2 | 34.7 | 19.23 |
| [52] | 7.4 | 12.8 | 15.9 | 18.4 | 16.6 | 27.7 | 16.46 |
| LBP [52] | 6.0 | 18.0 | 12.1 | 9.7 | 11.4 | 17.0 | 12.36 |
| Watershed [51] | 7.1 | 10.7 | 12.4 | 11.6 | 14.9 | 20.0 | 12.78 |
| MSBF [8] | 2.8 | 14.8 | 8.4 | 7.3 | 4.3 | 17.9 | 9.25 |
| U-Net [46] | 2.6 | 8.9 | 7.2 | 7.1 | 7.7 | 17.5 | 8.50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabağ, C.; Verhoeven, J.; Miller, N.R.; Reyes-Aldasoro, C.C. Texture Segmentation: An Objective Comparison between Five Traditional Algorithms and a Deep-Learning U-Net Architecture. Appl. Sci. 2019, 9, 3900. https://doi.org/10.3390/app9183900
Karabağ C, Verhoeven J, Miller NR, Reyes-Aldasoro CC. Texture Segmentation: An Objective Comparison between Five Traditional Algorithms and a Deep-Learning U-Net Architecture. Applied Sciences. 2019; 9(18):3900. https://doi.org/10.3390/app9183900
Chicago/Turabian StyleKarabağ, Cefa, Jo Verhoeven, Naomi Rachel Miller, and Constantino Carlos Reyes-Aldasoro. 2019. "Texture Segmentation: An Objective Comparison between Five Traditional Algorithms and a Deep-Learning U-Net Architecture" Applied Sciences 9, no. 18: 3900. https://doi.org/10.3390/app9183900
APA StyleKarabağ, C., Verhoeven, J., Miller, N. R., & Reyes-Aldasoro, C. C. (2019). Texture Segmentation: An Objective Comparison between Five Traditional Algorithms and a Deep-Learning U-Net Architecture. Applied Sciences, 9(18), 3900. https://doi.org/10.3390/app9183900






