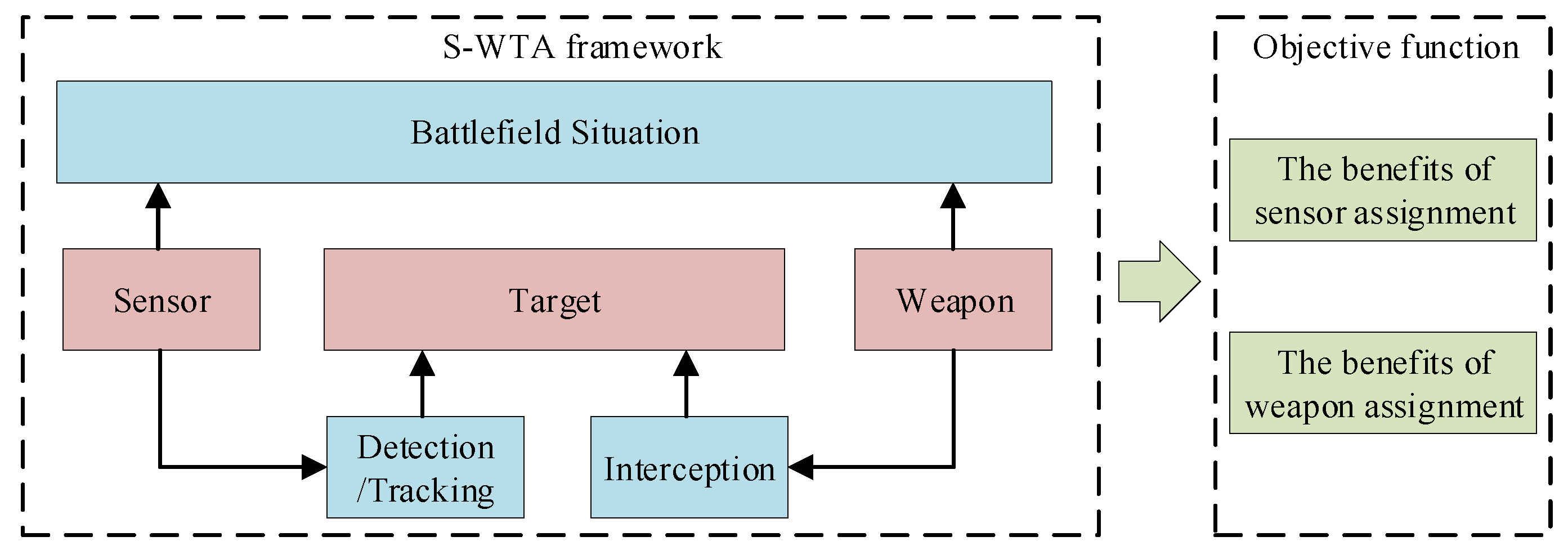
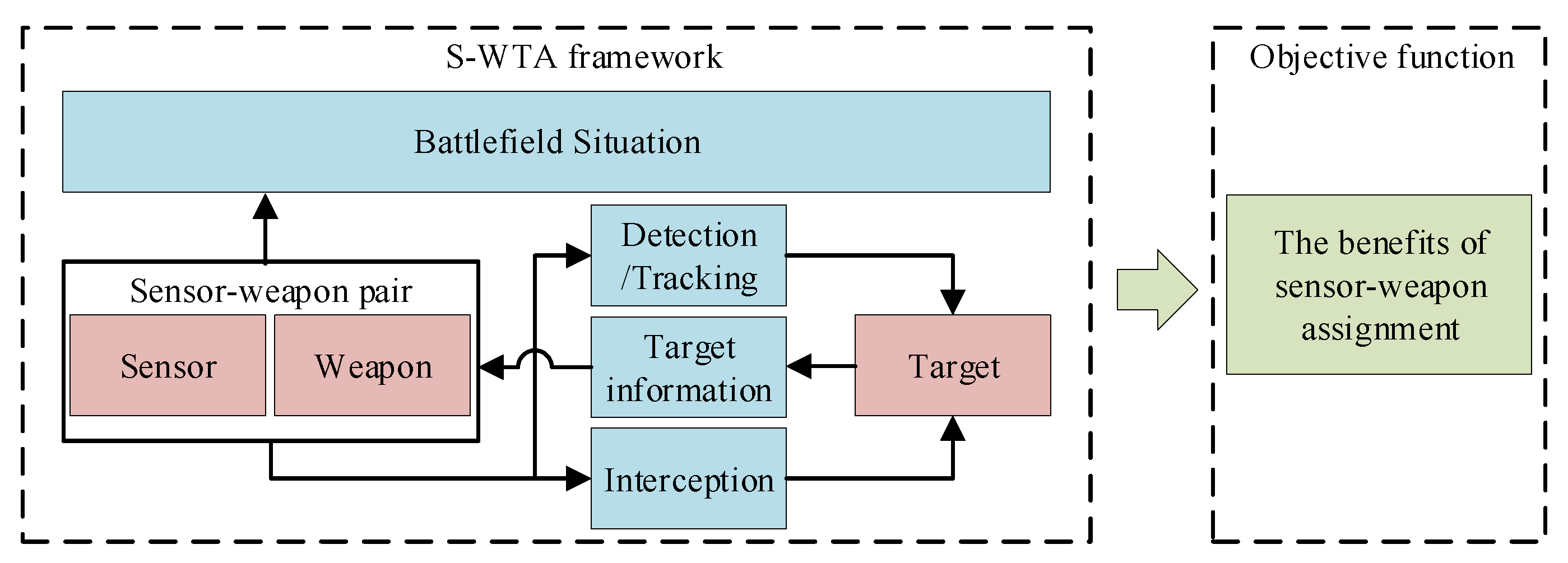
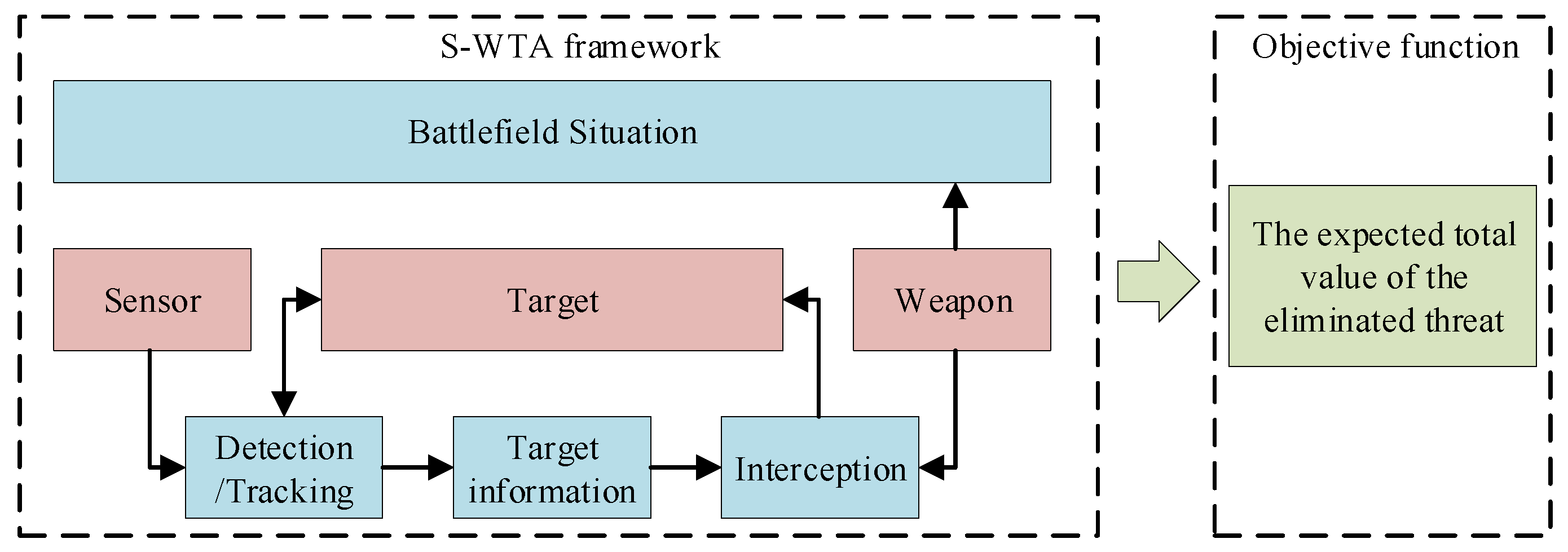
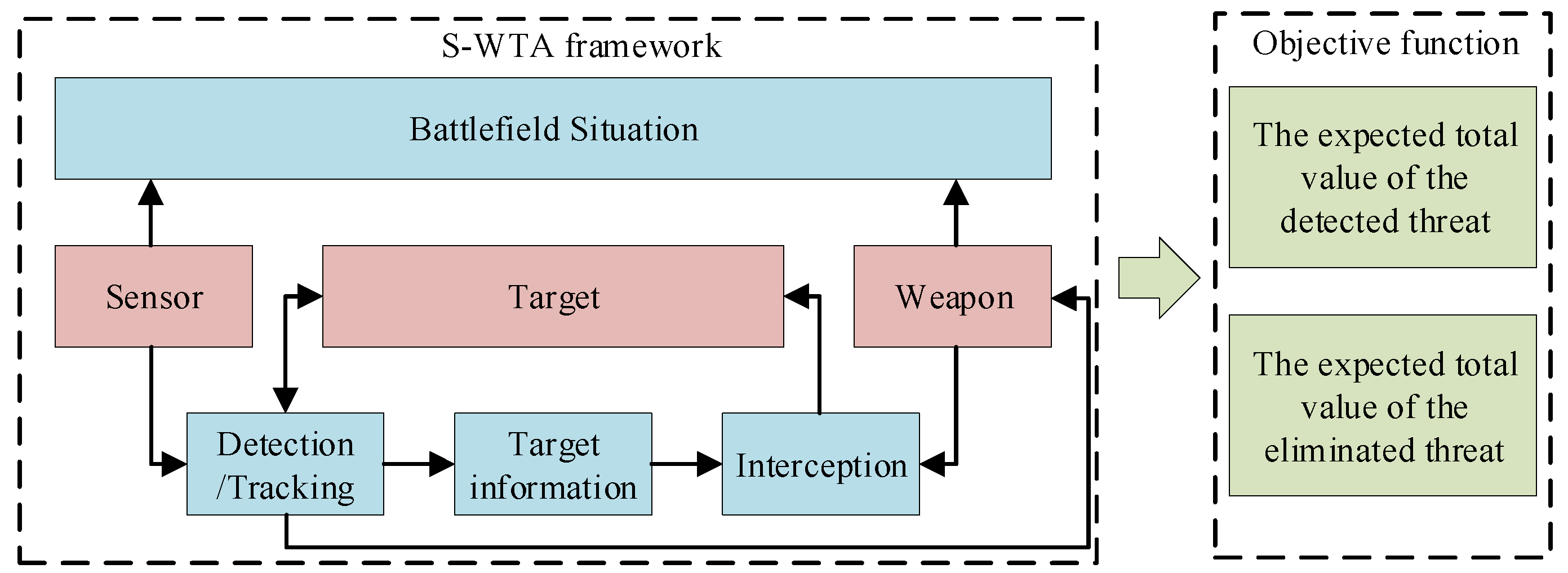
1. Introduction
The sensor-weapon–target assignment (S-WTA) problem, as one of the most important issues in C4ISR [
1,
2], has attracted great attention in recent years. Its objective is to find an appropriate assignment scheme for sensors and weapons to enemy targets with the goal of maximizing the benefit of the scheme. This problem is a constrained combinatorial optimization problem, which can be regarded as a nondeterministic polynomial time complete (NP-complete) problem [
3]. For certain cases, S-WTA can be considered as a composite of two independent parts, i.e., the sensor–target assignment (STA) [
4,
5,
6,
7,
8] and the weapon–target assignment (WTA) [
9,
10,
11,
12,
13,
14,
15,
16]. As the sensor is mainly used to obtain the information of the battlefield situation, the STA is performed in the mission of reconnaissance and surveillance to make decisions for the sensor management. As the weapon is used to protect the assets and obtain the superiority in the engagement, the WTA is implemented in the mission of attack to intercept and destroy the target. At present, as network-centric warfare (NCW) [
17] and knowledge-centric warfare (KCW) [
18] are the key operational architectures of the military operations, autonomy and cooperation are becoming more and more important. As a result, in this paper, we focus on the S-WTA problem, in which the sensors and weapons are allocated cooperatively. To be specific, the sensor can transmit the target information to the weapon in real-time and guide the weapon to attack the target accurately.
In the last few decades, some scholars have paid attention to the S-WTA problem. The S-WTA model was established by Bogdanowicz and Coleman [
19] for the first time. They deeply analyzed the characteristics of the S-WTA problem and proposed two types of S-WTA models: the independent S-WTA model and the dependent S-WTA model. Meanwhile, a heuristic algorithm based on auction algorithm was put forward in their paper to solve these S-WTA models. Afterwards, based on the proposed S-WTA model, Bogdanowicz further improved the auction algorithms named as Swt-opt [
20], which has been proved that Swt-opt can generate complete optimal assignment. In order to improve the efficiency of the allocation schemes over many dynamic network topologies, Li et al. [
21] proposed an improved Swt-opt, combining the consensus algorithm with Swt-opt. Li et al. [
22] introduced the temporal and spatial constraints into the S-WTA problem to establish an improved dependent model. They considered this specific S-WTA problem as a kind of dynamic weapon–target assignment (DWTA) [
23] problem and proposed an anytime algorithm based on decentralized cooperative auction to solve this problem. Chen et al. [
24] proposed an improved particle swarm optimization (PSO) to solve a similar dependent S-WTA problem. In this algorithm, some novel genetic operators were adopted to enhance the performance of the algorithm. Ezra et al. [
25,
26] analyzed the integrated relationship between sensor, weapon, and target. They proposed four integrated formulations combining the sensor resource management and weapon–target assignment to further demonstrate the characteristics of the independent and dependent S-WTA problem. Wang et al. [
27] proposed an improved genetic algorithm (GA) to solve the dependent S-WTA problem, considering the situation where the kill probability of the weapons was modified to a formula with regard to the detection precision of sensors. Taking into account the synergic relationship between weapons and sensors as well as some specific constraints, Xin et al. [
28] established a novel dependent S-WTA model. Moreover, they proposed a marginal-return-based constructive heuristic (MRBCH) to solve the formulated S-WTA model, so as to generate the allocation scheme rapidly and accurately. The work has been discussed thus far only focus on one aspect of the S-WTA problem. Consequently, some details of the collaborative operations of the sensors and weapons, which involve the cooperative engagement mode and the capacity constraints, are neglected. Therefore, in this paper, we focus on designing a comprehensive S-WTA model to demonstrate a more realistic S-WTA scenario.
In order to improve the solution of the S-WTA model, the optimization algorithm is also studied in this paper. The algorithms used to solve the S-WTA problem can be divided into two categories: The first category is the heuristic algorithm, such as Swt-opt and MRBCH. Heuristic algorithms can solve the S-WTA in real-time. It can be used in a dynamic environment and handle the uncertainties over the engagement. Although heuristic algorithms can solve the S-WTA problem in real-time, they are very difficult to achieve a satisfactory solution in such a NP-hard problem. This is because heuristic algorithms search for solutions using specific heuristic information, which traps them into the local optimal easily. The second category is the evolutionary algorithm (EA) [
29,
30], such as GA and PSO. As EA-based algorithms use many flexible mechanisms that fully consider the prior knowledge, they can achieve a satisfactory solution. However, the running time of EA-based algorithms are relatively large; they cannot solve the S-WTA problems in real-time. In this paper, as we focus on obtaining a high-quality assignment scheme, the running time of the algorithm is not considered. Since EA has many significant advantages in finding the optimal solution, we believe that choosing EA to solve the S-WTA problem can achieve a satisfactory assignment scheme.
EA has attracted massive interest from researchers for decades. At present, the well-known evolutionary algorithms are GA [
31], PSO [
32], ant colony algorithm (ACO) [
33], and differential evolution (DE) [
34]. Among these algorithms, GA is one of the most important algorithms. Because GA has a simple framework, high flexibility, and strong convergence ability, it has been successfully applied in many real-world problems [
35,
36,
37], especially in the WTA problem [
13,
23,
38]. For these reasons, we believe that choosing GA to solve the S-WTA problem is reasonable and promising. In this paper, we proposed a novel GA to solve the S-WTA problem named GA-SWTA. The contributions of this paper are described as follows.
- (1)
In the context that sensors and weapons are allocated cooperatively, a novel S-WTA model is presented. The traditional S-WTA model has only two frameworks: the dependent framework and the independent framework. In order to fully reflect the relationship between sensors and weapons, the S-WTA has been extended to the synthetical framework.
- (2)
For the proposed S-WTA model, a novel GA framework is proposed. Based on the characteristic of S-WTA, we redefine the form of chromosome encoding. We also adaptively improved the crossover operator to better match the redefined encoding. In addition, a problem-specific chromosome initialization method is proposed.
- (3)
In order to handle the constrains and improve the convergence ability of the algorithm, chromosome repair approaches are proposed. Based on the prior knowledge of S-WTA, two repair operations— R-STA operation and R-WTA operation—are designed to cooperatively repair the chromosome. The experiments validate the good performance of the proposed approaches.
The rest of this paper is organized as follows. In
Section 2, the frameworks of the S-WTA problem are analyzed first, then we present a mathematical optimization model for the synthetical S-WTA problem. In
Section 3, a novel GA, i.e., GA-SWTA, is proposed to solve the S-WTA problem. Meanwhile, a problem-specific initialization and a chromosome-repair mechanism are designed to improve the performance of the algorithm. In
Section 4, GA-SWTA is compared with three state-of-the-art S-WTA approaches, then the performance of the proposed initialization and a chromosome-repair mechanism are investigated. The conclusion and future work are described in
Section 5.
3. Description of the Proposed Method
In this section, the proposed novel GA method for solving S-WTA problem (GA-SWTA) is described. At the beginning, chromosome encoding is introduced. Then, the proposed population initialization method is presented. Afterwards, the evolutionary operations are demonstrated, and then the chromosome-repair mechanism is given. At last, the framework of GA-SWTA is elaborated.
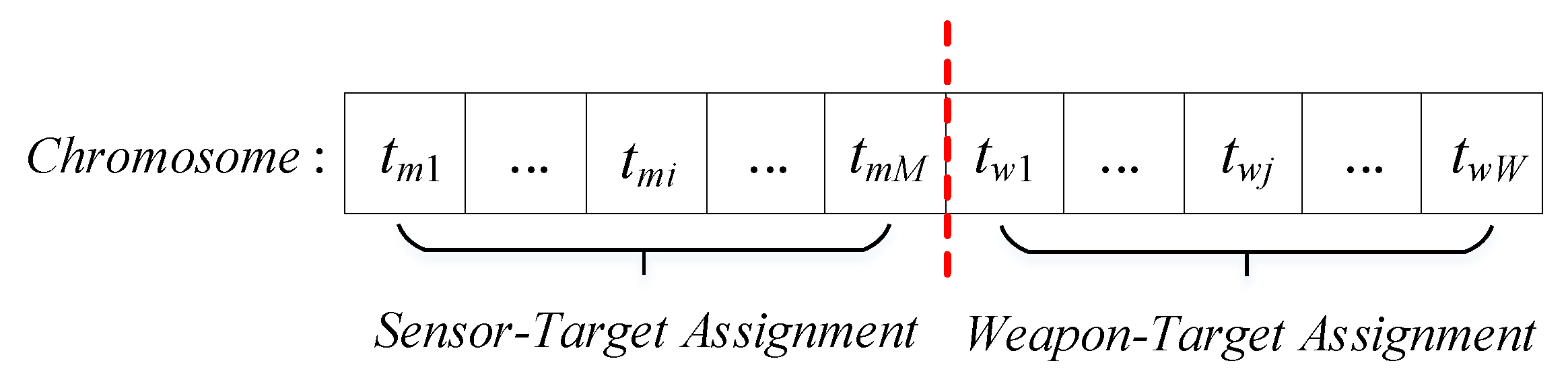
3.1. Chromosome Encoding
As the S-WTA problem has many similar characteristics to the WTA problem, the traditional encoding method of WTA [
13] can be used as a reference. Based on the WTA model, Wang [
27] proposed a chromosome encoding method for S-WTA. However, because the S-WTA model used in their paper is more difficult than the one we proposed, chromosome encoding needs to be further customized for better adaptation of the proposed S-WTA model. The chromosome encoding is defined as
, where
is the target that is detected or tracked by sensor
i and
is the target which is attacked by weapon
j.
Figure 5 is the illustration of the chromosome encoding.
As depicted in
Figure 5, the chromosome comprises two parts: The first part represents the assignment of sensors. The second part is the assignment of weapons. Based on the definition of chromosome encoding, the code can handle some basic constraints of the S-WTA. First, the dimension of the chromosome is
, which is the sum of the number of sensors and weapons. Therefore, the consumption of sensors and weapons can be ensured within the predefined amount.
3.2. Population Initialization
A population initialization method is an important part in the framework of GA. A common way to initialize the population for this problem is random initialization, which may generate initial solutions with an inferior fitness and redundancy. In addition, S-WTA has much prior knowledge, such as the benefits of detection or damage, which should be fully considered to improve the quality of the initial population to speed up algorithm to reach global optimum.
In this paper, some important prior knowledge, which was originally designed for the WTA problem [
13], is adaptively improved as the rules of initialization of the S-WTA problem. It is defined as in Rule 1 and Rule 2. Rule 1 is used for the sensor–target assignment. Rule 2 is used for the weapon–target assignment.
Rule 1: If is the highest value among all the sensor–target pair, the assignment scheme that the ith sensor is assigned to the kth target is the most appropriate scheme.
Rule 2: If is the highest value among all the weapon–target pair, the assignment scheme that the ith weapon is assigned to the kth target is the most appropriate scheme.
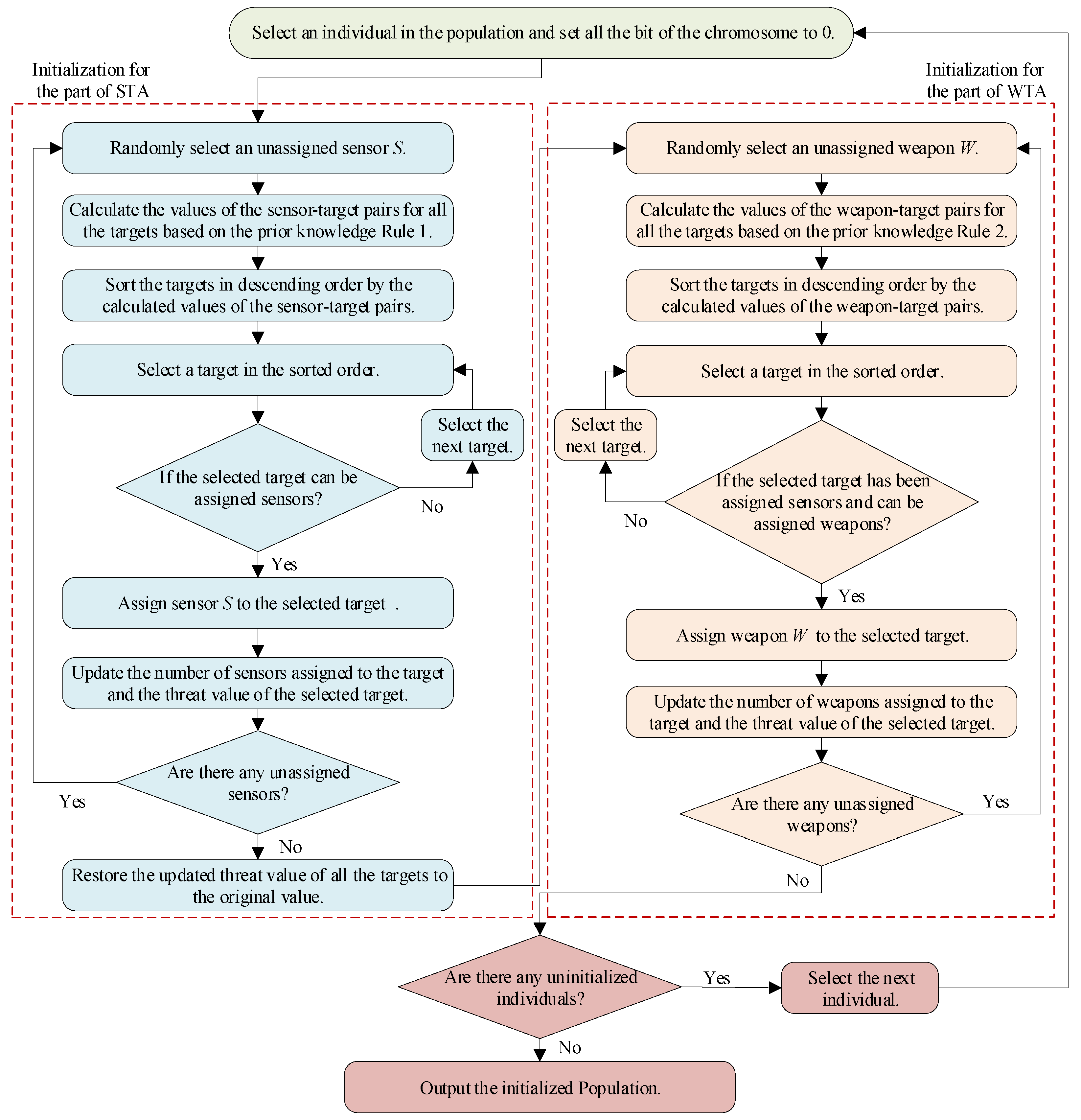
The flow chart of the proposed initialization method is shown in
Figure 6.
As shown in
Figure 6, the population is initialized by two procedures. First, the sensor is assigned to the target according to the Rule 1. Then, on the basis of the results of sensor assignment, the weapon is assigned according to the Rule 2. To facilitate further implementation of the algorithm, the pseudocode of the proposed method is given in Algorithm 1.
| Algorithm 1 Initialization |
Input: The number of sensors is M. The number of weapons is W. The number of targets is N. The matrix of the probability of detecting and tracking the targets by the sensors is . The matrix of the probability of destroying the targets by the weapons is . The maximum sensor cost of each target is . The maximum weapon cost of each target is . The threat value of each target is .
Output: The initialized population .- 1:
for to do - 2:
- 3:
for to M do - 4:
Randomly select an unassigned sensor . - 5:
for each target t do - 6:
- 7:
end for - 8:
Sort the targets in descending order by as . - 9:
Initial the sensor cost for as . - 10:
for to N do - 11:
if then - 12:
- 13:
- 14:
- 15:
break - 16:
end if - 17:
end for - 18:
end for - 19:
Restore the updated threat value to the original value. - 20:
for to W do - 21:
Randomly select an unassigned weapon . - 22:
for each target t do - 23:
- 24:
end for - 25:
Sort the targets in descending order by as . - 26:
Initial the weapon cost for as . - 27:
for to N do - 28:
if and then - 29:
- 30:
- 31:
- 32:
break - 33:
end if - 34:
end for - 35:
end for - 36:
end for
|
In Algorithm 1, the procedure of sensor–target assignment is from Step 3 to Step 18. In this procedure, Step 6 is to calculate the values of the sensor–target pairs. Based on Rule 1, Step 8 determines the optimal sensor–target pair. Afterwards, Step 11 ensures that the current assignment can meet the third constraint in model (
6). The weapon–target assignment is from Step 20 to Step 35. This procedure is similar to the sensor–target assignment. In this procedure, Step 25 is to determine the optimal weapon–target pair by the Rule 2. Step 28 ensures that the current weapon–target assignment can meet the last constraint in model (
6), and the target is detected and tracked by at least one sensor.
3.3. Evolutionary Operations
Evolutionary operation is an important mechanism in evolutionary algorithm. Therefore, we use crossover operation and mutation operation to find out better individuals. As the chromosome encoding of S-WTA problem is similar to the WTA problem, the evolutionary operations used in the WTA problem can be also suitable for the S-WTA problem. In this paper, we use the EX operator [
13] as the crossover operation. Meanwhile, we use the mutation operation to randomly change a gene. All of the above are commonly used evolutionary operations in WTA problems. However, as the chromosome encoding of S-WTA is different from WTA, the EX operator should be adaptively improved so it can be appropriately used in S-WTA. The improved EX operator is described as follows.
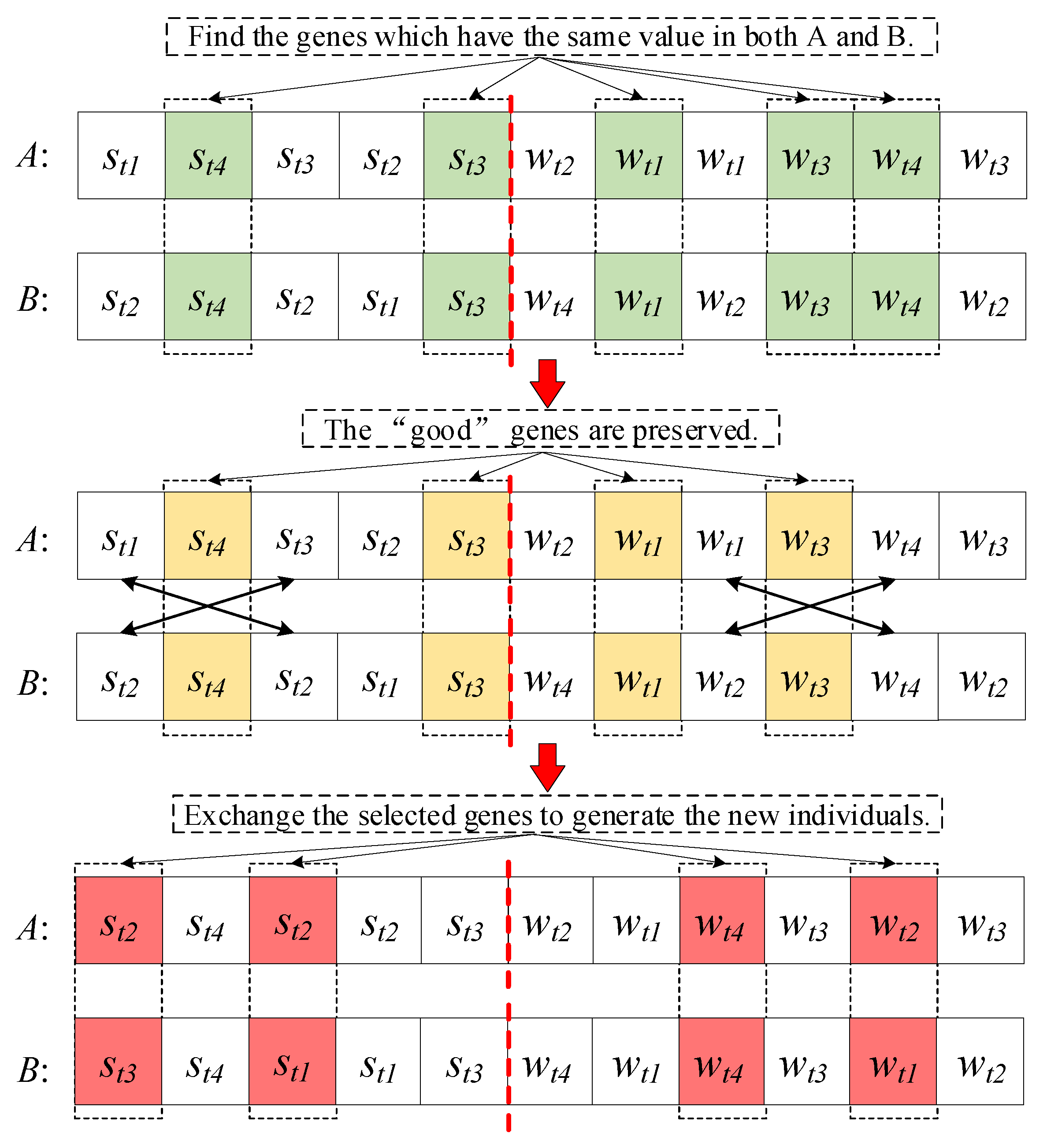
In the traditional EX operator, the so-called “good” genes contained in both parents are preserved. Therefore, for the S-WTA problem, the “good” genes represent the most appropriate assignment scheme from Rules 1 and 2. In addition, since the chromosome encoding of S-WTA is composed by two parts, the EX operator should be performed in the two parts, respectively. It is illustrated in
Figure 7.
As shown in
Figure 7, suppose that there are 4 targets, 5 sensors, and 6 weapons. We generate two individuals, A and B. First, genes 2, 5, 7, 9, and 10, which have the same value in both A and B, are selected to be evaluated. Assuming that the genes of 2, 5, 7, and 9 are the “good” genes. Then, these “good” genes are preserved, which means that they do not change during the crossover operation. Afterwards, two genes are randomly selected in the STA part and exchanged to generate the new individual. Similarly, the other two genes are randomly selected in the WTA part and exchanged.
3.4. Repair Operations
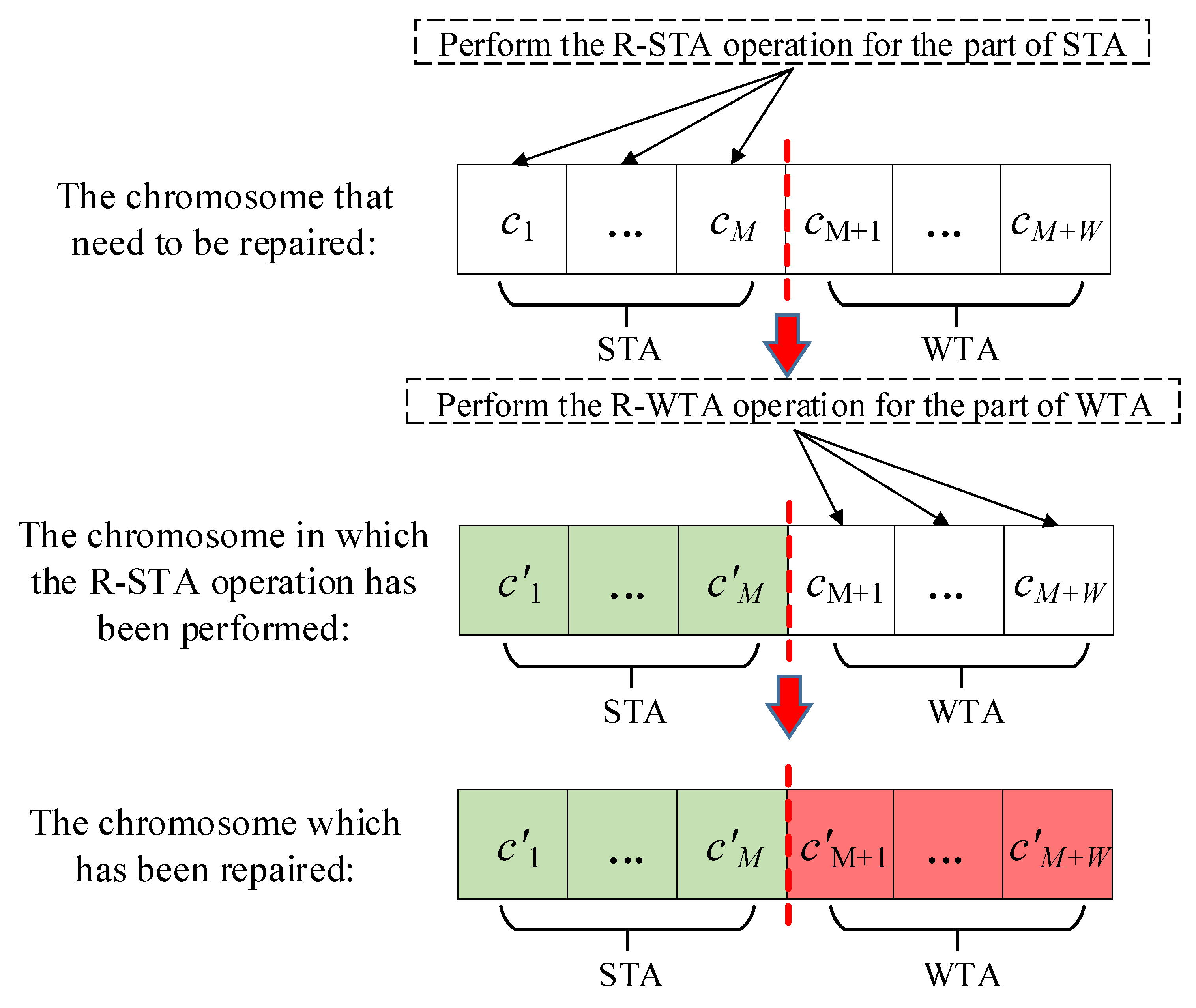
As the evolutionary operation mentioned above is unable to handle the constraints, some individuals may not satisfy the constraints of the S-WTA problem. Therefore, the repair operations should be adopted to repair the unsatisfactory individuals. In this paper, we propose two novel repair operations. The first repair operation is designed for the part of STA (R-STA operation). The second operation is designed for the part of WTA (R-WTA operation). The R-STA operation is performed first to repair the chromosome. Then, the R-WTA operation is performed. This process is illustrated in
Figure 8.
3.4.1. R-STA Operation
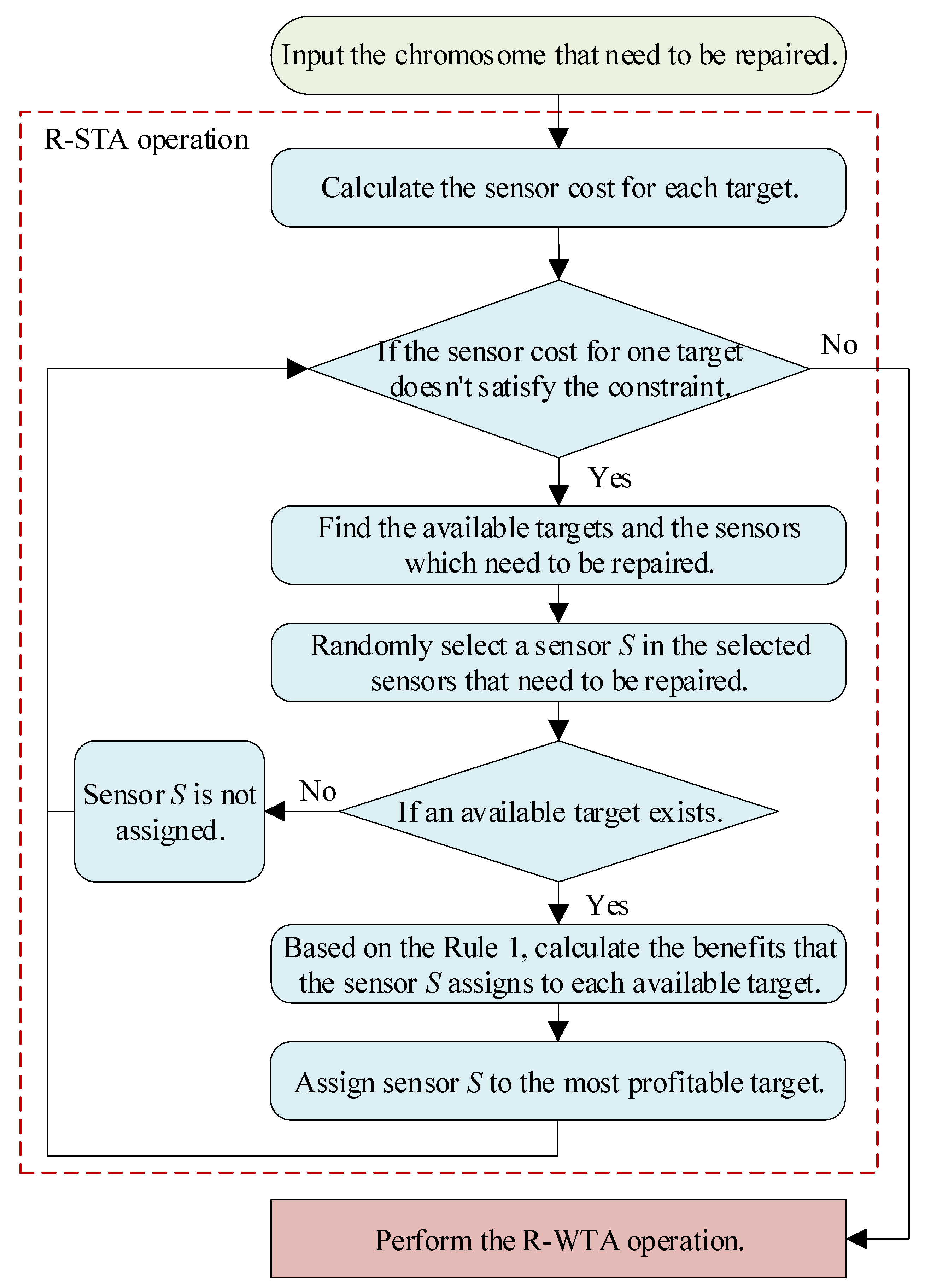
In the S-WTA problem, the target should be detected and tracked by sensors before it is attacked by weapons. Therefore, the R-STA operation is performed first to ensure that the sensors are appropriately assigned. The flow chart of the proposed R-STA operation is shown in
Figure 9.
To illustrate the details of the operation, the pseudocode is given in Algorithm 2. In this algorithm, step 2 ensures that all the improper assignment scheme can be repaired. In step 3, the available target means that the sensor cost of this target is no more than the maximum sensor cost. In step 4, the sensors assigned to the unavailable targets are selected to be repaired. Step 6 ensures that the STA scheme does not suffer overallocation. Therefore, if there are no available targets, the selected sensors are no longer assigned. In step 12, is the benefit of the assignment scheme of sensor and target . From step 7 to step 13, the benefits of all the assignment scheme for each available target and sensor are calculated based on Rule 1. Then the optimal sensor–target pair is determined according to the benefit of the assignment scheme by steps 14 and 15. Based on the procedures of R-STA operation, we can see that the prior knowledge Rule 1 is used to determine the sensor–target pair. In this way, the efficiency of the repair operation will be greatly improved.
| Algorithm 2 R-STA operation |
Input: The chromosome that need to be repaired is . The matrix of the probability of detecting and tracking the targets by the sensors is . The maximum sensor cost for target are . The threat value of each target is .
Output: The repaired chromosome .- 1:
Calculate the sensor cost for target as . - 2:
while () do - 3:
Find the available targets as . - 4:
Find the sensors which need to be repaired as . - 5:
Randomly select a sensor in as . - 6:
if then - 7:
for each in do - 8:
for each sensor s which is assigned to do - 9:
- 10:
end for - 11:
- 12:
- 13:
end for - 14:
Find the target in for which the corresponding is the largest. - 15:
- 16:
else - 17:
- 18:
end if - 19:
end
|
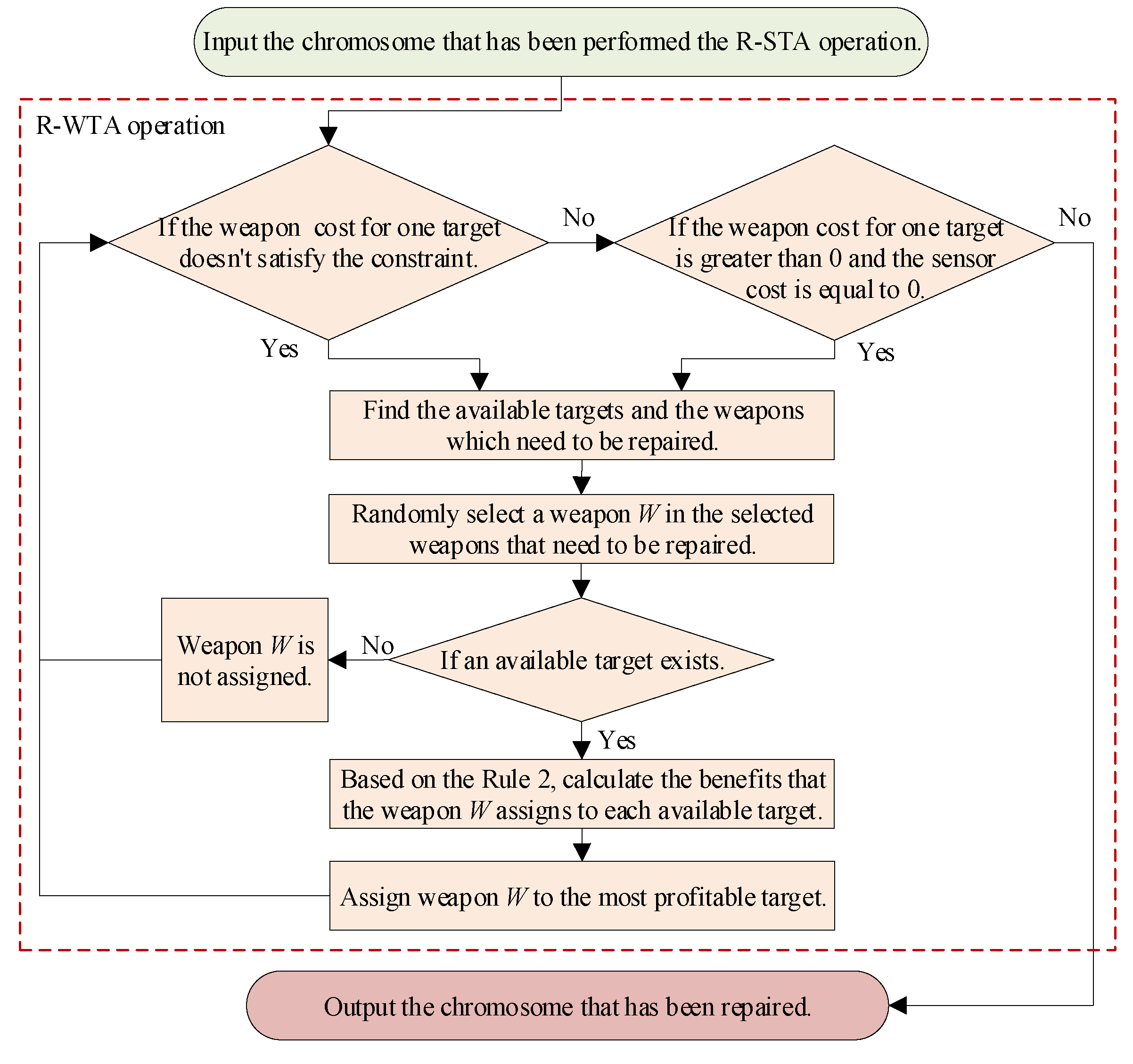
3.4.2. R-WTA Operation
In the S-WTA problem, if the targets are detected and tracked by sensors, the weapons can be launched to attack the target. Therefore, after the R-STA operation has been performed, the R-WTA operation should be implemented to ensure that the weapons are appropriately assigned. The flow chart of the proposed R-WTA operation is shown in
Figure 10.
In order to further illustrate the implementation process of the algorithm, the pseudocode of R-WTA operation is given in Algorithm 3. In this algorithm, most of the procedures are similar to the R-STA operation. However, as the sensors are assigned first, the effect of STA should be fully considered in R-WTA operation. According to the actual situation of S-WTA problem, only the target that has been detected and tracked by sensors can be attacked by weapons. Therefore, in the R-WTA operation, the weapons must be assigned to a target with sensor cost greater than zero. In step 3, in addition to determining whether the current WTA scheme satisfies the last constraint in model (
6), it is also necessary to determine whether the target of the assigned weapons has been allocated any sensors. In step 4, the available target means that the weapon cost of this target is no more than the maximum weapon cost and this target has been assigned any sensors. Similarly, in step 5, the weapons assigned to the unavailable targets are selected to be repaired. Step 7 to step 19 have a similar structure to step 6 to step 18 in R-STA operation. With these steps, the optimal weapon–target pair is determined. It should be noted that in the R-WTA operation, the prior knowledge in Rule 2 is used to enhance the efficiency of the repair operation.
| Algorithm 3 R-WTA operation |
Input: The chromosome in which the R-STA operation has been performed is . The matrix of the probability of destroying the targets by the weapons is . The maximum weapon cost for target are . The threat value of each target is .
Output: The repaired chromosome .- 1:
Calculate the weapon cost for target as . - 2:
Calculate the sensor cost for target as . - 3:
while () or ( and ) do - 4:
Find the available targets as . - 5:
Find the weapons which need to be repaired as . - 6:
Randomly select a sensor in as . - 7:
if then - 8:
for each in do - 9:
for each weapon w which is assigned to do - 10:
- 11:
end for - 12:
- 13:
- 14:
end for - 15:
Find the target in for which the corresponding is the largest. - 16:
- 17:
else - 18:
- 19:
end if - 20:
end
|
3.5. The Framework of GA-SWTA
In this paper, a novel genetic algorithm for the S-WTA problem (GA-SWTA) is proposed. This algorithm begins with a proposed problem-specific initialization method to generate the population. Then, it proceeds to the loop phase. Initially, the selection is performed to generate a new generation by some specific selection method, such as the roulette wheel selection and the tournament selection. Afterwards, the crossover and mutation operators are implemented to generate new individuals. Thereafter, in order to handle the constrains of the S-WTA problem, the proposed R-STA operation and R-WTA operation are performed to repair the individuals. At the end of the loop, the potential individuals are selected for the next evolution. The loop will continue until the iterations reaches the maximum number. The framework of GA-SWTA is shown in Algorithm 4.
| Algorithm 4 GA-SWTA |
Input: Max generation: . Population size: . Crossover probability: . Mutation probability: . Other necessary scenario information of S-WTA problem.
Output: The best individual .Step 1 Initialization: Generate an initial population by the proposed initialization method. Meanwhile, . Step 2 Selection: A proportion of population X are selected as a new generation by some specific selection method. Step 3 Reproduction: For do 3.1 Crossover: Generate a random number , if , randomly select an individual in , then perform the crossover operator on and to generate two new individuals as and . 3.2 Mutation: Generate a random number , if , randomly select an individual in , then perform the mutation operator on it to generate a new individual . Step 4 Repair: Perform the proposed R-STA operation and R-WTA operation for the reproduced population . Step 5: Let . Calculate the fitness for all the individuals in , then select the best individuals as the new generation X. Step 6:, then go to Step 2. If reaches , output the best individual .
|
4. Experimental Studies
4.1. Comparison Algorithms
In this paper, two heuristic algorithms, named MRBCH and Swt-opt, and one GA-based algorithm, referred to as ds-GA, are selected to compare with the proposed algorithm.
The MRBCH algorithm proposed in the work by the authors of [
28] is a real-time heuristic algorithm. It uses the concept of maximum marginal return (MMR), which is derived from economics, to handle the S-WTA problem. We choose it as our comparison algorithm because, as, to the best of our knowledge, it has the best performance among all the real-time heuristic algorithms in handling the S-WTA problem. We want to show that our proposed algorithm can achieve better optimization results.
The Swt-opt algorithm [
20] is another real-time heuristic algorithm based on the auction algorithm. In this algorithm, each sensor–weapon pair can be assigned to at most one target, and each target can be engaged by at most one sensor–weapon pair. We choose it as our comparison algorithm because it has many advantages in solving the S-WTA problem in which the number of sensors, weapons, and targets are the same. Our proposed algorithm cannot only get preferable optimization results in this special case, but also can achieve excellent optimization results in general S-WTA problem.
The ds-GA algorithm was proposed by Wang and Chen [
27], in which an improved genetic algorithm is used to solve the S-WTA problem. We choose it as our comparison algorithm because our proposed algorithm is also based on GA. We want to show that our proposed GA-based algorithm is more suitable to deal with the S-WTA problem.
4.2. Experimental Settings
The experiments are performed on a personal computer with i7-2.5GHz CPU and 8GB memory. All algorithms are written by Matlab. In our experiments, twenty-five S-WTA test instances are used for comparing GA-SWTA with MRBCH, Swt-opt and ds-GA. As these instances are carefully designed by Xin et al. [
28] and generated with different scales and features, they can comprehensively examine the performance of the proposed algorithm. These instances and their features are shown in
Table 3. Detailed data of these instances, such as the threat value of target, the constrains of sensors cost, and so on, are available online [
28].
In these experimental studies, all parameters of the MRBCH algorithm and Swt-opt algorithm are the same as the by the authors of [
28]. In addition, for our proposed algorithm, the population size is
, the selection method is the roulette wheel selection, the crossover probability is
, and the mutation probability is
. The crossover probability and the mutation probability are the recommended settings in the work by the authors of [
13].
For the ds-GA algorithm, the population size
, the crossover probability
, and the mutation probability
,
,
,
and
. All the parameters are the recommended settings in paper [
27]. Furthermore, in ds-GA, the penalty function is used for constraint handling. However, in this paper, as the proposed S-WTA model is different from the one in ds-GA, the penalty function should be redesigned to make it can be suitable for our proposed algorithm. We use the general constraint handling rules of the penalty function [
39], which are also used in ds-GA, to redesign the penalty function. In this way, as the redesigned function can maintain the same characteristics as the original function, the performance of the algorithm is not greatly affected. The penalty function of the
ith individual is shown as
where
is the fitness of the
ith individual,
is the penalized fitness, and
is the fitness set of the populations.
As the MRBCH and Swt-opt algorithms are deterministic, the result is an invariable for the same instance. Therefore, both are performed only once. In addition, because our proposed algorithm and the ds-GA algorithm are GA-based algorithms, each run of the algorithms produces a different result. Therefore, we perform 30 independent runs on both of the algorithms for each instance. Meanwhile, we stop both of the algorithms until the best solutions found so far remain unchanged in 500 generations.
4.3. Experiments on Comparison Algorithms
In these experiments, the performances of the comparison algorithms are analyzed. As the optimal S-WTA scheme is unknown for each instance, we use the fitness of individual as the comparative metric. Therefore, we propose that the greater the fitness of an individual, the better the corresponding S-WTA scheme.
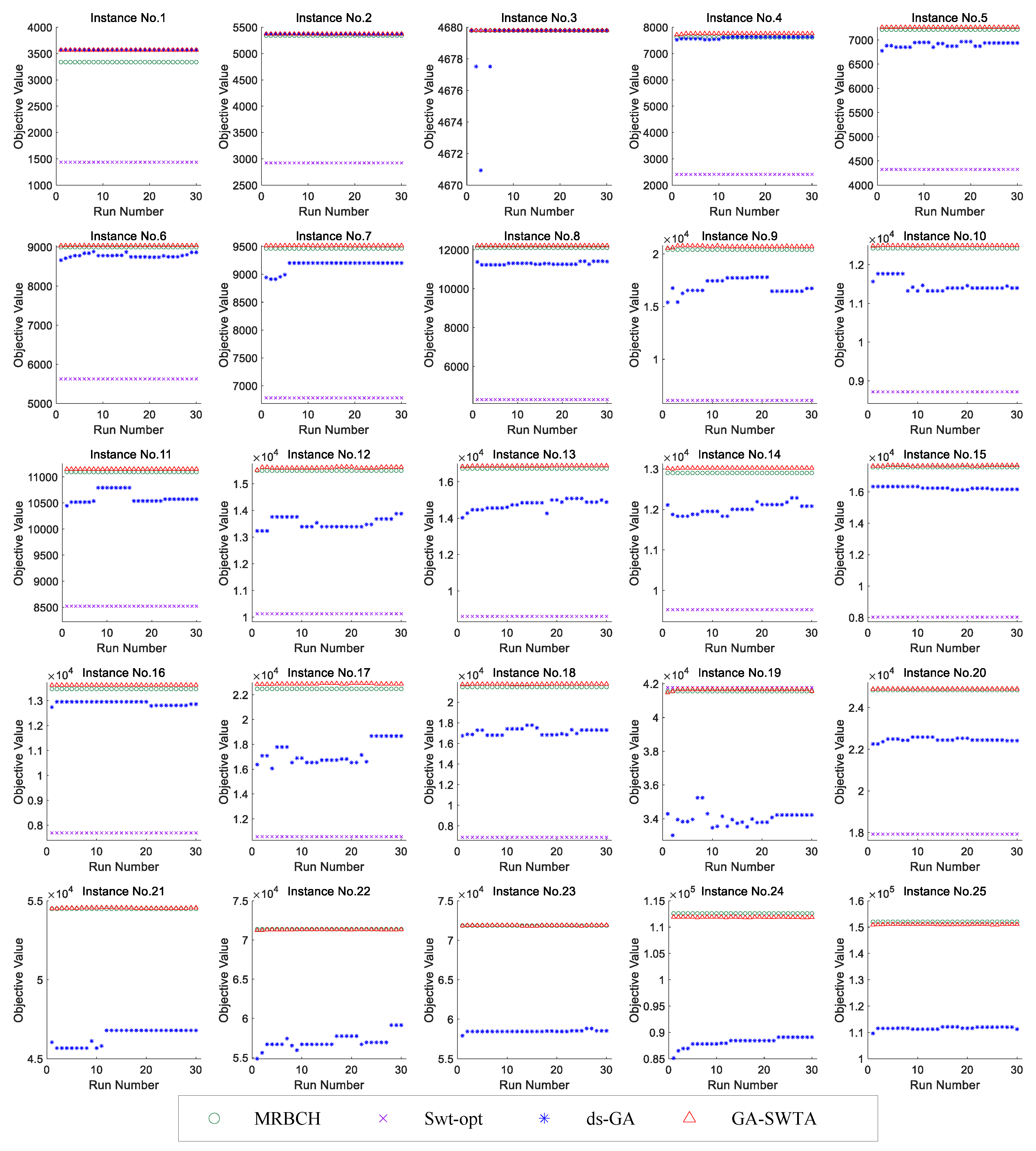
As the proposed GA-SWTA and ds-GA are performed for 30 independent runs for each instance, we demonstrate the results from 30 runs. Although the MRBCH and Swt-opt are deterministic algorithms, their results are also shown from 30 runs to facilitate the analysis. Furthermore, for instance 21 to instance 25, the results of Swt-opt are not available within the acceptable time (15,000 s). The experimental results are presented in
Figure 11.
As shown in
Figure 11, GA-SWTA performs better than other comparison algorithms in most instances. For the instance No. 1, ds-GA and GA-SWTA have the same performance. For the instance No. 3, all the algorithms can get their best result. For the instance No. 19, the performance of the Swt-opt outperforms other algorithms. For the instance No. 4 to the instance No. 25, GA-SWTA performs remarkably better than ds-GA. However, for the very large-scale instances, No. 24 and No. 25, MRBCH has the best performance.
Based on the experimental results presented above, it can be concluded that our proposed algorithm can effectively solve the S-WTA problem. Although the MRBCH and the Swt-opt outperforms GA-SWTA in a few cases, GA-SWTA can still provide high-quality solutions for all instances. In addition, if the scale of the problem is small, the MRBCH, ds-GA, and proposed GA-SWTA have the similar performance; as the solution space of the small-scale instances is small, these algorithms can easily search most areas of the solution space. Moreover, if the scale of the problem is very large, MRBCH can achieve better results in solving this problem. This is because the used evolutionary operators are originally designed for small-scale WTA problems that lose efficiency when solving the large-scale S-WTA problem. Additionally, the Swt-opt has the best performance for the instance No. 3 and No. 19. However, for most instances, its performance is worse than other algorithms. Because the Swt-opt is designed to solve the special instance described in the work by the authors of [
19], if more than one sensor or weapon can be assigned to one target, the objective cannot be calculated appropriately. Furthermore, the performance of ds-GA is worse than GA-SWTA for the vast majority of instances, which means that our proposed novel framework of GA is more suitable to solve the S-WTA problem.
4.4. Experiments on Initialization
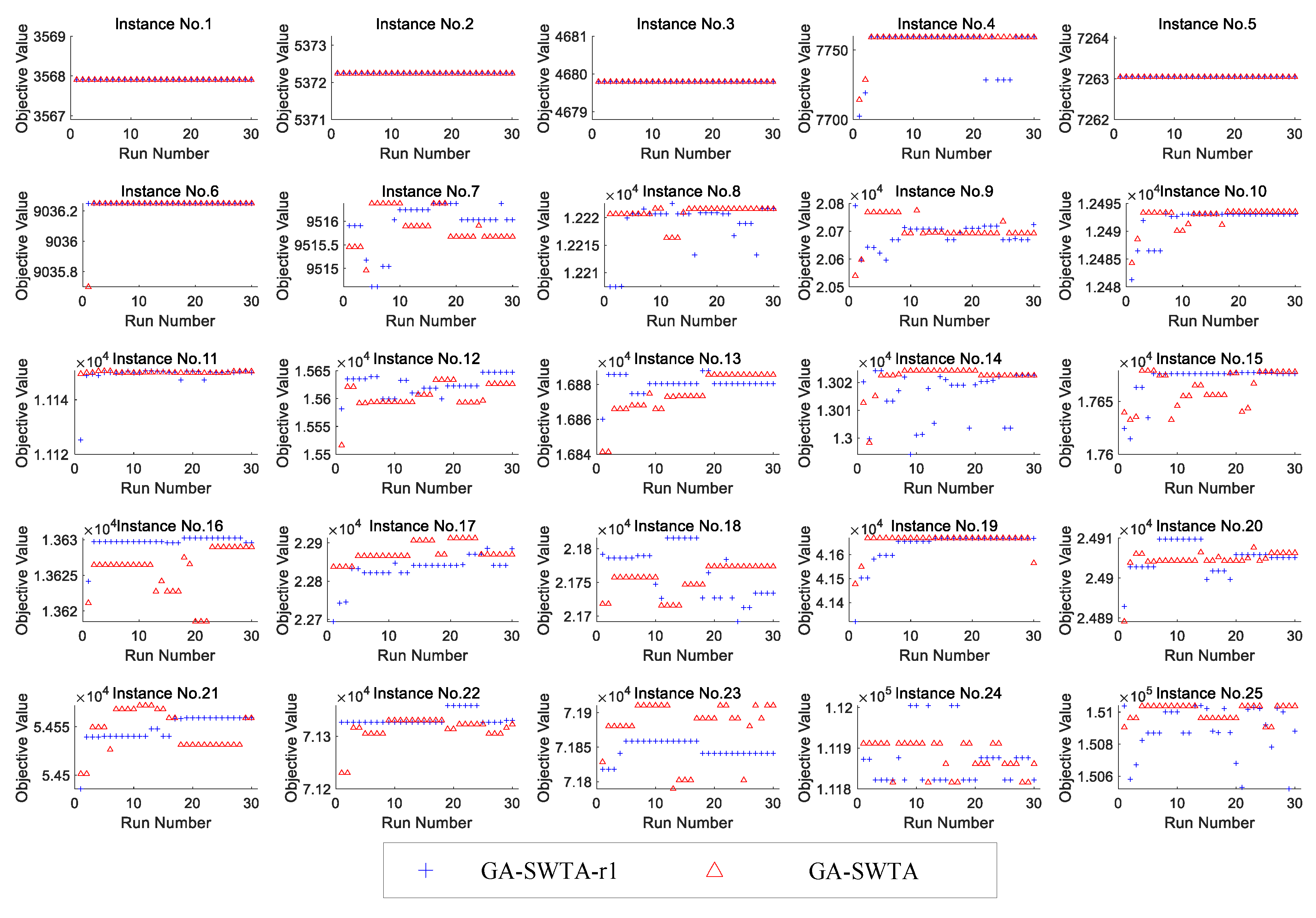
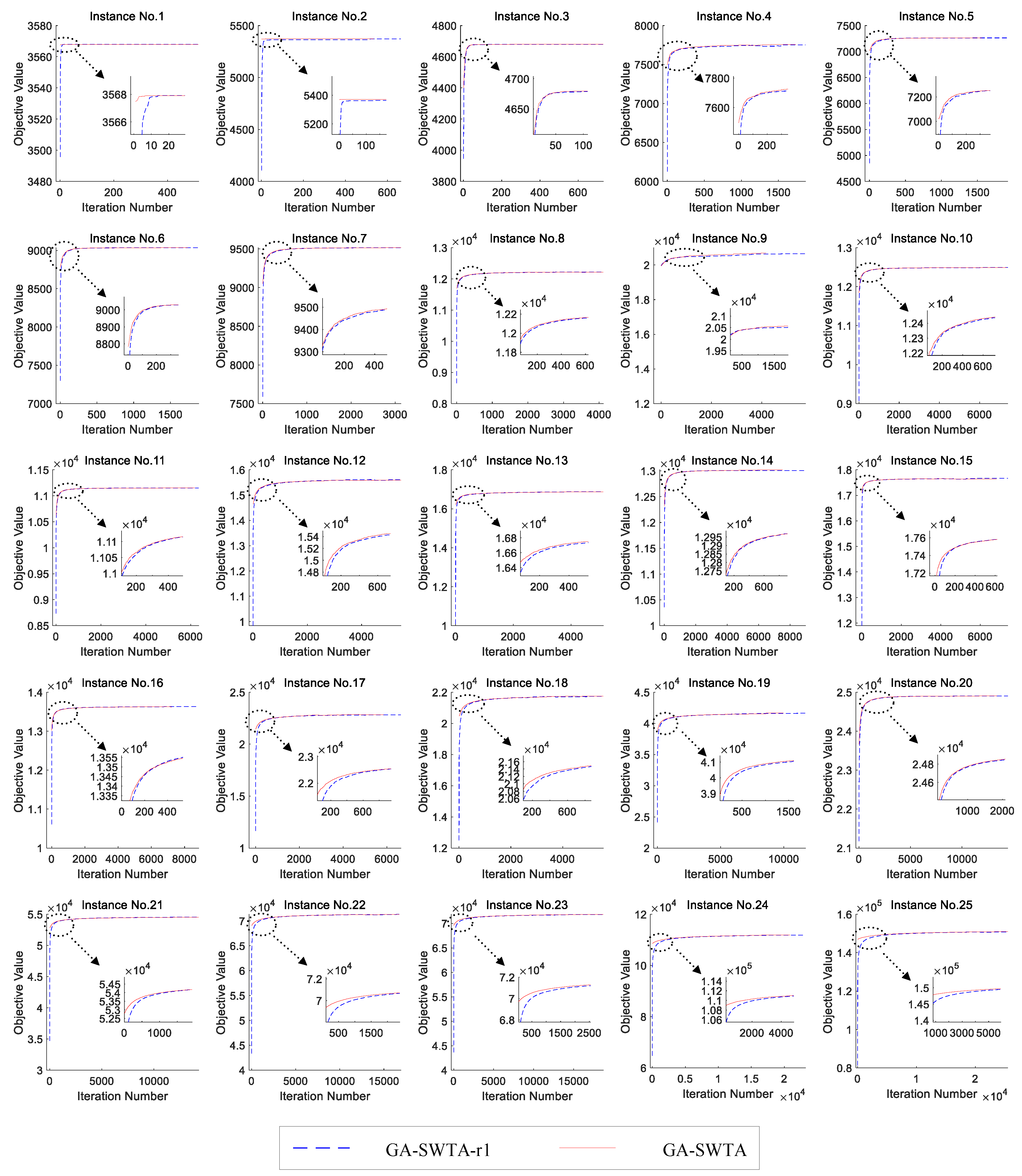
In order to verify the performance of the proposed initialization method, the random initialization method is used for comparison. Using the random initialization method means that the encoding of an individual is generated randomly without any prior knowledge. Since many of the evolutionary mechanisms used in ds-GA differ from the proposed algorithm, it is difficult to rule out the influence of different evolutionary mechanisms on algorithm performance. As a result, in order to ensure the fairness of the comparison, the proposed initialization method in GA-SWTA is replaced by the random initialization method. Meanwhile, the other mechanisms and parameters remain unchanged. The variant is called GA-SWTA-r1. We performed 30 independent runs on each algorithm for each instance.
Figure 12 shows the results of the two algorithms.
From
Figure 12, it can be found that the difference in the performance of the given indexes between GA-SWTA and GA-SWTA-r1 are very small. It means that the proposed initialization method does not affect the convergence of the algorithm. This is because the convergence of the proposed algorithm is mainly affected by the evolutionary operators. As the initialization method is designed to improve the quality of the initial population, its main function is to improve the efficiency of the convergence. In this paper, the evolution of the mean value of the objective value versus number of iterations is used to demonstrate the efficiency of the proposed initialization method. As we stop both of the algorithms until the best solutions found so far remain unchanged in 500 generations, the convergent generation of each run of the algorithm is different. Therefore, we calculate the maximum number of iterations of all the runs, then extend the number of iterations of all the runs to the same size as the maximum number. In this paper, the best objective value of each run is used as the value of the extended iteration. The results are shown in
Figure 13.
As presented in
Figure 13, the proposed initialization method can obtain a better initial value for almost all the instances. This means the proposed initialization method can generate a superior population at the beginning of the algorithm. In addition, for many instances, such as instances 2, 5, 9, 16, and 19, the maximum number of iterations of the proposed initialization method is remarkably less than the random method. This indicates our proposed method can effectively improve the convergence speed of the algorithm. Furthermore, for the very small-scale instances, instances No. 1 and No. 2, and the very large-scale instances, instances No. 21 to No. 25, our proposed initialization method is remarkably better than the random method. According to these experimental results, it can be concluded that the proposed initialization method can effectively improve the convergence efficiency of the algorithm, especially for the very small-scale and very large-scale S-WTA problems. This method cannot only improve the quality of the initial population, but also improve the convergence speed of the algorithm.
4.5. Experiments on Repair Operations
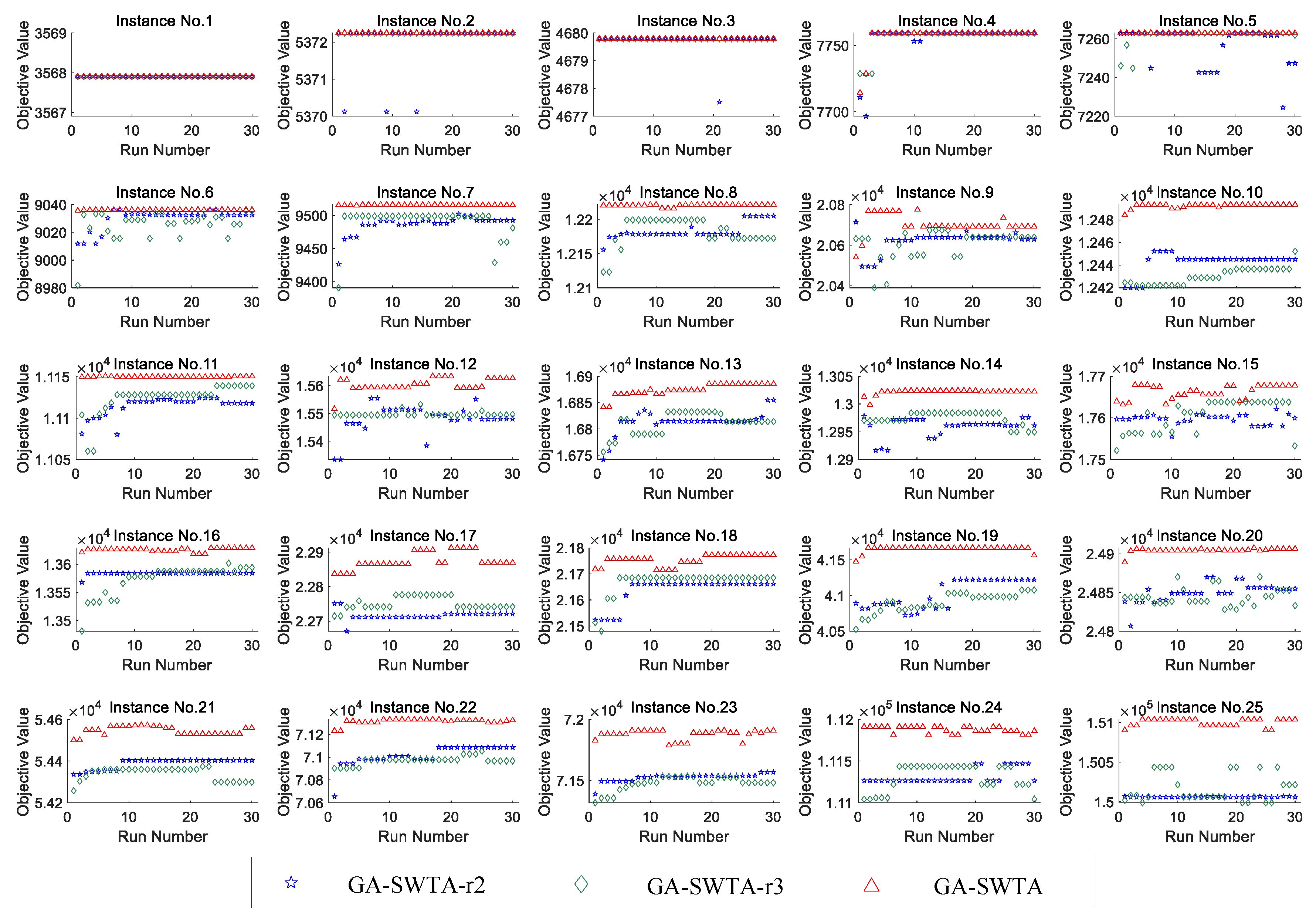
In this section, the performance of the repair operations is verified. In general, there are three methods to handle the individuals that do not satisfy the constraints. The first method is to delete the individuals. Although this method can quickly eliminate unsatisfactory individuals, it may reduce the efficiency of convergence. The second method is to punish the individuals. In this method, a penalty function is designed to adjust the objective values of the individuals, and the unsatisfactory individuals will be eliminated during the process of evolution. We should note that this method has been successful used in ds-GA to handling the constraints. The third method is to repair the individuals, which is used in our proposed algorithm. Therefore, the first and the second methods for handling constraints are selected for comparison.
Based on the proposed GA-SWTA, the repair operations are replaced by the first and the second methods. The variant is called GA-SWTA-r2, and GA-SWTA-r3, respectively. In GA-SWTA-r2, all unsatisfactory individuals are deleted instead of repair. In GA-SWTA-r3, the penalty function (
7) is used to handling the constraints. Meanwhile, other mechanisms and parameters remain unchanged. We performed 30 independent runs on each algorithm for each instance.
Figure 14 shows the results of the three algorithms.
As shown in
Figure 14, GA-SWTA has the best performance on the given indexes for all the 25 instances. For the instance No. 1, all algorithms have the same performance. For the small-scale instances, No. 2 to No. 5, the performance of all the algorithms are very similar. In addition, for the majority of other instances, GA-SWTA-r2 has the worst performance. Based on analyzing the experimental results in
Figure 14, we can conclude that the proposed repair method performs better than the other two methods in most of the instances. All the methods are work well on the small-scale problem. All these results show that the repair method proposed in this paper can effectively handle the constraints.
5. Conclusions
The STA and WTA problems have been widely concerned in the previous studies. However, few researches have focused on the S-WTA problem. In this paper, we proposed a novel genetic algorithm for the synthetical S-WTA problem. First, the frameworks of S-WTA are deeply analyzed. Then, a new model based on a novel framework of S-WTA is proposed. Furthermore, in order to solve the proposed model, a novel genetic algorithm, GA-SWTA, is presented. In the proposed GA-SWTA algorithm, a prior knowledge-based population initialization method is put forward to improve the efficiency of the convergence. Afterwards, two novel repair operations are designed to handle the constrains of the problem.
The performance of the GA-SWTA is analyzed in 25 test instances. Extensive experiments with two state-of-the-art heuristic algorithms and one GA-based algorithm demonstrate that our proposed algorithm outperforms other algorithms in most of the test instances. Furthermore, experiments on the proposed initialization method and random initialization method show that our proposed initialization method can improve the efficiency of the convergence. Moreover, the performance of the presented R-STA and R-WTA repair operations are detailed, which illustrate that these operations can effectively handle the constraints of the S-WTA problem as well as enhance the convergence of the algorithm.
According to these experimental results, we can conclude that our proposed algorithm can effectively solve the S-WTA problem. Compared with the traditional heuristic algorithms and evolutionary algorithm, the proposed algorithm has better convergence performance, which means that it can achieve better S-WTA scheme. However, since this algorithm is based on the framework of evolutionary computation, it cannot be performed in a real-time environment. Therefore, this proposed algorithm can be used in a non real-time and high-precision environment.
Although GA-SWTA can effectively solve the S-WTA problem in most of the test instances, its performance is worse than MRBCH in very large-scale problems. This is because the evolution operators used in this paper, which are the key factors to affect the convergence of GA-SWTA, are originally designed for the WTA problem, so they may lose their efficiency in solving S-WTA problems. Therefore, in our future work, we will focus on the design of evolution operators. We hypothesize that if the evolution operators are designed appropriately, the performance of the proposed algorithms in the very large-scale problems can be greatly enhanced.
In this paper, as we mainly focus on the framework of the S-WTA problem and the design of the solving algorithm, the configuration of the sensor–weapon system in practical application environment is neglected. Due to the rapid technological development of sensors like the array and wide range sensor systems, the sensor signal data can greatly affect the performance of the target detection and weapon guidance. In addition, the damage effect of the weapon on the target mainly depends on the type of targets and duration of destroying targets. Therefore, in our future work, we will also focus on these important elements, which may truly reflect the actual situation of the S-WTA problem, to build a more reasonable model.