1. Introduction
Currently, large-scale and fast-speed marine vessels are widely used in numerous operations and missions. High-speed ships and large container ships can exceed 28 knots in speed, while existing patrol vessels for maritime surveillance reach lower speeds [
1]. The operational conditions of patrol vessels give rise to disadvantages such as short visual range and slow response, rendering them unable to control the overall situation, and to continuously and effectively track illegal vessels for the efficient collection of evidence of illegal acts. The high-speed and high-efficiency of UAVs can effectively compensate for speed limitations of law enforcement vessels. A complete operational cycle of a UAV includes the three stages of launching, mission flight, and recycling. Both launching and autonomous flight technologies are considered relatively mature, whereas recycling is still a heated research topic in UAV technology [
2].
Moreover, the autonomous landing of UAVs on moving vessels is a more complex scientific and engineering issue [
3]. The landing environment of a ship-borne UAV is rather more complicated than that of a land-based UAV. Since the vessel is constantly moving during the landing of the UAV, a land-based UAV landing methodology should be applicable otherwise the UAV might fall directly into the sea. In particular, the sea cannot provide the necessary landmarks and the space required for landing. Even in aircraft carriers, the flight deck space is very limited, much smaller than the length of an onshore airport runway [
4]. In the course of unmanned land or sea monitoring missions, the timestamp and trajectory of the carrying vessel are necessary for the required relay transmission of monitoring information [
5]. Furthermore, the motion characteristics of the UAV and the vessel are essential for calculating the position of the vessel while the UAV is landing. Flight path planning of UAVs around dangerous areas have been studied in the literature [
6]. Additionally, algorithms for the UAV minimum path length have been also considered in the literature [
7,
8]. Researches for optimizing such flight paths, while preventing collision accidents and improving flight safety, have been also proposed [
9,
10]. Finally, guidance challenges of UAVs flying along a predetermined trajectory have been presented [
11].
Yi Feng et al. [
12] proposed a UAV autonomous landing system based on model predictive control. The system dynamically models the UAV through a universal camera and uses the Kalman filter to come to the best location of the mobile platform. A model predictive controller was developed to land safely under various uncertainties and wind disturbances. Sánchez López et al. [
13] proposed an autonomous landing algorithm that combines the Kalman filter with vision. By simulating the dynamics of different sea conditions and vessel decks and using a well-designed computer vision system, the ship deck is measured related to the posture of the drone. Wang Kai et al. [
14] proposed a network-based UAV ship with a self-adaptive guidance system. By controlling the line-of-sight angle to track the angle of the flight path, the angle guidance law and the reverse guidance law are introduced. The purpose is to reduce the sensitivity of drone motion changes in ship parameters. Wang Liyang and other scholars [
15] proposed a drone autonomous landing system based on airborne monocular vision, which can improve the ability of autonomous tracking and landing for drones under simulated sea conditions. Moriarty, P et al. [
16] provided an artificial neural network-based autonomous landing method for UAVs. Using the data generated by simulating the sea motion, the current relative azimuth and distance of the UAV to the landing platform were calculated, and the coordinate pairs were calculated, which normalized processing for training neural networks.
Currently, research on the planning of a fixed-wing UAV landing trajectory on moving vessels is very rare. The above-mentioned UAV flight path planning research is mainly focused on land-based UAVs; thus further improvements are needed for meeting the requirements of sea flight and landing. However, when the flight procedure is executed, depending on the result of the current monitoring information, the change in the weather condition or the movement path of the carrier, the UAV movement set by the flight task can be significantly changed according to commands from the control panel. In this regard, it is necessary to control the possibility of the drone returning to the vessel carrier during the flight. In order to do this, it is necessary to determine the length of the minimum return path, taking into account the handling of the drone steering carrier and the proximity landing device. The ship-borne landing device used in this work is similar to the SideArm system published by Defense Advanced Research Projects Agency (DARPA) [
17], with the current research proposing a method for calculating the optimal approach landing trajectory between the UAV and the small vessel. In this project, the possibility of a UAV return in any moment of the mission flight was analyzed. The planned landing flight trajectory can be divided into several stages, and in each stage the corresponding landing track parameters are calculated according to the flight mission and UAV flight performance.
The simulation results demonstrate the effectiveness of our proposed method allowing the UAV to consistently fly along the designed track with a smooth, safe, and reliable altitude. The proposed landing trajectory planning for fixed-wing UAVs can ensure for a safe and efficient UAV recovery task.
2. Approach Landing Trajectory Estimation between Drone and Vessel
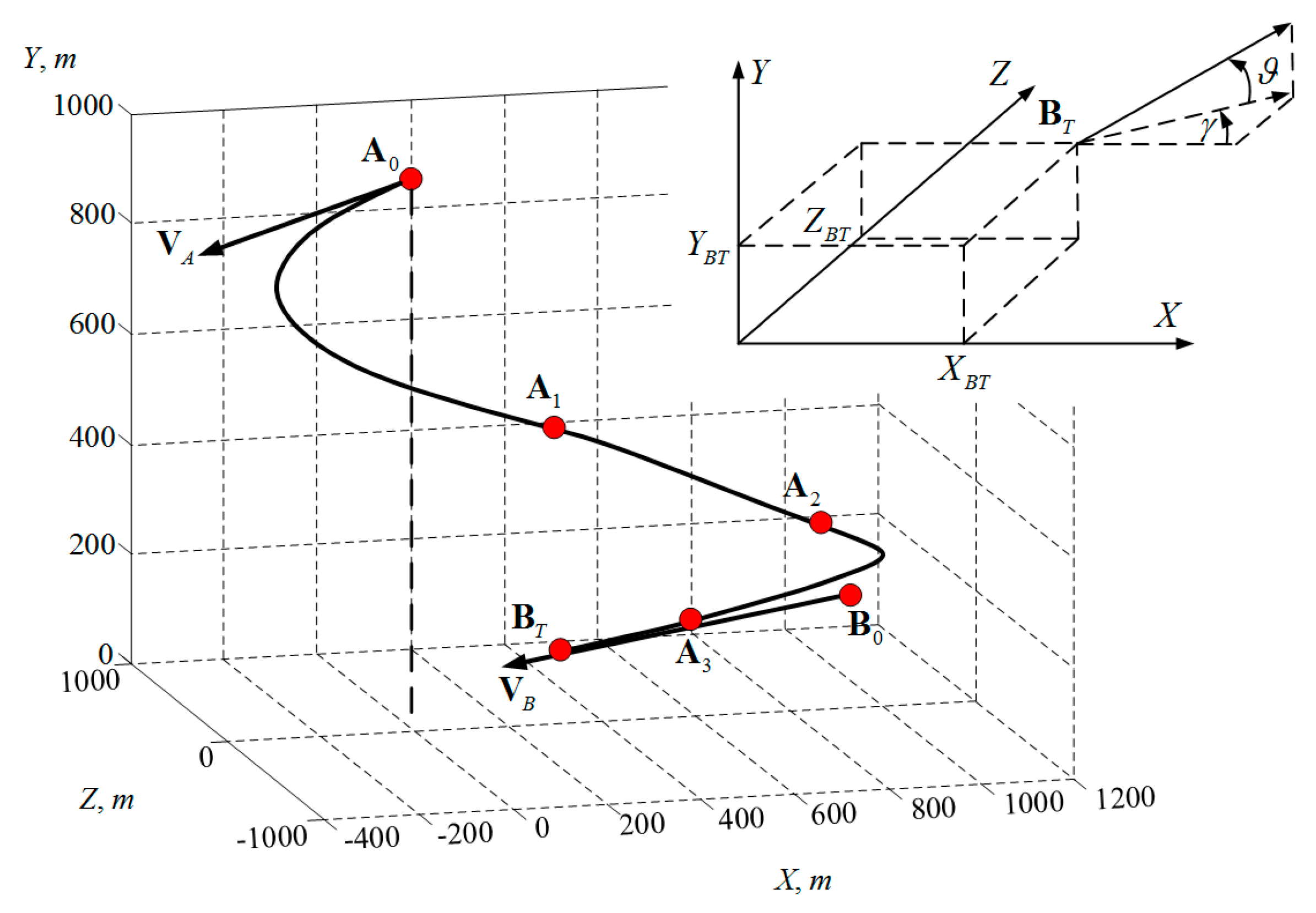
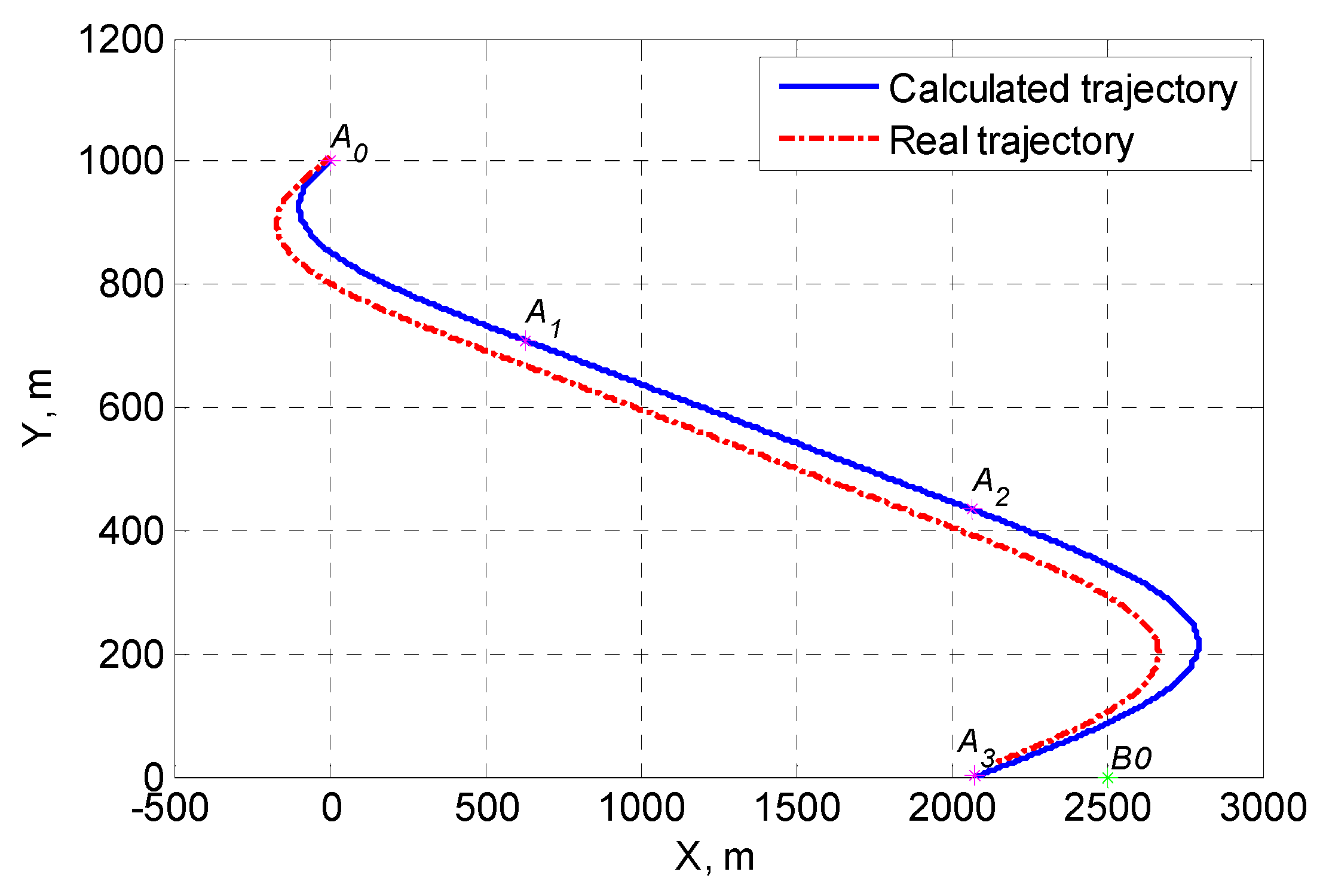
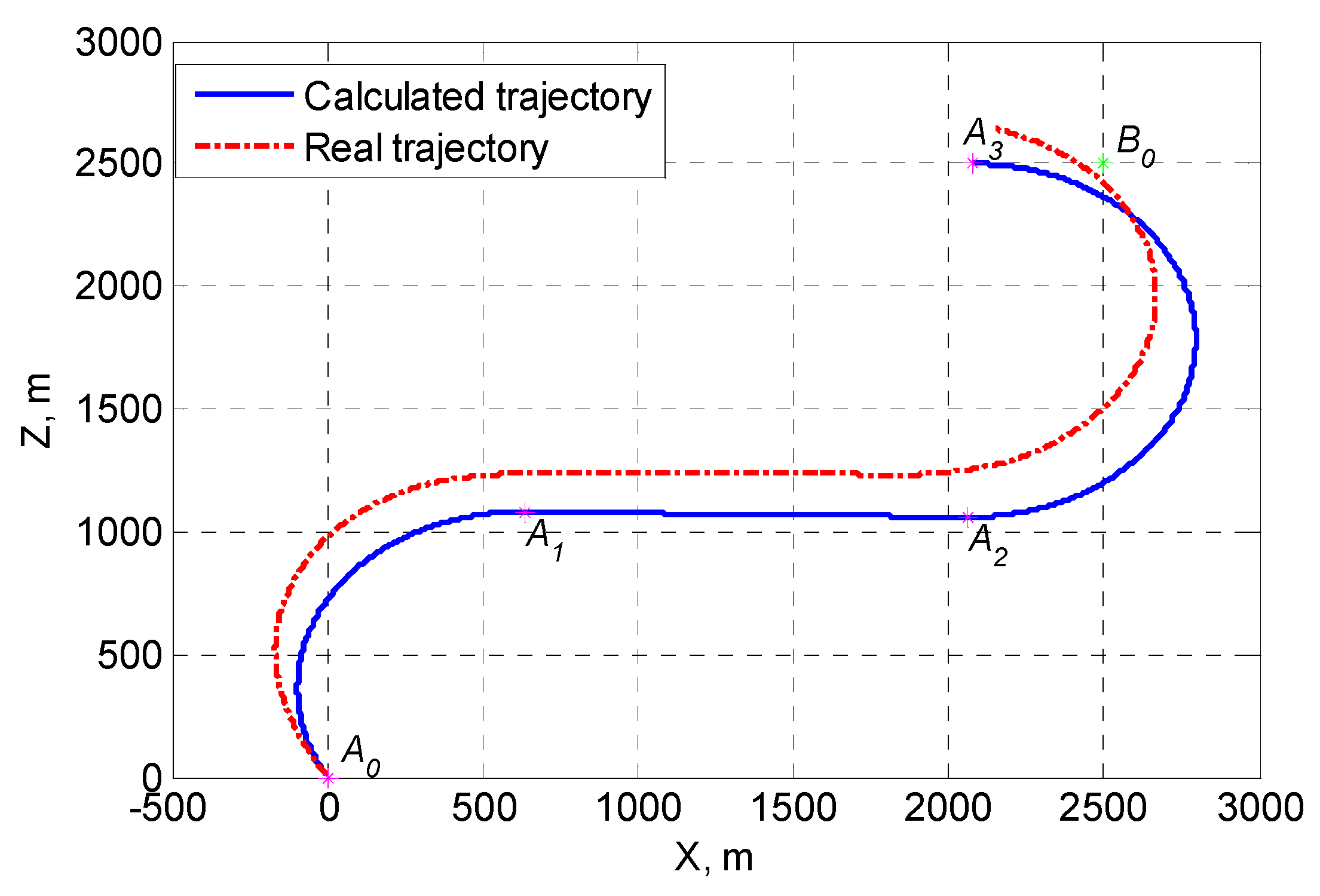
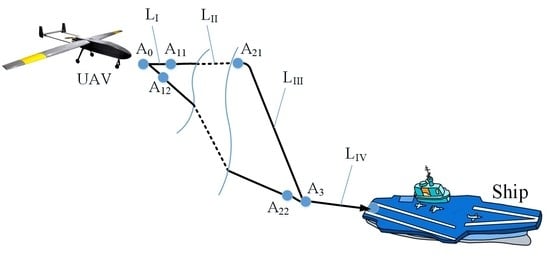
A typical approach landing trajectory between a common UAV and a vessel is shown in
Figure 1. At the time t = 0 (starting of the approach maneuver), the UAV is at the point
, with coordinates
, speed
, and speed direction expressed as
. Similarly, at the time t = 0, the vessel carrying the land-based device is located at a point
, with coordinates
, speed
, and speed direction of
.
It is assumed that during the UAV landing approach, the mode of the UAV motion velocity vector is , the mode of the vessel motion velocity vector is , and the vessel motion velocity direction are known constants. For the UAV landing time , the predicted position of the vessel is . At this time, the mode of the vessel’s motion velocity vector is constant with its direction .
Assuming that the approach landing trajectory is in the plane
, and the origin of the initial coordinate system is selected at the point
, the coordinates of the point in the new obtained coordinate system are:
where
,
,
, are the coordinates of the points in the new coordinate system, and
,
are the coordinates of the points in the original coordinate system.
In order for the ship’s velocity vector to lie in the horizontal plane, the resulting coordinate system needs to be rotated by
along the axis
. The new point coordinates in the resulting coordinate system are:
Finally, we rotate the obtained coordinate system along the axis
by an angle:
The point coordinates in the resulting new coordinate system are:
The complete approach trajectory from point
to point
in the resulting coordinate system will be in the plane
(as shown in
Figure 2).
The case shown in
Figure 2 occurs when the pitch angle of both the UAV and the vessel is numerically close to each other. For example, when the UAV flies at a constant altitude before starting the approach landing decision. The sum direction of the axis
and axis
and the positive direction of the angle in the plane
are given in
Figure 2.
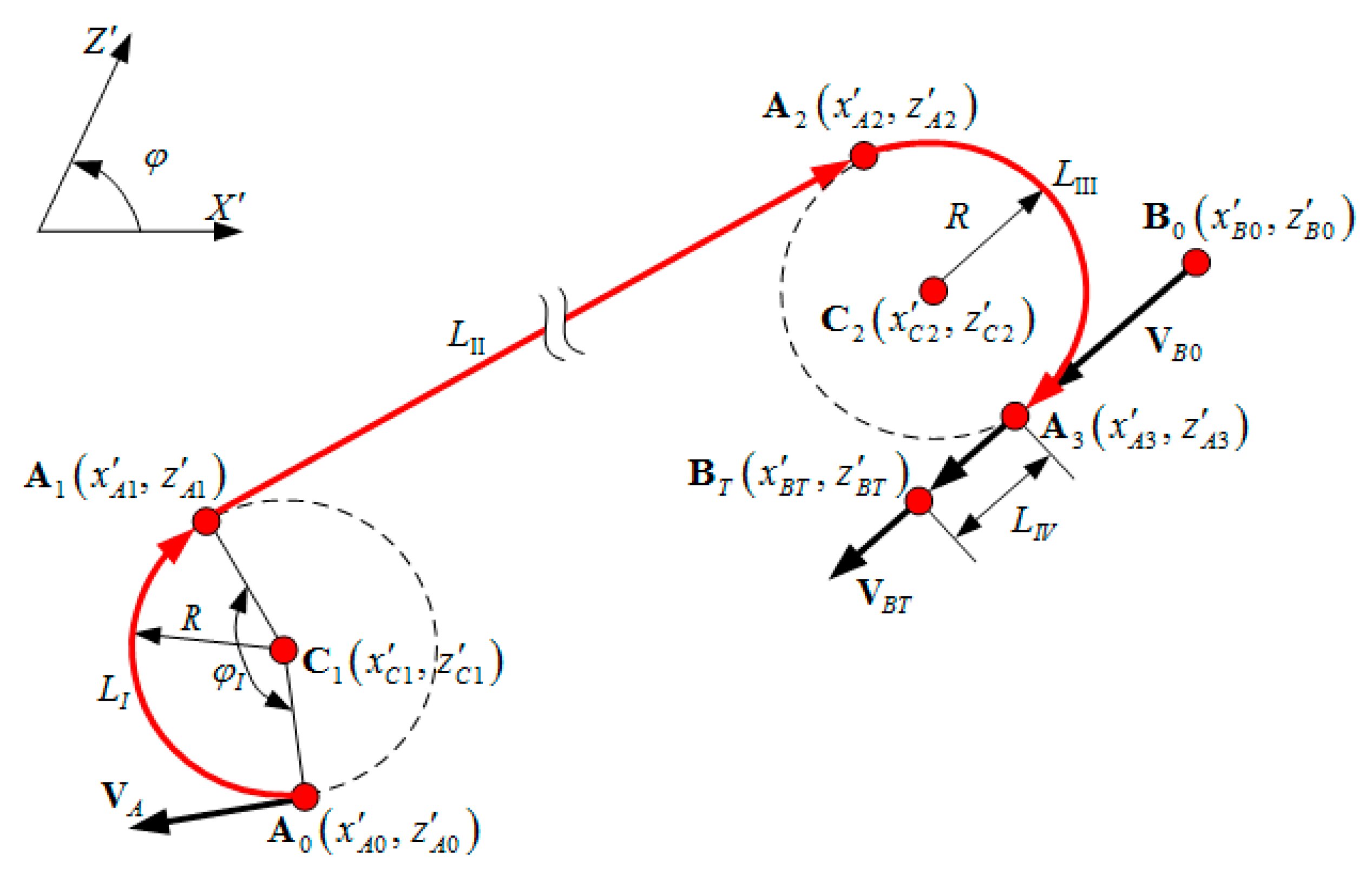
In general, a landing trajectory approach consists of four feature segments. The first segment corresponds to the UAV landing turn, from the initial UAV position
to point
at the end of the turn. If the inertia of the UAV control system in the horizontal plane is neglected, then the maneuvering process can be considered to be done along the center of the circle
, with a minimum allowable turning radius
(in plane
). At this time:
The length of the first track is:
of which the angular distance between
and
is
, and
is the turning radius of the UAV. On this trajectory, the value of
is determined by the lateral overload allowable value
[
18]. For example, for
,
, we can get:
In this case, the angular velocity of turn is:
The second segment of the landing trajectory approach corresponds to a straight line segment, between the first maneuver completion point
and the second maneuver start point
. The UAV enters the vessels navigation direction. The length of the trajectory is equal to the distance between the center of the first and second turns of the UAV, namely:
On this trajectory, the direction angle
of the UAV’s motion trajectory is calculated by:
In the third segment, along the center of the circle
, the arc of radius
is flying from the point
to the point
. At the point
, the UAV direction lies in the same direction of the ship carrying the landing device (ship). The length of the path is:
of which
refers to the angular distance between
and
.
In the fourth section of the landing trajectory approach, the UAV moves along the direction of the vessel, making an approximate linear motion between the second maneuver completion point and the landing end point . The length of the section is a constant value, about 200 to 300 m. The length of this passage is selected in advance based on the conditions that accurately guide the UAV to the landing device. On this path segment, a compensation of the calculated landing error, as well as a reduction in the UAV flight speed to the minimum required for landing, is achieved.
Assuming that
is the time when the UAV ends its turn (return to point
), then, in general, the following equation can be obtained:
For a specific uniform linear motion of the ship in the plane, we can get:
where the coordinates of the end point
, the UAV and the vessel are connected at this point:
After determining the coordinates of the point
, the coordinates of the turning circle center
of the third segment of the landing trajectory can be obtained with the following relationship:
In addition, according to Equation (7), the angle
can be obtained, and then the coordinates of the point
and
are obtained as follows:
The difficulty in solving Equations (4)–(13) is that the value
is indeterminate. To this end, this paper proposes an iterative method to determine the values of
. For the approximation of
, we can use:
where if the UAV and the vessel are facing each other, the symbol “
” is selected, but if not, the symbol “
” is selected. In formula (14), the angle between the UAV flight speed vector and the ship’s navigation speed vector cannot be equal to 90°.
The error
of a single approximation does not exceed the following value:
Within the interval
, the value
is searched and determined by the binary method. The search termination condition is:
where
—sets the coordinate error of point
in the track segment
and
. The value
is determined by the accuracy of the actual landing trajectory approach, and in this paper is selected as
.
refers to the point at the end of the left side trajectory of point
(the second trajectory);
refers to the point at the end of the right side trajectory of point
(the third trajectory).
When the vessel is cruising at a constant speed, at
according to Equation (7), the coordinates of the point
are:
With the coordinates of the point
being:
After the value
is determined, the total length
of the approach landing trajectory is determined by the sum of the length of the four-part trajectory segments:
By calculating the length
of the shortest approach landing trajectory in real time, according to Equation (19), we can control the likelihood of the UAV returning to the landing device on the vessel. If the remaining fuel amount of the aircraft is less than the fuel amount
required to return to the vessel, then the UAV must perform a return maneuver. Among them,
is determined according to Equation (20).
where
refers to the amount of fuel consumed by the drone unit path.
It is worth noting that, if
, the approximate calculation Formula (21) can be used to replace the exact calculation formula of the landing trajectory approach
(14).
where
or
is used when the UAV and the vessel are facing or are opposite each other, respectively.
The ratio of average speeds is defined by:
In order to estimate the error of the approximate calculation Formula (21), it is preferable to perform a more accurate calculation of the average speed ratio.
Based on the above-mentioned transformation relationship among coordinate systems, the coordinates in the reference coordinate system are calculated according to the coordinates , , , , of the approaching landing trajectory feature points in the new coordinate system. At this time, the transformation order is reversed, and the sign of the corner of the coordinate system and the sign of the displacement of the coordinate origin are also opposite.
The research work in this paper is applicable in an ideal UAV control system, regardless of the inertia of the UAV control system. The actual approach landing trajectory between the UAV and the vessel can be determined by simulating the movement of the UAV along with an ideal landing trajectory.
4. Improving the Accuracy of the Optimal Approach Landing Trajectory
In order to improve the accuracy of the optimal approach landing trajectory between UAV and vessel, we introduce the pre-position
n in the calculation formula of the direction angle
and the dip angle
of the UAV flight speed vector. More precisely, we replace Equation (29) with Equation (35) and calculate the direction angle
and dip angle
as follows:
with
n denoting the initial lead steps.
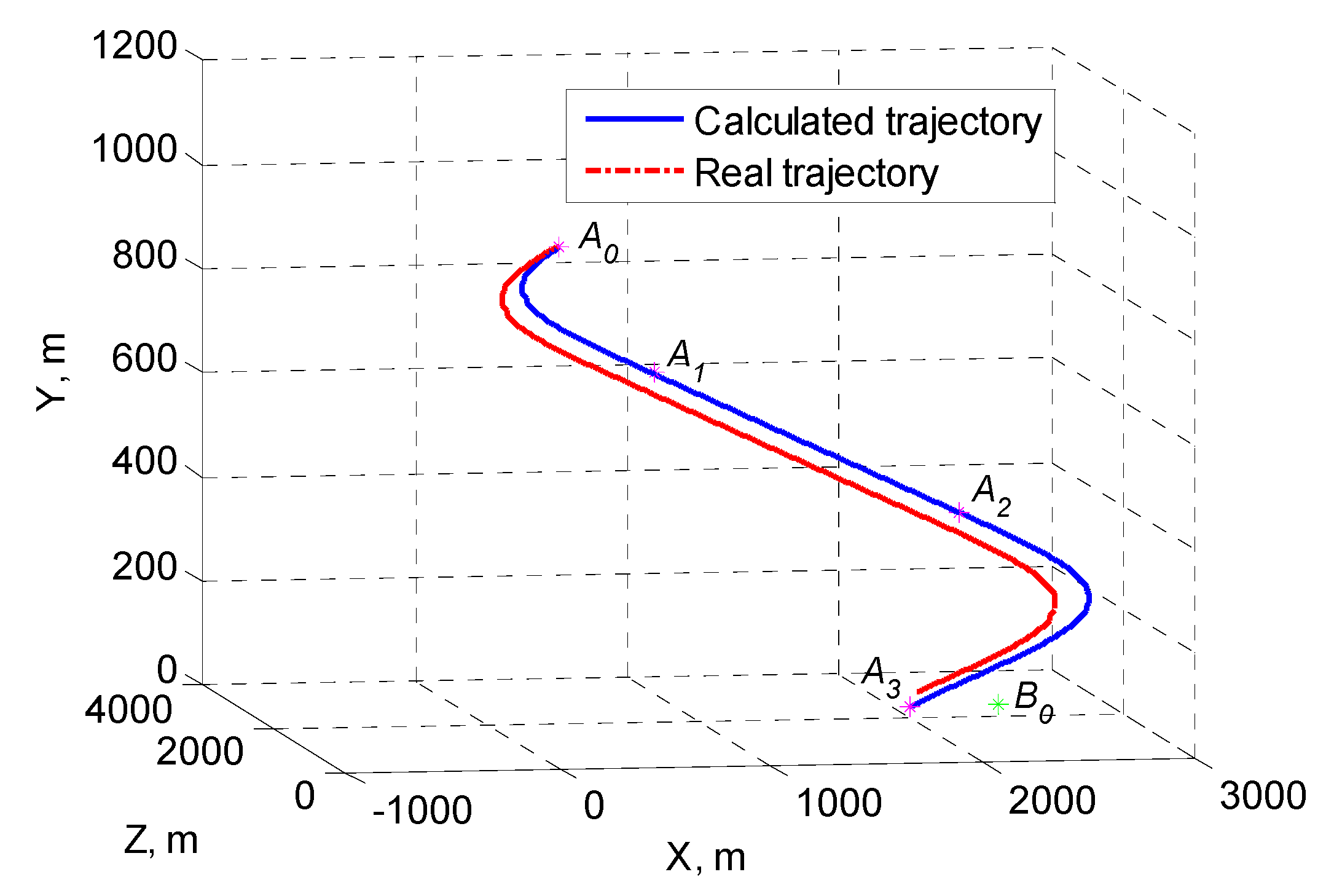
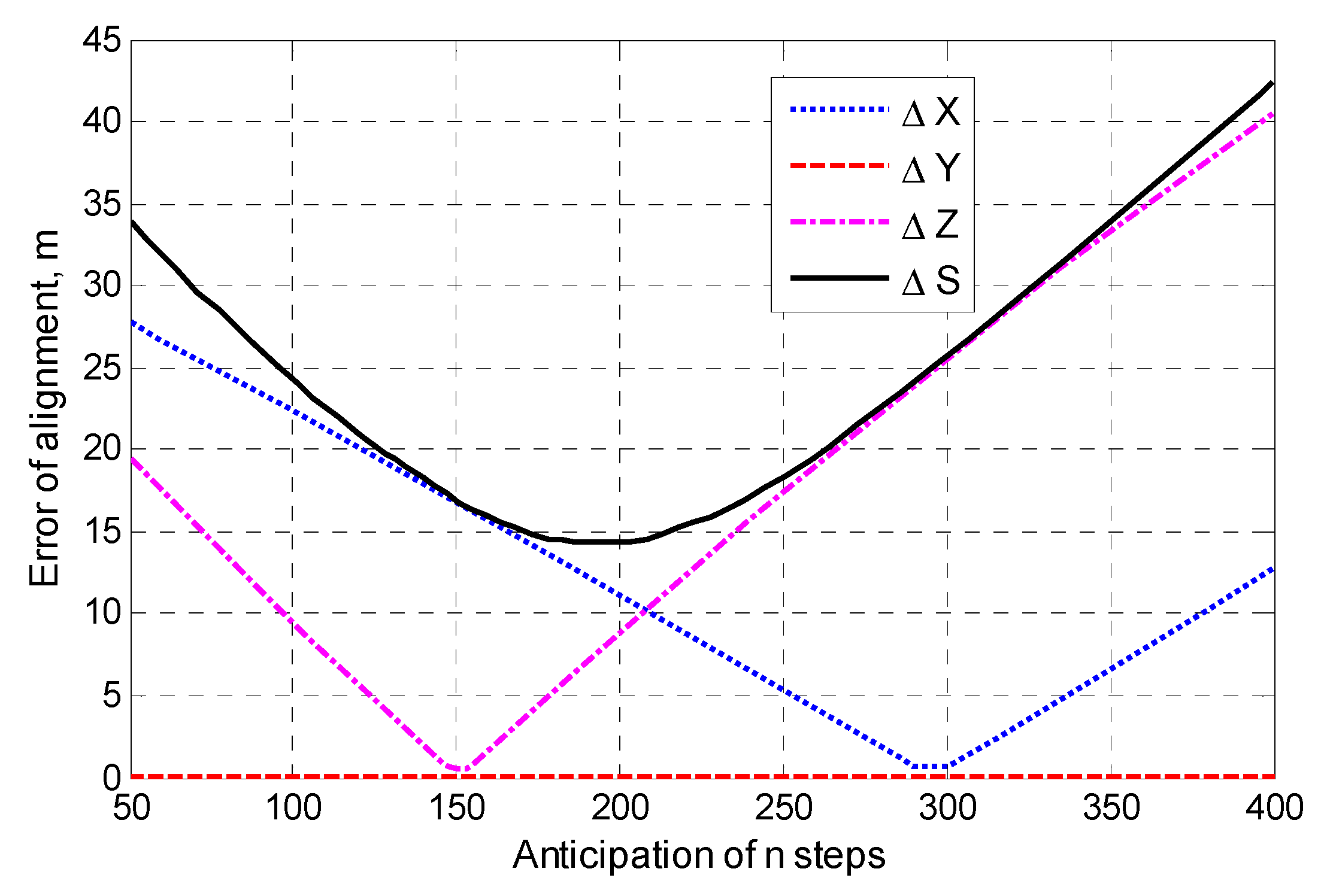
By selecting the optimal value of the initial lead steps
n, the guidance error of the UAV’s flying to point
can be greatly reduced. For the control system with the above parameters, different pre-step values are evaluated, and the coordinate deviation error
,
,
and the total error
between the UAV actual trajectory and the optimal calculated trajectory at the point
are shown in
Figure 8.
In
Figure 8,
is achieved by artificial compensation for systematic errors of
. From the simulation results shown in
Figure 8, it can be concluded that the optimal value of the initial lead is
. At this value, the total error between the actual UAV approach landing trajectory and the vessel at the point
is
and the calculated optimal approach landing trajectory, which is compared with the total error when
, is reduced by nearly 3.5 times.
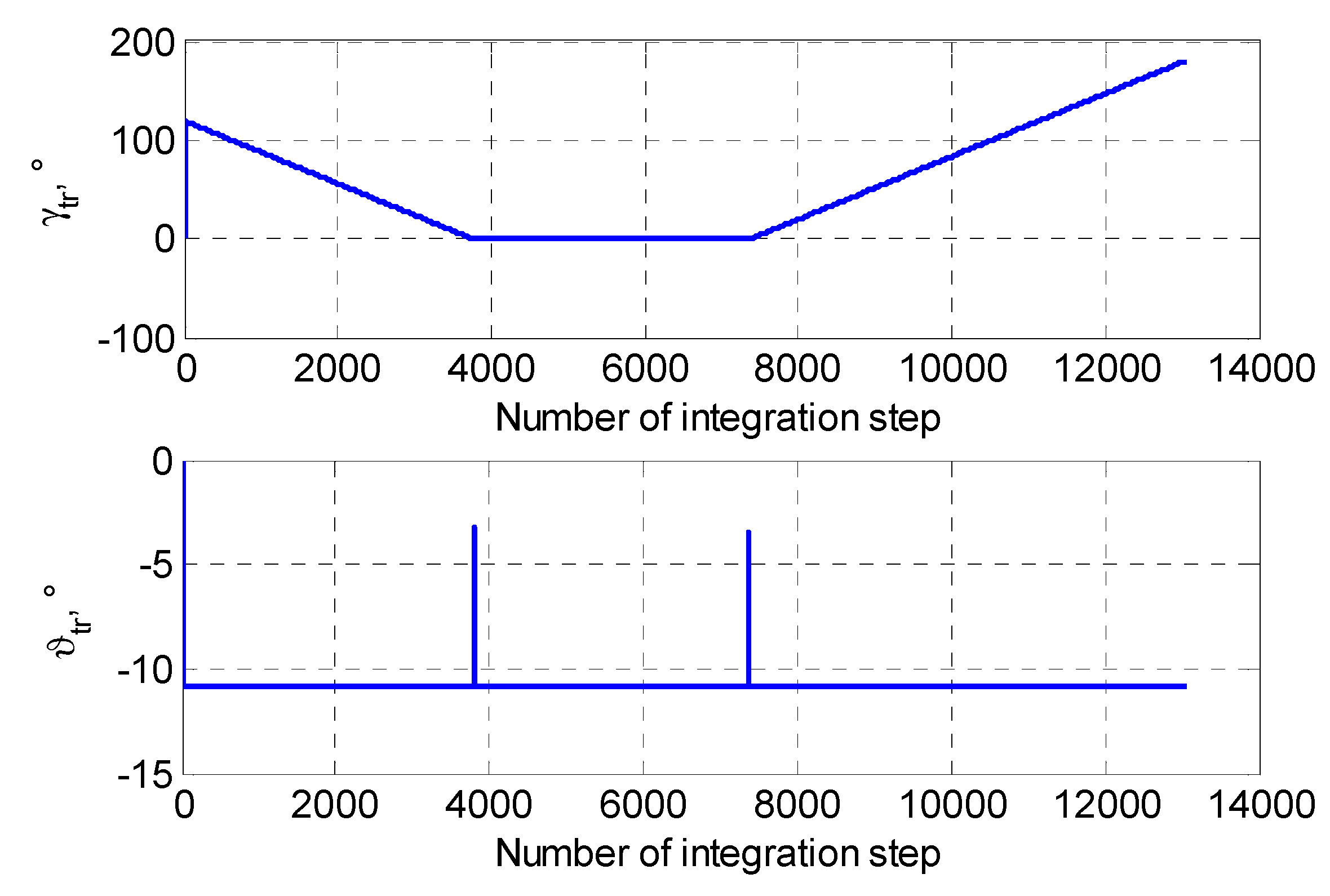
The direction angle
and the dip angle
of the flight speed vector between the UAV and the vessel are shown in
Figure 9.
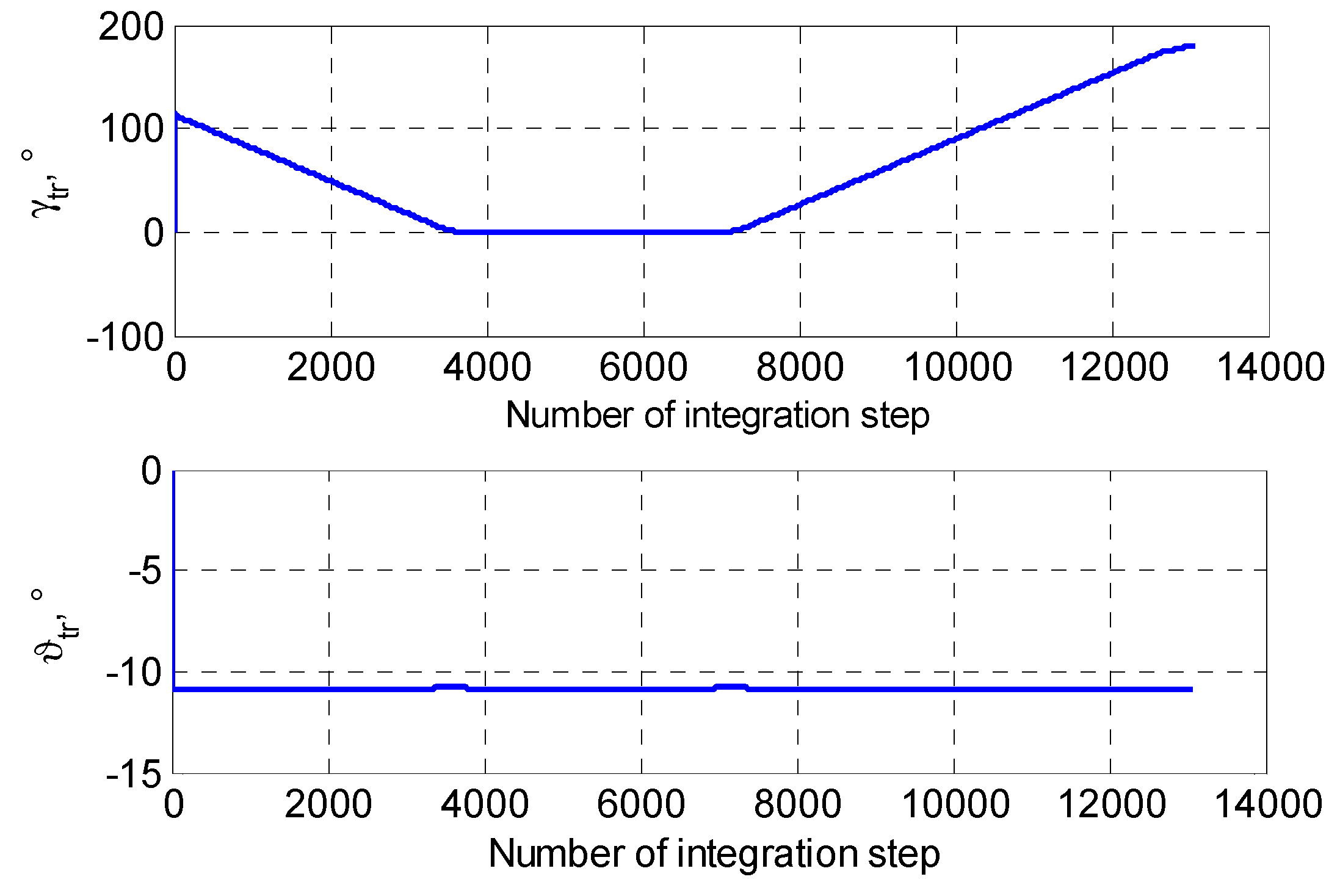
From the simulation results shown in
Figure 9, it can be seen that when the initial lead is
, the direction angle
change process of the UAV flight speed vector almost sees the same trend compared with the results of
Figure 7, showing a more gradual correction. By contrast, in the calculation process of the complete approach landing trajectory, the flight vector’s dip angle
changed significantly compared with the results of
Figure 7, with the change process at the approach point
and
being smoother. This behavior is considered beneficial to an optimal UAV landing trajectory tracking planning during actual flight.
By introducing the initial lead in the control signal, it can be concluded that the UAV inertia can be compensated for a certain extent, assuring a more efficient approach landing trajectory.