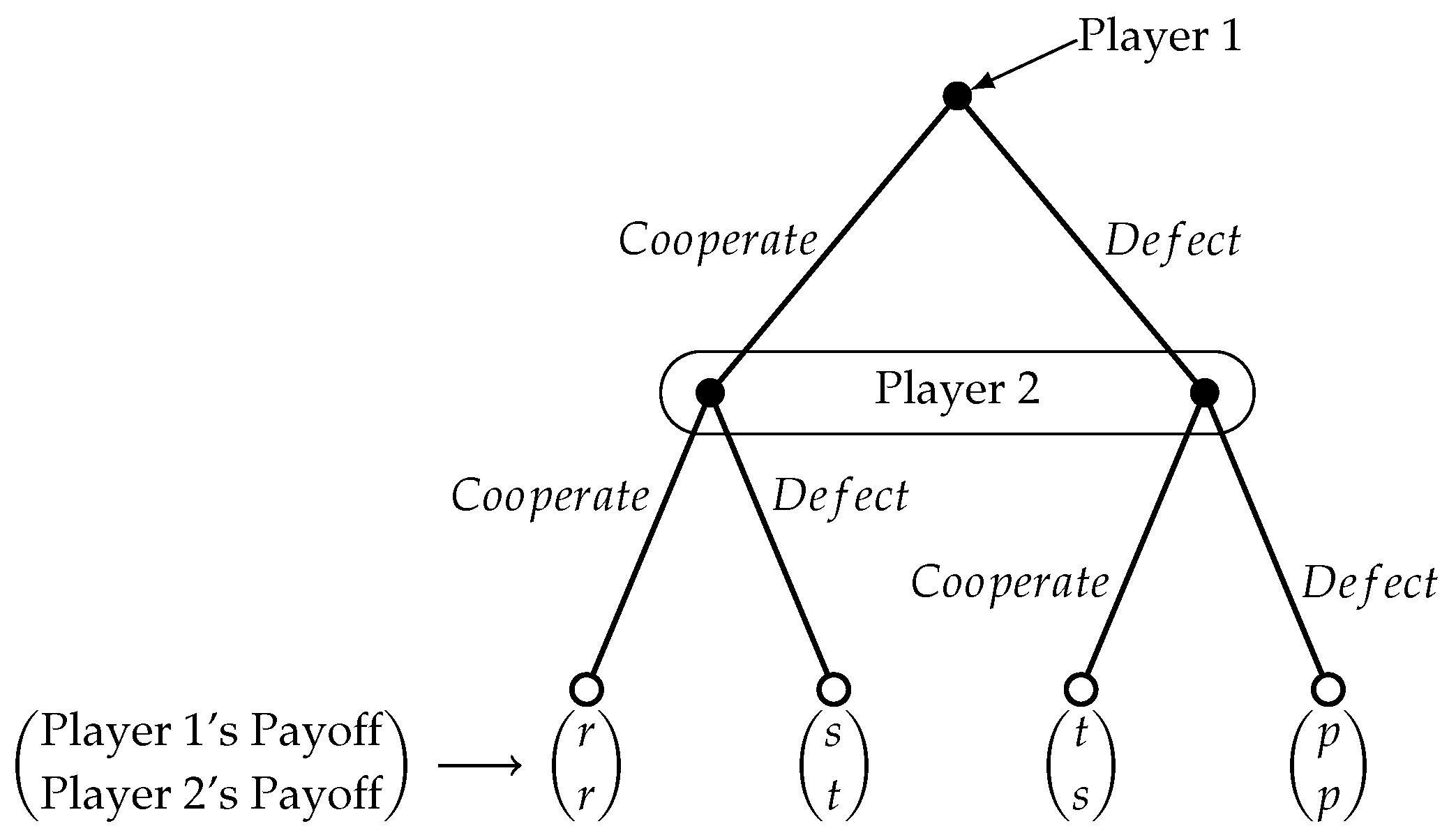
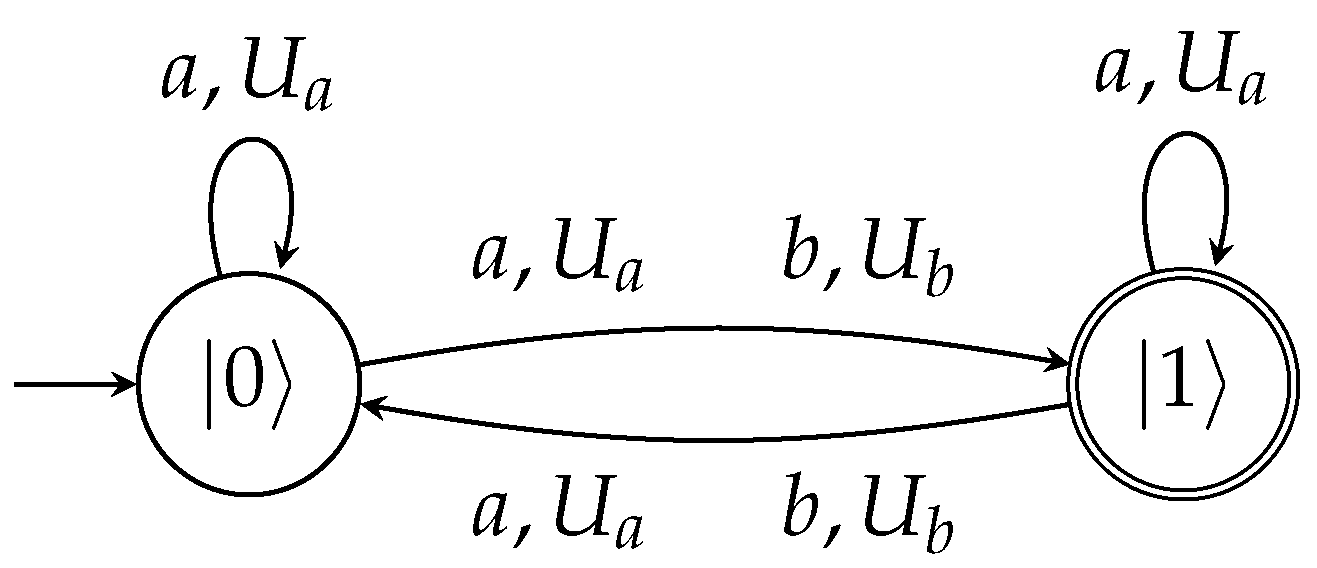5.1. Classical Pavlov in PD and Automata
In this part, we discuss the outputs of the the repeated PD game for
stages, where
is an arbitrary positive integer that defines the number of plays. It is imperative to emphasize that this number
is unknown to the players in order not to have a predefined series of actions [
27], which would lead to a dominant strategy of always “Defect” for both of them. We follow the actions-to-letter association of
Table 4. The associated automata in every case recognize the respective language with probability cut-point
. We clarify that the projective measurement, with respect to the orthonormal basis of the automaton’s states, is performed after the reading of the
input symbols. Furthermore, in all scenarios, the measurement period
is equal to the number of stages or, equivalently, to the number of input symbols (and consequently, in the case of repeated versions of the game,
). Thus, a measurement is imposed after reading a total of
symbols. But this can be easily extended to the infinite case by requiring measurements to take place periodically in
time-steps after
symbols are read. For example, if the accepted language is
, this means that there are
input symbols in total, that is,
stages of the game are played, which in turn implies that
.
5.1.1. Player 1 Plays Pavlov
Initially, we assume that Player 1 chooses to follow the Pavlov strategy. At first, Player 2 always defects, which means that regardless of what Player 1 chooses, Player 2 defects. As seen from the series of plays, the Pavlov strategy can be exploited by the all-defect strategy.
The regular expression for this sequence can be described as . This enables us to associate it with a variant of the quantum periodic automata that is able to recognize such languages, even if they are infinitely repeated. The automaton defined below can achieve this task.
The language is recognized with a probability of 1 by the -periodic quantum automaton that is defined as the tuple , where = , and = .
For the next scenario, we assume that Player 2 always cooperates.
The regular expression for this sequence can be described as . This leads us to associate it with a variant of the quantum periodic automata that is able to recognize such languages, even if they are infinitely repeated. The following automaton does the work.
The language is recognized with a probability of 1 by the -periodic quantum automaton that is defined as the tuple , where = .
Next, suppose that Player 2 chooses to follow the Pavlov strategy, similarly to Player 1.
For this case, the associated automaton is the same as the above (i.e., ) since the underlying language is the same, i.e., .
Next, Player 2 applies the tit for tat strategy.
Again, the associated automaton is the same as the previous one since the accepted language is .
Finally, we consider the case where Player 2 follows the reversed tit for tat strategy.
The regular expression for this sequence is , which is recognized with a probability of 1 by the -periodic quantum automaton that is defined as the tuple , where , , and .
5.1.2. Player 1 Plays Tit for Tat
In this series of PD games, we assume that Player 1 chooses to follow the tit for tat strategy, whereas Player 2 always defects.
The regular expression for this sequence is , and the corresponding -periodic quantum automaton is exactly the same as .
When Player 2 always cooperates, we have:
Its associated automaton is again the same as .
When Player 2 follows the Pavlov logic, we have:
Again, the resulting automaton is .
Then, if Player 2 applies the tit for tat strategy, we have:
The corresponding automaton is the same as .
For the scenario where Player 2 follows the reversed tit for tat strategy, we have:
In this case, the resulting automaton is a bit more complicated than those previously encountered since this series yields the regular language . With , we denote the length of the string (in this case, it is equal to 4, but we prefer to use in order to emphasize its derivation). The associated -periodic quantum automaton is the tuple , where , ,
, , and is a positive multiple of , i.e., , for some positive integer k.
For this particular scenario that seems a bit more complicated, it is important to emphasize that the measurement period
has to be a multiple of the length of the substring
in order to guarantee that the measurement will return an accepting outcome with a probability of 1 (as stated in the definition of
-periodic quantum automata in
Section 4), otherwise the acceptance cut-point
is
. This means that the read symbols (or the number of PD stages) have to be multiples of this length (in this case
).
5.1.3. Player 1 Plays Reversed Tit for Tat
Assuming Player 1 chooses to follow the reversed tit for tat strategy, whereas Player 2 always defects, we have:
The regular expression for this sequence is , and the associated -periodic quantum automaton is similar to by swapping the letter b with the letter d.
When Player 2 always cooperates, we have:
The associated automaton for this scenario is the same as , where the unary language is accepted with a probability of 1. For this scenario, all we have to do is to replace the letter a with c.
When the Pavlov strategy is followed by Player 2, we have:
The regular expression for this sequence is the , which is recognized with a probability of 1 by the -periodic quantum automaton that is defined as the tuple , where , , and .
When Player 2 follows tit for tat, we have the series of plays shown below.
The associated automaton for this scenario is the same as , where instead of the substring , we now have the substring . The language for this scenario is the regular language . Regarding the period , the same restrictions as those of must also hold.
Finally, if Player 2 follows the reversed tit for tat behavior, it holds that:
For this scenario, the measurement period has to be a multiple of the length of the substring in order to guarantee the desired outcome with a probability of 1. This is equivalent to saying that the number of input symbols (or the number of PD stages) must be multiples of this length (in this case ).