A Software Reliability Model Considering the Syntax Error in Uncertainty Environment, Optimal Release Time, and Sensitivity Analysis
Abstract
1. Introduction
2. Proposed Software Reliability Model
2.1. Non Homogeneous Poisson Process Model
2.2. Proposed Software Reliability Model
3. Numerical Example
3.1. Criteria
3.2. Data Sets Information
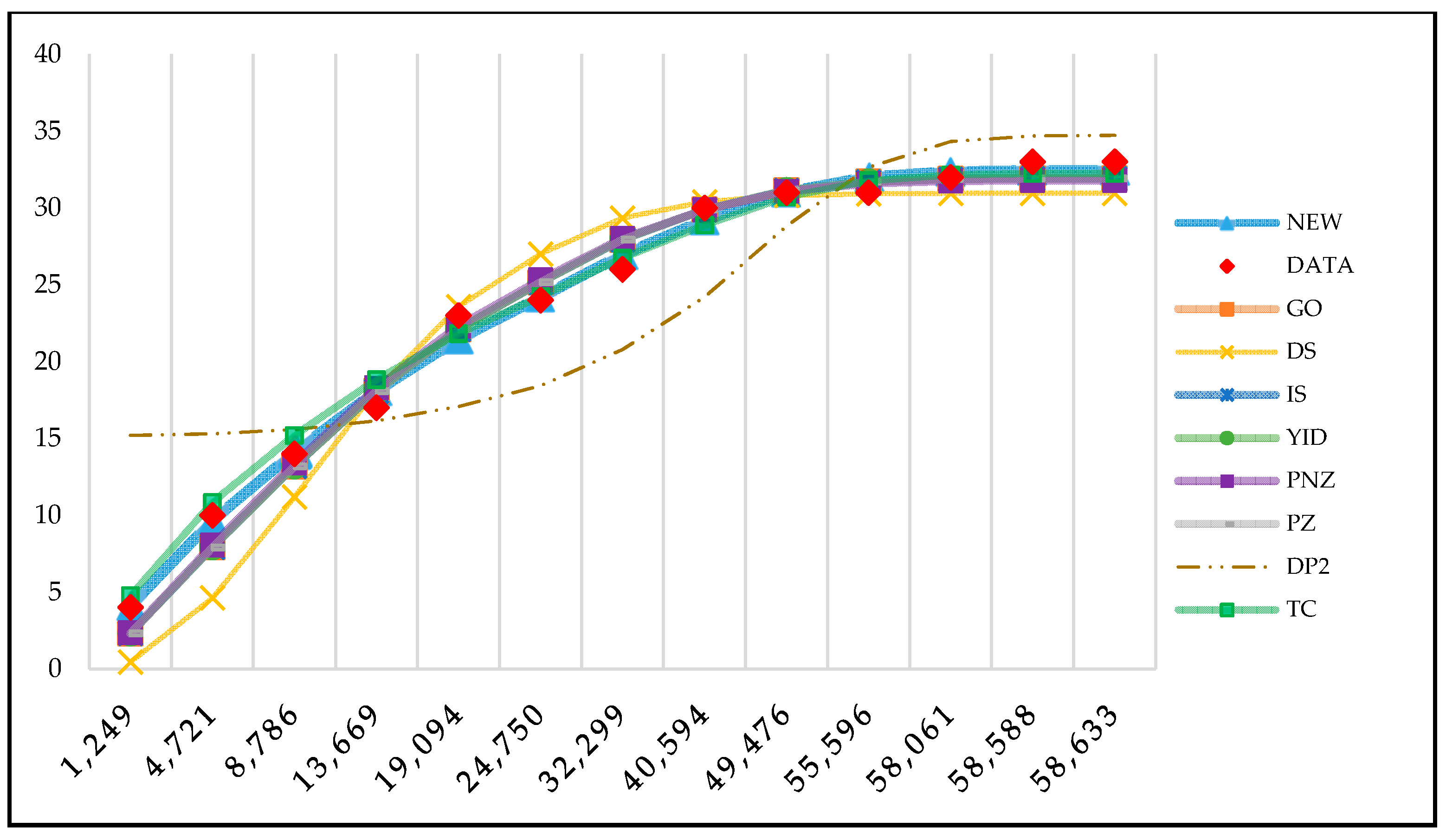
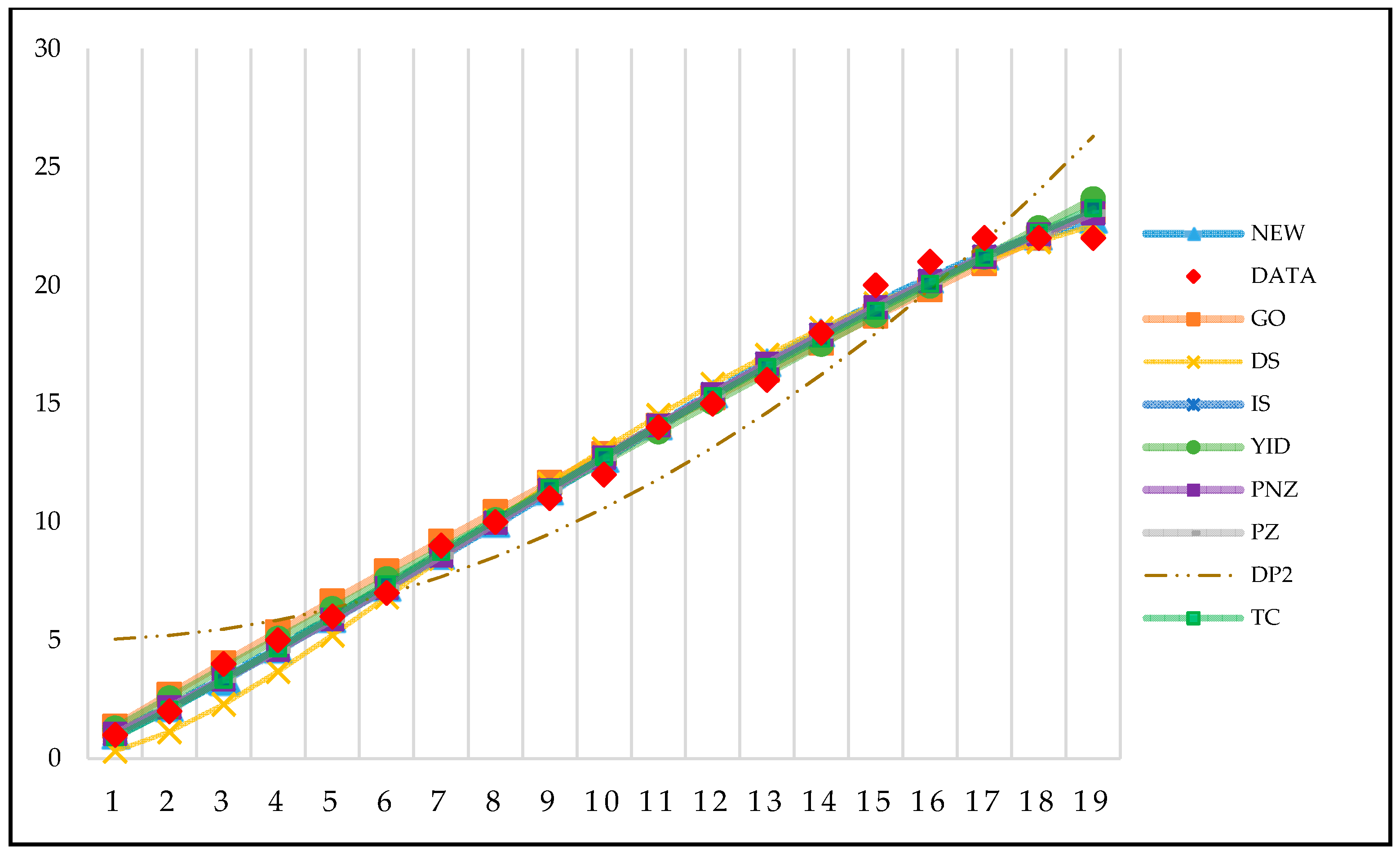
4. Results
4.1. Comparison of Goodness of Fit
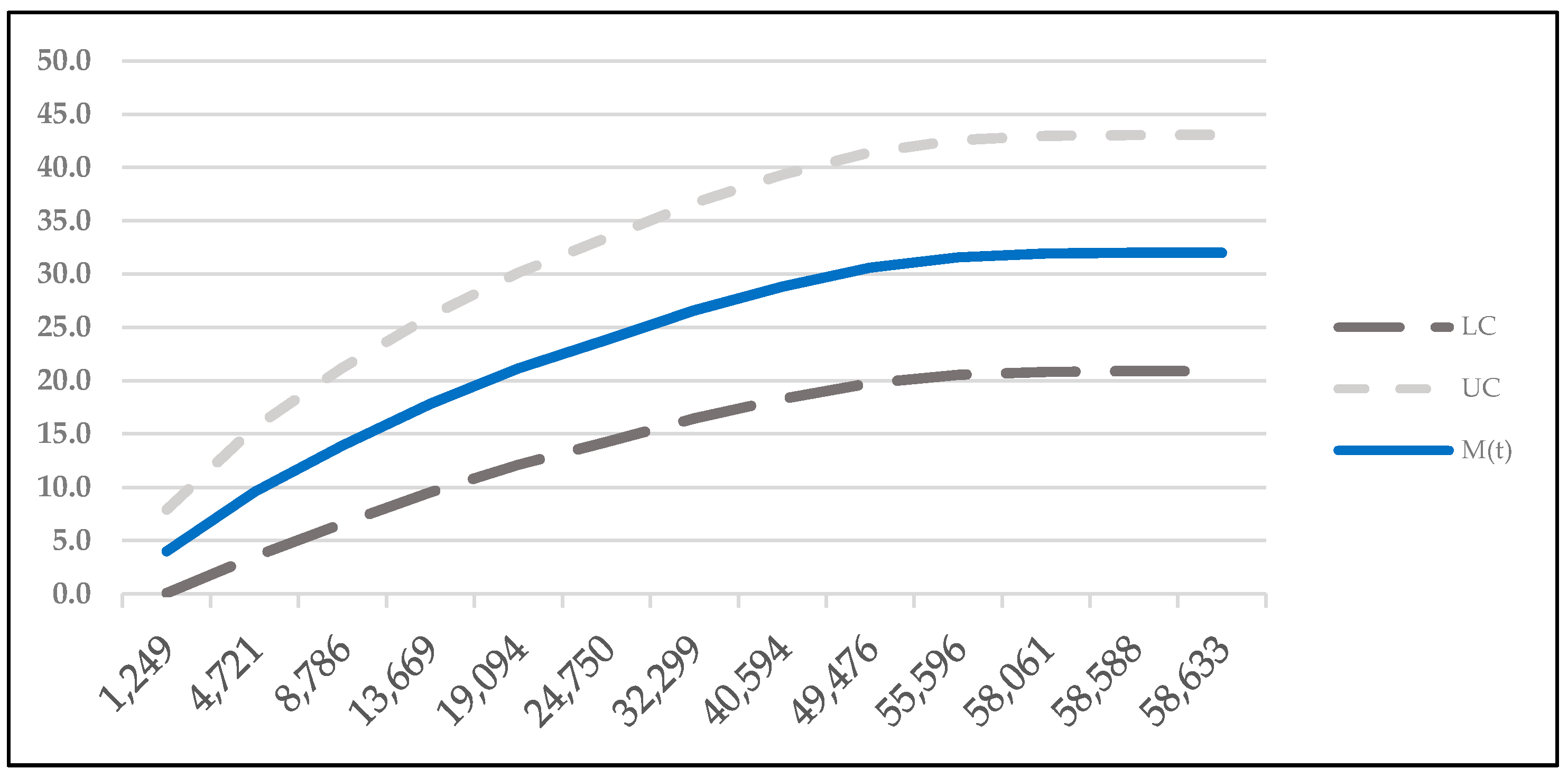
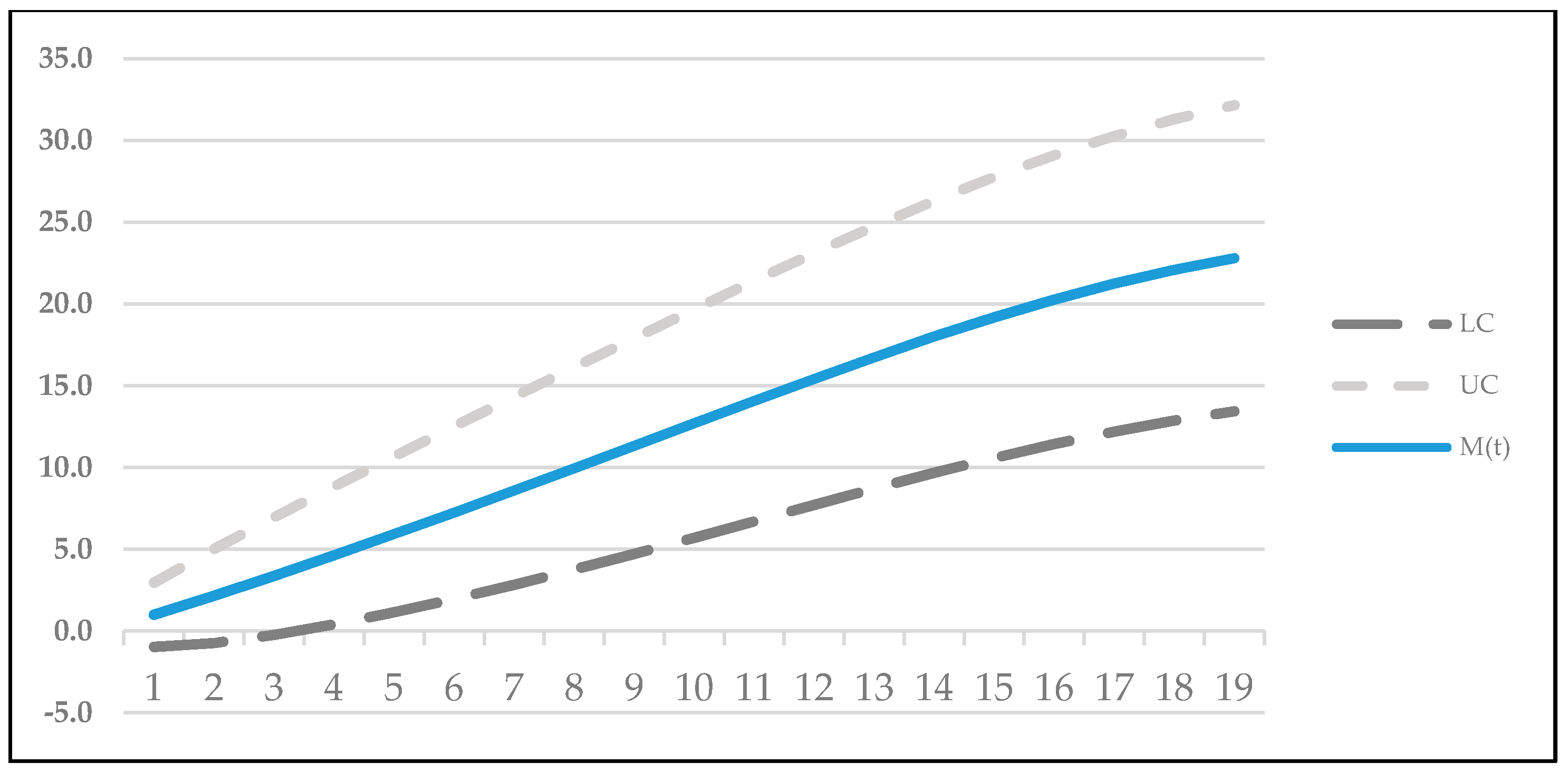
4.2. Confidence Interval
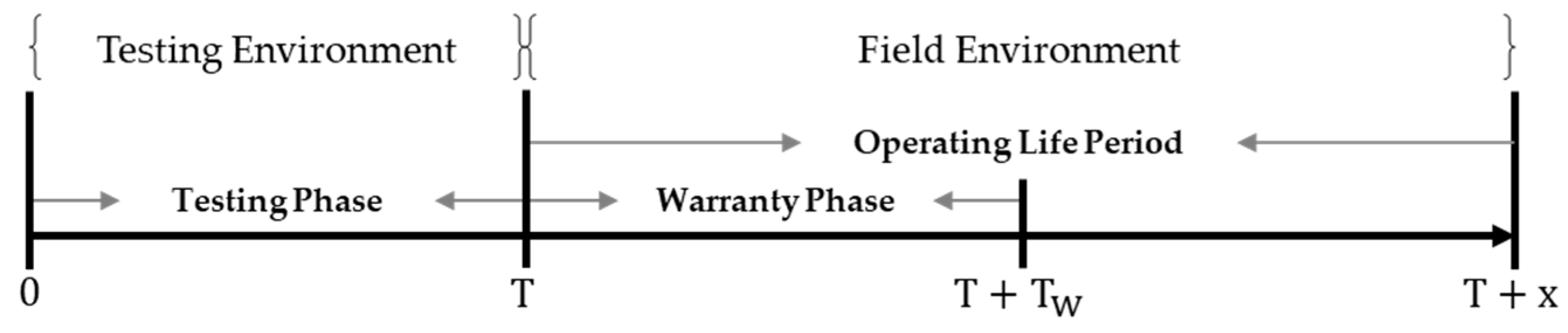
5. Software Release Policy
5.1. Optimal Release Time and Cost
5.2. Results of Optimal Release Time and Cost
6. Sensitivity Analysis
6.1. Sensitivity Analysis of Parameters
6.2. Results of Sensitivity Analysis
7. Conclusions
8. Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Acronyms
| SRGM | Software Reliability Growth Model |
| NHPP | Non Homogenous Poisson Process |
| LSE | Least Squares Estimation |
| MLE | Maximum Likelihood Estimation |
| MSE | Mean Squared Error |
| PRR | Predictive Ratio Risk |
| PP | Predictive Power |
| R2 | R-square |
| AIC | Akaike’s Information Criteria |
| SAE | Sum of Absolute Error |
| PRV | Predicted Relative Variation |
| RMSPE | Root Mean Square Prediction Error |
References
- Clarke, P.; O’Connor, R.V. The situational factors that affect the software development process: Towards a comprehensive reference framework. Inf. Softw. Technol. 2012, 54, 433–447. [Google Scholar] [CrossRef]
- Musa, J.D.; Iannino, A.; Okumoto, K. Software Reliability: Measurement, Prediction, and Application; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped reliability growth modeling for software fault detection. IEEE Trans. Reliab. 1983, 32, 475–484. [Google Scholar] [CrossRef]
- Yamada, S.; Ohba, M.; Osaki, S. Software Reliability Growth Models with Testing-effort. IEEE Trans. Reliab. 1986, 35, 19–23. [Google Scholar] [CrossRef]
- Quadri, S.M.K.; Ahmad, N.; Peer, M.A. Software optimal release policy and reliability growth modeling. In Proceedings of the 2nd National Conference on Computing for Nation Development, New Delhi, India, 8–9 February 2008; pp. 423–431. [Google Scholar]
- Ahmd, N.; Khan, M.G.M.; Rafi, L.S. A study of testing-effort dependent inflection S-shaped software reliability growth models with imperfect debugging. Int. J. Qual. Reliab. Manag. 2009, 27, 89–110. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. An NHPP software reliability models and its comparison. Int. J. Reliab. Qual. Saf. Eng. 1997, 4, 269–282. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. Software Reliability and Cost Models with Testing Coverage. Eur. J. Oper. Res. 2003, 145, 443–454. [Google Scholar] [CrossRef]
- Teng, X.; Pham, H. A new methodology for predicting software reliability in the random field environments. IEEE Trans. Reliab. 2006, 55, 458–468. [Google Scholar] [CrossRef]
- Pham, H. Loglog Fault-Detection Rate and Testing Coverage Software Reliability Models Subject to Random Environments. Vietnam J. Comput. Sci. 2014, 1, 39–45. [Google Scholar] [CrossRef]
- Inoue, S.; Ikeda, J.; Yamda, S. Bivariate change-point modeling for software reliability assessment with uncertainty of testing-environment factor. Ann. Oper. Res. 2016, 244, 209–220. [Google Scholar] [CrossRef]
- Li, Q.; Pham, H. A testing-coverage software reliability model considering fault removal efficiency and error generation. PLoS ONE 2017, 12, e0181524. [Google Scholar] [CrossRef] [PubMed]
- Song, K.Y.; Chang, I.H.; Pham, H. A three-parameter fault-detection software reliability model with the uncertainty of operating environments. J. Syst. Sci. Syst. Eng. 2017, 26, 121–132. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A Software Reliability Model with a Weibull Fault Detection Rate Function Subject to Operating Environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. An NHPP Software Reliability Model with S-Shaped Growth Curve Subject to Random Operating Environments and Optimal Release Time. Appl. Sci. 2017, 7, 1304. [Google Scholar] [CrossRef]
- Zhu, M.; Pham, H. A two-phase software reliability modeling involving with software fault dependency and imperfect fault removal. Comput. Lang. Syst. Struct. 2018, 53, 27–42. [Google Scholar] [CrossRef]
- Zhu, M.; Pham, H. A software reliability model incorporating martingale process with gamma-distributed environmental factors. Ann. Oper. Res. 2018, 1–22. [Google Scholar] [CrossRef]
- Zeephongsekul, P.; Jayasinghe, C.L.; Fiondella, L.; Nagaraju, V. Maximum-Likelihood Estimation of Parameters of NHPP Software Reliability Models Using Expectation Conditional Maximization Algorithm. IEEE Trans. Reliab. 2016, 65, 1571–1583. [Google Scholar] [CrossRef]
- Candini, F.; Gioletta, A. A Bayesian Monte Carlo-based algorithm for the estimation of small failure probabilities of systems affected by uncertainties. Reliab. Eng. Syst. Saf. 2016, 153, 15–27. [Google Scholar] [CrossRef]
- Caiuta, R.; Pozo, A.; Vergilio, S.R. Meta-learning based selection of software reliability models. Automat. Softw. 2017, 24, 575–602. [Google Scholar] [CrossRef]
- Tamura, Y.; Yamda, S. Software Reliability Model Selection Based on Deep Learning with Application to the Optimal Release Problem. J. Ind. Eng. Manag. Sci. 2018, 2016, 43–58. [Google Scholar] [CrossRef]
- Tamura, Y.; Matsumoto, S.; Yamada, S. Software Reliability Model Selection Based on Deep Learning. In Proceedings of the International Conference on Industrial Engineering Management Science and Application, Jeju, Korea, 23–26 May 2016; pp. 1–5. [Google Scholar]
- Wang, J.; Zhang, C. Software reliability prediction using a deep learning model based on the RNN encoder-decoder. Reliab. Eng. Syst. Saf. 2018, 170, 73–82. [Google Scholar] [CrossRef]
- Kim, K.C.; Kim, Y.H.; Shin, J.H.; Han, K.J. A Case Study on Application for Software Reliability Model to Improve Reliability of the Weapon System. J. KIISE 2011, 38, 405–418. [Google Scholar]
- Goel, A.L.; Okumoto, K. Time dependent error detection rate model for software reliability and other performance measures. IEEE Trans. Reliab. 1979, 28, 206–211. [Google Scholar] [CrossRef]
- Ohba, M. Inflexion S-shaped software reliability growth models. In Stochastic Models in Reliability Theory; Osaki, S., Hatoyama, Y., Eds.; Springer: Berlin, Germany, 1984; pp. 144–162. [Google Scholar]
- Yamada, S.; Tokuno, K.; Osaki, S. Imperfect debugging models with fault introduction rate for software reliability assessment. Int. J. Syst. Sci. 1992, 23, 2241–2252. [Google Scholar] [CrossRef]
- Pham, H.; Nordmann, L.; Zhang, X. A general imperfect software debugging model with S-shaped fault detection rate. IEEE Trans. Reliab. 1999, 48, 169–175. [Google Scholar] [CrossRef]
- Pham, H. Software Reliability Models with Time Dependent Hazard Function Based on Bayesian Approach. Int. J. Autom. Comput. 2007, 4, 325–328. [Google Scholar] [CrossRef]
- Chang, I.H.; Pham, H.; Lee, S.W.; Song, K.Y. A testing-coverage software reliability model with the uncertainty of operation environments. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 220–227. [Google Scholar]
- Pham, H. System Software Reliability; Springer: London, UK, 2006; p. 13. [Google Scholar]
- Li, Q.; Pham, H. NHPP software reliability model considering the uncertainty of operating environments with imperfect debugging and testing coverage. Appl. Math. Model. 2017, 51, 68–85. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–719. [Google Scholar] [CrossRef]
- Pillai, K.; Nair, V.S. A model for software development effort and cost estimation. IEEE Trans. Softw. Eng. 1997, 23, 485–497. [Google Scholar] [CrossRef]
- Xu, J.; Yao, S. Software Reliability Growth model with Partial Differential Equation for Various Debugging Processes. Math. Probl. Eng. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Anjum, M.; Haque, M.A.; Ahmad, N. Analysis and ranking of software reliability models based on weighted criteria value. J. Inform. Technol. Comput. Sci. 2013, 2, 1–14. [Google Scholar] [CrossRef]
- Daniel, R.J.; Zhang, X. Some successful approaches to software reliability modeling in industry. J. Syst. Softw. 2005, 74, 85–99. [Google Scholar]
- Li, X.; Xie, M.; Ng, S.H. Sensitivity analysis of release time of software reliability models incorporating testing effort with multiple change-points. Appl. Math. Model. 2010, 34, 3560–3570. [Google Scholar] [CrossRef]


| No. | MODEL | m(t) |
|---|---|---|
| 1 | Goel Okumoto [25] | |
| 2 | Delayed S-shaped [3] | |
| 3 | Inflection S-shaped [26] | |
| 4 | Yamada Imperfect [27] | |
| 5 | Pham–Nordmann–Zhang (PNZ) [28] | |
| 6 | Pham–Zhang (PZ) [7] | |
| 7 | Dependent Parameter 2 [29] | |
| 8 | Testing Coverage [30] | |
| 9 | New model |
| Index | Time | Failure | Cum. Failure | Index | Time | Failure | Cum. Failure |
|---|---|---|---|---|---|---|---|
| 1 | 1249 | 4 | 4 | 8 | 40,594 | 4 | 30 |
| 2 | 4721 | 6 | 10 | 9 | 49,476 | 1 | 31 |
| 3 | 8786 | 4 | 14 | 10 | 55,596 | 0 | 31 |
| 4 | 13,669 | 3 | 17 | 11 | 58,061 | 1 | 32 |
| 5 | 19,094 | 6 | 23 | 12 | 58,588 | 1 | 33 |
| 6 | 24,750 | 1 | 24 | 13 | 58,633 | 0 | 33 |
| 7 | 32,299 | 2 | 26 | - | - | - | - |
| Time | Failure | Cum. Failure | Time | Failure | Cum. Failure |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 11 | 2 | 14 |
| 2 | 1 | 2 | 12 | 1 | 15 |
| 3 | 2 | 4 | 13 | 1 | 16 |
| 4 | 1 | 5 | 14 | 2 | 18 |
| 5 | 1 | 6 | 15 | 2 | 20 |
| 6 | 1 | 7 | 16 | 1 | 21 |
| 7 | 2 | 9 | 17 | 1 | 22 |
| 8 | 1 | 10 | 18 | 0 | 22 |
| 9 | 1 | 11 | 19 | 0 | 22 |
| 10 | 1 | 12 | - | - | - |
| Model | Data Set 1 | Data Set 2 |
|---|---|---|
| GO | ||
| DS | ||
| IS | , | , |
| YID | , | , |
| PNZ | ||
| PZ | , | , |
| DP2 | ||
| TC | , | , |
| New model | , , |
| Model | MSE | PRR | PP | SAE | AIC | PRV | RMSPE | |
|---|---|---|---|---|---|---|---|---|
| GO | 1.6260 | 0.6277 | 0.2425 | 0.9839 | 12.9385 | 49.4088 | 1.1979 | 1.2191 |
| DS | 7.3713 | 65.1778 | 1.1664 | 0.9269 | 25.6464 | 72.2377 | 2.5922 | 2.3315 |
| IS | 1.7887 | 0.6279 | 0.2426 | 0.9839 | 12.9397 | 51.4089 | 1.2191 | 1.2940 |
| YID | 1.7870 | 0.6278 | 0.2426 | 0.9839 | 12.9216 | 51.3945 | 1.2187 | 1.2922 |
| PNZ | 2.0232 | 0.5604 | 0.2266 | 0.9836 | 12.9766 | 53.6534 | 1.2307 | 1.4418 |
| PZ | 2.2359 | 0.6280 | 0.2426 | 0.9839 | 12.9400 | 55.4091 | 1.2192 | 1.6175 |
| DP2 | 33.5928 | 1.0252 | 8.3639 | 0.7273 | 50.9805 | 131.6861 | 5.0194 | 5.6645 |
| TC | 1.3975 | 0.0547 | 0.0696 | 0.9899 | 10.6421 | 52.2273 | 0.9640 | 1.3303 |
| New model | 1.0029 | 0.0165 | 0.0152 | 0.9922 | 8.1965 | 54.1355 | 0.7760 | 0.8417 |
| Model | MSE | PRR | PP | R2 | SAE | AIC | PRV | RMSPE |
|---|---|---|---|---|---|---|---|---|
| GO | 0.5472 | 0.1919 | 0.3174 | 0.9898 | 10.9960 | 48.9315 | 0.7004 | 0.7179 |
| DS | 0.7472 | 6.2594 | 0.9673 | 0.9858 | 13.6902 | 48.5178 | 0.8226 | 0.8492 |
| IS | 0.3395 | 0.0715 | 0.0605 | 0.9941 | 8.1437 | 49.3896 | 0.5489 | 0.5493 |
| YID | 0.4886 | 0.1210 | 0.1786 | 0.9915 | 9.2881 | 50.5397 | 0.6564 | 0.6589 |
| PNZ | 0.3621 | 0.0721 | 0.0606 | 0.9941 | 8.1484 | 51.3791 | 0.5488 | 0.5493 |
| PZ | 0.3880 | 0.0722 | 0.0606 | 0.9941 | 8.1485 | 53.3790 | 0.5488 | 0.5493 |
| DP2 | 5.2747 | 1.3468 | 19.3541 | 0.9135 | 32.4992 | 70.1656 | 2.0966 | 2.0966 |
| TC | 0.4558 | 0.0797 | 0.0648 | 0.9930 | 8.5831 | 53.8763 | 0.5951 | 0.5954 |
| New model | 0.3481 | 0.0621 | 0.0522 | 0.9951 | 7.3657 | 54.7293 | 0.5011 | 0.5014 |
| Data Set 1 | Data Set 2 | ||||
|---|---|---|---|---|---|
| Time | LC | UC | Time | LC | UC |
| 1249 | 0.076714 | 7.910112 | 1 | −0.95994 | 2.962066 |
| 4721 | 3.510316 | 15.64006 | 2 | −0.72276 | 5.029449 |
| 8786 | 6.608054 | 21.23353 | 3 | −0.22797 | 6.968153 |
| 13,669 | 9.550651 | 26.10079 | 4 | 0.413007 | 8.848266 |
| 19,094 | 12.13476 | 30.16134 | 5 | 1.153972 | 10.6953 |
| 24,750 | 14.27082 | 33.41065 | 6 | 1.969788 | 12.52126 |
| 32,299 | 16.47781 | 36.68851 | 7 | 2.844421 | 14.33204 |
| 40,594 | 18.29813 | 39.34200 | 8 | 3.766162 | 16.12977 |
| 49,476 | 19.76057 | 41.44564 | 9 | 4.725129 | 17.91337 |
| 55,596 | 20.55722 | 42.58206 | 10 | 5.71162 | 19.67833 |
| 58,061 | 20.83969 | 42.98349 | 11 | 6.71484 | 21.41613 |
| 58,588 | 20.89753 | 43.06561 | 12 | 7.721905 | 23.1137 |
| 58,633 | 20.90243 | 43.07256 | 13 | 8.717243 | 24.75315 |
| - | - | - | 14 | 9.682677 | 26.31238 |
| - | - | - | 15 | 10.59846 | 27.76699 |
| - | - | - | 16 | 11.44533 | 29.09345 |
| - | - | - | 17 | 12.20722 | 30.27298 |
| - | - | - | 18 | 12.87369 | 31.29499 |
| - | - | - | 19 | 13.44132 | 32.15873 |
| C0 | C1 | C2 | C3 | C4 | x | μx | μw | Tw |
|---|---|---|---|---|---|---|---|---|
| 500 | 10 | 50 | 5000 | 500 | 10 | 0.1 | 0.1 | 10 |
| Tw = 5 | Tw = 10 | Tw = 15 | Tw = 20 | |||||
|---|---|---|---|---|---|---|---|---|
| T* | C(T) | T* | C(T) | T* | C(T) | T* | C(T) | |
| New | 46.6 | 1166.8328 | 47 | 1172.8471 | 47.2 | 1176.2287 | 47.4 | 1178.2435 |
| C0 | Tw = 5 | Tw = 10 | Tw = 15 | Tw = 20 | ||||
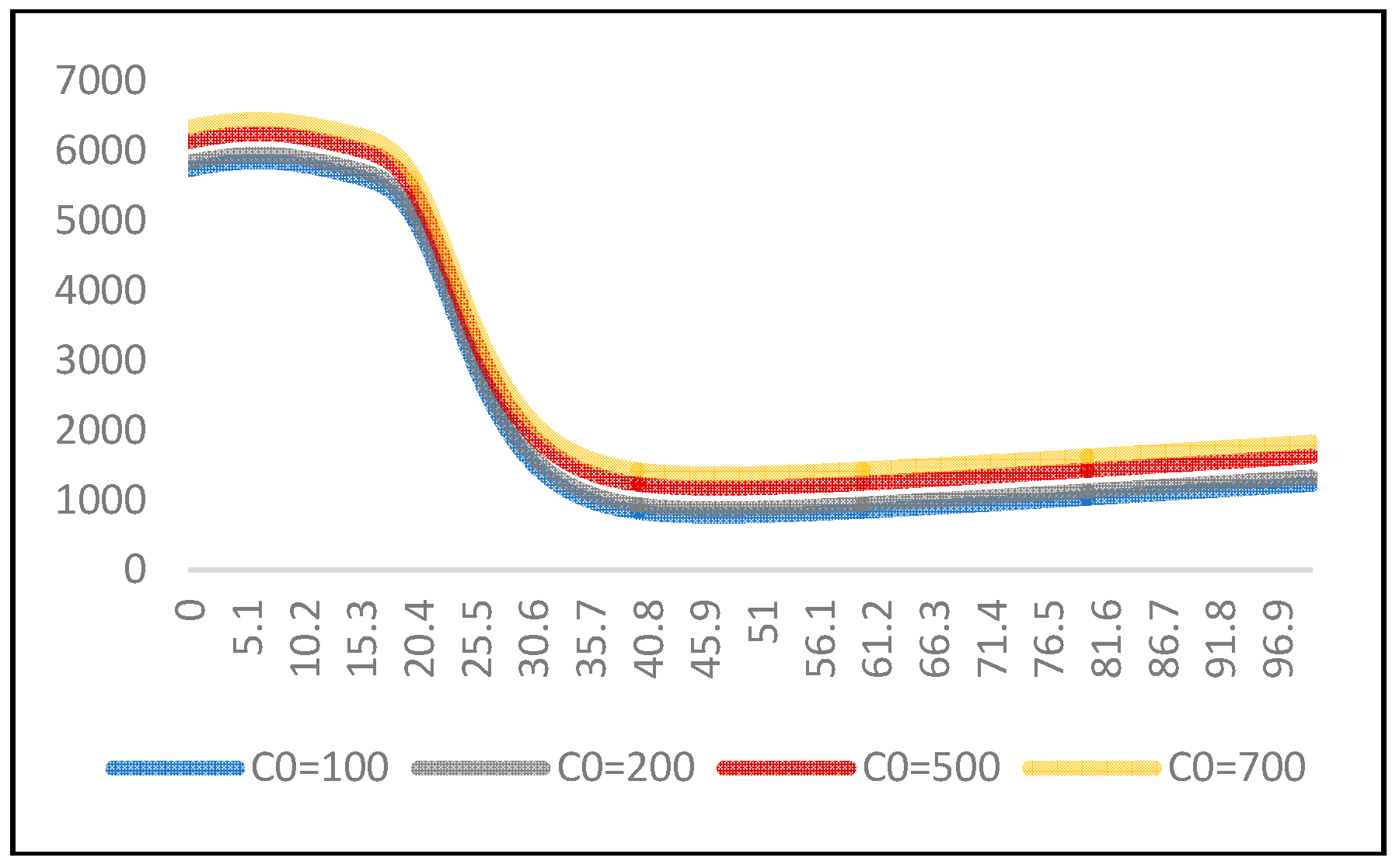
|---|---|---|---|---|---|---|---|---|
| T* | C(T) | T* | C(T) | T* | C(T) | T* | C(T) | |
| 100 | 46.6 | 766.8328 | 47 | 772.8471 | 47.2 | 776.2287 | 47.4 | 778.2435 |
| 200 | 46.6 | 866.8328 | 47 | 872.8471 | 47.2 | 876.2287 | 47.4 | 878.2435 |
| 500 | 46.6 | 1166.8328 | 47 | 1172.8471 | 47.2 | 1176.2287 | 47.4 | 1178.2435 |
| 700 | 46.6 | 1366.8328 | 47 | 1372.8471 | 47.2 | 1376.2287 | 47.4 | 1378.2435 |
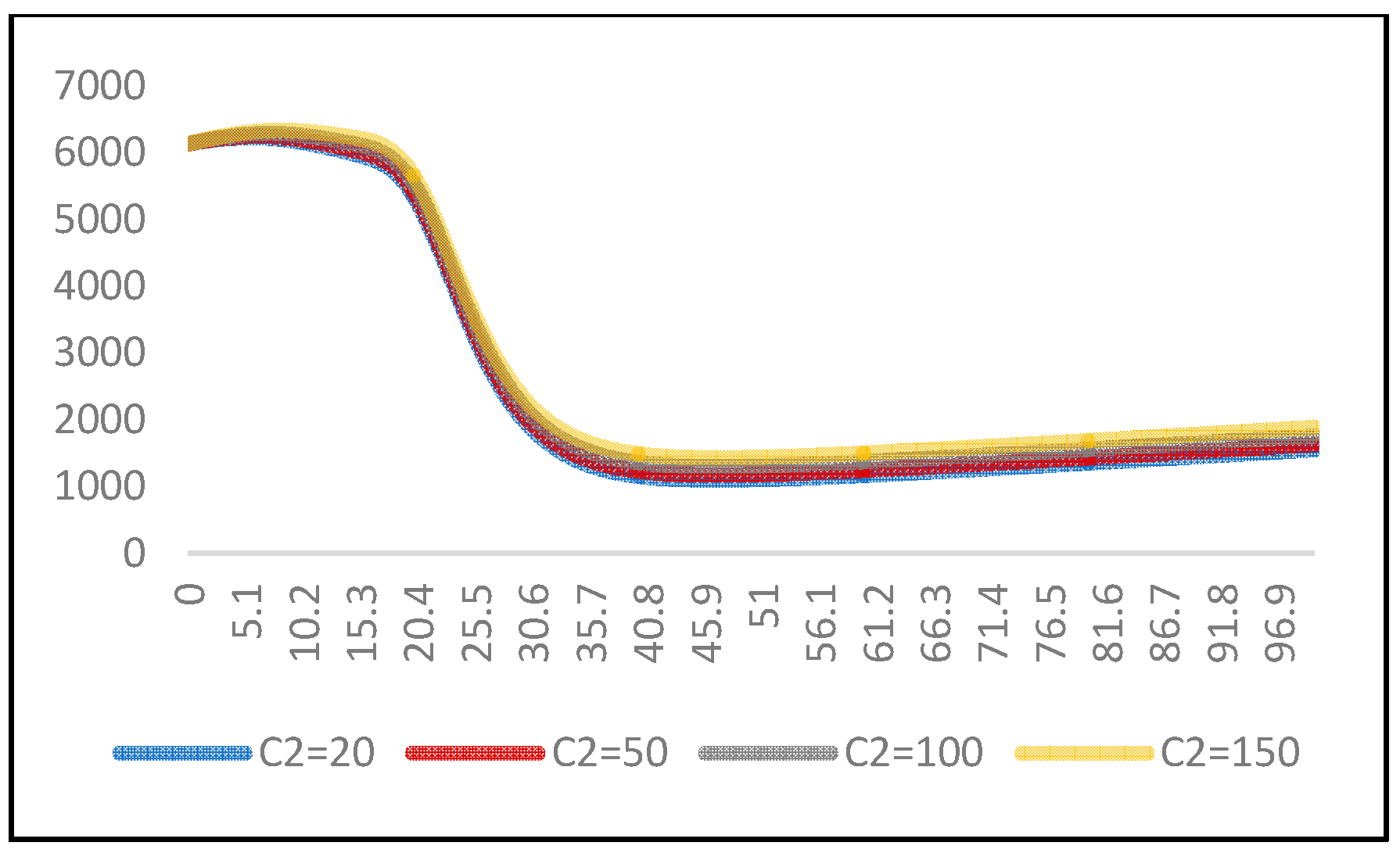
| C2 | Tw = 5 | Tw = 10 | Tw = 15 | Tw = 20 | ||||
|---|---|---|---|---|---|---|---|---|
| T* | C(T) | T* | C(T) | T* | C(T) | T* | C(T) | |
| 20 | 46.6 | 1089.6537 | 47 | 1095.6652 | 47.2 | 1099.0456 | 47.4 | 1101.0591 |
| 50 | 46.6 | 1166.8328 | 47 | 1172.8471 | 47.2 | 1176.2287 | 47.4 | 1178.2435 |
| 100 | 46.6 | 1295.4647 | 47 | 1301.4835 | 47.2 | 1304.8673 | 47.3 | 1306.8837 |
| 150 | 46.6 | 1424.0966 | 47 | 1430.1199 | 47.2 | 1433.5059 | 47.3 | 1435.5233 |
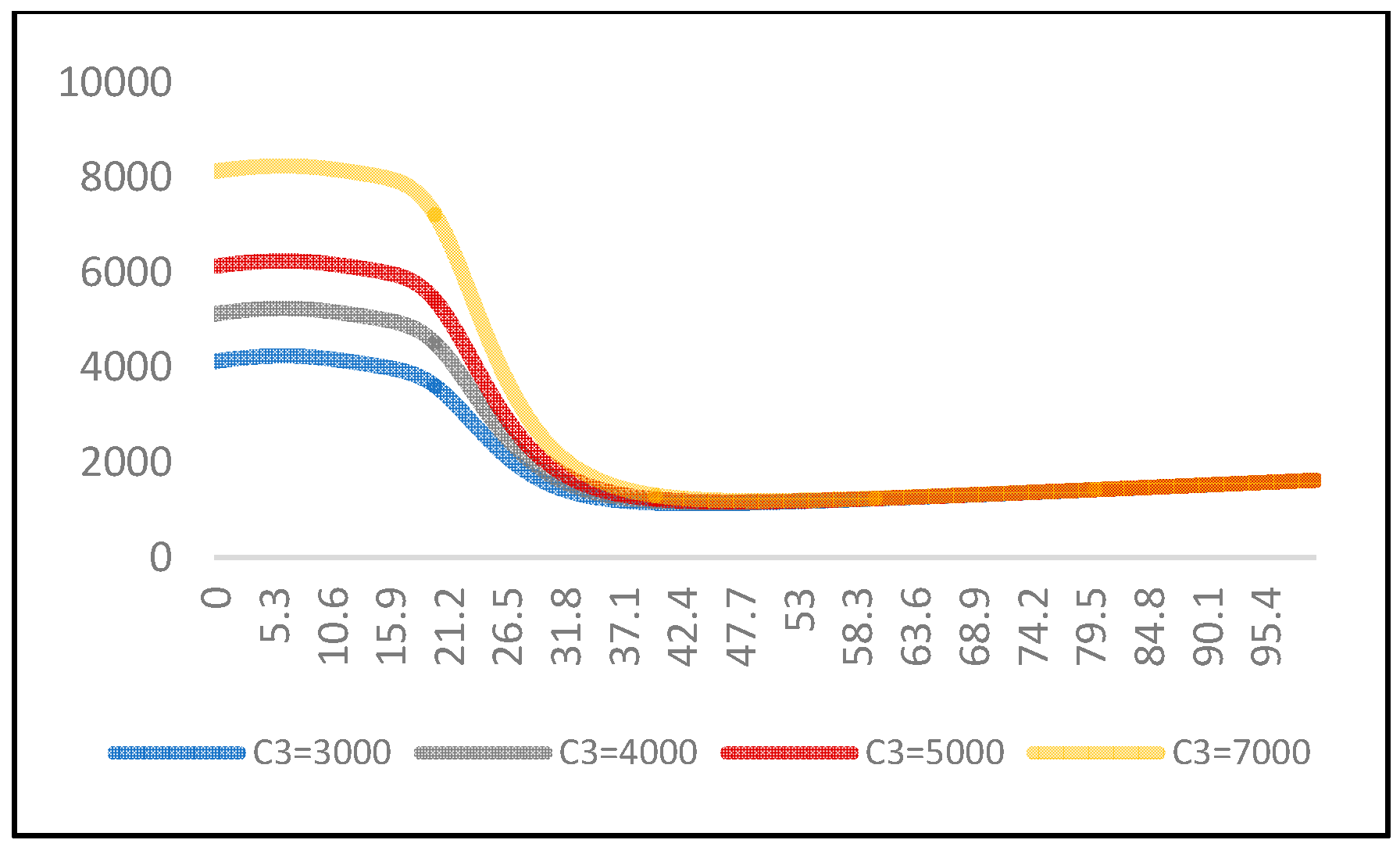
| C3 | Tw = 5 | Tw = 10 | Tw = 15 | Tw = 20 | ||||
|---|---|---|---|---|---|---|---|---|
| T* | C(T) | T* | C(T) | T* | C(T) | T* | C(T) | |
| 3000 | 43.4 | 1131.1875 | 43.8 | 1136.4696 | 44 | 1139.3614 | 44.1 | 1141.0439 |
| 4000 | 45.2 | 1150.9796 | 45.6 | 1156.6584 | 45.8 | 1159.8148 | 45.9 | 1161.6762 |
| 5000 | 46.6 | 1166.8328 | 47 | 1172.8471 | 47.2 | 1176.2287 | 47.4 | 1178.2435 |
| 7000 | 48.7 | 1191.5935 | 49.2 | 1198.1598 | 49.5 | 1201.9114 | 49.6 | 1204.1773 |
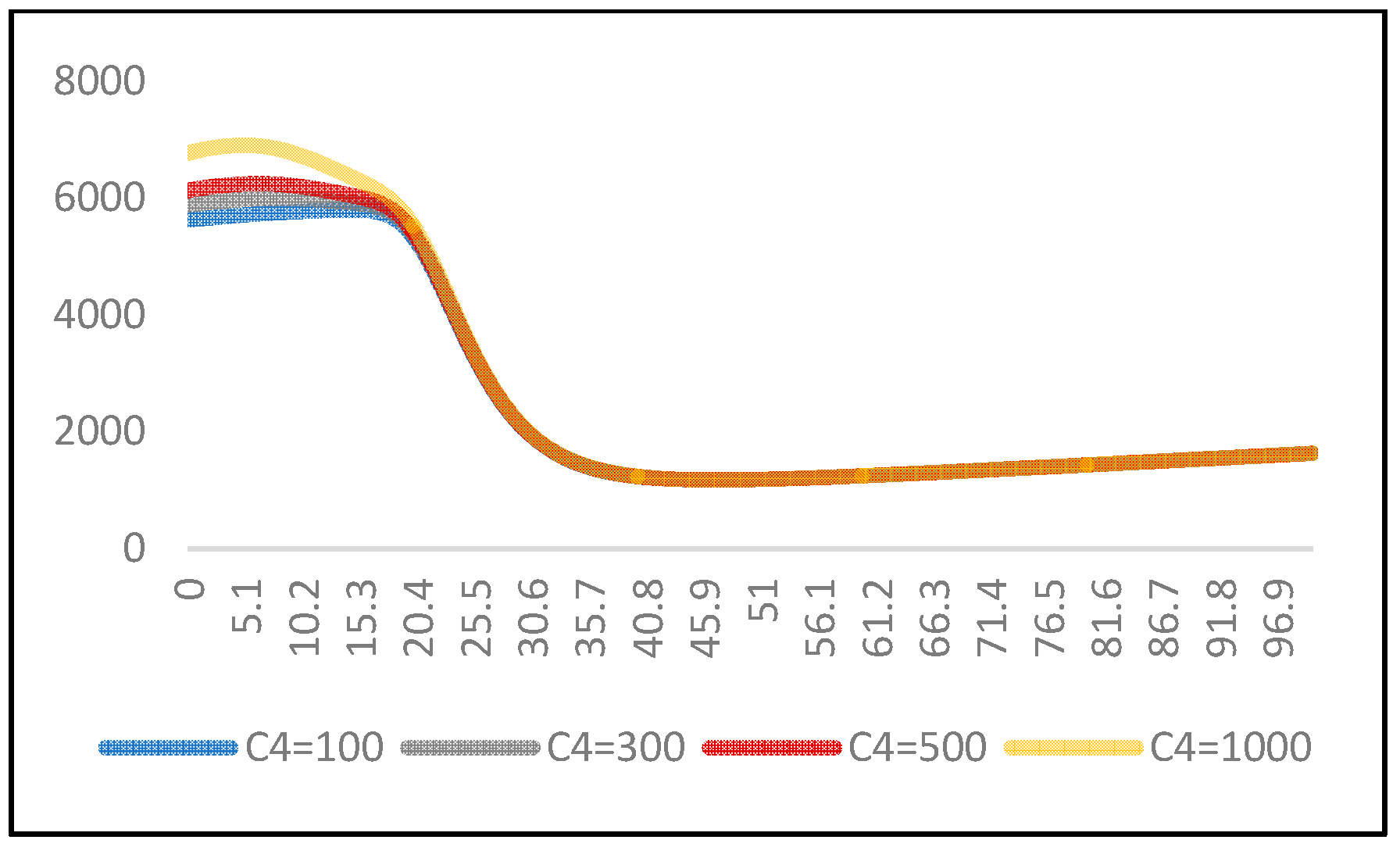
| C4 | Tw = 5 | Tw = 10 | Tw = 15 | Tw = 20 | ||||
|---|---|---|---|---|---|---|---|---|
| T* | C(T) | T* | C(T) | T* | C(T) | T* | C(T) | |
| 100 | 46.5 | 1166.5033 | 47 | 1172.3822 | 47.2 | 1175.6963 | 47.3 | 1177.6743 |
| 300 | 46.6 | 1166.6685 | 47 | 1172.6146 | 47.2 | 1175.9625 | 47.3 | 1177.9591 |
| 500 | 46.6 | 1166.8328 | 47 | 1172.8471 | 47.2 | 1176.2287 | 47.4 | 1178.2435 |
| 1000 | 46.6 | 1167.2435 | 47.1 | 1173.4273 | 47.3 | 1176.8886 | 47.4 | 1178.9461 |
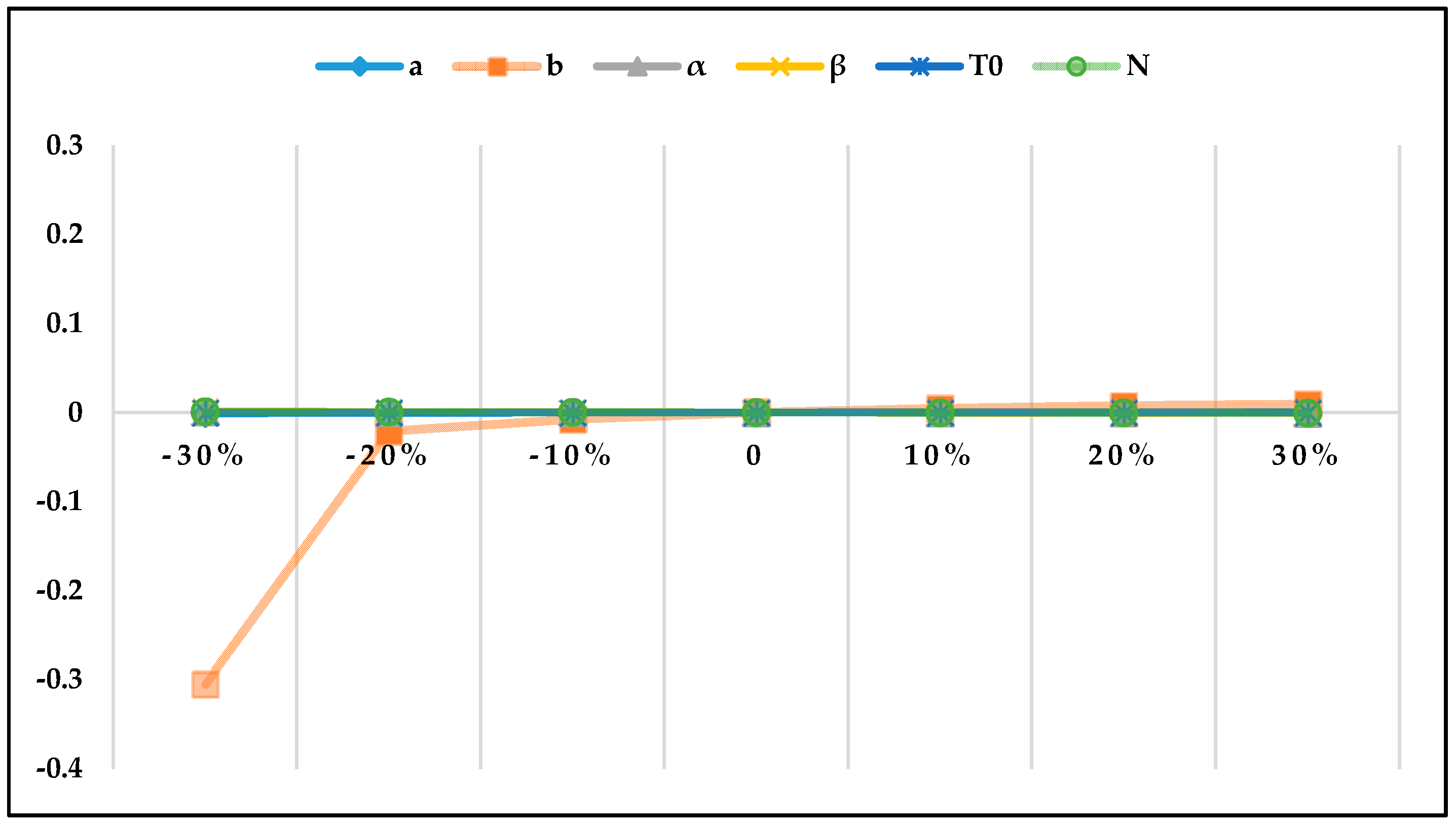
| −30% | −20% | −10% | 0 | 10% | 20% | 30% | |
|---|---|---|---|---|---|---|---|
| a | 0.022837 | 0.014165 | 0.006637 | 0 | −0.005927 | −0.011273 | −0.016140 |
| b | 1.739638 | 0.498721 | 0.187518 | 0 | −0.118787 | −0.197279 | −0.251138 |
| −0.021859 | −0.013792 | −0.006561 | 0 | 0.006012 | 0.011565 | 0.016728 | |
| −0.021811 | −0.013763 | −0.006547 | 0 | 0.006000 | 0.011543 | 0.016696 | |
| −0.000003 | −0.000002 | −0.000001 | 0 | 0.000001 | 0.000002 | 0.000003 | |
| −0.054793 | −0.035748 | −0.017538 | 0 | 0.016989 | 0.033519 | 0.049658 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.H.; Chang, I.H.; Pham, H.; Song, K.Y. A Software Reliability Model Considering the Syntax Error in Uncertainty Environment, Optimal Release Time, and Sensitivity Analysis. Appl. Sci. 2018, 8, 1483. https://doi.org/10.3390/app8091483
Lee DH, Chang IH, Pham H, Song KY. A Software Reliability Model Considering the Syntax Error in Uncertainty Environment, Optimal Release Time, and Sensitivity Analysis. Applied Sciences. 2018; 8(9):1483. https://doi.org/10.3390/app8091483
Chicago/Turabian StyleLee, Da Hye, In Hong Chang, Hoang Pham, and Kwang Yoon Song. 2018. "A Software Reliability Model Considering the Syntax Error in Uncertainty Environment, Optimal Release Time, and Sensitivity Analysis" Applied Sciences 8, no. 9: 1483. https://doi.org/10.3390/app8091483
APA StyleLee, D. H., Chang, I. H., Pham, H., & Song, K. Y. (2018). A Software Reliability Model Considering the Syntax Error in Uncertainty Environment, Optimal Release Time, and Sensitivity Analysis. Applied Sciences, 8(9), 1483. https://doi.org/10.3390/app8091483




