Scale Analysis of Wavelet Regularization Inversion and Its Improved Algorithm for Dynamic Light Scattering
Abstract
1. Introduction
2. Principle of WRIM for DLS
2.1. Regularization Inversion of DLS
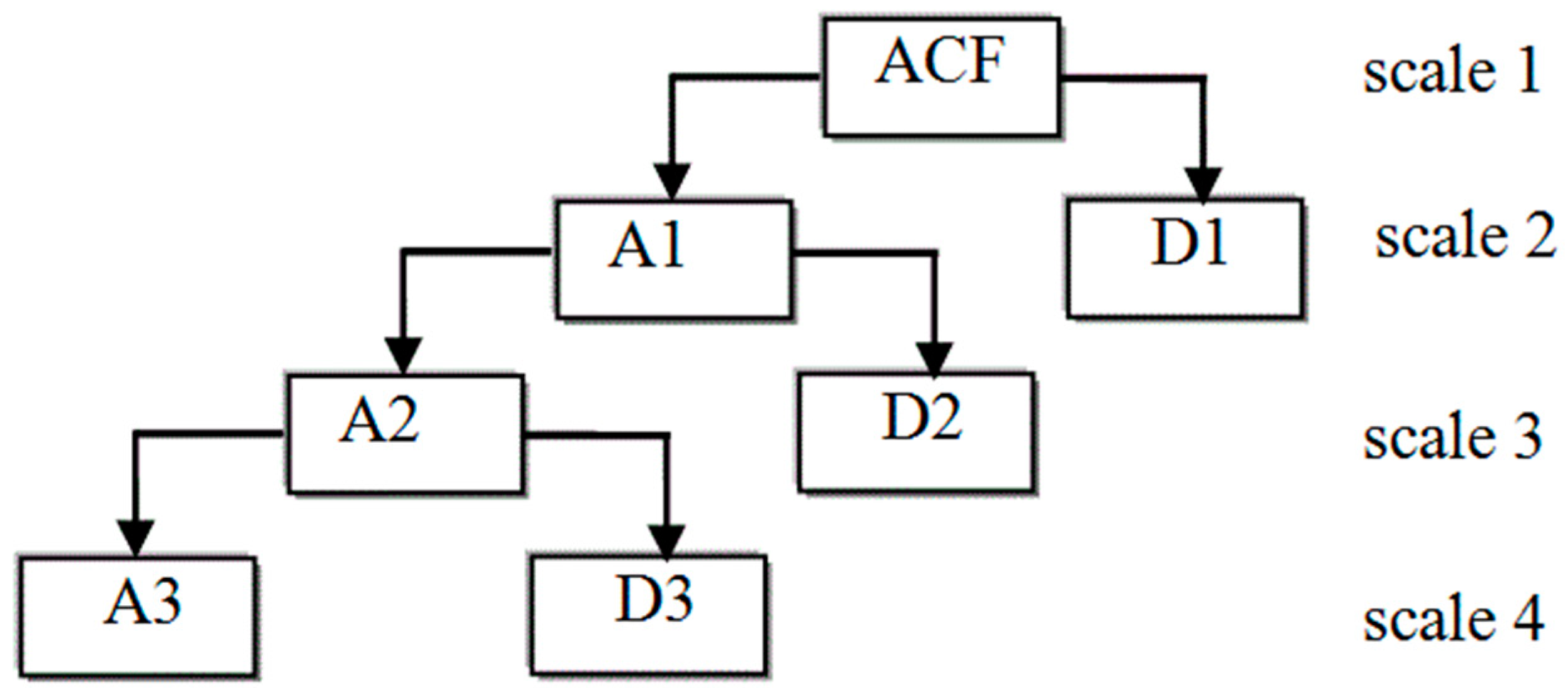
2.2. Inversion Principle of WRIM
3. Analysis of Scale Effect of Simulation Data
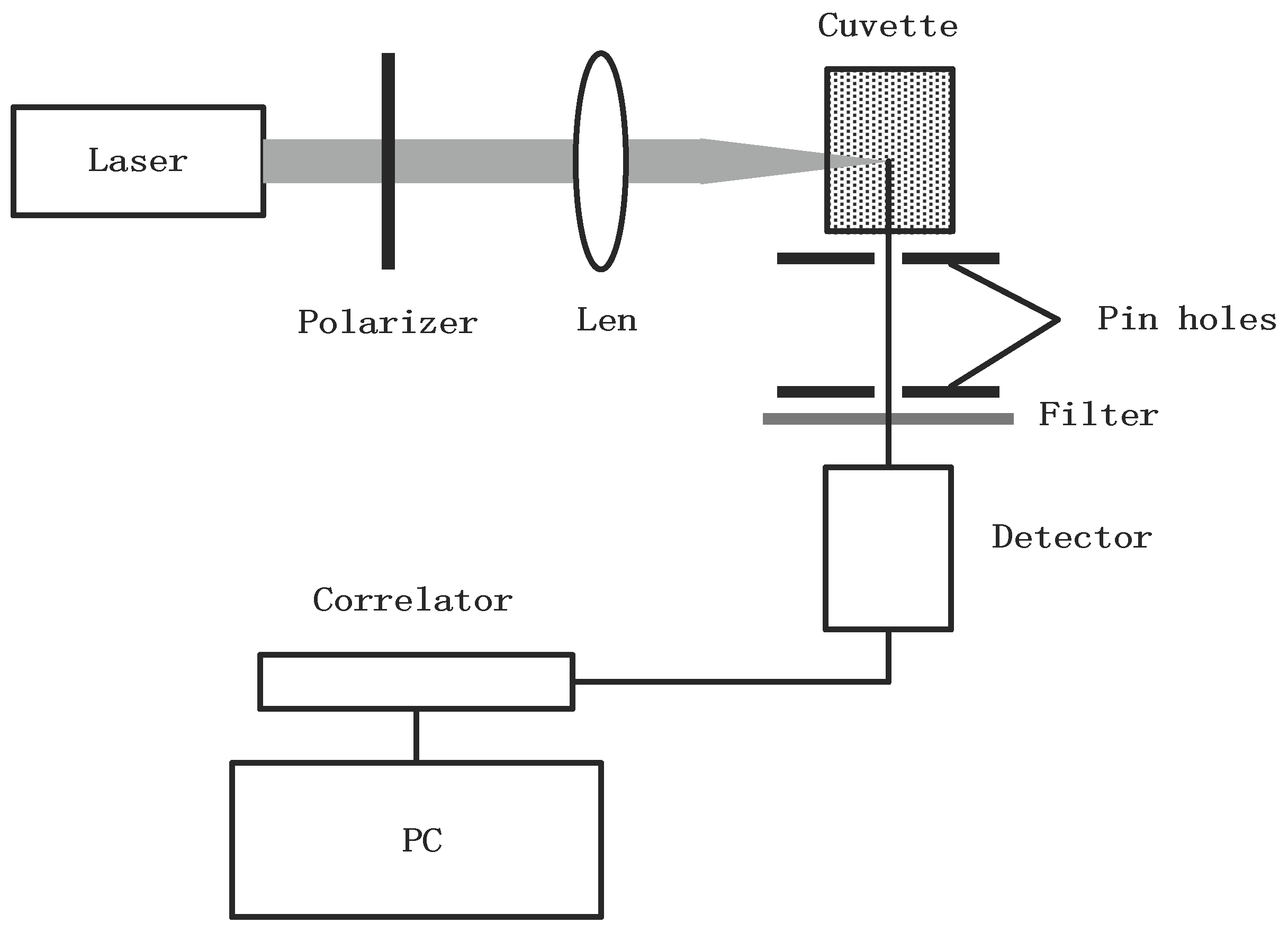
3.1. Simulation Experiment Parameters and Conditions
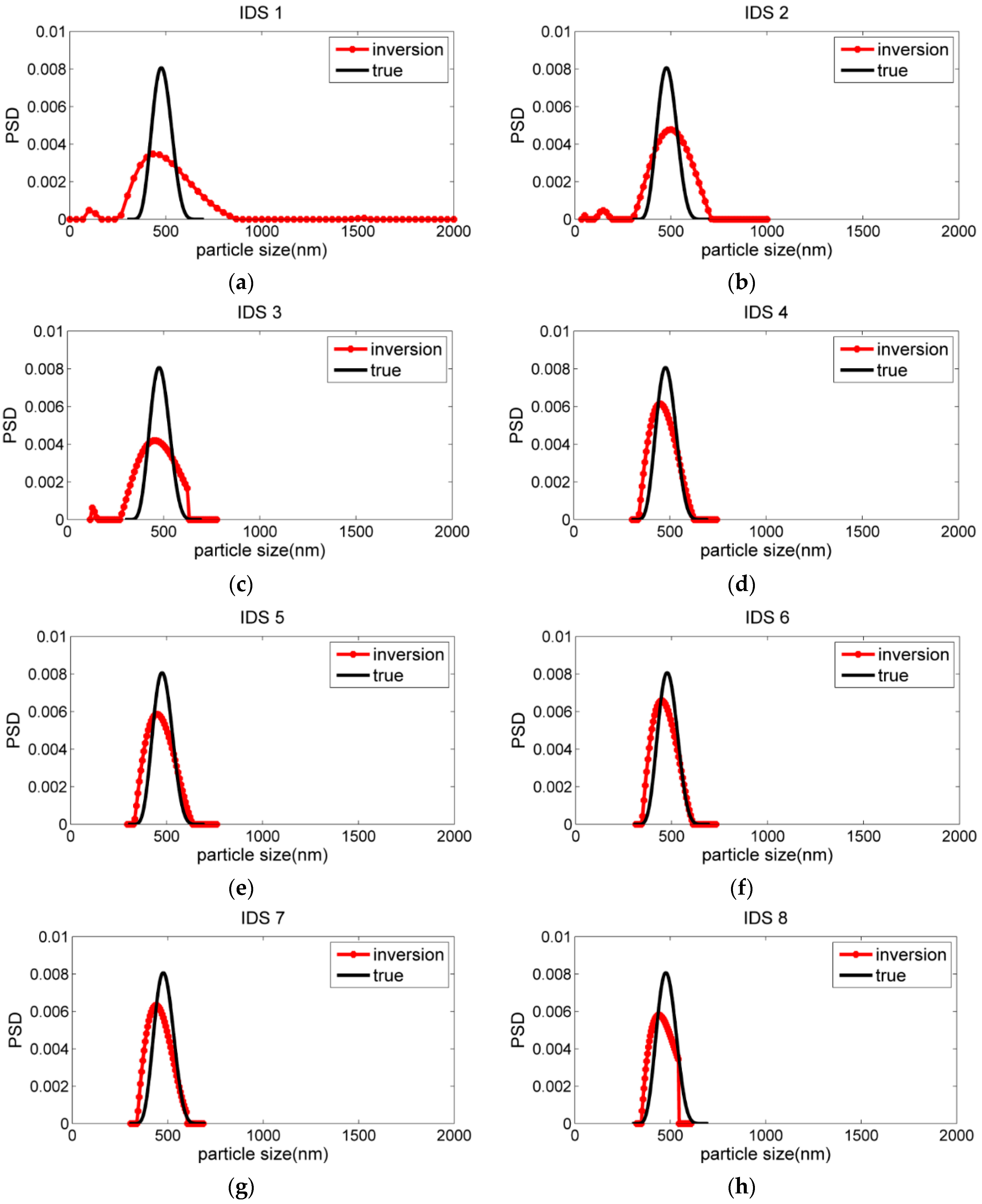
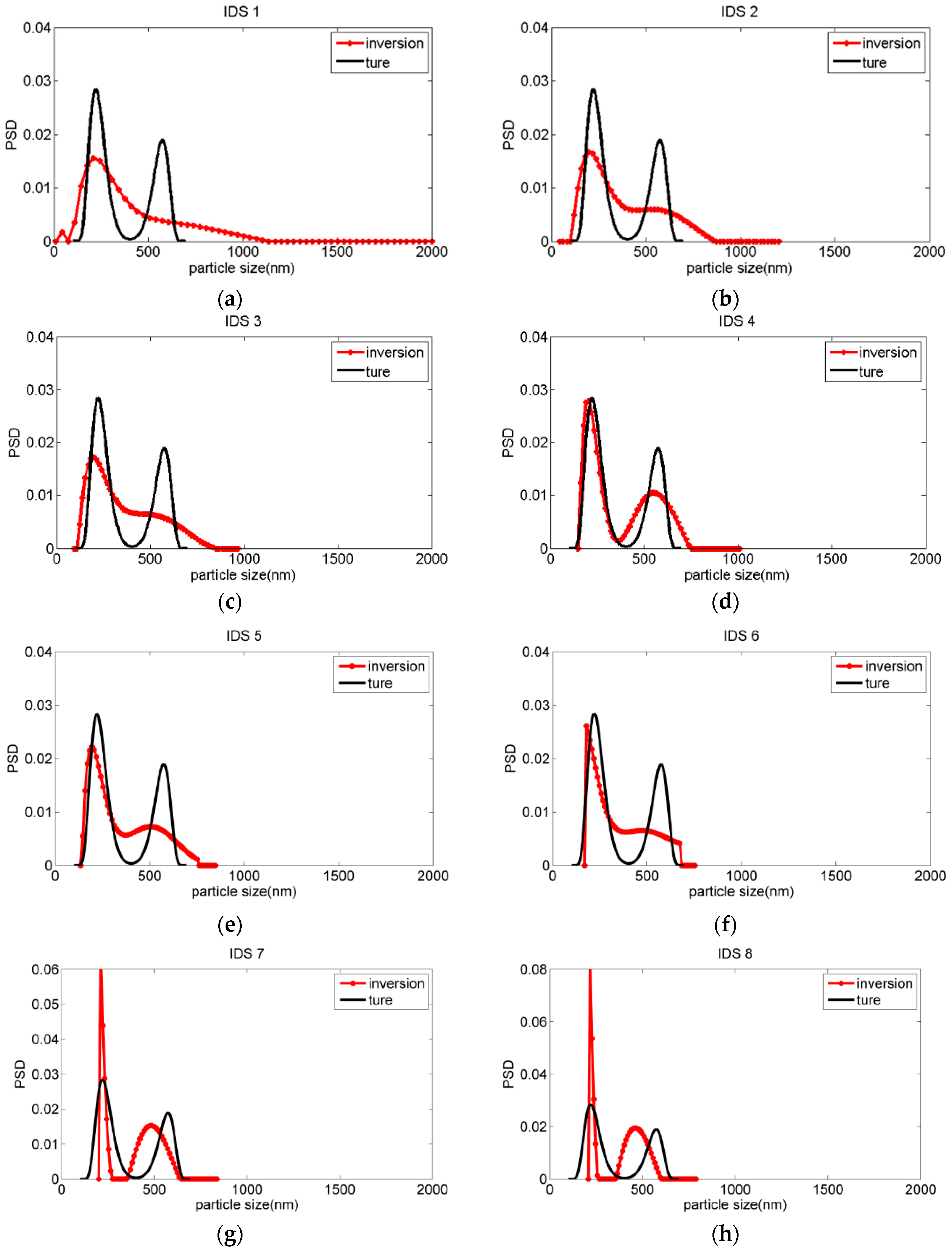
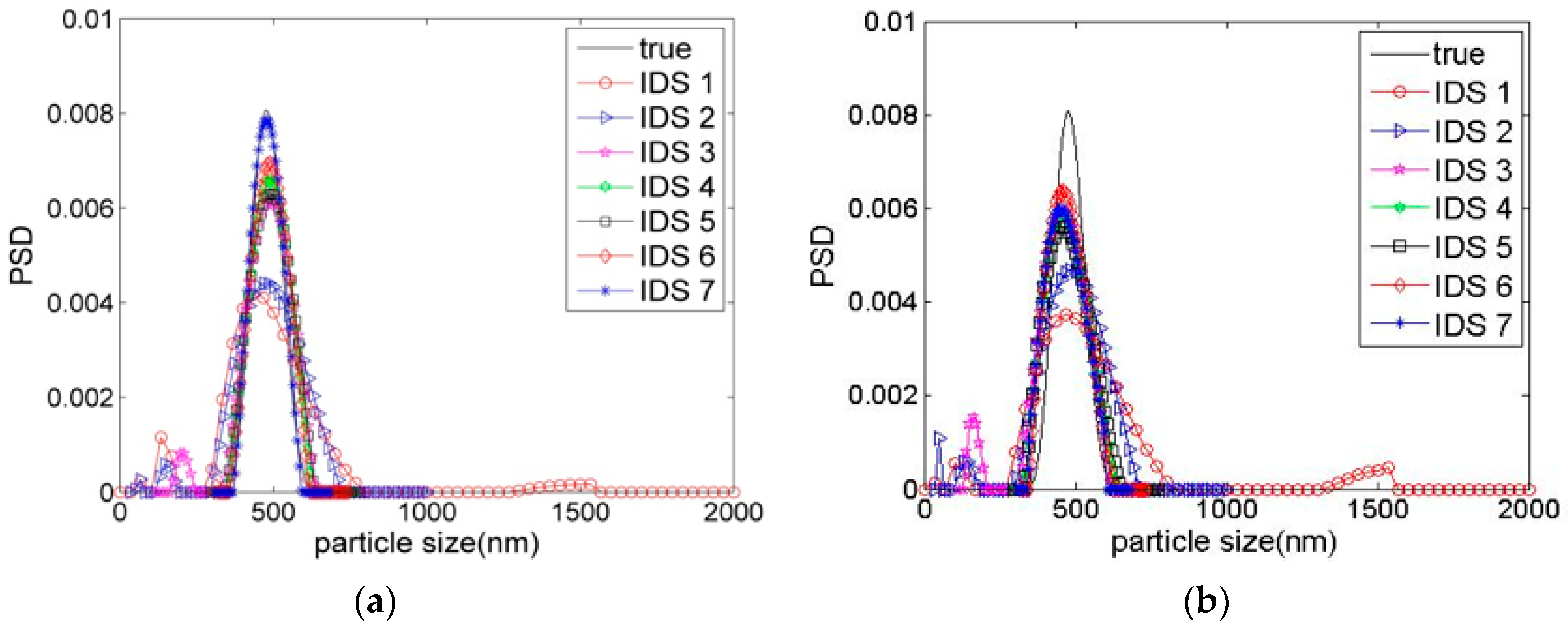
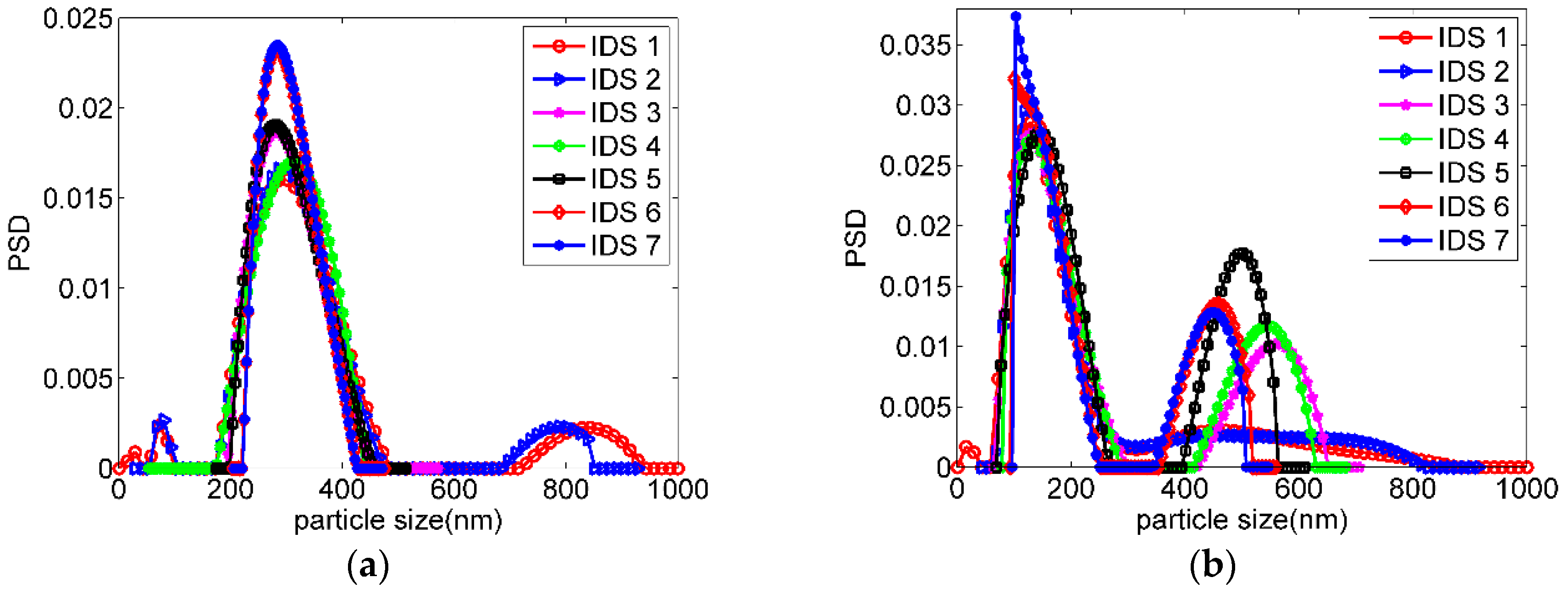
3.2. Inversion Analysis on Different IDSs
3.3. Effect of ACF Noise on Optimal IDS
4. Improved WRIM with Optimal IDS
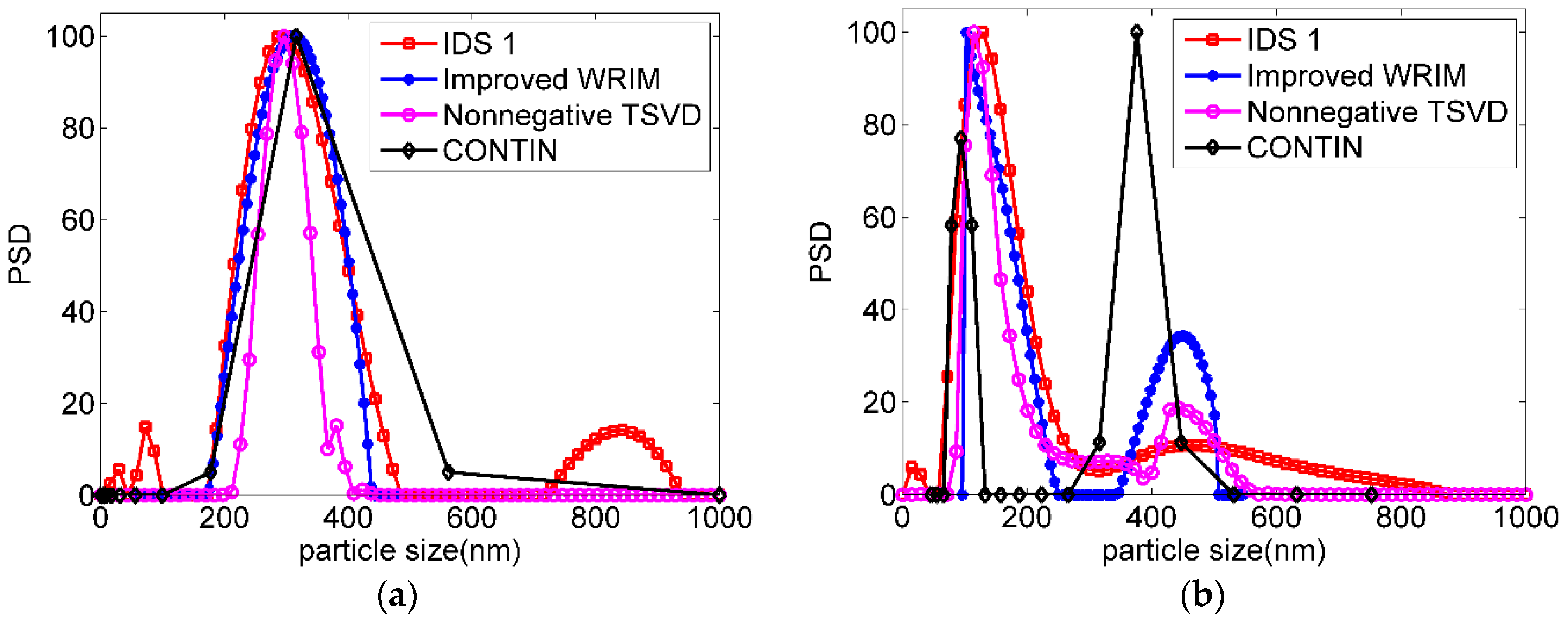
5. Inversion Analysis of Experimental Data
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Yang, K.C.; Li, W.; Wang, W.Y.; Guo, W.P. A recursive regularization algorithm for estimating the particle size distribution from multiangle dynamic light scattering measurements. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 244–254. [Google Scholar] [CrossRef]
- Zhu, X.; Shen, J.; Song, L. Accurate Retrieval of Bimodal Particle Size Distribution in Dynamic Light Scattering. IEEE Photonics Technol. Lett. 2015, 28, 311–314. [Google Scholar] [CrossRef]
- Robert, F. Particle Sizing in the Submicron Range by Dynamic Light Scattering. KONA Powder Part. 1993, 11, 17–32. [Google Scholar] [CrossRef]
- Takahashi, K.; Kato, H.; Saito, T. Precise measurement of the size of nanoparticles by dynamic light scattering with Uncertainty Analysis. Part. Part. Syst. Charact. 2008, 25, 31–38. [Google Scholar] [CrossRef]
- Li, Z.M.; Shen, J.; Sun, X.M.; Wang, Y.J. Nanoparticle Size Measurement from Dynamic Light Scattering Data Based on Autoregressive Model. Laser Phys. Lett. 2013, 10, 095701–095705. [Google Scholar] [CrossRef]
- Liu, W.; Sun, X.M.; Shen, J. A V-curve criterion for the parameter optimization of the Tikhonov regularization inversion algorithm for particle sizing. Opt. Laser Technol. 2012, 44, 1–5. [Google Scholar] [CrossRef]
- Koppel, D.E. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: The Method of Cumulants. J. Chem. Phys. 1972, 57, 4814–4820. [Google Scholar] [CrossRef]
- Frisken, B.J. Revisiting the method of cumulants for analysis of dynamic light scattering data. Appl. Opt. 2001, 40, 4087–4091. [Google Scholar] [CrossRef] [PubMed]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Provencher, S.W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- McWhirter, J.G.; Pike, E.R. On the numerical inversion of the Laplace transform and similar Fredholm integral equations of the first kind. J. Phys. A Math. Theor. 1978, 11, 1729–1745. [Google Scholar] [CrossRef]
- Varah, J.M. On the Numerical Solution of Ill-Conditioned linear systems with applications to Ill-Posed problems. Siam J. Numer. Anal. 1973, 10, 257–267. [Google Scholar] [CrossRef]
- Sun, Y.F.; Walker, J.G. Maximum likelihood data inversion for photon correlation spectroscopy. Meas. Sci Technol. 2008, 19, 115302. [Google Scholar] [CrossRef]
- Ostrowsky, N.; Sornette, D.; Parker, P.; Pike, E.R. Exponential sampling method for light scattering polydispersity analysis. J. Mod Opt. 1981, 28, 1059–1070. [Google Scholar] [CrossRef]
- Zhu, X.; Shen, J.; Liu, W.; Sun, X.; Wang, Y. Nonnegative least-squares truncated singular value decomposition to particle size distribution inversion from dynamic light scattering data. Appl. Opt. 2010, 49, 6591–6596. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M. On photon correlation measurements of colloidal size distributions using Bayesian strategies. J. Comput. Appl. Math. 2000, 126, 77–89. [Google Scholar] [CrossRef]
- Naiim, M.; Boualem, A.; Ferre, C.; Jabloun, M.; Jalocha, A.; Ravier, P. Multiangle dynamic light scattering for the improvement of multimodal particle size distribution measurements. Soft Matter 2015, 11, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Clementi, L.A.; Vega, J.R.; Gugliotta, L.M.; Orlande, H.R.B. A Bayesian inversion method for estimating the particle size distribution of latexes from multiangle dynamic light scattering measurements. Chemom. Intell. Lab. Syst. 2011, 107, 165–173. [Google Scholar] [CrossRef]
- Livesey, A.K.; Licinio, P.; Delaye, M. Maximum entropy analysis of quasielastic light scattering from colloidal dispersions. J. Chem. Phys. 1986, 84, 5102–5107. [Google Scholar] [CrossRef]
- Ye, M.; Wang, S.; Lu, Y. Inversion of particle-size distribution from angular light-scattering data with genetic algorithms. Appl. Opt. 1999, 38, 2677–2685. [Google Scholar] [CrossRef] [PubMed]
- Clementi, L.A.; Vega, J.R.; Gugliotta, L.M. Particle Size Distribution of Multimodal Polymer Dispersions by Multiangle Dynamic Light Scattering. Solution of the Inverse Problem on the Basis of a Genetic Algorithm. Part. Part. Syst. Charact. 2010, 27, 146–157. [Google Scholar] [CrossRef]
- Gugliotta, L.M.; Stegmayer, G.S.; Clementi, L.A.; Gonzalez, V.D.G. A neural network model for estimating the particle size distribution of dilute latex from multiangle dynamic light scattering measurements. Part. Part. Syst. Charact. 2009, 26, 41–52. [Google Scholar] [CrossRef]
- Chicea, D. Using neural networks for dynamic light scattering time series processing. Meas. Sci. Technol. 2017, 28, 055206. [Google Scholar] [CrossRef]
- Shen, J.; Cai, X. Optimized inversion procedure for retrieval of particle size distributions from dynamic light scattering signals in current detection mode. Opt. Lett. 2010, 35, 2010. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Shen, J.; Wang, Y.; Guan, J.; Sun, X.; Wang, X. The reconstruction of particle size distributions from dynamic light scattering data using particle swarm optimization techniques with different objective functions. Opt. Laser Technol. 2011, 43, 1128–1137. [Google Scholar] [CrossRef]
- Mailer, A.G.; Clegg, P.S.; Pusey, P.N. Particle sizing by dynamic light scattering: Non-linear cumulant analysis. J. Phys. Condens. Matter 2015, 27, 145102. [Google Scholar] [CrossRef] [PubMed]
- Arias, M.L.; Frontini, G.L. Particle size distribution retrieval from elastic light scattering measurement by a modified regularization method. Part. Part. Syst. Charact. 2006, 23, 374–380. [Google Scholar] [CrossRef]
- Wang, T.; Shen, J.; Liu, X.; Zhu, X.; Liu, W.; Sun, X. Particle Size Distribution Recovery from Dynamic Light Scattering (DLS) Data Using the Nonnegative Constraint Total Variation Regularization Method. Laser Eng. 2014, 28, 57–67. [Google Scholar]
- Mao, S.; Shen, J.; Zhu, X.; Liu, W.; Sun, X. Modifed Regularized Solution of Truncated Singular Value Decomposition with Chahine Algorithm in Dynamic Light Scattering (DLS) Measurements. Laser Eng. 2013, 26, 45–47. [Google Scholar]
- Ruigang, L.; Xia, G.; Wilhelm, O. Dynamic light scattering studies on random cross-linking of polystyrene in semi-dilute solution. Polymer 2006, 47, 8488–8494. [Google Scholar] [CrossRef]
- Karl, F.; Manfred, S. Pitfalls and novel applications of particle sizing by dynamic light scattering. Biomaterials 2016, 98, 79–91. [Google Scholar] [CrossRef]
- Tomohisa, N.; Takashi, M.; Qui, T. Comparison of the gelation dynamics for polystyrenes prepared by conventional and living radical polymerizations: A time-resolved dynamic light scattering study. Polymer 2005, 46, 1982–1994. [Google Scholar] [CrossRef]
- Wang, Y.J.; Shen, J.; Zheng, G. Wavelets-regularization Method for Particles Size Inversion in Photon Correlation Spectroscopy. Opt. Laser Technol. 2012, 44, 1529–1535. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization Tools version 4.0 for Matlab 7.3. Numer. Algorithms 2007, 46, 189–194. [Google Scholar] [CrossRef]
- Kindermann, S.; Navasca, C. Optimal control as a regularization method for ill-posed problems. J. Inverse Ill-Posed Probl. 2006, 14, 685–703. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization TOOLS: A Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef]
- Hansen, P.C. The Use of the L-Curve in the Regularization of Discrete Ill-posed Problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Mingsian, R.B.; Chun, C.; Po-Chen, W. Solution trategies for Linear Inverse Problems in Spatial Audio Signal Processing. Appl. Sci. 2017, 7, 582. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the l-curve. SIAM Rev. 1992, 1, 561–580. [Google Scholar] [CrossRef]
- Sun, L.; Qian, Z. Multi-scale wavelet transform filtering of non-uniform pavement surface image background for automated pavement distress identification. Measurement 2016, 86, 26–40. [Google Scholar] [CrossRef]
- Mount, N.J.; Tate, N.J.; Sarker, M.H.; Thorne, C.R. Evolutionary, multi-scale analysis of river bank line retreat using continuous wavelet transforms: Jamuna River, Bangladesh. Geomorphology 2013, 183, 82–95. [Google Scholar] [CrossRef]
- Wu, Q.J.; Tian, X.B.; Zhang, N.L. Inversion of receiver function by wavelet transformation. Acta Seismol. Sin. 2003, 25, 601–607. [Google Scholar] [CrossRef]
- Hu, G.S. Modern Signal Processing; Tsinghua University Press: Beijing, China, 2004; pp. 10–13. [Google Scholar]
- Deng, H.; Wang, X.; Ma, P. A study of wavelet analysis based error compensation for the angular measuring system of high-precision test turntables. ISA Trans. 2005, 44, 15–21. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. A study of particle size distribution. Powder Technol. 1990, 62, 101–118. [Google Scholar] [CrossRef]
- Yu, L.S.; Yang, G.L.; He, Z.J. Iterative CONTIN algorithm for particle sizing in dynamic light scattering. Opto-Electron. Eng. 2006, 33, 64–69. [Google Scholar]

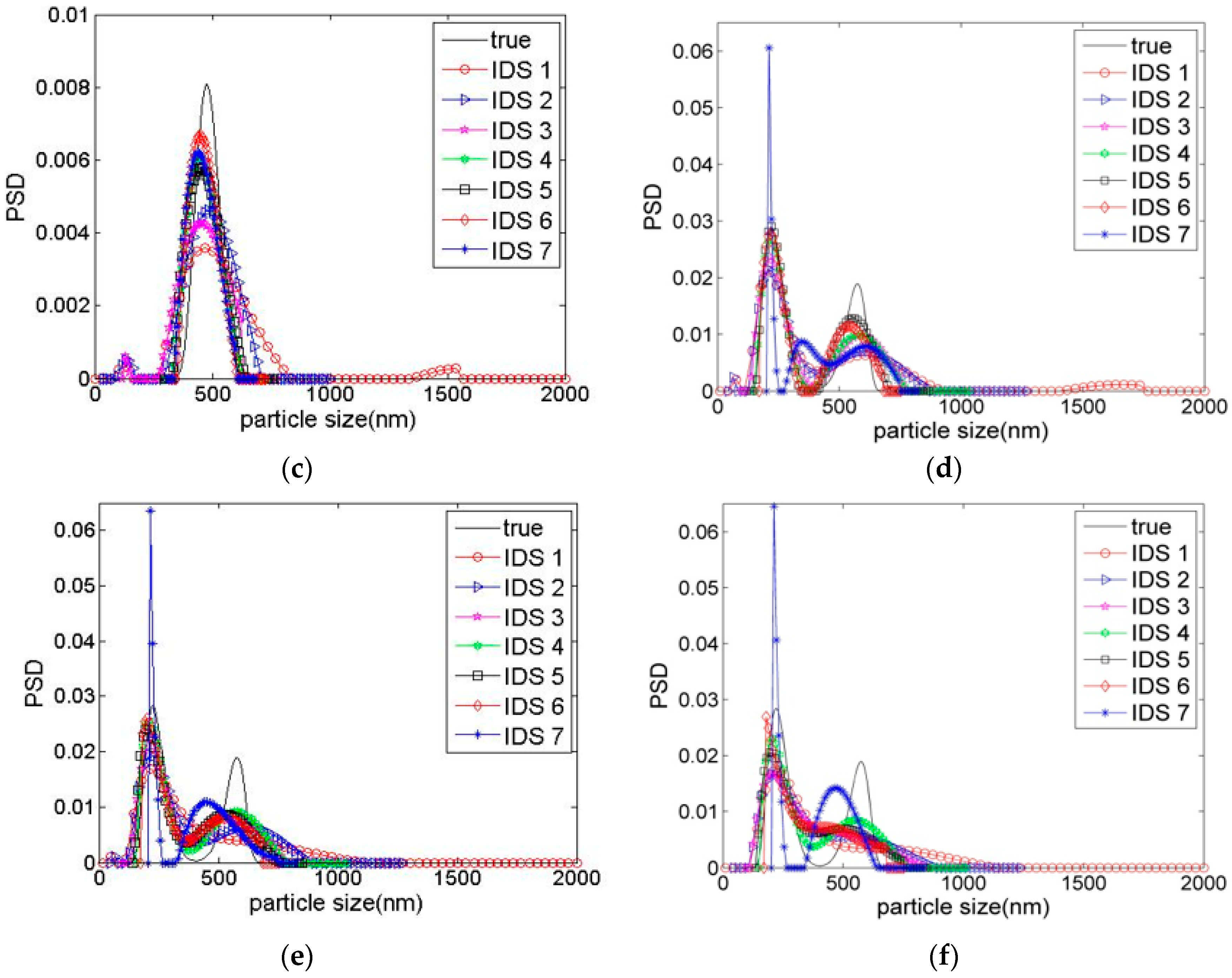
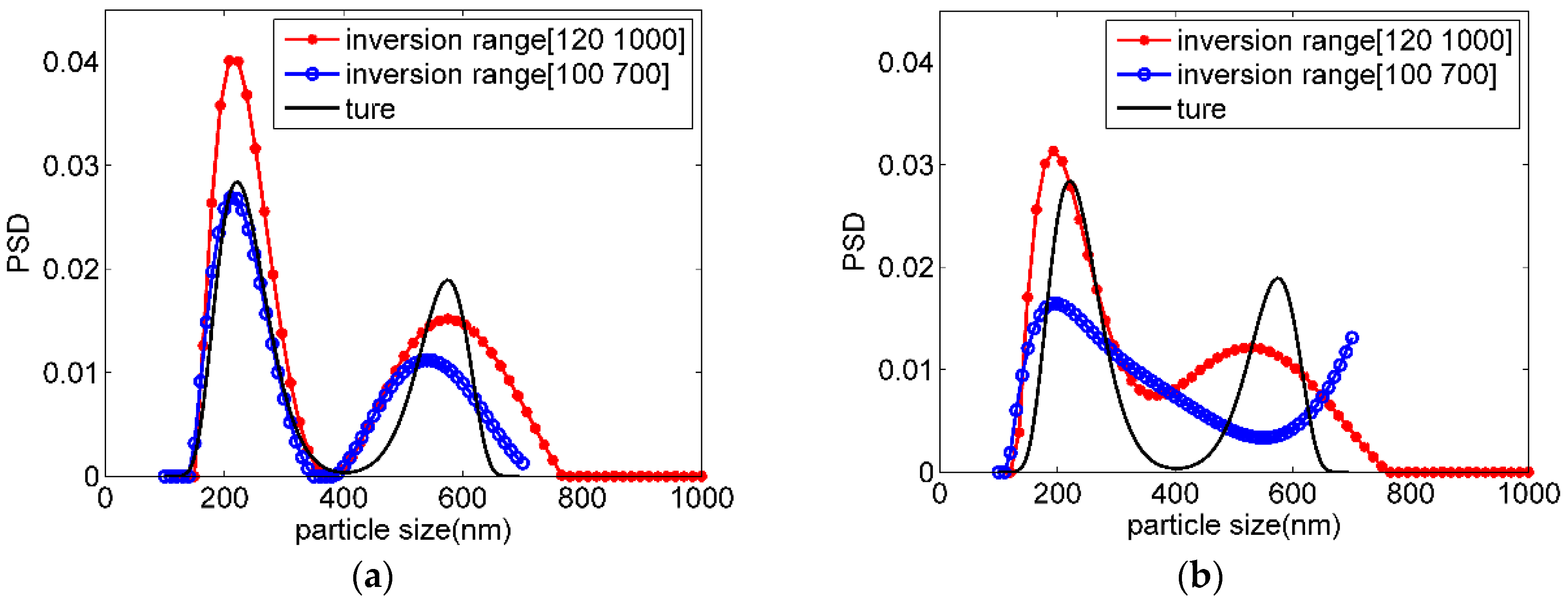
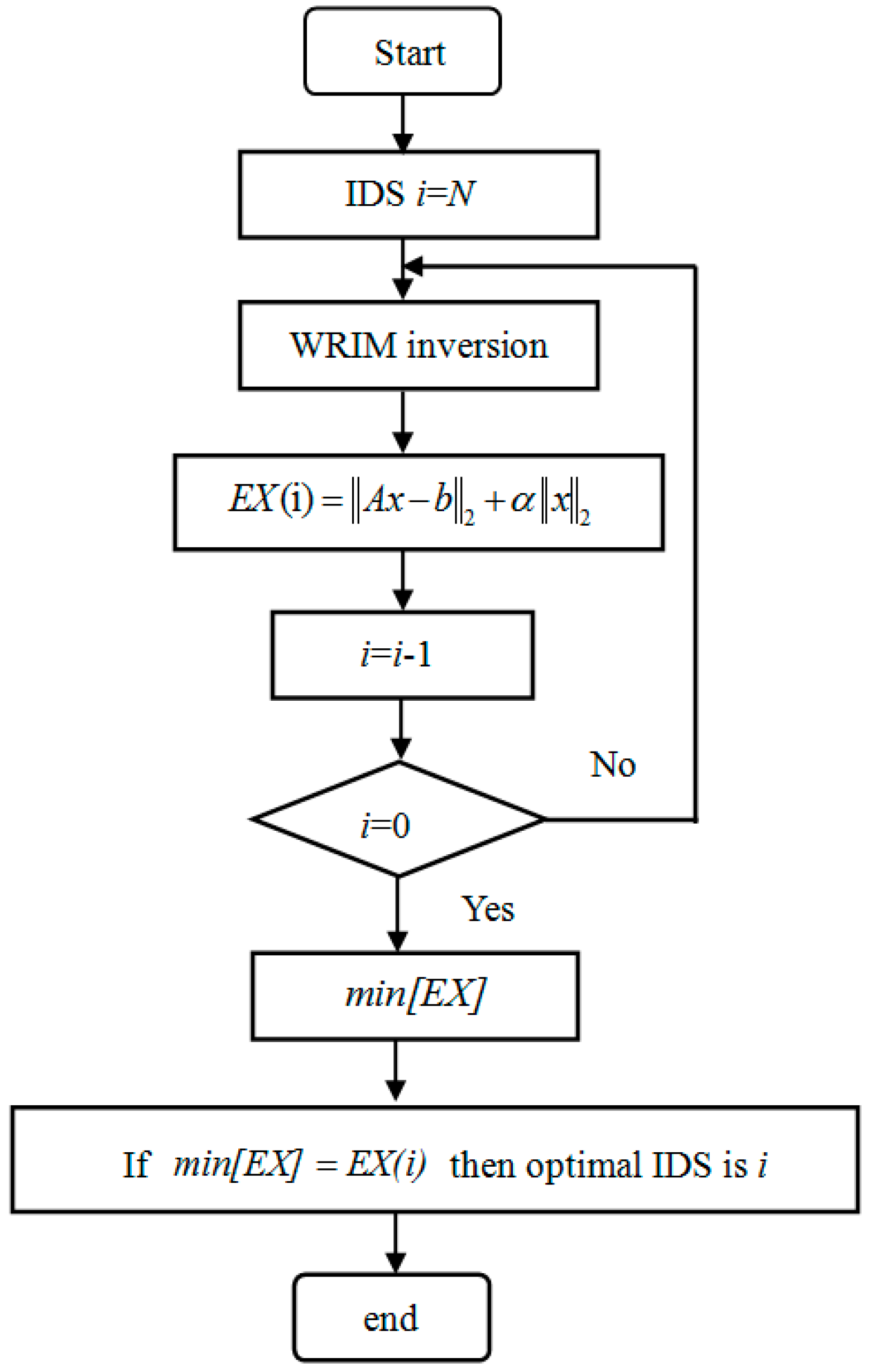
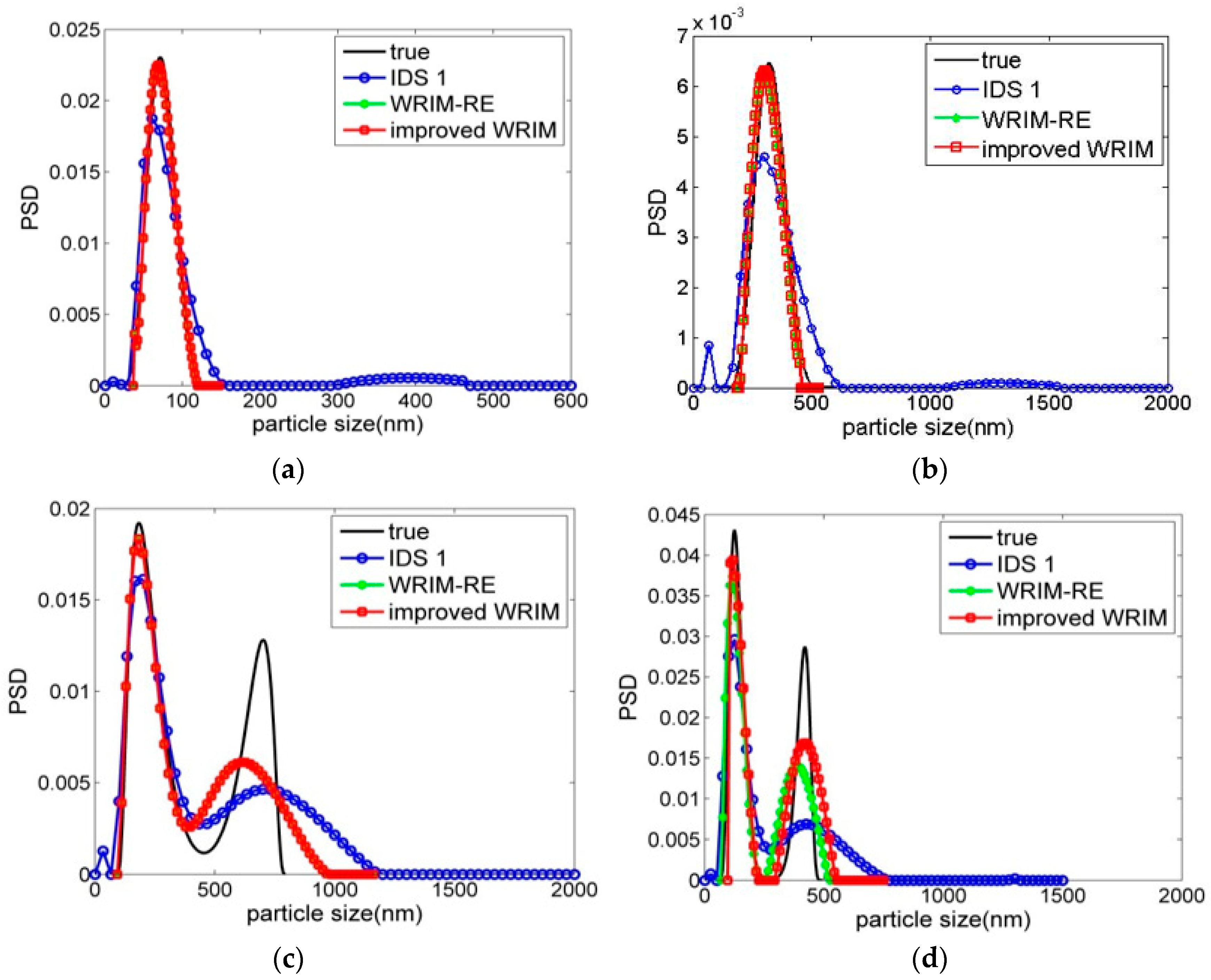
| IDS | Unimodal Distribution Particles | Bimodal Distribution Particles | ||
|---|---|---|---|---|
| Peak Value (nm) | RE | Peak Value (nm) | RE | |
| 1 | 434.11 | 0.6129 | —, — | 0.6174 |
| 2 | 501.30 | 0.5261 | 197.94, 526.84 | 0.5485 |
| 3 | 458.40 | 0.5207 | 196.72, 459.41 | 0.5511 |
| 4 | 449.96 | 0.3471 | 205.79, 579.47 | 0.3334 |
| 5 | 451.36 | 0.3598 | 193.96, 502.70 | 0.4668 |
| 6 | 452.81 | 0.3257 | 188.89, 479.82 | 0.4998 |
| 7 | 439.28 | 0.3963 | 222.10, 487.17 | 0.8255 |
| 8 | 437.74 | 0.4051 | 217.95, 460.08 | 1.1538 |
| Noise Level | Unimodal Particles | Bimodal Particles | ||||
|---|---|---|---|---|---|---|
| Peak Value (nm) | RE | Optimal IDS | Peak Value (nm) | RE | Optimal IDS | |
| 0.0001 | 477.22 | 0.1037 | 7 | 233.35, 551.45 | 0.2411 | 5 |
| 0.0005 | 457.98 | 0.2711 | 6 | 208.26, 562.04 | 0.3402 | 4 |
| 0.001 | 454.81 | 0.3118 | 6 | 205.79, 550.72 | 0.3725 | 4 |
| Particles | Inversion Range | WRIM-RE | Improved WRIM | ||
|---|---|---|---|---|---|
| True Optimal IDS | RE | Practice Optimal IDS | RE | ||
| 10 nm~150 nm | [1, 600] | 3 | 0.0672 | 3 | 0.0672 |
| 100 nm~600 nm | [1, 2000] | 5 | 0.1325 | 5 | 0.1325 |
| 90 nm~800 nm | [1, 2000] | 3 | 0.3181 | 3 | 0.3181 |
| 50 nm~500 nm | [1, 1500] | 3 | 0.3879 | 5 | 0.4015 |
| Method | 300 nm Unimodal Particles | 100 nm/450 nm Bimodal Particles | ||
|---|---|---|---|---|
| Peak Value (nm) | Peak Value Error % | Peak Value (nm) | Peak Value Error % | |
| IDS 1 | — | — | — | — |
| CONTIN | 316.23 | 5.41 | 94.06,376.27 | 5.94, 16.38 |
| Improved WRIM | 385.56 | 4.81 | 109.06, 455.52 | 9.06, 1.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shen, J.; Yuan, X.; Dou, Z.; Liu, W.; Mao, S. Scale Analysis of Wavelet Regularization Inversion and Its Improved Algorithm for Dynamic Light Scattering. Appl. Sci. 2018, 8, 1473. https://doi.org/10.3390/app8091473
Wang Y, Shen J, Yuan X, Dou Z, Liu W, Mao S. Scale Analysis of Wavelet Regularization Inversion and Its Improved Algorithm for Dynamic Light Scattering. Applied Sciences. 2018; 8(9):1473. https://doi.org/10.3390/app8091473
Chicago/Turabian StyleWang, Yajing, Jin Shen, Xi Yuan, Zhenhai Dou, Wei Liu, and Shuai Mao. 2018. "Scale Analysis of Wavelet Regularization Inversion and Its Improved Algorithm for Dynamic Light Scattering" Applied Sciences 8, no. 9: 1473. https://doi.org/10.3390/app8091473
APA StyleWang, Y., Shen, J., Yuan, X., Dou, Z., Liu, W., & Mao, S. (2018). Scale Analysis of Wavelet Regularization Inversion and Its Improved Algorithm for Dynamic Light Scattering. Applied Sciences, 8(9), 1473. https://doi.org/10.3390/app8091473




