Simulation of Motion Interactions of a 2-DOF Linear Piezoelectric Impact Drive Mechanism with a Single Friction Interface
Abstract
:Featured Application
Abstract
1. Introduction
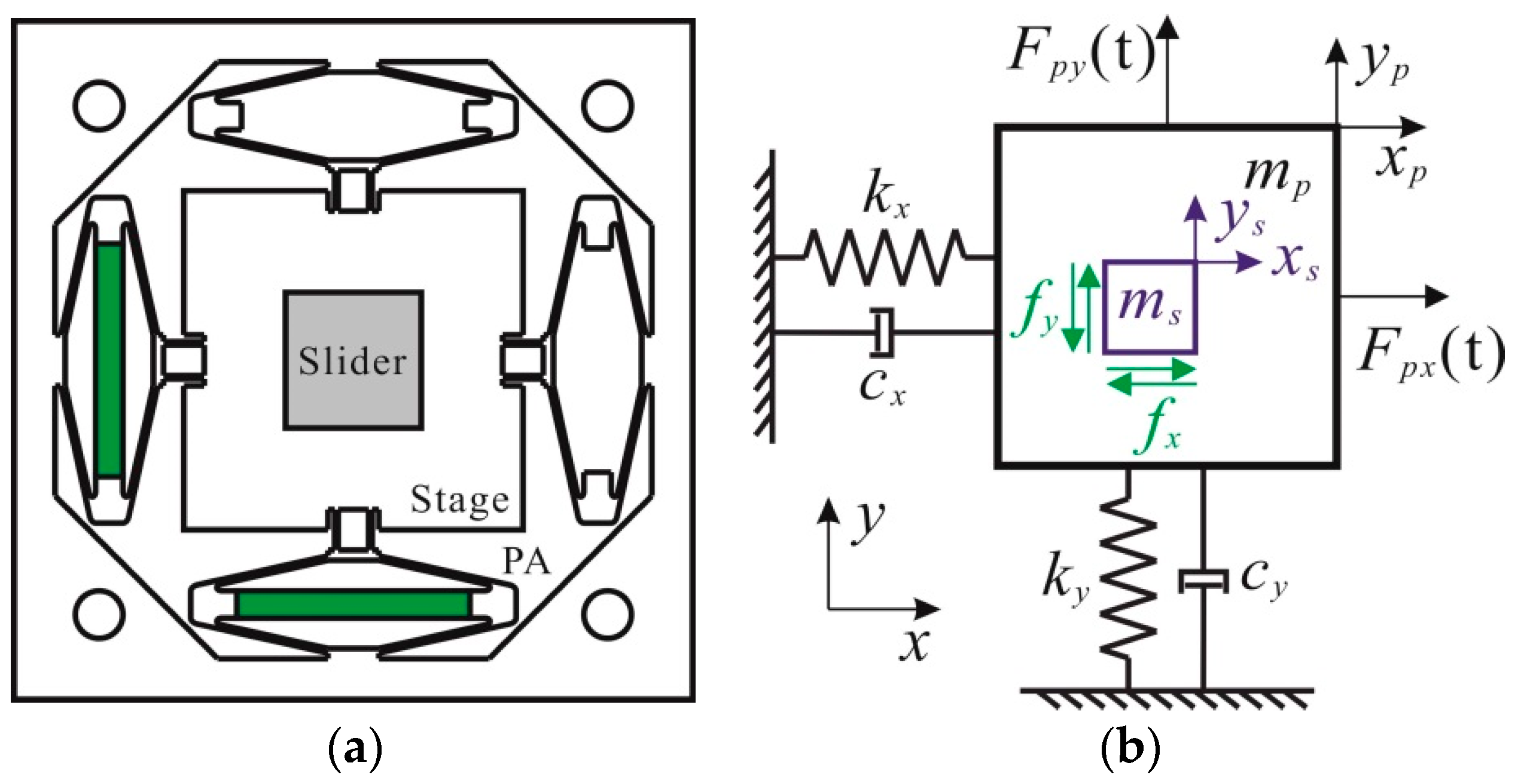
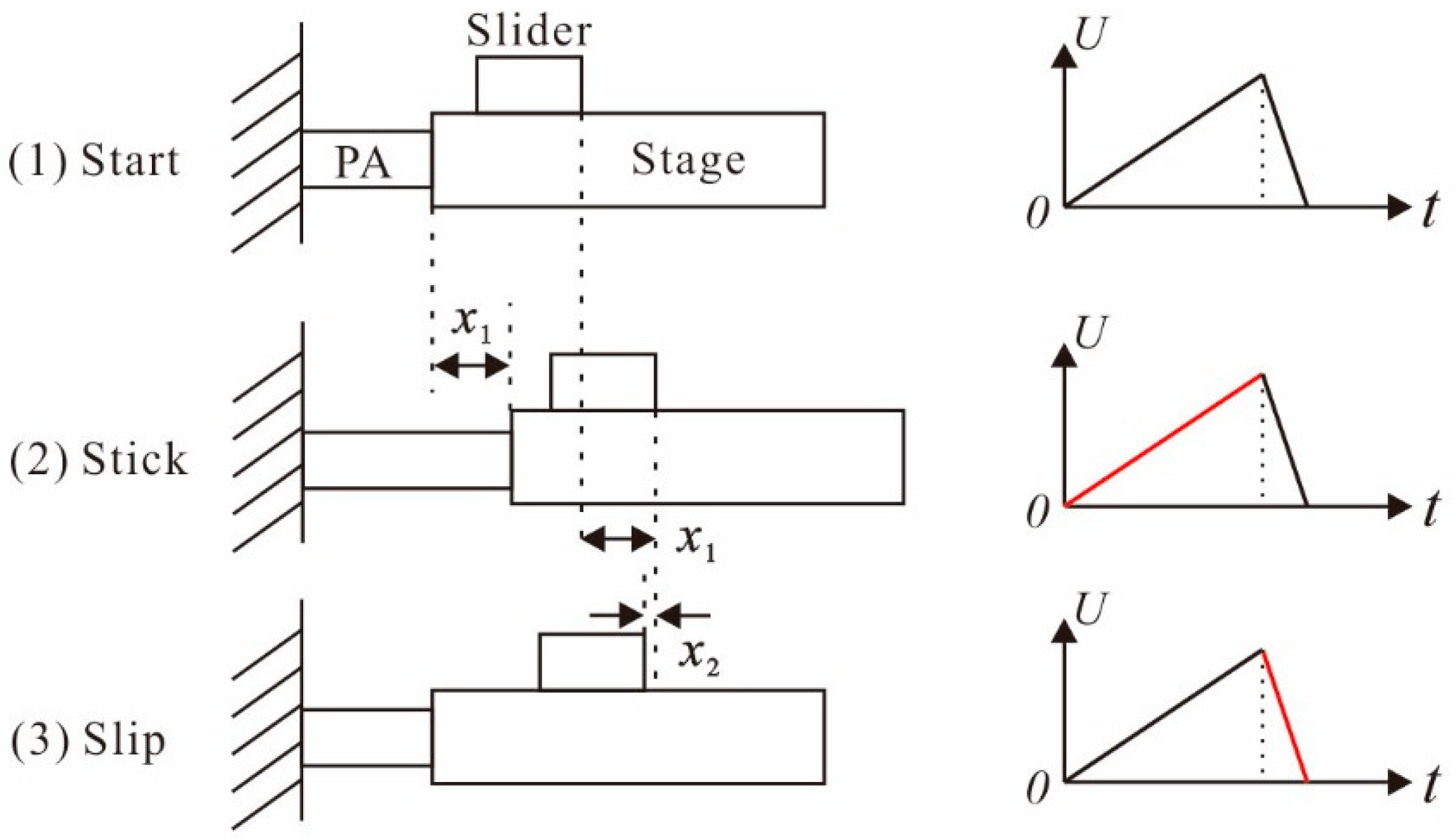
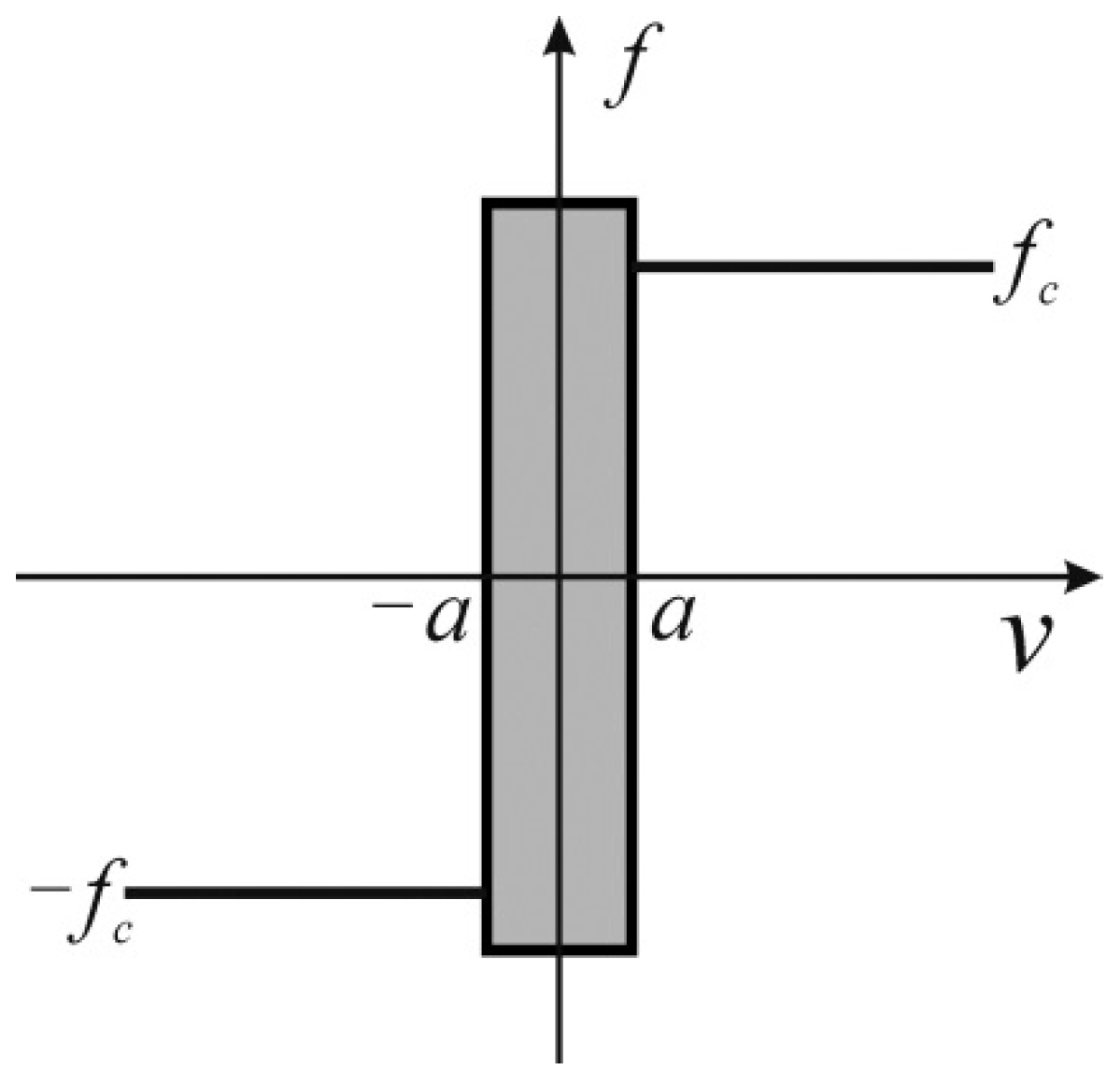
2. Structure Design, Working Process, and Dynamic Model Analysis
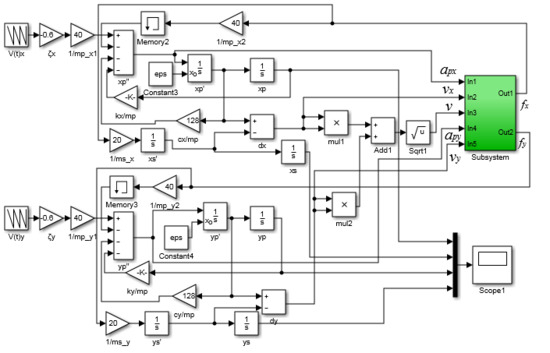
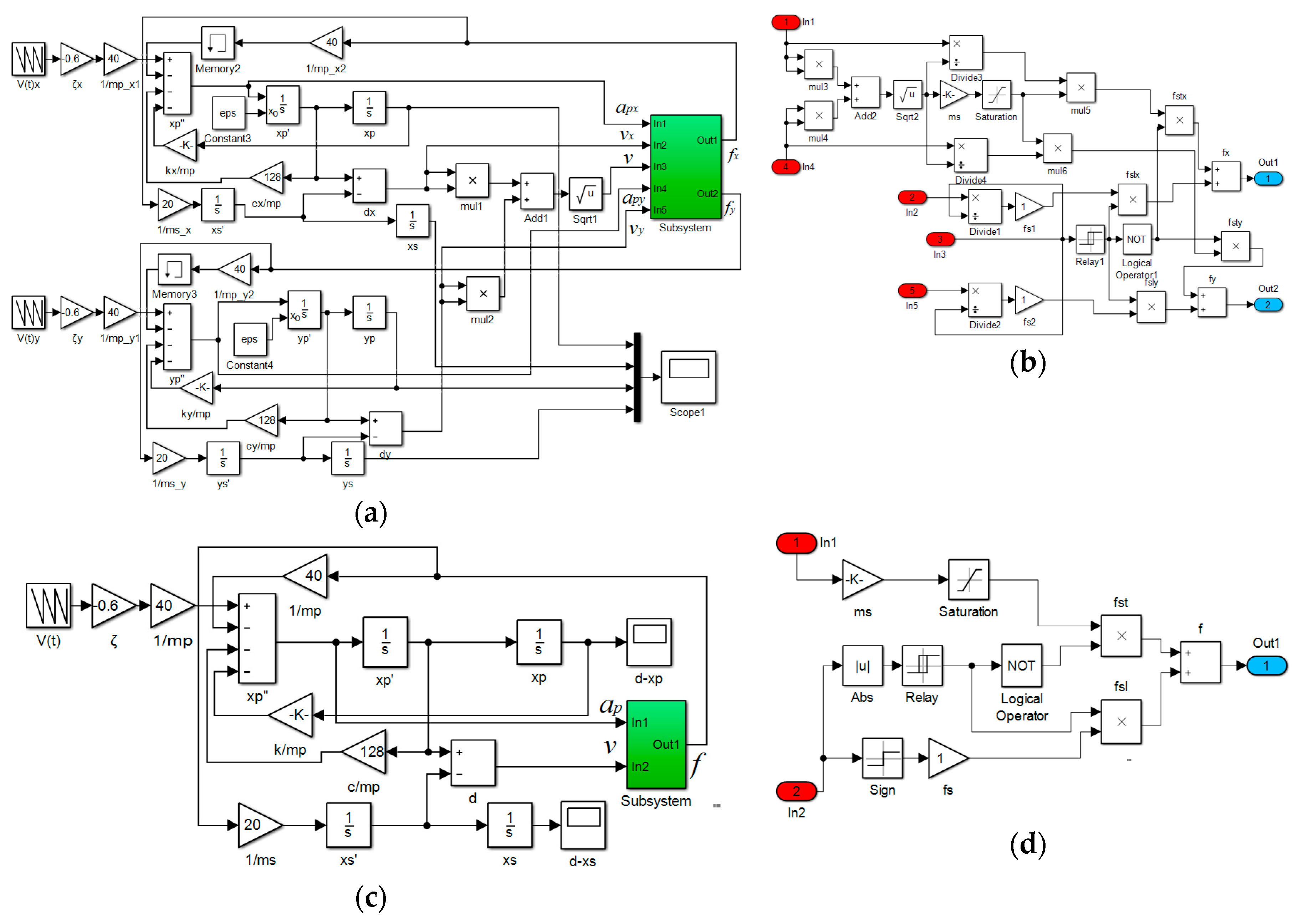
3. Numerical Simulation Processes
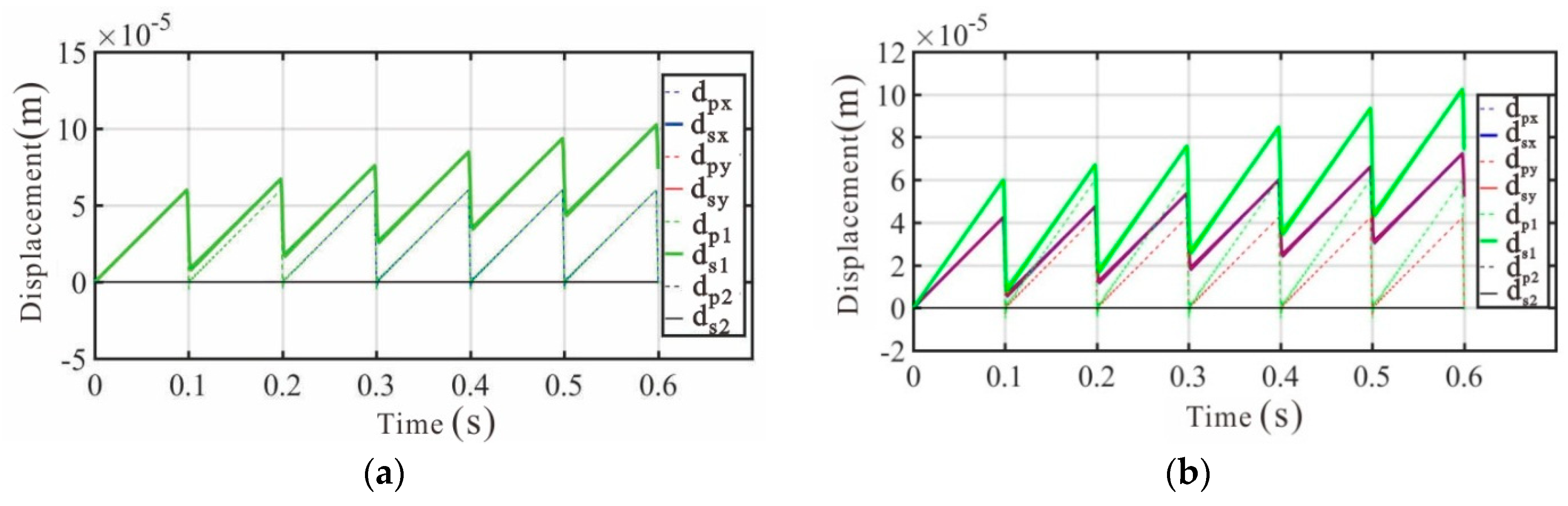
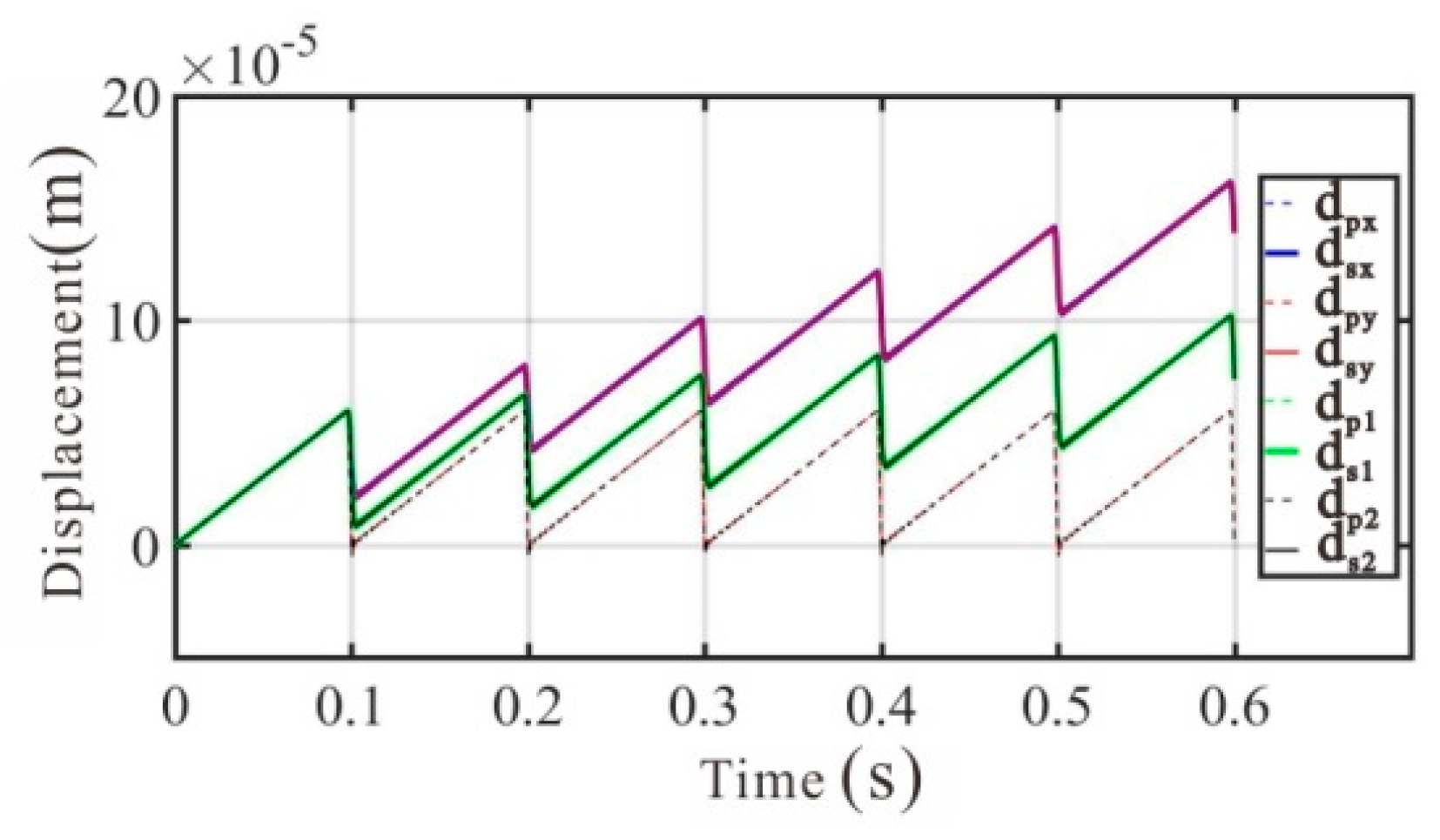
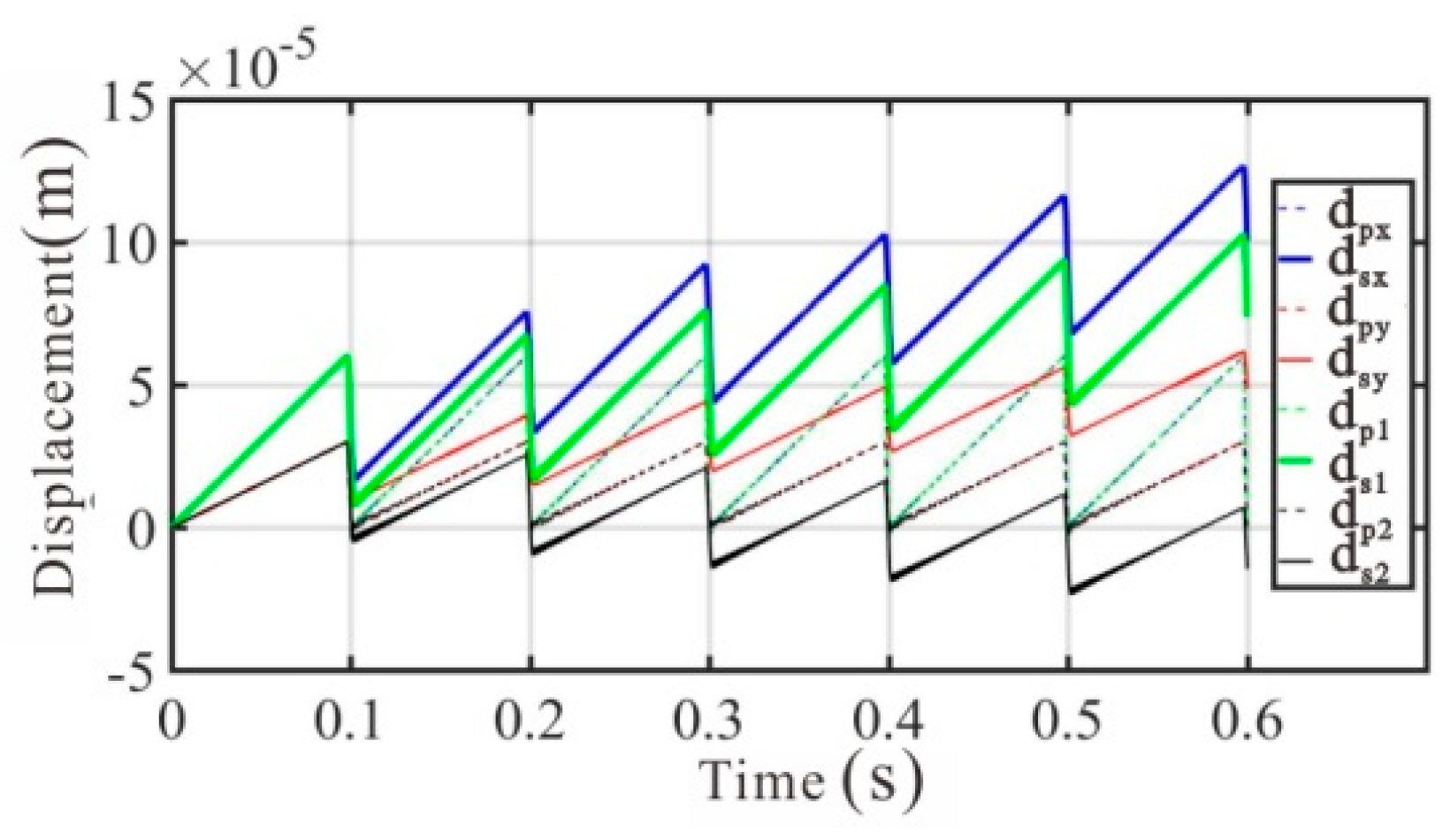
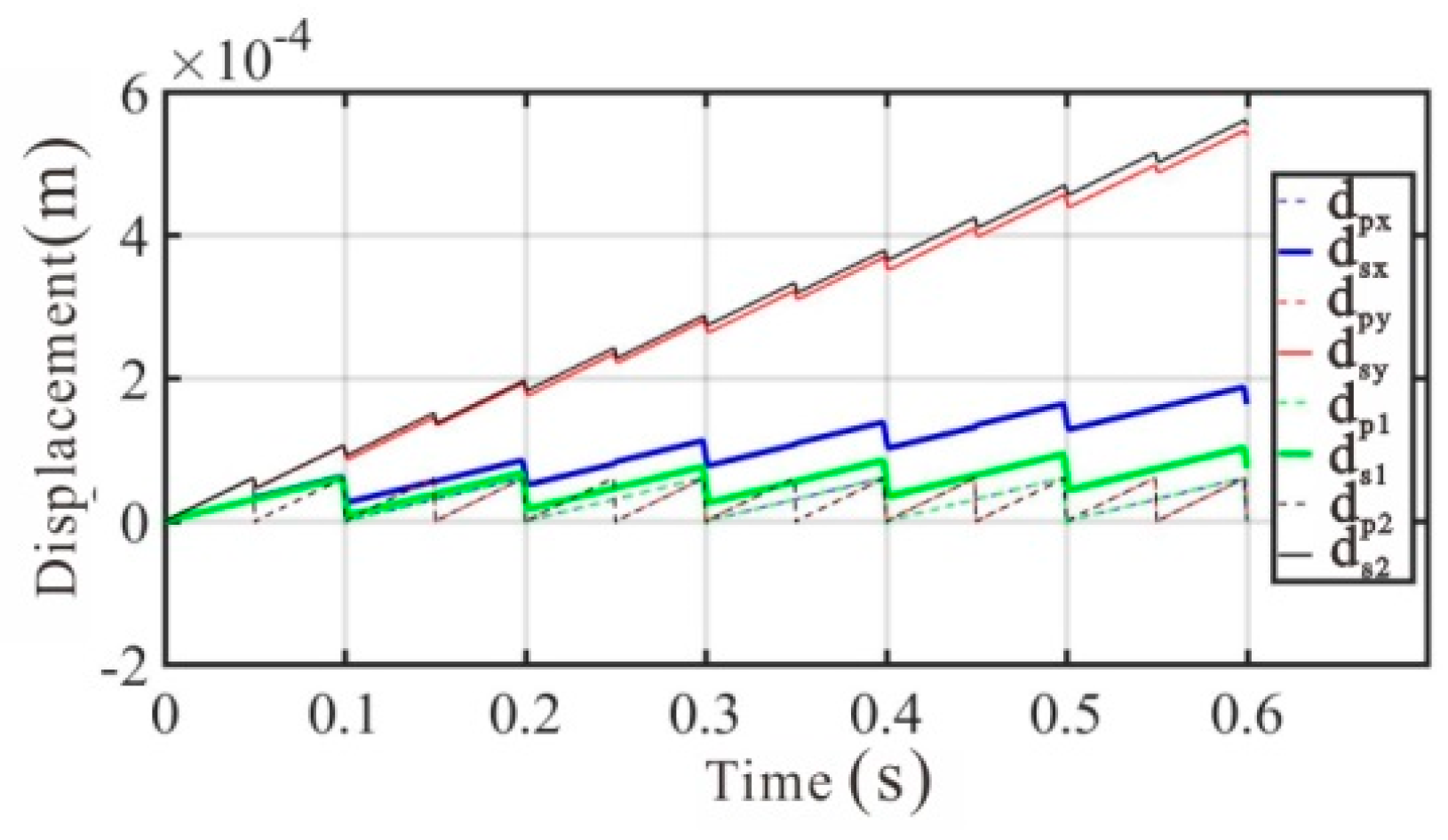
4. Simulation Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, H.; Quan, Q.Q.; Deng, Z.Q.; Hua, Y.X.; Wang, Y.C.; Bai, D. A novel noncontact ultrasonic levitating bearing excited by piezoelectric ceramics. Appl. Sci. 2016, 6, 280. [Google Scholar] [CrossRef]
- Liu, Y.X.; Xu, D.M.; Yu, Z.Y.; Yan, J.P.; Yang, X.H.; Chen, W.S. A novel rotary piezoelectric motor using first bending hybrid transducers. Appl. Sci. 2015, 5, 472–484. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zhang, Y.; Ru, C.; Chen, B.K.; Sun, Y. A load-lock-compatible nanomanipulation system for scanning electron micro scope. IEEE/ASME Trans. Mechatron. 2012, 18, 230–237. [Google Scholar] [CrossRef]
- Sun, X.T.; Chen, W.H.; Zhang, J.B.; Zhou, R.; Chen, W.J. A novel piezo-driven linear-rotary inchworm actuator. Sens. Actuators A Phys. 2015, 224, 78–86. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.J.; Hesselbach, J.; Kerle, H. Development of a two-degree-of-freedom piezoelectric rotary-linear actuator with high driving force and unlimited linear movement. Rev. Sci. Instrum. 2006, 77, 465–481. [Google Scholar] [CrossRef]
- Li, H.Y.; Wang, L.; Cheng, T.H.; He, M.; Zhao, H.W.; Gao, H.B. A high-thrust screw-type piezoelectric ultrasonic motor with three-wavelength exciting mode. Appl. Sci. 2016, 6, 442. [Google Scholar] [CrossRef]
- Dong, W.; Li, H.; Du, Z. A planar nano-positioner driven by shear piezoelectric actuators. Aip Adv. 2016, 6, 669–671. [Google Scholar] [CrossRef]
- Mashimo, T.; Toyama, S. Rotary-linear piezoelectric microactuator with a cubic stator of side length 3.5 mm. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 1825. [Google Scholar] [CrossRef] [PubMed]
- Morita, T.; Yoshida, R.; Okamoto, Y.; Higuchi, T. Three dof parallel mechanism utilizing smooth impact drive mechanism. Precis. Eng. 2002, 26, 289–295. [Google Scholar] [CrossRef]
- Shim, J.Y.; Gweon, D.G. Piezo-driven metrological multiaxis nanopositioner. Rev. Sci. Instrum. 2001, 72, 4183–4187. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Liu, G.; Dong, S. A two degrees-of-freedom piezoelectric single-crystal micromotor. J. Appl. Phys. 2014, 116, 224101. [Google Scholar] [CrossRef]
- Guo, M.; Hu, J.; Zhu, H.; Zhao, C.; Dong, S. Three-degree-of-freedom ultrasonic motor using a 5-mm-diameter piezoelectric ceramic tube. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 1446–1452. [Google Scholar] [CrossRef]
- Lee, D.J.; Lee, S.K. Ultraprecision XY stage using a hybrid bolt-clamped Langevin-type ultrasonic linear motor for continuous motion. Rev. Sci. Instrum. 2015, 86, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yan, J.; Wang, L.; Chen, W. A two-dof ultrasonic motor using a longitudinal-bending hybrid sandwich transducer. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Gu, Z.; Quan, Q.; Deng, J. Development of a two-dimensional linear piezoelectric stepping platform using longitudinal-bending hybrid actuators. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Hesselbach, J. On Development of a Rotary–Linear Actuator Using Piezoelectric Translators. IEEE/ASME Trans. Mechatron. 2006, 11, 647–650. [Google Scholar] [CrossRef]
- Peng, Y.; Ito, S.; Sakurai, Y.; Shimizu, Y.; Gao, W. Construction and verification of a linear-rotary microstage with a millimeter-scale range. Int. J. Precis. Eng. Manuf. 2013, 14, 1623–1628. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Shi, Y.; Wang, X.; Guan, K.; Ju, B.F. Design, modeling, analysis and testing of a novel piezo-actuated XY compliant mechanism for large workspace nano-positioning. Smart Mater. Struct. 2016, 25, 115033. [Google Scholar] [CrossRef]
- Zhang, Z.M.; An, Q.; Li, J.W.; Zhang, W.J. Piezoelectric friction-inertia actuator-a critical review and future perspective. Int. J. Adv. Manuf. Technol. 2012, 62, 669–685. [Google Scholar] [CrossRef]
- Liu, Y.F.; Li, J.; Hu, X.H.; Zhang, Z.M.; Cheng, L.; Lin, Y.; Zhang, W.J. Modeling and control of piezoelectric inertia-friction actuators: Review and future research directions. Mechanicalences 2015, 6, 95–107. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Olejnik, P. Analysis of dynamic systems with various friction laws. Appl. Mech. Rev. 2005, 58, 389–411. [Google Scholar] [CrossRef]
- Karnopp, D. Computer simulation of stick-slip friction in mechanical dynamic systems. Trans. ASME J. Dyn. Syst. Meas. Control 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Astrom, K.J.; Canudas-De-Wit, C. Revisiting the Lugre friction model. IEEE Control Syst. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Ha, J.L.; Fung, R.F.; Han, C.F.; Chang, J.R. Effects of frictional models on the dynamic response of the impact drive mechanism. J. Vib. Acoust. 2006, 128, 88–96. [Google Scholar] [CrossRef]
- Dupont, P.; Hayward, V.; Armstrong, B.; Altpeter, F. Single state elastoplastic friction models. IEEE Trans. Autom. Control 2002, 47, 787–792. [Google Scholar] [CrossRef]
- Edeler, C.; Meyer, I.; Fatikow, S. Modeling of stick-slip micro-drives. J. Micro-Nano Mechatron. 2011, 6, 65–87. [Google Scholar] [CrossRef]
- Peng, J.Y.; Chen, X.B. Modeling of piezoelectric-driven stick-slip actuators. IEEE/ASME 2011, 16, 394–399. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Edeler, C.; Fatikow, S. Contact mechanics modeling of piezo-actuated stick-slip microdrives. Phys. Mesomech. 2012, 15, 280–286. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. 1997, 20, 99–111. [Google Scholar] [CrossRef]
- Wang, D.H.; Zhu, W.; Yang, Q. Linearization of stack piezoelectric ceramic actuators based on bouc-wen model. J. Intell. Mate Syst. Struct. 2010, 22, 401–413. [Google Scholar] [CrossRef]
- Karpinskii, D.N.; Parinov, I.A. Computer simulation of microstructure formation in a piezoelectric ceramic. J. Appl. Mech. Tech. Phys. 1992, 33, 134–138. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Edeler, C.; Fatikow, S. Modeling of piezo-actuated stick-slip micro-drives: An overview. Adv. Sci. Technol. 2013, 81, 39–48. [Google Scholar] [CrossRef]
- Szufnarowski, F.; Schneider, A. Two-dimensional dynamics of a quasi-static legged piezoelectric actuator. Smart Mater. Struct. 2012, 21, 055007. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.H.; Han, L.L.; Zhang, R.; Pan, C.L.; Yu, L.D. Dynamic responses of piezoelectric inertia friction motors with different friction models. In Proceedings of the 2016 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Xi’an, China, 21–24 October 2016. [Google Scholar] [CrossRef]
- Han, L.L.; Zhao, H.N.; Xia, H.J.; Pan, C.L.; Jiang, Y.Z.; Li, W.S.; Yu, L.D. A compact impact rotary motor based on a piezoelectric tube actuator with helical interdigitated electrodes. Sensors 2018, 18, 2195. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value | Unit |
|---|---|---|
| mpx (mpy) | 2.5 × 10−3 | kg |
| msx (msy) | 5.0 × 10−3 | kg |
| kx (ky) | 1.0 × 106 | N·m−1 |
| cx (cy) | 3.2 | N·s·m−1 |
| δx (δy) | −0.6 | N·V−1 |
| fs | 1.2 | N |
| fc | 1.0 | N |
| a | 1.0 × 10−6 | m·s−1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, H.; Han, L.; Pan, C.; Jia, H.; Yu, L. Simulation of Motion Interactions of a 2-DOF Linear Piezoelectric Impact Drive Mechanism with a Single Friction Interface. Appl. Sci. 2018, 8, 1400. https://doi.org/10.3390/app8081400
Xia H, Han L, Pan C, Jia H, Yu L. Simulation of Motion Interactions of a 2-DOF Linear Piezoelectric Impact Drive Mechanism with a Single Friction Interface. Applied Sciences. 2018; 8(8):1400. https://doi.org/10.3390/app8081400
Chicago/Turabian StyleXia, Haojie, Liling Han, Chengliang Pan, Huakun Jia, and Liandong Yu. 2018. "Simulation of Motion Interactions of a 2-DOF Linear Piezoelectric Impact Drive Mechanism with a Single Friction Interface" Applied Sciences 8, no. 8: 1400. https://doi.org/10.3390/app8081400