Study on the Dynamic Mechanical Properties of Viscoelastic Materials Based on Asymmetrical Sandwich Beams
Abstract
:1. Introduction
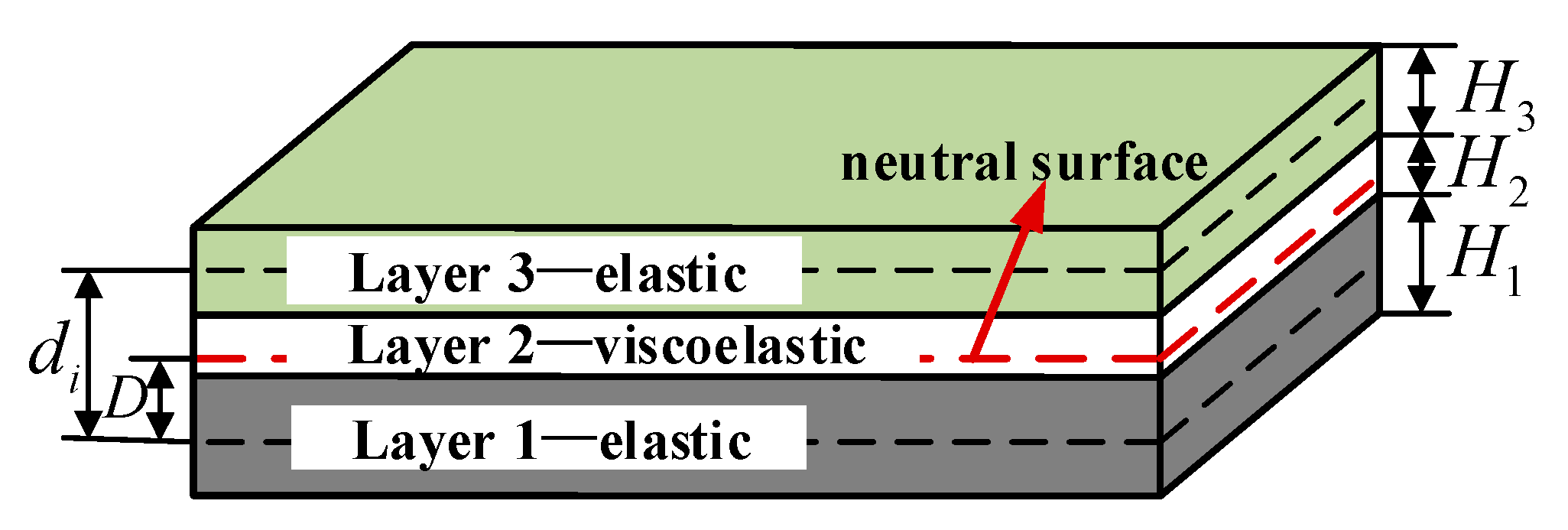
2. Theoretical Modelling
2.1. General Sandwich Beam Specimens
2.2. Symmetrical Sandwich Beam Specimens
3. Simulations and Discussions
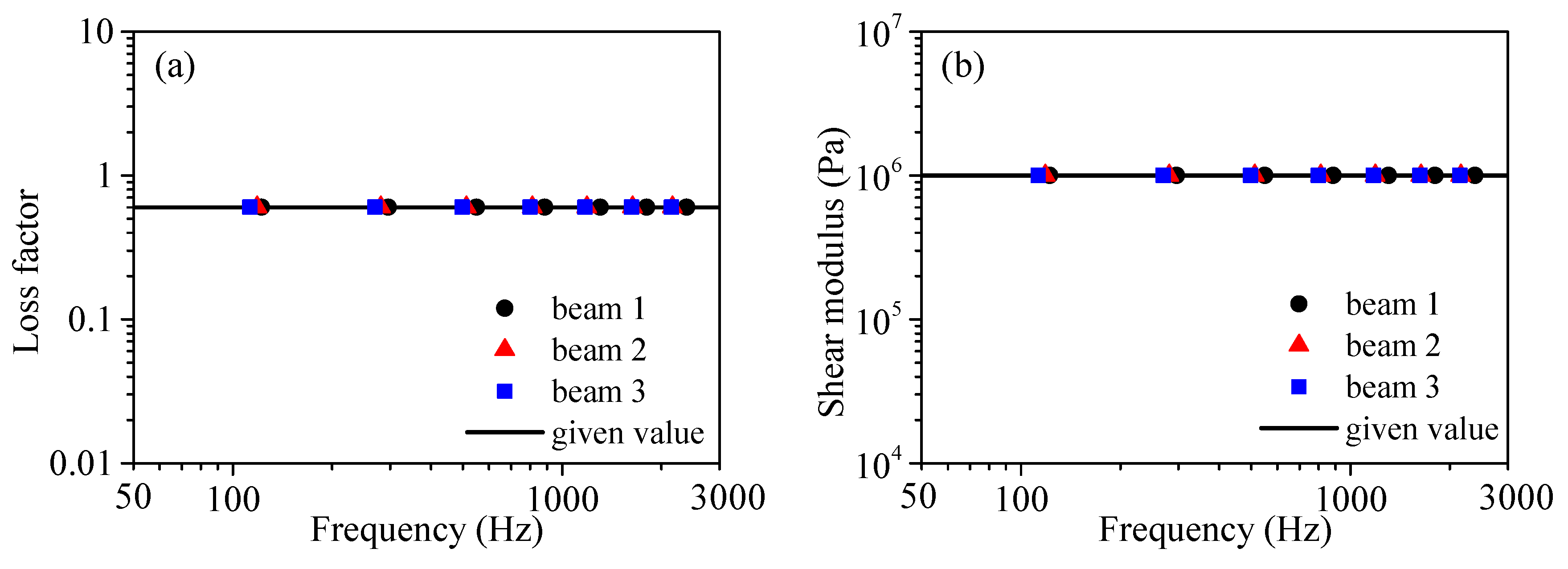
3.1. Constant Damping Model
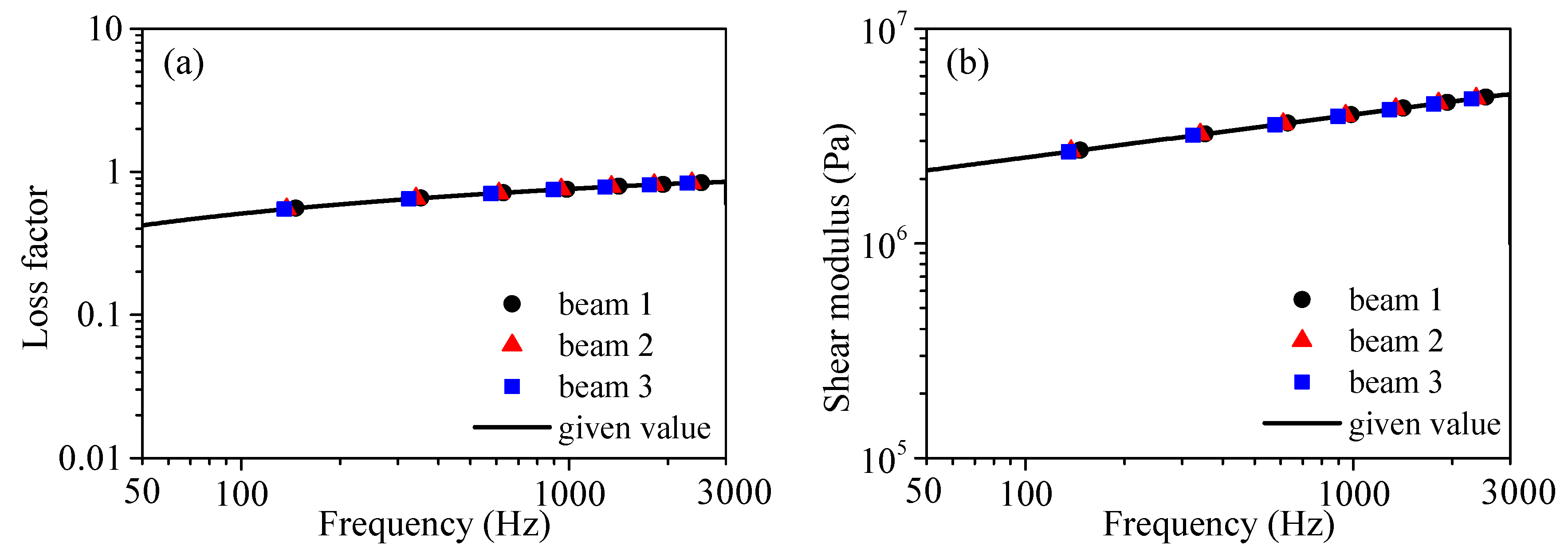
3.2. Frequency-Dependent Viscoelastic Model
4. Experimental Validation
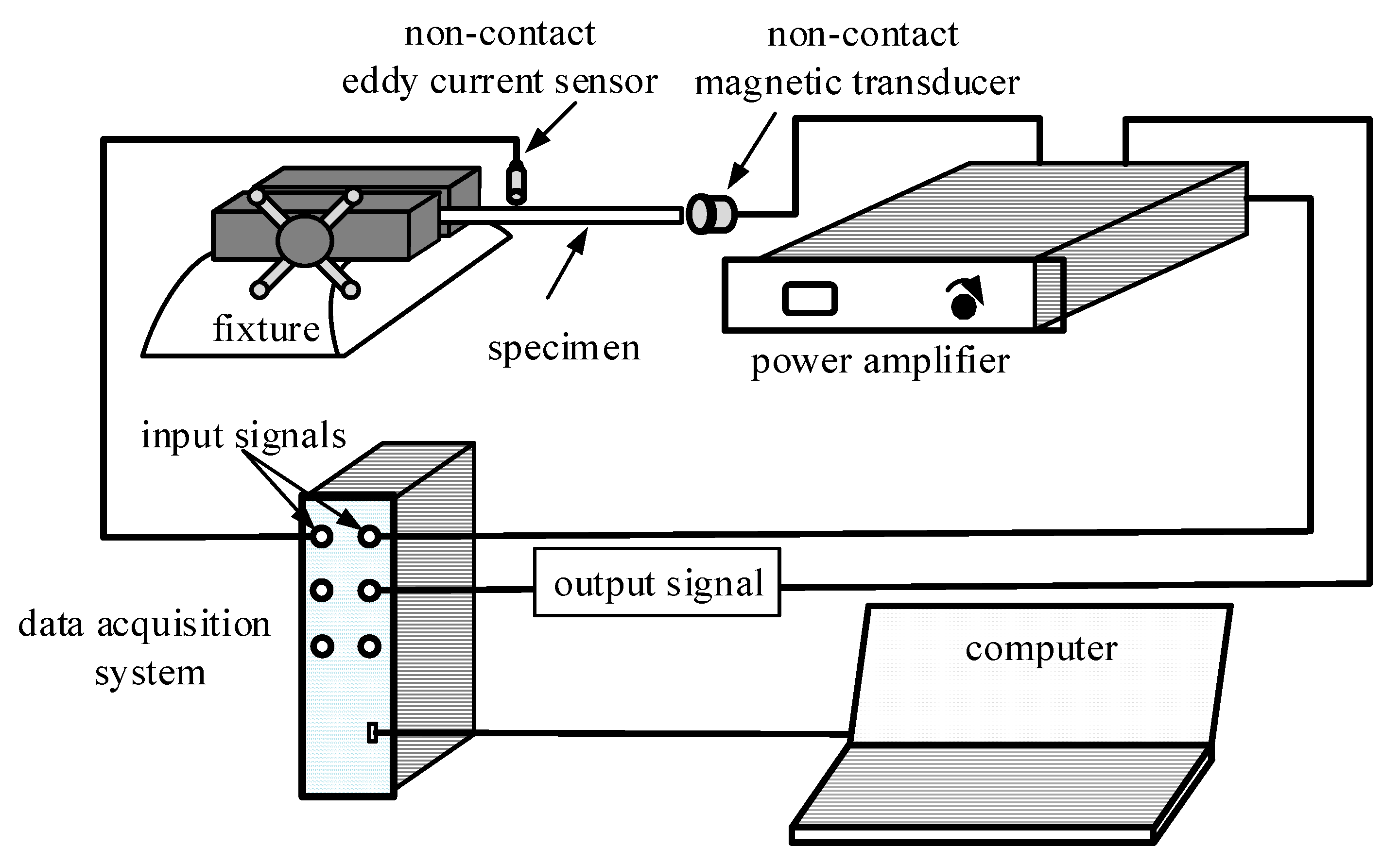
4.1. Experimental Apparatus
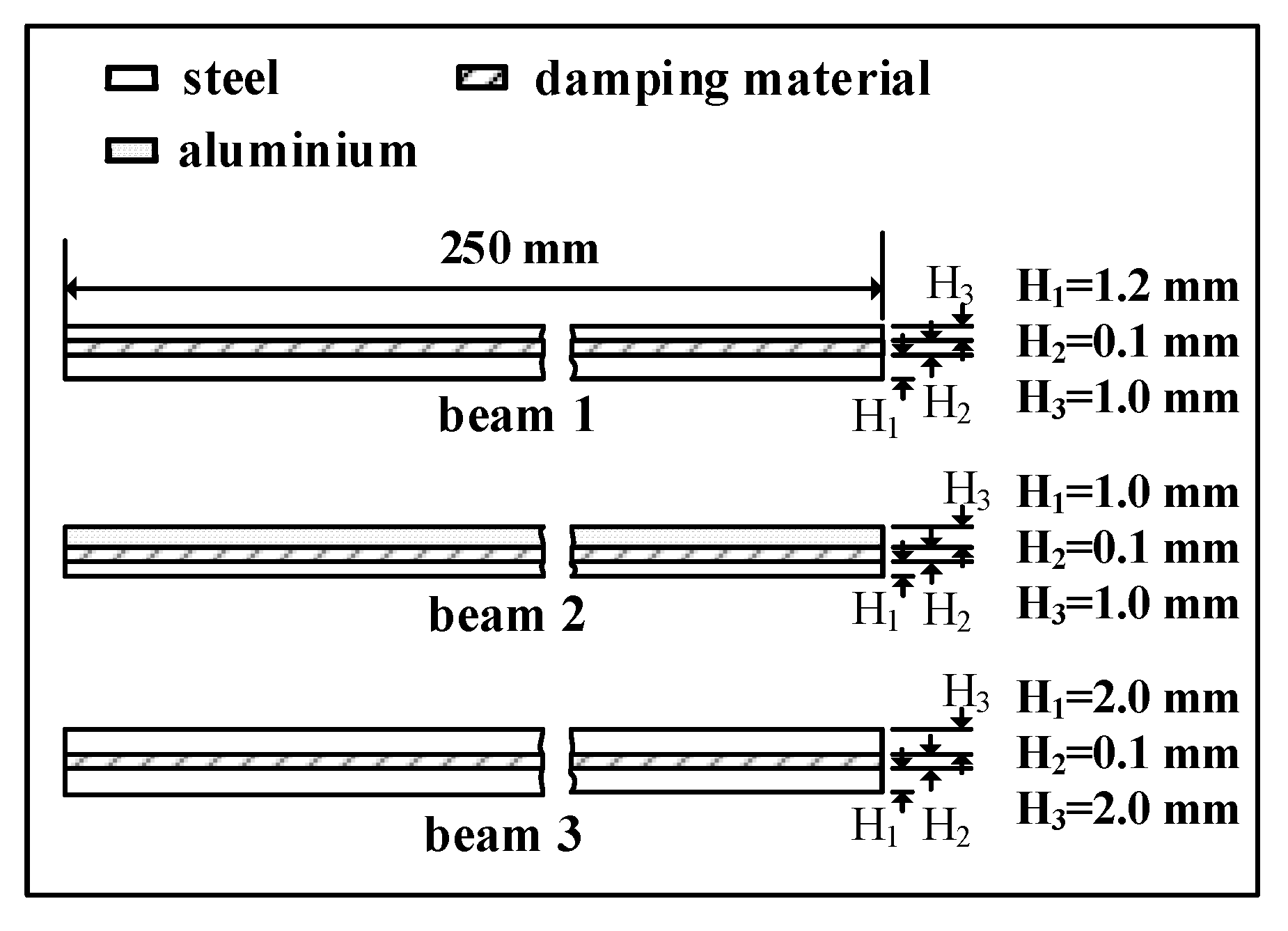
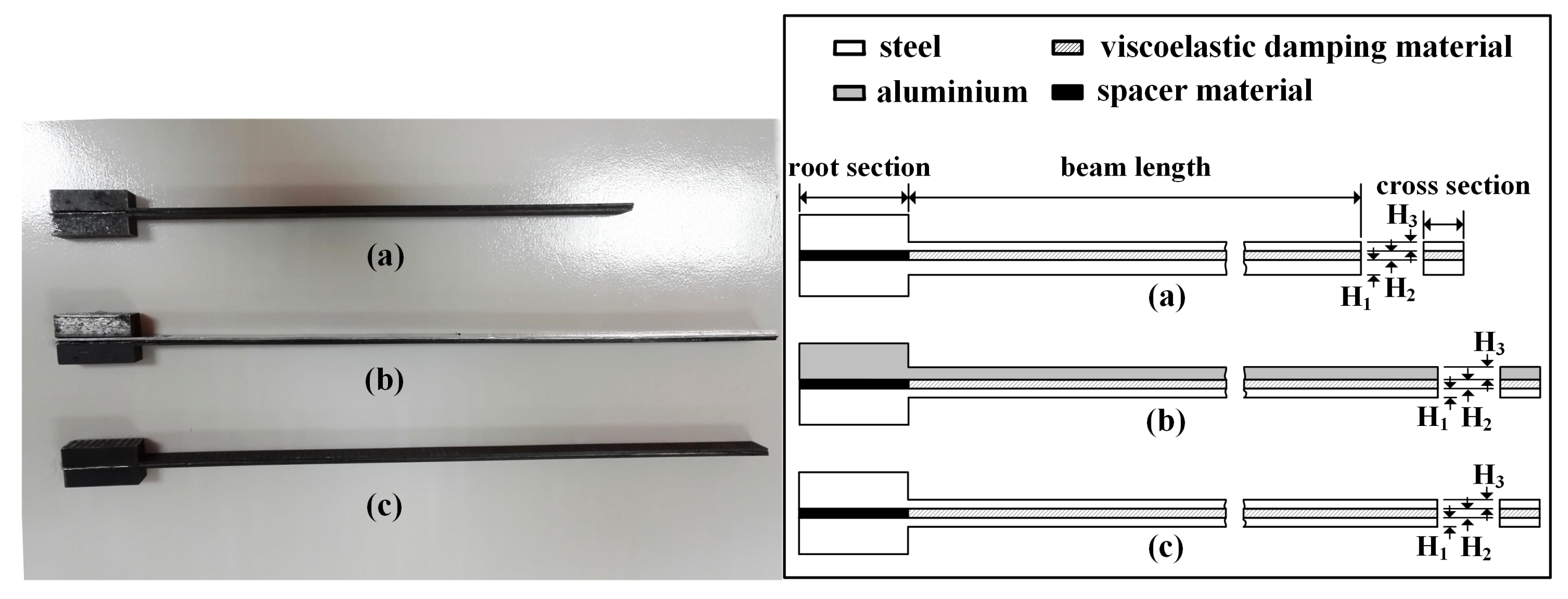
4.2. Test Specimens
4.3. Experimental Results
4.3.1. Normalized Displacement Frequency Responses
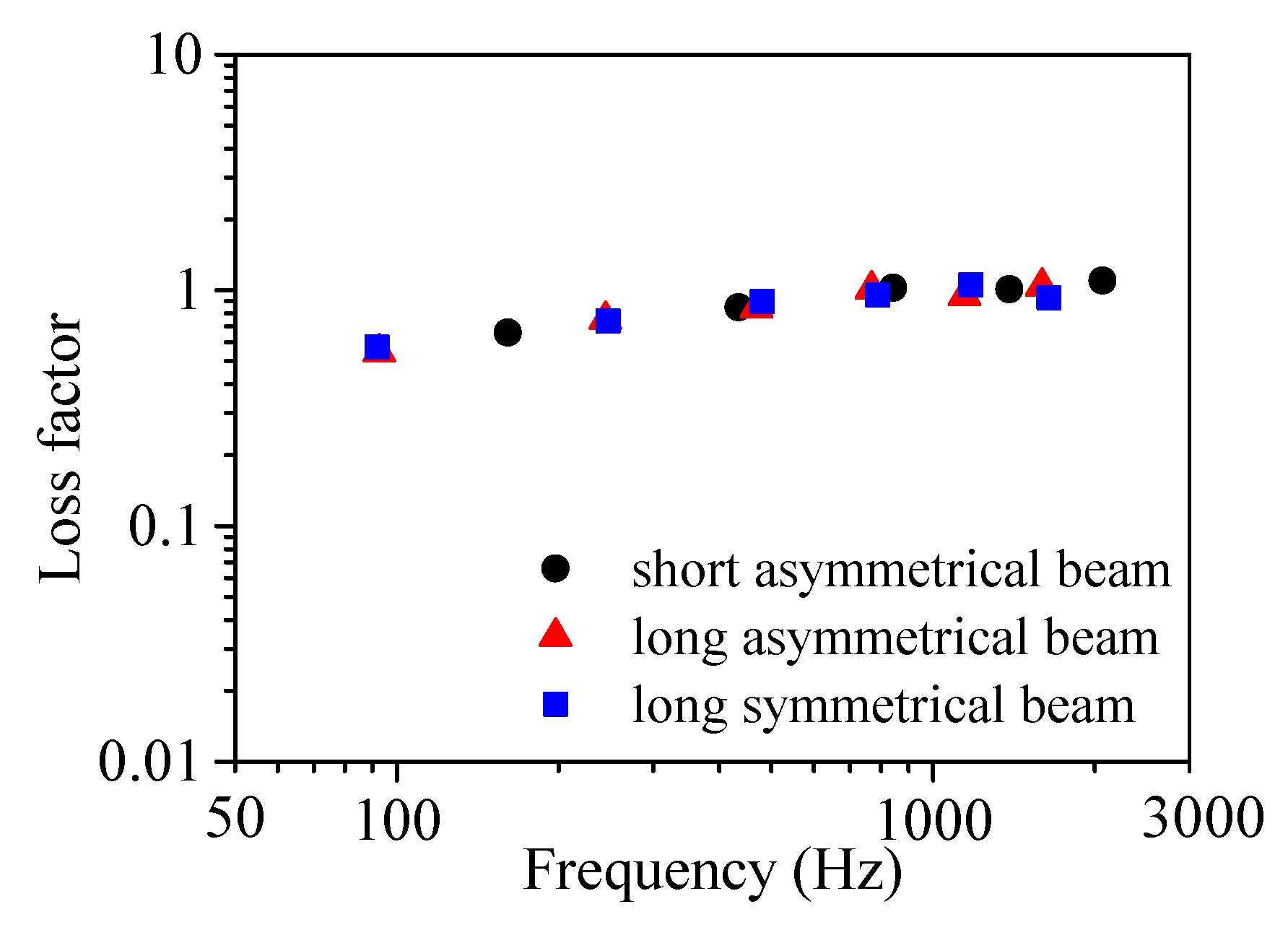
4.3.2. Modal Frequencies and Loss Factors of Sandwich Specimens
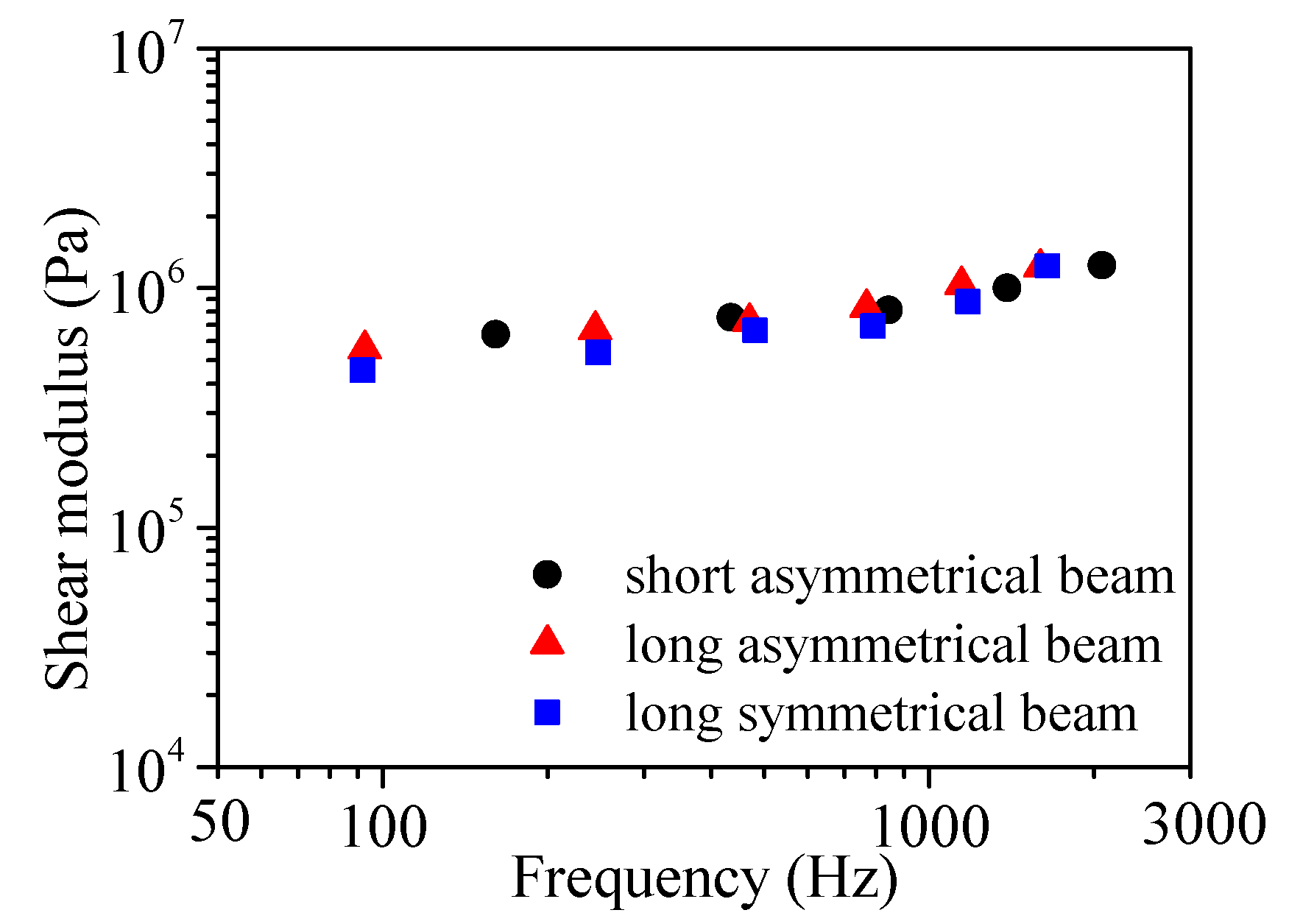
4.3.3. Modal Shear Moduli and Modal Loss Factors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ISO. Mechanical Vibration and Shock—Characterization of the Dynamic Mechanical Properties of Visco-Elastic Materials; ISO 18437; ISO: Geneva, Switzerland, 2005. [Google Scholar]
- ASTM. Standard Test Method for Measuring Dynamic Mechanical Properties of Materials; ASTM E. 756705; ASTM: West Conshohocken, PA, USA, 2005; pp. 1–14. [Google Scholar]
- Bies, D.A.; Hamid, S. In situ determination of loss and coupling loss factors by the power injection method. J. Sound Vib. 1980, 70, 187–204. [Google Scholar] [CrossRef]
- Bloss, B.C.; Rao, M.D. Estimation of frequency-averaged loss factors by the power injection and the impulse response decay methods. J. Acoust. Soc. Am. 2005, 117, 240–249. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.P. A new theoretical basis for the bandwidth method and optimal power ratios for the damping estimation. Mech. Syst. Sig. Process. 2008, 22, 1869–1881. [Google Scholar] [CrossRef]
- Carfagni, M.; Pierini, M. Determining the Loss Factor by the Power Input Method (PIM), Part 2: Experimental Investigation with Impact Hammer Excitation. J. Vib. Acoust. 1999, 121, 422–427. [Google Scholar] [CrossRef]
- Liu, W.B.; Marks, S.E. Experimental and analytical estimation of loss factors by the power input method. AIAA J. 2007, 45, 477–484. [Google Scholar] [CrossRef]
- Srikanth, N.; Gupta, M. Damping characterization of magnesium based composites using an innovative circle-fit approach. Compos. Sci. Technol. 2003, 63, 559–568. [Google Scholar] [CrossRef]
- Guo, Z.W.; Sheng, M.P.; Ma, J.G. Damping identification in frequency domain using integral method. J. Sound Vib. 2015, 338, 237–249. [Google Scholar] [CrossRef]
- Kerwin, E.M. Damping of flexural waves by a constrained viscoelastic layer. J. Acoust. Soc. Am. 1959, 31, 952–962. [Google Scholar] [CrossRef]
- Ungar, E.E. Loss factors of viscoelastically damped beam structures. J. Acoust. Soc. Am. 1962, 34, 1082–1089. [Google Scholar] [CrossRef]
- Derby, T.F.; Ruzicka, J.E. Loss Factor and Resonant Frequency of Viscoelastic Shear-Damped Structural Composites; NASA CR 1269: Springfield, VA, USA, 1969. [Google Scholar]
- Li, J.; Narita, Y. Analysis and optimal design for the damping property of laminated viscoelastic plates under general edge conditions. Compos. B Eng. 2013, 45, 972–980. [Google Scholar] [CrossRef]
- Adessina, A.; Hamdaoui, M.; Xu, C. Damping properties of bi-dimensional sandwich structures with multi-layered frequency-dependent visco-elastic cores. Compos. Struct. 2016, 154, 334–343. [Google Scholar] [CrossRef]
- Ablitzer, F.; Pezerat, C.; Genevaux, J.M.; Bégué, J. Identification of stiffness and damping properties of plates by using the local equation of motion. J. Sound Vib. 2014, 333, 2454–2468. [Google Scholar] [CrossRef]
- Mcdaniel, J.G.; Dupont, P.; Salvino, L. A wave approach to estimating frequency-dependent damping under transient loading. J. Sound Vib. 2000, 231, 433–449. [Google Scholar] [CrossRef]
- Rak, M.; Ichchou, M.; Holnicki-Szulc, J. Identification of structural loss factor from spatially distributed measurements on beams with viscoelastic layer. J. Sound Vib. 2008, 310, 801–811. [Google Scholar] [CrossRef] [Green Version]
- Ichchou, M.N.; Bareille, O.; Berthaut, J. Identification of effective sandwich structural properties via an inverse wave approach. Eng. Struct. 2008, 30, 2591–2604. [Google Scholar] [CrossRef]
- Cherif, R.; Chazot, J.D.; Atalla, N. Damping loss factor estimation of two-dimensional orthotropic structures from a displacement field measurement. J. Sound Vib. 2015, 356, 61–71. [Google Scholar] [CrossRef]
- Barkanov, E.; Skukis, E.; Petitjean, B. Characterisation of viscoelastic layers in sandwich panels via an inverse technique. J. Sound Vib. 2009, 327, 402–412. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Liu, R.; Yan, X. Inverse Identification of the Frequency-Dependent Mechanical Parameters of a Viscoelastic Core Layer Based on the Vibration Response. Appl. Sci. 2017, 7, 455. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, L.; Zeiger, A.S.; Li, Y.; Vliet, K.J.V.; Tompson, C.V. Compositional dependence of Young’s moduli for amorphous Cu–Zr films measured using combinatorial deposition on microscale cantilever arrays. Scr. Mater. 2011, 64, 41–44. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Collet, C.; Guillemet, R. Determination of the elastic moduli and residual stresses of freestanding Au-TiW bilayer thin films by nanoindentation. Mater. Des. 2016, 106, 436–445. [Google Scholar] [CrossRef]
- Yun, Y.K. Young’s modulus measurement of a silicon nitride thin-film using an ultrasonically actuated microcantilever. Measurement 2018, 115, 133–138. [Google Scholar] [CrossRef]
- Zeng, H.; Sharpe, W. A system for measuring biaxial creep strains over short gage lengths. Exp. Mech. 1996, 36, 84–91. [Google Scholar] [CrossRef]
- Zhang, F.; Krishnaswamy, S.; Lilley, C.M. Bulk-wave and guided-wave photoacoustic evaluation of the mechanical properties of aluminum/silicon nitride double-layer thin films. Ultrasonics 2006, 45, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Hwangbo, Y.; Park, J.M.; Brown, W.L.; Goo, J.H.; Lee, H.J.; Hyun, S. Effect of deposition conditions on thermo-mechanical properties of free standing silicon-rich silicon nitride thin film. Microelectron. Eng. 2012, 95, 34–41. [Google Scholar] [CrossRef]




| Beam Type | Materials | Thickness (mm) | Modal Frequency (Hz) | ||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | |||
| Base 1 | Steel | 0.90 | 143.55 | 402.80 | 792.30 | 1311.0 | 1957.0 |
| Base 2 | Steel | 1.02 | 164.50 | 459.50 | 900.30 | 1488.0 | 2221.0 |
| Sandwich | —— | 2.42 | 161.31 | 434.50 | 842.50 | 1388.0 | 2068.0 |
| Beam Type | Materials | Thickness (mm) | Modal Frequency (Hz) | |||||
|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | |||
| Base 1 | Steel | 0.97 | 87.63 | 246.06 | 482.80 | 798.50 | 1193.0 | 1668.0 |
| Base 2 | Aluminium | 0.90 | 76.13 | 219.00 | 432.00 | 717.60 | 1078.5 | 1512.0 |
| Sandwich | —— | 2.37 | 92.94 | 245.00 | 469.00 | 768.50 | 1145.0 | 1597.0 |
| Beam Type | Materials | Thickness (mm) | Modal Frequency (Hz) | |||||
|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | |||
| Base 1 | Steel | 0.97 | 87.63 | 246.30 | 483.00 | 799.50 | 1195.0 | 1669.0 |
| Base 2 | Steel | 0.97 | 87.50 | 246.10 | 483.00 | 798.50 | 1194.0 | 1668.0 |
| Sandwich | —— | 2.44 | 91.94 | 248.00 | 480.75 | 789.25 | 1177.5 | 1645.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Wang, M. Study on the Dynamic Mechanical Properties of Viscoelastic Materials Based on Asymmetrical Sandwich Beams. Appl. Sci. 2018, 8, 1359. https://doi.org/10.3390/app8081359
Wu Q, Wang M. Study on the Dynamic Mechanical Properties of Viscoelastic Materials Based on Asymmetrical Sandwich Beams. Applied Sciences. 2018; 8(8):1359. https://doi.org/10.3390/app8081359
Chicago/Turabian StyleWu, Qingqing, and Minqing Wang. 2018. "Study on the Dynamic Mechanical Properties of Viscoelastic Materials Based on Asymmetrical Sandwich Beams" Applied Sciences 8, no. 8: 1359. https://doi.org/10.3390/app8081359




