Dynamic Response Evaluation of Long-Span Reinforced Arch Bridges Subjected to Near- and Far-Field Ground Motions
Abstract
:1. Introduction
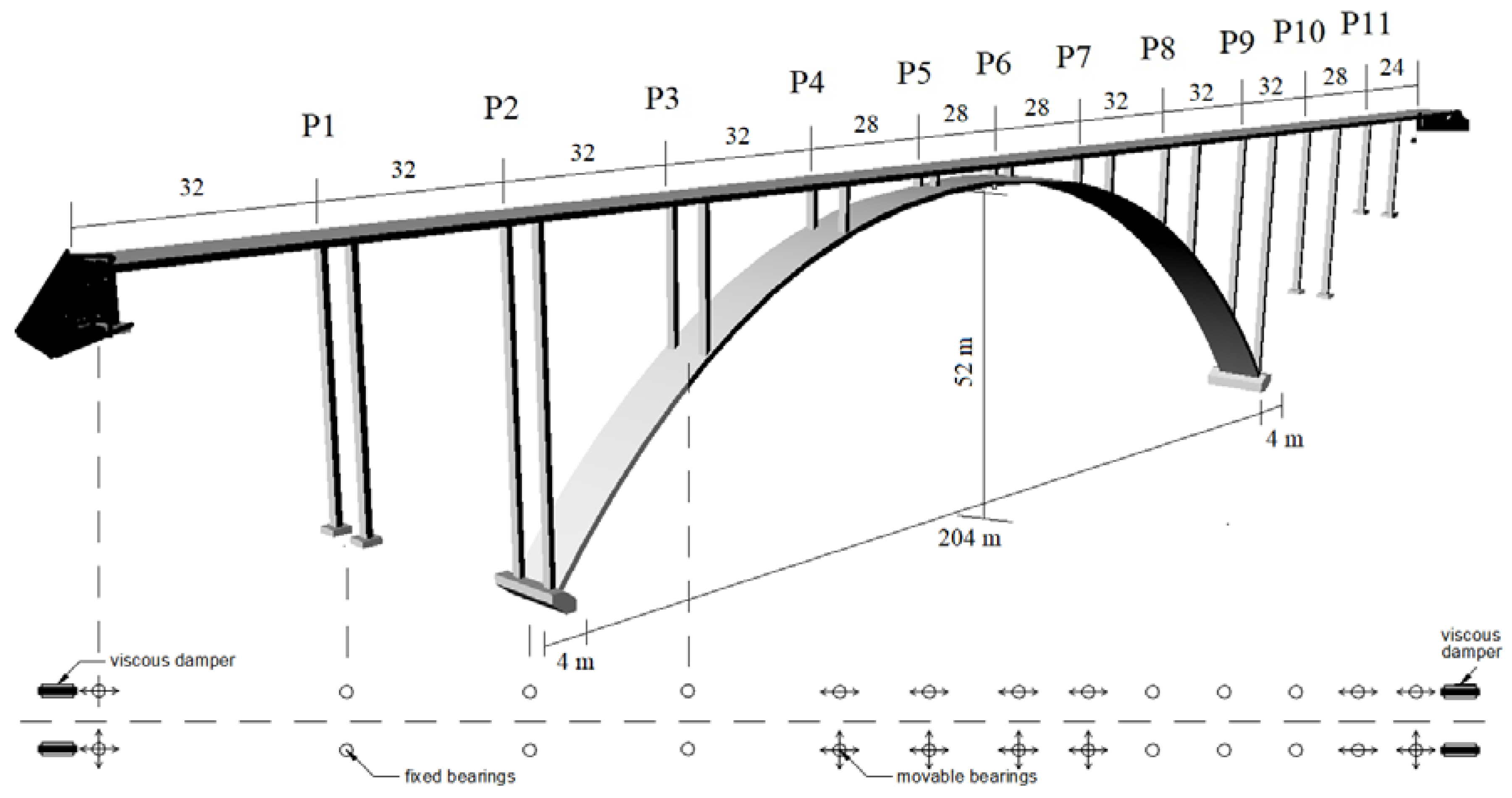
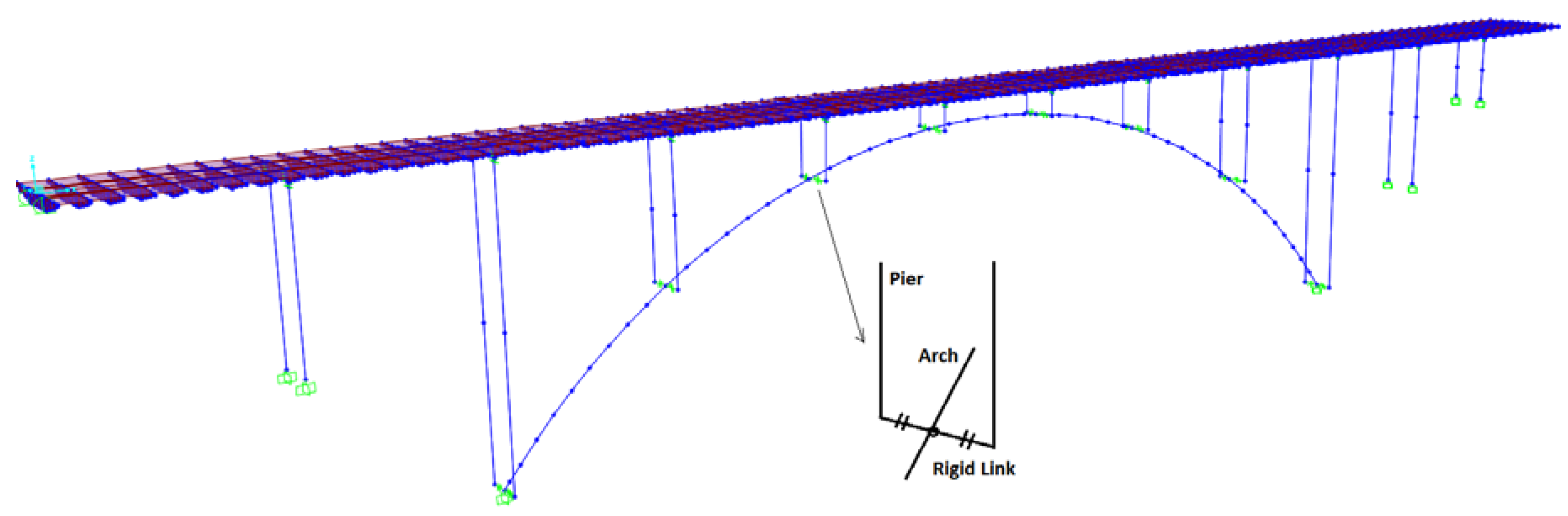
2. Structure of the Representative Bridge Used in the Case Study
3. Modeling the Forces Acting on the Representative Bridge
4. Case Study of a Representative Bridge
4.1. Moment-Curvature Analysis for Piers
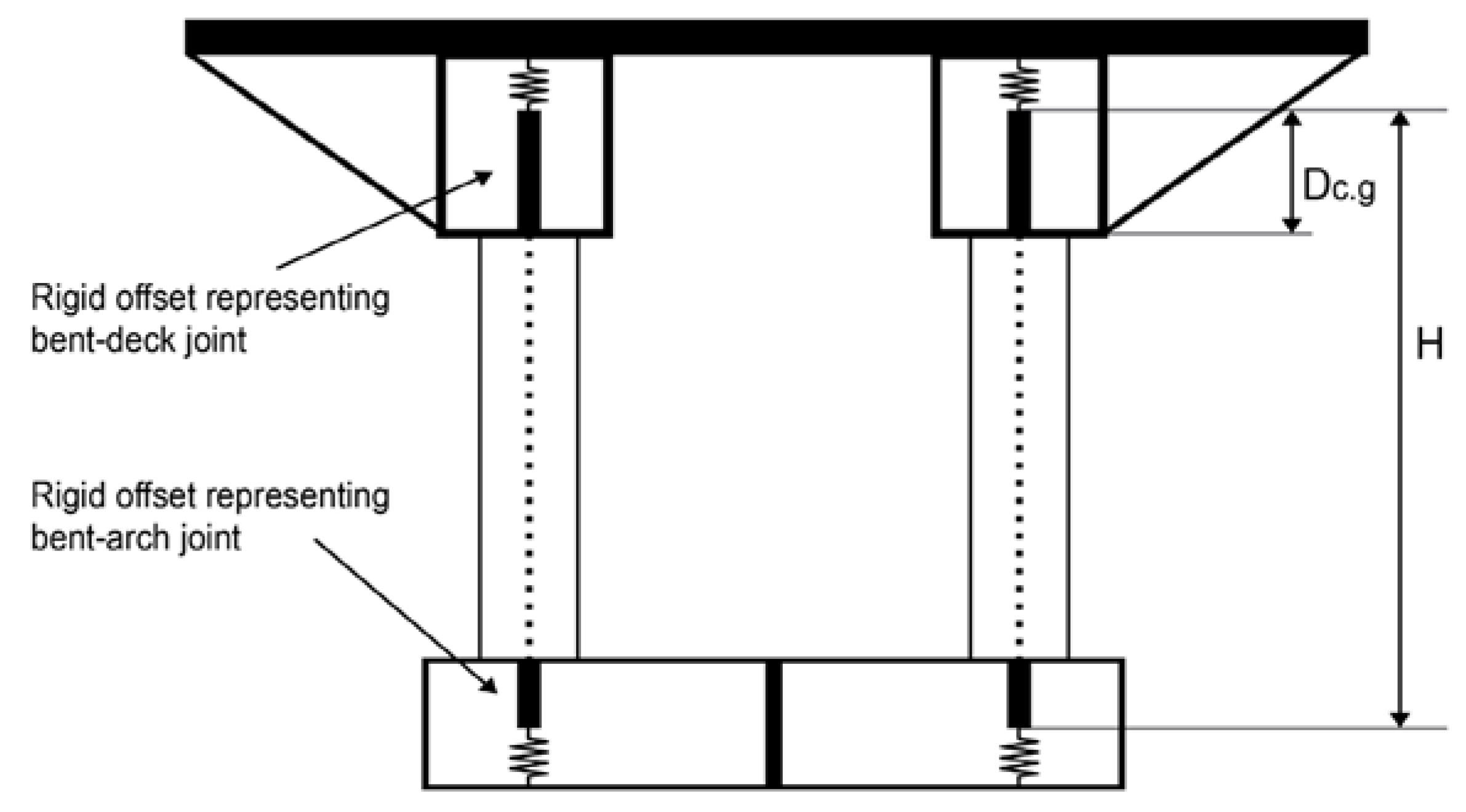
4.2. Assigning the Plastic Hinges
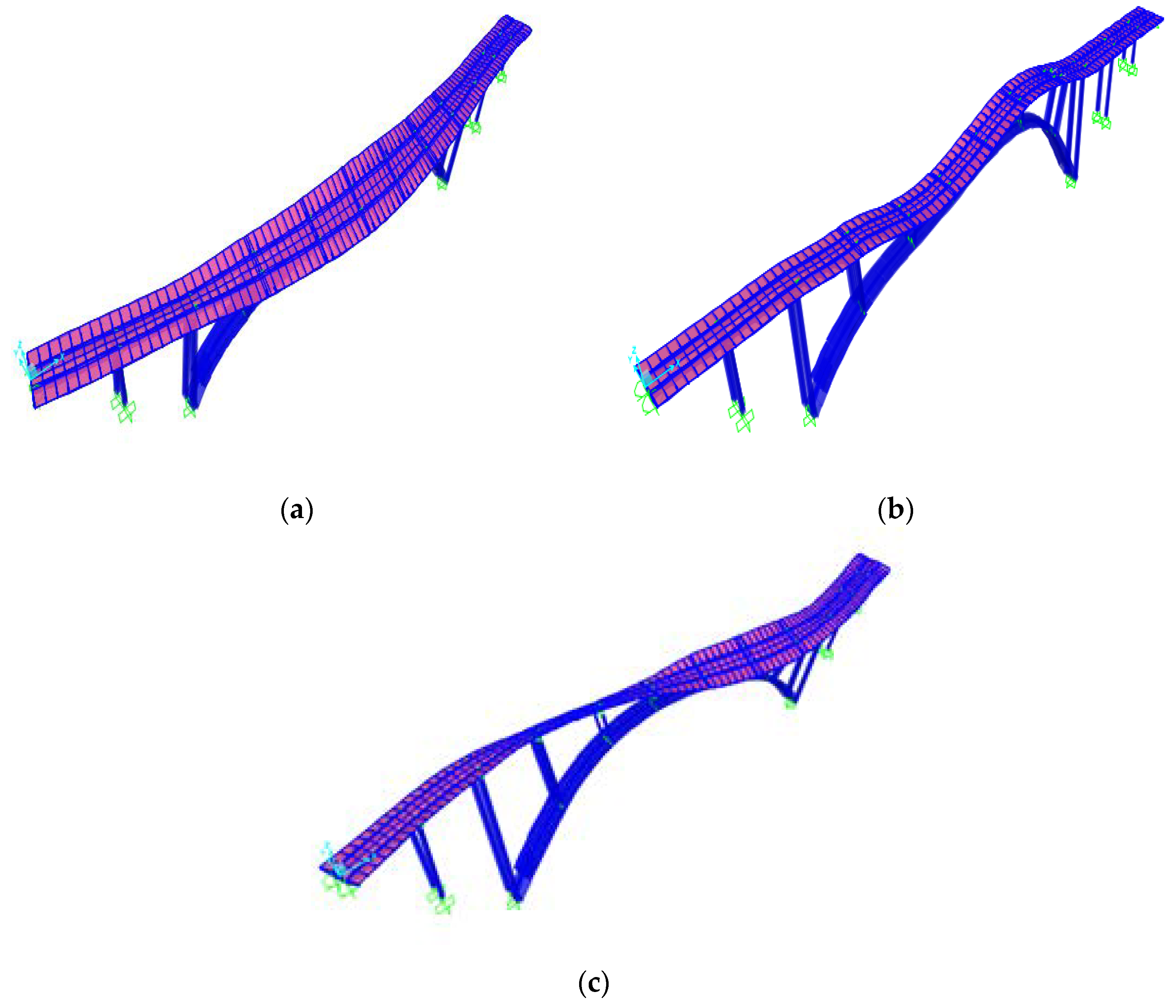
5. Bridge Modal Analysis
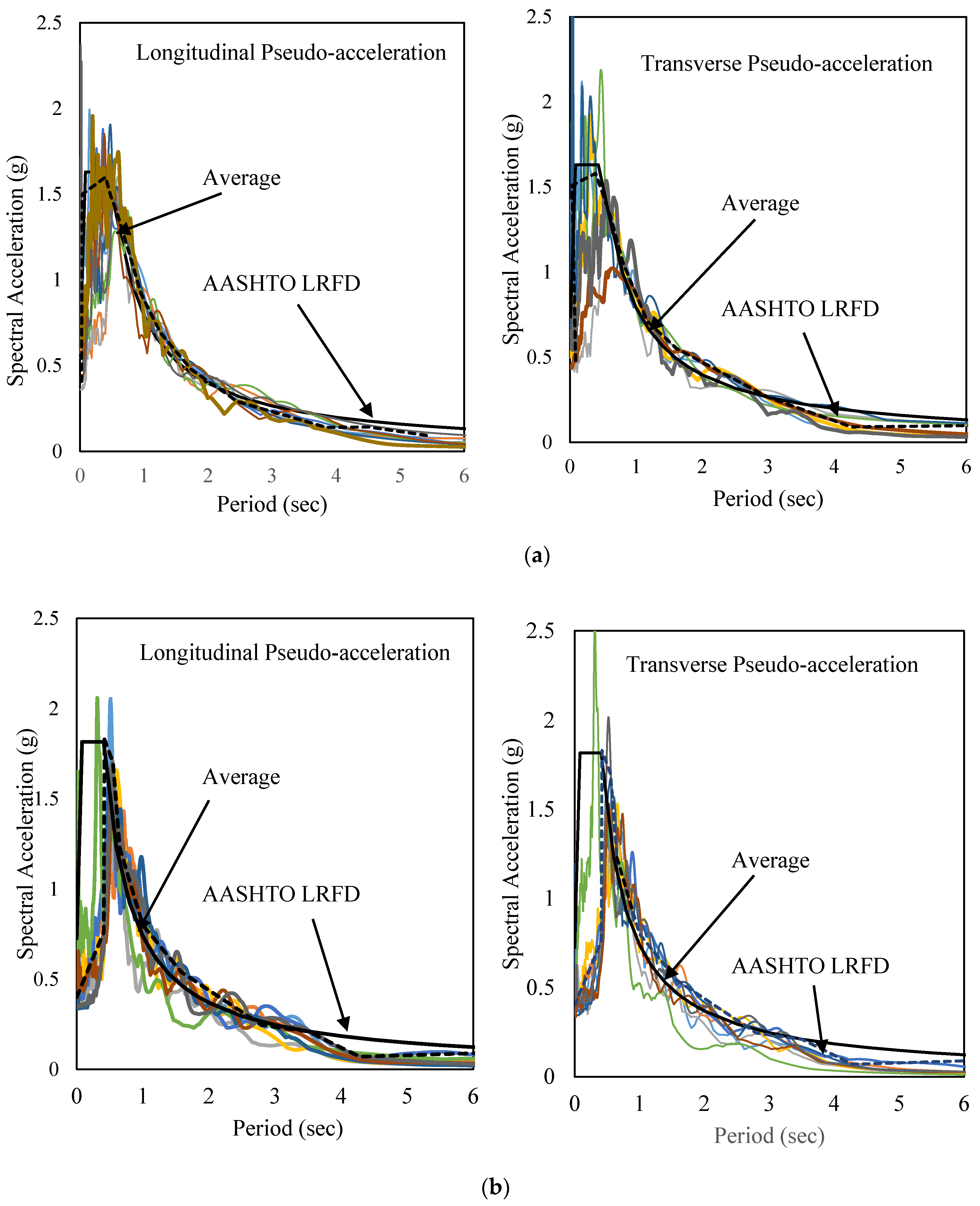
6. Ground Motion Database
7. Dynamic Analysis
8. Seismic Performance Evaluation
8.1. Seismic Displacement Demand Estimation
8.2. Distribution of Internal Forces and Bending Moments
8.3. Demand/Capacity Evaluation
8.4. Effect of Vertical Acceleration
9. Conclusions
- The eigenvalue analysis demonstrated that an unexpectedly high number of modes of vibration contributed to the seismic behavior of the model RC arch bridge. In order to achieve the 90% modal contribution recommended by the AASHTO [19] specifications, it was necessary to include 1850 modes of vibration.
- The DCR less than unity indicated that the arch bridge modeled in this study showed no sign of gross damage under either near- or far-field ground motion, although insignificant hazard levels for the DCR were reported for two piers. This is likely due to installing fixed bearings at both ends of the model bridge.
- A significant relative difference between the deck and arch displacement can be observed in longitudinal direction, while the deck and arch displacement in the other directions show almost identical results for the time history analysis. This indicates that no significant residual deck displacement remains at the end of the analysis; hence, no damage has occurred in either the piers or the arch, which play the greatest role in supporting the internal forces of the deck.
- The diagram representing the distribution of axial forces and out-of-plane bending moments along the main arch shows that for both near- and far-field ground motions, the average of maximum values calculated from the time history analyses has increased with a rather steep gradient near the abutment of the RC arch. The distribution of the in-plane shear force is almost uniform along the RC arch.
- The average discrepancies, 53%, for displacement in vertical direction and up to 16% in DCR were observed when considering the vertical component of earthquake in dynamic analysis. It was concluded that ignoring the effect of the vertical component of ground motion highlighted the importance of including this effect when modeling the dynamic responses of long-span arch bridges. Hence, it is strongly recommended that this be taken into account when designing RC arch bridges.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, B.; Ye, L. An overview of long span concrete arch bridges in China. In Proceedings of the Chinese-Croatian Joint Colloquium, Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Fuzhou University: Fuzhou, China, 2008. [Google Scholar]
- Radic, J.; Kindij, A.; Ivankovic, A.M. History of concrete application in development of concrete and hybrid arch bridges. In Proceedings of the Chinese-Croatian Joint Colloquium, Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Fuzhou University: Fuzhou, China, 2008. [Google Scholar]
- Mantzaris, G.; Pnevmatikos, N.; Tsiboukaki, G.; Mantzaris, A. Standardization of bridge structures for spans up to 100 m. Concr. Plant Int. J. 2010, 3, 164–172. [Google Scholar]
- Pnevmatikos, N.; Sentzas, V. Preliminary estimation of response of curved bridges subjected to earthquake loading. J. Civ. Eng. Archit. 2010, 6, 1530–1535. [Google Scholar]
- Chen, B. Long span arch bridges in China. In Proceedings of the Chinese-Croatian Joint Colloquium, Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Fuzhou University: Fuzhou, China, 2008. [Google Scholar]
- Kawashima, K.; Mizoguti, A. Seismic response of a reinforced concrete arch bridge. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; New Zealand Society for Earthquake Engineering: Upper Hutt, New Zealand, 2000. [Google Scholar]
- McCallen, D.; Noble, C.; Hoehler, M. The Seismic Response of Concrete Arch Bridges: With Focus on the Bixby Creek Bridge; Report No.: UCRL-ID-134419; Lawrence Livermore National Laboratory: Springfield, VA, USA, 1999. Available online: https://e-reports-ext.llnl.gov/pdf/236014.pdf (accessed on 15 March 2018).
- Cetinkaya, O.T.; Nakamura, S.; Takahashi, K. Expansion of a static analysis-based out-of-plane maximum inelastic seismic response estimation method for steel arch bridges to in-plane response estimation. Eng. Struct. 2009, 31, 2209–2212. [Google Scholar] [CrossRef] [Green Version]
- Torkamani, M.; Lee, H.K. Dynamic behavior of steel deck tension-tied arch bridges to seismic excitation. J. Bridge Eng. 2002, 7, 57–67. [Google Scholar] [CrossRef]
- Nazmy, A.S. Seismic response analysis of long-span steel arch bridges. Proc. Inst. Civ. Eng. 2003, 156, 91–97. [Google Scholar] [CrossRef]
- Lu, Z.; Usami, T.; Ge, H. Seismic performance evaluation of steel arch bridges against major earthquakes. Part 2: Simplified verification procedure. Earthq. Eng. Struct. Dyn. 2004, 33, 1355–1372. [Google Scholar] [CrossRef]
- Usami, T.; Lu, Z.; Ge, H.; Kono, T. Seismic performance evaluation of steel arch bridges against major earthquakes. Part 1: Dynamic analysis approach. Earthq. Eng. Struct. Dyn. 2004, 33, 1337–1354. [Google Scholar] [CrossRef]
- Kandemir, E.C.; Mazda, T.; Nurui, H.; Miyamoto, H. Seismic retrofit of an existing steel arch bridge using viscous damper. In Proceedings of the Twelfth East Asia-Pacific Conference on Structural Engineering and Construction, Hong Kong, China, 26–28 January 2011; Elsevier: New York, NY, USA, 2011. [Google Scholar]
- Khan, E.; Sullivan, J.T.; Kowalsky, M. Direct displacement–based seismic design of reinforced concrete arch bridges. J. Bridge Eng. 2014, 19, 44–58. [Google Scholar] [CrossRef]
- Franetovic, M.; Ivankovic, A.M.; Radic, J. Seismic assessment of existing reinforced-concrete arch bridges. Građevinar 2014, 8, 691–703. [Google Scholar] [CrossRef]
- Chen, K.; Song, J.Y. Survey and analysis of exiting reinforced concrete ribbed arch bridges. Adv. Mater. Res. 2011, 255–260, 1187–1191. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Direct Displacement Based Design of Structures, 2nd ed.; EUcentre Foundation, Istituto Universitario di Studi Superiori di Pavia (IUSS) Press: Pavia, Italy, 2018; ISBN 978-8861980006. [Google Scholar]
- Salonga, J.; Gauvreau, P. Comparative study of the proportions, form, and efficiency of concrete arch bridges. J. Bridge Eng. 2014, 19. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Guide Specifications for LRFD Seismic Bridge Design, 2nd ed.; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- California Department of Transportation. Caltrans Seismic Design Criteria (SDC), V1.7; California Department of Transportation: Sacramento, CA, USA, 2016.
- Hatzigeorgiou, G. Ductility demand spectra for multiple near- and far-fault earthquakes. Soil Dyn. Earthq. Eng. 2010, 30, 170–183. [Google Scholar] [CrossRef]
- Alavi, B.; Krawinkler, H. Behavior of moment-resisting frame structures subjected to near-fault ground motions. Earthq. Eng. Struct. Dyn. 2004, 33, 687–706. [Google Scholar] [CrossRef]
- Baker, J. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Žderić, Z.; Runjić, A.; Hrelja, G. Design and construction of Cetina arch bridge. In Proceedings of the Chinese-Croatia Joint Colloquium on Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Fuzhou University: Fuzhou, China, 2008; pp. 285–292. [Google Scholar]
- Seleemah, A.A.; Constantinou, M.C. Investigation of Seismic Response of Buildings with Linear and Nonlinear Fluid Viscous Dampers; Technical Report NCEER-97-0004; State University of New York at Buffalo: Buffalo, NY, USA, 1997. [Google Scholar]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures Part 1: General Rules and Rules for Buildings; EN1992-1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Computer & Structures Inc. (CSI). Integrated 3D Bridge Design Software, v20; CSiBridge Advanced; CSI: Berkeley, CA, USA, 2017. [Google Scholar]
- Finke, J.E. Static and Dynamic Characterization of Tied Arch Bridges. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2016. [Google Scholar]
- Mander, J.B.; Priestley, J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- American Concrete Institute. Building Code Requirements for Structural Concrete; Commentary on Building Code Requirements for Structural Concrete (ACI 318R-14); Reported by ACI Committee 318; American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- Berry, M.; Eberhard, M.O. Performance Modeling Strategies for Modern Reinforced Concrete Bridge Columns; PEER Report 2007/07; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures; ASCE Standard ASCE/SEI 7-10; American Society of Civil Engineers: Reston, VA, USA, 2010; ISBN 978-0-7844-1085-1. [Google Scholar]
- Computer & Structures Inc. (CSI). Integrated Analysis, Design and Drafting of Building Systems; ETABS, v16.2.1; CSI: Berkeley, CA, USA, 2016. [Google Scholar]
- Hilber, H.M.; Hughes, T.J.; Taylor, R.L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, J. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Papazoglou, A.; Elnashai, A. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1138. [Google Scholar] [CrossRef]
- Kim, S.J.; Curtis, J.H.; Elnashai, A. Analytical assessment of the effect of vertical earthquake motion on RC bridge piers. J. Struct. Eng. 2011, 137, 252–260. [Google Scholar] [CrossRef]








| (a) Mass Participation Factors | |||||||
| Mode No. | Period (s) | Translational Masses (%) | Rotational Masses (%) | ||||
| L | T | V | L | T | V | ||
| 1 | 2.34 | 7.3 × 10−8 | 6.6 × 10−1 | 1.0 × 10−7 | 2.8 × 10−1 | 6.6 × 10−8 | 4.4 × 10−4 |
| 2 | 1.66 | 1.1 × 10−1 | 2.6 × 10−6 | 5.6 × 10−6 | 3.8 × 10−7 | 8.2 × 10−2 | 1.8 × 10−7 |
| 3 | 1.20 | 2.5 × 10−7 | 2.6 × 10−3 | 1.6 × 10−9 | 1.4 × 10−3 | 2.4 × 10−8 | 5.0 × 10−1 |
| 4 | 1.08 | 2.2 × 10−2 | 3.1 × 10−6 | 2.1 × 10−2 | 7.0 × 10−6 | 1.4 × 10−3 | 2.1 × 10−6 |
| 5 | 0.80 | 1.6 × 10−7 | 1.7 × 10−6 | 9.4 × 10−5 | 1.0 × 10−1 | 1.8 × 10−6 | 4.9 × 10−5 |
| 6 | 0.71 | 3.3 × 10−2 | 5.6 × 10−5 | 1.9 × 10−3 | 3.7 × 10−5 | 3.2 × 10−3 | 5.7 × 10−6 |
| 7 | 0.64 | 1.6 × 10−2 | 1.4 × 10−5 | 2.6 × 10−3 | 4.9 × 10−6 | 4.4 × 10−2 | 1.7 × 10−6 |
| 8 | 0.63 | 2.4 × 10−7 | 6.4 × 10−2 | 9.6 × 10−7 | 3.3 × 10−3 | 4.2 × 10−6 | 3.5 × 10−4 |
| 9 | 0.59 | 3.1 × 10−7 | 1.7 × 10−6 | 1.0 × 10−8 | 3.1 × 10−4 | 1.0 × 10−6 | 1.0 × 10−3 |
| 10 | 0.55 | 1.5 × 10−7 | 6.8 × 10−4 | 3.4 × 10−5 | 3.4 × 10−4 | 6.2 × 10−7 | 1.5 × 10−2 |
| 11 | 0.52 | 3.4 × 10−7 | 1.7 × 10−4 | 1.2 × 10−5 | 1.8 × 10−4 | 6.4 × 10−6 | 1.1 × 10−3 |
| 12 | 0.52 | 3.0 × 10−3 | 3.7 × 10−4 | 1.9 × 10−4 | 8.3 × 10−5 | 3.6 × 10−4 | 6.1 × 10−3 |
| 13 | 0.51 | 3.7 × 10−1 | 1.5 × 10−5 | 4.7 × 10−3 | 8.8 × 10−8 | 2.9 × 10−2 | 3.0 × 10−5 |
| 14 | 0.50 | 1.8 × 10−5 | 1.3 × 10−5 | 1.9 × 10−4 | 1.1 × 10−4 | 6.8 × 10−5 | 3.0 × 10−4 |
| 15 | 0.48 | 3.2 × 10−5 | 1.6 × 10−4 | 1.6 × 10−3 | 7.8 × 10−4 | 6.4 × 10−5 | 2.6 × 10−5 |
| 61 | 0.31 | 1.9 × 10−5 | 4.0 × 10−4 | 1.8 × 10−1 | 1.2 × 10−3 | 7.4 × 10−4 | 3.1 × 10−7 |
| 441 | 0.13 | 9.0 × 10−8 | 7.8 × 10−6 | 4.1 × 10−6 | 1.1 × 10−4 | 8.3 × 10−2 | 9.2 × 10−9 |
| 1850 | 0.03 | 2.1 × 10−5 | 6.7 × 10−8 | 5.0 × 10−8 | 2.2 × 10−8 | 7.6 × 10−5 | 2.4 × 10−9 |
| (b) Percentage of Modal Mass Participation | |||||||
| Mode No. | Period (s) | Translational Masses (%) | Rotational Masses (%) | ||||
| L | T | V | L | T | V | ||
| 1 | 2.34 | 0 | 0.66 | 0 | 0.27 | 0 | 0 |
| 2 | 1.66 | 0.11 | 0.66 | 0 | 0.27 | 0.08 | 0 |
| 3 | 1.2 | 0.11 | 0.66 | 0 | 0.28 | 0.08 | 0.5 |
| 4 | 1.08 | 0.13 | 0.66 | 0 | 0.28 | 0.09 | 0.5 |
| 5 | 0.8 | 0.13 | 0.66 | 0 | 0.38 | 0.09 | 0.5 |
| 6 | 0.71 | 0.17 | 0.66 | 0 | 0.38 | 0.1 | 0.5 |
| 7 | 0.64 | 0.18 | 0.66 | 0 | 0.38 | 0.14 | 0.5 |
| 8 | 0.63 | 0.18 | 0.73 | 0 | 0.39 | 0.14 | 0.51 |
| 9 | 0.59 | 0.18 | 0.73 | 0 | 0.39 | 0.14 | 0.51 |
| 10 | 0.55 | 0.18 | 0.73 | 0 | 0.39 | 0.14 | 0.52 |
| 11 | 0.52 | 0.18 | 0.73 | 0 | 0.39 | 0.14 | 0.52 |
| 12 | 0.52 | 0.18 | 0.73 | 0 | 0.39 | 0.14 | 0.53 |
| 13 | 0.51 | 0.56 | 0.73 | 0.01 | 0.39 | 0.17 | 0.53 |
| 14 | 0.5 | 0.56 | 0.73 | 0.01 | 0.39 | 0.17 | 0.53 |
| 15 | 0.48 | 0.56 | 0.73 | 0.01 | 0.39 | 0.17 | 0.53 |
| 61 | 0.31 | 0.58 | 0.79 | 0.32 | 0.42 | 0.32 | 0.66 |
| 441 | 0.13 | 0.81 | 0.85 | 0.67 | 0.55 | 0.51 | 0.76 |
| 1850 | 0.03 | 0.91 | 0.93 | 0.9 | 0.74 | 0.88 | 0.89 |
| No. | Year | Earthquake | Mw | Mech a | Station | Dist b | PGA (g) |
|---|---|---|---|---|---|---|---|
| 1 | 1979 | Imperial Valley-06 | 6.53 | SS | EC County Center FF | 7.31 | 0.35 |
| 2 | 1979 | Imperial Valley-06 | 6.53 | SS | El Centro Array #7 | 1.56 | 0.51 |
| 3 | 1986 | N. Palm Springs | 6.06 | RO | North Palm Springs | 4.04 | 0.84 |
| 4 | 1994 | Northridge-01 | 6.9 | REV | Rinaldi Receiving | 6.50 | 0.62 |
| 5 | 1994 | Northridge-01 | 6.69 | REV | Sylmar—Converter | 5.35 | 0.52 |
| 6 | 1995 | Kobe_Japan | 6.90 | SS | Takarazuka | 1.27 | 0.71 |
| 7 | 1995 | Kobe_Japan | 6.90 | SS | Takatori | 2.47 | 0.39 |
| 8 | 1992 | Erzican_Turkey | 6.69 | SS | Erzican | 4.38 | 0.57 |
| No. | Year | Earthquake | Mw | Mech a | Station | Dist b | PGA (g) |
|---|---|---|---|---|---|---|---|
| 1 | 1978 | Tabas | 7.35 | REV | Ferdows | 91.40 | 0.41 |
| 2 | 1952 | Kern County | 7.36 | REV | Taft Lincoln School | 38.89 | 0.44 |
| 3 | 1994 | Northridge-01 | 6.69 | REV | La Puente—Rimgrove | 56.59 | 0.32 |
| 4 | 1994 | Northridge-01 | 6.69 | REV | Downey—Co Maint | 46.74 | 0.41 |
| 5 | 1999 | Kocaeli | 7.51 | SS | Ambarli | 69.62 | 0.45 |
| 6 | 1987 | Whittier Narrows | 5.99 | RO | Tarzana—Cedar Hill | 41.22 | 0.61 |
| 7 | 1956 | El Alamo | 6.80 | SS | El Centro Array #9 | 121.3 | 0.31 |
| 8 | 1994 | Northridge-01 | 6.69 | REV | Montebello—Bluff Rd. | 45.30 | 0.39 |
| No. | Station | Deck (m) | Arch Crown (m) | ||||
|---|---|---|---|---|---|---|---|
| L | T | V | L | T | V | ||
| 1 | EC County | 0.080 | 0.480 | 0.164 | 1.110 | 0.509 | 0.170 |
| 2 | El Centro #7 | 0.096 | 0.592 | 0.168 | 0.084 | 0.503 | 0.168 |
| 3 | North Palm | 0.111 | 0.678 | 0.247 | 0.108 | 0.562 | 0.192 |
| 4 | Rinaldi | 0.120 | 0.765 | 0.180 | 0.103 | 0.615 | 0.174 |
| 5 | Sylmar | 0.123 | 0.406 | 0.155 | 0.077 | 0.317 | 0.154 |
| 6 | Takarazuka | 0.103 | 0.483 | 0.165 | 0.105 | 0.596 | 0.165 |
| 7 | Takatori | 0.131 | 0.728 | 0.158 | 0.098 | 0.581 | 0.163 |
| 8 | Erzican | 0.103 | 0.732 | 0.156 | 0.091 | 0.590 | 0.158 |
| 9 | Average | 0.112 | 0.627 | 0.177 | 0.224 | 0.545 | 0.165 |
| No. | Station | Deck (m) | Arch Crown (m) | ||||
|---|---|---|---|---|---|---|---|
| L | T | V | L | T | V | ||
| 1 | Ferdows | 0.127 | 0.451 | 0.150 | 0.077 | 0.353 | 0.148 |
| 2 | Taft Lincoln | 0.087 | 0.593 | 0.168 | 0.098 | 0.470 | 0.171 |
| 3 | La Puente | 0.093 | 0.316 | 0.122 | 0.067 | 0.240 | 0.125 |
| 4 | Downey-Maint | 0.087 | 0.670 | 0.167 | 0.092 | 0.527 | 0.171 |
| 5 | Ambarli | 0.118 | 0.470 | 0.152 | 0.103 | 0.373 | 0.152 |
| 6 | Tarzana | 0.109 | 0.335 | 0.122 | 0.055 | 0.280 | 0.112 |
| 7 | El Centro #9 | 0.101 | 0.540 | 0.162 | 0.091 | 0.433 | 0.162 |
| 8 | Montebello | 0.090 | 0.542 | 0.170 | 0.091 | 0.423 | 0.174 |
| 9 | Average | 0.101 | 0.490 | 0.151 | 0.084 | 0.388 | 0.151 |
| No. | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | R | L | R | L | R | L | R | L | R | L | R | L | R | L | R | L | R | L | R | L | R | |
| 1 | 0.77 | 0.85 | 0.63 | 0.69 | 0.92 | 0.95 | 0.70 | 0.31 | 0.46 | 0.18 | 0.48 | 0.18 | 0.81 | 0.41 | 0.65 | 0.70 | 0.52 | 0.53 | 0.61 | 0.61 | 0.54 | 0.57 |
| 2 | 0.79 | 0.91 | 0.66 | 0.68 | 0.95 | 0.95 | 0.73 | 0.32 | 0.48 | 0.17 | 0.47 | 0.18 | 0.83 | 0.44 | 0.66 | 0.73 | 0.56 | 0.59 | 0.72 | 0.72 | 0.63 | 0.64 |
| 3 | 0.85 | 0.95 | 0.71 | 0.71 | 0.94 | 0.96 | 0.79 | 0.36 | 0.63 | 0.18 | 0.60 | 0.19 | 0.85 | 0.48 | 0.74 | 0.80 | 0.58 | 0.60 | 0.73 | 0.75 | 0.65 | 0.68 |
| 4 | 0.94 | 0.92 | 0.77 | 0.80 | 0.93 | 0.95 | 0.78 | 0.46 | 0.65 | 0.24 | 0.68 | 0.20 | 0.80 | 0.58 | 0.85 | 0.83 | 0.62 | 0.59 | 0.80 | 0.82 | 0.66 | 0.62 |
| 5 | 0.70 | 0.62 | 0.54 | 0.48 | 0.71 | 0.72 | 0.59 | 0.32 | 0.44 | 0.17 | 0.43 | 0.16 | 0.66 | 0.41 | 0.62 | 0.58 | 0.48 | 0.41 | 0.48 | 0.46 | 0.47 | 0.42 |
| 6 | 0.88 | 0.78 | 0.69 | 0.71 | 0.92 | 0.94 | 0.89 | 0.44 | 0.96 | 0.22 | 0.90 | 0.22 | 0.99 | 0.61 | 0.76 | 0.71 | 0.54 | 0.52 | 0.64 | 0.67 | 0.56 | 0.56 |
| 6 * | 0.87 | 0.76 | 0.64 | 0.63 | 0.85 | 0.86 | 0.83 | 0.38 | 0.85 | 0.16 | 0.75 | 0.17 | 0.90 | 0.51 | 0.69 | 0.63 | 0.52 | 0.50 | 0.56 | 0.57 | 0.59 | 0.55 |
| 7 | 0.88 | 0.89 | 0.72 | 0.70 | 0.95 | 0.96 | 0.87 | 0.36 | 0.74 | 0.17 | 0.75 | 0.17 | 0.95 | 0.45 | 0.74 | 0.70 | 0.60 | 0.61 | 0.73 | 0.71 | 0.64 | 0.63 |
| 8 | 0.81 | 0.91 | 0.71 | 0.71 | 0.93 | 0.91 | 0.76 | 0.35 | 0.56 | 0.17 | 0.51 | 0.18 | 0.82 | 0.53 | 0.76 | 0.79 | 0.59 | 0.65 | 0.78 | 0.76 | 0.67 | 0.66 |
| Avg. | 0.83 | 0.85 | 0.68 | 0.68 | 0.90 | 0.91 | 0.76 | 0.36 | 0.61 | 0.19 | 0.60 | 0.18 | 0.84 | 0.49 | 0.72 | 0.73 | 0.56 | 0.56 | 0.69 | 0.69 | 0.60 | 0.60 |
| ESA | 0.71 | 0.74 | 0.56 | 0.57 | 0.72 | 0.65 | 0.59 | 0.14 | 0.58 | 0.09 | 0.53 | 0.46 | 0.57 | 0.21 | 0.61 | 0.60 | 0.51 | 0.52 | 0.74 | 0.73 | 0.72 | 0.71 |
| RSA | 0.64 | 0.64 | 0.51 | 0.51 | 0.77 | 0.76 | 0.70 | 0.47 | 0.80 | 0.12 | 0.78 | 0.13 | 0.78 | 0.63 | 0.51 | 0.52 | 0.44 | 0.44 | 0.53 | 0.53 | 0.52 | 0.52 |
| No. | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | R | L | R | L | R | L | R | L | R | L | L | R | L | R | L | R | L | R | L | R | L | |
| 1 | 0.72 | 0.79 | 0.62 | 0.64 | 0.78 | 0.81 | 0.62 | 0.32 | 0.46 | 0.19 | 0.49 | 0.18 | 0.73 | 0.43 | 0.60 | 0.63 | 0.45 | 0.46 | 0.50 | 0.51 | 0.50 | 0.50 |
| 1 * | 0.70 | 0.76 | 0.58 | 0.58 | 0.79 | 0.76 | 0.57 | 0.31 | 0.40 | 0.17 | 0.43 | 0.16 | 0.67 | 0.40 | 0.55 | 0.56 | 0.42 | 0.44 | 0.48 | 0.49 | 0.48 | 0.49 |
| 2 | 0.76 | 0.79 | 0.64 | 0.61 | 0.93 | 0.91 | 0.72 | 0.33 | 0.49 | 0.18 | 0.52 | 0.19 | 0.83 | 0.44 | 0.71 | 0.71 | 0.56 | 0.53 | 0.62 | 0.61 | 0.55 | 0.56 |
| 3 | 0.64 | 0.58 | 0.56 | 0.46 | 0.59 | 0.55 | 0.48 | 0.30 | 0.38 | 0.16 | 0.37 | 0.15 | 0.59 | 0.40 | 0.51 | 0.48 | 0.40 | 0.38 | 0.47 | 0.42 | 0.47 | 0.40 |
| 4 | 0.78 | 0.78 | 0.66 | 0.65 | 0.91 | 0.90 | 0.74 | 0.32 | 0.56 | 0.18 | 0.50 | 0.17 | 0.74 | 0.43 | 0.75 | 0.71 | 0.55 | 0.57 | 0.64 | 0.63 | 0.57 | 0.58 |
| 5 | 0.75 | 0.72 | 0.65 | 0.58 | 0.76 | 0.82 | 0.58 | 0.31 | 0.42 | 0.17 | 0.42 | 0.16 | 0.70 | 0.41 | 0.59 | 0.61 | 0.49 | 0.45 | 0.57 | 0.50 | 0.50 | 0.48 |
| 6 | 0.62 | 0.65 | 0.51 | 0.50 | 0.58 | 0.55 | 0.59 | 0.38 | 0.66 | 0.19 | 0.66 | 0.18 | 0.67 | 0.45 | 0.51 | 0.49 | 0.42 | 0.40 | 0.45 | 0.43 | 0.45 | 0.42 |
| 7 | 0.72 | 0.75 | 0.58 | 0.62 | 0.81 | 0.84 | 0.66 | 0.32 | 0.45 | 0.19 | 0.51 | 0.18 | 0.76 | 0.45 | 0.60 | 0.60 | 0.51 | 0.49 | 0.55 | 0.54 | 0.53 | 0.51 |
| 8 | 0.73 | 0.80 | 0.61 | 0.61 | 0.84 | 0.86 | 0.66 | 0.35 | 0.49 | 0.18 | 0.52 | 0.18 | 0.81 | 0.46 | 0.63 | 0.67 | 0.53 | 0.51 | 0.58 | 0.59 | 0.58 | 0.58 |
| Avg. | 0.71 | 0.73 | 0.60 | 0.59 | 0.80 | 0.80 | 0.63 | 0.33 | 0.49 | 0.18 | 0.50 | 0.18 | 0.73 | 0.43 | 0.61 | 0.61 | 0.49 | 0.47 | 0.55 | 0.53 | 0.52 | 0.50 |
| ESA | 0.71 | 0.74 | 0.56 | 0.57 | 0.72 | 0.65 | 0.59 | 0.14 | 0.58 | 0.09 | 0.53 | 0.46 | 0.57 | 0.21 | 0.61 | 0.60 | 0.51 | 0.52 | 0.74 | 0.73 | 0.72 | 0.71 |
| RSA | 0.64 | 0.64 | 0.51 | 0.51 | 0.77 | 0.76 | 0.70 | 0.47 | 0.80 | 0.12 | 0.78 | 0.13 | 0.78 | 0.63 | 0.51 | 0.52 | 0.44 | 0.44 | 0.53 | 0.53 | 0.52 | 0.52 |
| Earthquake Name | Three Orthogonal Accelerations | Two Horizontal Accelerations | Difference (%) | ||
|---|---|---|---|---|---|
| Kobe (Takarazuka) | Arch | L | 0.105 | 0.098 | 6.70 |
| T | 0.596 | 0.535 | 10.2 | ||
| V | 0.165 | 0.041 | 75.2 | ||
| Deck | L | 0.103 | 0.095 | 7.76 | |
| T | 0.483 | 0.442 | 8.50 | ||
| V | 0.165 | 0.045 | 72.7 | ||
| Tabas (Ferdows) | Arch | L | 0.077 | 0.070 | 9.10 |
| T | 0.353 | 0.322 | 8.78 | ||
| V | 0.148 | 0.038 | 74.3 | ||
| Deck | L | 0.127 | 0.116 | 8.66 | |
| T | 0.451 | 0.418 | 7.31 | ||
| V | 0.150 | 0.039 | 74.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohseni, I.; Lashkariani, H.A.; Kang, J.; Kang, T.H.-K. Dynamic Response Evaluation of Long-Span Reinforced Arch Bridges Subjected to Near- and Far-Field Ground Motions. Appl. Sci. 2018, 8, 1243. https://doi.org/10.3390/app8081243
Mohseni I, Lashkariani HA, Kang J, Kang TH-K. Dynamic Response Evaluation of Long-Span Reinforced Arch Bridges Subjected to Near- and Far-Field Ground Motions. Applied Sciences. 2018; 8(8):1243. https://doi.org/10.3390/app8081243
Chicago/Turabian StyleMohseni, Iman, Hamidreza Alinejad Lashkariani, Junsuk Kang, and Thomas H.-K. Kang. 2018. "Dynamic Response Evaluation of Long-Span Reinforced Arch Bridges Subjected to Near- and Far-Field Ground Motions" Applied Sciences 8, no. 8: 1243. https://doi.org/10.3390/app8081243
APA StyleMohseni, I., Lashkariani, H. A., Kang, J., & Kang, T. H.-K. (2018). Dynamic Response Evaluation of Long-Span Reinforced Arch Bridges Subjected to Near- and Far-Field Ground Motions. Applied Sciences, 8(8), 1243. https://doi.org/10.3390/app8081243






