Numerical Investigation of the Dynamics of ‘Hot Spots’ as Models of Dissipative Rogue Waves
Abstract
:1. Introduction
2. Effect of Background Gain/Loss
2.1. Preliminary Theoretical Considerations
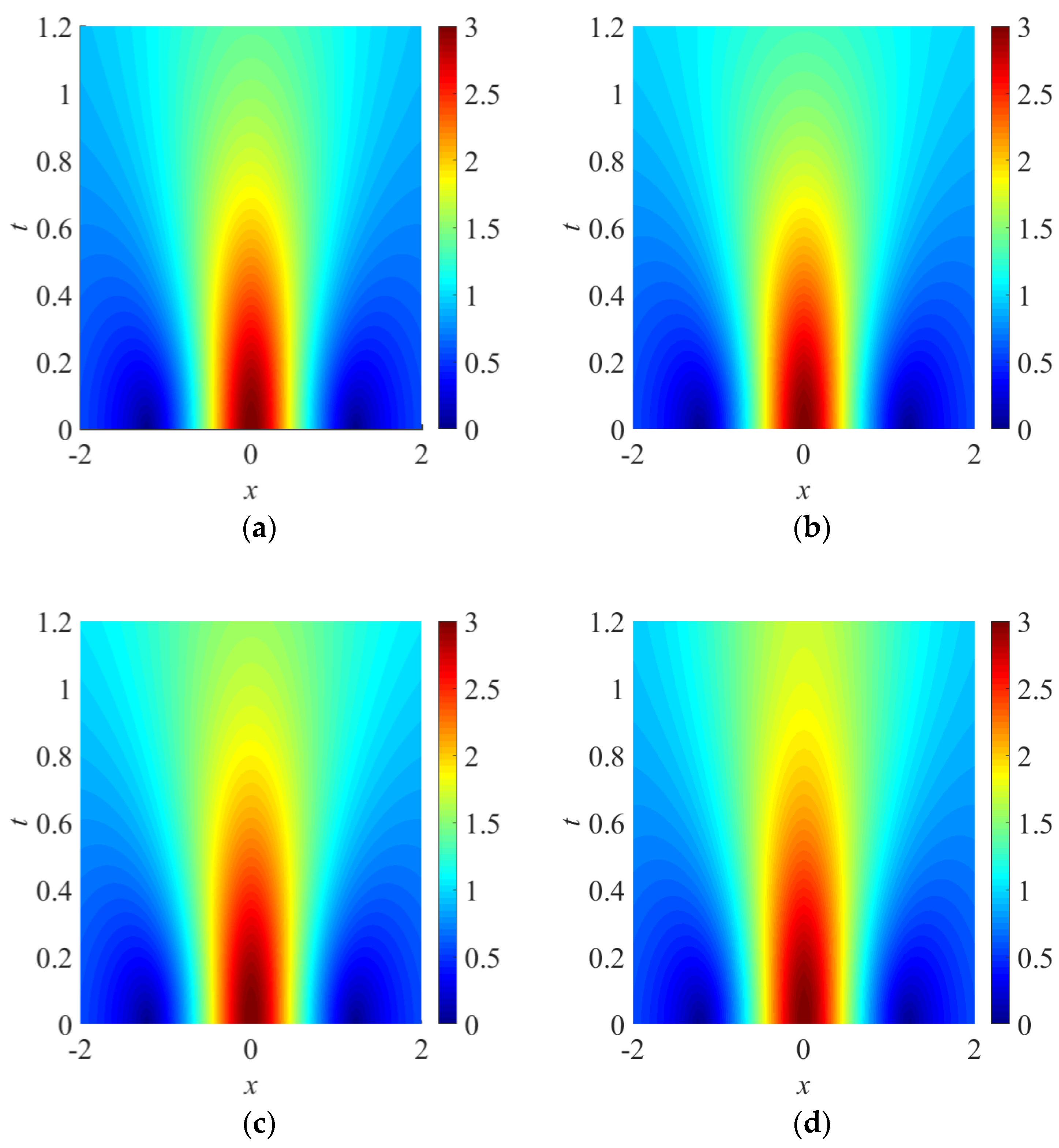
2.2. Linear Background Gain/Loss
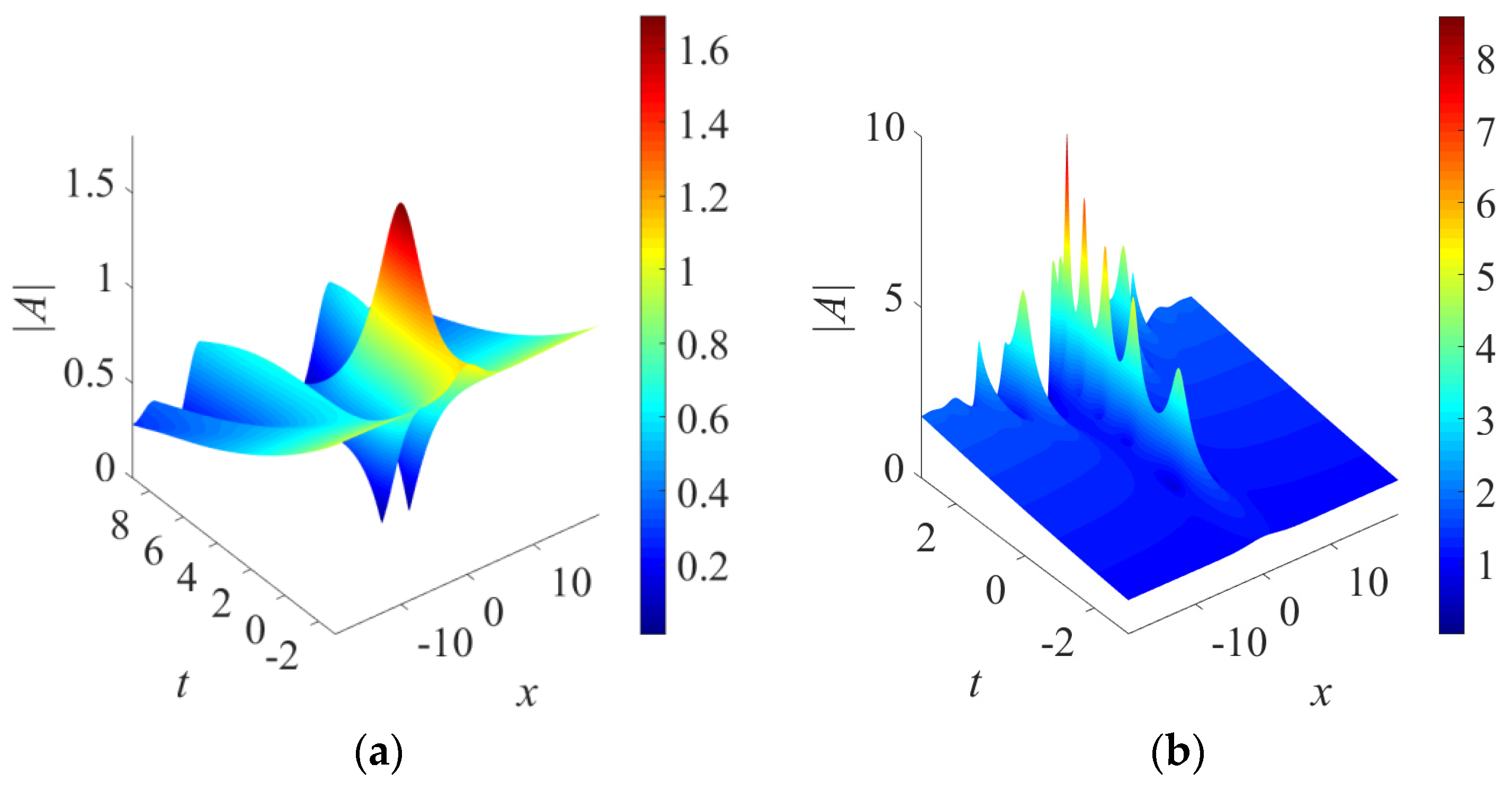
2.3. Cubic Background Gain
3. Gain Localized in Space
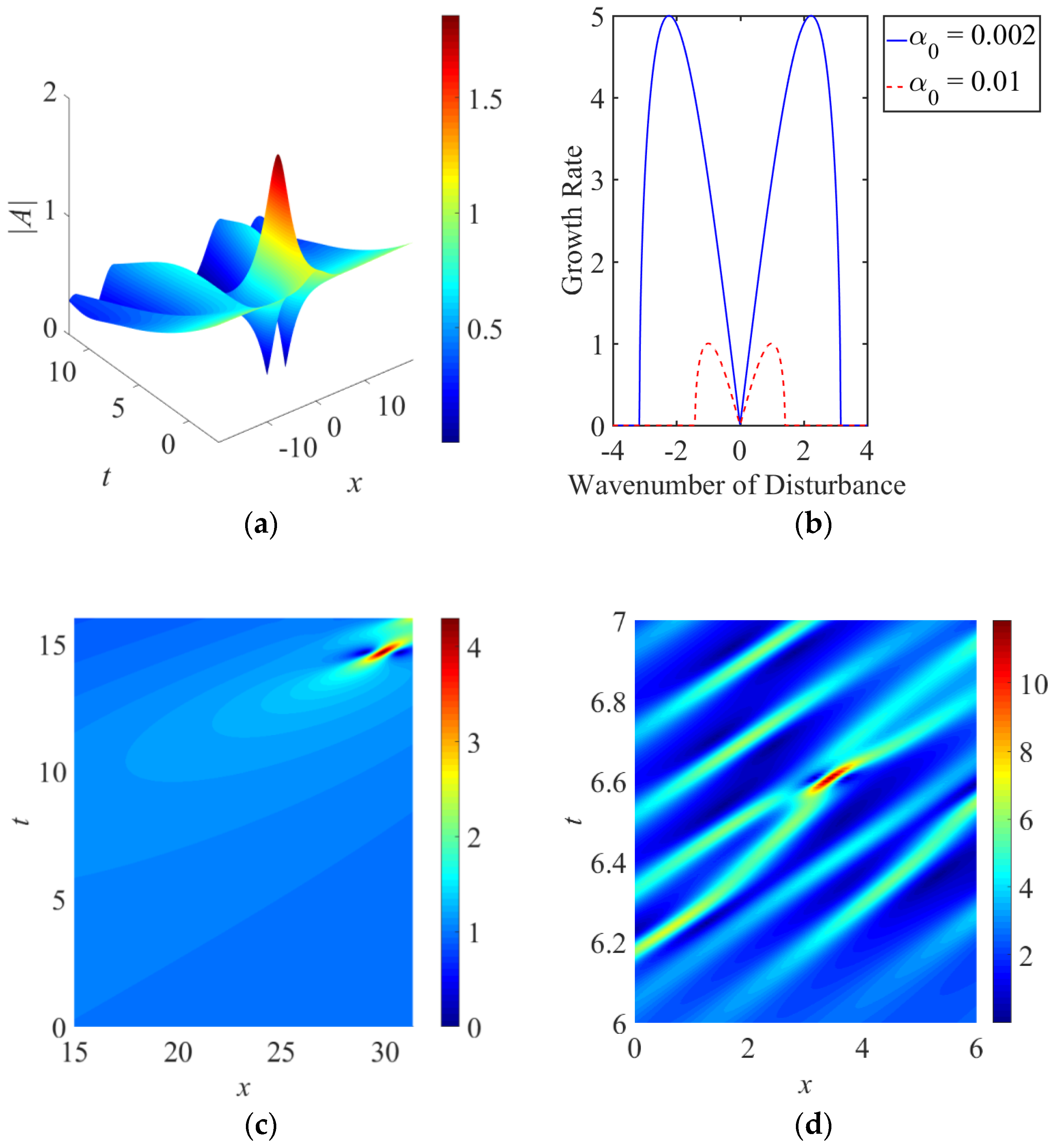
3.1. Linear Gain
Emergence of a Pinned Mode
3.2. Cubic Gain
4. Gain Localized in Both Space and Time
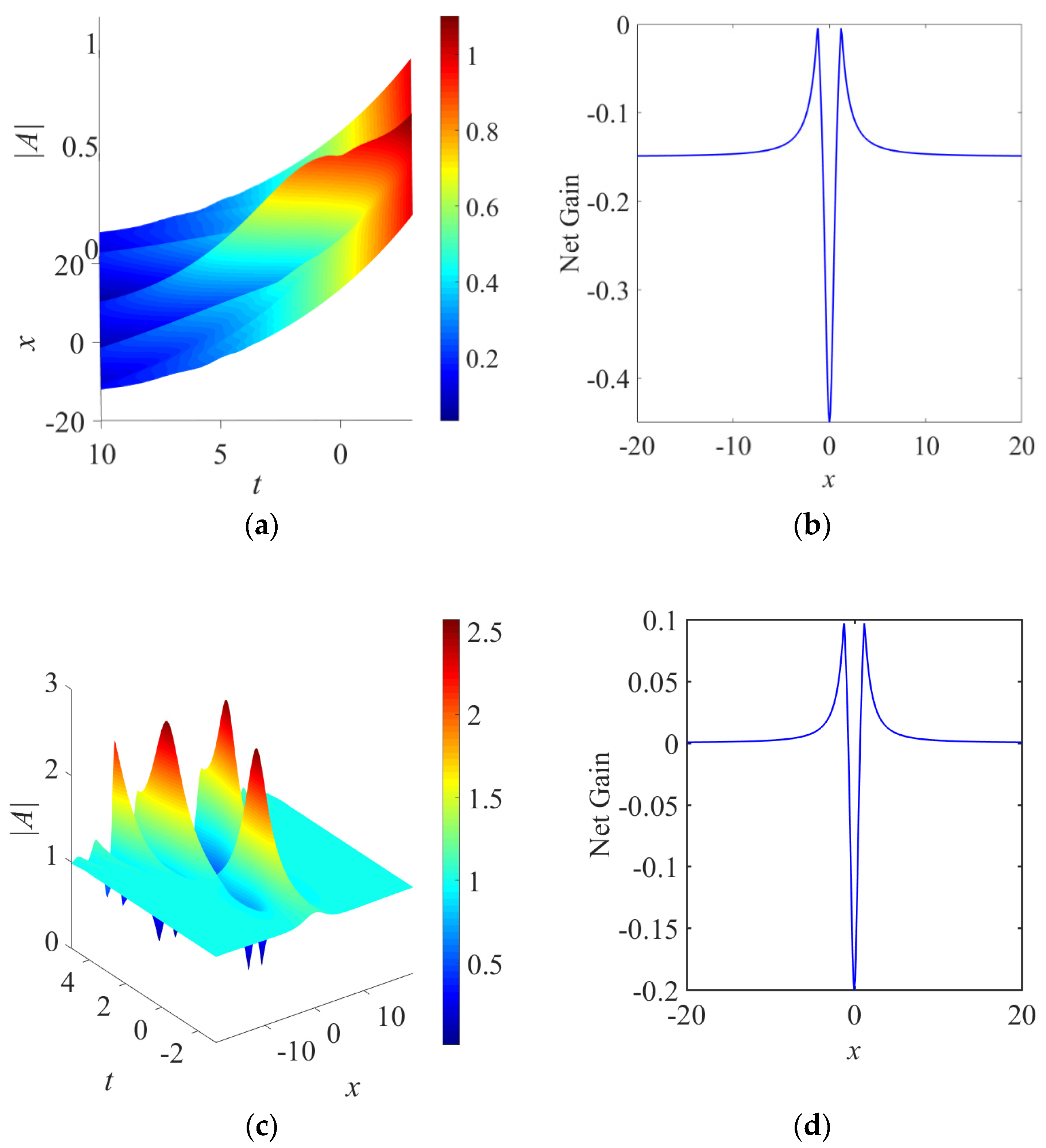
4.1. Linear Gain
4.2. Cubic Gain
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| β0 | t | Adiabatic Approximation of |A(0,t)| by Equation (A2) | Numerical Approximation of |A(0,t)| by Simulation | Absolute Percentage Error | |
|---|---|---|---|---|---|
| 0.05 | −1 | 0.5 | 2.18 | 2.15 | 1.4% |
| 0.05 | −1 | 1 | 1.53 | 1.47 | 4.08% |
| 0.05 | 1 | 0.5 | 2.29 | 2.33 | 1.72% |
| 0.05 | 1 | 1 | 1.7 | 1.79 | 5.03% |
References
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef] [Green Version]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 220, 755–764. [Google Scholar] [CrossRef]
- Akhmediev, N.; Kibler, B.; Baronio, F.; Belić, M.; Zhong, W.-P.; Zhang, Y.; Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Grelu, P.; et al. Roadmap on optical rogue waves and extreme events. J. Opt. 2016, 18, 063001. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Baronio, F.; Soto-Crespo, J.M.; Grelu, P.; Mihalache, D. Versatile rogue waves in scalar, vector, and multidimensional nonlinear systems. J. Phys. A: Math. Theor. 2017, 50, 463001. [Google Scholar] [CrossRef] [Green Version]
- Zhong, W.P.; Belić, M.R.; Huang, T. Rogue wave solutions to the generalized nonlinear Schrödinger equation with variable coefficients. Phys. Rev. E 2013, 87, 065201. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, K.; Muruganandam, P.; Senthilvelan, M.; Lakshmanan, M. Manipulating localized matter waves in multicomponent Bose-Einststen condensates. Phys. Rev. E 2016, 93, 032212. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Wang, J.; Li, J. Controllable rogue waves in coupled nonlinear Schrödinger equations with varying potentials and nonlinearities. Nonlinear Dyn. 2014, 77, 545–552. [Google Scholar] [CrossRef]
- Tlidi, M.; Panajotov, K. Two-dimensional dissipative rogue waves due to time-delayed feedback in cavity nonlinear optics. Chaos 2017, 27, 013119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tlidi, M.; Panajotov, K.; Ferré, M.; Clerc, M.G. Drifting cavity solitons and dissipative rogue waves induced by time-delayed feedback in Kerr optical frequency comb and in all fiber cavities. Chaos 2017, 27, 114312. [Google Scholar] [CrossRef] [PubMed]
- Panajotov, K.; Clerc, M.G.; Tlidi, M. Spatiotemporal chaos and two-dimensional dissipative rogue waves in Lugiato-Lefever model. Eur. Phys. J. D 2017, 71, 176. [Google Scholar] [CrossRef]
- Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-replicating spots in the Brusselator model and extreme events in the one-dimensional case with delay. Entropy 2016, 18, 64. [Google Scholar] [CrossRef]
- Liu, M.; Luo, A.P.; Xu, W.C.; Luo, Z.C. Dissipative rogue waves induced by soliton explosions in an ultrafast fiber laser. Opt. Lett. 2016, 41, 3912–3915. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Cai, Z.R.; Hu, S.; Luo, A.P.; Zhao, C.J.; Zhang, H.; Xu, W.C.; Luo, Z.C. Dissipative rogue waves induced by long-range chaotic multi-pulse interactions in a fiber laser with a topological insulator-deposited microfiber photonic device. Opt. Lett. 2015, 40, 4767–4770. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Tarasov, N.; Sugavanam, S.; Churkin, D. Rogue waves generation via nonlinear soliton collision in multiple-soliton state of a mode-locked fiber laser. Opt. Expr. 2016, 24, 24256–24263. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.M.; Devine, N.; Akhmediev, N. Dissipative solitons with extreme spikes: Bifurcation diagrams in the anomalous dispersion. J. Opt. Soc. Am. B 2017, 34, 1542–1549. [Google Scholar] [CrossRef]
- Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Akhmediev, N. Spiny solitons and noise-like pulses. J. Opt. Soc. Am. B 2015, 32, 1377–1383. [Google Scholar] [CrossRef]
- Shemer, L.; Alperovich, L. Peregrine breather revisited. Phys. Fluids 2013, 25, 051701. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Tang, W.; Xue, H.X.; Zhang, X.Y. Numerical study of rogue waves as nonlinear Schrödinger breather solutions under finite water depth. Wave Motion 2015, 52, 81–90. [Google Scholar] [CrossRef]
- Lam, C.K.; Malomed, B.A.; Chow, K.W.; Wai, P.K.A. Spatial solitons supported by localized gain in nonlinear optical waveguides. Eur. Phys. J. Spec. Top. 2009, 173, 233–243. [Google Scholar] [CrossRef]
- Tsang, C.H.; Malomed, B.A.; Lam, C.K.; Chow, K.W. Solitons pinned to hot spots. Eur. Phys. J. D 2010, 59, 81–89. [Google Scholar] [CrossRef]
- Davey, A.; Stewartson, K. 3-Dimensional packets of surface-waves. Proc. R. Soc. 1974, 338, 101–110. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Evolution of packets of water waves. J. Fluid Mech. 1979, 92, 691–715. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super rogue waves: Observation of a higher-order breather in water waves. Phys. Rev. X 2012, 2, 011015. [Google Scholar] [CrossRef]
- Dong, G.; Liao, B.; Ma, Y.; Perlin, M. Experimental investigation of the Peregrine breather of gravity waves on finite water depth. Phys. Rev. Fluids 2018, 3, 064801. [Google Scholar] [CrossRef]
- Menyuk, C.R.; Schiek, R.; Torner, L. Solitary waves due to χ(2): χ(2) cascading. J. Opt. Soc. Am. B 1994, 11, 2434–2443. [Google Scholar] [CrossRef]
- Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Rogue waves in space dusty plasma. Phys. Plasma 2017, 24, 113701. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclass. Opt. 2005, 7, R53–R72. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel soliton solutions of the nonlinear Schrödinger equation model. Phys. Rev. Lett. 2000, 85, 4502–4505. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhang, J.H.; Liu, C.; Li, M.; Qi, F.H. Breather transition dynamics, Peregrine combs and walls, and modulation instability in a variable-coefficient nonlinear Schrödinger equation with high-order effects. Phys. Rev. E 2016, 93, 062217. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.P.; Belić, M.; Malomed, B.A. Rogue waves in a two-component Manakov system with variable coefficients and an external potential. Phys. Rev. E 2015, 92, 053201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Zhong, W.P.; Belić, M.; Zhang, Y. Controllable optical rogue waves via nonlinearity management. Opt. Express 2018, 26, 7587–7597. [Google Scholar] [CrossRef] [PubMed]
- Estelle Temgoua, D.D.; Tchoula Tchokonte, M.B.; Kofane, T.C. Combined effects of nonparaxiality, optical activity, and walk-off on rogue wave propagation in optical fibers filled with chiral materials. Phys. Rev. E 2018, 97, 042205. [Google Scholar] [CrossRef] [PubMed]
- Baronio, F.; Chen, S.; Grelu, P.; Wabnitz, S.; Conforti, M. Baseband modulation instability as the origin of rogue waves. Phys. Rev. A 2015, 91, 033804. [Google Scholar] [CrossRef]
- Chan, H.N.; Chow, K.W. Rogue waves for an alternative system of coupled Hirota equations: Structural robustness and modulation instabilities. Stud. Appl. Math. 2017, 139, 78–103. [Google Scholar] [CrossRef]
- Chan, H.N.; Chow, K.W. Rogue wave modes for the coupled nonlinear Schrödinger system with three components: A computational study. Appl. Sci. 2017, 7, 559. [Google Scholar] [CrossRef]
- Cuevas-Maraver, J.; Malomed, B.A.; Kevrekidis, P.G.; Frantzeskakis, D.J. Stabilization of the Peregrine soliton and Kuznetsov-Ma breathers by means of nonlinearity and dispersion management. Phys. Lett. A 2018, 382, 968–972. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Konotop, V.V.; Vysloukh, V.A.; Torner, L. Dissipative defect modes in periodic structures. Opt. Lett. 2010, 35, 1638–1640. [Google Scholar] [CrossRef] [PubMed]
- Torner, L. Amplification of quadratic solitons. Opt. Commun. 1998, 154, 59–64. [Google Scholar] [CrossRef]
- Malomed, B.A. Spatial solitons supported by localized gain. J. Opt. Soc. Am. B 2014, 31, 2460–2475. [Google Scholar] [CrossRef]
- Descalzi, O.; Cartes, C. Stochastic and higher-order effects on exploding pulses. Appl. Sci. 2017, 7, 887. [Google Scholar] [CrossRef]
- He, J.; Malomed, B.A.; Mihalache, D. Localized modes in dissipative lattice media: An overview. Philos. Trans. R. Soc. A 2014, 372, 20140017. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.V.; Torner, L. Rotation-managed dissipative solitons. Opt. Lett. 2013, 38, 2317–2320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fochesato, C.; Grilli, S.; Dias, F. Numerical modeling of extreme rogue waves generated by directional energy focusing. Wave Motion 2007, 44, 395–416. [Google Scholar] [CrossRef]
- Porubov, A.V.; Tsuji, H.; Lavrenov, I.V.; Oikawa, M. Formation of the rogue wave due to non-linear two-dimensional waves interaction. Wave Motion 2005, 42, 202–210. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Todorov, M.D.; Kyuldjiev, A.V. Adiabatic interactions of Manakov solitons-Effects of cross-modulation. Wave Motion 2017, 71, 71–81. [Google Scholar] [CrossRef]
- Dang Koko, A.; Tabi, C.B.; Ekobena Fouda, H.P.; Mohamadou, A.; Kofané, T.C. Nonlinear charge transport in the helicoidal DNA molecule. Chaos 2012, 22, 043110. [Google Scholar] [CrossRef] [PubMed]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Böhm, M.; Mitschke, F. Solitons in lossy fibers. Phys. Rev. A 2007, 76, 063822. [Google Scholar] [CrossRef]
- Mitschke, F.; Mahnke, C.; Hause, A. Soliton content of fiber-optic light pulses. Appl. Sci. 2017, 7, 635. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, H.N.; Chow, K.W. Numerical Investigation of the Dynamics of ‘Hot Spots’ as Models of Dissipative Rogue Waves. Appl. Sci. 2018, 8, 1223. https://doi.org/10.3390/app8081223
Chan HN, Chow KW. Numerical Investigation of the Dynamics of ‘Hot Spots’ as Models of Dissipative Rogue Waves. Applied Sciences. 2018; 8(8):1223. https://doi.org/10.3390/app8081223
Chicago/Turabian StyleChan, Hiu Ning, and Kwok Wing Chow. 2018. "Numerical Investigation of the Dynamics of ‘Hot Spots’ as Models of Dissipative Rogue Waves" Applied Sciences 8, no. 8: 1223. https://doi.org/10.3390/app8081223
APA StyleChan, H. N., & Chow, K. W. (2018). Numerical Investigation of the Dynamics of ‘Hot Spots’ as Models of Dissipative Rogue Waves. Applied Sciences, 8(8), 1223. https://doi.org/10.3390/app8081223




