A Modified Polynomial Expansion Algorithm for Solving the Steady-State Allen-Cahn Equation for Heat Transfer in Thin Films
Abstract
:Featured Application
Abstract
1. Introduction
2. The Steady-State Allen-Cahn Equation and a Modified Polynomial Expansion Method
Do i = 1, m
Do j = 1, i
k = k + 1
pk = pij
Enddo.
K = ATA > 0.
3. The Iterative Process for the Steady-State Allen-Cahn Equation
- (i)
- Given n1, n2 (nk = n1 × n2), and m [n = m(m + 1)/2].
- (ii)
- Given .
- (iii)
- Given collocation points (xi, yi), i = 1, …, nk.
- (iv)
- One-time only:Generate sij,Generate Q from Mk = sij and Equation (18),I = AQ.
- (v)
- For k = 0, 1, 2 ,…, reiteration as follows:Compute u, ux, uy from Equations (20)–(22)Generate bk from the right-hand side of Equation (1)Resolve the normal form of Ip = bk to acquire
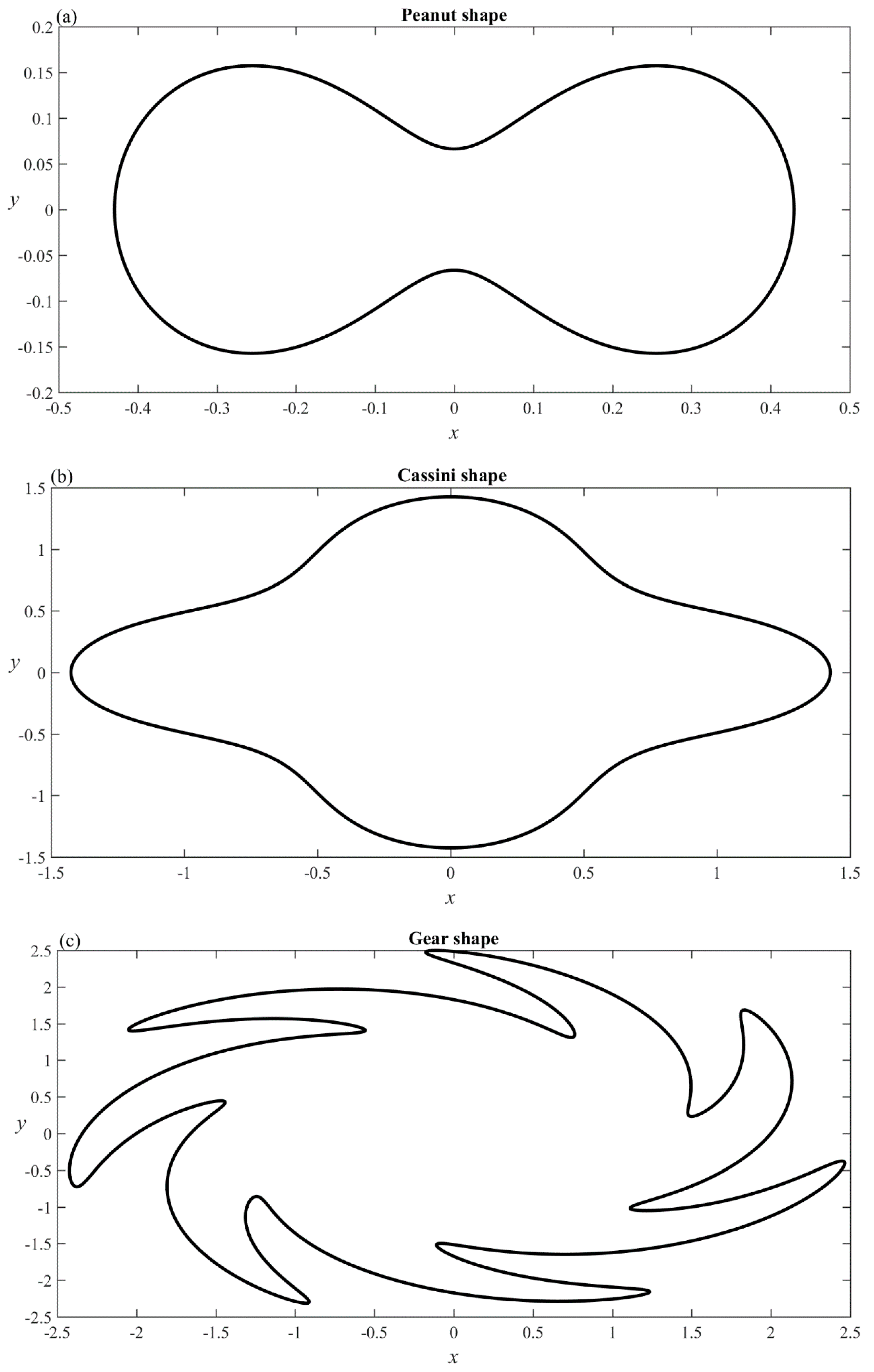
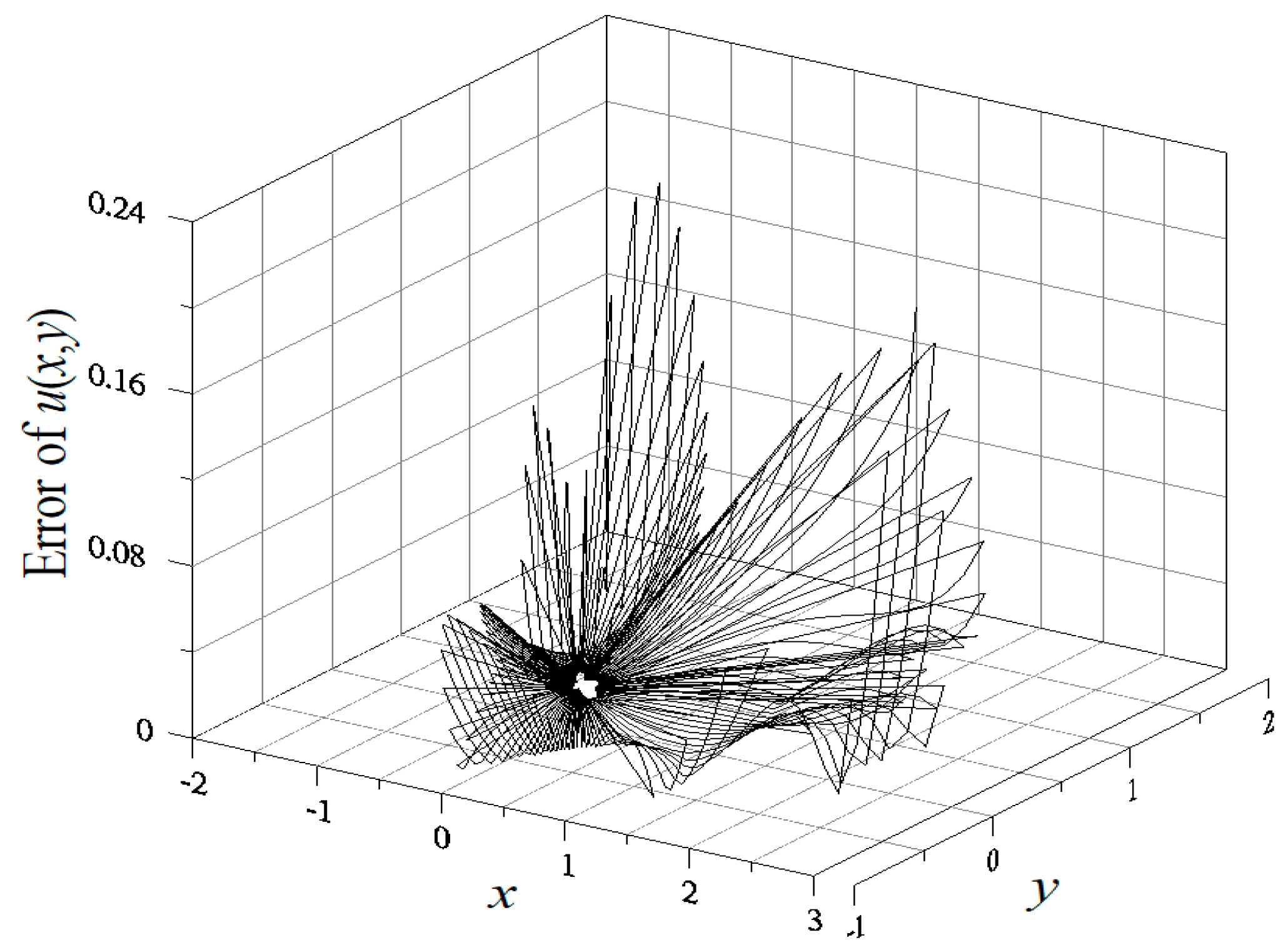
4. Numerical Examples
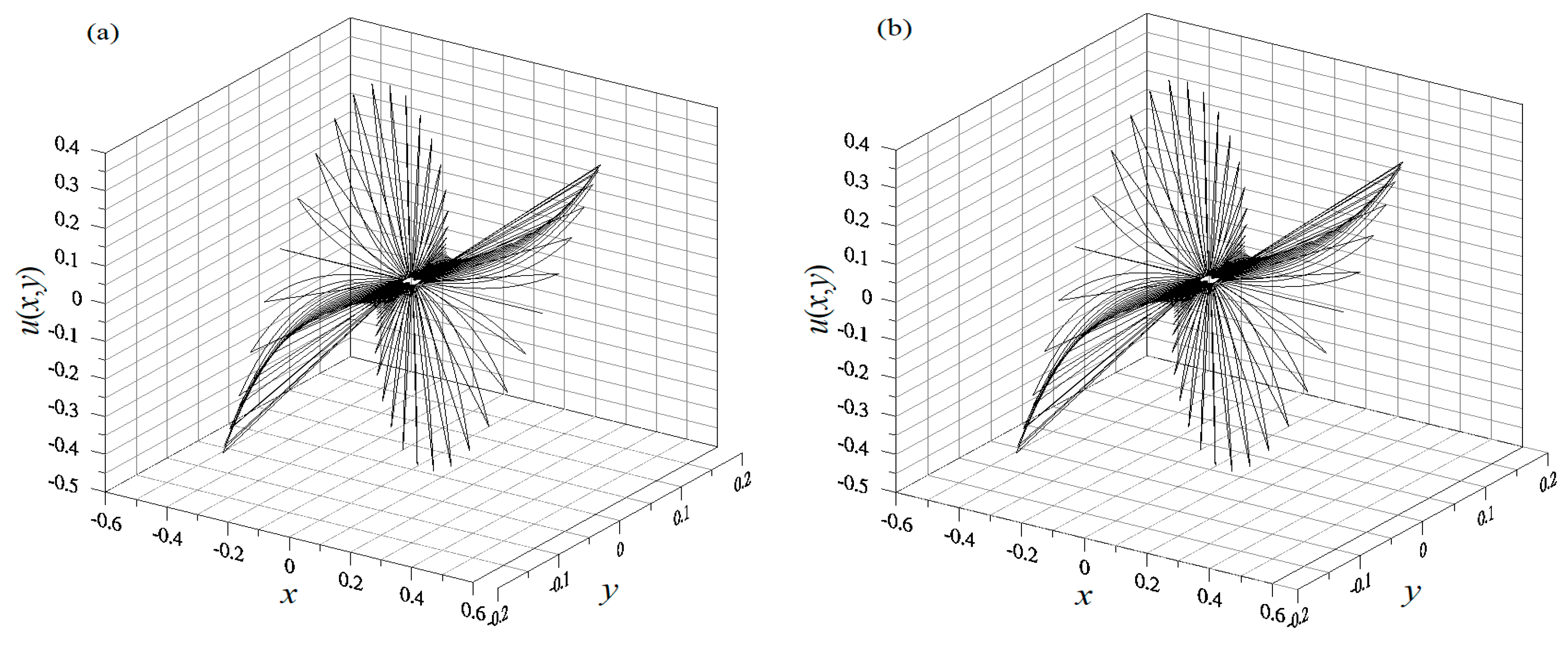
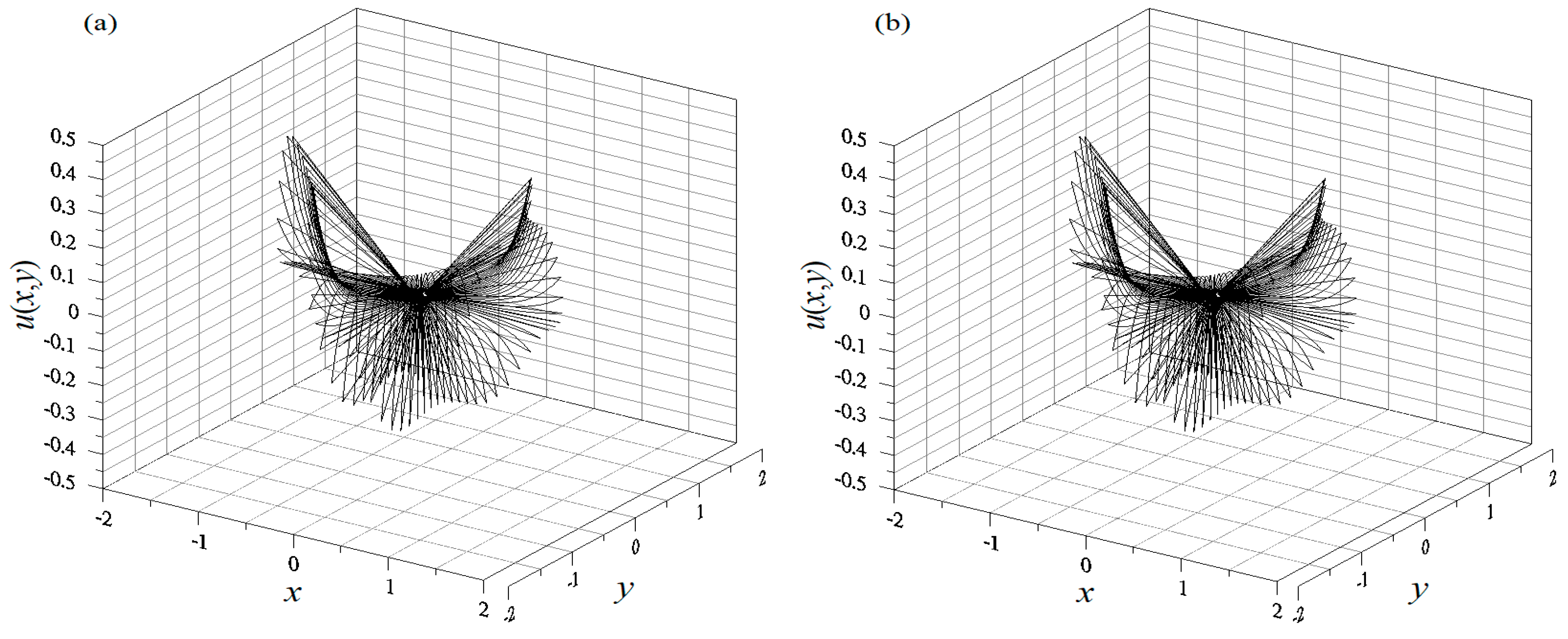
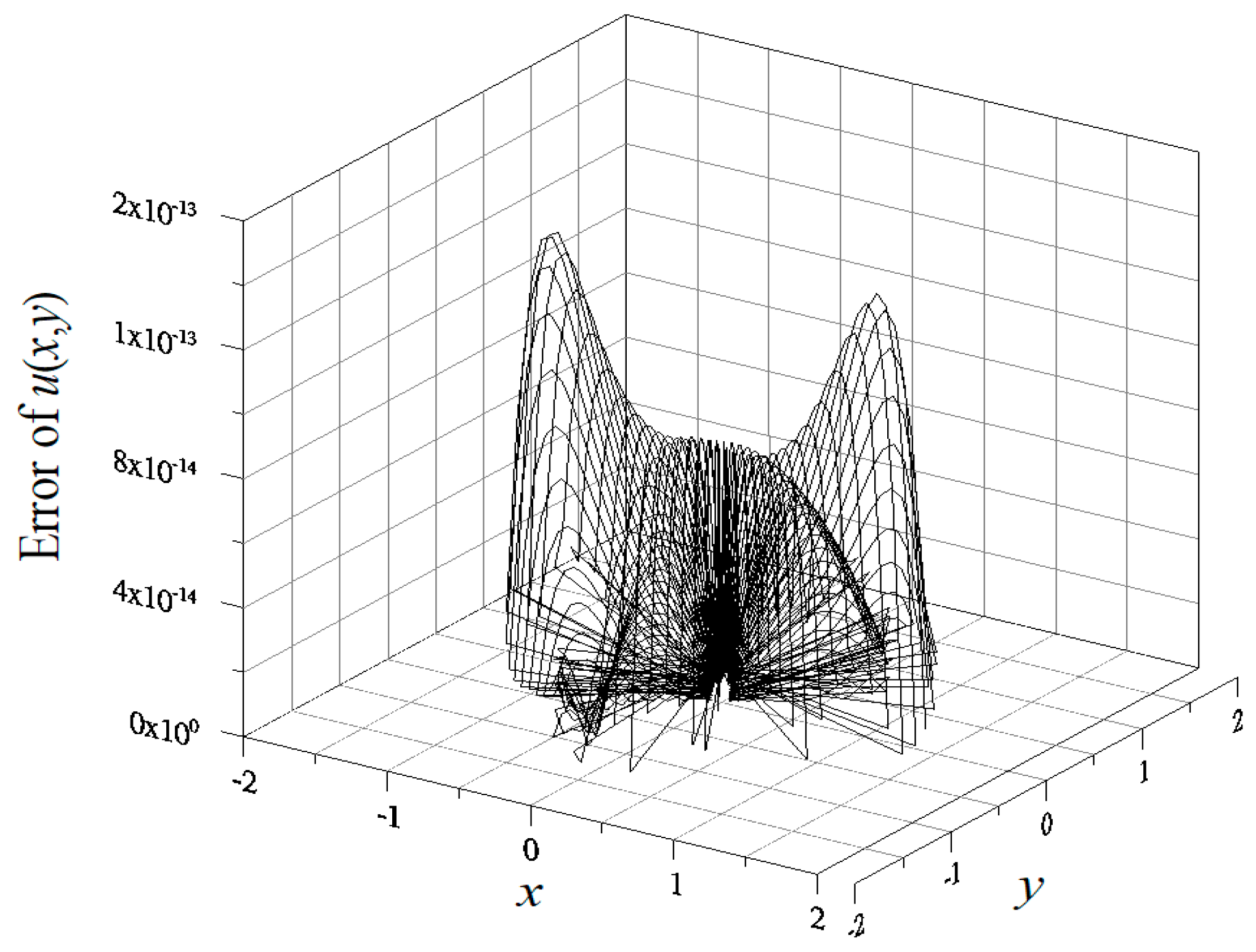
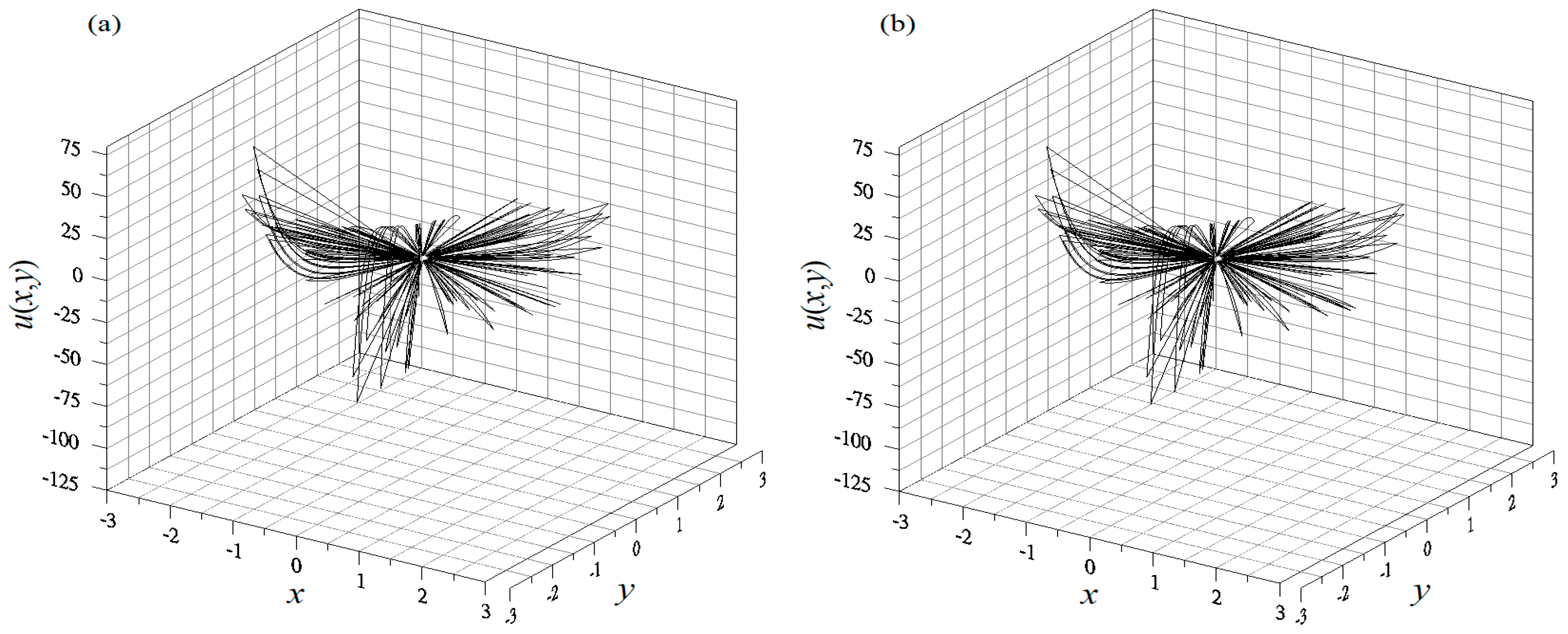
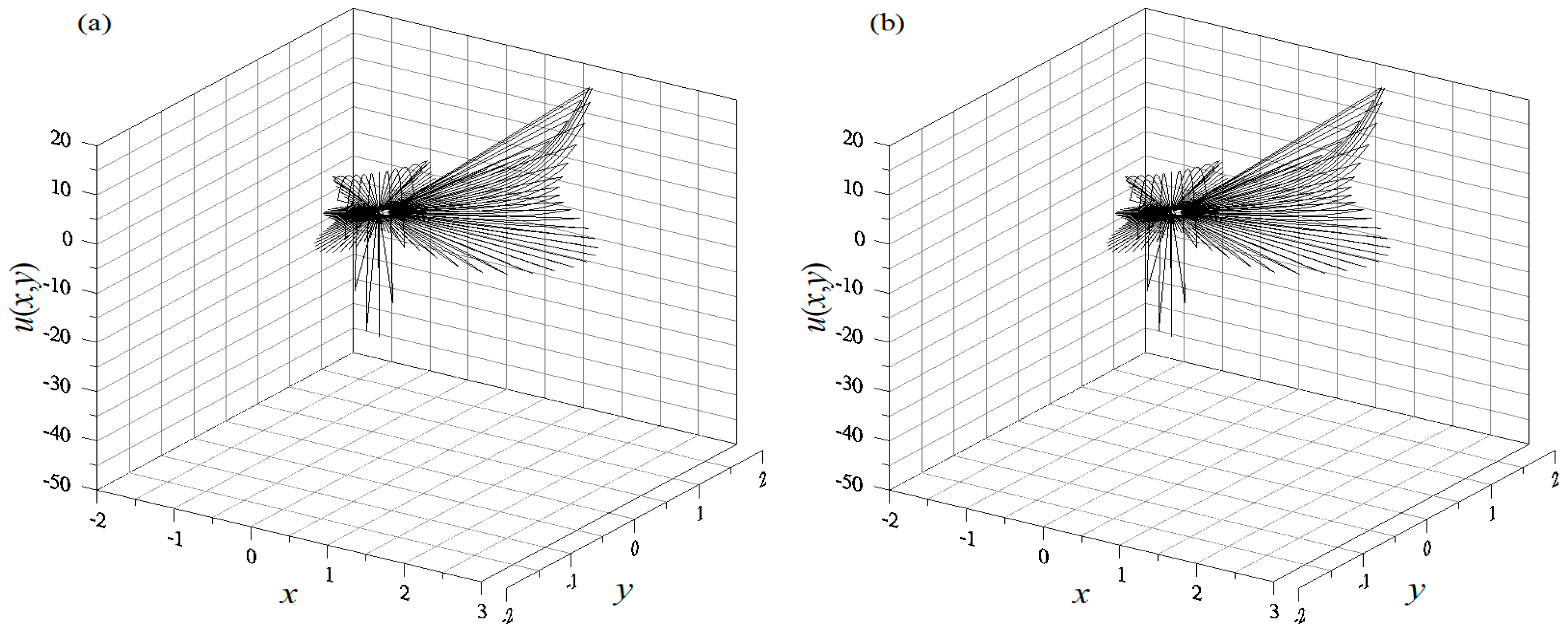
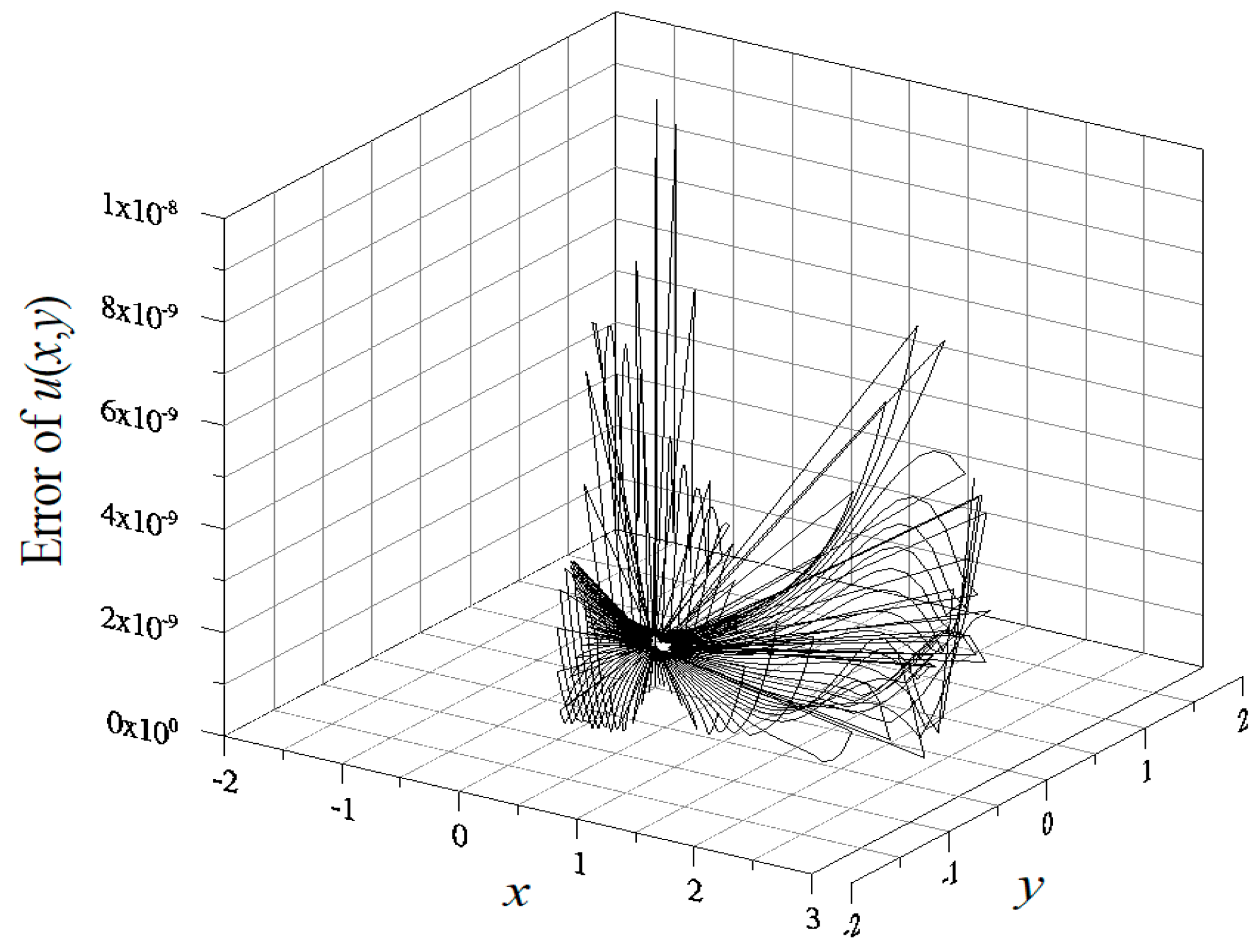
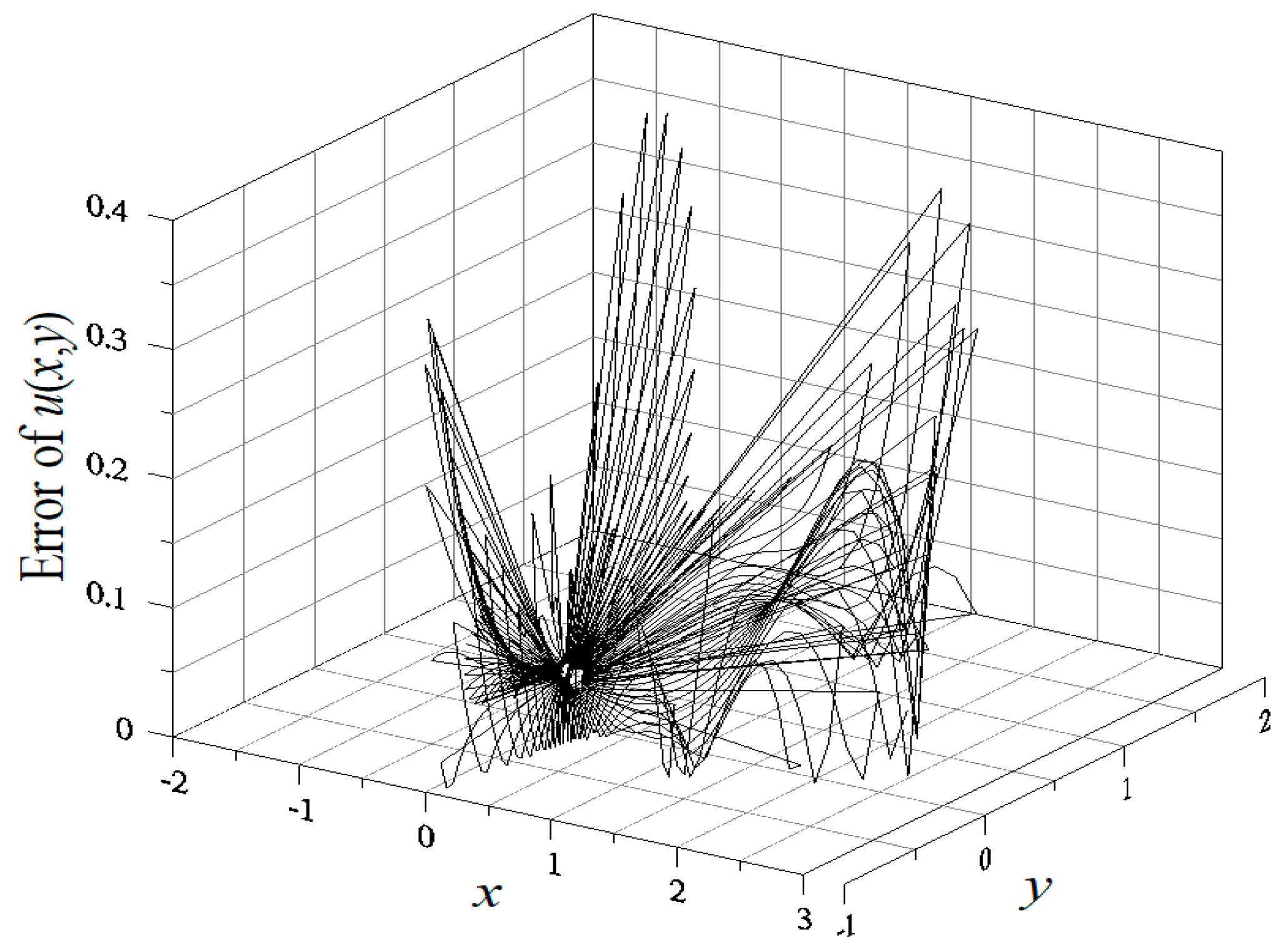
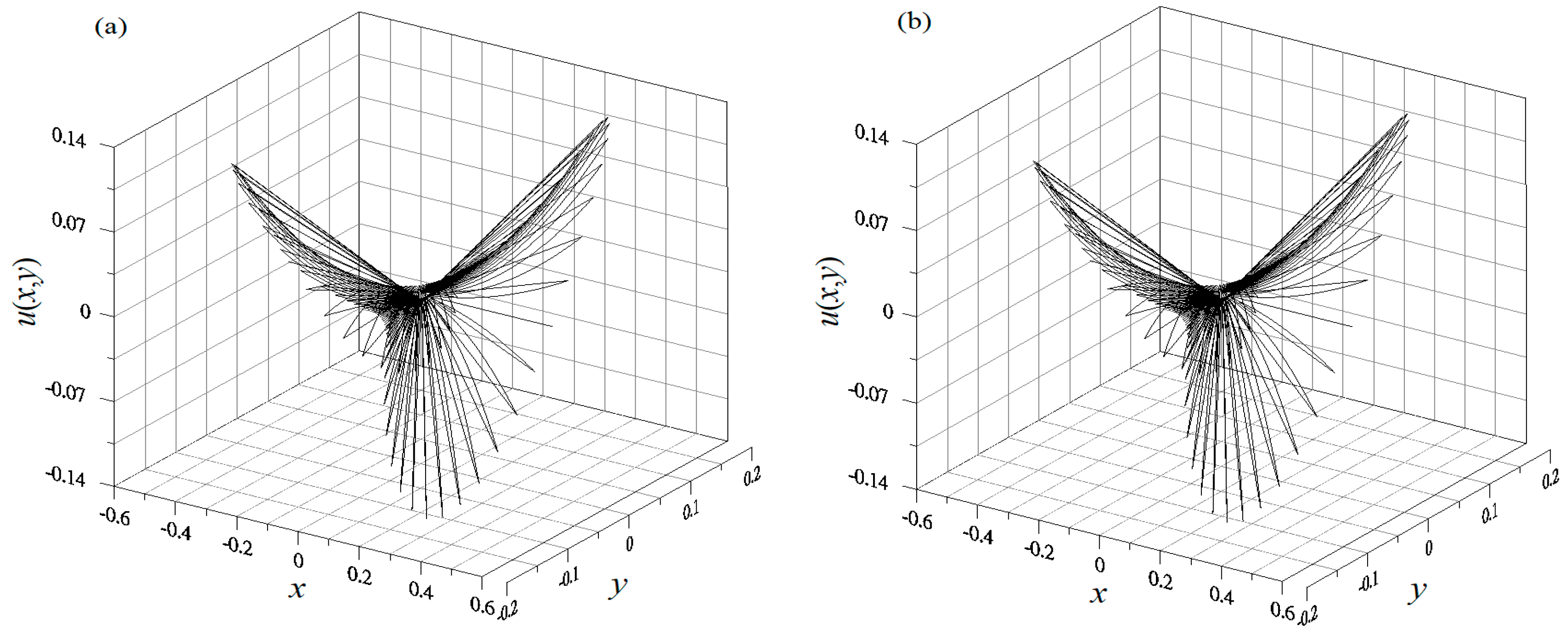
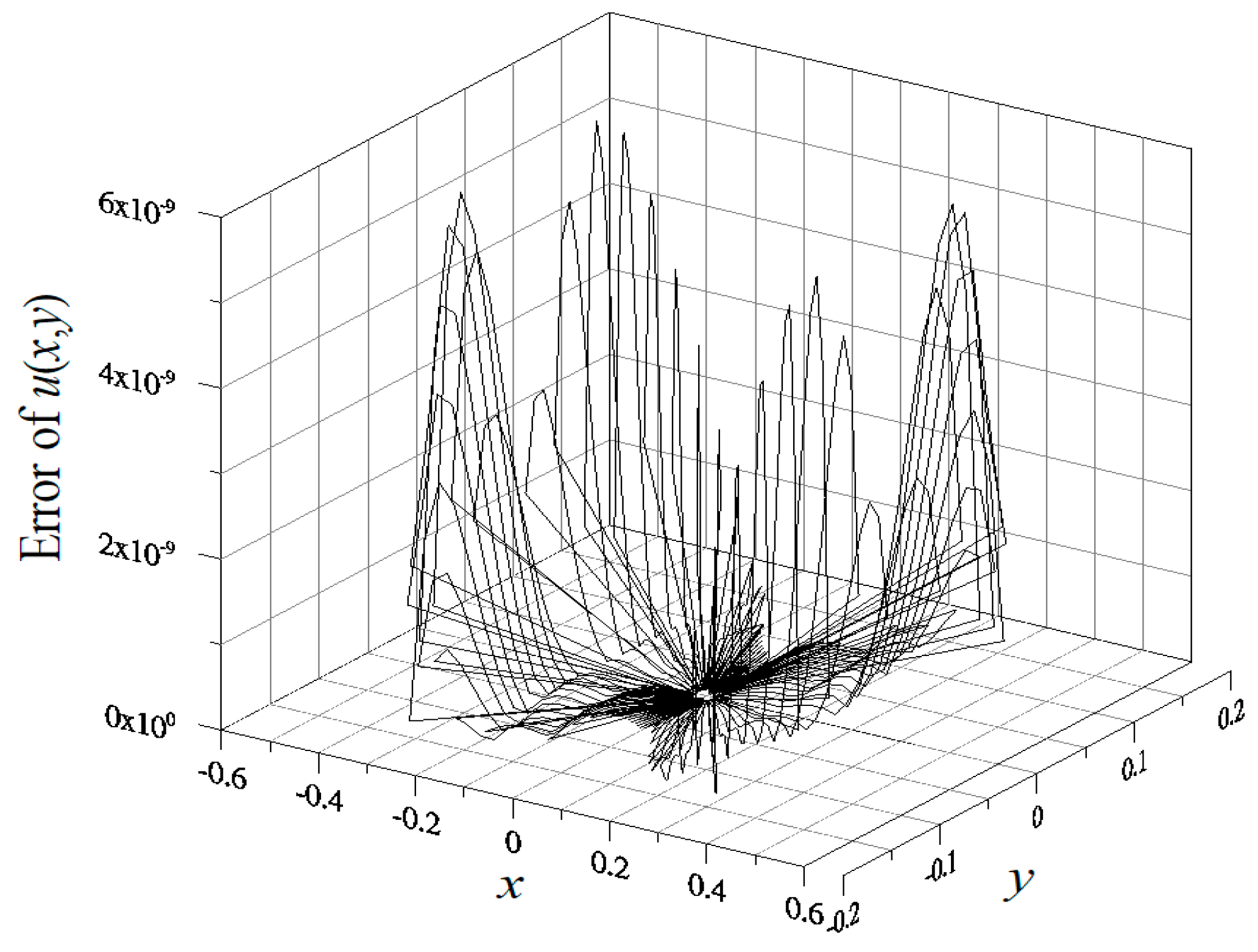
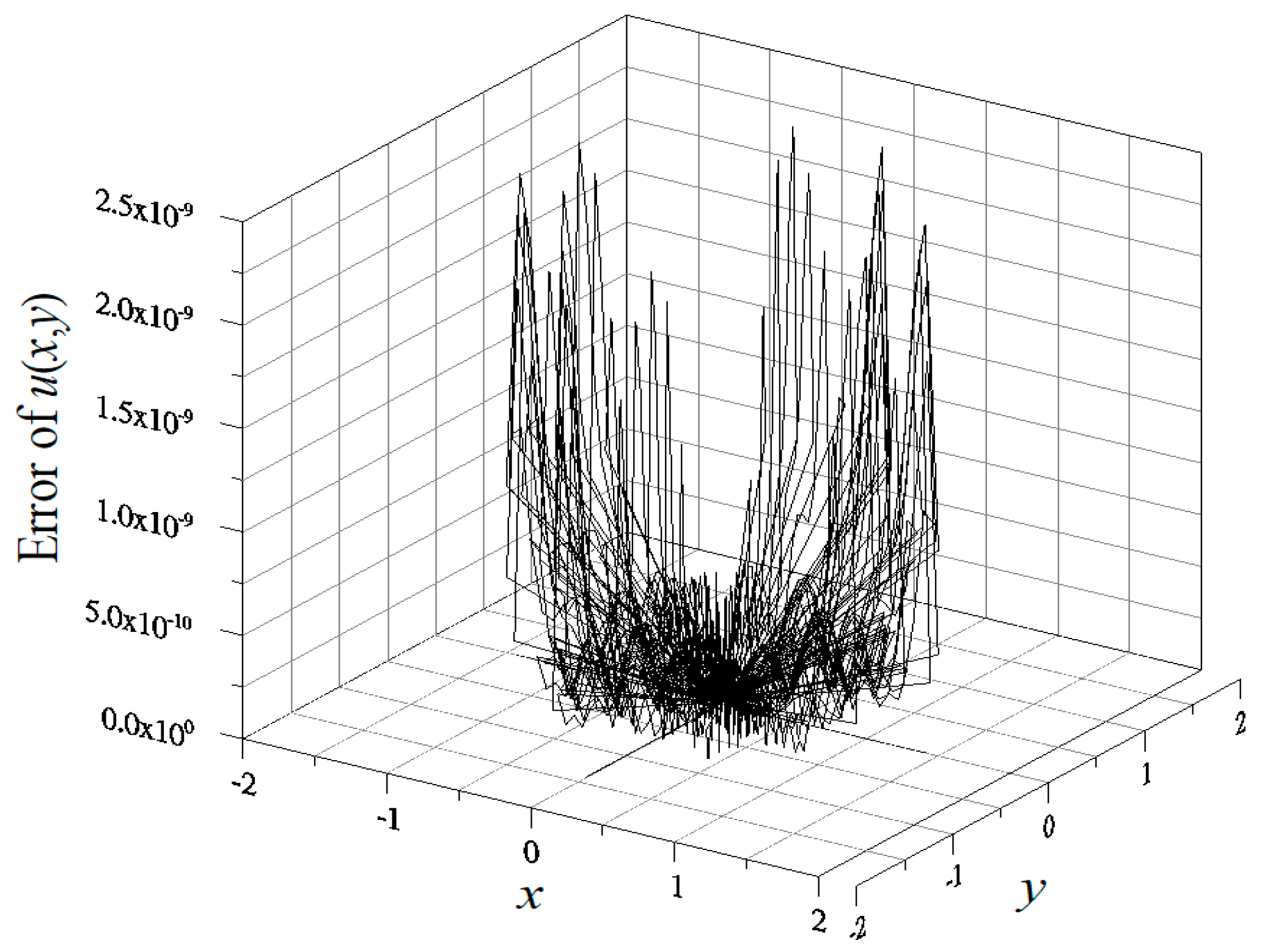
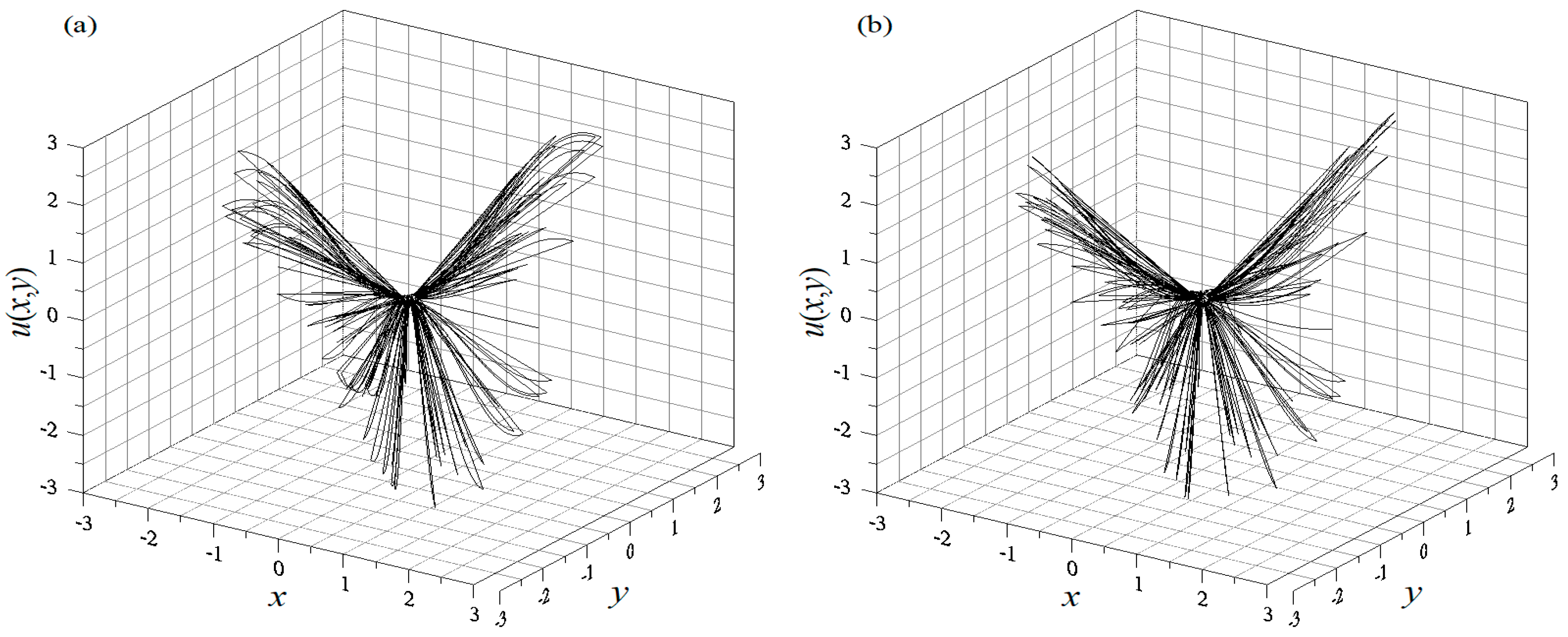
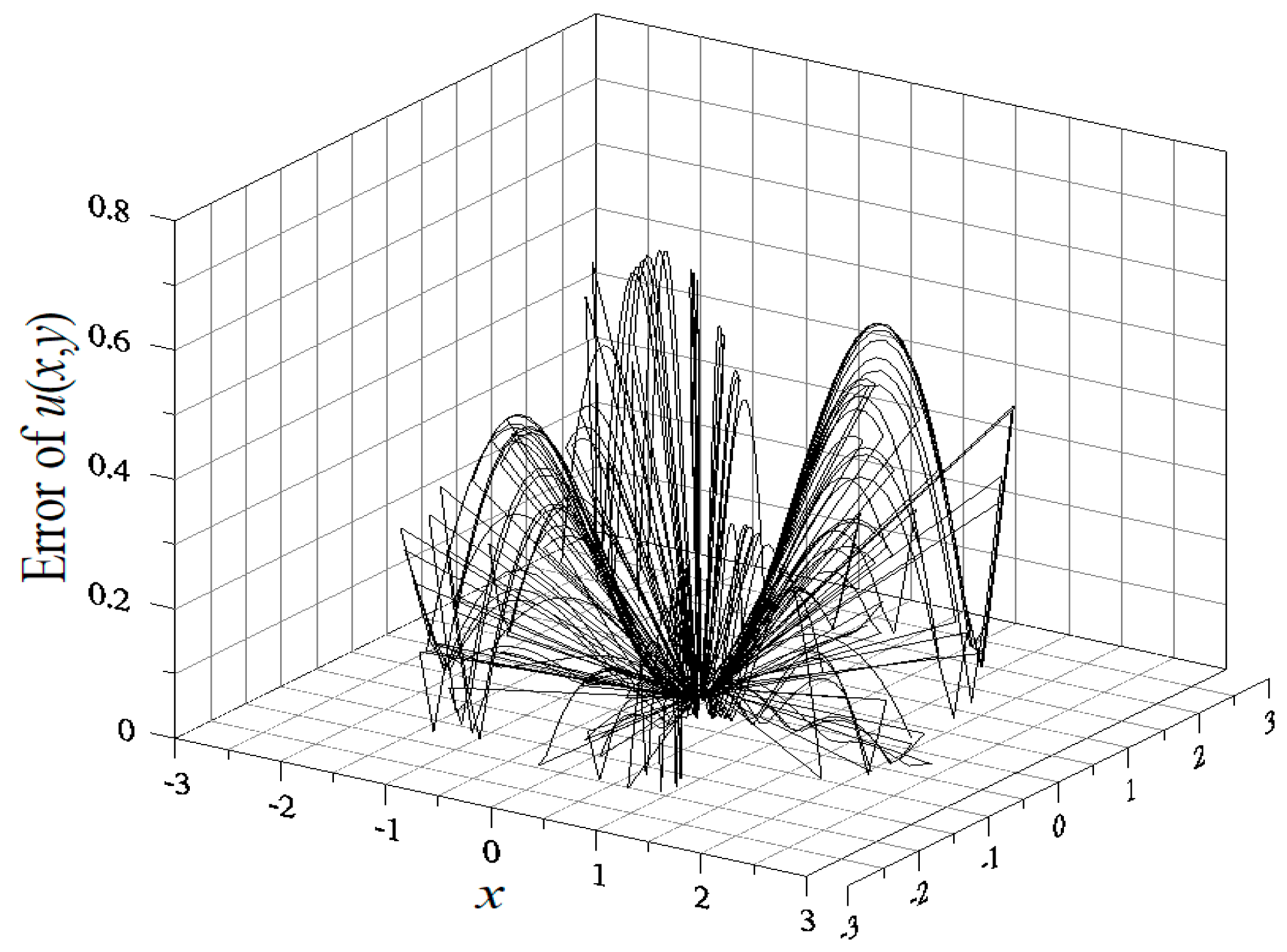
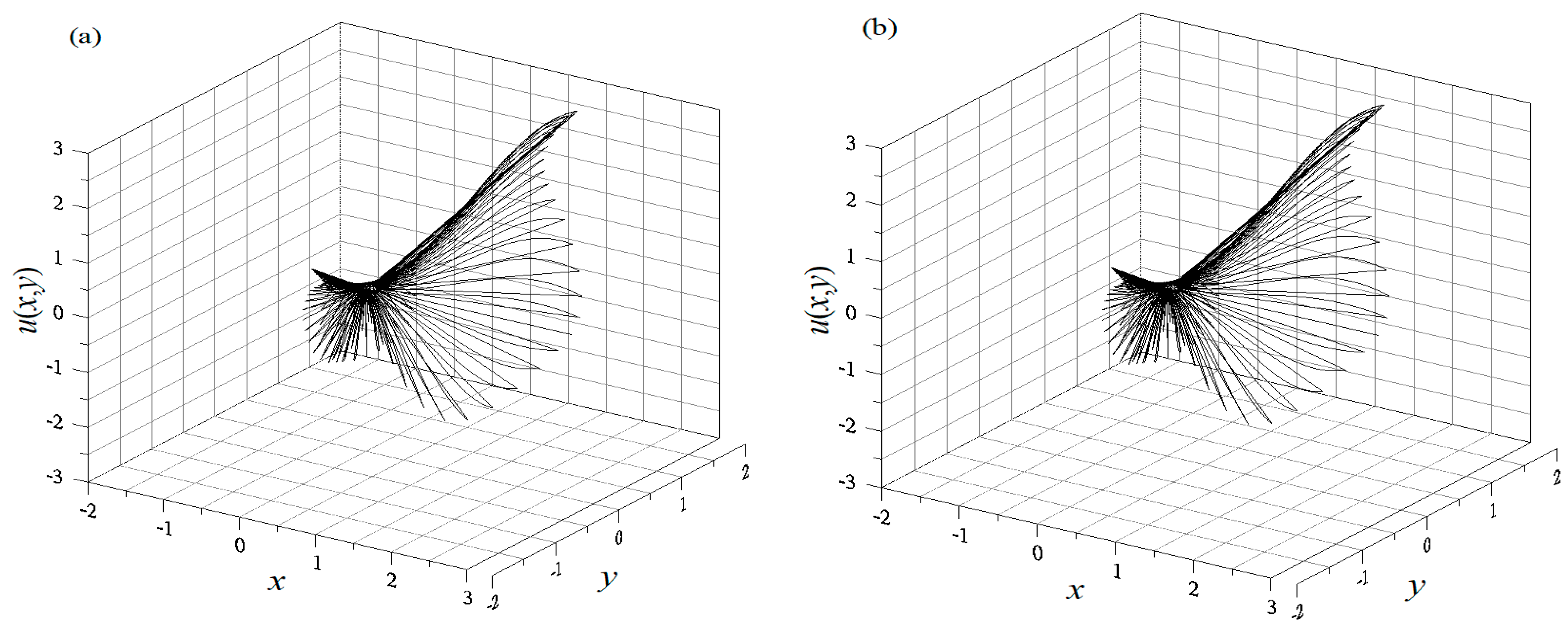
4.1. Example 1
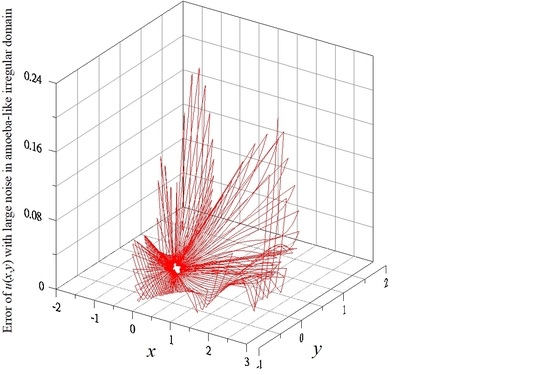
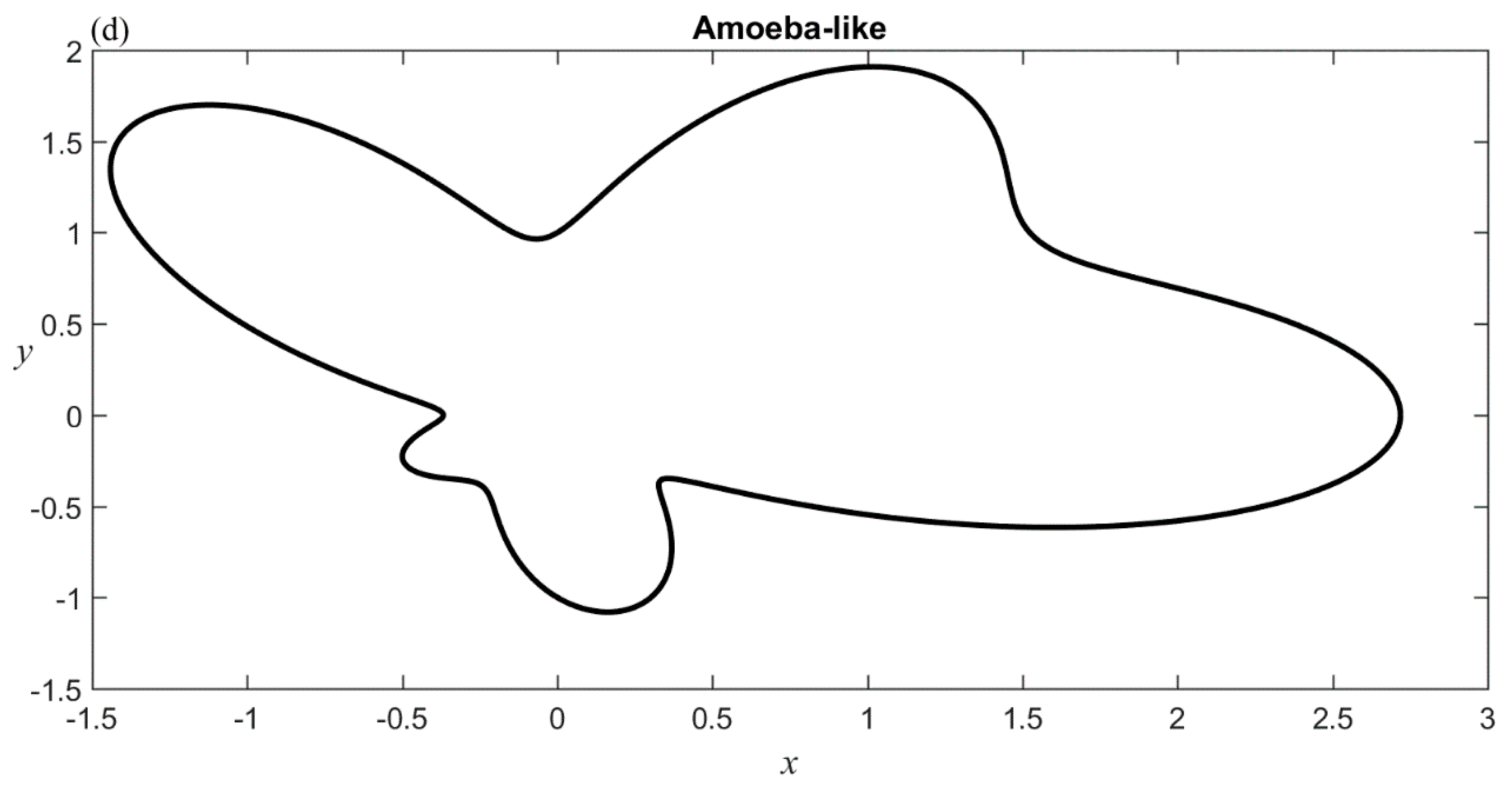
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allen, M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. Mater. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Shah, A.; Sabir, M.; Bastain, M.P. An efficient time-stepping scheme for numerical simulation of dendritic crystal growth. Eur. J. Comput. Mech. 2017, 25, 475–488. [Google Scholar] [CrossRef]
- Gerish, A.; Moelans, A.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar]
- Rizwan, M.; Shah, A.; Yuan, L. A central compact scheme for numerical solution of two phase incompressible flow using Allen-Cahn phase-field model. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 433–441. [Google Scholar] [CrossRef]
- Chen, L.-Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef]
- Biben, T. Phase-field models for free-boundary problems. Eur. J. Phys. 2005, 26, 47–55. [Google Scholar] [CrossRef]
- Jay, D.; Lee, B.-J. Effect of constriction on phonon transport in silicon thin films and nanowires. Smart Sci. 2016, 4, 173–179. [Google Scholar]
- Beneš, M.; Chalupecky, V.; Mikula, K. Geometrical image segmentation by the Allen-Cahn equation. Appl. Numer. Math. 2004, 51, 187–205. [Google Scholar] [CrossRef]
- Feng, X.B.; Prohl, A. Numerical analysis of the Allen-Cahn equation and approximation for mean curvature flows. Numer. Math. 2003, 94, 33–65. [Google Scholar] [CrossRef]
- Wheeler, A.A.; Boettinger, W.J.; Mcfadden, G.B. Phase-field model for isothermal phase transitions in binary alloys. Phys. Rev. A 1992, 45, 7424–7439. [Google Scholar] [CrossRef] [PubMed]
- Sabir, M.; Shah, A.; Muhammad, W.; Ali, I.; Bastian, P. A mathematical model of tumor hypoxia targeting in cancer treatment and its numerical simulation. Comput. Math. Appl. 2017, 74, 3250–3259. [Google Scholar] [CrossRef]
- Kolobov, A.V.; Gubernov, V.V.; Polezhaev, A.A. Autowaves in a model of invasive tumor growth. Biophysics 2009, 54, 232–237. [Google Scholar] [CrossRef]
- Avila, J.A.; Lozada-Cruz, G. On a model for the growth of an invasive avascular tumor. Appl. Math. Inf. Sci. 2013, 7, 1857–1863. [Google Scholar] [CrossRef]
- Zahra, W.K. Trigonometric B-Spline collocation method for solving PHI-Four and Allen-Cahn equations. Mediterr J. Math. 2017, 14, 122–141. [Google Scholar] [CrossRef]
- Karasözen, B.; Uzunca, M.; Sariaydin-Filibelioğlu, A.; Yücel, H. Energy stable discontinuous Galerkin finite element method for the Allen-Cahn equation. Int. J. Comp. Methods 2018, 15, 1850013. [Google Scholar] [CrossRef]
- Yang, J.; Du, Q.; Zhang, W. Uniform Lp-bound of the Allen-Cahn equation and its numerical discretization. Int. J. Numer. Anal. Model. 2018, 15, 213–227. [Google Scholar]
- Liu, C.-S.; Kuo, C.-L. A multiple-scale Pascal polynomial triangle solving elliptic equations and inverse Cauchy problems. Eng. Anal. Bound. Elem. 2016, 62, 35–43. [Google Scholar] [CrossRef]
- Liu, C.-S.; Young, D.-L. A multiple-scale Pascal polynomial for 2D Stokes and inverse Cauchy-Stokes problems. J. Comput. Phys. 2016, 312, 1–13. [Google Scholar] [CrossRef]
- Chang, C.-W. A new meshless method for solving steady-state nonlinear heat conduction problems in arbitrary plane domain. Eng. Anal. Bound. Elem. 2016, 70, 56–71. [Google Scholar] [CrossRef]
- Chang, C.-W.; Huang, J.-H.; Wang, C.-C. A new meshfree method for solving steady-state modified Burgers’ equation in transport problems. Smart Sci. 2017, 5, 14–20. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-W.; Liu, C.-H.; Wang, C.-C. A Modified Polynomial Expansion Algorithm for Solving the Steady-State Allen-Cahn Equation for Heat Transfer in Thin Films. Appl. Sci. 2018, 8, 983. https://doi.org/10.3390/app8060983
Chang C-W, Liu C-H, Wang C-C. A Modified Polynomial Expansion Algorithm for Solving the Steady-State Allen-Cahn Equation for Heat Transfer in Thin Films. Applied Sciences. 2018; 8(6):983. https://doi.org/10.3390/app8060983
Chicago/Turabian StyleChang, Chih-Wen, Chein-Hung Liu, and Cheng-Chi Wang. 2018. "A Modified Polynomial Expansion Algorithm for Solving the Steady-State Allen-Cahn Equation for Heat Transfer in Thin Films" Applied Sciences 8, no. 6: 983. https://doi.org/10.3390/app8060983
APA StyleChang, C.-W., Liu, C.-H., & Wang, C.-C. (2018). A Modified Polynomial Expansion Algorithm for Solving the Steady-State Allen-Cahn Equation for Heat Transfer in Thin Films. Applied Sciences, 8(6), 983. https://doi.org/10.3390/app8060983