Review on Structural Health Evaluation with Acoustic Emission
Abstract
1. Introduction
2. Signal Attenuation
2.1. Guided Wave Attenuation
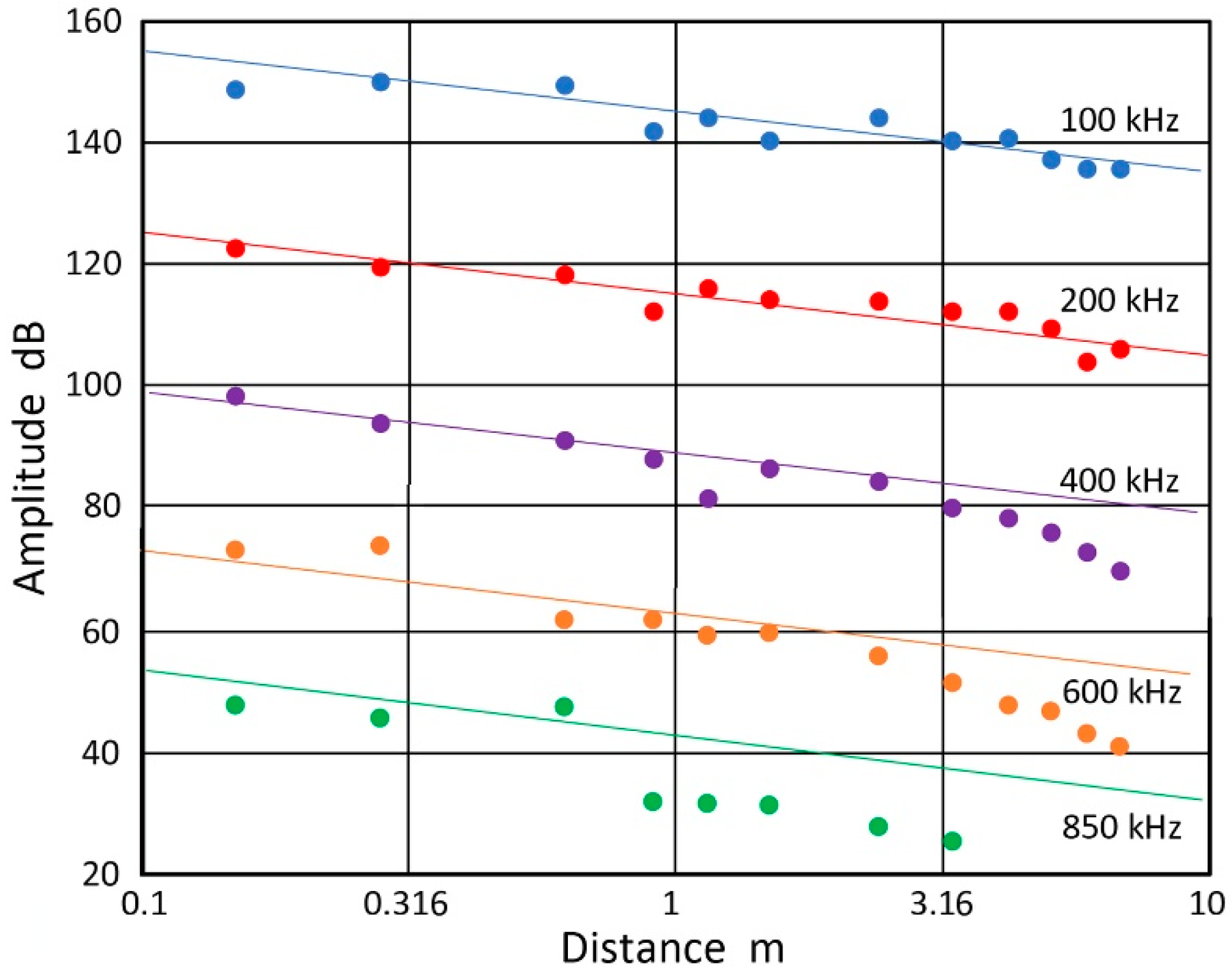
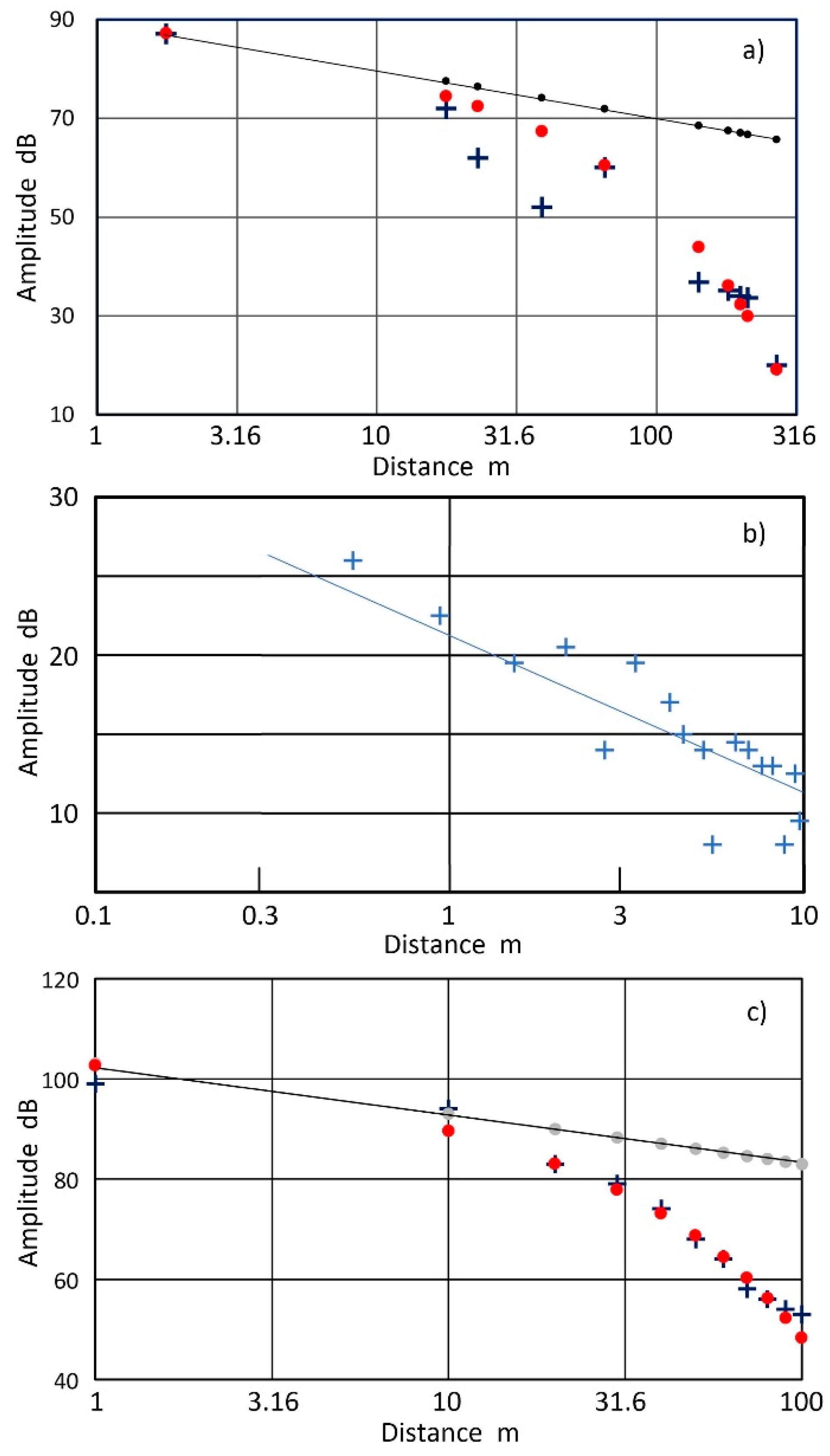
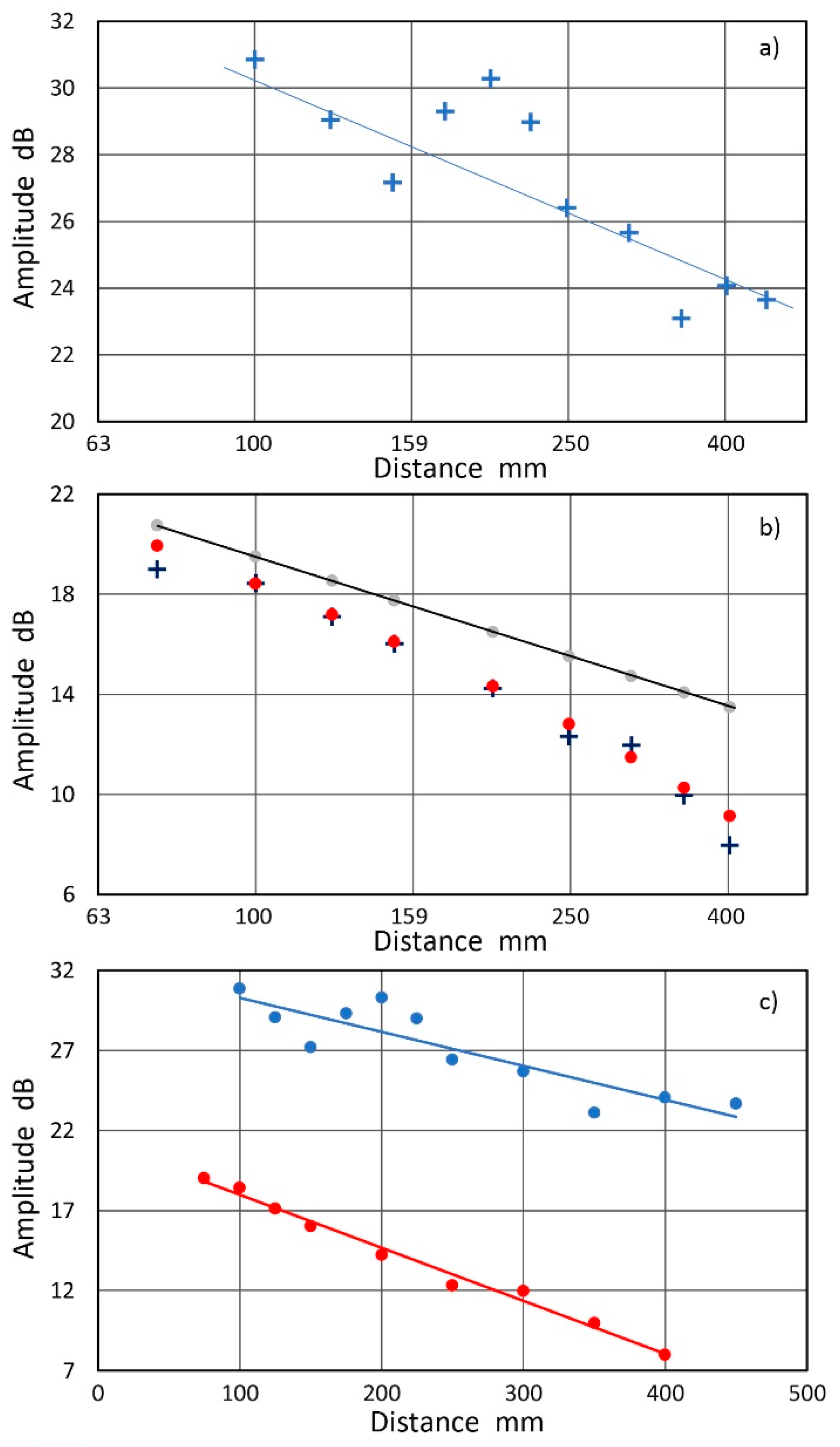
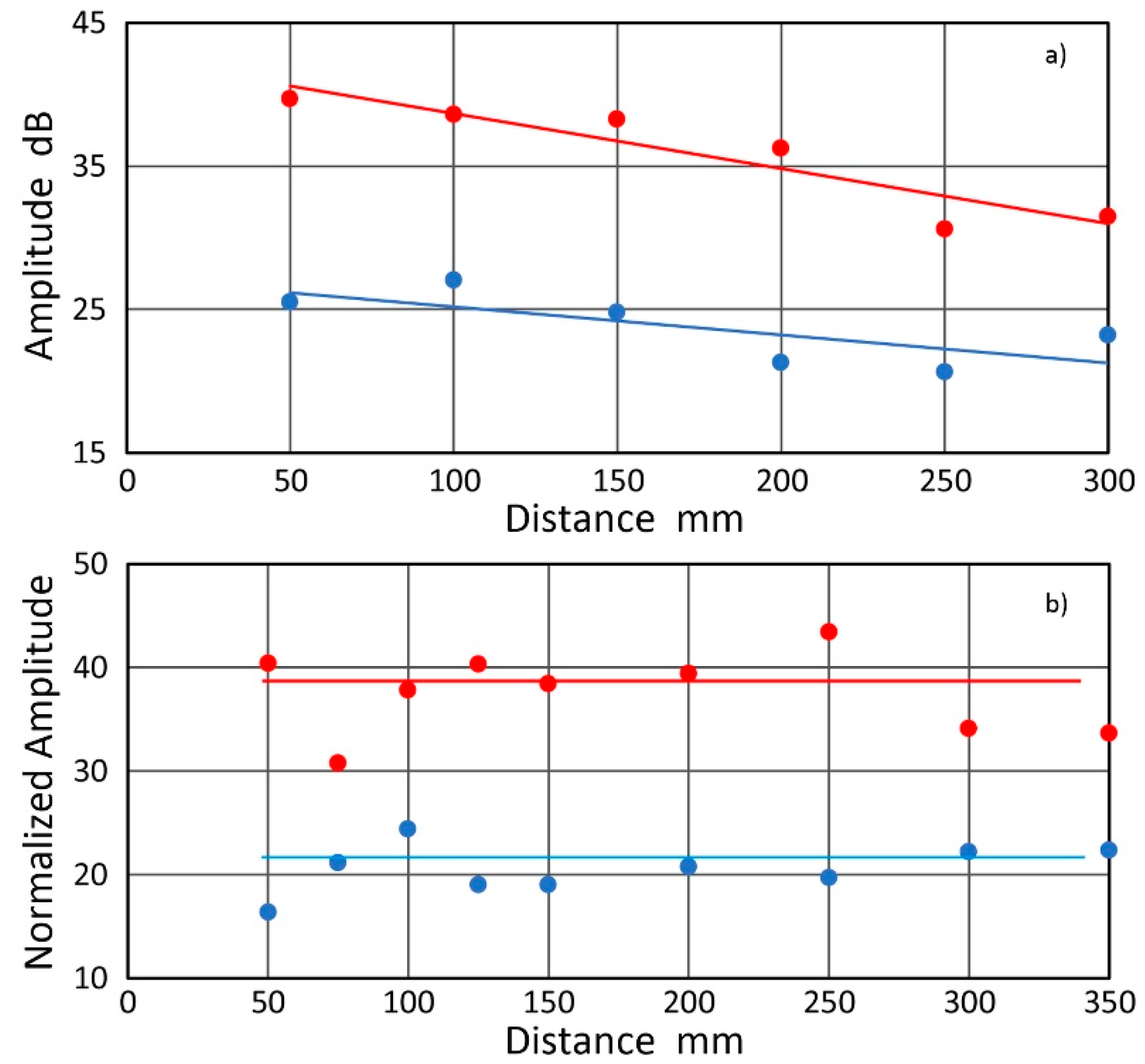
2.2. Attenuation Measurements on Large Metallic Structures
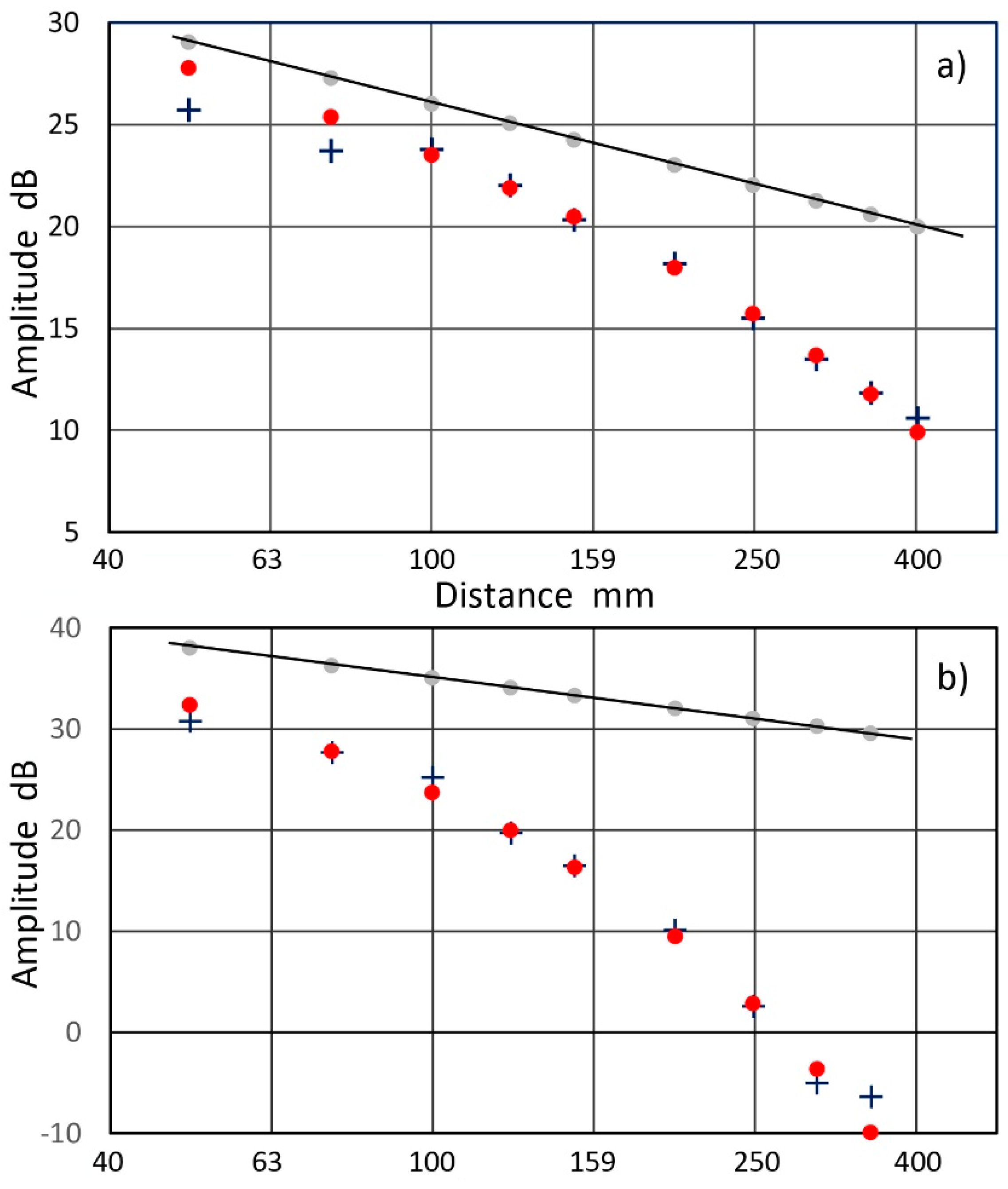
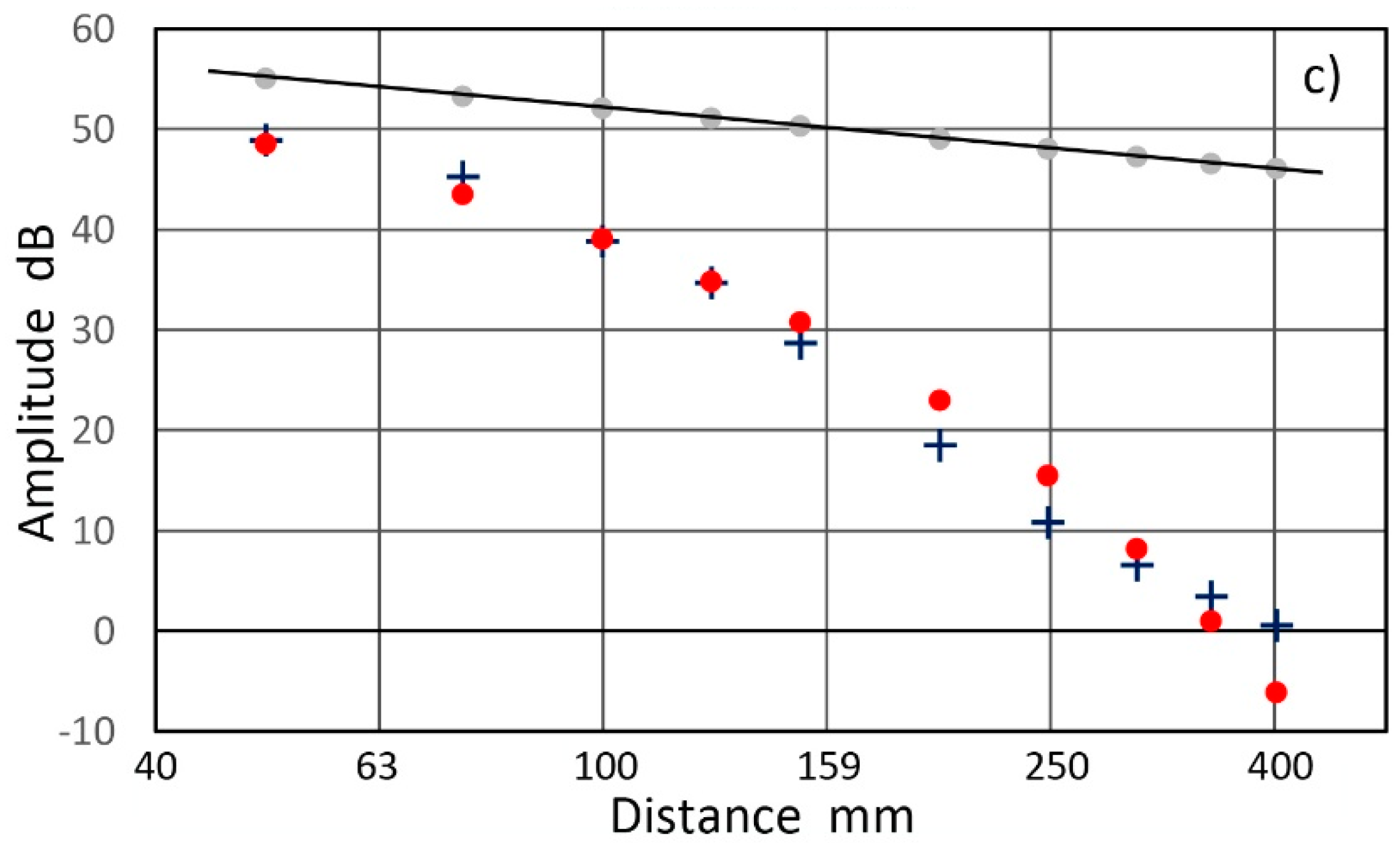
2.3. Laboratory Attenuation Measurements
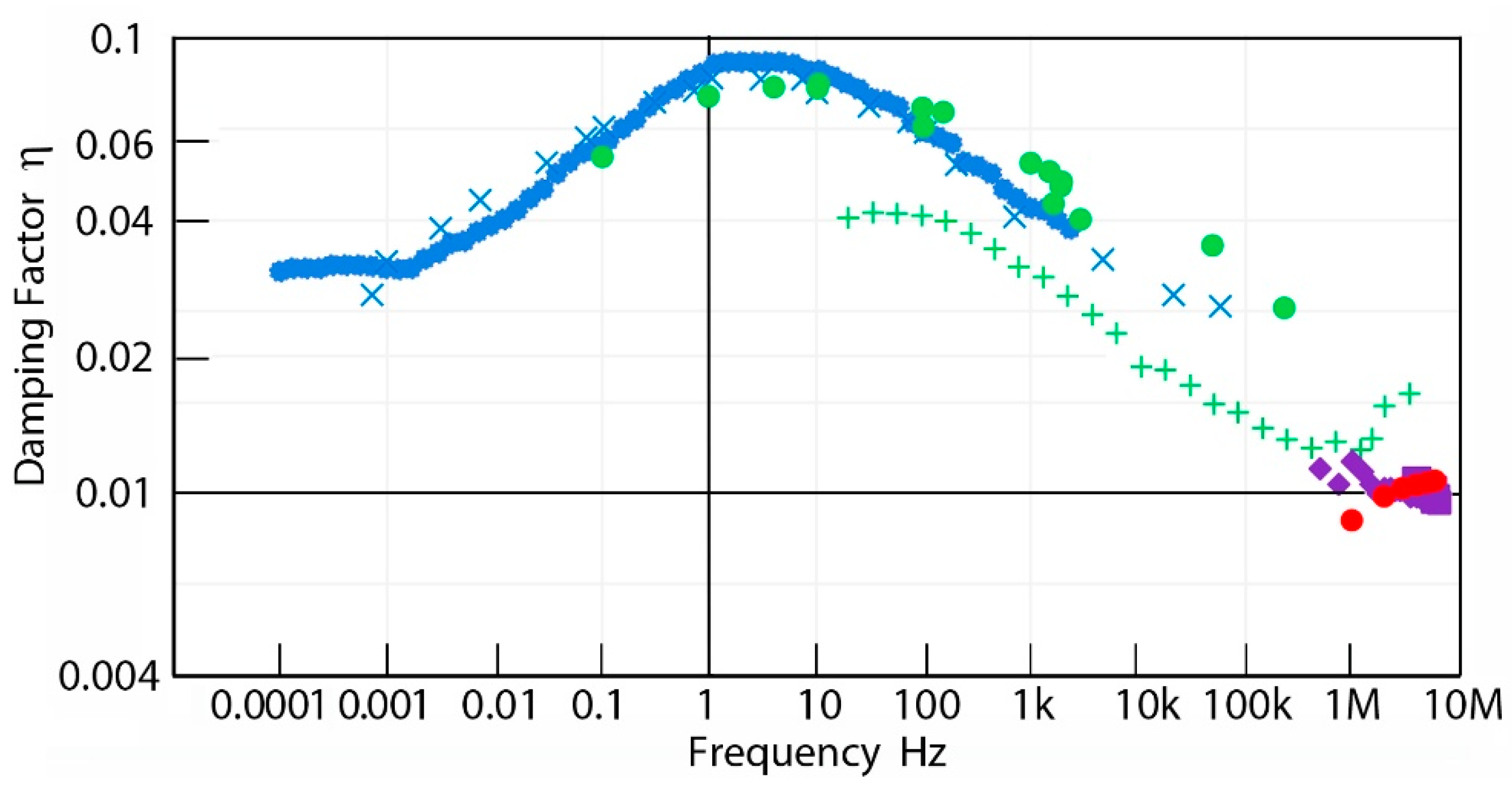
2.4. Complex Elastic Moduli Measurements
2.5. Survey of Ultrasonic Attenuation of Metallic Alloys
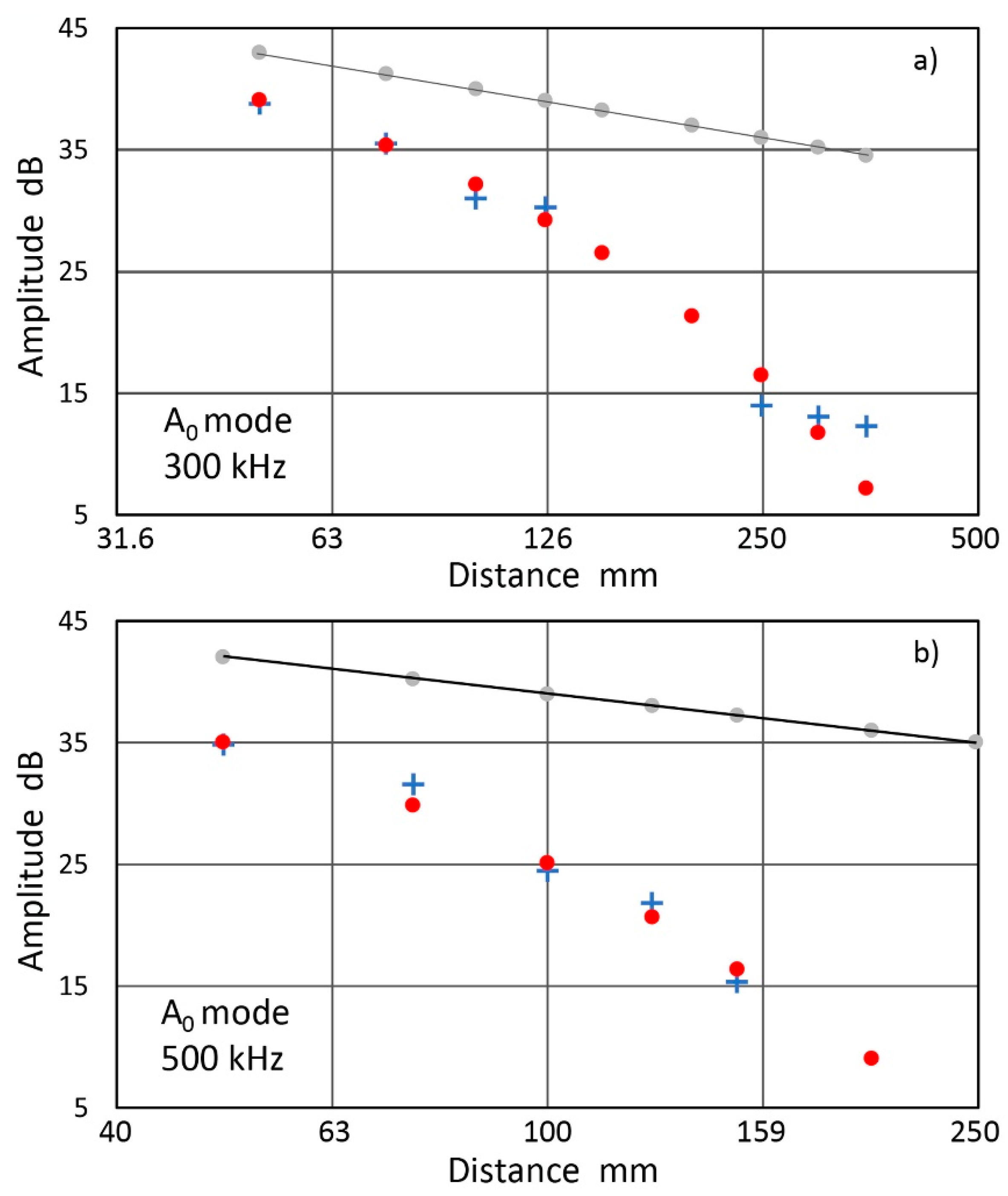
2.6. Guided Wave Attenuation on Fiber-Reinforced Composites
2.7. Summaries
3. Source Location
4. Bridge Monitoring
5. Sensing and Signal Processing
6. Pressure Vessels and Tanks
7. AE Inspection of Miscellaneous Processes
8. General Summary and Follow-Up Studies
9. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
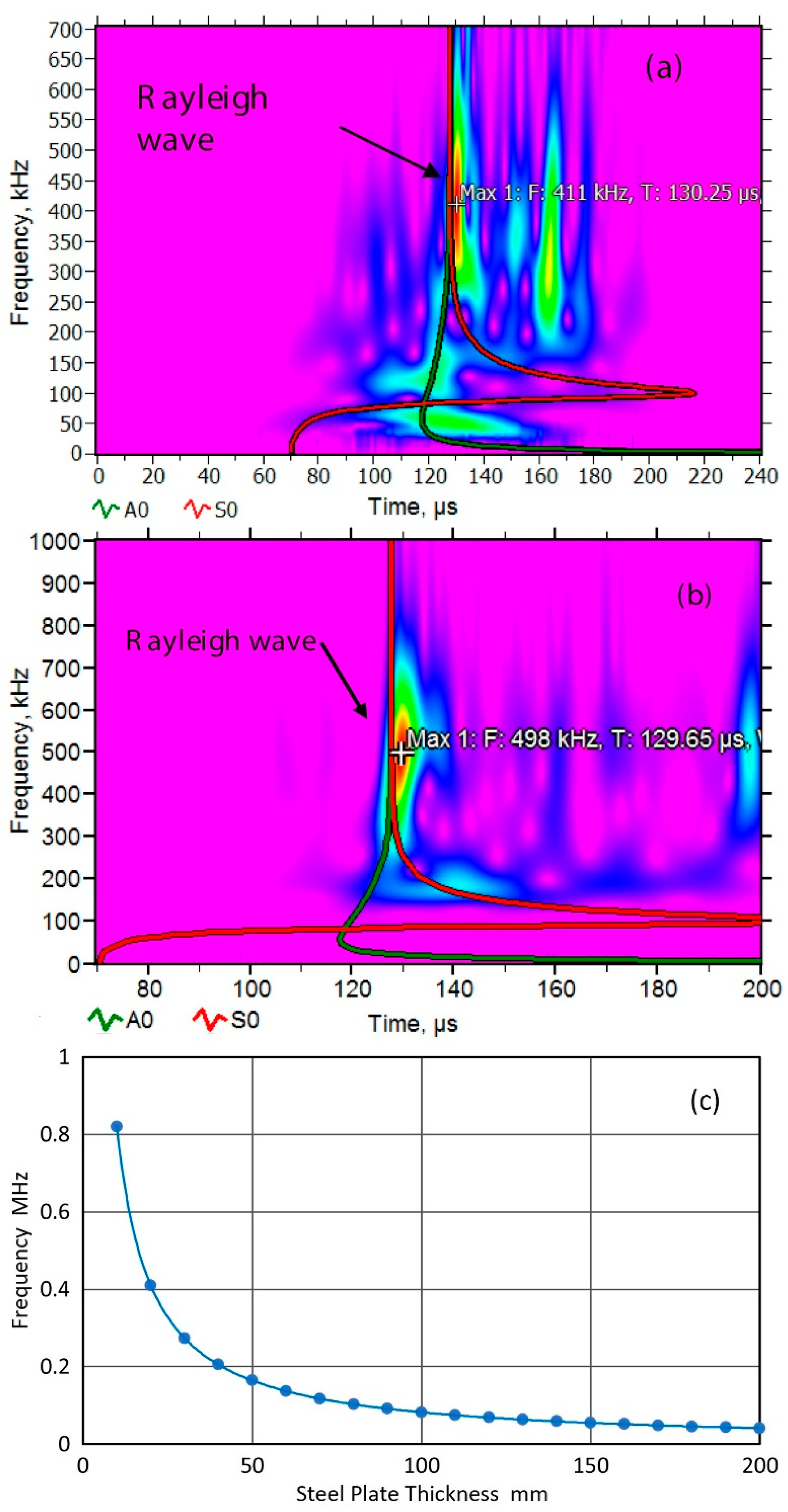
Appendix A. Limiting Frequency of Rayleigh Wave Propagation
References
- Green, A.T.; Lockman, C.S.; Steele, R.K. Acoustic verification of structural integrity of Polaris chambers. Mod. Plast. 1964, 41, 137–139. [Google Scholar]
- Liptai, R.G.; Harris, D.O.; Tatro, C.A. (Eds.) Acoustic Emission; STP-505; American Society for Testing and Materials: Philadelphia, PA, USA, 1972; 337p. [Google Scholar]
- Spanner, J.C.; McElroy, J.W. Monitoring Structural Integrity by Acoustic Emission; STP-571; American Society for Testing and Materials: Philadelphia, PA, USA, 1975; 289p. [Google Scholar]
- Fowler, T.J.; Blessing, J.A.; Conlisk, P.J.; Swanson, T.L. The MONPAC system. J. Acoust. Emiss. 1989, 8, 1–10. [Google Scholar]
- Miller, R.K. (Ed.) Acoustic emission. In Nondestructive Testing Handbook, 3rd ed.; American Society for Nondestructive Testing: Columbus, OH, USA, 2005; Volume 6, 446p. [Google Scholar]
- Ono, K. (Ed.) Journal Acoustic Emission. 1982–. Available online: www.aewg.org (accessed on 15 April 2017).
- Shiotani, T. Recent advances of AE technology for damage assessment of infrastructures. J. Acoust. Emiss. 2012, 30, 76–99. [Google Scholar]
- Bohse, J. Acoustic emission. In Handbook of Technical Diagnostics: Fundamentals and Application to Structures and Systems; Czichos, H., Ed.; Springer: Berlin, Germany, 2013; pp. 137–160. [Google Scholar]
- Hay, D.R.; Cavaco, J.A.; Mustafa, V. Monitoring the civil infrastructure with acoustic emission: Bridge case studies. J. Acoust. Emiss. 2009, 27, 1–9. [Google Scholar]
- Gorman, M.R. Modal AE analysis of fracture and failure in composite materials, and the quality and life of high pressure composite pressure vessels. J. Acoust. Emiss. 2011, 29, 1–28. [Google Scholar]
- Rumsey, M.A.; Paquette, J.; White, J.R.; Werlink, R.J.; Beattie, A.G.; Pitchford, C.W.; van Dam, J. Experimental results of structural health monitoring of wind turbine blades, AIAA Paper AIAA-2008-1348. 2008. Available online: www.sandia.gov/wind/asme/AIAA-2008-1348.pdf (accessed on 25 April 2012).
- Ono, K. Application of acoustic emission for structure diagnosis. Diagnostyka Diagn. Struct. Health Monit. 2011, 2, 3–18. [Google Scholar]
- Ono, K.; Gallego, A. Research and applications of AE on advanced composites. J. Acoust. Emiss. 2012, 30, 180–229. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring of Aerospace Composites; Academic Press: New York, NY, USA, 2015; 470p. [Google Scholar]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Gresil, M.; Giurgiutiu, V. Prediction of attenuated guided waves propagation in carbon fiber composites using Rayleigh damping model. J. Intell. Mater. Syst. Struct. 2015, 26, 2151–2169. [Google Scholar] [CrossRef]
- Treviso, A.; Van Genechten, B.; Mundo, D.; Tournour, M. Damping in composite materials: Properties and models. Compos. Part B Eng. 2015, 78, 144–152. [Google Scholar] [CrossRef]
- Jarzynski, J.; Balizer, E.; Fedderly, J.J.; Lee, G. Acoustic Properties—Encyclopedia of Polymer Science and Technology; Wiley: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Sinha, M.; Buckly, D.J. Acoustic properties of polymers. In Physical Properties of Polymers Handbook; Part X; Springer: Berlin, Germany, 2007; pp. 1021–1031. [Google Scholar]
- Viktorov, I.A. Rayleigh and Lamb Waves: Physical Theory and Applications; Plenum: New York, NY, USA, 1967; p. 154. [Google Scholar]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999; 476p. [Google Scholar]
- Mal, A.K.; Bar-Cohen, Y.; Lih, S.-S. Wave attenuation in fiber reinforced composites. In Mechanics and Mechanisms of Material Damping; ASTM STP-1169; American Society for Testing and Materials: Philadelphia, PA, USA, 1992; pp. 245–261. [Google Scholar]
- Press, F.; Healy, J. Absorption of Rayleigh waves in low-loss media. J. Appl. Phys. 1957, 28, 1323–1325. [Google Scholar] [CrossRef]
- Zhukov, K.V.; Merkulov, L.G.; Pigulevskii, E.D. Normal mode damping in a plate with free edges. Sov. Phys. Acoust. 1964, 10, 133–136. [Google Scholar]
- Krautkramer, J.; Krautkramer, H. Ultrasonic Testing of Materials; Springer: Berlin, Germany, 1969; p. 521. [Google Scholar]
- Mason, W.J.; McSkimin, H.J. Attenuation and scattering of high frequency sound waves in metals and glasses. J. Acoust. Soc. Am. 1947, 19, 464–473. [Google Scholar] [CrossRef]
- Roderick, R.L.; Truell, R. The measurement of ultrasonic attenuation in solids by the pulse technique and some results in steel. J. Appl. Phys. 1952, 23, 267–279. [Google Scholar] [CrossRef]
- Kamigaki, K. Ultrasonic attenuation in steel and cast iron. Sci. Rep. Res. Inst. Tohoku Univ. Ser. A 1957, 9, 48–77. [Google Scholar]
- Papadakis, E.P. Ultrasonic attenuation and velocity in three transformation products in steel. J. Acoust. Soc. Am. 1963, 35, 1884. [Google Scholar] [CrossRef]
- Papadakis, E.P. Ultrasonic attenuation in SAE 3140 and 4150 steel. J. Acoust. Soc. Am. 1960, 32, 1628–1639. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 3rd ed.; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Cai, C.; Zheng, H.; Khan, M.S.; Hung, K.C. Modeling of Material Damping Properties in ANSYS. 2002 International ANSYS Conference Proceedings. Available online: https://support.ansys.com/staticassets/ANSYS/staticassets/resourcelibrary/confpaper/2002-Int-ANSYS-Conf-197.PDF (accessed on 19 May 2018).
- Graham, L.J.; Alers, G.A. Acoustic emission in the frequency domain. In Monitoring Structural Integrity by Acoustic Emission; STP-571; American Society for Testing and Materials: Philadelphia, PA, USA, 1975; pp. 11–39. [Google Scholar]
- Pollock, A.A. Classical wave theory in practical AE testing. In Progress in AE III; The Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 1986; pp. 708–721. [Google Scholar]
- Blackburn, P.R. Acoustic emission from fatigue cracks in Cr-Mo steel cylinders. J. Acoust. Emiss. 1988, 7, 49–56. [Google Scholar]
- Baran, I.; Lyasota, I.; Skrok, K. Acoustic emission testing of underground pipelines of crude oil of fuel storage depots. In Proceedings of the 32nd European Conference on Acoustic Emission Testing, Prague, Czech Republic, 7–9 September 2016; pp. 15–26. [Google Scholar]
- Šofer, M.; Crha, J.; Zengerle, H. From near field to far field and beyond. In Proceedings of the 32nd European Conference on Acoustic Emission Testing, Prague, Czech Republic, 7–9 September 2016; pp. 475–483. [Google Scholar]
- Bryla, P.; Walaszek, H.; Herve, C.; Catty, J. Real time & long term acoustic emission monitoring: A new way to use acoustic emission—Application to hydroelectric penstocks and paper machine. In Proceedings of the 31st European Conference on Acoustic Emission Testing, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- El-Shaib, M.N. Predicting Acoustic Emission Attenuation in Solids Using Ray-Tracing within a 3D Solid Model. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2012; 230p. [Google Scholar]
- Ono, K.; Hayashi, T.; Cho, H. Bar-wave calibration of acoustic emission sensors. Appl. Sci. 2017, 7, 964. [Google Scholar] [CrossRef]
- Ono, K. On the piezoelectric detection of guided ultrasonic waves. Materials 2017, 10, 1325. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Perez, R.J.; Lavernia, E.J. Documentation of damping capacity of metallic, ceramic and metal-matrix composite materials. J. Mater. Sci. 1993, 28, 2395–2404. [Google Scholar] [CrossRef]
- Papadakis, E.P. Ultrasonic attenuation caused by scattering in polycrystalline metals. J. Acoust. Soc. Am. 1965, 37, 711–717. [Google Scholar] [CrossRef]
- Drinkwater, B.W.; Castaings, M.; Hosten, B. The interaction of Lamb waves with solid-solid interfaces. AIP Conf. Proc. 2003, 657, 1064–1071. [Google Scholar] [CrossRef]
- Zhang, F.; He, G.; Xu, K.; Wu, H.; Guo, S. The damping and flame-retardant properties of poly(vinyl chloride)/chlorinated butyl rubber multilayered composites. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Povolo, F.; Goyanes, S.N. Amplitude-dependent dynamical behavior of poly(methyl methacrylate). Polym. J. 1994, 26, 1054–1062. [Google Scholar] [CrossRef]
- Lee, T.; Lakes, R.S.; Lal, A. Resonant ultrasound spectroscopy for measurement of mechanical damping: Comparison with broadband viscoelastic spectroscopy. Rev. Sci. Instrum. 2000, 71, 2855–2861. [Google Scholar] [CrossRef]
- Castaings, M.; Hosten, B. The use of electrostatic, ultrasonic, air-coupled transducers to generate and receive Lamb waves in anisotropic, viscoelastic plates. Ultrasonics 1998, 36, 361–365. [Google Scholar] [CrossRef]
- Castaings, M.; Hosten, B. Air-coupled measurement of plane wave, ultrasonic plate transmission for characterising anisotropic, viscoelastic materials. Ultrasonics 2000, 38, 781–786. [Google Scholar] [CrossRef]
- Castaings, M.; Hosten, B.; Kundu, T. Inversion of ultrasonic, plane-wave transmission data in composite plates to infer viscoelastic material properties. NDT E Int. 2000, 33, 377–392. [Google Scholar] [CrossRef]
- Capodagli, J.; Lakes, R. Isothermal viscoelastic properties of PMMA and LDPE over 11 decades of frequency and time: A test of time–temperature superposition. Rheol. Acta 2008, 47, 777–786. [Google Scholar] [CrossRef]
- Wang, Y.C.; Ko, C.C.; Wu, H.K.; Wu, Y.T. Pendulum-type viscoelastic spectroscopy for damping measurement of solids. J. Jpn. Soc. Exp. Mech. 2013, 13, s137–s142. [Google Scholar]
- Thakur, V.K.; Vennerberg, D.; Madbouly, S.A.; Kessler, M.R. Bio-inspired green surface functionalization of PMMA for multifunctional capacitors. RSC Adv. 2014, 4, 6677–6684. [Google Scholar] [CrossRef]
- Treiber, M.; Kim, J.Y.; Jacobs, L.J. Correction for partial reflection in ultrasonic attenuation measurements using contact transducers. J. Acoust. Soc. Am. 2009, 125, 2946–2953. [Google Scholar] [CrossRef] [PubMed]
- Carlson, J.E.; van Deventer, J.; Scolan, A.; Carlander, C. Frequency and temperature dependence of acoustic properties of polymers used in pulse-echo systems. In Proceedings of the 2003 IEEE Symposium on Ultrasonics, Honolulu, HI, USA, 5–8 October 2003; pp. 885–888. [Google Scholar]
- Pouet, B.F.; Rasolofosaon, N.J.P. Measurement of broadband intrinsic ultrasonic attenuation and dispersion in solids with laser techniques. J. Acoust. Soc. Am. 1993, 93, 1286–1292. [Google Scholar] [CrossRef]
- Hartmann, B.; Jarzynski, J. Ultrasonic hysteresis absorption in polymers. J. Appl. Phys. 1972, 43, 4304–4312. [Google Scholar] [CrossRef]
- Merkulov, L.G. Damping of normal mode in a plate immersed in a liquid. Sov. Phys. Acoust. 1964, 10, 169–173. [Google Scholar]
- Shehadeh, M.F. Monitoring of Long Steel Pipes Using Acoustic Emission. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2006; 204p. [Google Scholar]
- European Coop. Space Standardization (ECSS). In Space Engineering, Structural Materials Handbook, Part I, Overview and Materials Properties and Applications; EDSS-E-HB-32-20 Part 1A; Sec. 5.4; ECSS: Noordwijk, The Netherlands, 2011; 535p. [Google Scholar]
- Neau, G.; Lowe, M.J.S.; Deschamps, M. Propagation of Lamb waves in anisotropic and absorbing plates: Theoretical derivation and experiments. AIP Conf. Proc. 2002, 615, 1062–1069. [Google Scholar] [CrossRef]
- Matt, H.M. Structural Diagnostics of CFRP Composite Aircraft Components by Ultrasonic Guided Waves and Built-in Piezoelectric Transducers. Ph.D. Thesis, University of California, San Diego, CA, USA, 2006; 242p. [Google Scholar]
- Calomfirescu, M.; Herrmann, A.S. On the propagation of Lamb waves in viscoelastic composites for SHM applications. Key Eng. Mater. 2007, 347, 543–548. [Google Scholar] [CrossRef]
- Calomfirescu, M. Lamb Waves for Structural Health Monitoring in Viscoelastic Composite Materials. Ph.D. Thesis, Universitat Bremen, Bremen, Germany, 2008; 128p. [Google Scholar]
- Schmidt, D.; Sadri, H.; Szewieczek, A.; Sinapius, M.; Wierach, P.; Siegert, I.; Wendemuth, A. Characterization of Lamb wave attenuation mechanisms. In Health Monitoring of Structural and Biological Systems; SPIE: San Diego, CA, USA, 2013; Volume 8695, p. 869503. [Google Scholar] [CrossRef]
- Schmidt, D.; Wierach, P.; Sinapius, M. Mode selective actuator-sensor system for Lamb wave-based structural health monitoring. In Proceedings of the 7th European Workshop on SHM, Nantes, France, 8–11 July 2014. [Google Scholar]
- Papadakis, E.P. The measurement of ultrasonic attenuation. In Methods of Experimental Physics; Edmonds, P.D., Ed.; Academic Press: New York, NY, USA, 1981; Chapter 3; pp. 108–156. [Google Scholar]
- Klinman, R.; Webster, G.R.; Marsh, F.J.; Stephenson, E.T. Ultrasonic prediction of grain size, strength, and toughness in plain carbon steel. Mater. Eval. 1980, 38, 26–32. [Google Scholar]
- Klinman, R.; Stephenson, E.T. Ultrasonic prediction of grain size and mechanical properties in plain carbon steel. Mater. Eval. 1981, 39, 1116–1120. [Google Scholar]
- Smith, R.L.; Reynolds, W.N.; Wadley, H.N.G. Ultrasonic attenuation and microstructure in low-carbon steels. Met. Sci. 1981, 15, 554–558. [Google Scholar] [CrossRef]
- Smith, R.L.; Rusbridge, K.L.; Reynolds, W.N.; Hudson, B. Ultrasonic attenuation, microstructure, ductile to brittle transition temperature in Fe-C alloys. Mater. Eval. 1983, 41, 219–222. [Google Scholar]
- Papadakis, E.P. Ultrasonic Attenuation and velocity in SAE 52100 steel quenched from various temperatures. Met. Trans. 1970, 1, 1053–1057. [Google Scholar]
- Latiff, R.H.; Fiore, N.F. Ultrasonic attenuation in spheroidized steel. J. Appl. Phys. 1974, 45, 5182–5186. [Google Scholar] [CrossRef]
- Coronel, V.F.; Beshers, D.N. Magnetomechanical damping in iron. J. Appl. Phys. 1988, 64, 2006–2015. [Google Scholar] [CrossRef]
- Ohtani, T.; Ogi, T.; Hirao, M. Ultrasonic attenuation peak during creep of a nickel-base superalloy with electromagnetic acoustic resonance. J. Soc. Mater. Sci. Jpn. 2004, 53, 692–698. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. EMATS for Science and Industry, Noncontacting Ultrasonic Measurements; Kluwer: Boston, MA, USA, 2003; p. 369. [Google Scholar]
- Ohtani, T.; Ogi, H.; Hirao, M. Change of ultrasonic attenuation and microstructure evolution in crept 2.25%Cr-1%Mo steels. J. Soc. Mater. Sci. Jpn. 2002, 51, 195–201. (In Japanese) [Google Scholar] [CrossRef]
- Ohtani, T.; Ogi, H.; Hirao, M. Electromagnetic acoustic resonance to assess creep damage in Cr–Mo–V steel, Japan. J. Appl. Phys. 2006, 45, 4526–4533. [Google Scholar] [CrossRef]
- Ohtani, T.; Takei, K. Change of ultrasonic attenuation and microstructure evolution during creep of SUS316L austenite stainless steels. J. Soc. Mater. Sci. Jpn. 2005, 54, 607–614. (In Japanese) [Google Scholar] [CrossRef]
- Reynolds, W.N.; Smith, R.N. Ultrasonic wave attenuation spectra in steels. J. Phys. D Appl. Phys. 1984, 17, 109–116. [Google Scholar] [CrossRef]
- Generazio, E.R. The Role of the Reflection Coefficient in Precision Measurement of Ultrasonic Attenuation; NASA Technical Memorandum 83788; NASA Lewis Research Center: Cleveland, OH, USA, 1984; 32p.
- Hikata, A.; Truell, R. Frequency dependence of ultrasonic attenuation and velocity on plastic deformation. J. Appl. Phys. 1957, 28, 522–523. [Google Scholar] [CrossRef]
- Mason, W.P.; McSkimin, H.J. Energy losses of sound waves in metals due to scattering and diffusion. J. Appl. Phys. 1948, 19, 940–946. [Google Scholar] [CrossRef]
- Zeng, F.; Agnew, S.R.; Raeisinia, B.; Myneni, G.R. Ultrasonic attenuation due to grain boundary scattering in pure niobium. J. Nondestruct. Eval. 2010, 29, 93–103. [Google Scholar] [CrossRef]
- Ahn, B.; Lee, S.S. Effect of microstructure of low carbon steels on ultrasonic attenuation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 620–629. [Google Scholar] [PubMed]
- Du, H.; Turner, J.A. Ultrasonic attenuation in pearlitic steel. Ultrasonics 2014, 54, 882–887. [Google Scholar] [CrossRef] [PubMed]
- Wan, T.; Naoe, T.; Wakui, T.; Futakawa, M.; Obayashi, H.; Sasa, T. Effects of grain size on ultrasonic attenuation in type 316L stainless steel. Materials 2017, 10, 753. [Google Scholar] [CrossRef] [PubMed]
- Nadeau, F.; Bussiere, J.F.; Van Drunen, G. On the relation between ultrasonic attenuation and fracture toughness in type 403 stainless steel. Mater. Eval. 1985, 43, 101–107. [Google Scholar]
- Ramuhalli, P.; Good, M.S.; Diaz, A.A.; Anderson, M.T.; Watson, B.E.; Peters, T.J.; Dixit, M.; Bond, L.J. Ultrasonic Characterization of Cast Austenitic Stainless Steel Microstructure: Discrimination between Equiaxed- and Columnar-Grain Material—An Interim Study; PNNL-18912; Pacific Northwest National Laboratory: Richland, WA, USA, 2009; 84p.
- Jennes, J.R., Jr.; Kline, D.E. The dynamic mechanical properties of some epoxy matrix composites. J. Appl. Polym. Sci. 1973, 17, 3391–3422. [Google Scholar] [CrossRef]
- Dokun, O.D.; Jacobs, L.J.; Haj-Ali, R.M. Ultrasonic techniques to quantify material degradation in FRP composites. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1999; pp. 1365–1371. [Google Scholar]
- Roman, I.; Ono, K. Acoustic emission characterization of failure mechanisms in Woven roving glass-epoxy composites. In Progress in Acoustic Emission II; Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 1984; pp. 496–503. [Google Scholar]
- Crane, R.M. Vibration Damping Response of Composite Materials; US Navy Report; DTRC-SME-91/12; April 1991 AD A235 614; David Taylor Research Center: Bethesda, MD, USA, 1991; 303p. [Google Scholar]
- Vantomme, J. A parametric study of material damping in fibre-reinforced plastics. Composites 1995, 26, 147–153. [Google Scholar] [CrossRef]
- Yim, J.H.; Gillespie, J.W., Jr. Damping characteristics of 0° and 90° AS4/3501-6 unidirectional laminates including the transverse shear effect. Compos. Struct. 2000, 50, 217–225. [Google Scholar] [CrossRef]
- Jalili, M.M.; Mousavi, S.Y.; Pirayeshfa, A.S. Investigating the acoustical properties of carbon fiber-, glass fiber-, and hemp fiber-reinforced polyester composites. Polym. Compos. 2014, 35, 2103–2111. [Google Scholar] [CrossRef]
- Kim, H.C.; Park, J.M. Ultrasonic wave propagation in carbon fibre-reinforced plastics. J. Mater. Sci. 1987, 22, 4536–4540. [Google Scholar] [CrossRef]
- Watanabe, Y.; Biwa, S.; Ohno, N. Experimental investigation of ultrasonic attenuation behavior in carbon fiber reinforced epoxy composites. J. Soc. Mater. Sci. Jpn. 2002, 51, 451–457. [Google Scholar] [CrossRef]
- Williams, J.H., Jr.; Lee, S.S.; Nayeb-Hashemi, H. Ultrasonic wave propagation loss factor in composite in terms of constituent properties. J. Nondestruct. Eval. 1980, 1, 191–199. [Google Scholar] [CrossRef]
- Seki, H.; Granato, A.; Truell, R. Diffraction effects in the ultrasonic field of a piston source and their importance in the accurate measurement of attenuation. J. Acoust. Soc. Am. 1956, 28, 230–238. [Google Scholar] [CrossRef]
- Papadakis, E.P. Ultrasonic velocity and attenuation: Measurement methods with scientific and industrial applications. In Physical Acoustics; Academic Press: New York, NY, USA, 1976; Volume XII, pp. 277–375. [Google Scholar]
- Ono, K. Acoustic emission behavior of flawed unidirectional carbon fiber-epoxy composites. J. Reinf. Plast. Compos. 1988, 7, 90–105. [Google Scholar] [CrossRef]
- Adams, R.D. The dynamic longitudinal shear modulus and damping of carbon fibres. J. Phys. D Appl. Phys. 1975, 8, 738. [Google Scholar] [CrossRef]
- Ishikawa, M.; Kogo, Y.; Koyanagi, J.; Tanaka, F.; Okabe, T. Torsional modulus and internal friction of polyacrylonitrile and pitch-based carbon fibers. J. Mater. Sci. 2015, 50, 7018–7025. [Google Scholar] [CrossRef]
- Olivier, P.A.; Marguerès, P.; Mascaro, B.; Collombet, F. CFRP with voids: Ultrasonic characterization of localized porosity, acceptance criteria and mechanical characteristics. In Proceedings of the 16th International Conference on Composite Materials, Kyoto, Japan, 3–8 July 2007. [Google Scholar]
- Ono, K.; Gallego, A. Attenuation of Lamb waves in CFRP plates. J. Acoust. Emiss. 2012, 30, 109–123. [Google Scholar]
- Weihnacht, B.; Schulze, E.; Frankenstein, B. Acoustic emission analysis in the dynamic fatigue testing of fiber composite components. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Ge, M. Analysis of source location algorithms, Part I: Overview and non-iterative methods. J. Acoust. Emiss. 2003, 21, 14–28. [Google Scholar]
- Ge, M. Analysis of source location algorithms, Part II: Iterative methods. J. Acoust. Emiss. 2003, 21, 29–51. [Google Scholar]
- Summerscales, J. Acoustic Emission Source Location in Fibre-Reinforced Composite Materials; Advanced Composites Manufacturing Centre at Plymouth University: Plymouth, UK, 2013; 36p, ISBN 978-1-870918-04-6. [Google Scholar]
- Kundu, T. Acoustic source localization. Ultrasonics 2014, 54, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Holford, K.M.; Eaton, M.J.; Hensman, J.J.; Pullin, R.; Evans, S.L.; Dervilis, N.; Worden, K. A new methodology for automating acoustic emission detection of metallic fatigue fractures in highly demanding aerospace environments: An overview. Prog. Aerosp. Sci. 2017, 90, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.D.; Rauchenstein, L.T.; Carlson, T.J. Contributed Review: Source-localization algorithms and applications using time of arrival and time difference of arrival measurements. Rev. Sci. Instrum. 2016, 87, 041502. [Google Scholar] [CrossRef] [PubMed]
- Hutton, P.H.; Jolly, W.D.; Vetrano, J.B. Acoustic emission for periodic and continuous flaw detection in pressure vessels. In Proceedings of the U.S.-Japan Joint Symposium on Acoustic Emission, Tokyo, Japan, 4–6 July 1972. [Google Scholar]
- Crostack, H.A.; Böhm, P. Monitoring of a pressure vessel (ZB2) by means of acoustic emission. J. Acoust. Emiss. 1990, 9, 29–36. [Google Scholar]
- Aljets, D.; Chong, A.; Wilcox, S.; Holford, K. Acoustic emission source location in plate-like structures using a closely arranged triangular sensor array. J. Acoust. Emiss. 2010, 28, 85–98. [Google Scholar]
- Kundu, T.; Nakatani, H.; Takeda, N. Acoustic source localization in anisotropic plates. Ultrasonics 2012, 52, 740–746. [Google Scholar] [CrossRef] [PubMed]
- Scholey, J.J.; Wilcox, P.D.; Wisnom, M.R.; Friswell, M.; Pavier, M.; Aliha, M.R. A generic technique for acoustic emission source location. J. Acoust. Emiss. 2009, 27, 291–298. [Google Scholar]
- Boller, C.; Chang, F.K.; Fujino, Y. (Eds.) Encyclopedia of Structural Health Monitoring; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- He, T.; Pan, Q.; Liu, Y.; Liu, X.; Hu, D. Near-field beamforming analysis for acoustic emission source localization. Ultrasonics 2012, 52, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Dong, L. An efficient closed-form solution for acoustic emission source location in three-dimensional structures. AIP Adv. 2014, 4, 027110. [Google Scholar] [CrossRef]
- Spencer, S.J. Closed-form analytical solutions of the time difference of arrival source location problem for minimal element monitoring arrays. J. Acoust. Soc. Am. 2010, 127, 2943–2954. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Milios, E. Acoustic positioning using multiple microphone arrays. J. Acoust. Soc. Am. 2005, 117, 2772–2782. [Google Scholar] [CrossRef] [PubMed]
- Mellen, G.; Pachter, M.; Raquet, J. Closed-form solution for determining emitter location using time difference of arrival measurements. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1056–1058. [Google Scholar] [CrossRef]
- Hensman, J.J.; Mills, R.; Pierce, S.G.; Worden, K.; Eaton, M.J. Locating acoustic emission sources in complex structures using Gaussian processes. Mech. Syst. Signal Process. 2010, 24, 211–223. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. A probabilistic framework for single-sensor acoustic emission source localization in thin metallic plates. Smart Mater. Struct. 2017, 26, 095026. [Google Scholar] [CrossRef]
- Jiang, M.; Lu, S.; Sai, Y.; Sui, Q.; Jia, L. Acoustic emission source localization technique based on least squares support vector machine by using FBG sensors. J. Mod. Opt. 2014, 61, 1634–1640. [Google Scholar] [CrossRef]
- Worden, K.; Staszewski, W.J. Impact location and quantification on a composite panel using neural networks and a genetic algorithm. Strain 2000, 36, 61–70. [Google Scholar] [CrossRef]
- Gorman, M.R. Plate wave acoustic emission. J. Acoust. Soc. Am. 1991, 90, 358–364. [Google Scholar] [CrossRef]
- Ziola, S.M.; Gorman, M.R. Source location in thin plates using cross-correlation. J. Acoust. Soc. Am. 1991, 90, 2551–2556. [Google Scholar] [CrossRef]
- Gorman, M.R.; Prosser, W.H. AE source location by plate wave analysis. J. Acoust. Emiss. 1990, 9, 283–288. [Google Scholar]
- Yamada, H.; Mizutani, Y.; Nishino, H.; Takemoto, M.; Ono, K. Lamb wave source location of impact on anisotropic plates. J. Acoust. Emiss. 2000, 18, 51–60. [Google Scholar]
- Maji, A.K.; Satpathi, D.; Kratochvil, T. Acoustic emission source location using Lamb wave modes. J. Eng. Mech. 1997, 123, 154–161. [Google Scholar] [CrossRef]
- Park, W.H.; Packo, P.; Kundu, T. Acoustic source localization in an anisotropic plate without knowing its material properties—A new approach. Ultrasonics 2017, 79, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimkhanlou, A.; Salamone, S. AE source localization in thin metallic plates: A single sensor approach based on multimodal edge reflections. Ultrasonics 2017, 78, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Al-Jumaili, S.K.; Pearson, M.R.; Holford, K.M.; Eaton, M.J.; Pullin, R. Acoustic emission source location in complex structures using full automatic delta T mapping technique. Mech. Syst. Signal Process. 2016, 72–73, 513–524. [Google Scholar] [CrossRef]
- Dorme, C.; Fink, M. Focusing in transmit-receive mode through inhomogeneous media: The TR matched filter approach. J. Acoust. Soc. Am. 1995, 98, 1155–1162. [Google Scholar] [CrossRef]
- Tanter, M.; Thomas, J.L.; Fink, M. Time reversal and the inverse filter. J. Acoust. Soc. Am. 2000, 108, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Ing, R.-K.; Quieffin, N.; Catheline, S.; Fink, M. In solid localization of finger impacts using acoustic time-reversal process. Appl. Phys. Lett. 2005, 87, 204104. [Google Scholar] [CrossRef]
- Ciampa, F.; Meo, M. Impact detection in anisotropic materials using a time reversal approach. Struct. Health Monit. 2011, 11, 43–49. [Google Scholar] [CrossRef]
- Douma, J.; Niederleithinger, E.; Snieder, R. Locating events using time reversal and deconvolution: Experimental application and analysis. J. Nondestruct. Eval. 2015, 34, 2. [Google Scholar] [CrossRef]
- Robert, E.; Jurg, D. Acoustic emission source detection using the time reversal principle on dispersive waves in beams. In Proceedings of the 2013 International Congress on Ultrasonics (ICU 2013), Singapore, 2–5 May 2013. [Google Scholar] [CrossRef]
- Liu, F.; Ding, S.; Hu, D.; Wang, Q.; Xu, Y.; Kong, S.; Zheng, M. Sound source location error analysis of acoustic emission technique for thick-wall pressure vessel inspection. In Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009; pp. 485–491. [Google Scholar] [CrossRef]
- Iliopoulos, S.; Aggelis, D.G.; Pyl, L.; Vantomme, J.; Van Marcke, P.; Coppens, E.; Areias, E. Detection and evaluation of cracks in the concrete buffer of the Belgian nuclear waste container using combined NDT techniques. Constr. Build. Mater. 2015, 78, 369–378. [Google Scholar] [CrossRef]
- Ozevin, D. Geometry-based spatial acoustic source location for spaced structures. Struct. Health Monit. 2010, 10, 503–510. [Google Scholar] [CrossRef]
- Nair, A.; Cai, C.S. Acoustic emission monitoring of bridges, review and case studies. Eng. Struct. 2010, 32, 1704–1714. [Google Scholar] [CrossRef]
- Washer, G. Nondestructive evaluation methods for bridge elements. In Bridge Engineering Handbook, 2nd ed.; Construction and Maintenance; CRC Press: Boca Raton, FL, USA, 2014; pp. 301–335. [Google Scholar]
- Kosnik, D.E.; Hopwood, T.; Corr, D.J. Acoustic emission monitoring for assessment of steel bridge details. AIP Conf. Proc. 2011, 1335, 1410–1417. [Google Scholar]
- Attanayake, U.; Aktan, H.; Hay, R.; Catbas, N. Remote Monitoring of Fatigue-Sensitive Details on Bridges; Report MDOT RC-1629; Michigan Department of Transport: Kalamazoo, MI, USA, 2015; 49p.
- Johnson, M.B.; Ozevin, D.; Washer, G.; Ono, K.; Gostautas, R.; Tamutus, T. Acoustic Emission Method for Real-Time Detection of Steel Fatigue Crack in Eyebar; National Academy of Sciences: Washington, DC, USA, 2012; pp. 72–79. [Google Scholar]
- Ley, O.; Gostautas, R.; Godinez-Azcuaga, V.F. Recent advances in structural health monitoring using acoustic emission. In Progress in Acoustic Emission XVIII; Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 2016; pp. 153–156. [Google Scholar]
- Hovhanessian, G.; Laurent, E. Instrumentation and monitoring of critical structural elements unique to suspension bridges. In Advances in Cable-Supported Bridges; Taylor & Frances: London, UK, 2006; Chapter 8; pp. 111–119. [Google Scholar]
- Sluszka, P. Studies on the Longevity of Suspension Bridge Cables; Transportation Research Record 1290; National Academy of Sciences: Washington, DC, USA, 1990; pp. 272–278. [Google Scholar]
- Colford, B. The maintenance of long span bridges. In Proceedings of the 8th International Cable Supported Bridge Operators Conference, Edinburgh, UK, 3–5 June 2013. [Google Scholar]
- Mayrbaurl, R.M.; Camo, S. Guidelines for Inspection and Strength Evaluation of Suspension Bridge Parallel Wire Cables; National Cooperative Highway Research Program Report; NCHRP 534; National Academy of Sciences: Washington, DC, USA, 2004. [Google Scholar]
- Beabes, S.; Faust, D.; Cocksedge, C. Suspension bridge main cable dehumidification—An active system for cable preservation, Sustainable bridge structures. In Proceedings of the 8th New York City Bridge Conference, New York, NY, USA, 24–25 August 2015; pp. 3–18. [Google Scholar]
- Ono, K. Calibration methods of acoustic emission sensors. Materials 2016, 9, 508. [Google Scholar] [CrossRef] [PubMed]
- Ono, K. Critical examination of ultrasonic transducer characteristics and calibration methods. Res. Nondestruct. Eval. 2017, 1–46. [Google Scholar] [CrossRef]
- Vallen, H. Proposal for an absolute AE sensor calibration setup. In Proceedings of the World Conference on Acoustic Emission, Xi’an, China, 11–13 October 2017. [Google Scholar]
- NDIS 2109-91. Method for Absolute Calibration of Acoustic Emission Transducers by Reciprocity Technique; The Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 1991; 13p. [Google Scholar]
- Hatano, H.; Watanabe, T. Reciprocity calibration of acoustic emission transducers in Rayleigh-wave and longitudinal-wave sound fields. J. Acoust. Soc. Am. 1997, 101, 1450–1455. [Google Scholar] [CrossRef]
- Monnier, T.; Friedrich, P.; Zhang, F. Primary calibration of acoustic emission sensors by the method of reciprocity-industrial exploitation of the calibration bench. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Wild, G.; Hinckley, S. Acousto-ultrasonic optical fiber sensors: Overview and state-of-the-art. IEEE Sens. J. 2008, 8, 1184–1193. [Google Scholar] [CrossRef]
- Teixeira, J.G.V.; Leite, I.T.; Silva, S.; Frazão, O. Advanced fiber-optic acoustic sensors. Photonic Sens. 2014, 4, 198–208. [Google Scholar] [CrossRef]
- Yu, F.; Okabe, Y.; Wu, Q.; Shigeta, N. Damage type identification based on acoustic emission detection using a fiber-optic sensor in carbon fiber reinforced plastic laminates. In Proceedings of the 32nd European Conference on Acoustic Emission, Prague, Czech Republic, 7–9 September 2016; pp. 543–550. [Google Scholar]
- Innes, M.; Davis, C.; Rosalie, C.; Norman, P.; Rajic, N. Acoustic emission detection and characterisation using networked FBG sensors. Procedia Eng. 2017, 188, 440–447. [Google Scholar] [CrossRef]
- Shrestha, P.; Kim, J.H.; Park, Y.; Kim, C.G. Impact localization on composite wing using 1D array FBG sensor and RMS/correlation based reference database algorithm. Compos. Struct. 2015, 125, 159–169. [Google Scholar] [CrossRef]
- Barat, V.; Borodin, Y.; Kuzmin, A. Intelligent AE signal filtering methods. J. Acoust. Emiss. 2010, 28, 109–119. [Google Scholar]
- Elizarov, S.; Barat, V.; Shimansky, A. Nonthreshold acoustic emission data registration principles. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Lokajícek, T.; Klíma, K. A first arrival identification system of acoustic emission (AE) signals by means of a high-order statistics approach. Meas. Sci. Technol. 2006, 17, 2461. [Google Scholar] [CrossRef]
- Pomponi, E.; Vinogradov, A. Wavelet based approach to acoustic emission phase picking. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Manhertz, G.; Csicso, G.; Gardonyi, G.; Por, G. Real-time acoustic emission event detection with data evaluation for supporting material research. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Kharrat, M.; Ramasso, E.; Placet, V.; Boubakar, L. Acoustic emission in composite materials under fatigue tests: Effect of signal-denoising input parameters on the hits detection and data clustering. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Sagasta, F.A.; Zitto, M.; Piotrokowski, R.; Gallego, A.; Benavent-Climent, A. A novel wavelet b-value of acoustic emissions to evaluate local damage in RC frames subjected to earthquakes. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Sibil, A.; Godin, N.; R’Mili, M.; Maillet, M.; Fantozzi, G. Optimization of acoustic emission data clustering by a genetic algorithm method. J. Nondestruct. Eval. 2012, 31, 169–180. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Reading, MA, USA, 1989; 412p. [Google Scholar]
- Anastassopoulos, A.A.; Philippidis, T.P. Clustering methodology for the evaluation of acoustic emission from composites. J. Acoust. Emiss. 1995, 13, 11–22. [Google Scholar]
- Godin, N.; Huguet, S.; Gaertner, R.; Salmon, L. Clustering of acoustic emission signals collected during tensile tests on unidirectional glass/polyester composite using supervised and unsupervised classifiers. NDT E Int. 2004, 37, 253–264. [Google Scholar] [CrossRef]
- Katsuyama, K.; Seto, M.; Kiyama, T.; Utagawa, M. Three-dimensional AE tomography for image processing of the deteriorated material. Saf. Eng. (Anzen Kogaku) 1992, 31, 321–326. (In Japanese) [Google Scholar]
- Schubert, F. Principle of AE tomography. J Acoust. Emiss. 2004, 22, 147–158. [Google Scholar]
- Kobayashi, Y.; Shiotani, T. Computerized AE tomography. In Innovative AE and NDT Techniques for On-Site Measurement of Concrete and Masonry Structures; Ohtsu, M., Ed.; Springer: Dordrecht, Germany, 2016; pp. 47–68. [Google Scholar]
- Kobayashi, Y.; Shiotani, T.; Oda, K. Three-dimensional AE-tomography with accurate source location technique. In Proceedings of the Structural Faults and Repair Conference, London, UK, 8–10 July 2014. [Google Scholar]
- Kobayashi, Y.; Shiotani, T.; Oda, K. System identification for three-dimensional AE-tomography with Kalman filter. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Nishida, T.; Shiotani, T.; Asaue, H.; Maejima, T.; Kobayashi, Y. Damage evaluation for CR bridge deck under wheel loading test by means of AE tomography. In Progress in Acoustic Emission XVIII; The Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 2016; pp. 111–116. [Google Scholar]
- Fukuda, M.; Shiotani, T.; Nishida, T.; Asaue, H.; Watabe, K.; Kobayashi, Y. Damage evaluation for in-field bridge deck by AE tomography. In Progress in Acoustic Emission XVIII; The Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 2016; pp. 481–486. [Google Scholar]
- Takamine, H.; Watabe, K.; Miyata, H.; Asaue, H.; Nishida, T.; Shiotani, T. Efficient damage inspection of deteriorated RC bridge deck with rain-induced elastic wave. Constr. Build. Mater. 2018, 162, 908–913. [Google Scholar] [CrossRef]
- Lackner, G.; Tscheliesnig, P. Requalification of LPG tanks in Europe: Verifying the structural integrity by monitoring the pressure test with acoustic emission. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Di Fratta, C.; Ferraro, A.; Tscheliesnig, P.; Lackner, G.; Correggia, V.; Altamura, N. AT on buried LPG tanks over 13 m3: An innovative and practical solution. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Newhouse, N.L.; Rawls, G.B.; Rana, M.D.; Shelley, B.F.; Gorman, M.R. Development of ASME section X code rules for high pressure composite hydrogen pressure vessels with non-load sharing liners. In Proceedings of the 2010 ASME Pressure Vessels and Piping Conference, PVP 2010, Bellevue, WA, USA, 18–22 July 2010; 10p. [Google Scholar]
- ASME Boiler and Pressure Vessel Code, Sec. X, Fiber-Reinforced Plastic Pressure Vessels; Mandatory Appendix 8-620 and NB10-0601, Supplement 9; The American Society of Mechanical Engineers: New York, NY, USA, 2017; 323p.
- Digital Wave Corp. Use of Modal Acoustic Emission (MAE) for Life Extension of Civilian Self-Contained Breathing Apparatus (SCBA) DOT-CFFC Cylinders; Final Report; US DOT Contract DTPH56-13-P-000029; Digital Wave Corp: Centennial, CO, USA, 2014; 204p. Available online: www.phmsa.dot.gov/sites/phmsa.dot.gov/files/docs/technical-resources/56376/finalreport-june20-2014.pdf (accessed on 20 May 2018).
- Anderson, M. A Review of Composite SCBA Cylinders and DOT Life Extension; Digital Wave Corp: Centennial, CO, USA, 2016; 7p, Available online: www.digitalwavecorp/scba-life-extension-1 (accessed on 1 May 2018).
- Flage, D.; Hunter, D.; Robinson, S.; Ceres, R.; Gorman, M.; Ziola, S. Self-Contained Breathing Apparatus (SCBA) Cylinder Life-Extension Study; Final Report; NAVSEA Contract N00024-11-C-4314; CACI International: Fairfax, VA, USA, 2012; 23p, Available online: navy-self-contained-breathing-apparatus-scba-composite-cylinder-life-extension-research-project.pdf (accessed on 20 May 2018).
- US DOT Pipeline and Hazardous Materials Safety Administration. Modal Acoustic Emission (MAE) Examination Specification for Requalification of Composite Overwrapped Pressure Vessels (Cylinders and Tubes); Tech. Report; US Dept. Transportation: Washington, DC, USA, 3 May 2018; 23p. Available online: www.phmsa.dot.gov/technical-resources/hazmat-technical-resources/technical-reports (accessed on 20 May 2018).
- Chang, J.B. Implementation Guidelines for ANSI/AIAA S-081: Space Systems Composite Overwrapped Pressure Vessels; Aerospace Report No. TR-2003(8504)-1; AD A413531; Aerospace Corp: El Segundo, CA, USA, 2003; 83p. [Google Scholar]
- Carpinteri, A.; Lacidogna, G. (Eds.) Acoustic Emission and Critical Phenomena: From Structural Mechanics to Geophysics; CRC Press: Boca Raton, FL, USA, 2008; 282p. [Google Scholar]
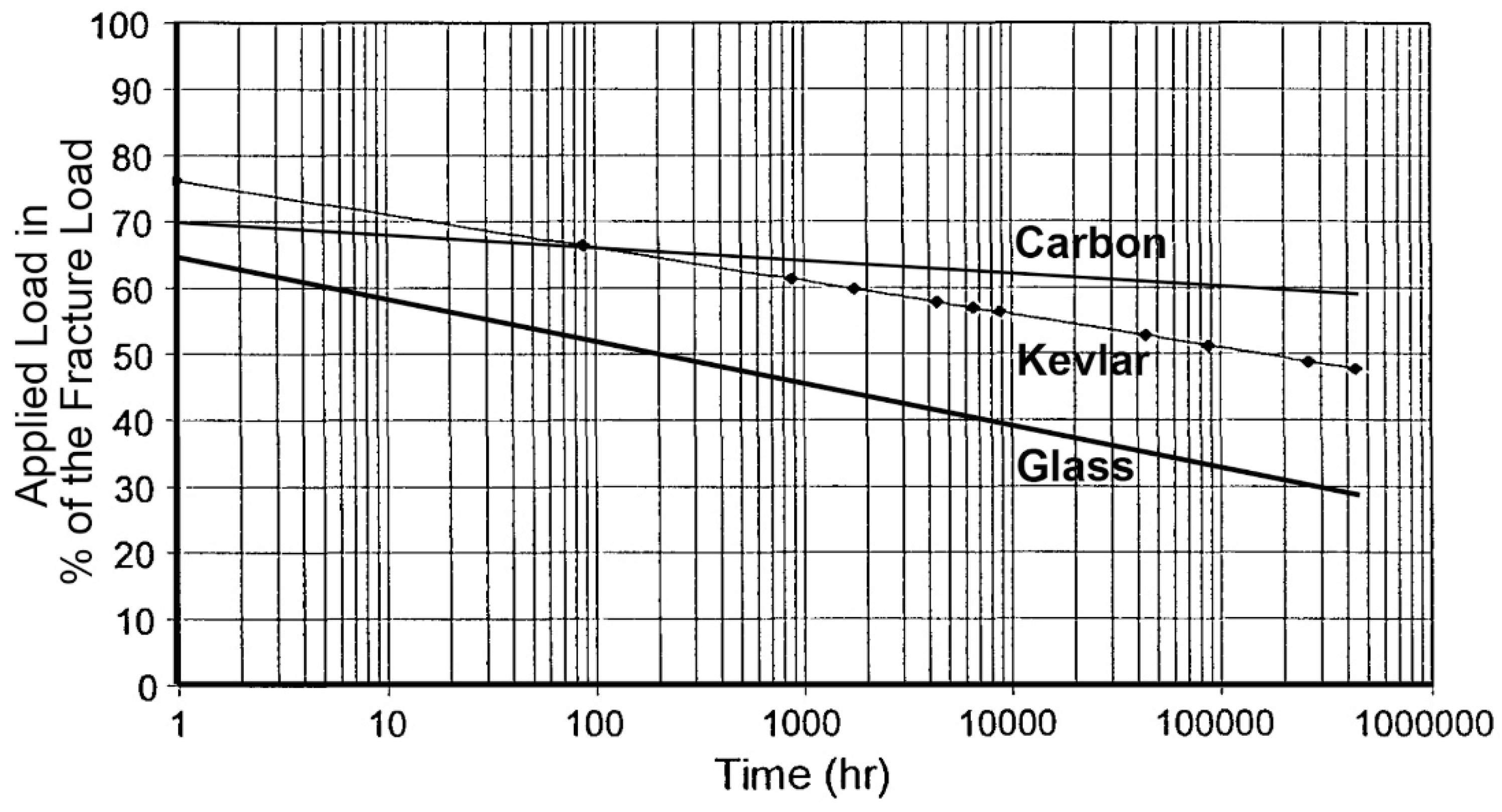
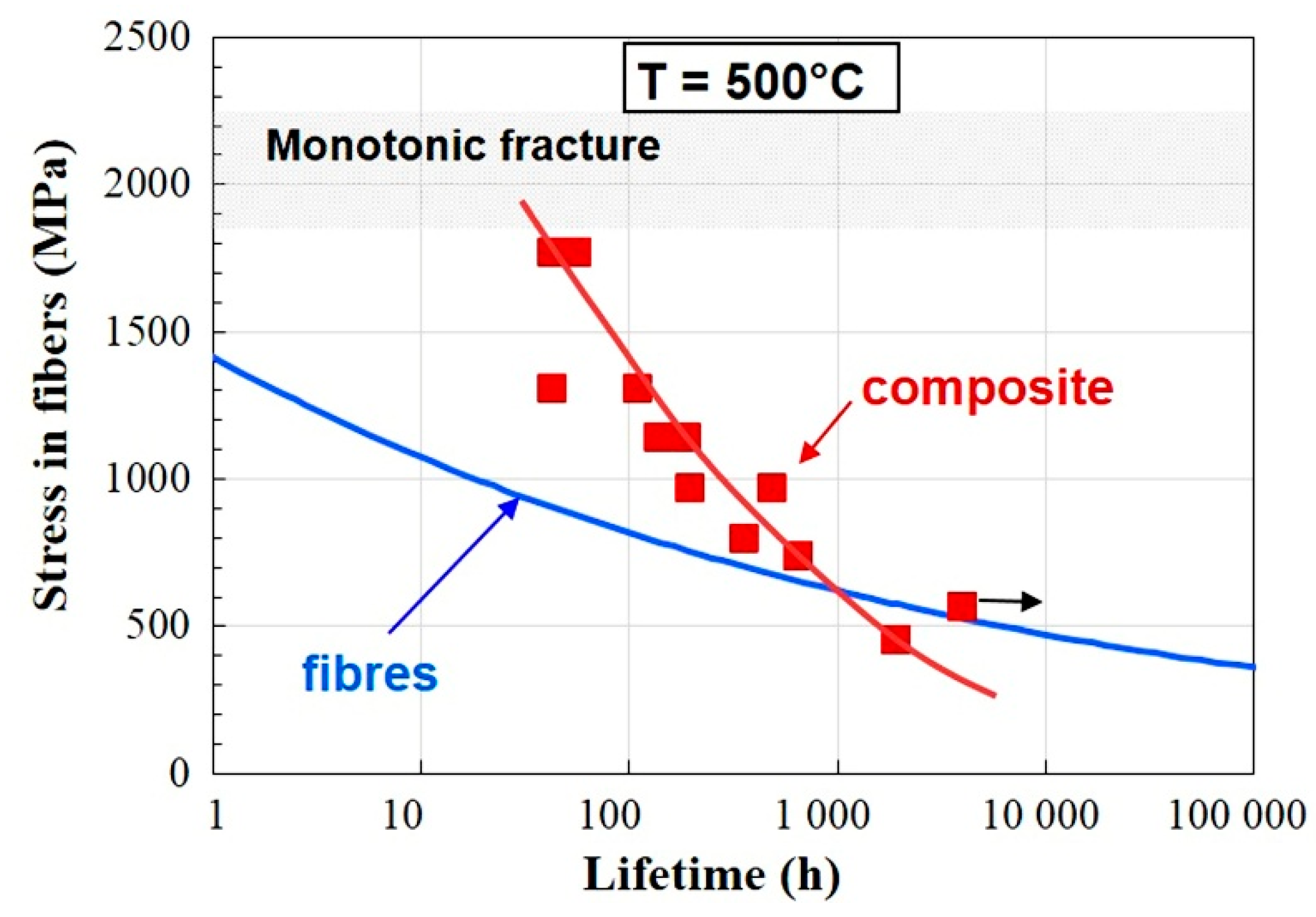
- Maillet, E.; Godin, N.; R’Mili, M.; Reynaud, P.; Lamon, J.; Fantozzi, G. Analysis of acoustic emission release during static fatigue tests at intermediate temperatures on ceramic matrix composites: Towards rupture time prediction. Compos. Sci. Technol. 2012, 72, 1001–1007. [Google Scholar] [CrossRef]
- Godin, N.; Reynaud, P.; R’Mili, M.; Fantozzi, G. Identification of a critical time with acoustic emission monitoring during static fatigue tests on ceramic matrix composites: Towards lifetime prediction. Appl. Sci. 2016, 6, 43. [Google Scholar] [CrossRef]
- Dassios, K.G.; Aggelis, D.G.; Kordatos, E.Z.; Matikas, T.E. Cyclic loading of a SiC-fiber reinforced ceramic matrix composite reveals damage mechanisms and thermal residual stress state. Compos. Part A 2013, 44, 105–113. [Google Scholar] [CrossRef]
- Tracey, J.; Waes, A.; Daly, S. A new experimental approach for in situ damage assessment in fibrous ceramic matrix composites at high temperature. J. Am. Ceram. Soc. 2015, 98, 1896–1906. [Google Scholar] [CrossRef]
- Li, L.B. Damage development in fiber-reinforced ceramic-matrix composites under cyclic fatigue loading using hysteresis loops at room and elevated temperatures. Int. J. Fract. 2016, 199, 39–58. [Google Scholar] [CrossRef]
- Papasalouros, D.; Bollas, K.; Kourousis, D.; Anastasopoulos, A. Acoustic emission tank floor testing: A study on the data-base of tests and follow-up inspections. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Kim, D.H.; Lee, S.B.; Yang, B.S.; Bae, D.M. Structural health monitoring of blast furnace in steel mill using acoustic emission technique. In Progress in Acoustic Emission XVIII; The Japanese Society for Non-Destructive Inspection: Tokyo, Japan, 2016; pp. 37–42. [Google Scholar]
- Seretti, A.; Boyer, L.; Adam, L.; Proust, A. Acoustic emission monitoring of cold forming automated operation on airplane wing panels. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Zielke, R.; Tillmann, W.; Abdulgader, M.; Sievers, N.; Wang, G. Process control of thermal spraying. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Manthei, G.; Alter, C.; Kolling, S. Localization of initial cracks in laminated glass using acoustic emission analysis—Part I. In Proceedings of the 31st European Working Group on Acoustic Emission, Dresden, Germany, 3–5 September 2014. [Google Scholar]
- Ravnik, F.; Grum, J. Identification of machine components cracking with sound emission during steel quenching. In Proceedings of the 32nd European Working Group on Acoustic Emission, Prague, Czech Republic, 7–9 September 2016; pp. 419–431. [Google Scholar]
- Sause, M.G.R. In Situ Monitoring of Fiber-Reinforced Composites; Springer: Berlin, Germany, 2016; 633p. [Google Scholar]
- Asamene, K.; Hudson, L.; Sundaresan, M. Influence on acoustic emission signals in carbon fiber reinforced composites. Ultrasonics 2015, 59, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Schubert, K.; Herrmann, A.S. On attenuation and measurement of Lamb waves in viscoelastic composites. Compos. Struct. 2011, 94, 177–185. [Google Scholar] [CrossRef]
- Ibrahim, M.E. Nondestructive evaluation of thick-section composites and sandwich structures: A review. Compos. Part A 2014, 64, 36–48. [Google Scholar] [CrossRef]
- Schaal, C.; Mal, A. Core-skin disbond detection in a composite sandwich panel using guided ultrasonic waves. ASME J. Nondest. Eval. 2017, 1, 011006. [Google Scholar] [CrossRef]
- Ohtsu, M. (Ed.) Acoustic Emission and Related Non-Destructive Evaluation Techniques in the Fracture Mechanics of Concrete; Woodhead: Cambridge, UK, 2015; 318p. [Google Scholar]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G. Multidimensional approaches to study of Italian seismicity. In Acoustic Emission and Critical Phenomena: From Structural Mechanics to Geophysics; CRC Press: Boca Raton, FL, USA, 2008; pp. 245–270. [Google Scholar]
- De Santis, S.; Tomor, A.K. Laboratory and field studies on the use of acoustic emission for masonry bridges. NDT E Int. 2013, 55, 64–74. [Google Scholar] [CrossRef]
- Verstrynge, E.; De Wilder, K.; Drougkas, A.; Voet, E.; Van Balen, K.; Wevers, M. Crack monitoring in historical masonry with distributed strain and acoustic emission sensing techniques. Constr. Build. Mater. 2018, 162, 898–907. [Google Scholar] [CrossRef]
- Hamstad, M.A. Some observations on Rayleigh waves and acoustic emission in thick steel plates. J. Acoust. Emiss. 2009, 27, 114–136. [Google Scholar]
| Ref. No. 1 | Material | Axis 2 | η11 | η22 | η33 | η44 | η55 | η66 | H12 | η13 | η23 | Freq (MHz) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [60] | Epoxy | 0.01 | 0.01 | 0.011 | ||||||||
| [49] | PMMA | 0.023 | 0.056 | 0.026 | 0.046 | 0.3 | ||||||
| [49] | GFRP-UD | 3 | 0.047 | 0.043 | 0.033 | 0.050 | 0.038 | 0.033 | 0.036 | 0.3 | ||
| [61] | GFRP-UD | 3 | 0.051 | 0.038 | 0.056 | 0.100 | 0.070 | 0.091 | 0.014 | 0.106 | 0.05–0.2 | |
| [61] | CFRP-UD | 3 | 0.027 | 0.05 | 0.075 | 0.06 | 0.063 | 0.11 | 0.037 | 0.1 | 0.05–0.2 | |
| [62] | CFRP-UD | 1 | 0.061 | 0.024 | 0.046 | 0.084 | 0.062 | 0.055 | 0.114 | 0.105 | 0.029 | |
| [63] | CFRP-UD | 1 | 0.086 | 0.045 | 0.06 | 0.037 | 0.033 | 0.005–0.2 | ||||
| [64] | CFRP-UD | 1 | 0.024 | 0.043 | 0.041 | 0.032 | 0.056 | 0.093 | 0.143 | 0.074 | 0.2–0.93 | |
| [64] | CFRP-QI | 1 | 0.041 | 0.067 | 0.034 | 0.045 | 0.044 | 0.068 | 0.071 | 0.016 | 0.2–0.93 | |
| [65,66] | CFRP XP | 1 | 0.020 | 0.018 | 0.001 | 0.010 | 0.017 | 0.026 | 0.018 | 0.016 | 0.001 | 0.01–1 |
| [65,66] | CFRP-UD | 1 | 0.015 | 0.099 | 0.099 | 0.010 | 0.045 | 0.045 | 0.015 | 0.015 | 0.261 | 0.01–1 |
| Material | Type | α-p 1 | α-t 1 | Method 2 | Condition 3 | Reference | Ref. No. |
|---|---|---|---|---|---|---|---|
| Al | 1100 (2S) | 0.16 (5), 1(10) | Q | Hikata (1957) | [82] | ||
| Al | Al (99.99%) | 28 (6.3) | E | Anneal 200 °C 1 h | Hirao (2003) | [76] | |
| 2017 (17ST) | 5.6 (5) | 13.1 (4) | Q | GS: 0.23 mm | Mason (1947) | [26] | |
| 2017 (17ST) | 2.6 (5) | 7.9 (5) | Q | GS: 0.13 mm | Mason (1947) | [26] | |
| Cu | Cu (99.99%) | 88 (2.3) | E | GS: 35 µm | Hirao (2003) | [76] | |
| Brass (360) | 45.7 (10) | 286 (5) | Q | GS: 49 µm | Papadakis (1965) | [43] | |
| Mg | -- | 32.3 (10) | Q | GS: 0.2 mm | Mason (1948) | [83] | |
| AZ31 (FS1) | 6.9 (10) | 4.1 (10) | Q | GS: 0.12 mm | Mason (1948) | [83] | |
| Nb | Nb | 280–510 (5) | GS: 43–124 µm | Zeng (2010) | [84] | ||
| Ni | Grade A | 115 (3.5) | 240 (2) | Q | GS: 55 µm | Papadakis (1965) | [43] |
| Waspaloy | 51 (4.5) | E | solution + aged | Ohtani (2004) | [75] | ||
| Fe | Fe-0.004%C | 339 (8.2) | GS: 50 µm | Ahn (2000) | [85] | ||
| Fe-0.02%C | 300–1350 (10) | GS: 18–137 µm | Smith (1981) | [70] | |||
| Fe-0.06%C | 46–101 (5) | GS: 22–30 µm | Klinman (1980) | [68] | |||
| Steel | Fe-0.15%C | 33–60 (5) | GS: 14–40 µm | Klinman (1980) | [68] | ||
| Fe-0.15%C | 116 (5) | E | GS: 49 µm | Hirao (2003) | [76] | ||
| Fe-0.2%C | 220–340 (5) | GS: 120–290 µm | Ahn (2000) | [85] | |||
| Fe-0.25%C | 45–91 (5) | GS: 12–29 µm | Klinman (1980) | [68] | |||
| Fe-low C | 83–237 (5) | GS: 50–120 µm | Klinman (1980) | [68] | |||
| Fe-0.4%C | 53 (5) | GS: 12–20 µm | Klinman (1980) | [68] | |||
| Fe-0.4%C | 86–127 (5) | GS: 50–65 µm | Klinman (1980) | [68] | |||
| 4150 | 78.7 (10) | RHC: 14 | Roederick (1952) | [27] | |||
| 4150 | 19.7 (20) | RHC: 61 | Roederick (1952) | [27] | |||
| 4145 | 14.5 (5) | Q | VHN: 746 | Kamigaki (1957) | [28] | ||
| 4145 | 22.5 (5) | Q | VHN: 265 | Kamigaki (1957) | [28] | ||
| 3140 | 21.2 (10) | Q | RHC: 45 | Papadakis (1960) | [30] | ||
| 4150 | 21.2 (10) | Q | RHC: 54 | Papadakis (1960) | [30] | ||
| 4150 | 12.2 (10) | Q | pearlie-bainite | Papadakis (1964) | [29] | ||
| 4150 | 6.4 (20) | Q | martensite (M) | Papadakis (1964) | [29] | ||
| 4150 | 11.0 (20) | Q | tempered M | Papadakis (1964) | [29] | ||
| 1Cr-Mo-V | 33 (5) | E | tempered M | Ohtani (2002) | [77] | ||
| 2.25Cr-1Mo | 25.6 (3.9) | E | annealed | Ohtani (2006) | [78] | ||
| 1075 | 10 (5) | Q | GSc: 27 µm | Kamigaki (1957) | [28] | ||
| 1075 | 35 (5) | Q | GSc: 38 µm | Kamigaki (1957) | [28] | ||
| 1075 | 68 (5) | Q | GSc: 68 µm | Kamigaki (1957) | [28] | ||
| 1075 | 174 (5) | Q | GSc: 174 µm | Kamigaki (1957) | [28] | ||
| 1075 | 73.5 (10) | Q | VHN: 696 | Kamigaki (1957) | [28] | ||
| 1075 | 90 (10) | Q | VHN: 274 | Kamigaki (1957) | [28] | ||
| 1075 | 174 (10) | Q | VHN: 270 | Kamigaki (1957) | [28] | ||
| 1080 | 19.2–33.9 (10) | Q | spheroidized | Latiff (1974) | [83] | ||
| 1080 | 230–290 (5) | normalized | Ahn (2000) | [85] | |||
| Rail steel | 26–150 (10) | Quenched | Du (2014) | [86] | |||
| 52100 | 2.4–22 (10) | 6.8–44 (10) | Q | RHC: 55–61 | Papadakis (1970) | [72] | |
| Plain C | 150–1000 (15) | GS: 15–33 µm | Smith (1983) | [71] | |||
| Plain C | 150–1690 (10) | GS: 10–31 µm | Klinman (1981) | [69] | |||
| 316L SS | 230 (5), 360 (10) | GS: 37 µm | Wan (2017) | [87] | |||
| 316L SS | 5.0 (5) | E | GS: 19.5 µm | Ohtani (2005) | [79] | ||
| 403 SS | 26 (10) | Q | GSc: 25 µm | Nadeau (1985) | [88] | ||
| 416 SS | 27.8 (5) | 159 (5) | Q | GS: 30 µm | Papadakis (1965) | [43] | |
| 416 SS | 348 (10) | Q | GS: 30 µm | Papadakis (1965) | [43] | ||
| 440C austenitic SS | 313 (5) | 814 (5) | Q | GS: 50 µm | Papadakis (1965) | [43] | |
| Cast austenitic SS | 192 (0.5), 174 (1) | columnar 2.5 mm | Ramuhalli (2009) | [89] | |||
| Cast austenitic SS | 264 (0.5), 272 (1) | equiaxed 2.3 mm | Ramuhalli (2009) | [89] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ono, K. Review on Structural Health Evaluation with Acoustic Emission. Appl. Sci. 2018, 8, 958. https://doi.org/10.3390/app8060958
Ono K. Review on Structural Health Evaluation with Acoustic Emission. Applied Sciences. 2018; 8(6):958. https://doi.org/10.3390/app8060958
Chicago/Turabian StyleOno, Kanji. 2018. "Review on Structural Health Evaluation with Acoustic Emission" Applied Sciences 8, no. 6: 958. https://doi.org/10.3390/app8060958
APA StyleOno, K. (2018). Review on Structural Health Evaluation with Acoustic Emission. Applied Sciences, 8(6), 958. https://doi.org/10.3390/app8060958





