Variable Tap-Length Algorithm with Mixed Parameter
Abstract
Featured Application
Abstract
1. Introduction
2. Variable Tap-Length Algorithm
2.1. Least Mean Square Algorithm
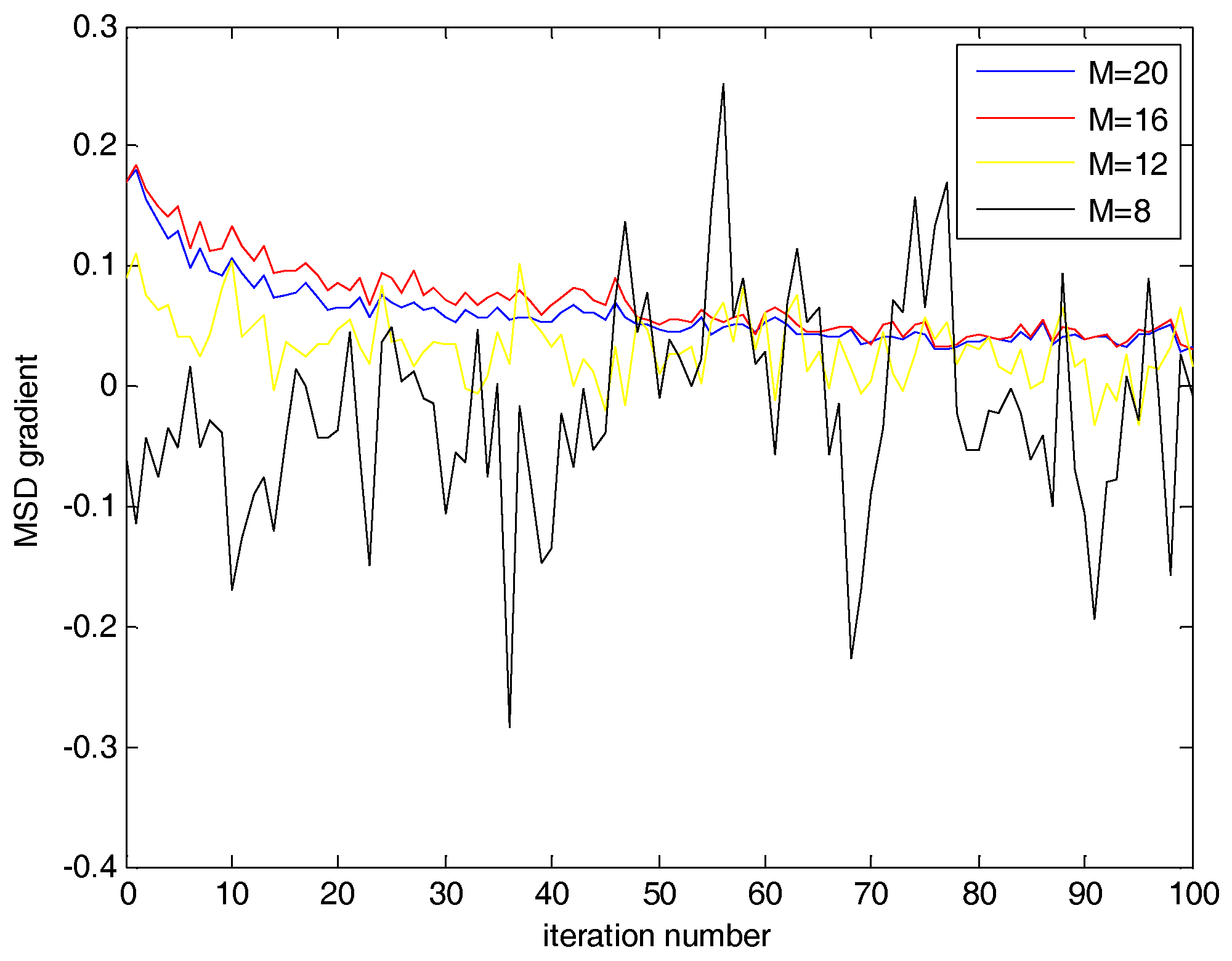
2.2. Mean Square Deviation Gradient
2.3. Fractional Variable Tap-Length Algorithm
3. Mixed Parameter Fractional Variable Tap-Length Algorithm
4. Performance Analysis
4.1. Parameter Analysis
4.2. Performance Analysis
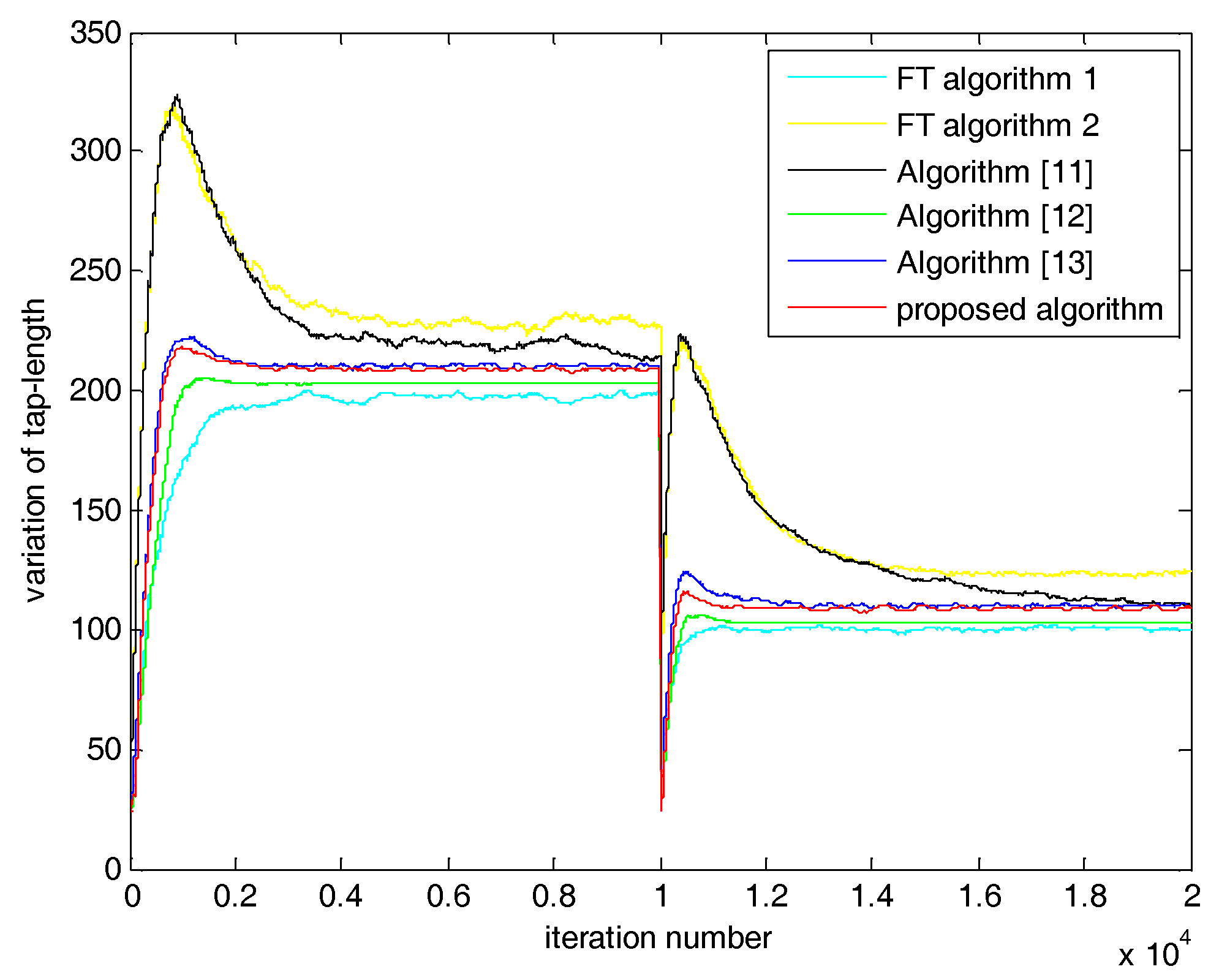
5. Simulations and Results
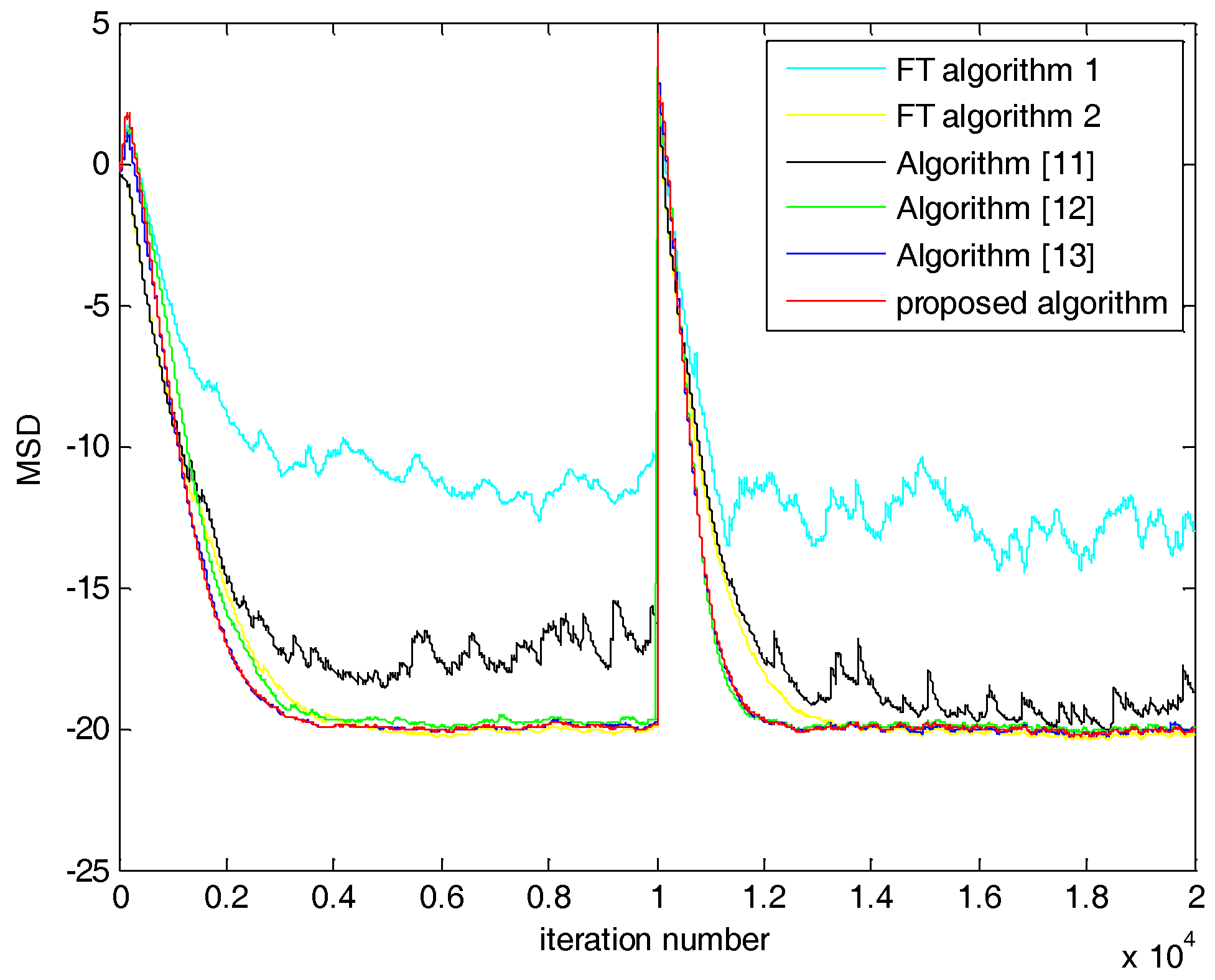
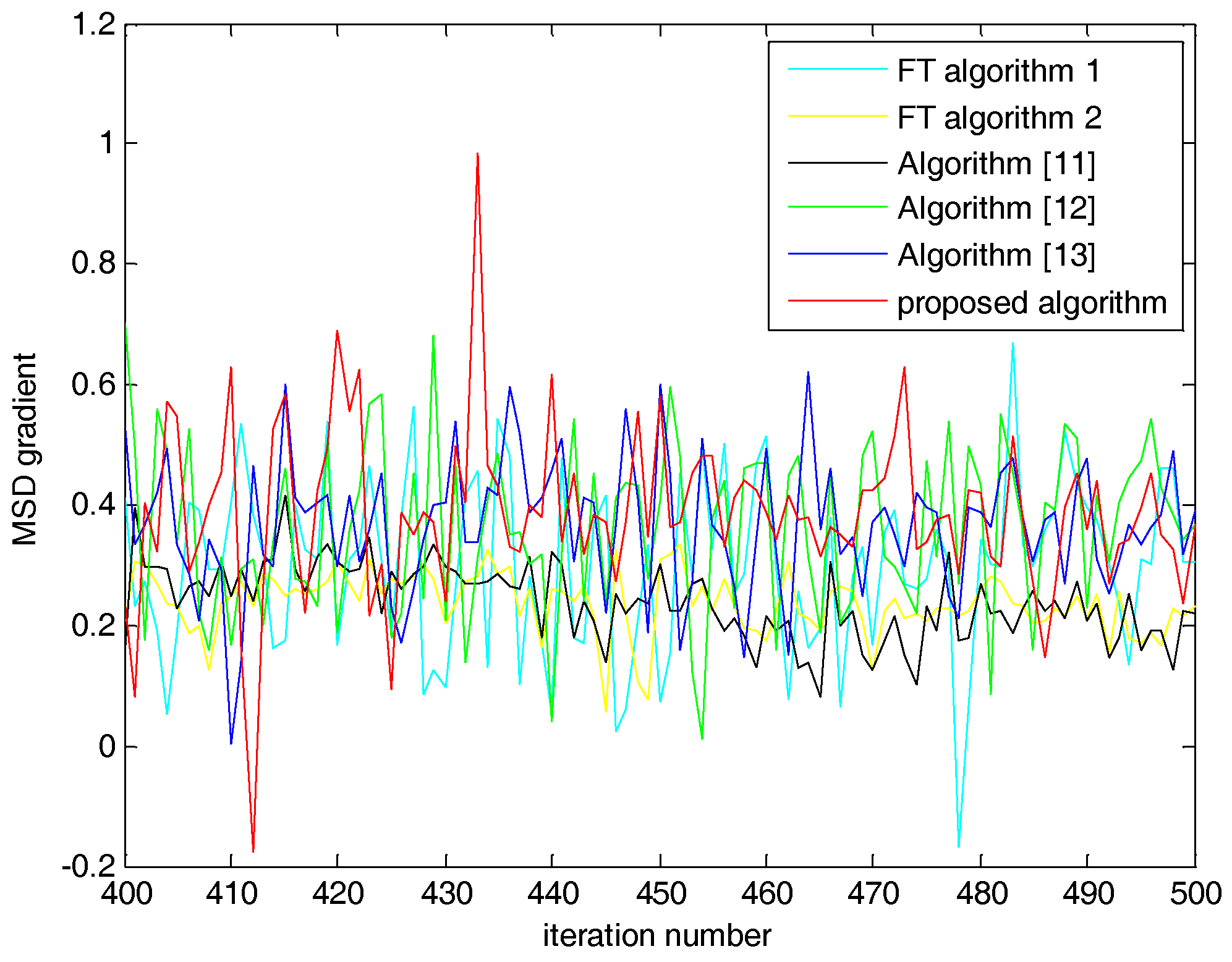
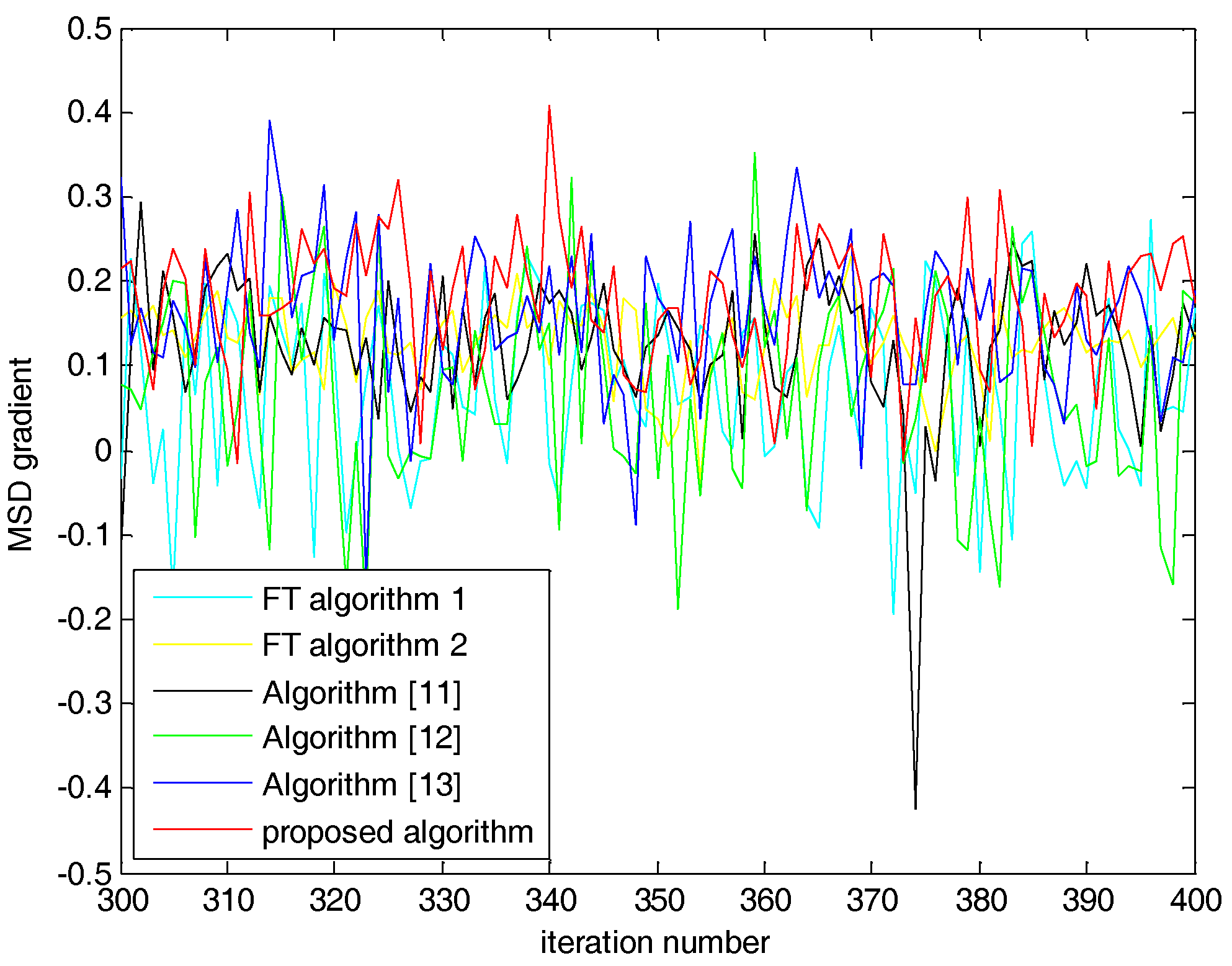
5.1. Case 1: SNR = 20 dB
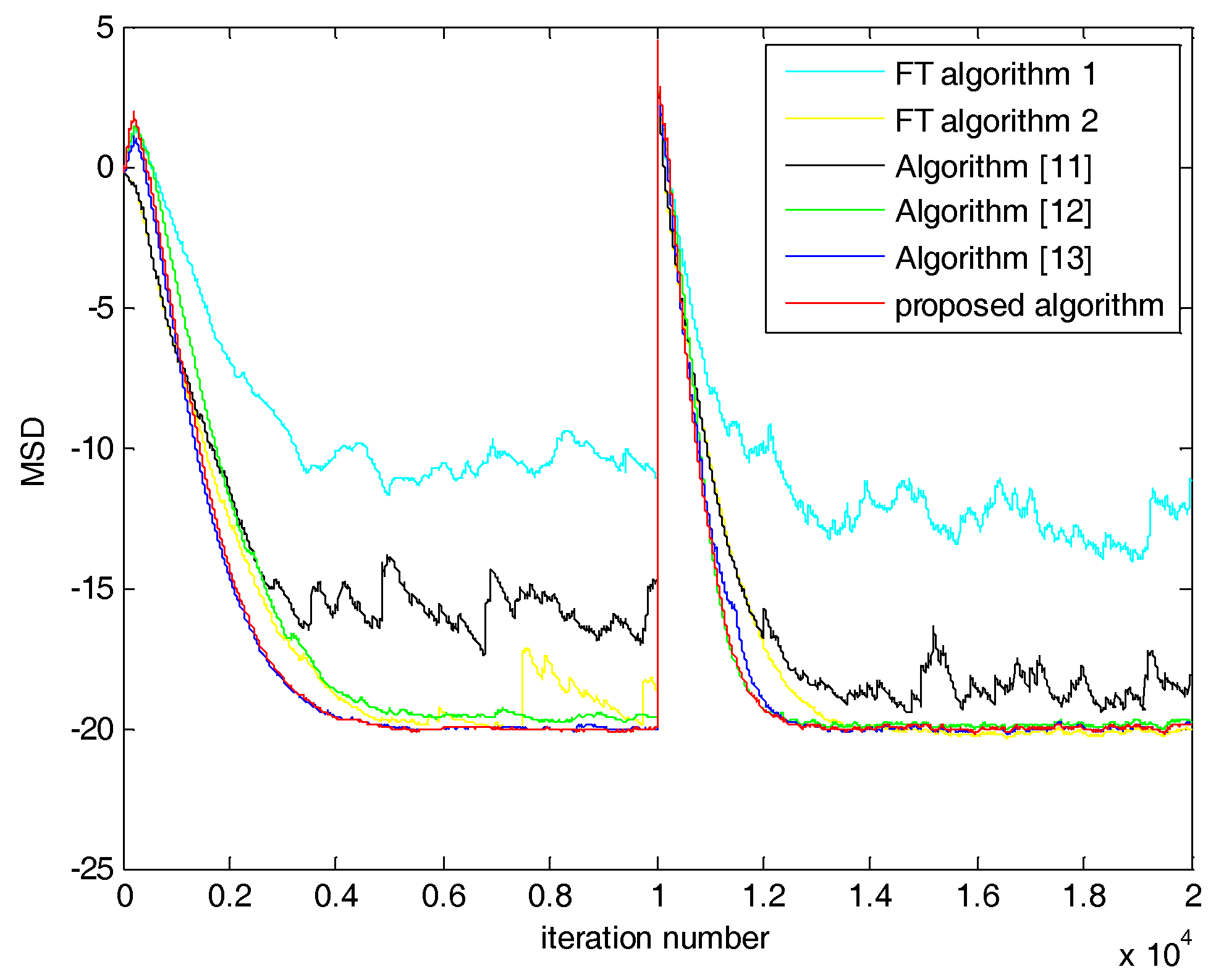
5.2. Case 2: SNR = 0 dB
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magliacano, D.; Viscardi, M.; Dimino, I.; Concilio, A. Active vibration control by piezoceramic actuators of a car floor panel. In Proceedings of the 23rd International Congress on Sound and Vibration (ICSV), Athens, Greece, 10–14 July 2016. [Google Scholar]
- Qu, Y.; He, D. An adaptive remaining useful life prediction method for hybrid ceramic bearing. In Proceedings of the 2016 International Conference on Mechanics Design, Manufacturing and Automation (MDM 2016), Suzhou, China, 14–15 May 2016. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Gu, Y.; Tang, K.; Cui, H. LMS algorithm with gradient descent filter length. IEEE Signal Process. Lett. 2004, 11, 305–307. [Google Scholar] [CrossRef]
- Riera-Palou, F.; Noras, J.M.; Cruickshank, D.G.M. Linear equalisers with dynamic and automatic length selection. Electron. Lett. 2001, 37, 1553–1554. [Google Scholar] [CrossRef]
- Yu, G.; Cowan, C.F.N. An LMS style variable tap-length algorithm for structure adaptation. IEEE Trans. Signal Process. 2005, 53, 2400–2407. [Google Scholar]
- Zhang, Y.; Li, N.; Chambers, J.A.; Sayed, A.H. Steady-state performance analysis of a variable tap-length LMS algorithm. IEEE Trans. Signal Process. 2008, 56, 839–845. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.; Zhao, Y.; Hao, Y. An improved variable tap-length LMS algorithm. Signal Process. 2009, 89, 908–912. [Google Scholar] [CrossRef]
- Xu, D.J.; Yin, B.; Wang, W.; Zhu, W. Variable tap-length LMS algorithm based on adaptive parameters for TDL structure adaption. IEEE Signal Process. Lett. 2014, 21, 809–813. [Google Scholar]
- Mayyas, K.; Abuseba, H.A. A new variable length NLMS adaptive algorithm. Digit. Signal Process. 2014, 34, 82–91. [Google Scholar] [CrossRef]
- Han, Y.; Wang, M.; Zhao, B. Variable tap-length NLMS algorithm with adaptive parameter. IEEE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 100, 1720–1723. [Google Scholar] [CrossRef]
- Han, Y.; Wang, M.; Liu, M. An improved variable tap-length algorithm with adaptive parameters. Digit. Signal Process. 2018, 74, 111–118. [Google Scholar] [CrossRef]
- Almeida, S.J.M.D.; Bermudez, J.C.M.; Bershad, N.J.; Costa, M.H. A statistical analysis of the affine projection algorithm for unity step size and autoregressive inputs. IEEE Trans. Circ. Syst. 2005, 52, 1394–1405. [Google Scholar] [CrossRef]
- Mayyas, K. Performance analysis of deficient length LMS adaptive algorithm. IEEE Trans. Signal Process. 2005, 53, 2727–2734. [Google Scholar] [CrossRef]
- Shin, H.C.; Sayed, A.H. Mean-square performance of a family of affine projection algorithms. IEEE Trans. Signal Process. 2004, 52, 90–102. [Google Scholar] [CrossRef]

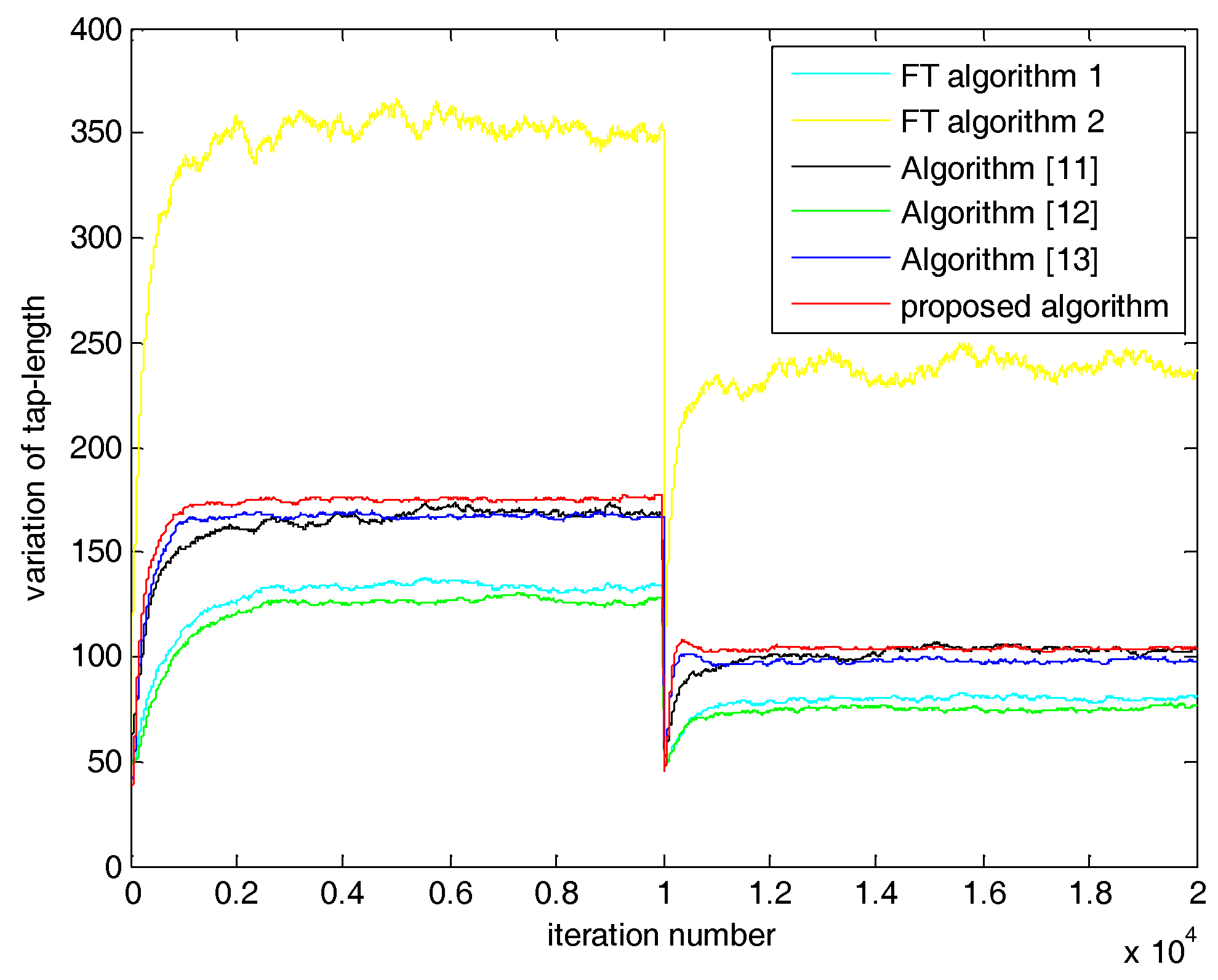
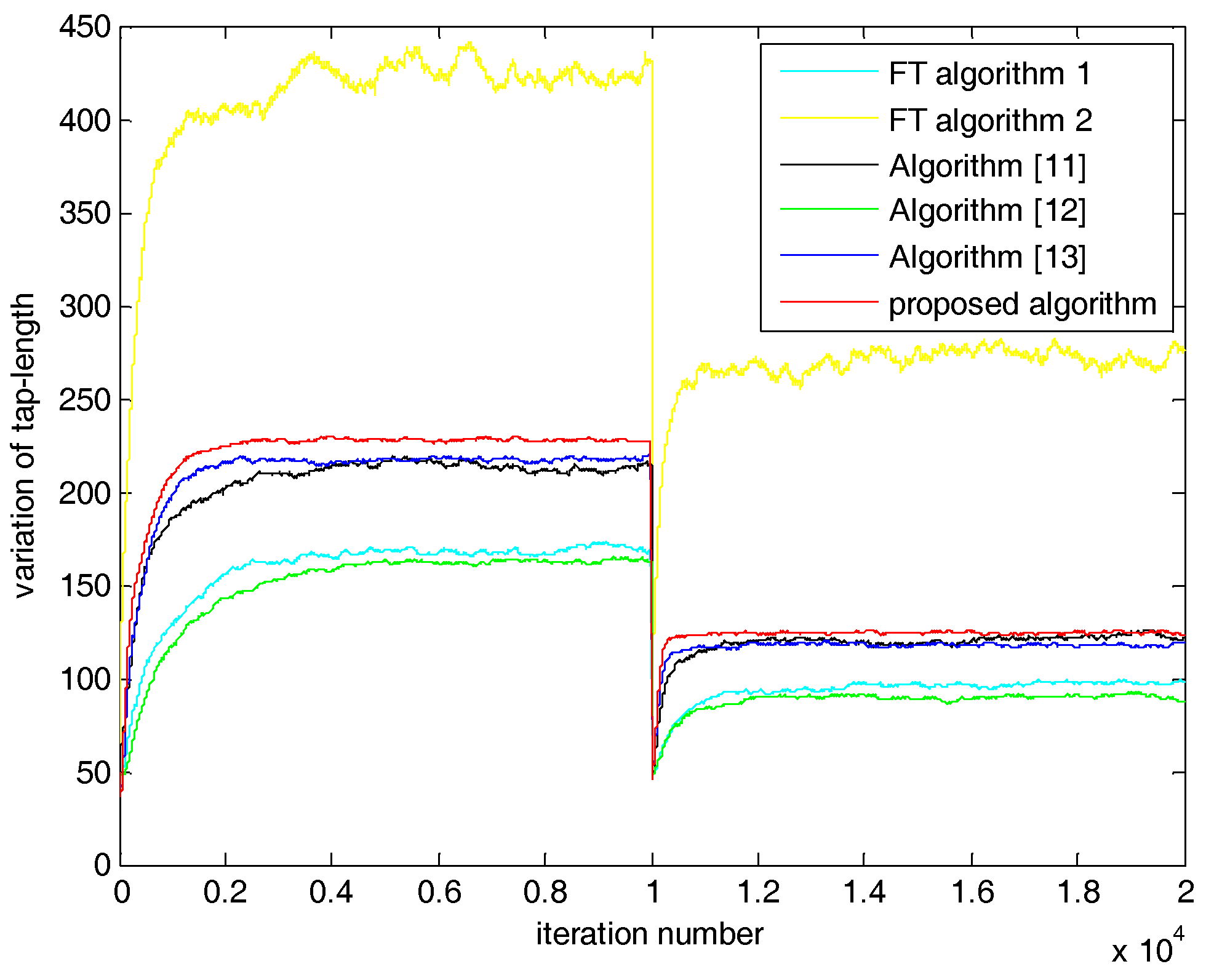
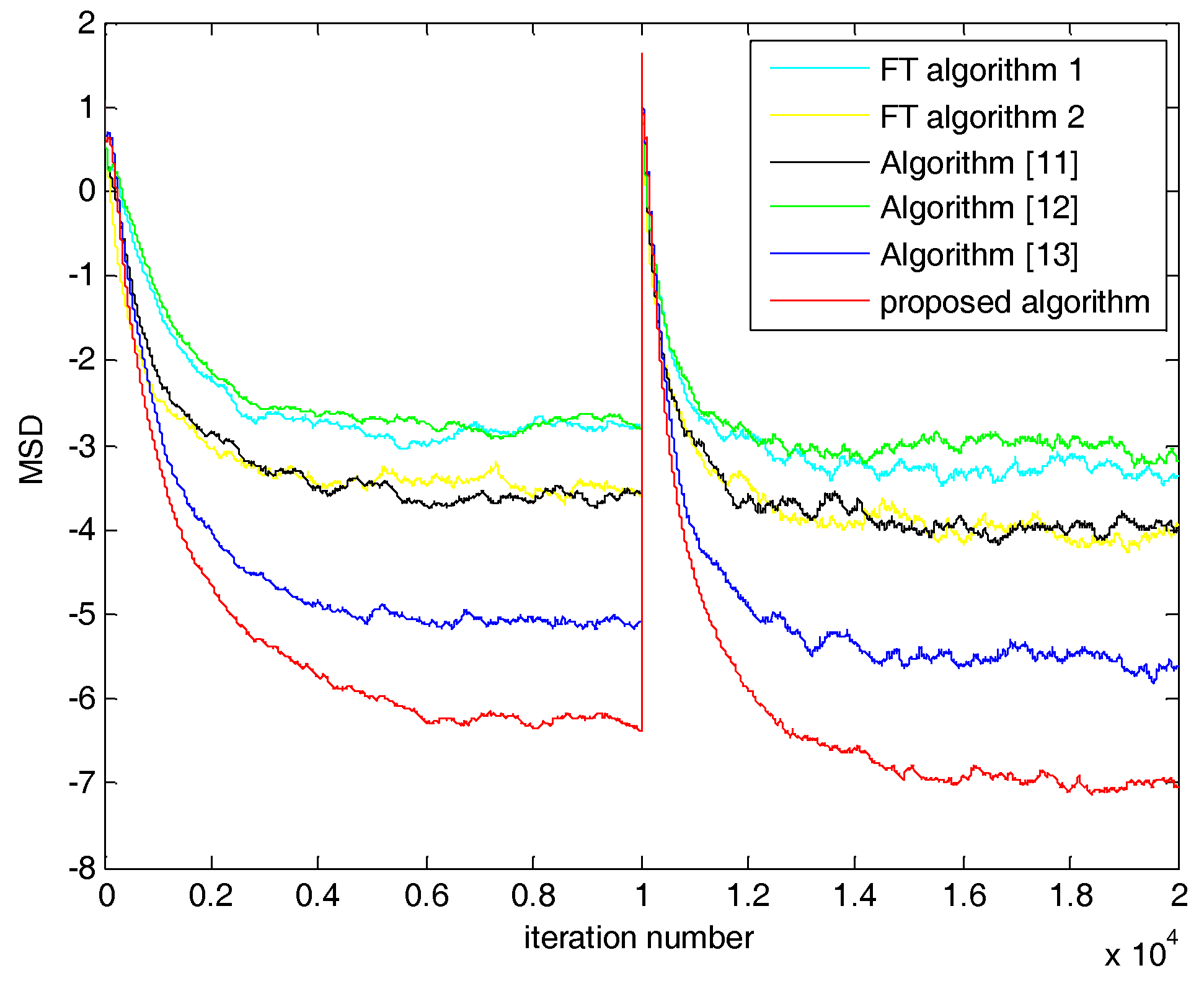
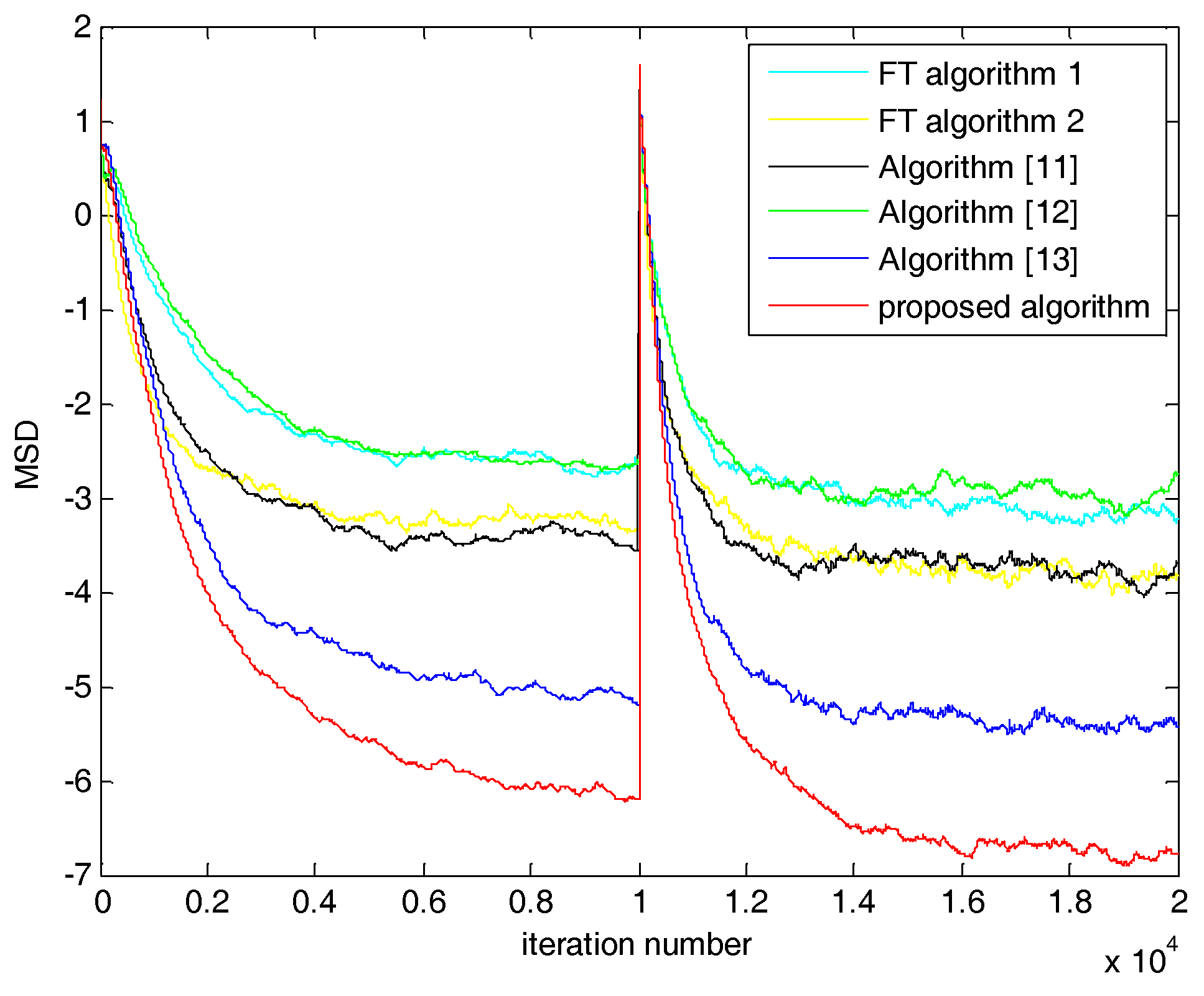
| Algorithm | SNR = 20 dB | SNR = 0 dB |
|---|---|---|
| General | ,,, , , , , , | , ,, , , , , , |
| FT Algorithm 1 | , | , |
| FT Algorithm 2 | , | , |
| Algorithm [11] | , , | , , |
| Algorithm [12] | , , C = 0.02 | ,, C = 0.02 |
| Algorithm [13] | , , , C = 0.5, , | , , , C = 0.5, , |
| Proposed algorithm | , , , , C = 0.5, , | , , , , C = 0.5, , |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Wang, M.; Lu, Y. Variable Tap-Length Algorithm with Mixed Parameter. Appl. Sci. 2018, 8, 939. https://doi.org/10.3390/app8060939
Han Y, Wang M, Lu Y. Variable Tap-Length Algorithm with Mixed Parameter. Applied Sciences. 2018; 8(6):939. https://doi.org/10.3390/app8060939
Chicago/Turabian StyleHan, Yufei, Mingjiang Wang, and Yun Lu. 2018. "Variable Tap-Length Algorithm with Mixed Parameter" Applied Sciences 8, no. 6: 939. https://doi.org/10.3390/app8060939
APA StyleHan, Y., Wang, M., & Lu, Y. (2018). Variable Tap-Length Algorithm with Mixed Parameter. Applied Sciences, 8(6), 939. https://doi.org/10.3390/app8060939





