Evaluation of the Change in Undrained Shear Strength in Cohesive Soils due to Principal Stress Rotation Using an Artificial Neural Network

Abstract

This paper presents a method describing the application of artificial neural networks to evaluate the change in undrained shear strength in cohesive soils due to principal stress rotation. For analysis, the results of torsional shear hollow cylinder (TSHC) tests were used. An artificial neural network with an architecture of 7–6–1 was able to predict the real value of normalized undrained shear strength, τ_fu/σ’_v, based on soil type, over-consolidation ratio (OCR), plasticity index, I_P, and the angle of principal stress rotation, α, with an average relative error of around ±3%, and a single maximum value of relative error around 6%.

1. Introduction

Undrained shear strength is one of the basic parameters that characterizing the mechanical properties of cohesive soils. The value of this parameter depends on soil type, consistency, stress state, history, and also depends on factors such as loading type and loading mode [1,2]. The loading of subsoil changes the stress state of the soil, and thereby causes principal stress rotation in comparison with the soil’s initial state obtained during the sedimentation process [3]. Research performed in a torsional shear hollow cylinder apparatus (TSHCA), both on undisturbed and reconstituted cohesive soils, has shown that principal stress rotation has a significant impact on the value of undrained shear strength. Undrained shear strength had a major principal stress value in the σ₁ horizontal, which was about 0.70 of the value of that of the vertical σ₁, as previously observed in the literature [4,5,6,7,8]. Therefore, when determining the bearing capacity of the subsoil, changes resulting from this phenomenon should be taken into account. Test investigations that determine the impact of principal stress rotation on the undrained shear strength of subsoil are costly and time-consuming. Hence, other methods to evaluate the change in undrained shear strength are used.

The impact of principal stress rotation on undrained shear strength may be estimated using the relationship proposed by Bishop [9]:

$$C_u=C_{uV}·\left(1-a_B·si{n}^2\theta \right)·\left(1-b_B·si{n}^{2}2\theta \right),$$

(1)

where C_uV is the undrained shear strength with a vertical direction of applied stress, a_B and b_B are empirical coefficients, and $\theta$ is the inclination of major principal stress with respect to the vertical axis.

In the Bishop relationship, only undrained shear strength with a vertical direction of applied stress is determined in the tests, while the change in undrained shear strength depends on empirical parameters.

Kulhavy and Mayne [10] proposed a systematic framework to estimate normalized undrained shear strength as a function of normalized undrained shear strength, under an isotropically-consolidated undrained compression test with a strain rate equal to 1%/h on normally-consolidated clay. The following dimensionless modifiers were also taken into account: test mode, over-consolidation ratio, strain rate. Ching and Phoon [11] constructed a multivariate probability distribution of undrained shear strength from various test procedures, based on a large clay database. This multivariate distribution provided an estimate of normalized undrained shear strength based on four factors: test mode, over-consolidation ratio, strain rate, and plasticity. Houlsby and Houlsby [12] performed a statistical fitting of undrained strength data using Bayesian statistical methods. The presented approach allowed the fitting of a design profile to a set of measurements of undrained shear strength.

Artificial neural networks (ANNs) are tools of information technology, often used in science and various fields of technology for modeling complex phenomena (e.g., [13,14,15,16]). ANNs are alternatively used for statistical analysis methods, as they are often more useful compared to traditional methods [17].

Reviews of the application of ANNs in civil engineering were presented by Adeli [18], Ghaboussi [19], and Rojas [20]. Waszczyszyn [21,22] presented applications of ANNs in various subjects: analysis of regression problems, hybrid computational systems, development of ANNs, Bayesian neural networks (BNNs), principal component analysis (PCA), and recurrent cascade neural networks (RCNNs). Rafiq et al. [23] provided guidelines and examples of engineering applications of three types of neural networks: multilayer perceptrons (MLPs), radial basis function (RBF) networks, and normalized RBF (NRBF) networks.

In geotechnical engineering, ANNs have been used to analyze many issues, as reviewed by Dihoru et al. [24], Pichler et al. [25], Rafiq et al. [23], Shahin et al. [26,27], Tian et al. [28], Sulewska [29], and Zhou et al. [30]. Constitutive modeling of soils in triaxial tests, based on neural networks, were carried out by Basheer [31], Ellis et al. [32], Fu et al. [33], Najjar and Huang [34], Penumadu and Zhao [35], and Sidarta and Ghaboussi [36]. Lee et al. [37] presented neural network models for evaluating unsaturated shear strength. The use of ANNs for the prediction of the lateral earth pressure ratio, K_o, based on a dilatometer test was shown by Das and Basudhar [38], and the prediction of undrained shear strength was shown by Byeon et al. [39] and Lee et al. [37]. However, artificial neural networks have not been applied to the evaluation of the change in undrained shear strength in cohesive soils due to principal stress rotation. For this purpose, a series of undrained shear strength tests in a torsional shear hollow cylinder apparatus, both on undisturbed and reconstituted cohesive soil samples, was carried out.

2. Materials and Methods

Laboratory tests to determine undrained shear strength were performed in the Water Center Laboratory at the Warsaw University of Life Sciences (SGGW) using the torsional shear hollow cylinder apparatus (Figure 1). Tests were carried out on undisturbed (U) and reconstituted (R) soil samples of clay (Cl(U)), sandy silty clay (sasiCl(U) and sasiCl(R)), and clayey sand (clSa(R)). The clay samples had an over-consolidation ratio (OCR) of 3.5 and a plasticity index I_P of 77.6%. The samples of sandy silty clay had an OCR of 2.7 and an I_P of 34.7%, whereas the samples of clayey sand had an OCR of 8.0 and an I_P of 10.5%. The index properties of the tested soils are presented in

Table 1. Index properties of the tested soils [40,41].

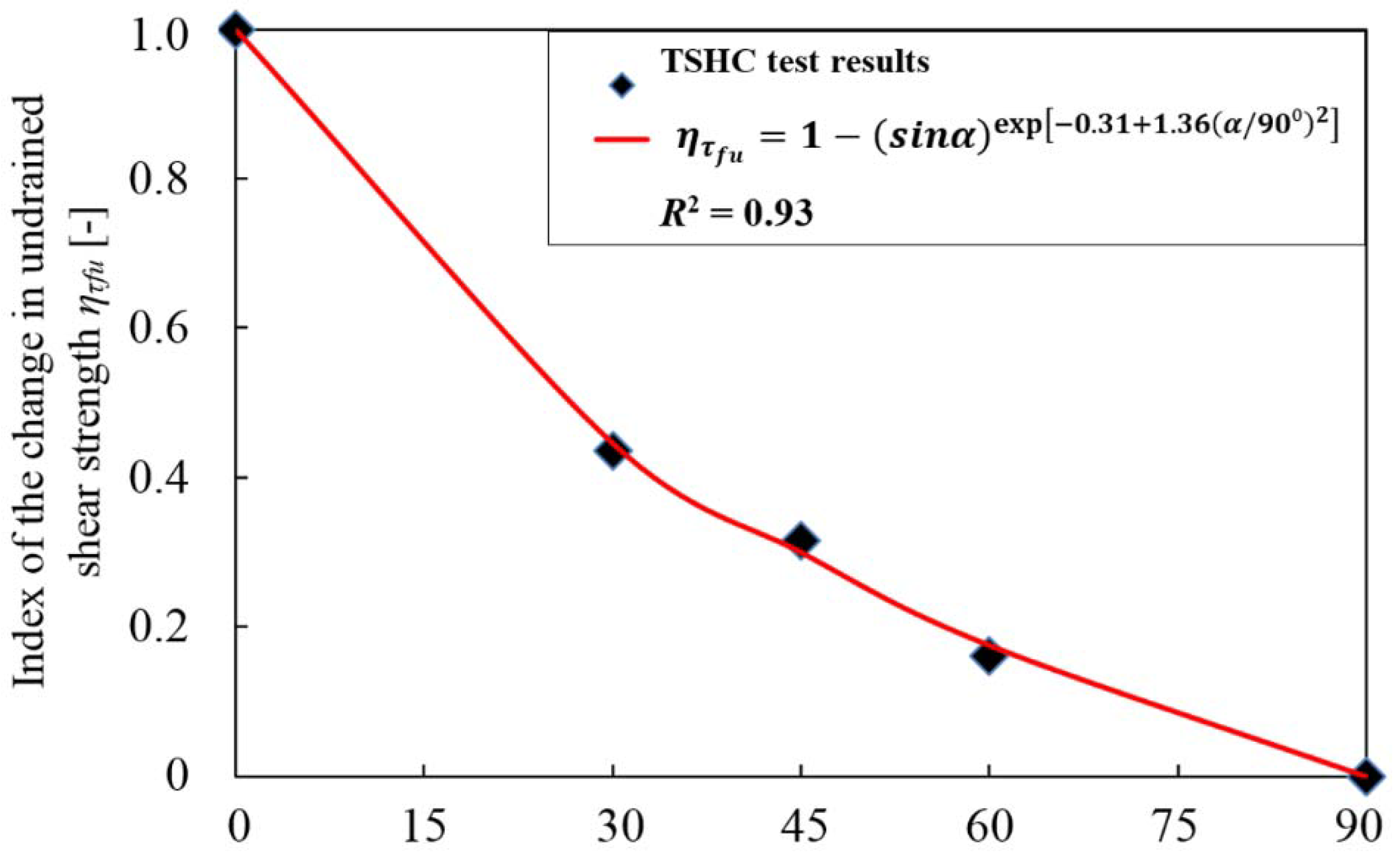
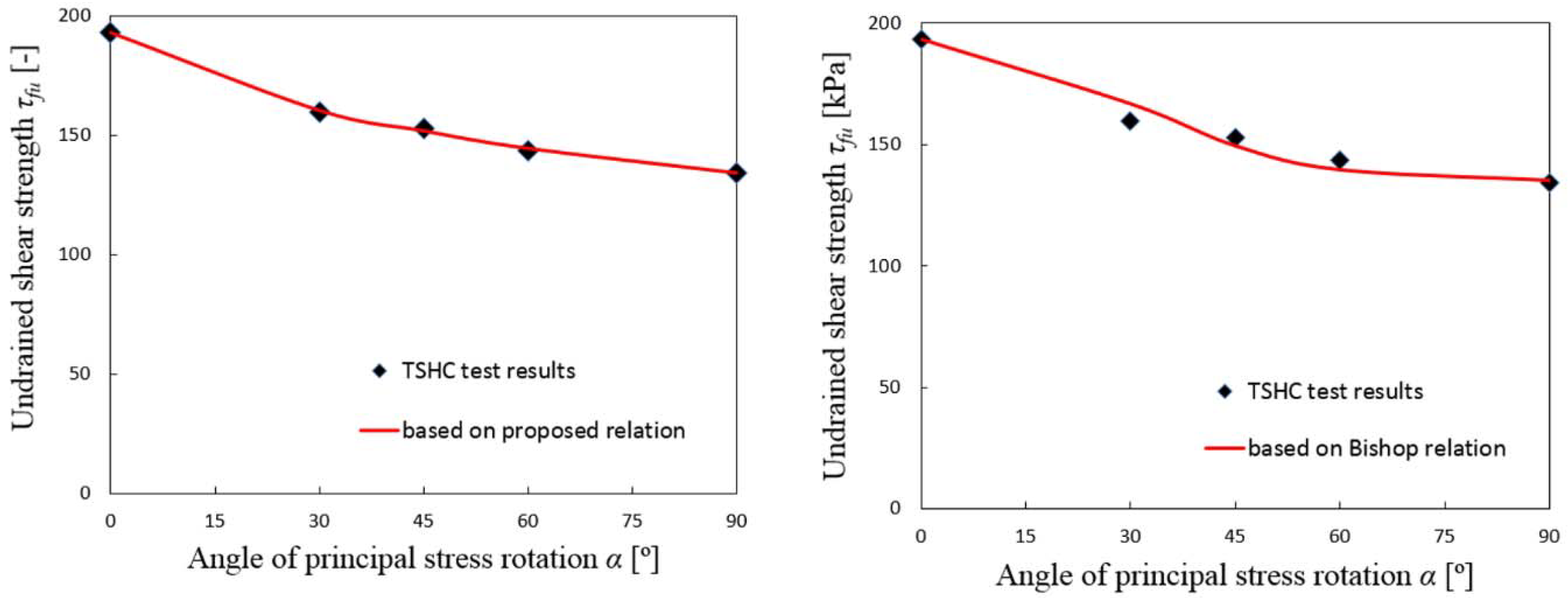
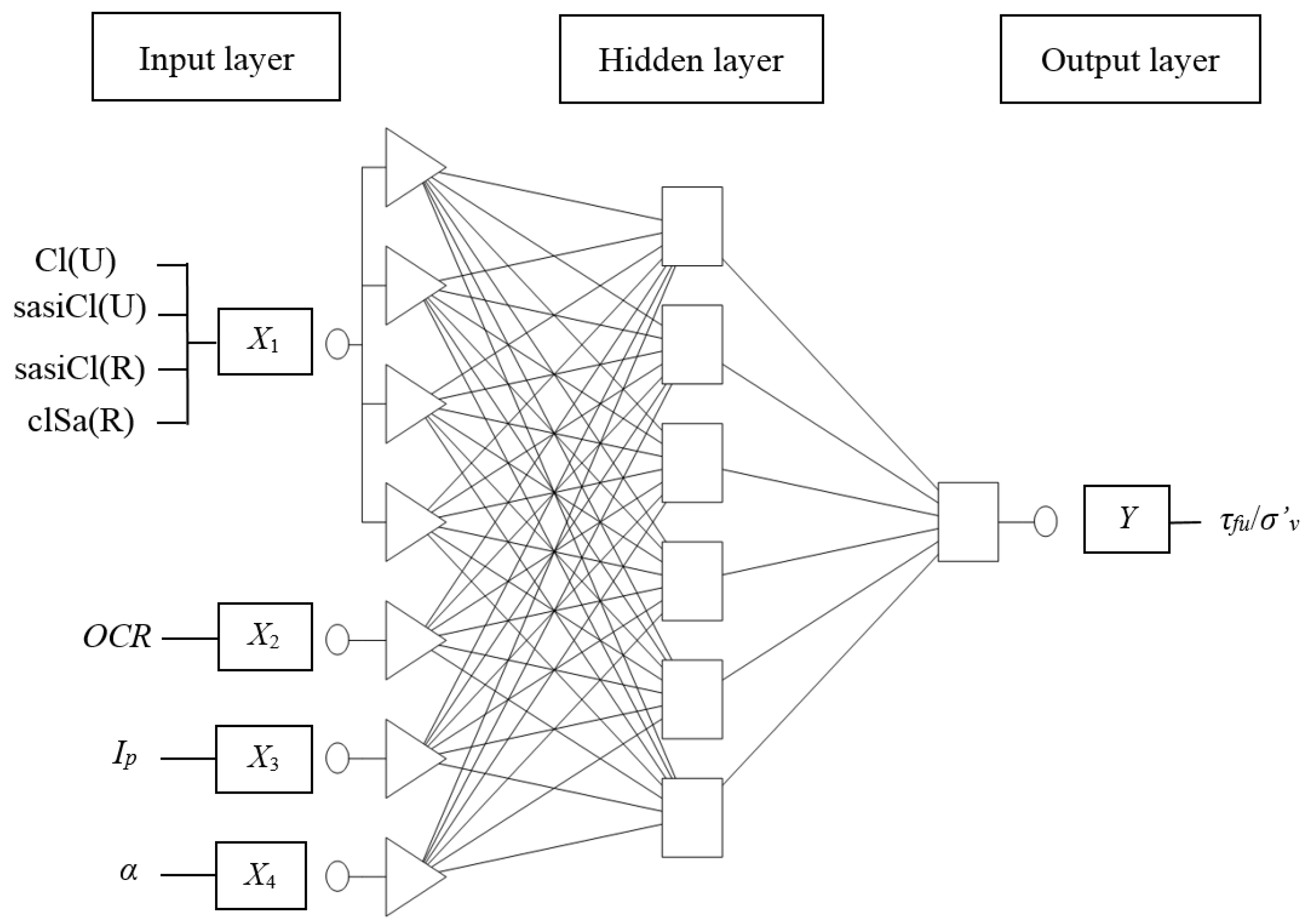
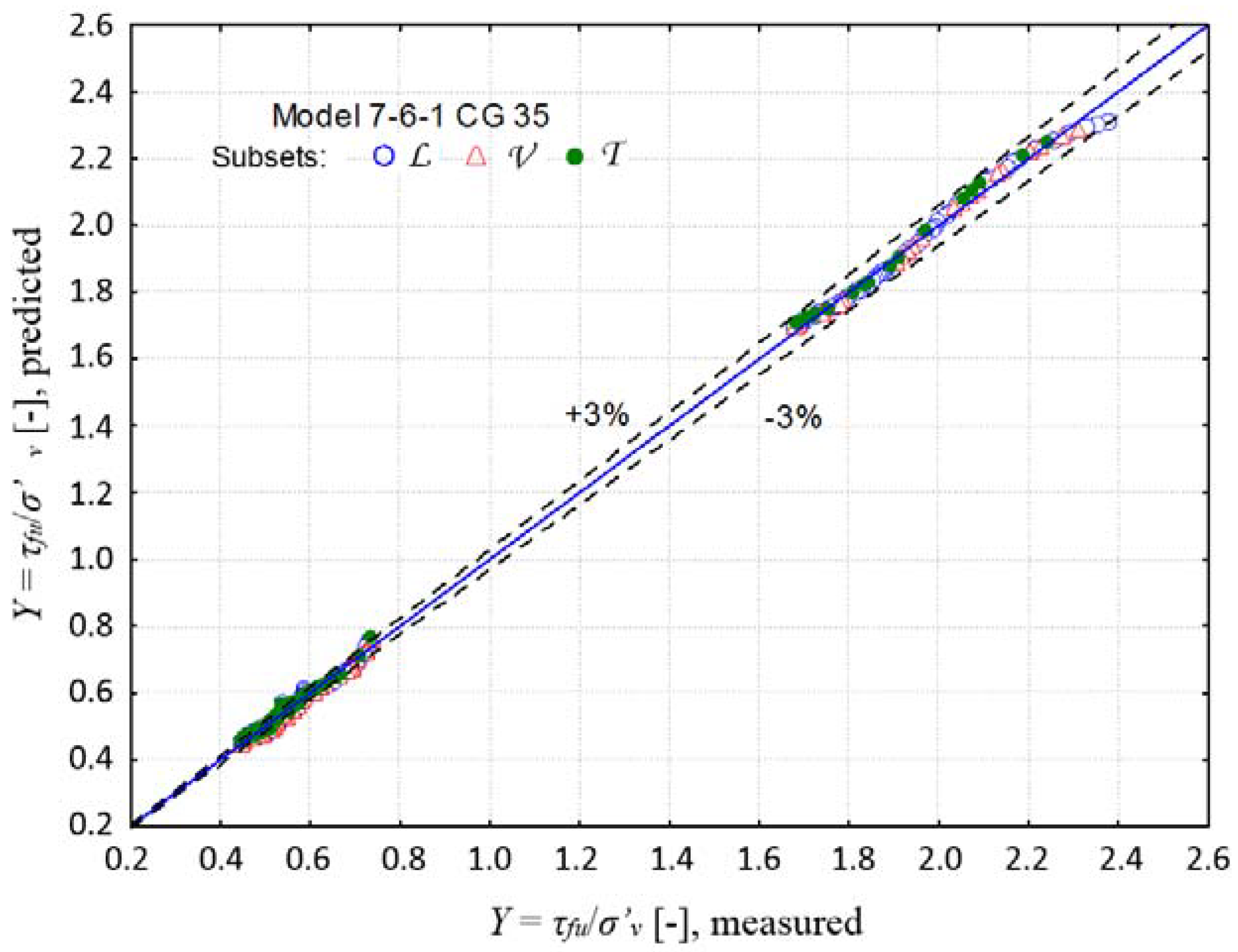
Soil type [42]	wL (%)	wP (%)	IL (-)	IC (-)	Fraction [43] (%)
					Gr	Sa	Si	Cl
Cl(U)	112.9	35.3	−0.06	1.06	0	5	36	59
sasiCl(U) sasiCl(R)	59.0	24.3	0.13	0.87	0	21	50	29
clSa(R)	19.4	8.7	0.75	0.25	0	70	19	11

Notes: w_L—liquid limit, w_P—plastic limit, I_L—liquidity index, I_C—consistency index. Gr—gravel, Sa—sand, Si—silt, Cl—clay, R—reconstituted, U—undisturbed.

. The undrained shear strength was determined at angles of principal stress rotation, α, equal to 0°, 30°, 45°, 60°, and 90° for clay and clayey sand, and equal to 0°, 15°, 30°, 45°, 60°, 75°, and 90° for sandy silty clay. Undisturbed soil samples were taken directly from the excavation site at the Copernicus Science Center station of the II underground line in Warsaw, while reconstituted samples were prepared in the laboratory using material from undisturbed samples, following their failure.

The TSHC tests were performed on soil samples in the shape of a hollow cylinder (Figure 2). Tests, both on undisturbed and reconstituted soils, were performed in six consecutive stages: flushing, saturation, consolidation, change of the intermediate principal stress parameter, b, change of the angle of principal stress rotation, α, and finally, shearing in undrained conditions. Parameter b is defined as:

$$b=\frac{\left({\sigma }_2-{\sigma }_3\right)}{\left({\sigma }_1-{\sigma }_3\right)},$$

(2)

where σ₁ is the major principal stress, σ₂ is the intermediate principal stress, and σ₃ is the minor principal stress.

Flushing was carried out to remove air and gases from soil samples and tubes having the largest dimensions. Saturation of soil samples was performed using the back pressure method. This stage lasted until the value of Skempton’s parameter, B, exceeded 0.95. Next, anisotropic consolidation was performed. In the case of clay, the value of K_o during the consolidation process was equal to 0.97, whereas for sandy silty clay, K_o was equal to 0.83. After dissipation of excess pore water pressure, parameter b was changed to 0.5 (Equation (1)) [44].

In the next step, the value of angle α was changed to the determined value in particular test. Finally, the process of sample shearing was carried out in the stress path, involving an increase in deviator stress, q, and a constant value of total mean stress, p. During the entire shearing process of the soil samples, values of parameter b and angle α were kept constant. An example of the soil samples after the TSHC tests is shown in Figure 3.

3. Results

The TSHC tests allowed the values of undrained shear strength to be obtained at selected angles of principal stress rotation for undisturbed clay, undisturbed and reconstituted sandy silty clay, as well as reconstituted clayey sand (

Table 2. Results of the TSHC tests for clay (Cl), sandy silty clay (sasiCl), and clayey sand (clSa), as well as empirical coefficients for Equation (5) [40,41,45].

Soil Type (X1)	Over-Consolidation Ratio OCR (-) (X2)	Plasticity Index IP (%) (X3)	Angle of the Principal Stress Rotation α (°) (X4)	Undrained Shear Strength τfu (kPa)	Effective Vertical Stress σ’v (kPa)	Normalized Undrained Shear Strength τfu/σ’vo (-) (Y)	Coefficients of Equation (5)
							ao	a1	n
Cl(U)	3.5	77.6	0	228.5	310	0.737	0.34	−0.80	2
			30	201.8		0.651
			45	178.5		0.576
			60	172.4		0.556
			90	160.1		0.516
sasiCl(U)	2.7	34.7	0	129.3	220	0.588	0.52	−2.14	2
			15	125.8		0.572
			30	117.7		0.535
			45	106.6		0.485
			60	101.4		0.461
			75	99.8		0.454
			90	98.4		0.447
sasiCl(R)	2.7	34.7	0	118.7	220	0.54	0.64	−0.20	2
			15	117.5		0.534
			30	115.2		0.524
			45	110.6		0.503
			60	107.4		0.488
			75	105.5		0.48
			90	104.2		0.478
clSa(R)	8	10.5	0	193.2	80	2.415	−0.31	1.36	2
			30	159.9		1.999
			45	152.7		1.909
			60	143.6		1.795
			90	134.1		1.676

). To determine these parameters, the maximum deviator stress was used as the failure criterion. All obtained values of undrained shear strength were normalized based on the vertical effective stress, σ’_v, to obtain comparable values of normalized undrained shear strength.

Based on research carried out by Wrzesiński [41] in a torsional shear hollow cylinder apparatus, a relationship was proposed to evaluate undrained shear strength at any angle of principal stress rotation [45]. The proposed relationship differs from the commonly known equation proposed by Bishop [9], because undrained shear strengths at α values of 0° and 90° are determined based on strength tests. This allows a more accurate determination of undrained shear strength for α values between 0° and 90°.

The undrained shear strength at any angle of principal stress rotation, ${\tau }_{fu}^{\alpha }$, can be evaluated as [45]:

$${\tau }_{fu}^{\alpha }={\tau }_{fu}^{90°}+{\eta }_{{\tau }_{fu}}\left({\tau }_{fu}^{0°}-{\tau }_{fu}^{90°}\right),$$

(3)

where ${\eta }_{{\tau }_{fu}}$ is the index of change in undrained shear strength, ${\tau }_{fu}^{90°}$ is the undrained shear strength at α = 90°, and ${\tau }_{fu}^{0°}$ is the undrained shear strength at α = 0°.

The index of change in undrained shear strength due to a change in angle of principal stress rotation is defined as:

$${\eta }_{{\tau }_{fu}}=\left({\tau }_{fu}^{\alpha }-{\tau }_{fu}^{90°}\right)/\left({\tau }_{fu}^{0°}-{\tau }_{fu}^{90°}\right).$$

(4)

Based on the TSHC test results, the following relationship between the indexes of change in undrained shear strength at any angle, α, was proposed by Wrzesiński [41]:

$${\eta }_{{\tau }_{fu}}=1-{\left(sin\alpha \right)}^{exp\left[a_o+a_1{\left(\frac{\alpha }{{90}^{°}}\right)}^n\right]},$$

(5)

where a_o, a₁, and n are empirical coefficients.

The obtained relationship in Equation (5) for over-consolidated clayey sand (clSa(R)), tested by Kiziewicz [40], is presented in Figure 4. The coefficient of determination, R², for the relationship determining the change in undrained shear strength for clayey sand was equal to 0.93. The values of empirical coefficients a_o, a₁, and n for all tested soils are shown in Table 2. Test results showed that the values of empirical coefficients in Equation (5) depended on the type and structure of the soil, and its stress history. The proposed equation was derived on the basis of tests performed on over-consolidated clays with a low impact of glaciotectonic disturbances on the soil structure.

Figure 5 presents the undrained shear strength of clayey sand, clSa(R), based on Equation (3), with the index ${\eta }_{{\tau }_{fu}}$ obtained from Equation (5), and empirical coefficients presented in Table 2. In Figure 5, undrained shear strength evaluated based on Bishop’s relationship is also presented. The undrained shear strength at α = 90° determined in the TSHC test was different from the result based on Bishop’s relationship. In this case, the relative error was equal to 0.82. Using Bishop’s relationship to determine undrained shear strength for clayey sand clSa(R), the biggest relative error was at an α value of 30°, and was equal to 4.19%. However, when using the proposed method, the error was equal to 0.38%.

4. Artificial Neural Network Analysis

4.1. Architecture of the Artificial Neural Network

The class of neural network used in this study was a multilayer perceptron (MLP) with one hidden layer. The architecture of the network’s N–H–M type is defined by the number of nodes, N, in the input layer X₁–X_N; the number of nodes, H, in the hidden layer; and the number of nodes, M = Y, in the output layer.

Neural networks were constructed according to the criterion of minimization of the error function, which was the sum of squares of differences (SOS), expressed by the following formula (for one output):

$$E_{SOS}= {\displaystyle \sum }_{i=1}^P{\left(d_i-y_i\right)}^2,$$

(6)

where P is the number of cases of set P, i ∈ {1, …, P}, d_i represents the known values of the tests, and y_i corresponds to values predicted from neural networks.

Measures of errors were calculated separately for each subset: learning, $L$, testing, $T$, and validation, $V$. To assess the predictive quality of the neural network, values of error measures in the testing subset, $T$, were taken into account. Selected error measures for neural networks with one output are given by the following formulae:

−

Relative error (for individual cases):

$$R{E}_i=\left|\frac{d_i-y_i}{d_i}\right|·100\%,$$

(7)

−

Determination coefficient, R²:

$$R^2=\frac{{{\displaystyle \sum }}_{i=1}^P{\left(y_i-{\overline{d}}_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^P{\left(d_i-{\overline{d}}_i\right)}^2},$$

(8)

−

Mean absolute error:

$$MAE=\frac{{{\displaystyle \sum }}_{i=1}^P\left|d_i-y_i\right|}{P},$$

(9)

−

Root mean squared error:

$$RMS=\sqrt{\frac{1}{P}·{\displaystyle \sum }_{i=1}^P{\left(d_i-y_i\right)}^2},$$

(10)

where d_i is the measured value, y_i is the value predicted by the neural network, d_i is the measured mean value in a given subset, and denotes the case number from subsets $L$, $T$, or $V$ with cardinality P, where i ∈ {1, ..., P}.

4.2. Datasets

Two datasets were used in the ANN analysis. Set $A$ consisted of results of the TSHC tests, where n_A was equal to 24 cases, described by the following five variables: X₁ = soil type ∈ {Cl(U), sasiCl(U), sasiCl(R), clSa(R)} X₂ = over-consolidation ratio, OCR ∈ {3.5, 2.7, 8.0}; X₃ = plasticity index, I_P ∈ {77.6, 34.7, 10.5%}; X₄ = angle of principal stress rotation, α ∈ {0, 30, 45, 60, 90°} or {0, 15, 30, 45, 60, 75, 90°}; Y = normalized undrained shear strength, τ_fu/σ’_v (Table 2). The variables used were selected based on statistical analysis [41]. Variable X₁ was treated as a quality (linguistic) variable. Variable X₁ required the introduction of as many input neurons as there were soils (i.e., four neurons) [46].

Set $B$ was a set of “artificial” data, and consisted of n_B = 340 cases, described by independent variables X₁–X₃ shown in Table 2, and dependent variable Y, representing normalized undrained sheer strength, τ_fu/σ’_v, calculated from Equations (3) and (4) using empirical coefficients shown in Table 2 for the independent variable, α, in the range 1–89° in 1° increments. Set $B$ was used to create and train the neural networks. The selected artificial neural network was used to predict τ_fu/σ’_v values based on new, actual data from the TSHC tests in set $A$.

4.3. Training and Testing

Set $B$ was randomly assigned to 50%, 25%, and 25% of the learning, $L$, testing, $T$, and validation, $V$ subsets, respectively. The testing subset was used to periodically check the generalizability acquired by the network, and the validation subset was used for the final evaluation of the trained neural network.

The predictive quality of the neural regression model was evaluated on the basis of error analysis, and calculated independently for the following subsets: learning, $L$, testing, $T$, and validation, $V$. Neural networks were optimized for the number of neurons in the hidden layer, the activation function in the neurons of the hidden and output layers, and the learning method. The conjugate gradient (CG) algorithm was chosen for network learning. An early-stopping method of training was used [47]. Learning was stopped after 35 learning cycles (epochs). Neural networks with the best predictive quality were determined on the basis of the highest values of the determination coefficient (R²), the lowest values of root mean squared errors (RMSs), and the lowest mean values of relative errors (REs) [47].

Based on the analysis of many neural networks, a neural network of 7–6–1 was selected, meaning seven input neurons, six neurons in one hidden layer, and one output neuron (Figure 6). Activation functions were identified. For the hidden neurons, this was a tanh sigmoid curve, and for the output neuron, this was a logistic function. The errors in the $L$, $T$, and $V$ subsets of dataset $B$ were small, while the determination coefficients (R²) were very high (

Table 3. Measures of network errors in the 7–6–1 network of subsets $L$, $T$, and $V$ of set $B$. MAE: mean absolute error; R²: coefficient of determination; RMS: root mean squared error.

Measures of Errors	Subset learning, $\mathit{ℒ}$	Subset testing, $\mathit{𝒯}$	Subset validation, $\mathit{𝒱}$
RMS	0.0057	0.0054	0.0052
MAE	0.0109	0.0110	0.0105
R2	0.998	0.998	0.998

). The relative prediction error (RE) of the proposed neural network had a maximum value of about ±3% (Figure 7) in all subsets of dataset $B$.

Statistical analysis performed by Wrzesiński [41] indicated that, from linear regression models (simple and multiple), the highest value of the determination coefficient was 0.951, and the lowest mean relative error was about ±20%.

4.4. Neural Network Prediction

The trained artificial neural network, 7–6–1, was tested by applying it to the prediction of τ_fu/σ’_v, based on laboratory data from set $A$. Independent variables X₁, X₂, X₃, and X₄ (Table 2) were introduced into the network, and τ_fu/σ’_v values predicted by the network were obtained. A comparison between measured values of τ_fu/σ’_v obtained from the TSHC tests and values of τ_fu/σ’_v predicted using the proposed neural network 7–6–1 are shown in

Table 4. Comparison between measured values of τ_fu/σ’_v obtained from the TSHC tests and values of τ_fu/σ’_v predicted using the proposed neural network 7–6–1, in set $A$.

No.	Measured Values τfu/σ’v from Set $\mathit{A}$ di (-)	Predicted Values τfu/σ’v Based on 7–6–1 Network yi (-)	Relative Errors of Individual Case REi (%)
1	0.737	0.775	5.16
2	0.651	0.634	2.61
3	0.576	0.59	2.43
4	0.556	0.554	0.36
5	0.516	0.512	0.77
6	0.588	0.612	4.08
7	0.572	0.558	2.45
8	0.535	0.52	2.8
9	0.485	0.491	1.24
10	0.461	0.468	1.52
11	0.454	0.455	0.22
12	0.447	0.452	1.12
13	0.54	0.572	5.92
14	0.534	0.531	0.56
15	0.524	0.5	4.58
16	0.503	0.48	4.57
17	0.488	0.47	3.69
18	0.48	0.47	2.08
19	0.478	0.478	0
20	2.415	2.322	3.85
21	1.999	2.019	1
22	1.909	1.885	1.26
23	1.795	1.789	0.33
24	1.676	1.694	1.07
			Max RE13 = 5.92%

. The single maximum value of relative error was about 6%.

5. Conclusions

The presented neural network, with the architecture 7–6–1, predicted the real value of the variable, τ_fu/σ’_v, based on the following data: soil type, over-consolidation ratio (OCR), plasticity index (I_P), and angle of principal stress rotation (α) for tested pre-consolidated cohesive soils.

The 7–6–1 artificial neural network was selected with a determination coefficient of 0.998 and a mean relative error of around ±3% in set $B$, and the single maximum relative error was about 6%. It had better predictive quality of normalized undrained shear strength (τ_fu/σ’_v) than linear regression models, where the highest determination coefficient was 0.951, and the lowest mean relative error was about ±20%.

Conclusions from the analysis only concern the tested types of cohesive soils. As further tests are carried out in the torsional shear hollow cylinder apparatus, the ANN models can be upgraded and extended, taking into account other soil types, and possibly generalizing for most types of cohesive soils.