An Ultrasonic Through-Metal-Wall Power Transfer System with Regulated DC Output
Abstract
:Featured Application
Abstract
1. Introduction
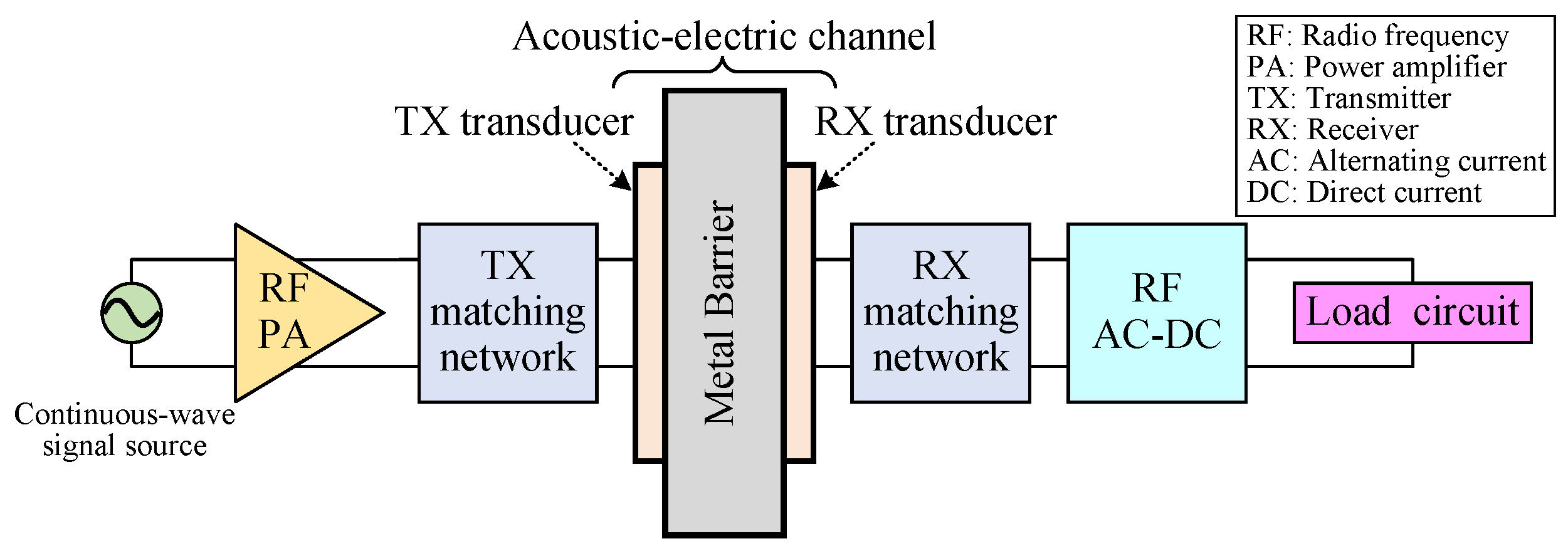
2. System Description
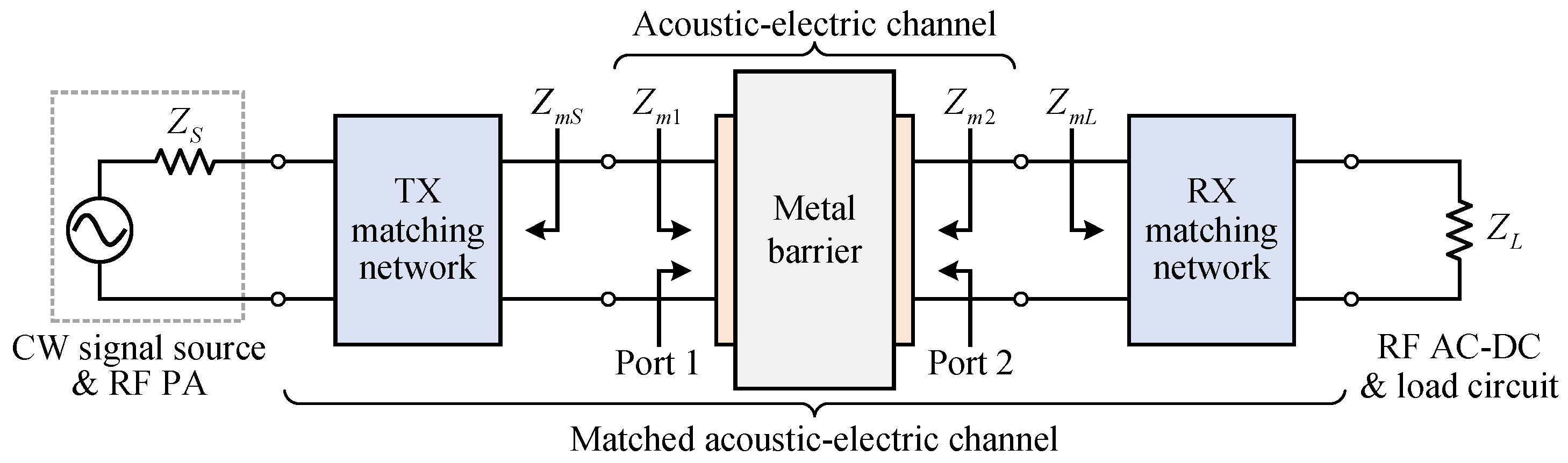
2.1. Acoustic-Electric Channel
2.2. Simultaneous Conjugate Impedance Matching
2.3. RF AC-DC Converter with Input Impedance Matching
- Operation Mode I
- Operation Mode II
- Operation Mode III
- Operation Mode IV
- Step 1: Derivation of the input voltage amplitude
- Step 2: Decision of the resonant-type rectifier output voltage
- Step 3: Calculation of the voltage ratio
- Step 4: Derivation of the frequency ratio
- Step 5: Derivation of a non-dimensional parameter
- Step 6: Calculation of the resonant inductance
- Step 7: Calculation of the resonant frequency
- Step 8: Calculation of the resonant capacitance C
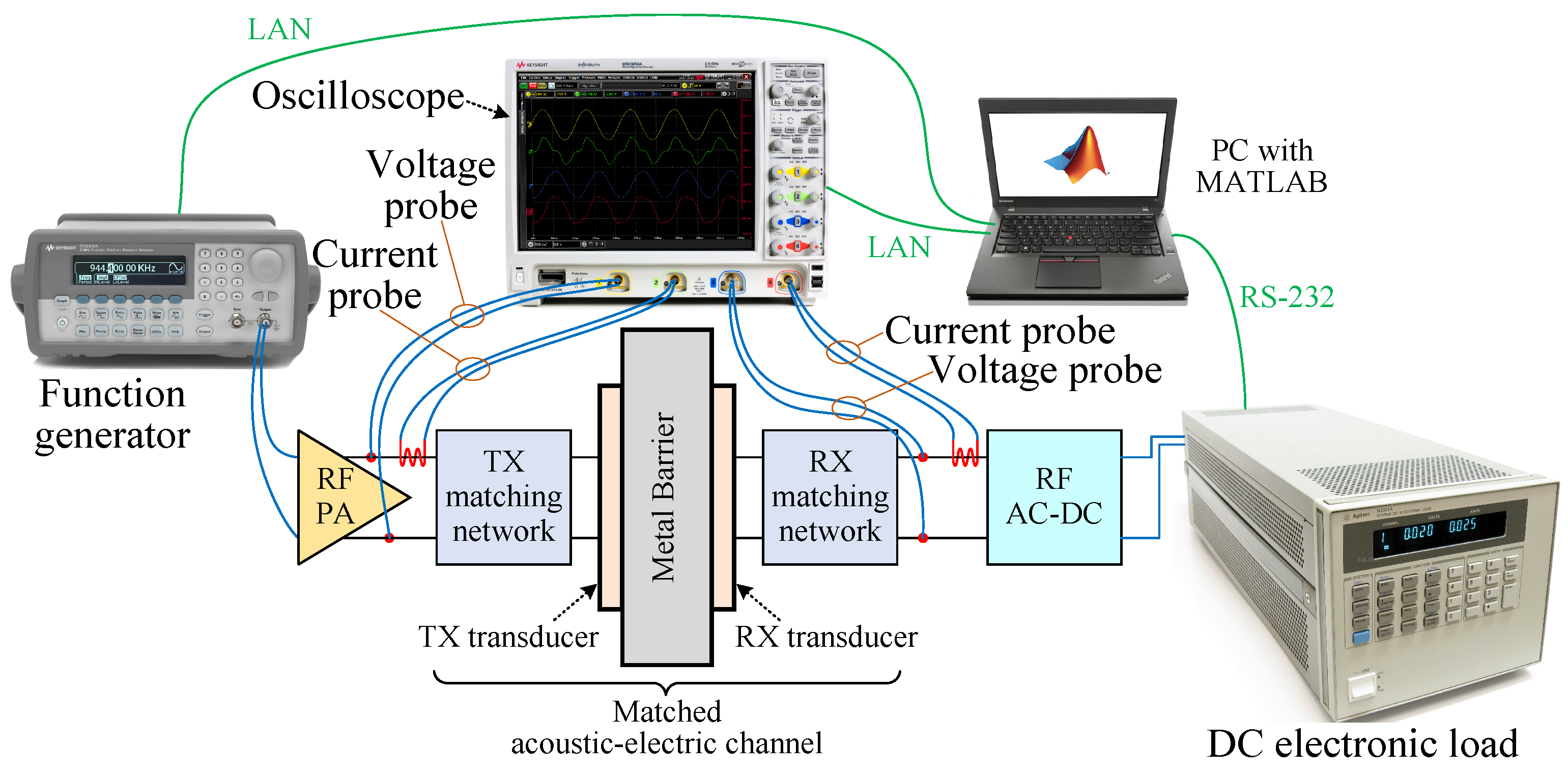
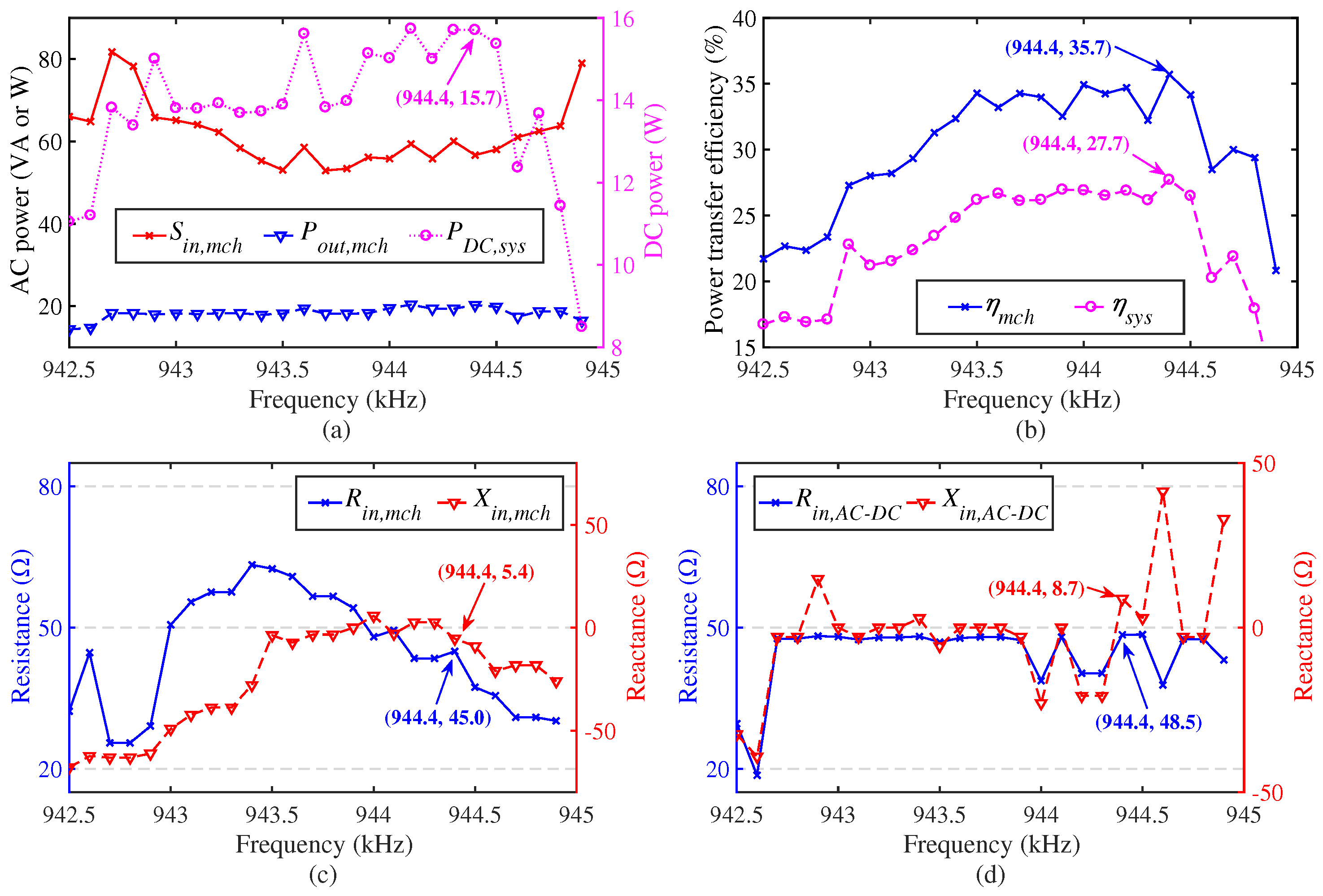
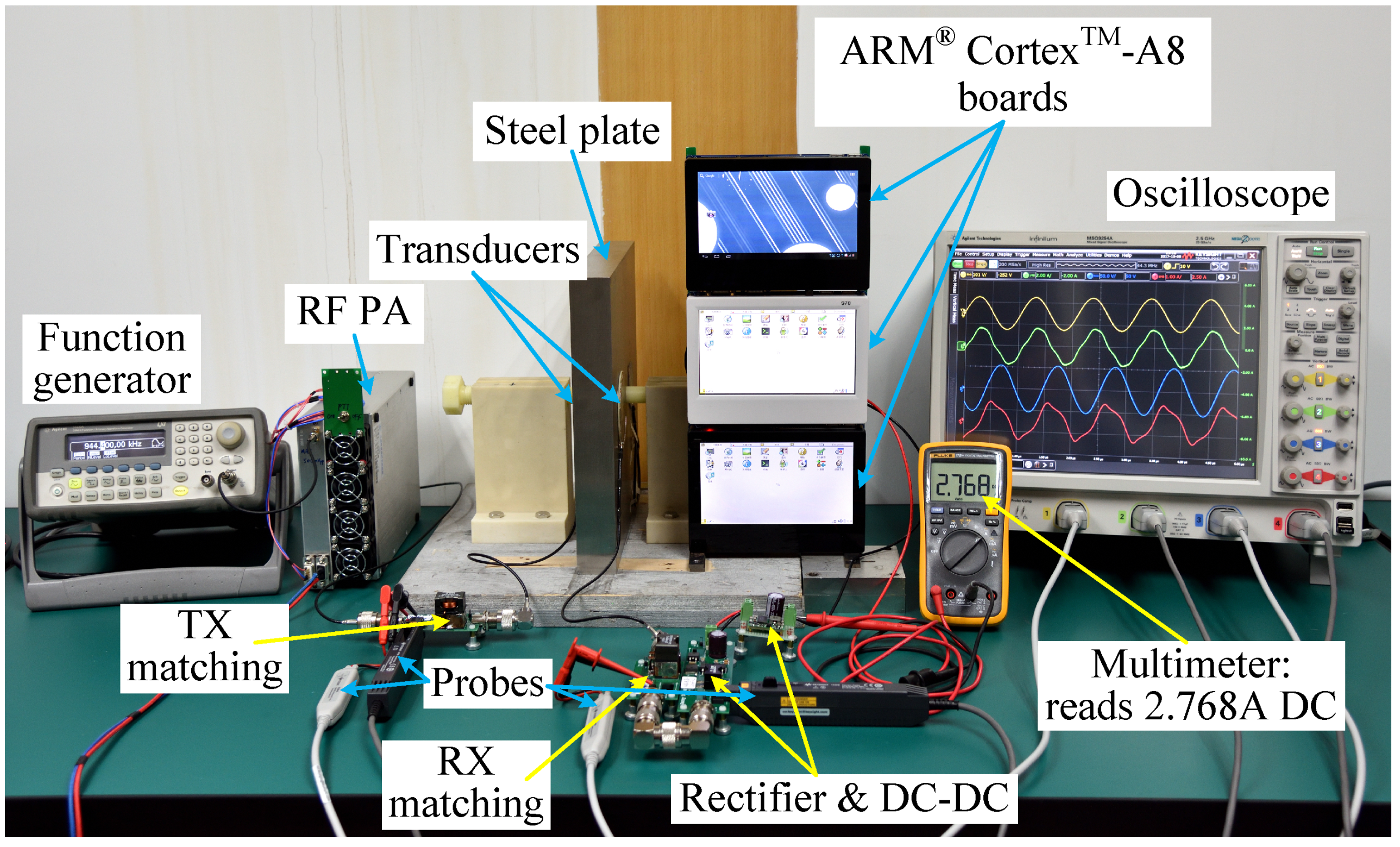
3. Measurements
| Algorithm 1 Automated measurement algorithm of the system. |
|
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–986. [Google Scholar] [CrossRef] [PubMed]
- Moradewicz, A.J.; Kazmierkowski, M.P. Contactless Energy Transfer System With FPGA-Controlled Resonant Converter. IEEE Trans. Ind. Electron. 2010, 57, 3181–3190. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, X.; Yang, J.; Jiang, Q. Transmitting electric energy through a metal wall by acoustic waves using piezoelectric transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 773–781. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.X.; Hu, Z.; Zhao, H.; Hu, H.F.; Sun, Y.Z.; Hou, B.J. Through-Metal-Wall Power Delivery and Data Transmission for Enclosed Sensors: A Review. Sensors 2015, 15, 31581–31605. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yu, Z.; Yang, H.; Wu, M.; Yang, J. In Wireless communication using ultrasound through metal barriers: Experiment and analysis. In Proceedings of the 2015 10th International Conference on Information, Communications and Signal Processing (ICICS), Singapore, 2–4 December 2015. [Google Scholar]
- Cotte, B.; Lafon, C.; Dehollain, C.; Chapelon, J.Y. Theoretical study for safe and efficient energy transfer to deeply implanted devices using ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1674–1685. [Google Scholar] [CrossRef] [PubMed]
- Denisov, A.; Yeatman, E. Ultrasonic vs. Inductive power delivery for miniature biomedical implants. In Proceedings of the 2010 International Conference on Body Sensor Networks, Singapore, 7–9 June 2010. [Google Scholar]
- Guida, R.; Santagati, G.E.; Melodia, T. A 700 khz ultrasonic link for wireless powering of implantable medical devices. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Basaeri, H.; Christensen, D.; Roundy, S.; Yu, Y.; Nguyen, T.; Tathireddy, P.; Young, D.J. Ultrasonically powered hydrogel-based wireless implantable glucose sensor. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Lin, Y.C.; Chiang, M.C.; Chen, J.H. A wireless sensor utilizing ultrasound for wireless power and data transmission. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017. [Google Scholar]
- Tseng, V.F.G.; Bedair, S.S.; Lazarus, N. Acoustic wireless power transfer with receiver array for enhanced performance. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017. [Google Scholar]
- Du, G.; Zhu, Z.; Gong, X. Fundamentals of Acoustics, 3rd ed.; Nanjing University Press: Nanjing, China, 2012; pp. 351–352. ISBN 9787305097782. [Google Scholar]
- International Telecommunication Union (ITU). Nomenclature of the Frequency and Wavelength Bands Used in Telecommunications; International Telecommunication Union (ITU): Geneva, Switzerlandm, 1865; Available online: https://www.itu.int/dms_pubrec/itu-r/rec/v/R-REC-V.431-7-200005-S!!PDF-E.pdf (accessed on 4 March 2018).
- Hu, H.; Hu, Y.; Chen, C.; Wang, J. A system of two piezoelectric transducers and a storage circuit for wireless energy transmission through a thin metal wall. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2312–2319. [Google Scholar] [CrossRef] [PubMed]
- Bao, X.Q.; Doty, B.J.; Sherrit, S.; Badescu, M.; Cohen, Y.B.; Aldrich, J.; Chang, Z.S. Wireless piezoelectric acoustic-electric power feedthru. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2007, San Diego, CA, USA, 19–22 March 2007; Tomizuka, M., Yun, C.-B., Giurgiutiu, V., Eds.; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Bao, X.Q.; Biederman, W.; Sherrit, S.; Badescu, M.; Cohen, Y.B.; Jones, C.; Aldrich, J.; Chang, Z.S. High-power piezoelectric acoustic-electric power feedthru for metal walls. In Proceedings of the Industrial and Commercial Applications of Smart Structures Technologies 2008, San Diego, CA, USA, 10–12 March 2008; Porter Davis, L., Henderson, B.K., Brett McMickell, M., Eds.; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- Lawry, T.J. A High Performance System for Wireless Transmission of Power and Data through Solid Metal Enclosures. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2011. [Google Scholar]
- Lawry, T.J.; Wilt, K.R.; Ashdown, J.D.; Scarton, H.A.; Saulnier, G.J. A high-performance ultrasonic system for the simultaneous transmission of data and power through solid metal barriers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Leung, H.F.; Hu, A.P. Theoretical modeling and analysis of a wireless ultrasonic power transfer system. In Proceedings of the 2015 IEEE PELS Workshop on Emerging Technologies: Wireless Power (2015 WoW), Daejeon, Korea, 5–6 June 2015. [Google Scholar]
- Dai, X.; Li, L.; Li, Y.; Hou, G.; Leung, H.F.; Hu, A.P. Determining the maximum power transfer condition for ultrasonic power transfer system. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016. [Google Scholar]
- Rezaie, H.; Hu, A.P.; Leung, H.F.; Cordell, R. New attachment method to increase the performance of ultrasonic wireless power transfer system. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017. [Google Scholar]
- Feng, R.; Yao, J.; Guan, L. Ultrasonics Handbook; Nanjing University Press: Nanjing, China, 1999; pp. 233–234. ISBN 9787305033544. [Google Scholar]
- Rahola, J. Power waves and conjugate matching. IEEE Trans. Circuits Syst. II Exp. Briefs 2008, 55, 92–96. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 165–192. ISBN 9781118298138. [Google Scholar]
- Matsui, K.; Yamamoto, I.; Guan, E.; Hasegawa, M.; Ando, K.; Ueda, F.; Mori, H. A High DC voltage Generator by LC Resonance in Commercial Frequency. In Proceedings of the 2007 Power Conversion Conference, Nagoya, Janpan, 2 April 2007. [Google Scholar]
- Kusaka, K.; Itoh, J.I. Experimental verifications and desing procedure of an AC-DC converter with input impedance matching for wireless power transfer systems. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15 September 2013. [Google Scholar]
- Kusaka, K.; Itoh, J.I. Input impedance matched AC-DC converter in wireless power transfer for EV charger. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012. [Google Scholar]
- Keysight Technologies, Inc. Keysight U1880A Deskew Fixture User’s Guide; Keysight Technologies, Inc.: Santa Rosa, CA, USA, 2014; Available online: https://literature.cdn.keysight.com/litweb/pdf/U1880-97000.pdf (accessed on 10 February 2018).
- Qiu, G.Y.; Luo, X.J. Circuit, 5th ed.; Higher Education Press: Beijing, China, 2006; pp. 233–238. ISBN 9787040196719. [Google Scholar]
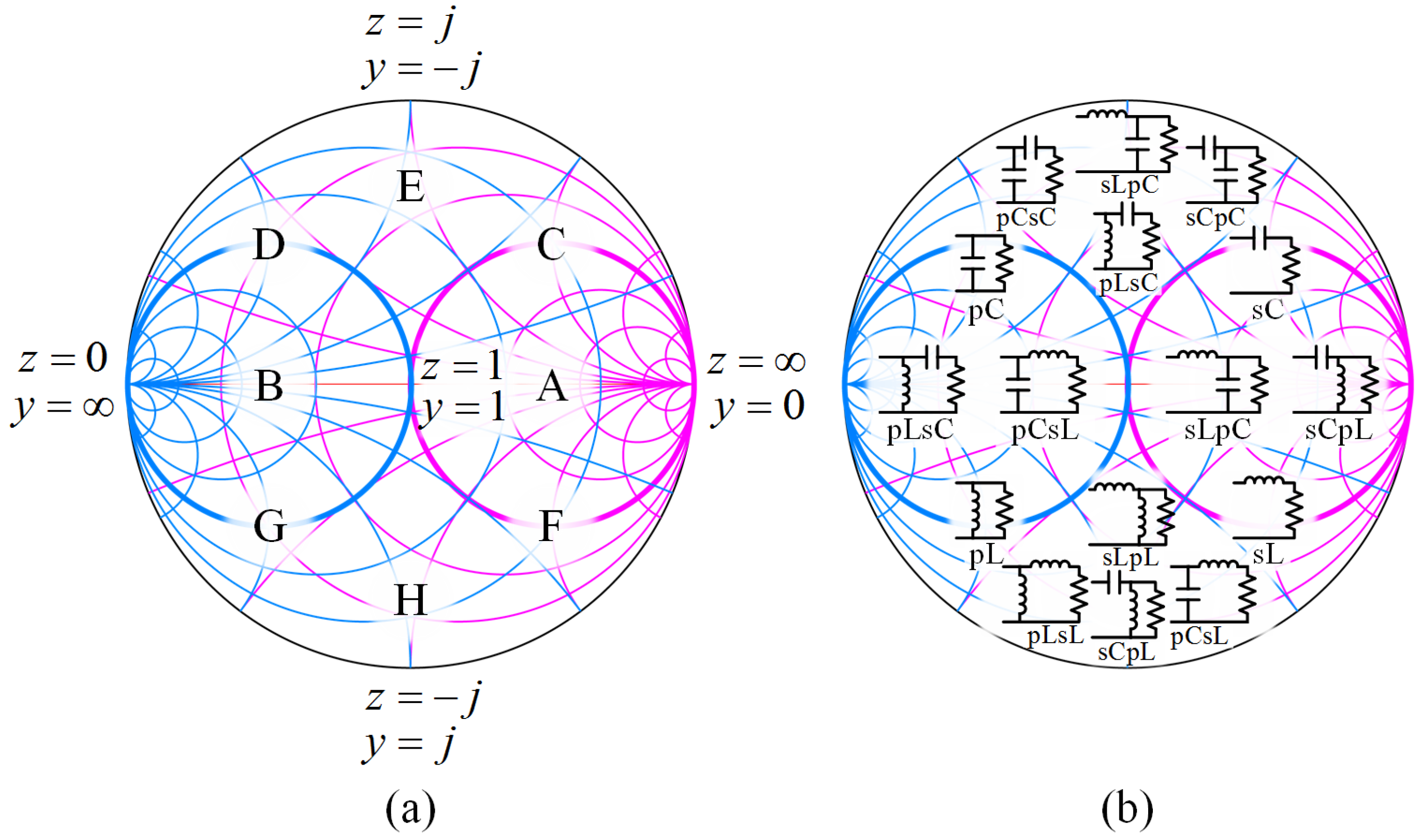

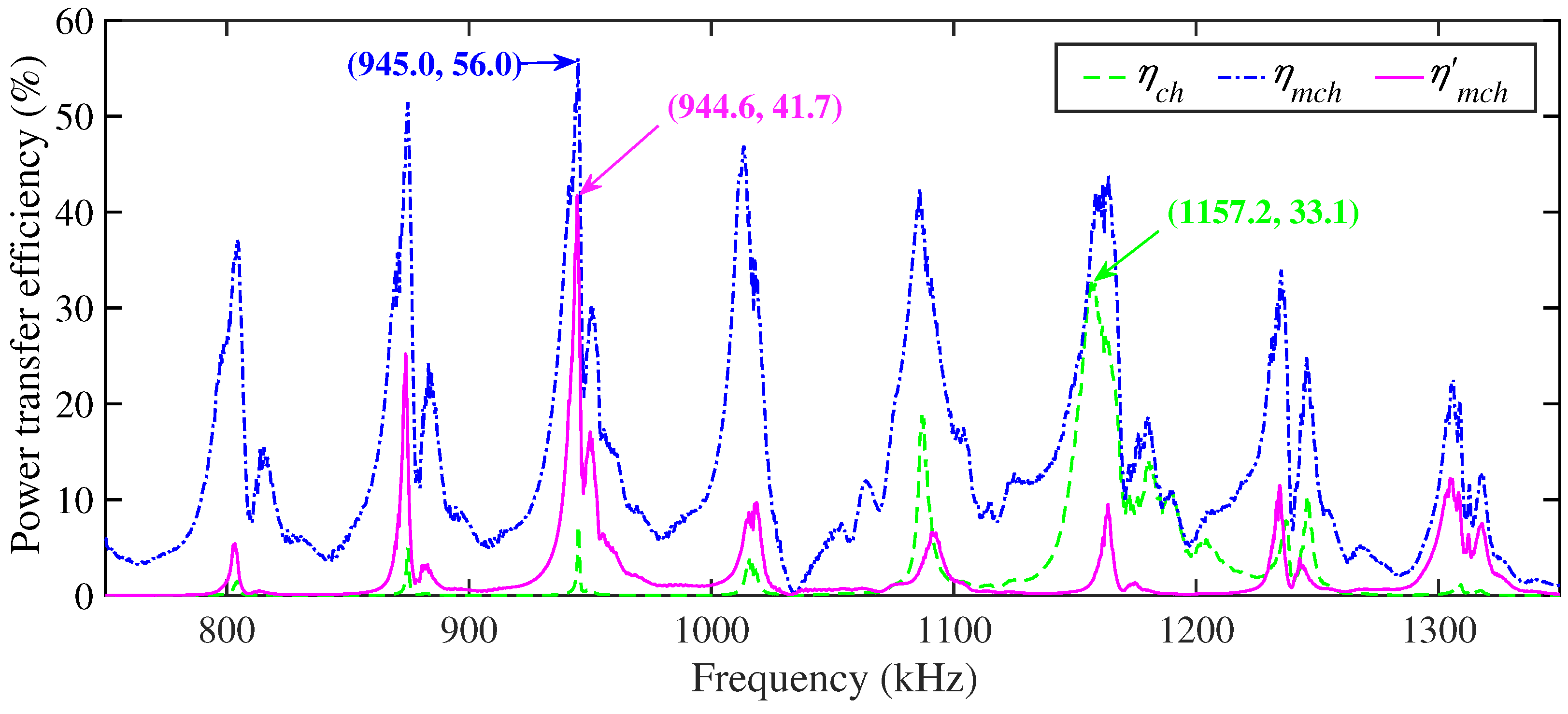
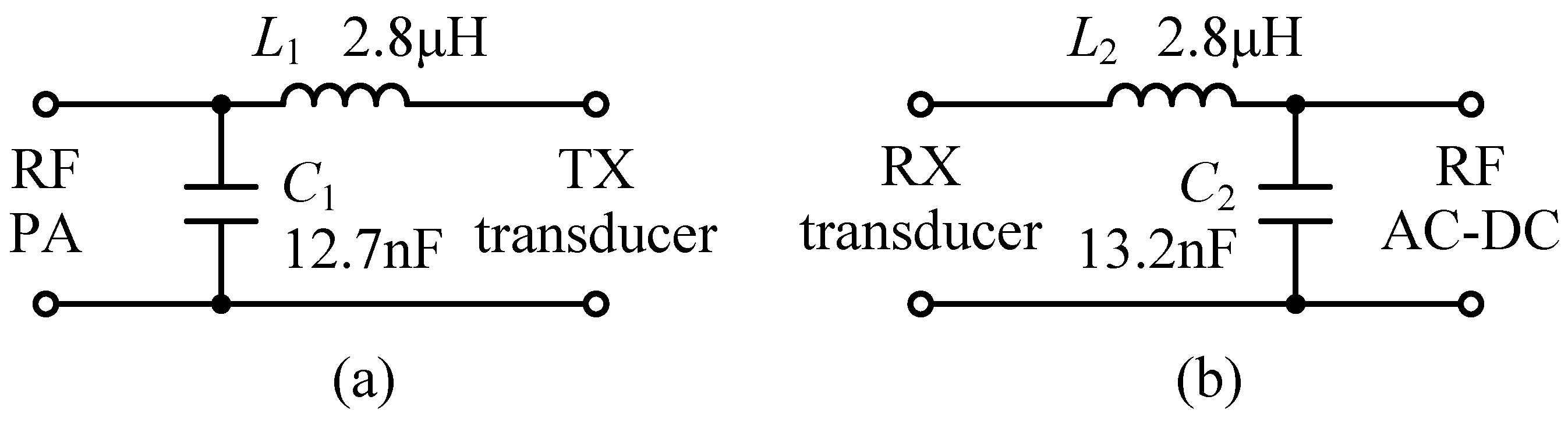
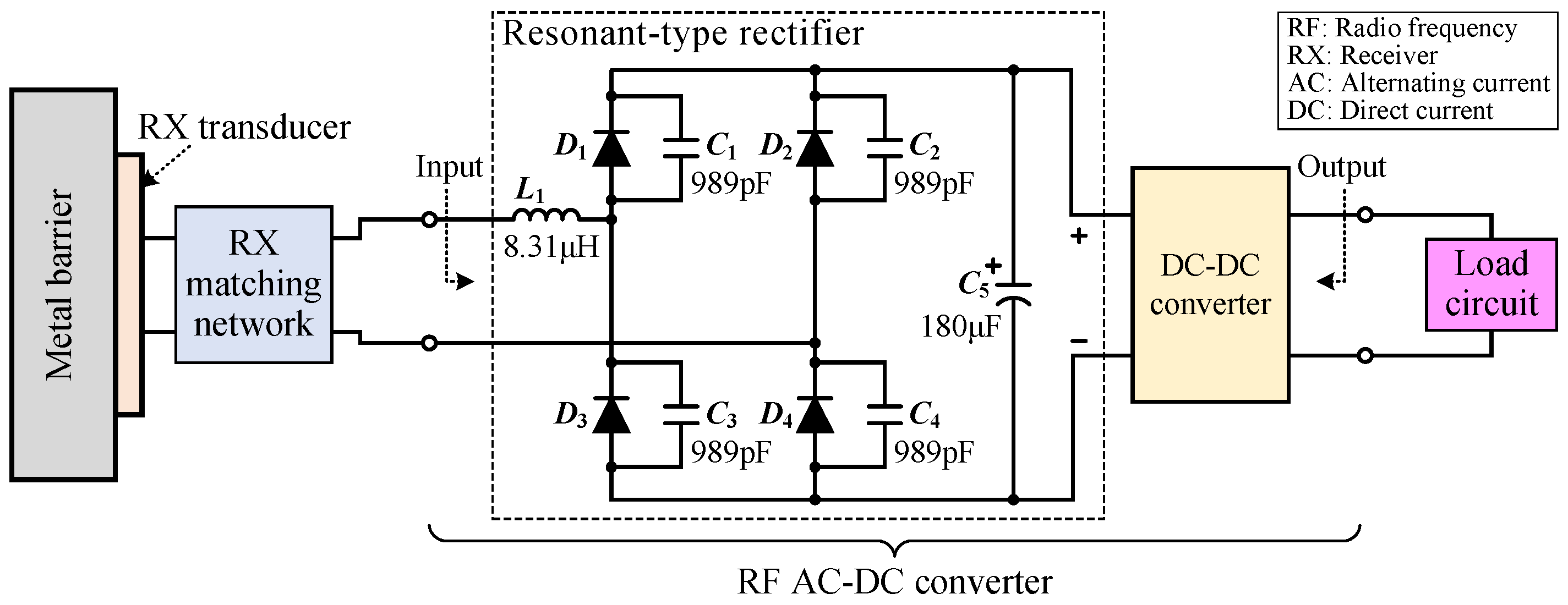
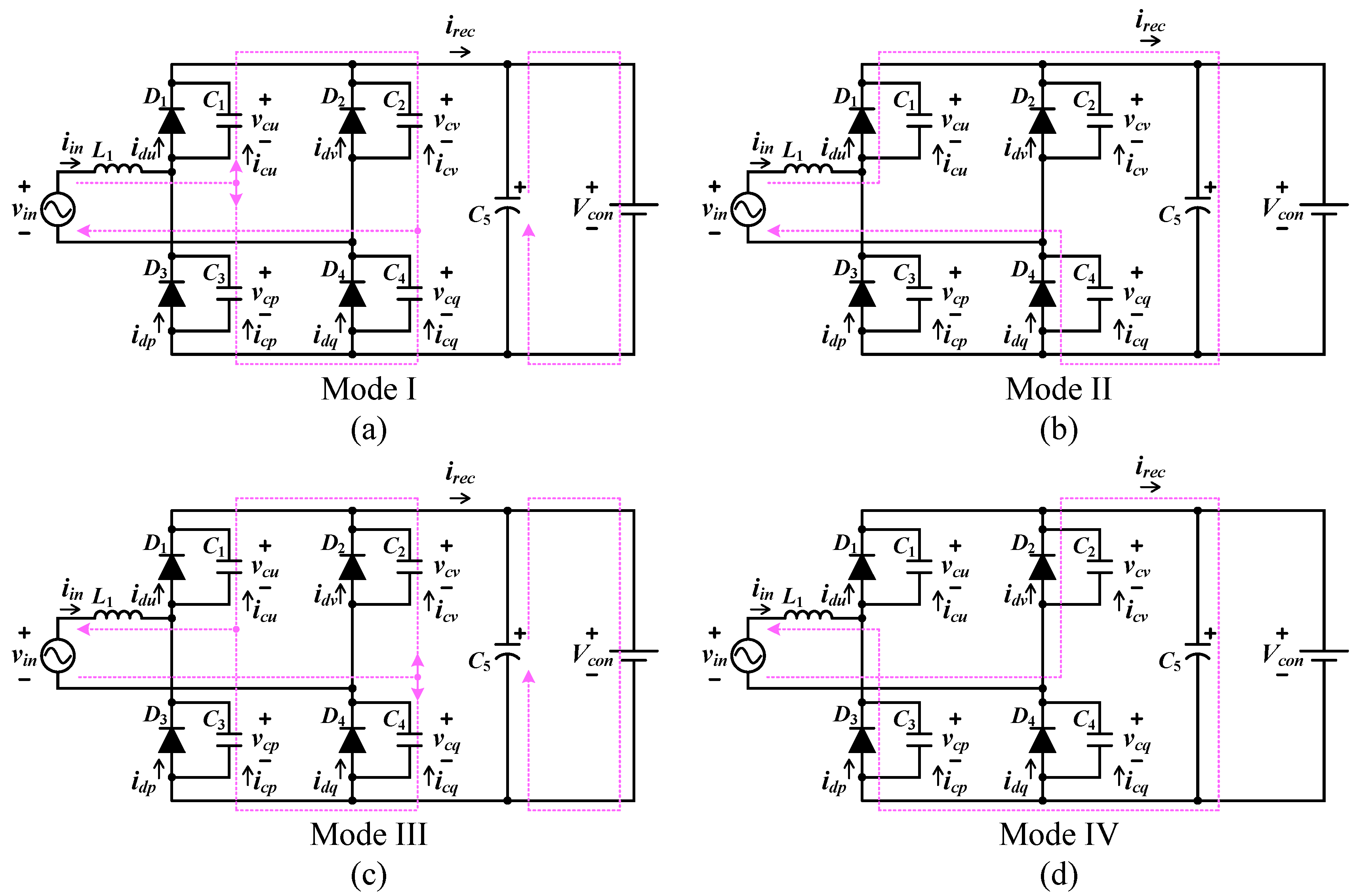


| Region | Range of Normalized Port Impedance & Admittance | Available Network Topologies |
|---|---|---|
| A | sCpL and sLpC | |
| B | pLsC and pCsL | |
| C | and | sC |
| D | and | pC |
| E | , and | sCpC, sLpC, pCsC and pLsC |
| F | and | sL |
| G | and | pL |
| H | , and | sLsL, sCpL, pLsL and pCsL |
| Parameter | Symbol | Value | Unit | |
|---|---|---|---|---|
| Design input parameters | Input impedance | |||
| Input frequency | 944.6 | kHz | ||
| Input power | 20.0 | W | ||
| Rectifier output voltage | 50.0 | V | ||
| Design output parameters | Resonance inductance | 8.3 | µH | |
| Resonance capacitance | C | 989 | pF | |
| Parameter | Our System | Lawry’s System |
|---|---|---|
| Transducer material | PZT-5 | PZT-5 |
| Transducer diameter | 80 mm | 66.68 mm |
| Transducer resonant frequency | About 945 kHz | About 1 MHz |
| Metal wall material | 304 stainless steel | Submarine steel |
| Metal wall dimensions | ||
| Channel operating frequency | 944.4 kHz | 1.102 MHz |
| Channel maximum efficiency | 35.7% | 51% |
| AC-DC converter | Cascaded combination of | CF-DFBR |
| a resonant-type rectifier | ||
| and a DC-DC converter | ||
| AC-DC converter | Yes | No |
| input impedance matched | ||
| Maximum DC output power | 15.7 W | 19 W |
| DC output regulated | Yes | No |
| System maximum efficiency | 27.7% | 19% |
| (DC output) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wu, M.; Yu, Z.; Yang, J. An Ultrasonic Through-Metal-Wall Power Transfer System with Regulated DC Output. Appl. Sci. 2018, 8, 692. https://doi.org/10.3390/app8050692
Yang H, Wu M, Yu Z, Yang J. An Ultrasonic Through-Metal-Wall Power Transfer System with Regulated DC Output. Applied Sciences. 2018; 8(5):692. https://doi.org/10.3390/app8050692
Chicago/Turabian StyleYang, Hengxu, Ming Wu, Ziying Yu, and Jun Yang. 2018. "An Ultrasonic Through-Metal-Wall Power Transfer System with Regulated DC Output" Applied Sciences 8, no. 5: 692. https://doi.org/10.3390/app8050692
APA StyleYang, H., Wu, M., Yu, Z., & Yang, J. (2018). An Ultrasonic Through-Metal-Wall Power Transfer System with Regulated DC Output. Applied Sciences, 8(5), 692. https://doi.org/10.3390/app8050692





