Noise Attenuation Based on Wave Vector Characteristics
Abstract
:1. Introduction
2. Principles
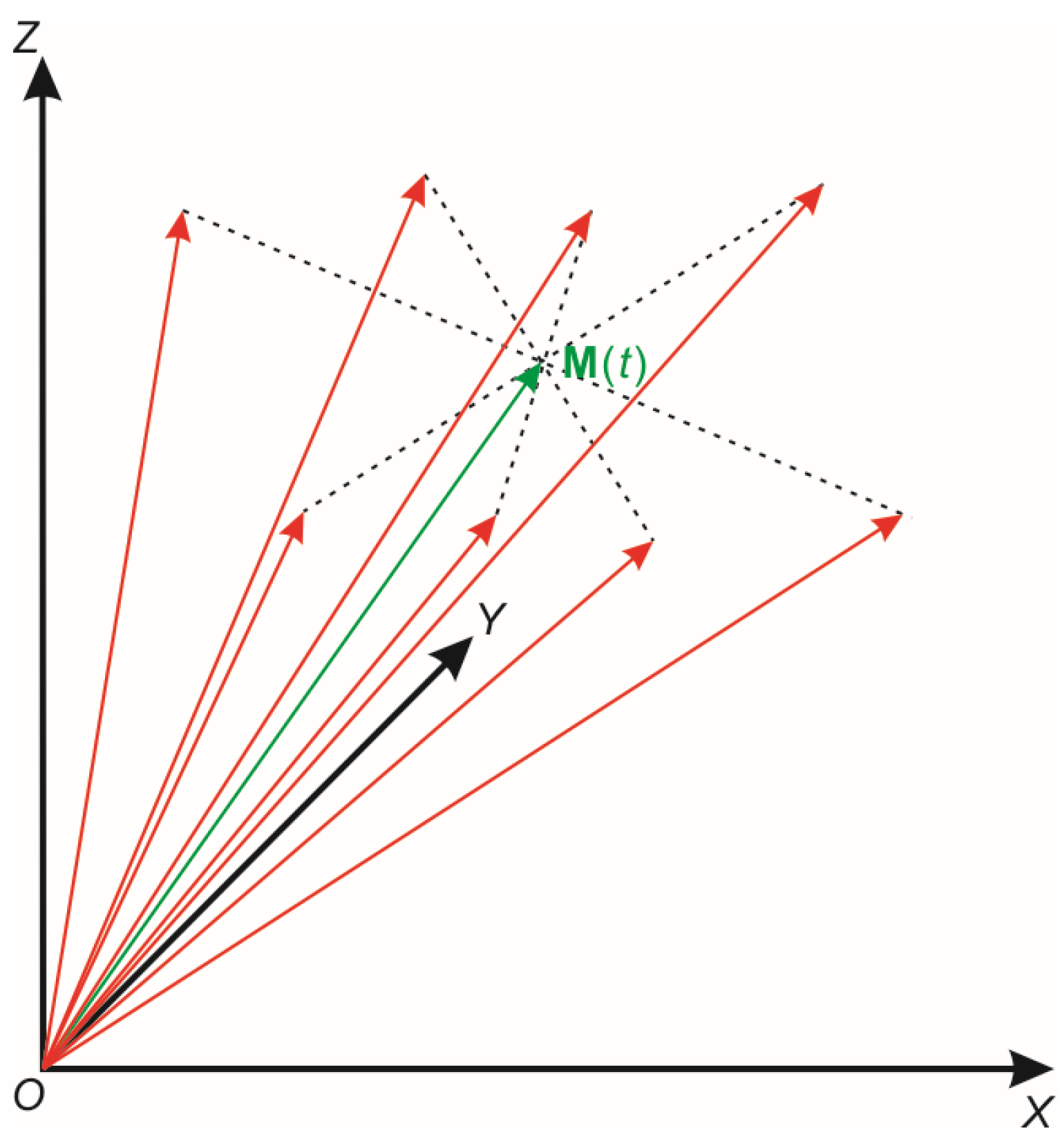
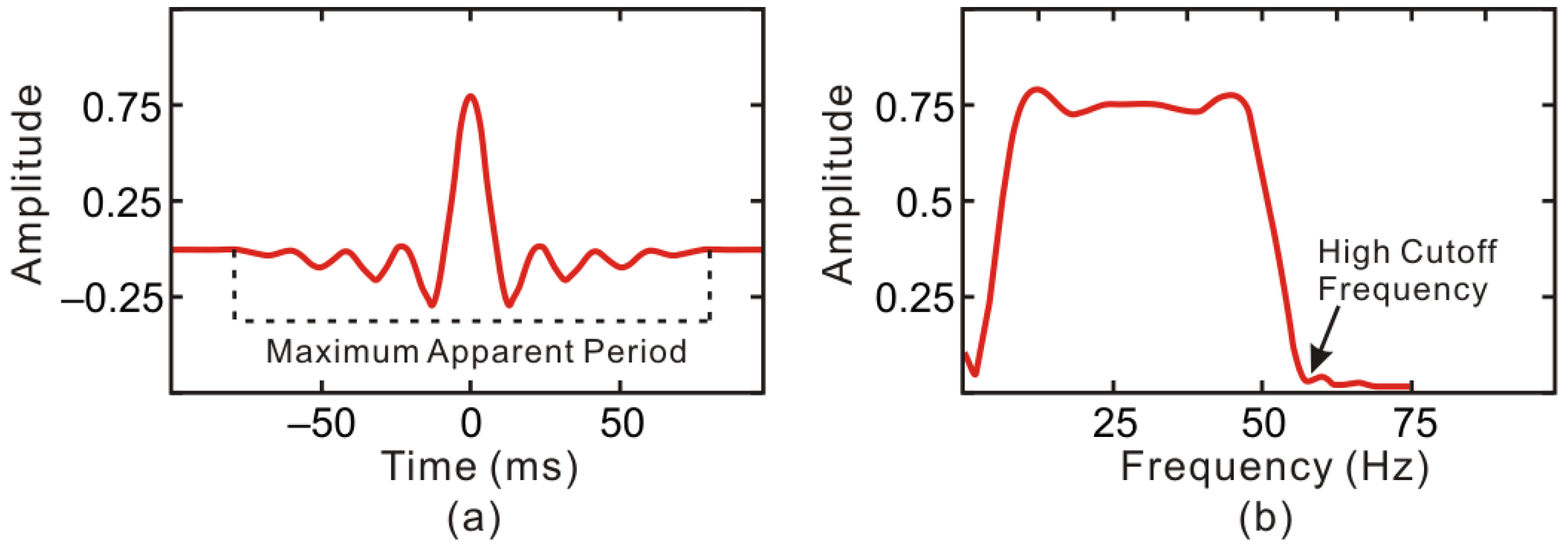
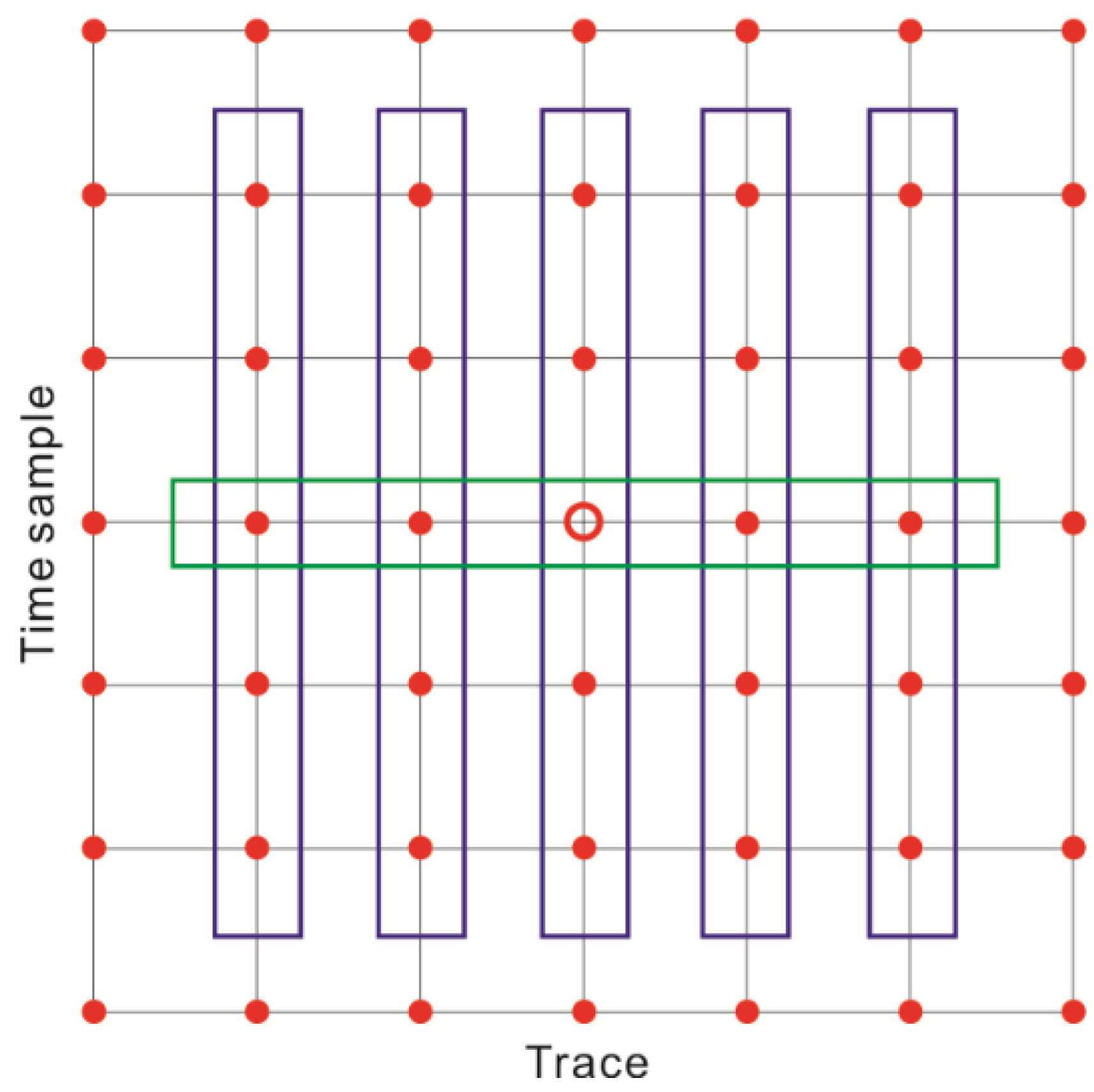
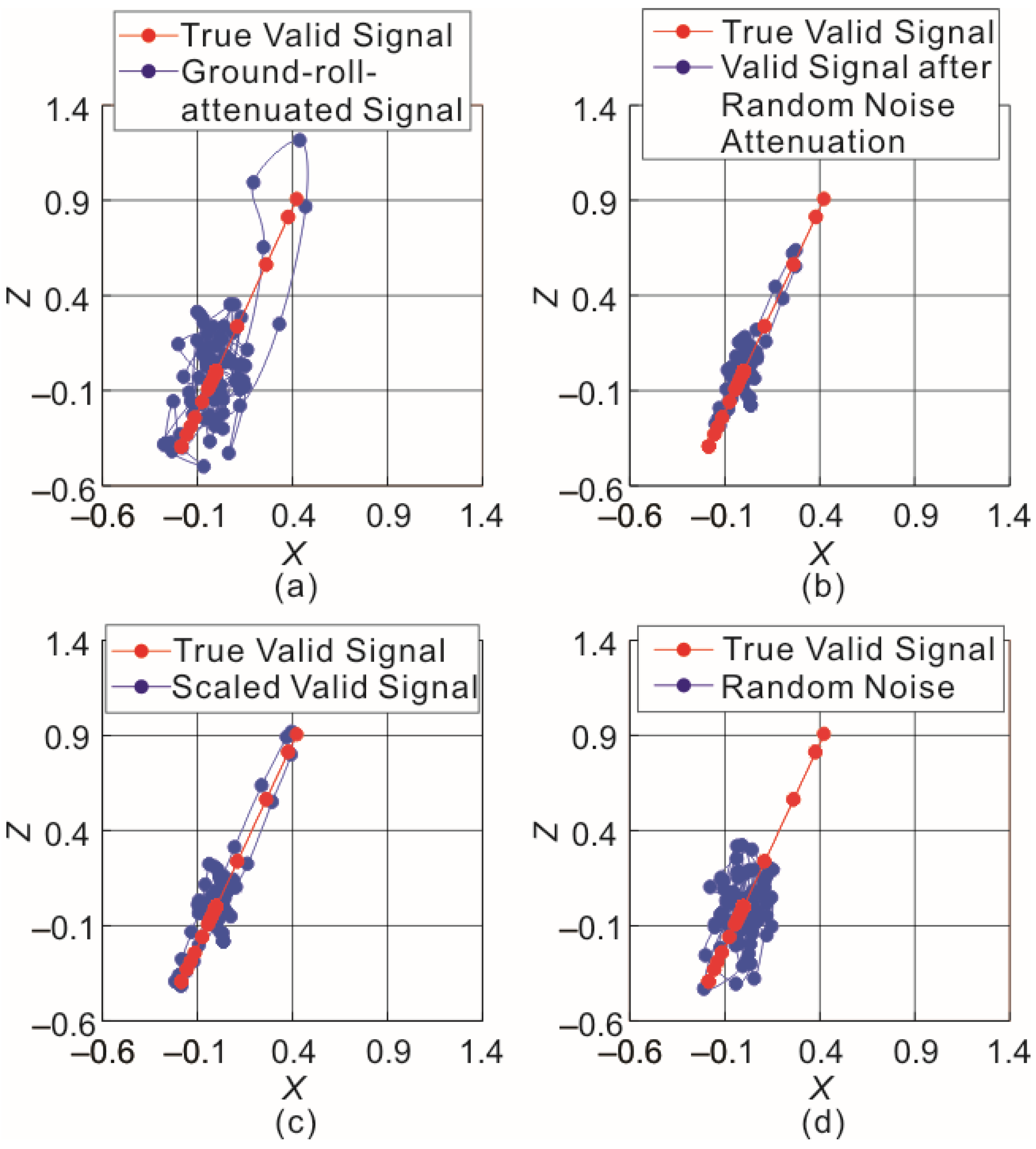
2.1. Wave Vector Estimation
2.2. Ground Roll Attenuation
2.3. Attenuation of Random Noise and Other Non-Ground-Roll Related Coherent Noise
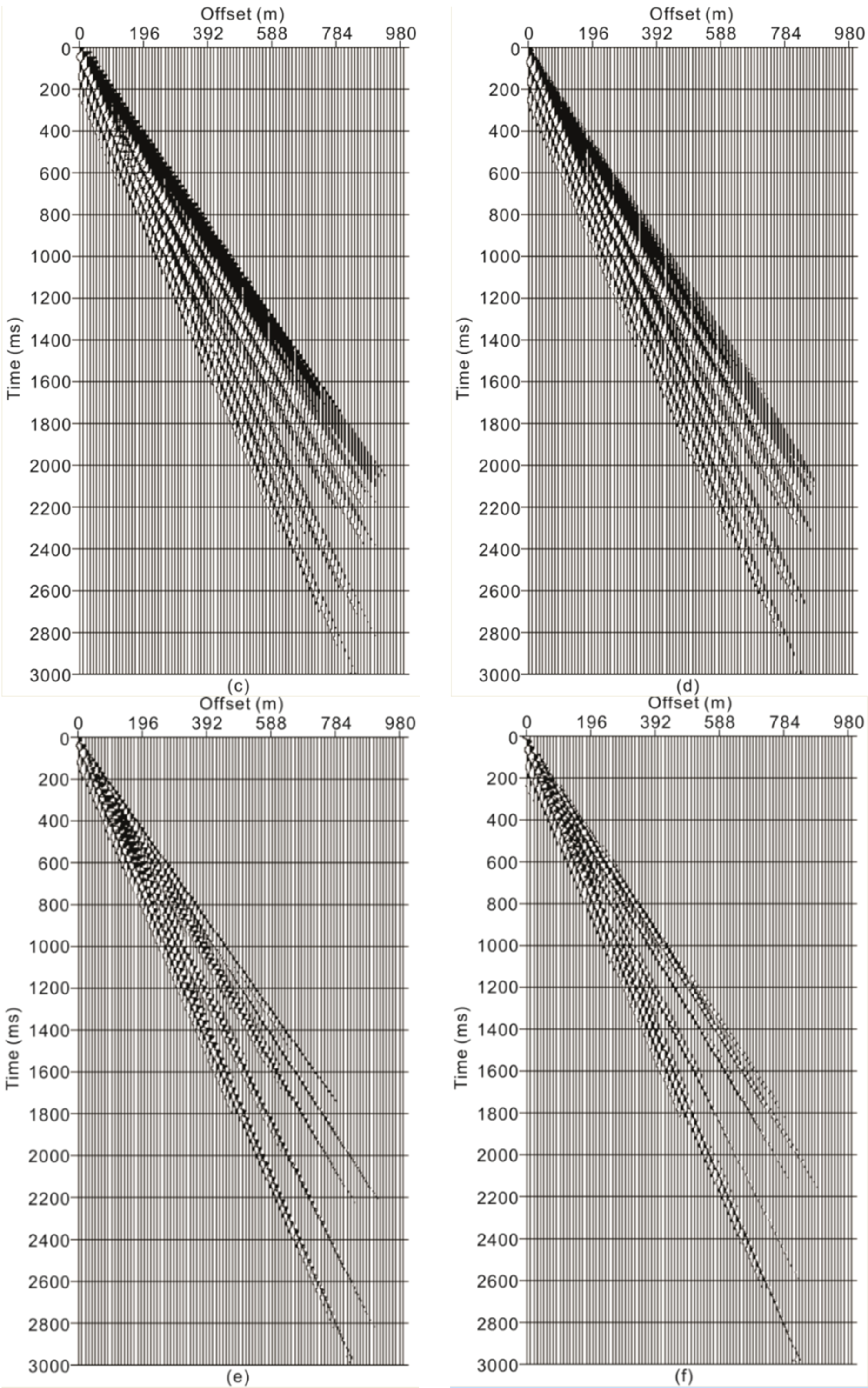
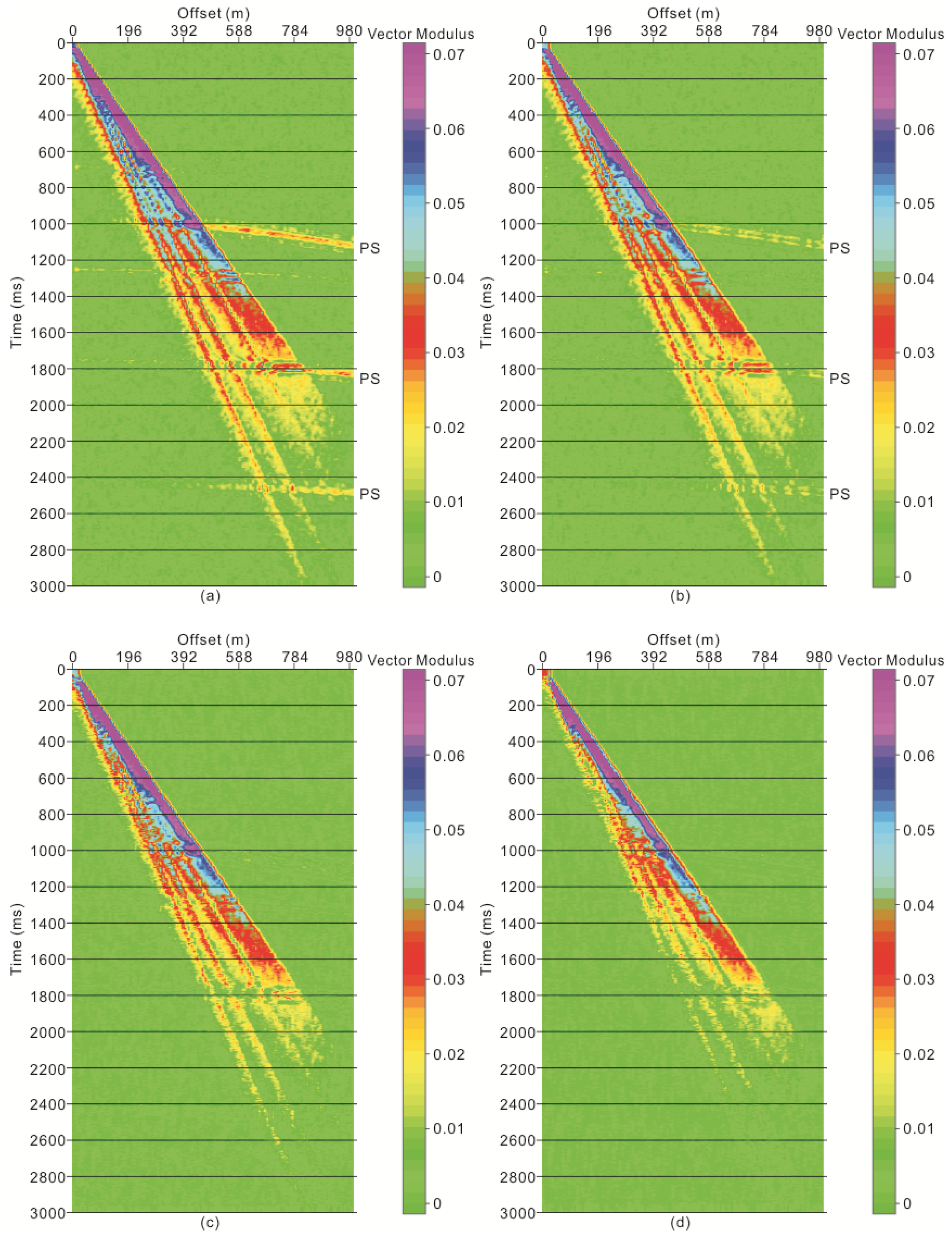
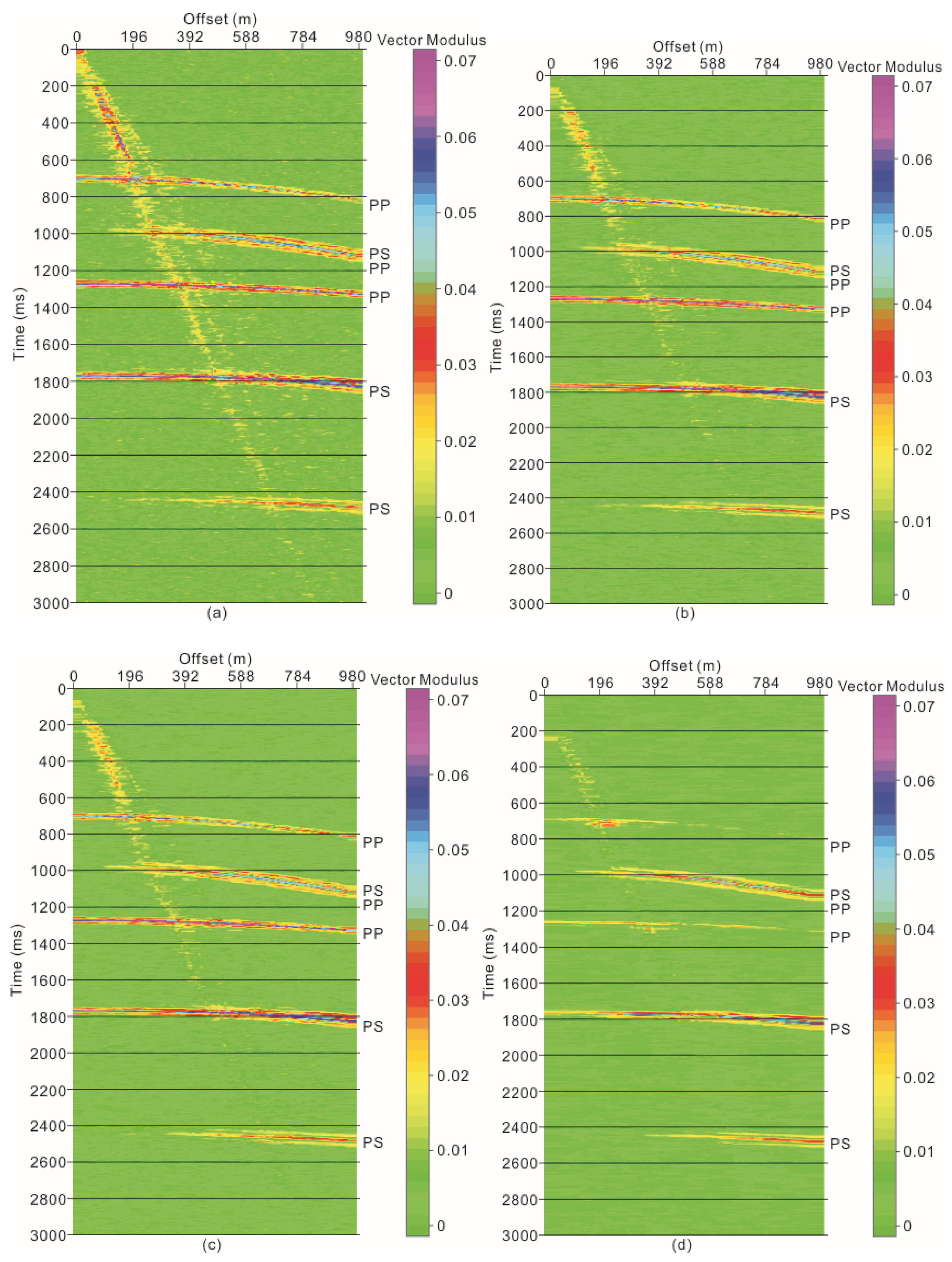
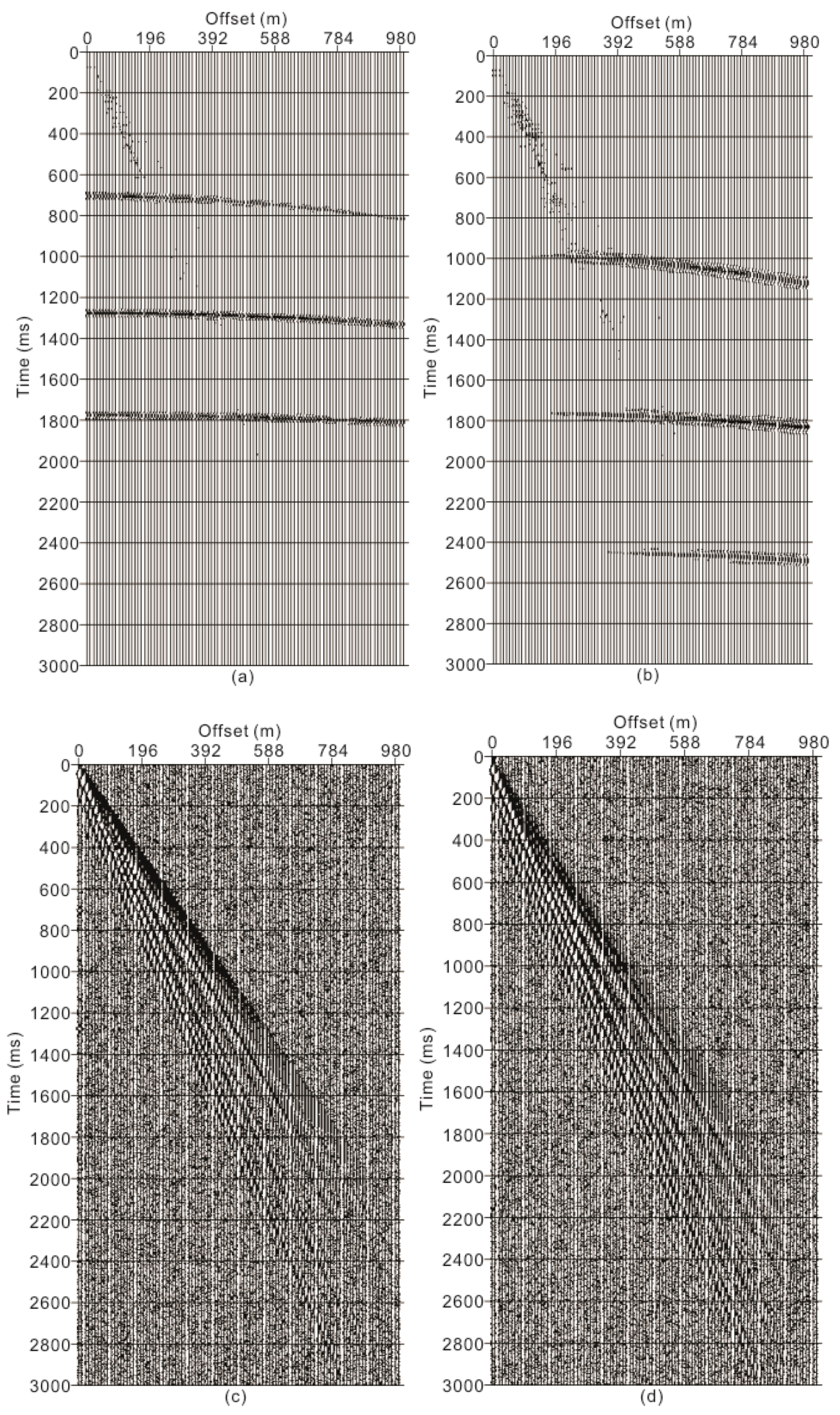
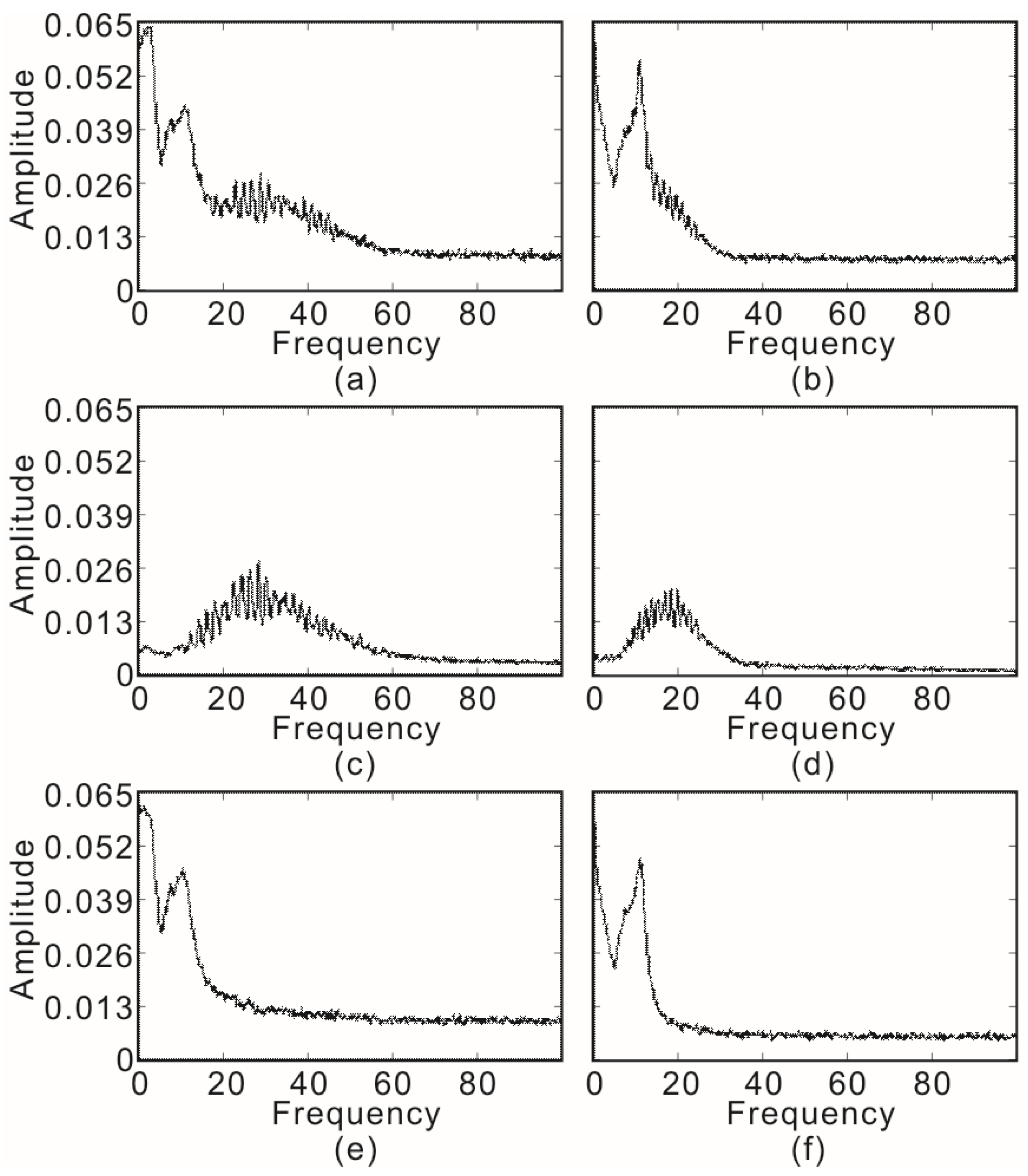
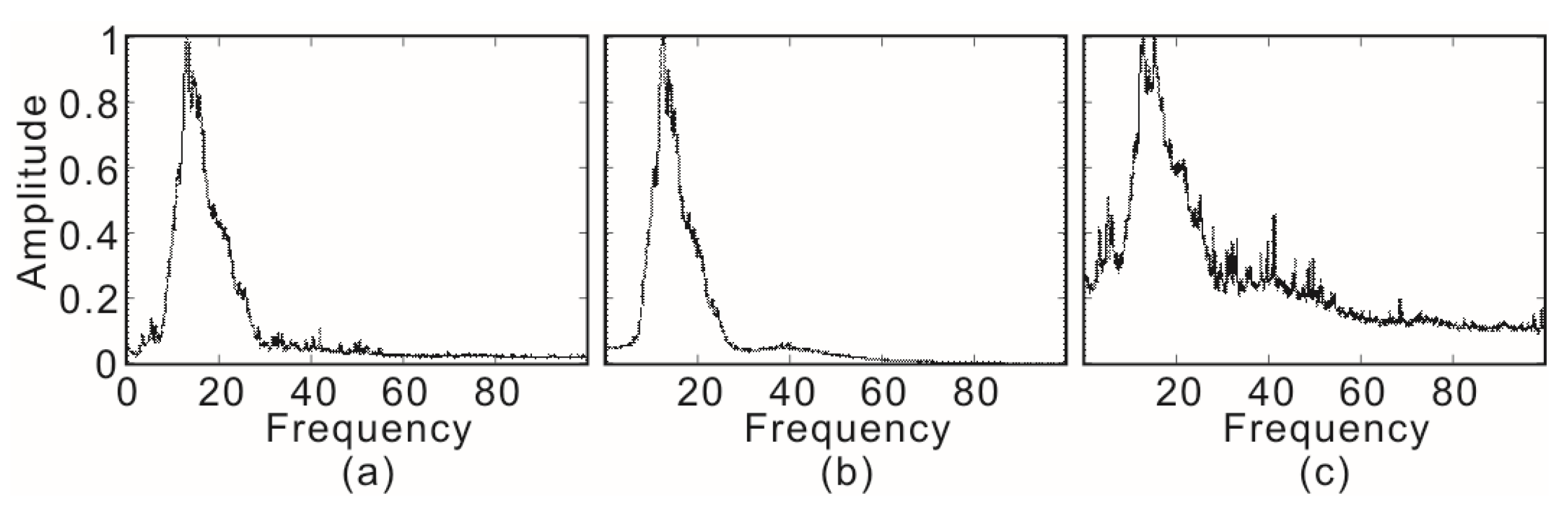
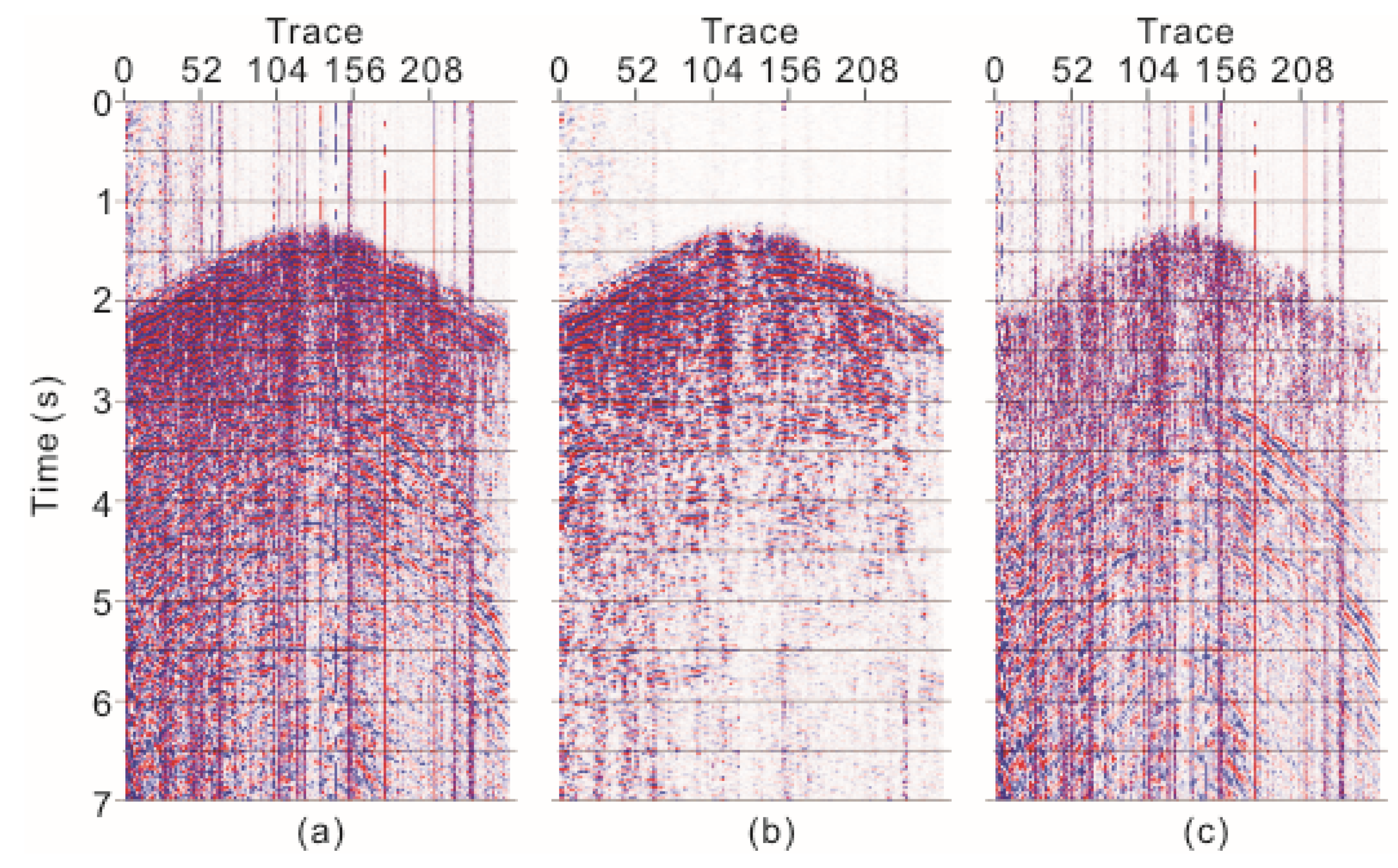
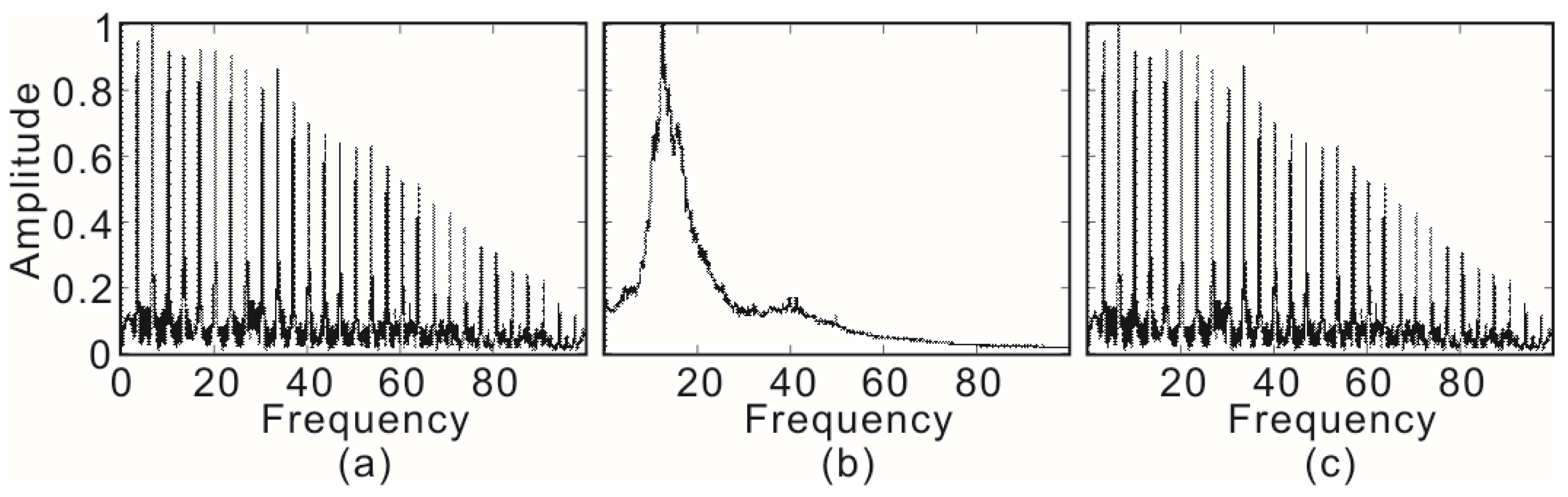
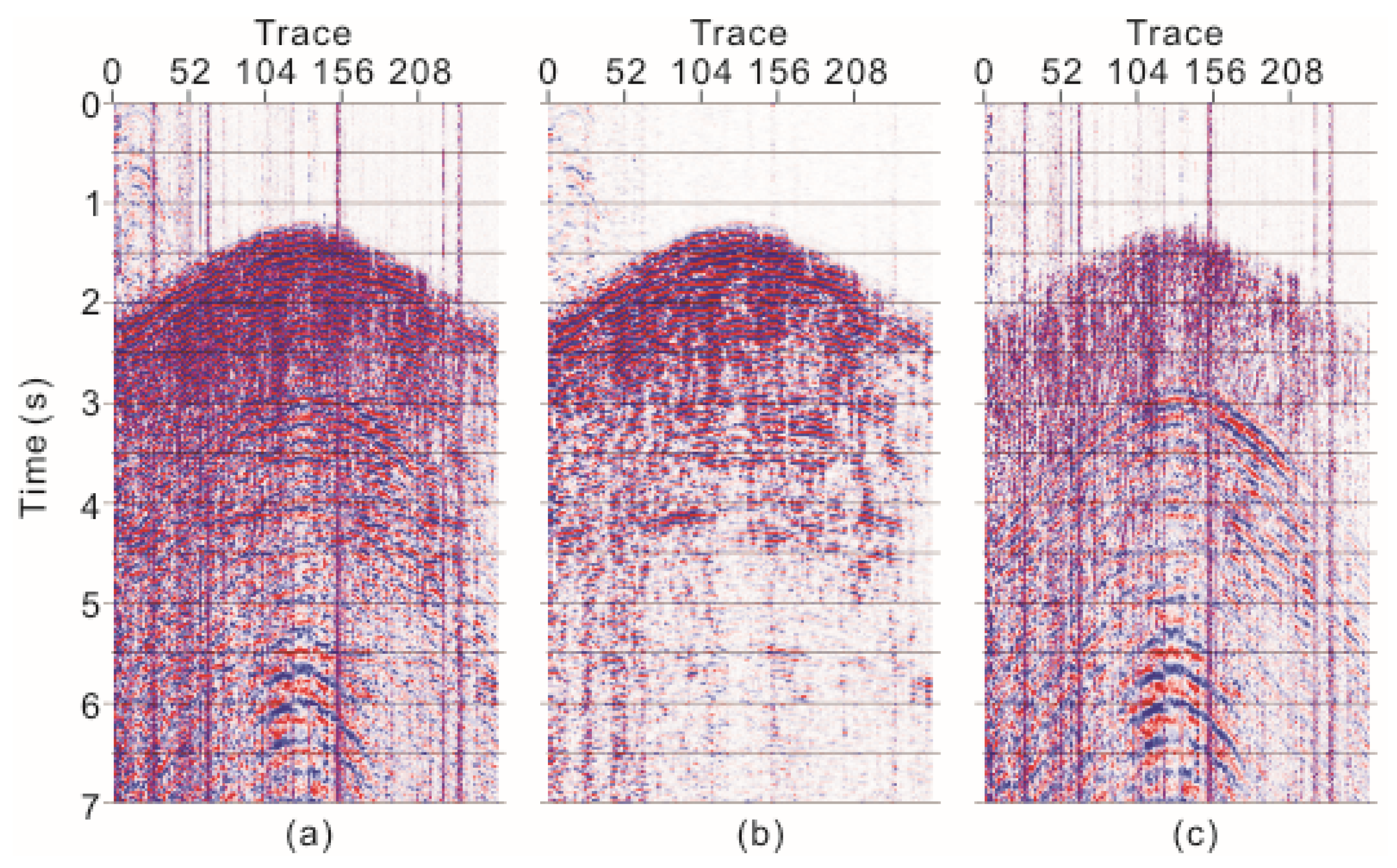
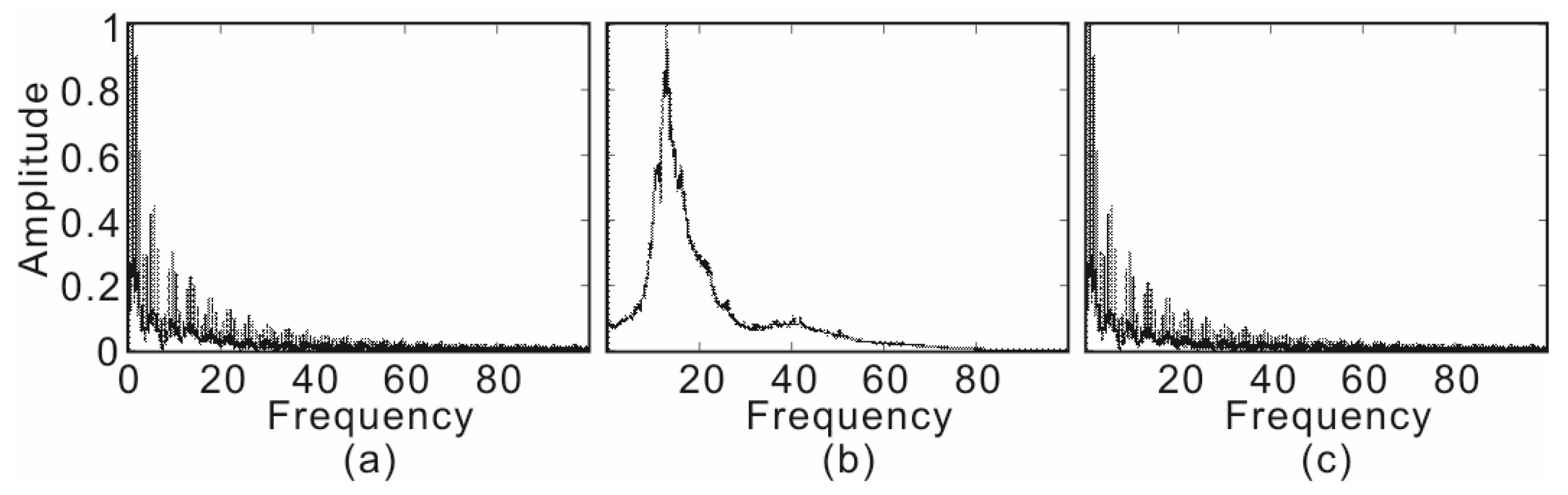
3. Numerical Data Test
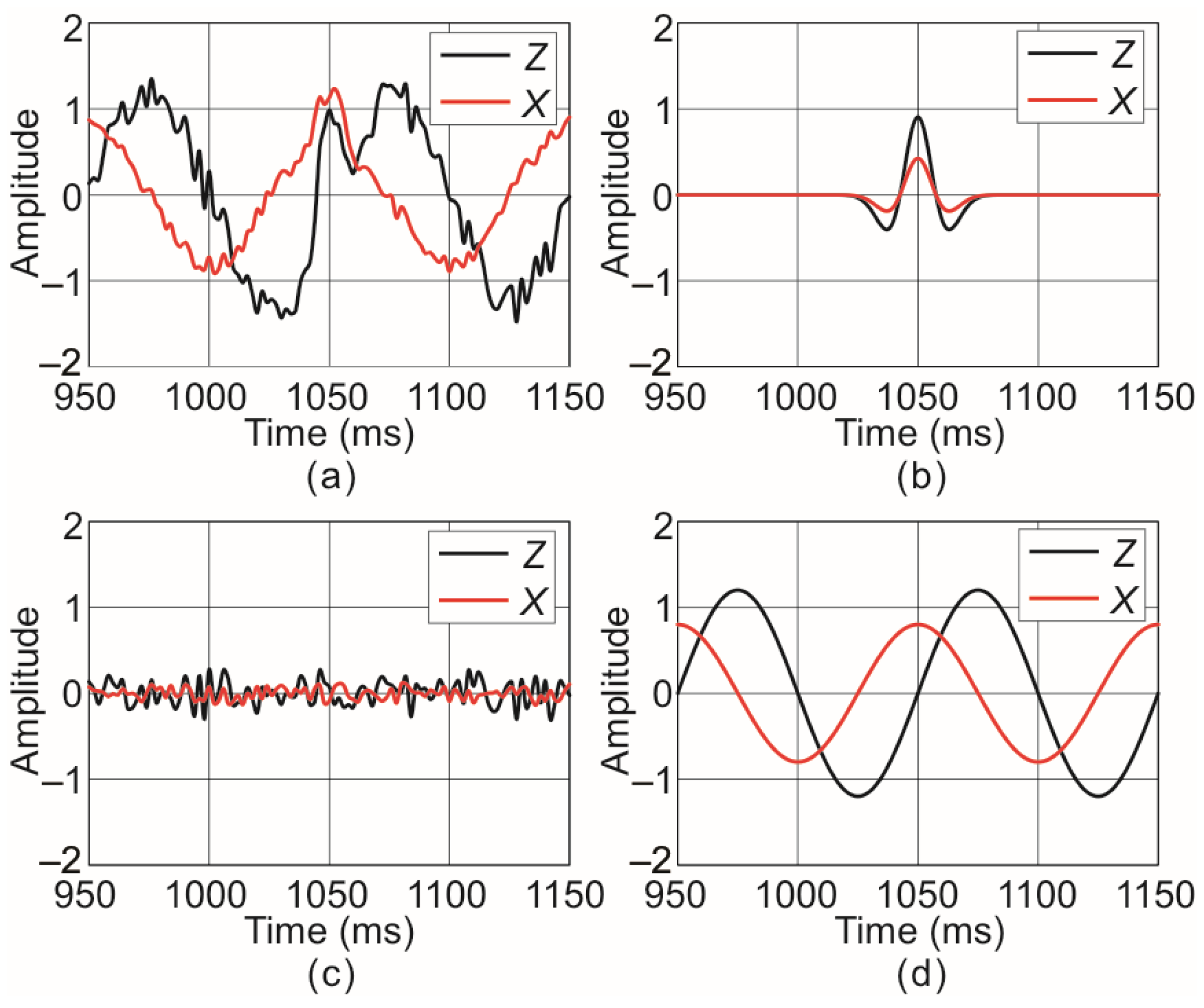
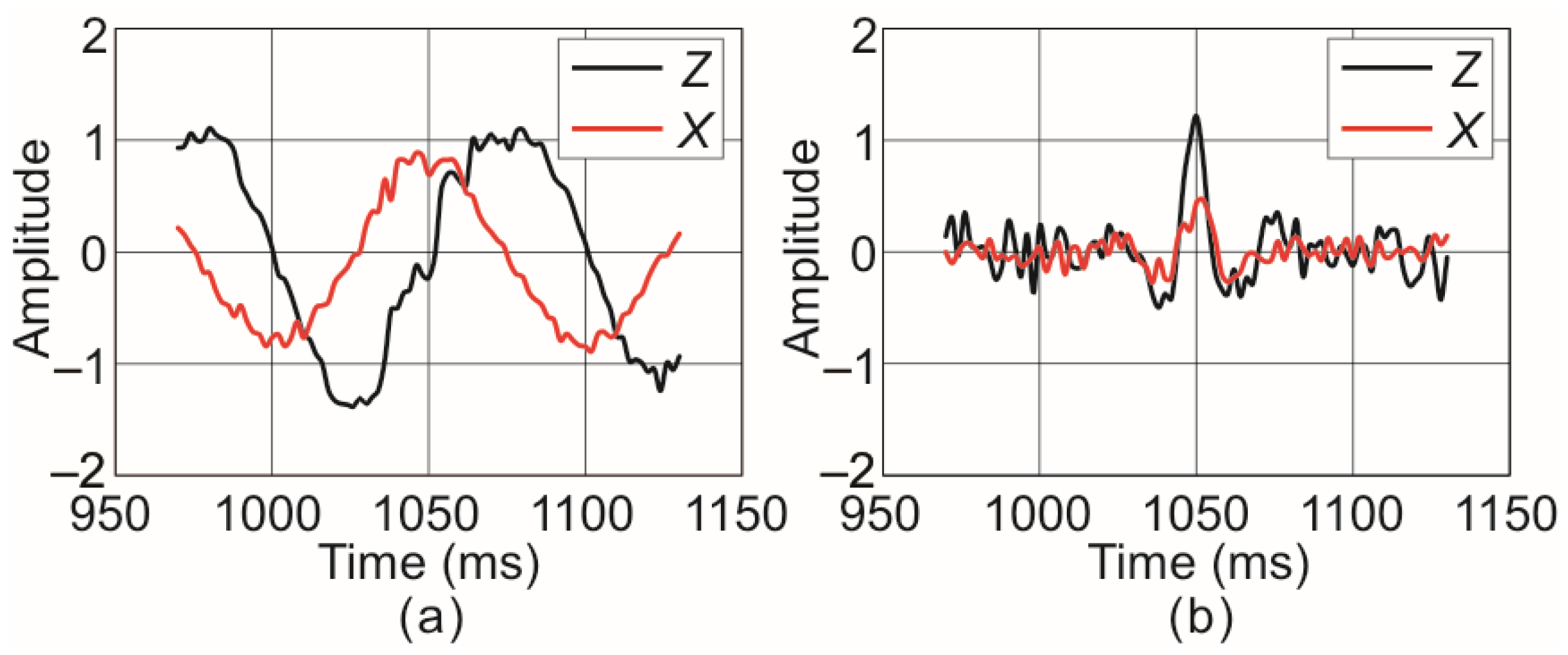
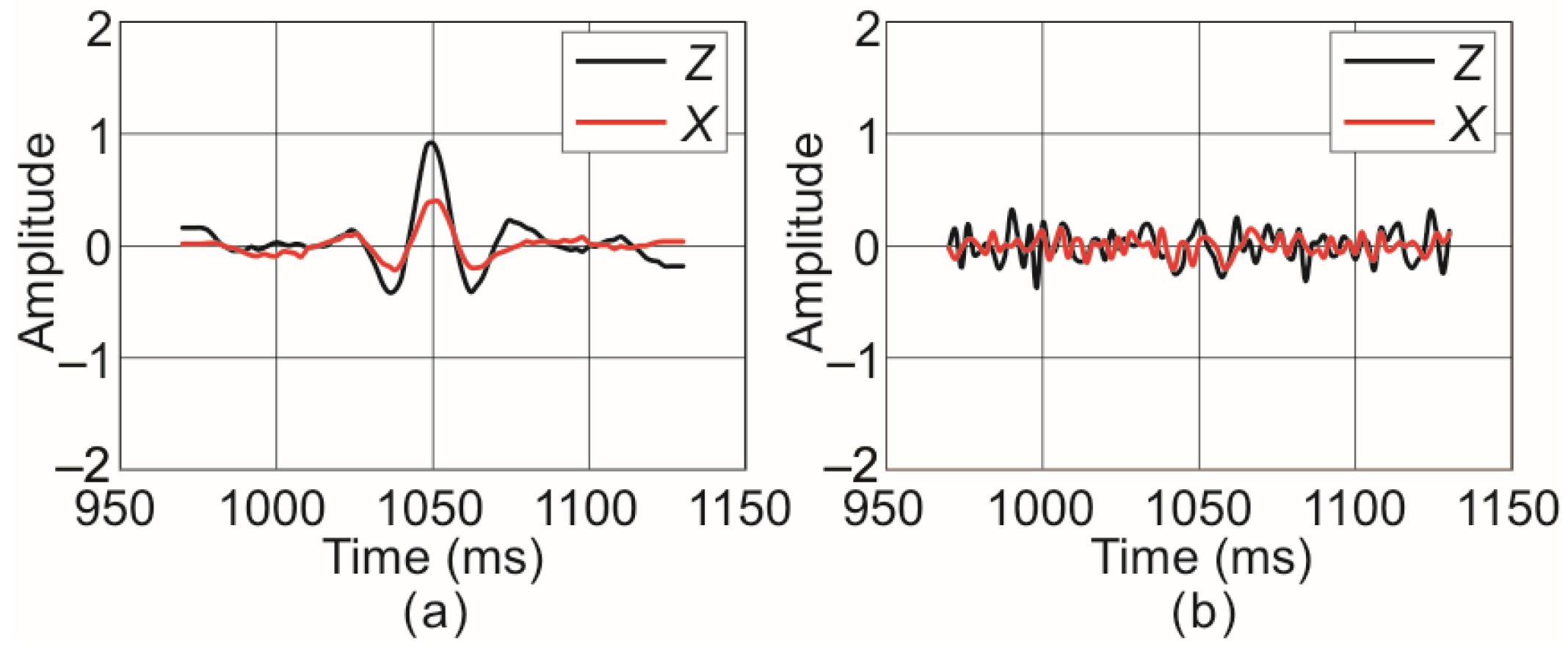
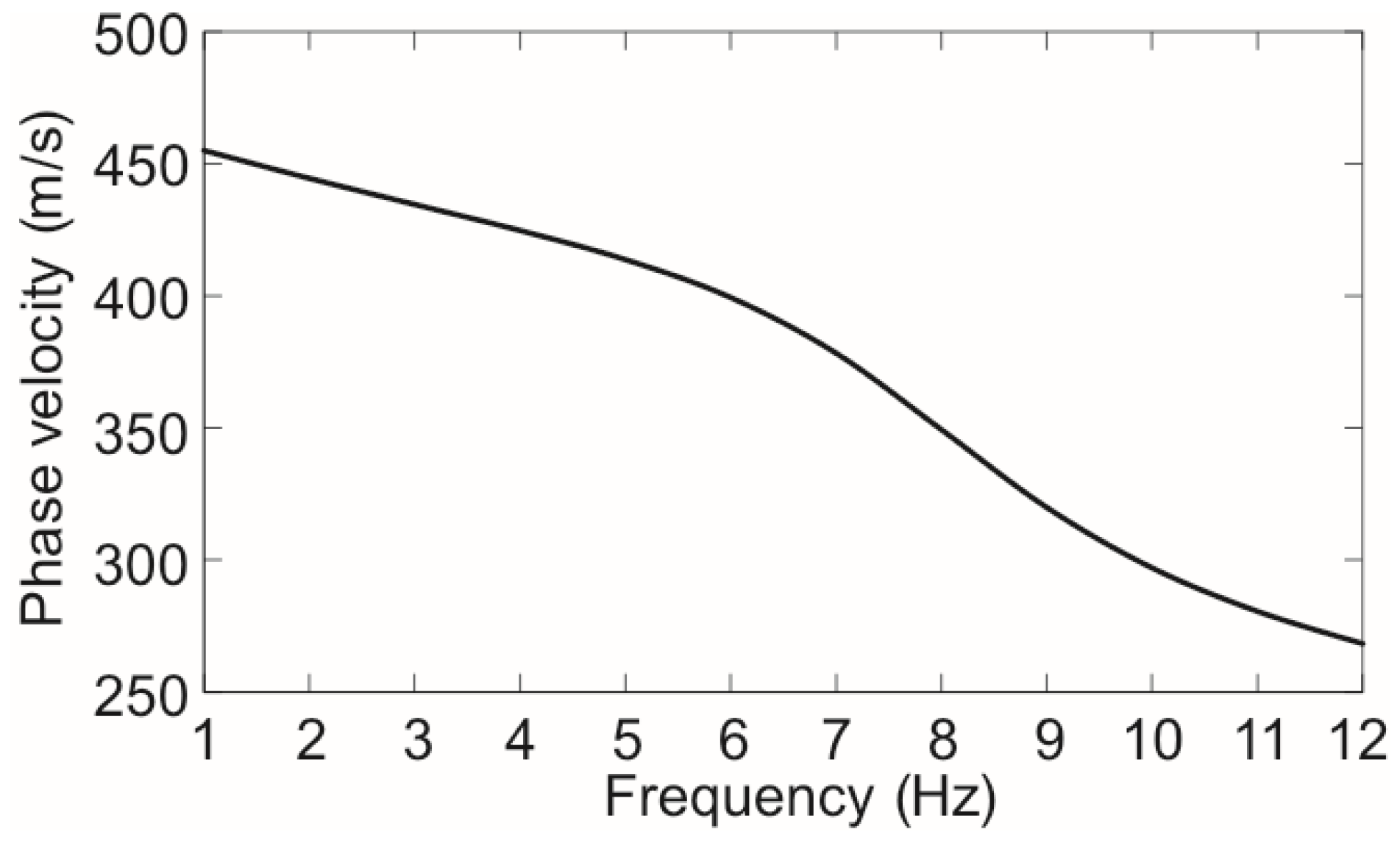
3.1. Numerical One-dimensioal Two-component Data
3.2. Two-dimensional Two-Component Synthetic Data
3.3. Comparison with Instantaneous Polarization Filtering
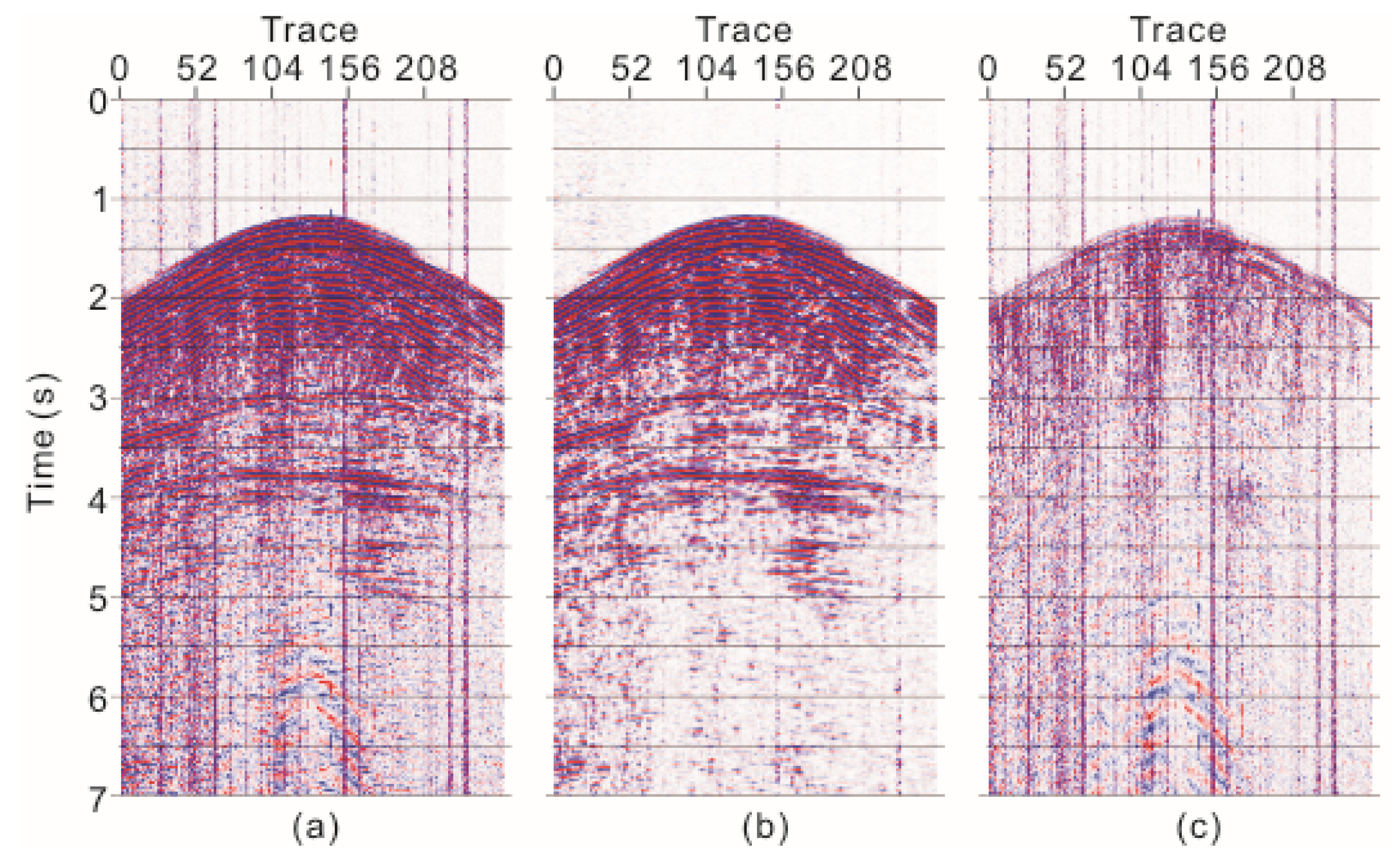
4. Application Results and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gaiser, J.E. Applications for vector coordinate systems of 3-D converted-wave data. Lead. Edge 1999, 18, 1290–1300. [Google Scholar] [CrossRef]
- Kishore, S.A.; Prosenjit, D.; Sastry, M.H.; Tewari, S.K.; Baloni, C.L. 3D-3C Seismic data acquisition—Survey design and implementation: A case study NAS Block, A & AA Basin. In Proceedings of the 9th Biennial International Conference & Exposition on Petroleum Geophysics, Hyderabad, India, 16–18 February 2012; pp. 260–264. [Google Scholar]
- Schimmel, M.; Gallart, J. Degree of polarization filter for frequency-dependent signal enhancement through noise suppression. Bull. Seismol. Soc. Am. 2004, 94, 1016–1035. [Google Scholar] [CrossRef]
- Perelberg, A.I.; Hornbostel, S.C. Applications of seismic polarization analysis. Geophysics 1994, 59, 119–130. [Google Scholar] [CrossRef]
- Schimmel, M.; Gallart, J. The use of instantaneous polarization attributes for seismic signal detection and image enhancement. Geophys. J. Int. 2003, 155, 653–668. [Google Scholar] [CrossRef]
- Flinn, E.A. Signal analysis using rectilinearity and direction of particle motion. Proc. IEEE 1965, 53, 1874–1876. [Google Scholar] [CrossRef]
- Montalbetti, J.F.; Kanasewich, E.R. Enhancement of teleseismic body phases with a polarization filter. Geophys. J. Int. 1970, 21, 119–129. [Google Scholar] [CrossRef]
- Kanasewich, E.R. Time Sequence Analysis in Geophysics, 3rd ed.; University of Alberta Press: Edmonton, AB, Canada, 1981. [Google Scholar]
- Vidale, J.E. Complex polarization analysis of particle motion. Bull. Seismol. Soc. Am. 1986, 76, 1393–1405. [Google Scholar]
- Du, Z.; Foulger, G.R.; Mao, W. Noise reduction for broad-band, three-component seismograms using data-adaptive polarization filters. Geophys. J. Int. 2000, 141, 820–828. [Google Scholar] [CrossRef]
- Kulesh, M.; Diallo, M.S.; Holschneider, M.; Kurennaya, K.; Krüger, F.; Ohrnberger, M.; Scherbaum, F. Polarization analysis in the wavelet domain based on the adaptive covariance method. Geophys. J. Int. 2007, 170, 667–678. [Google Scholar] [CrossRef]
- Benhama, A.; Cliet, C.; Dubesset, M. Study and applications of spatial directional filtering in three-component recordings. Geophys. Prospect. 1988, 36, 591–613. [Google Scholar] [CrossRef]
- Shieh, C.-F.; Herrmann, R.B. Ground roll: Rejection using polarization filters. Geophysics 1990, 55, 1216–1222. [Google Scholar] [CrossRef]
- Kragh, E.; Peardon, L. Ground roll and polarization. First Break 1995, 13, 369–378. [Google Scholar] [CrossRef]
- De Franko, R.; Musacchio, G. Polarization filter with singular value decomposition. Geophysics 2001, 66, 932–938. [Google Scholar] [CrossRef]
- Tiapkina, O.; Landrø, M.; Tyapkin, Y.; Link, B. Single-station SVD-based polarization filtering of ground roll: Perfection and investigation of limitations and pitfalls. Geophysics 2012, 77, V41–V59. [Google Scholar] [CrossRef]
- Samson, J.C. The spectral matrix, eigenvalues, and principal components in the analysis of multichannel geophysical data. Ann. Geophys. 1983, 1, 115–119. [Google Scholar]
- Park, J.; Vernon, F.L., III; Lindberg, C.R. Frequency dependent polarization analysis of high-frequency seismograms. J. Geophys. Res. 1987, 92, 12664–12674. [Google Scholar] [CrossRef]
- Jurkevics, A. Polarization analysis of three-component array data. Bull. Seismol. Soc. Am. 1988, 78, 1725–1743. [Google Scholar]
- Morozov, I.B.; Smithson, S.B. Instantaneous polarization attributes and directional filtering. Geophysics 1996, 61, 872–881. [Google Scholar] [CrossRef]
- Diallo, M.S.; Kulesh, M.; Holschneider, M.; Scherbaum, F. Instantaneous polarization attributes in the time-frequency domain and wavefield separation. Geophys. Prospect. 2005, 53, 723–731. [Google Scholar] [CrossRef]
- Diallo, M.S.; Kulesh, M.; Holschneider, M.; Kurennaya, K.; Scherbaum, F. Instantaneous polarization attributes based on an adaptive approximate covariance method. Geophysics 2006, 71, V99–V104. [Google Scholar] [CrossRef]
- Diallo, M.S.; Kulesh, M.; Holschneider, M.; Scherbaum, F.; Adler, F. Characterization of polarization attributes of seismic waves using continuous wavelet transforms. Geophysics 2006, 71, V67–V77. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Y.; Yang, C.Y. Instantaneous polarization filtering focused on suppression of surface waves. Appl. Geophys. 2010, 7, 88–97. [Google Scholar] [CrossRef]
- Diallo, M.S.; Ross, W.S.; Shatilo, A.P.; Dura-Gomez, I.; Szurek, G.C. Application of constrained polarization filtering for surface-wave mitigation: Three case studies. Geophysics 2012, 77, V169–V181. [Google Scholar] [CrossRef]
- Hou, S.; Luo, Y.; Kelamis, P.G. Simultaneous sources separation via multidirectional vector-median filtering. Geophysics 2012, 77, V123–V131. [Google Scholar]
- Liu, Y. Noise reduction by vector median filtering. Geophysics 2013, 78, V79–V86. [Google Scholar] [CrossRef]
- Al-Dossary, S.; Marfurt, K.J. Lineament-preserving filtering. Geophysics 2007, 72, P1–P8. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Y.; Yang, Y.; Chen, J. Pre-stack separation of PP and split PS waves in HTI media. Geophys. J. Int. 2017, 210, 510–524. [Google Scholar] [CrossRef]
- Knopoff, L. A matrix method for elastic wave problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar]
- Schwab, F.; Knopoff, L. Surface-wave dispersion computations. Bull. Seismol. Soc. Am. 1970, 60, 321–344. [Google Scholar]
- Mao, W.; Stuart, G.M. Rapid multi-wave-type ray tracing in complex 2-D and 3-D isotropic media. Geophysics 1997, 62, 298–308. [Google Scholar] [CrossRef]
- René, R.M.; Fitter, J.L.; Forsyth, P.M.; Kim, K.Y.; Murray, D.J.; Walters, J.K.; Westerman, J.D. Multicomponent seismic studies using complex trace analysis. Geophysics 1986, 51, 1235–1251. [Google Scholar] [CrossRef]

| Density (g/cm3) | Thickness (m) | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) |
|---|---|---|---|
| 1.47 | 5 | 500 | 200 |
| 1.53 | 5 | 600 | 300 |
| 1.74 | 30 | 1000 | 500 |
| 2.19 | 760 | 2500 | 1443 |
| 2.26 | 800 | 2800 | 1617 |
| 2.33 | 800 | 3200 | 1848 |
| 2.4 | 600 | 3600 | 2078 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, Y.; Chen, J. Noise Attenuation Based on Wave Vector Characteristics. Appl. Sci. 2018, 8, 672. https://doi.org/10.3390/app8050672
Lu J, Wang Y, Chen J. Noise Attenuation Based on Wave Vector Characteristics. Applied Sciences. 2018; 8(5):672. https://doi.org/10.3390/app8050672
Chicago/Turabian StyleLu, Jun, Yun Wang, and Jingyi Chen. 2018. "Noise Attenuation Based on Wave Vector Characteristics" Applied Sciences 8, no. 5: 672. https://doi.org/10.3390/app8050672
APA StyleLu, J., Wang, Y., & Chen, J. (2018). Noise Attenuation Based on Wave Vector Characteristics. Applied Sciences, 8(5), 672. https://doi.org/10.3390/app8050672






