Featured Application
The specific application of the research aims to the port transportation, the working efficiency can be improved considering findings of this article.
Abstract
A novel control algorithm combining the linear quadratic regulator (LQR) control and trajectory planning (TP) is proposed for the control of an underactuated crane system, targeting position adjustment and swing suppression. The TP is employed to control the swing angle within certain constraints, and the LQR is applied to achieve anti-disturbance. In order to improve the accuracy of the position control, a differential-integral control loop is applied. The weighted LQR matrices representing priorities of the state variables for the bridge crane motion are searched by the multi-objective genetic algorithm (MOGA). The stability proof is provided in order to validate the effectiveness of the proposed algorithm. Numerous simulation and experimental validations justify the feasibility of the proposed method.
1. Introduction
Nowadays, the development of port transportation brings with it increasing demands of cargo movement. The bridge crane system is widely applied in order to move the cargo with less cost compared to other transit systems [1]. For the crane system, it is imperative to design an effective controller that can achieve fast and safe cargo movement.
For the cargo movement control, in addition to satisfying the target position, some constraints and disturbances need to be properly dealt with, including maximum moving speed and distance, maximum swing angle, etc. Focusing on these practical challenges, the designed controller should satisfy the demands, including fast response, high robustness, and stability, as well as strong anti-disturbance. Among them, the most important task is to regulate the crane to the desired position, and meanwhile to suppress the payload swing. In terms of this, the traditional control methods can be divided into two categories, i.e., open loop and closed loop methods.
For open loop control methods, the control commands are determined in advance according to the requirements before operation. The popular methods include input shaping control [2,3], trajectory planning (TP) control [4,5], etc. The input shaping control is imposed in order to produce a series of pulses according to the ratio between the system frequency and the damping; then, the convolution between the pulse and the reference trajectory is conducted in order to generate the control command. This method can guarantee the control performance for the crane position when the cable length changes, whereas the residual swing of the payload cannot be eliminated. By TP, the crane trajectory can be designed based on the nonlinear coupling relationship between the crane position and the swing angle, thereby ensuring the cargo’s safety when moving and suppressing the residual oscillation. Both methods can satisfy the controlling target. However, when the system is under external disturbance, such as wind and human touch, the payload oscillation can be potentially triggered, and yet cannot be eliminated effectively based on the open loop methods.
In order to overcome the influence of the external disturbance, various closed loop methods are proposed, which can be divided into adaptive control [6,7,8], fuzzy logic-based control [9,10], genetic algorithms (GA) [11,12], feedback linearization control [13,14], linear quadratic regulator (LQR) control [15,16,17], proportional–integral–differential (PID) control [18,19,20], etc. In [21], Zhang and He considered the crane velocity, the position error, and the swing angle totally in a linearized manner, and an adaptive sliding mode controller is designed. However, the convergence and boundedness proof of the position error and swing angle are not given. Based on linearization, the PID control algorithm, regulated by the fuzzy logic algorithm, is employed in order to improve the crane’s transient performance and robustness. Since the GA is capable of finding the optimal solutions, a nonlinear control algorithm is proposed based on a real-time GA in order to solve the difficulty of regulating the control gain [12,22,23,24]. In this manner, the whole control performance of the crane system is improved. Actually, it is difficult for the GA algorithm to ensure the stability strictly at the equilibrium point theoretically, and the controller design is relatively complex, bringing inconvenience for practical application.
For sake of reducing the controller complexity and easily applying it in actual operation, the feedback linearization control algorithm is introduced based on the simplified crane model, which divides the crane motion and the payload swing into two subsystems [25,26,27,28]. A nonlinear coupling control method is designed to ensure that the crane position and the payload swing can finally converge to specified ranges. Based on the model linearization, the LQR method is harnessed to achieve the control using the feedback gain of the linear systems [29]. Although the LQR method is simple and highly efficient, the system states can possibly deviate from the equilibrium points when the system is disturbed by external signals, and thus, it is difficult to guarantee the stability of the control performance. To solve this problem, the constraint of the payload swing and the capability of anti-disturbances need to be taken into account, and some combined algorithms of open loop and closed loop methods are introduced [30,31,32]. In [30], Blajer and Kołodziejczyk employed the feedforward control and the feedback PID control together, according to the inverse dynamics analysis. However, this method lacks the stability analysis, and it is difficult to satisfy the demand of the payload angle and crane position simultaneously with the PID control.
Aiming at these considerations, a combined open loop and closed loop method is herein proposed to satisfy the constraint of the payload swing, and precisely realize the position control of the crane. First, the motion path of the crane is designed by TP, which keeps the payload swing states in the vicinity of the equilibrium point due to the underactuated characteristics. By this manner, the constraints of the swing angle can be satisfied, and the residual swing can be eliminated. Then, an updated LQR algorithm is introduced to improve the precision of the crane position and the payload swing control, which are immune from external disturbance. Here, for the sake of the multi-freedom control for the crane position, a differential and integral control loop is added to track the crane position with fast speed. In order to gain preferable control effects, a multi-objective GA (MOGA) algorithm is employed to achieve the different motion state optimization by searching the weighed matrices of the LQR [33]. The MOGA is characterized by the weight of the multi-objective functions being assigned randomly; thus, its search direction is not fixed. A set of Pareto optimal solutions can be retained and uniformly distributed during implementation [34,35]. By this manner, the MOGA exhibits the advantage of the diversity of solutions, and meanwhile, the computational complexity is lower compared with the traditional GA [36,37]. Finally, the quasioptimal control of the crane is reached by simulation and experiment validation.
The remainder of this paper is structured as follows. The detailed modeling and associated constraints are introduced in Section 2. The controller design and its stability proof are provided in Section 3. The feasibility of the proposed method is verified by the simulation and experiments in Section 4 and Section 5, respectively. Finally, conclusions are drawn in Section 6.
2. Dynamic Modeling of the Crane System
In order to design an algorithm with the target of precise position control and anti-disturbance, the physical model of the two-dimensional (2D) underactuated system is established, as shown in Figure 1. In order to simplify the modeling, some assumptions are made.
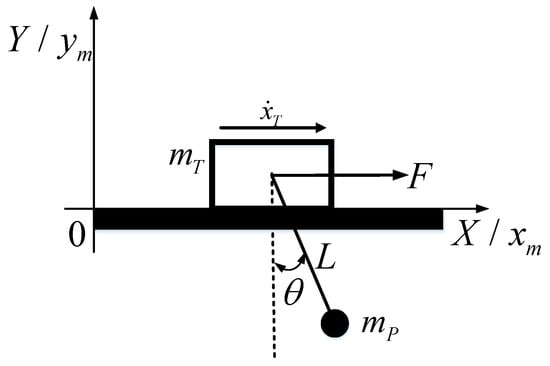
Figure 1.
Crane physical model.
Assumption 1.
The crane is a rigid driving system, and the payload is assumed to be a rigid body. Additionally, the air friction is neglected.
Assumption 2.
The cable length is unchanged.
Assumption 3.
The payload swing angle satisfies < < .
With these assumptions, dynamic equations can be formulated [32]:
where is the horizontal position of the payload, is the crane horizontal position, is the cable length, and are the mass of the crane and payload, respectively, presents the gravity factor, and is the driving force. Through the geometric operation and analysis, the payload position can be obtained:
It can be found that due to the underactuated characteristics, the payload swing cannot be designed directly, and instead it can be planned by the coupling relationship between the crane and the payload. From Equation (2), we can provide the theoretical analysis for the subsequent control methods.
During the process of the actual transportation, the payload swing should be imposed within the small angle, i.e.,:
According to Equations (2) and (4), the dynamic equations can be simplified as:
In order to fully consider the Stribeck effect, the friction, and the crane mass, is selected as the control command. Now, the matrix equation of model can be established according to Equation (5):
where is the state matrix of the bridge crane, T states the matrix transposition, and denotes the crane acceleration.
Aiming to satisfy the real-world requirement, three constraints are considered.
Constraint 1.
The crane is required to reach the target position within a limited time :
Constraint 2.
The velocity and acceleration of the crane should be restricted due to the actual limitation of actuators:
Constraint 3.
The maximum swing angle of the payload should be bounded:
where are defined as the maximum velocity and maximum acceleration, respectively, and is the limited maximum swing angle.
Next, the corresponding controller design is detailed in the following section.
3. Control Design
In this paper, a LQR algorithm based on the TP is proposed for the 2D underactuated system with the target of minimizing the regulating time and guaranteeing the swing angle under the constraints. The flowchart of the overall controller design is shown in Figure 2.
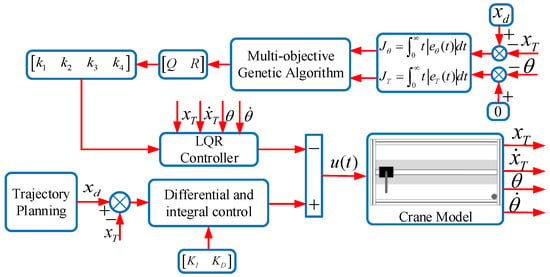
Figure 2.
Flowchart of the controller design.
As can be seen in Figure 2, the whole control framework consists of four parts, namely: the trajectory planning, the LQR controller, the crane model, and the MOGA algorithm. First, according to the desired position, the planning trajectory of the crane motion is planned in advance. Then, the modified LQR algorithm, which combines the differential and integral controllers, is implemented to control the bridge crane system with the help of the designed trajectory. The weighted matrixes of the improved LQR controller are determined based on the MOGA, with the target of minimizing the integration of the time-weighted absolute value of the errors (ITAEs) for the payload swing and the crane position. By this manner, the control merits of the TP and LQR can be combined to better reach the control target.
3.1. Trajectory Planning Control
Based on the geometrical analysis, an efficient trajectory imposed by Constraints 1 to 3 can be acquired. The second-order ordinary differential equation and its derivative equation are solved based on Equation (5):
where , , and denote the initial swing and the angle velocity of the payload, respectively.
Since the payload does not oscillate at the initial motion point, and equal zero. Based on Equations (10) and (11), we can get:
where .
Now, the phase plane is employed in terms of Equation (12) for further analysis, of which and refer to the longitudinal coordinate and the horizontal coordinate, respectively, as shown in Figure 3. To implement the intuitive illustration, the following three cases are discussed according to different values of the acceleration.
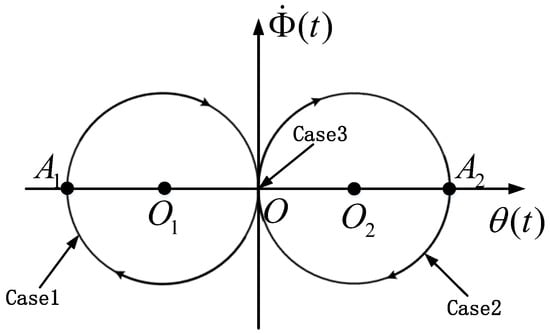
Figure 3.
Phase plane of the payload.
Case 1.
When , the vector in the phase plane moves in the clockwise direction at a constant angular velocity ;
Case 2.
When , the vector moves in the counterclockwise direction at the same velocity;
Case 3.
When , the vector stays in the original point; namely, there does not exist any relative motion between the crane and the payload.
Here, an appropriate trajectory is determined considering the geometric properties. Based on the above analysis, the primary expression can be furnished as:
where is the duration of the acceleration, and is the duration for the constant speed stage.
As shown in Figure 3, , and can be determined according to the geometric properties. At the beginning of acceleration, the vector starts to move from the original point towards with the angular velocity . After reaching , the maximum payload swing is achieved, and the relationship with respect to and can be determined, i.e.,:
and they should be satisfied with the following constraints:
The payload swing reaches zero after one complete acceleration cycle. At , the crane stops accelerating and keeps its speed unchanged, while the load’s swing angle maintains zero, as stated in Case 2. In addition, during the deceleration process presented in Case 3, the similar phenomenon can also be observed: that one cycle is required to be undergone in order to reach the target position through point , during which the residual angle can be eliminated.
Based on the previous analysis, the duration in terms of acceleration/deceleration stages requires the same time cost, i.e., . Given the chosen target position, the motion states can be determined after an integral calculation:
The displacement of the entire operation period can be calculated as:
where . Moreover, the duration during the acceleration and constant velocity period can be calculated:
where is the maximum velocity of the crane. Note that a pivotal condition versus should be considered here due to , which can be furnished as:
Combining with Equations (9), (14), and (19), the constraint can be set:
Now, based on Equations (8) and (21), the upper limit of the maximum acceleration can be yielded:
where indicates the boundary value of the acceleration, and finally, . The velocity constraint can be calculated considering Equation (20) in order to improve the efficiency, and thus, the maximum velocity can be defined as:
Meanwhile, the maximum acceleration can be determined:
Now, all of the parameters are determined considering the designed requirements. In the next step, the corresponding controller and its parameters are designed with care.
3.2. LQR Control Based on Trajectory Planning
The TP algorithm is easy to apply, which can take the moving efficiency and maximum payload swing into account. However, it is difficult to adaptively adjust the swing for the payload in practical conditions, and the oscillation cannot be suppressed when external disturbance exists. Hence, the TP algorithm combined with the closed-loop control can effectively solve these problems.
For the underactuated system, there exists multiple motion states, and thus, it is necessary to attain the feedback control. According to Equation (6), the LQR control law from the feedback input yields:
where can be calculated by minimizing the energy function of LQR , as:
where is a semi-definite matrix of , and is a positive define matrix constant of . Then, can be calculated as:
where is a positive definite symmetric matrix, which is evaluated from the Algebraic Riccati equation (ARE) as:
By this manner, the gain of LQR feedback = can be estimated, and the crane acceleration can thus be determined. In order to accomplish the position control accurately, the differential and integral control is introduced for the crane’s position adjustment. Hence, the improved controller can be expressed as:
where is the control input; and , , , and , belonging to , are defined as feedback gains for the crane position and velocity, the payload swing, and the angular velocity, respectively. is the error trajectory of the crane system, and can be determined based on and by engineering experience. However, it is difficult to find the optimal solution in this manner. and are integral and differential gains, which are designed by the response optimization, and the constraint of the response optimization can be expressed as:
where is the simulated response of the crane position, and is the piecewise linear bound of the crane position.
3.3. Multi-Objective Optimization
It is critical to determine the control parameters of the designed algorithm, i.e., , , , and , and thus, the weighted matrixes and need to be optimized. Here, integration of time-weighted absolute value of the error (ITAE) is introduced in order to evaluate the convergence and oscillation of the system, as:
where and denote the ITAEs of the payload swing and the crane position, respectively. Here, the MOGA is applied to find optimal solutions among multiple objective functions. According to the optimal method, a series of points reflecting the control effects can be presented based on the ITAEs of the crane and payload. In addition, the optimization process should be subject to the following constraints:
Here, we employed the MOGA algorithm to calculate the optimization parameters with the criteria of minimizing the ITAE of the crane position and the payload swing. As can be seen in the Figure 4, the whole process will first choose the initial weighted matrixes and randomly. Then, the control commands can be generated based on the constraints and the updated ITAE of the crane position, and the payload swing can be calculated based on the fitness function. In the next step, the MOGA is applied to search the optimal parameters through a series of the selection, crossover, and mutation, wherein the roulette wheel selection and the two-point crossover are adopted. For the MOGA algorithm, first, some existing populations are selected to generate the next generation, and this process is known as selection. Some existing populations are considered as elitists, and are directly selected as next generations without any change. The selection criteria is based on the fitness function and their corresponding constraints. During the crossover process, the parent chromosomes are hybridized to generate new offsprings, and meanwhile, some bits of chromosomes are uniformly or randomly changed with a certain possibility. This is the so-called mutation, of which the main function is to avoid falling into a local optimum. By means of these actions, a new chromosome group is generated, which is different from the previous version. The whole action is operated iteratively until the terminal condition is reached, which usually includes exceeding the budget time, reaching the maximum allowable amount, etc. Finally, the Pareto fronts and the optimized parameters can be found. In this paper, the population size, the crossover rate, and the mutation rate of the MOGA algorithm are set to 40, 0.8, and 0.05, respectively, and the number of iterations is set to 50 after repetitive tunning. Furthermore, the constraint of the payload swing is set to be less than 4°, the maximum acceleration is defined as 5 m/s2, the maximum crane velocity is 1.5 m/s, the target position is m, and the error of two objective functions is limited within .
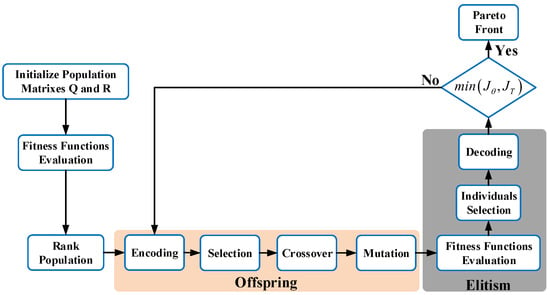
Figure 4.
Flowchart of multi-objective genetic algorithm.
Next, the stability analysis is conducted, and the stability proof is given.
3.4. Stability Analysis
Theorem.
Independently from the stochastic initial payload swing, the proposed algorithm given by Equation (29) can control the crane to the desired position and suppress the payload swing, i.e.,:
Proof.
In order to meet the demand of the theorem, a non-negative function is selected as:
Differentiating Equation (34) and combining Equation (2) with Equation (29), we can get:
According to the principle of the arithmetic mean–geometric mean (AM–GM) inequality, Equation (35) can be rewritten as:
By integrating Equation (34), we can further get:
In Equation (37), we can find that all of the integration items are bounded. Based on Equations (4) and (34), it can prove that:
Therefore, Equation (37) can be utilized to show that , Based on this fact, the following conclusion can be drawn from Equation (2). It can be proven that:
Then, Barbalat lemma [38] can then be directly utilized to show that:
And Equation (37) can be rewritten as:
Based on and Equation (38), Equation (41) can then be employed to conclude that:
According to Equations (37) and (42), it is easy to show that:
Based on Equations (2), (40), and (43), we can go through a similar analysis to show that:
Thus, Assumption 3 and Equation (4) can be employed to conclude that:
From Equations (29), (41) and (45), it is clear that:
Now, the designed controller is proved to be asymptotically stable. Next, numerical simulation and experimental validation are performed in order to validate the proposed algorithm.
4. Numerical Simulation
In this section, the simulation validation and control performance validation are conducted. All simulations are carried out based on Matlab/Simulink, and the MOGA is implemented with its built-in standard code. The crane trajectory is designed with the constraints provided by the TP. The anti-disturbance of the control is solved combining the LQR. The model parameters are shown in Table 1.

Table 1.
Model parameters.
Based on the MOGA, a series of Pareto fronts can be achieved in light of the different requirements after iterations. Since the security of the cargo has a higher priority, the swing optimal solution is considered chiefly in this section, and the optimal control solutions of the Pareto front are shown in Figure 5. The horizontal coordinate and the vertical coordinate denote the ITAEs of the swing angle and the crane’s position, respectively. According to the actual application, three solutions, including the time optimization, swing angle minimization, and the trade-off in between, are selected for further analysis, as marked in Figure 6. The weighted matrixes of three solutions, and , are obtained by the MOGA; then, the feedback gain is achieved with these weighted matrixes. The gain of the integration control and differential control, i.e., and , are acquired by the response optimization. The weighted matrixes and the parameters of these three solutions are displayed in Table 2, and the performances of them are shown in Table 3. The main tasks of Solutions 1 and 3 are to minimize the swing angle and the regulation time, respectively. The main destination of Solution 2 is the trade-off between solutions 1 and 3.
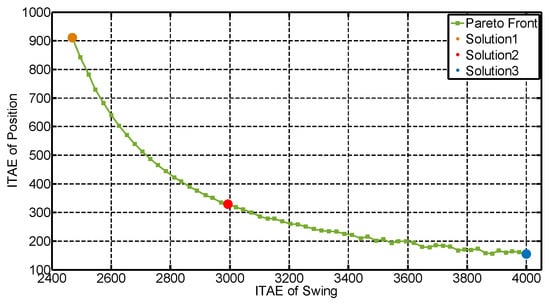
Figure 5.
Pareto optimal front.
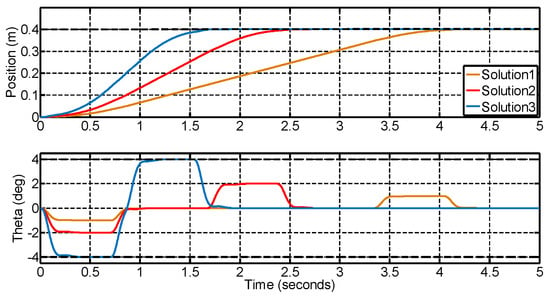
Figure 6.
The response of three kinds of solutions.

Table 2.
Performance of three solutions.

Table 3.
Performance of three solutions. ITAE: integration of the time-weighted absolute value of the errors.
It can be observed that Solution 1 is able to achieve the minimal payload swing. The maximum payload swing is 1°, and the ITAE of the swing is 2469.21, whereas it takes a longer time, i.e., 4.21 s, to reach control command. Solution 3 achieves the optimized time regulation, in which the minimum settling time is required to sacrifice the regulation swing. The settling time is 2.35 s, and the ITAE of the position control declines by 83.03%. However, the maximum payload swing increases by 3° compared with Solution 1. Solution 2 is the trade-off regulation, which means that the time is not at its minimum, and the swing is not yet smallest when compared with solutions 1 and 3. This solution is the most reasonable choice, since that its settling time is reduced by 1.53 s compared with Solution 1, and the payload swing decreases by 2° compared with Solution 3. Thus, Solution 2 can be selected as the control algorithm for the following study, since it can not only ensure the load swing angle within a small range, it can also control the load to reach the target position with fast speed.
By simulation, the parameters based on the LQR and the proposed algorithm are shown in Table 4, respectively. There exists obvious difference among the algorithm parameters, since the crane trajectory is predetermined by the proposed algorithm. From Figure 7, although the TP and LQR can achieve the effective control, the proposed controller can improve the efficiency that the TP algorithm cannot handle. As displayed in Figure 8, the performance indicators of the proposed algorithm are preferably superior to those of the other two control methods under the same swing constraint. Compared with the TP, the settling time shortens to be 1.35 s, the ITAE of the swing angle decreases by 3.24%, and the ITAE of the position decreases by 98.05%. Compared with LQR, the settling time reduced by 1.11 s, the ITAE of swing decreased by 12.82%, and the ITAE of position fell by 68.13%. Based on the above comparative analysis, we can conclude that the proposed method can achieve the position control rapidly, and meanwhile satisfy the swing constraint requirement.

Table 4.
Parameters of the linear quadratic regulator (LQR), and the proposed method.
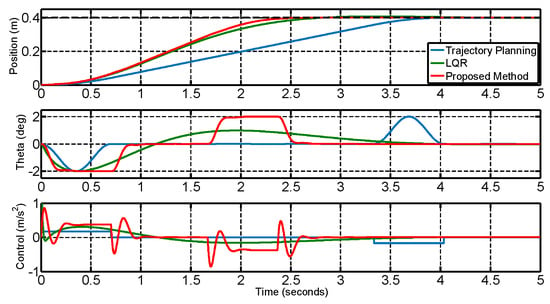
Figure 7.
Control response of trajectory planning (TP), linear quadratic regulator (LQR), and the proposed method.
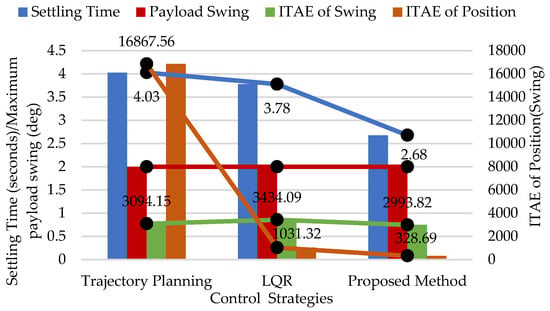
Figure 8.
Performance of three controllers.
In order to verify the anti-disturbance performance, an acceleration excitation is given to the crane, thereby leading to a certain swing angle for the payload. Here, the acceleration is set as 0.8 m/s2, and its duration as 0.2 s. The responses of the TP, LQR, and proposed algorithm are compared in Figure 9. It can be observed that the maximum payload swing of TP is 7.3° when the external disturbance occurs; obviously, it cannot meet the control demands. In addition, the LQR algorithm can suppress the swing, and the maximum swing is 2.03°. However, the whole duration is still 1.66 s. The performance of the proposed algorithm is superior to that of other control methods, and the settling time is 1.44 s. Thus, it proves that the algorithm can achieve fast, stable ability and realize immune control of external disturbances.
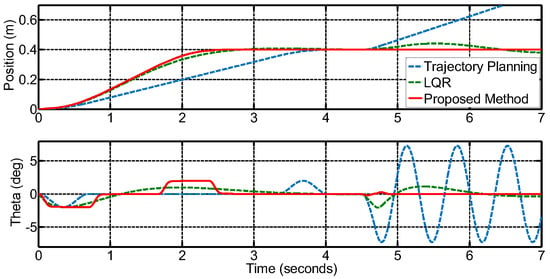
Figure 9.
Response of different controllers with external disturbances.
Next, experimental validation is performed to further justify the feasibility of the proposed algorithm.
5. Experimental Verification
In order to ensure the safety of the cargo, the payload swing should be the prior control object, and Solution 2 is selected as the method of the experiment. The experimental validation is conducted based on a test platform of B&R Industrial Automation Ltd., which supplies an integrated solution for automation systems [39]. The experimental equipment is designed based on a downsized model according to the actual bridge crane [40], as shown in Figure 10. It employs a metal lever and a metal load to simulate the actual crane line and the payload, respectively. The system applies a motor to move the crane system in a horizontal direction, thereby simulating the actual cargo transportation. Compared with actual cranes, the downsized model can meet the requirements of control algorithm regulation, and yet, the weight and vertical swing of the cable and the friction of the crane during movement cannot be taken into account [41].

Figure 10.
Anti-swing control equipment.
In the actual application, there are several factors that can possibly influence the control precision, e.g., the target position, the payload weight, the cable length, and the external disturbance. In order to justify the advance of the proposed algorithm, a series of experimental validations are carried out considering different constraints, different payloads, different cable lengths, and disturbances, respectively.
5.1. Constraints Condition
In order to verify whether the constraints of the payload swing and the settling time can be both satisfied under different target positions, two groups of experiments are conducted. Here, the maximum swing angle is set to be 2°. The corresponding responses with respect to different moving ranges are shown in Figure 11 and Table 5, respectively. It can be found that the actual maximum swing angle is 1.92°, which satisfies the setting requirement. The regulation time is almost the same, and the responses are shown in Figure 12 and Table 6. The results show that all of the regulated time is less than 1.64 s. When the target position changes, the regulated time basically remains unchanged. To summarize, for different target positions, the proposed algorithm can achieve effective control.
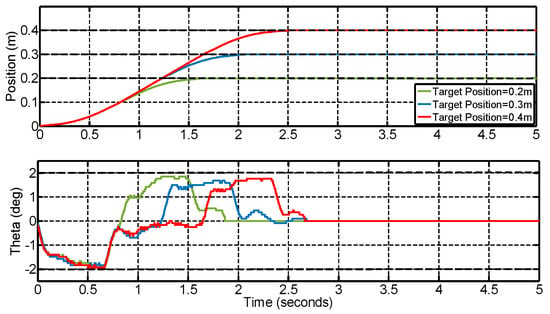
Figure 11.
The response within an angle constraint scheme.

Table 5.
Performance within angle constraint.
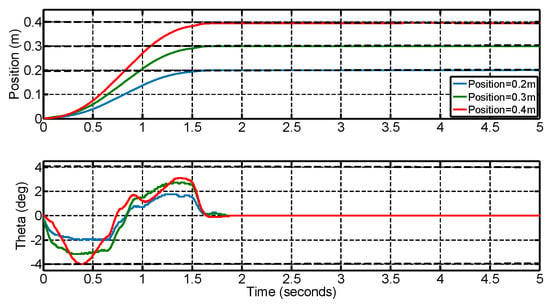
Figure 12.
The time-optimization response within a time-optimal scheme.

Table 6.
Performance within a time optimal solution.
5.2. Different Payload Condition
Some magnetic sheets are attached to the original load to simulate the weight variation, as shown in Figure 13. When the weight changes, the controller can still move the cargo to the desired position with almost the same maximum swing angle. The maximum difference is less than 0.06°. Thus, the variation of the payload cannot affect the settling time and the maximum swing, and the robustness of the proposed algorithm is proved to some extent.
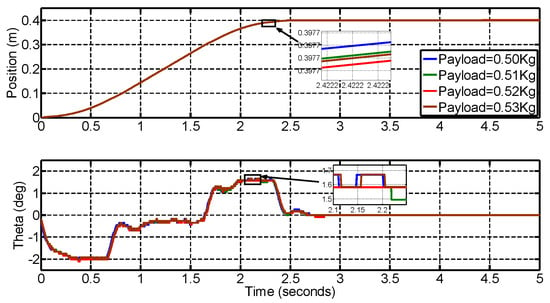
Figure 13.
The response for different weights of payloads.
5.3. Different Cable Length Condition
In addition, it is imperative to consider different cable lengths in order to verify the algorithm. The response is shown in Figure 14. The maximum payload swing increases by 0.2° when the cable length varies from 0.092 m to 0.122 m. Certainly, longer cable length brings larger swing angle. Nonetheless, it can still satisfy the constraint of the maximum angle, i.e., 2°. Thus, the controller can effectively control the crane to reach the target position, and meanwhile can satisfy the maximum angle constraint when the payload and cable length change.
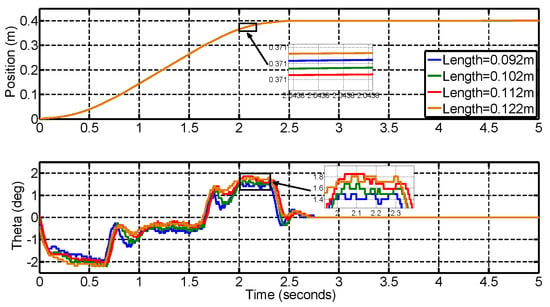
Figure 14.
The response in different cable lengths.
5.4. Disturbance Condition
Moreover, the control performance needs to be validated when external disturbance exists. Here, the disturbance is maintained for 3 s to 5 s. Similar to that of the simulation, an external acceleration of 0.8 m/s2 is added, and its duration is 0.2 s. By comparing the responses of three different controllers in Figure 15, the proposed algorithm can realize the optimal control effect compared with the other methods. The proposed algorithm can reach the target position with the shortest time. It can also be observed that the TP algorithm cannot suppress the payload swing, and the LQR algorithm can induce the swing angle by 1.41°. In this manner, conclusions can be made that the proposed method can effectively suppress the external disturbance.
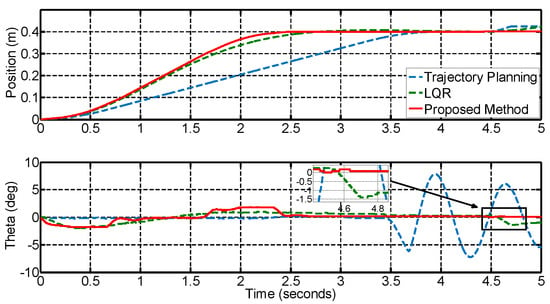
Figure 15.
The response of three controls with disturbance.
6. Conclusions
In this paper, a novel algorithm combining the TP and the LQR is employed to achieve control of the anti-swing crane system. The proposed algorithm takes the acceleration of the payload as the control variable, and the ITAEs of the position and the swing angle as the criterion of evaluation. The MOGA is applied to find the optimal algorithm parameters. Compared with the TP algorithm and the LQR algorithm, the proposed algorithm can reach the control settings. The regulation time can be shortened, and the maximum swing angle can be reduced. Simulation and experimental validation justify the feasibility of the proposed algorithm.
Following works will focus on the real implementation of the proposed algorithm in port cargo transportation.
Acknowledgments
The research is supported by National Science Foundation of China (Grant No. 51567012, 61763021) in part, the Innovation Foundation of Kunming University of Science and Technology (Grant No. 2015YB053) in part, the Innovation Team Program of Kunming University of Science and Technology (No. 14078368) in part, and the Scientific Research Start-up Funding of Kunming University of Science and Technology (Grant No. 14078337) in part. In addition, the authors would like to thank the B&R Automation LLC for their hardware and program training support. Moreover, the authors would also like to thank reviewers for their corrections and helpful suggestions.
Author Contributions
Renxin Xiao and Zelin Wang conceived the paper, discussed the multi-objective genetic optimization and the trajectory planning. Zheng Chen designed the bridge crane model and revised the paper. Ningyuan Guo and Yitao Wu performed the experiments and conducted the figures drawing. Jiangwei Shen analyzed the data and provided some valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z.N. Dynamics and Control of Cranes: A Review. J. Vib. Control 2003, 9, 863–908. [Google Scholar] [CrossRef]
- Maghsoudi, M.J.; Mohamed, Z.; Sudin, S.; Buyamin, S.; Jaafar, H.; Ahmad, S. An improved input shaping design for an efficient sway control of a nonlinear 3D overhead crane with friction. Mech. Syst. Signal Process. 2017, 92, 364–378. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.; Abidin, M.Z.; Buyamin, S.; Bature, A.A. Output-based command shaping technique for an effective payload sway control of a 3D crane with hoisting. Trans. Inst. Meas. Control 2017, 39, 1443–1453. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, X.; Gao, F.; Tian, X.; Li, Y. A motion planning method for underactuated 3D overhead crane systems. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 4286–4291. [Google Scholar]
- Sun, N.; Fang, Y.; Zhang, X.; Yuan, Y. Transportation task-oriented trajectory planning for underactuated overhead cranes using geometric analysis. IET Control Theory Appl. 2012, 6, 1410–1423. [Google Scholar] [CrossRef]
- Chiu, C.-H.; Lin, C.-H. Adaptive output recurrent neural network for overhead crane system. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 1082–1087. [Google Scholar]
- He, W.; Zhang, S.; Ge, S.S. Adaptive Control of a Flexible Crane System with the Boundary Output Constraint. IEEE Trans. Ind. Electron. 2014, 61, 4126–4133. [Google Scholar] [CrossRef]
- Fang, Y.; Ma, B.; Wang, P.; Zhang, X. A motion planning-based adaptive control method for an underactuated crane system. IEEE Trans. Control Syst. Technol. 2012, 20, 241–248. [Google Scholar] [CrossRef]
- Rahmani, R.; Karimi, H.; Yusof, R.; Othman, M.F. A precise fuzzy controller developed for overhead crane. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Sabah, Malaysia, 31 May–3 June 2015; pp. 1–5. [Google Scholar]
- Li, C.; Lee, C.-Y. Fuzzy motion control of an auto-warehousing crane system. IEEE Trans. Ind. Electron. 2001, 48, 983–994. [Google Scholar]
- Nakazono, K.; Ohnisihi, K.; Kinjo, H. Load swing suppression in jib crane systems using a genetic algorithm-trained neuro-controller. In Proceedings of the ICM2007 4th IEEE International Conference on Mechatronics, Tokyo, Japan, 8–10 May 2007; pp. 1–4. [Google Scholar]
- Kimiaghalam, B.; Homaifar, A.; Bikdash, M.; Dozier, G. Genetic algorithms solution for unconstrained optimal crane control. In Proceedings of the 1999 Congress on Evolutionary Computation CEC ’99, Washington, DC, USA, 6–9 July 1999; pp. 2124–2130. [Google Scholar]
- Le, T.A.; Kim, G.H.; Min, Y.K. Partial feedback linearization control of overhead cranes with varying cable lengths. Int. J. Precis. Eng. Manuf. 2012, 13, 501–507. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Zhang, X. Energy coupling output feedback control of 4-DOF underactuated cranes with saturated inputs. Automatica 2013, 49, 1318–1325. [Google Scholar] [CrossRef]
- Yang, B.; Xiong, B. Application of LQR techniques to the anti-sway controller of overhead crane. Adv. Mater. Res. 2010, 139, 1933–1936. [Google Scholar] [CrossRef]
- Win, T.M.; Hesketh, T.; Eaton, R. SimMechanics Visualization of Experimental Model Overhead Crane, Its Linearization and Reference Tracking-LQR Control. AIRCC Int. J. Chaos Control Model. Simul. 2013, 2, 1–16. [Google Scholar] [CrossRef]
- Abdullah, J.; Ruslee, R.; Jalani, J. Performance Comparison between LQR and FLC for Automatic 3 DOF Crane Systems. Int. J. Control Autom. 2011, 4, 163–178. [Google Scholar]
- Choi, S.; Kim, J.; Lee, J.; Lee, Y.; Lee, K. A study on gantry crane control using neural network two degree of PID controller. In Proceedings of the ISIE 2001 IEEE International Symposium on Industrial Electronics Proceedings, Pusan, Korea, 12–16 June 2001; pp. 1896–1900. [Google Scholar]
- Solihin, M.I.; Wahyudi; Legowo, A. Fuzzy-tuned PID anti-swing control of automatic gantry crane. J. Vib. Control 2010, 16, 127–145. [Google Scholar] [CrossRef]
- Lee, C.H.; Lee, Y.H.; Teng, C.C. A novel robust PID controllers design by fuzzy neural network. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 1561–1566. [Google Scholar]
- Zhang, S.; He, X. Adaptive HJI sliding mode control of three dimensional overhead cranes. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5820–5855. [Google Scholar]
- Solihin, M.I.; Kamal, M.; Legowo, A. Objective function selection of GA-based PID control optimization for automatic gantry crane. In Proceedings of the 2008 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 13–15 May 2008; pp. 883–887. [Google Scholar]
- Lin, J.; Zheng, Y. Vibration suppression control of smart piezoelectric rotating truss structure by parallel neuro-fuzzy control with genetic algorithm tuning. J. Sound Vib. 2012, 331, 3677–3694. [Google Scholar] [CrossRef]
- Petrenko, Y.N.; Alavi, S.E. Fuzzy logic and genetic algorithm technique for non-liner system of overhead crane. In Proceedings of the 2010 IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering (SIBIRCON), Irkutsk, Russia, 11–15 July 2010; pp. 848–851. [Google Scholar]
- Wang, X.J.; Chen, Z.M. Two-degree-of-freedom sliding mode anti-swing and positioning controller for overhead cranes. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 673–677. [Google Scholar]
- Wang, X.; Wang, H.; Tian, Y.; Christov, N. Predictive Observer based Lyapunov antiswing control for overhead visual crane. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1670–1675. [Google Scholar]
- Wu, X.; He, X.; Ou, X. A coupling control method applied to 2-D overhead cranes. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 1658–1662. [Google Scholar]
- Chen, H.; Fang, Y.; Sun, N. A swing constraint guaranteed MPC algorithm for underactuated overhead cranes. IEEE/ASME Trans. Mechatron. 2016, 21, 2543–2555. [Google Scholar] [CrossRef]
- Jafari, J.; Ghazal, M.; Nazemizadeh, M. A LQR Optimal Method to Control the Position of an Overhead Crane. IAES Int. J. Robot. Autom. 2014, 3, 252. [Google Scholar]
- Blajer, W.; Kołodziejczyk, K. Control of underactuated mechanical systems with servo-constraints. Nonlinear Dyn. 2007, 50, 781–791. [Google Scholar] [CrossRef]
- Wang, J.; Noda, Y.; Inomata, A. Straight transfer control system using PI control and trajectory planning in overhead traveling crane. In Proceedings of the 2015 IEEE/SICE International Symposium on System Integration (SII), Nagoya, Japan, 11–13 December 2015; pp. 522–527. [Google Scholar]
- Chen, H.; Fang, Y.; Sun, N. Optimal trajectory planning and tracking control method for overhead cranes. IET Control Theory Appl. 2016, 10, 692–699. [Google Scholar] [CrossRef]
- Summanwar, V.S.; Jayaraman, V.K.; Kulkarni, B.D.; Kusumakar, H.S.; Gupta, K.; Rajesh, J. Solution of constrained optimization problems by multi-objective genetic algorithm. Comput. Chem. Eng. 2002, 26, 1481–1492. [Google Scholar] [CrossRef]
- Coello, C.A.C. Multi-objective Evolutionary Algorithms in Real-World Applications: Some Recent Results and Current Challenges; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–18. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Yeh, W.C.; Chuang, M.C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Padula, F.; Adamini, R.; Finzi, G.; Visioli, A. Revealing the Hidden Technology by Means of an Overhead Crane. IFAC Papersonline 2017, 50, 9126–9131. [Google Scholar] [CrossRef]
- 2016 B&R Scholastic Union Competition. Available online: http://www.br-education.com/activities/index.asp?ColumnId=45&Style_ID=3&ID=376 (accessed on 18 March 2018).
- B&R Automation. Available online: https://www.br-automation.com/en-au/about-us/customer-magazine/2013/ 201303 /swift-steady/ (accessed on 18 March 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).