Hesitant Probabilistic Multiplicative Preference Relations in Group Decision Making
Abstract
:1. Introduction
- Consensus among decision-makers: In group decision-making, the diversity in nature, social backgrounds, education level, expertise, and experience of decision-makers may lead to differences in opinions, but it is important in many scenarios of group decision-making to develop a reasonable consensus between the decision-makers [22,25,35,38,41,47,48,49]. Thus, some measures are needed to remove the difference in opinion to some extent.
2. Preliminaries
3. Hesitant Probabilistic Multiplicative Sets and Relations
- If then ( is superior to ).
- For the case , compare the deviations. If then if then if , then
Consistency Measure of the Hesitant Probabilistic Multiplicative Preference Relation
| Algorithm 1 Algorithmic description to determine NHPMPR consistent HPMPR , and number of iterations |
|
- 1.
- 2.
- if and only if
- 3.
| Algorithm 2 Algorithmic description to determine the acceptably consistent. |
|
4. Consensus Measure in Group Decision Making
| Algorithm 3 Algorithmic description to modify the dissenter’s HPMPR to reach an acceptable consensus. |
|
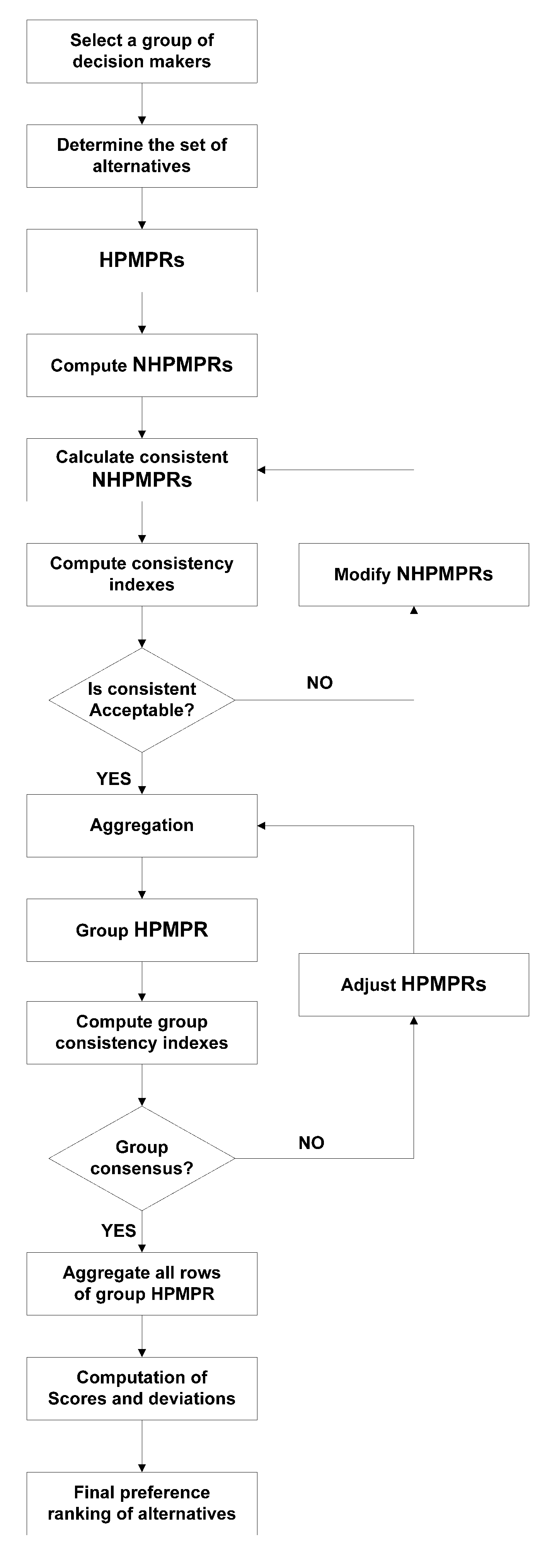
5. Decision Support Model for Group Decision Making with HPMPRs
| Algorithm 4 Algorithmic description to determine a complete decision model. |
|
6. Case Study
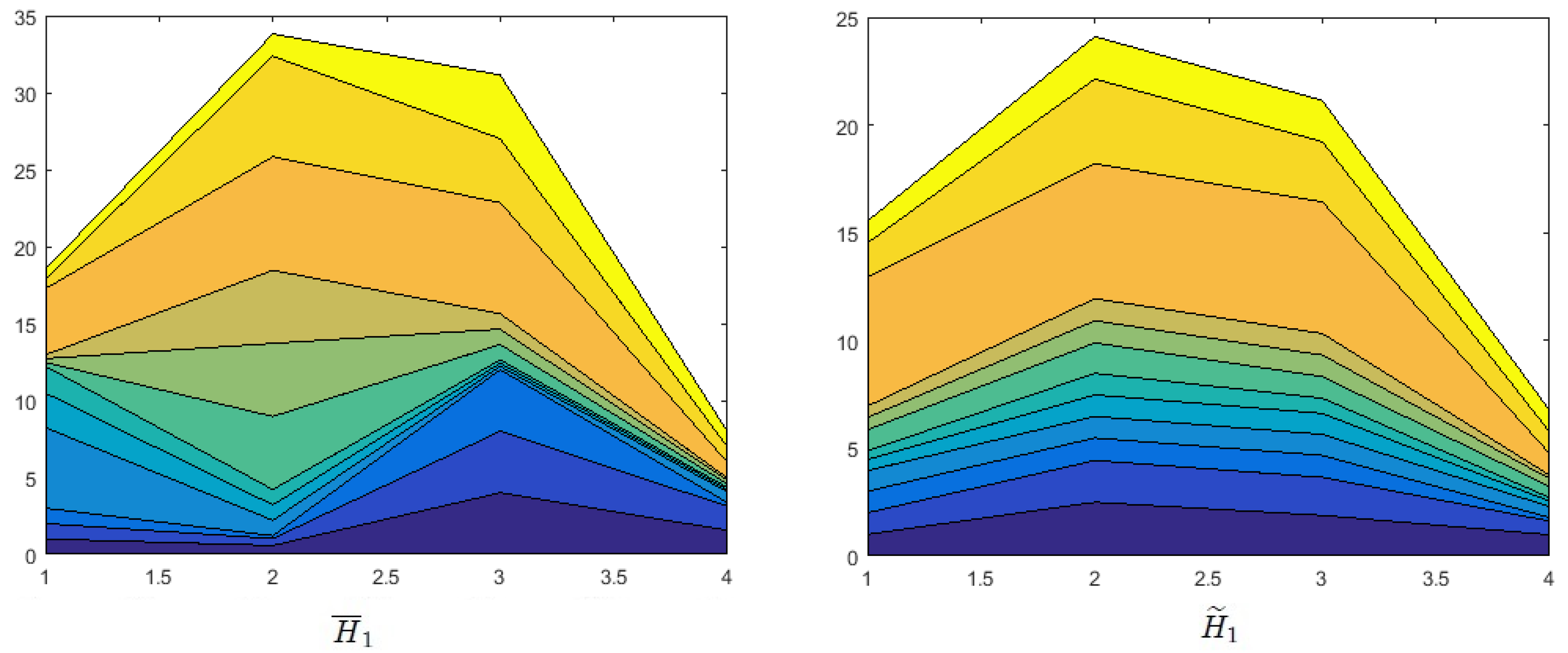
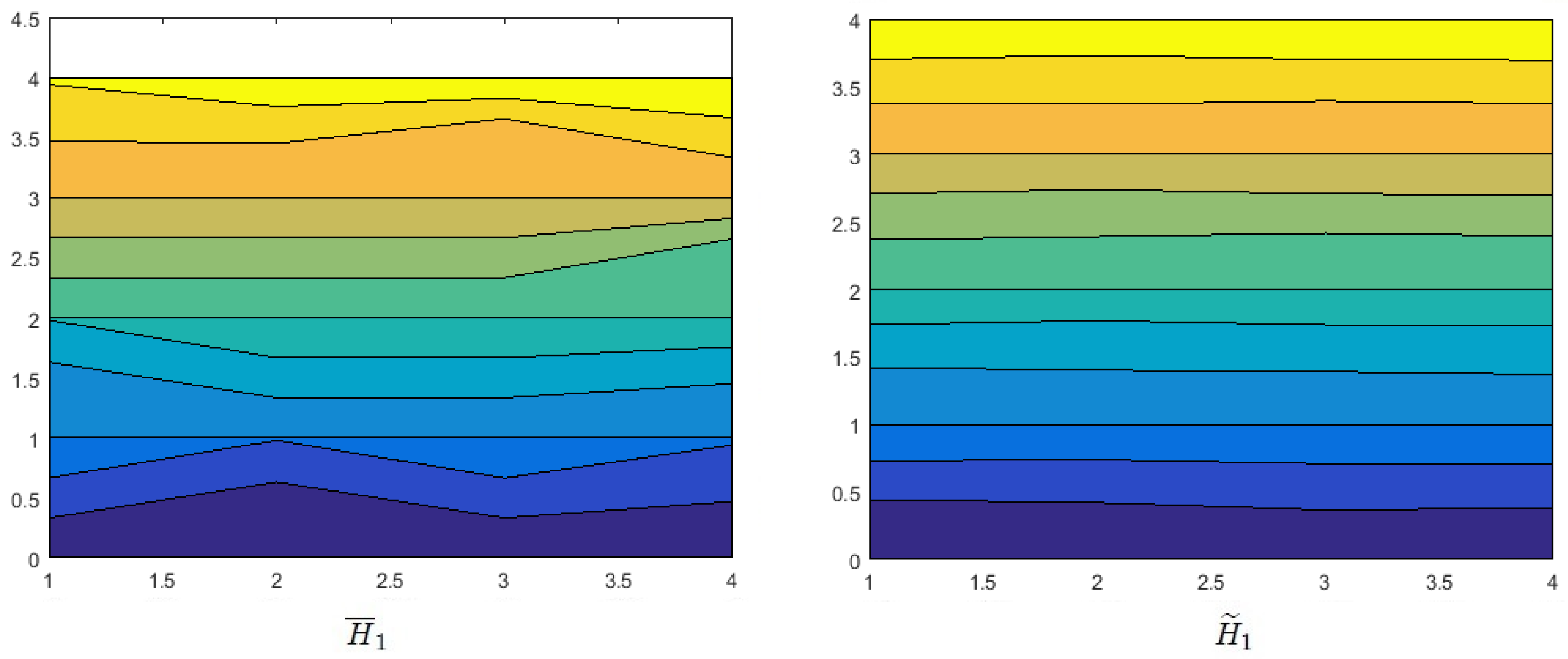
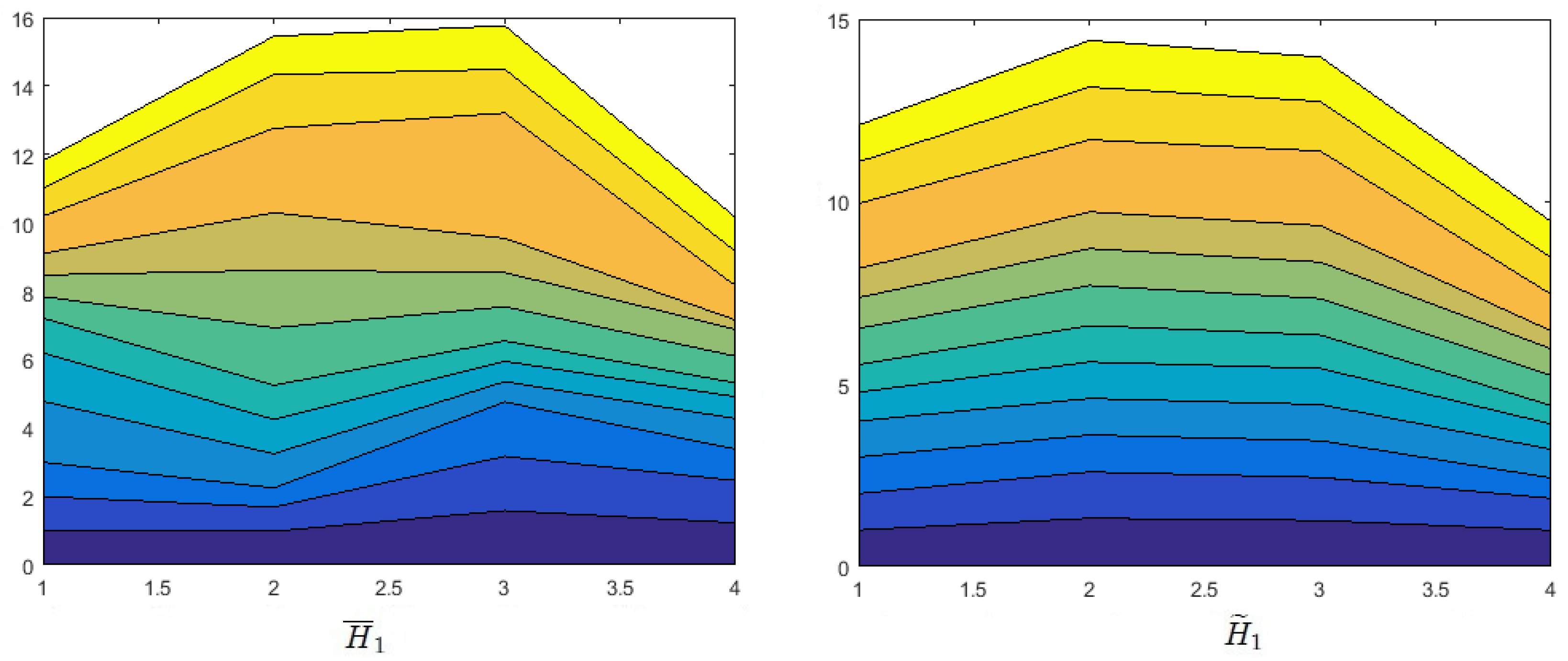
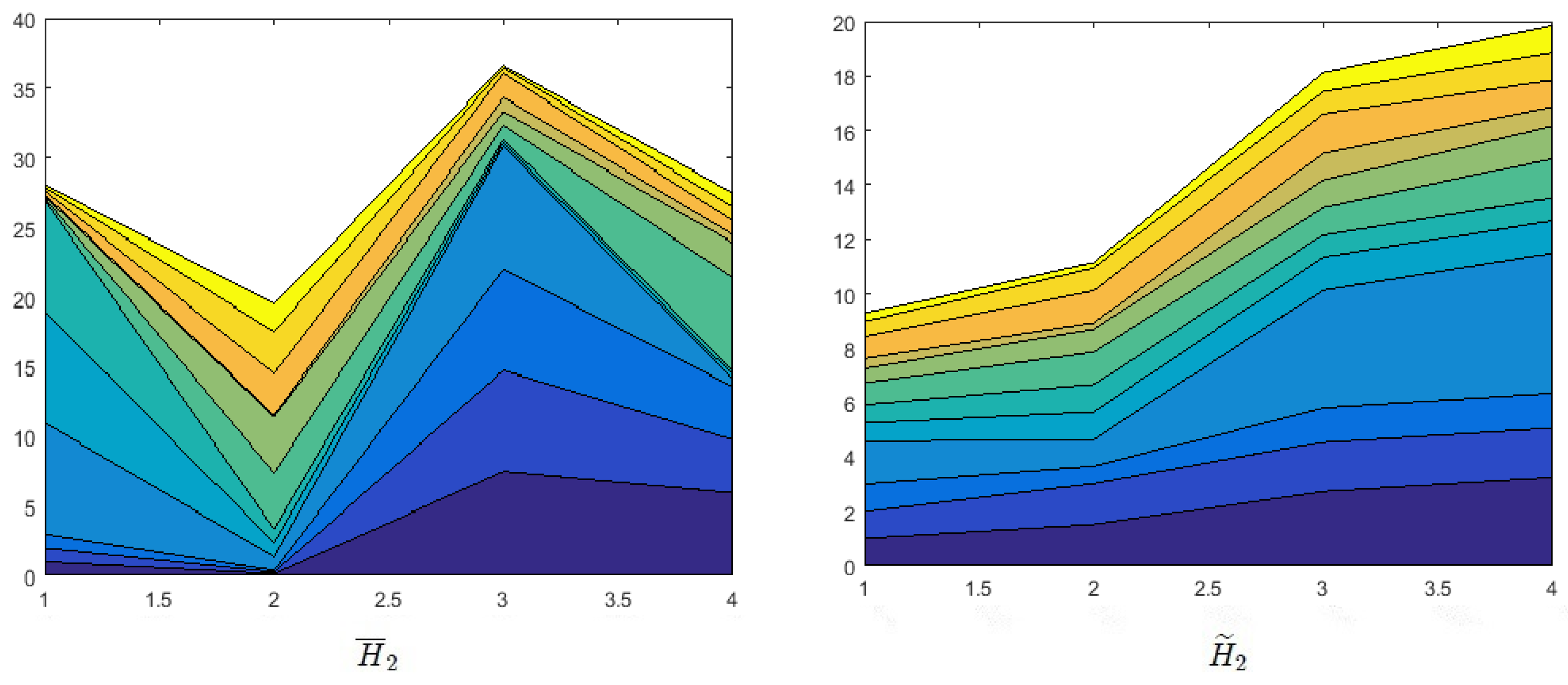
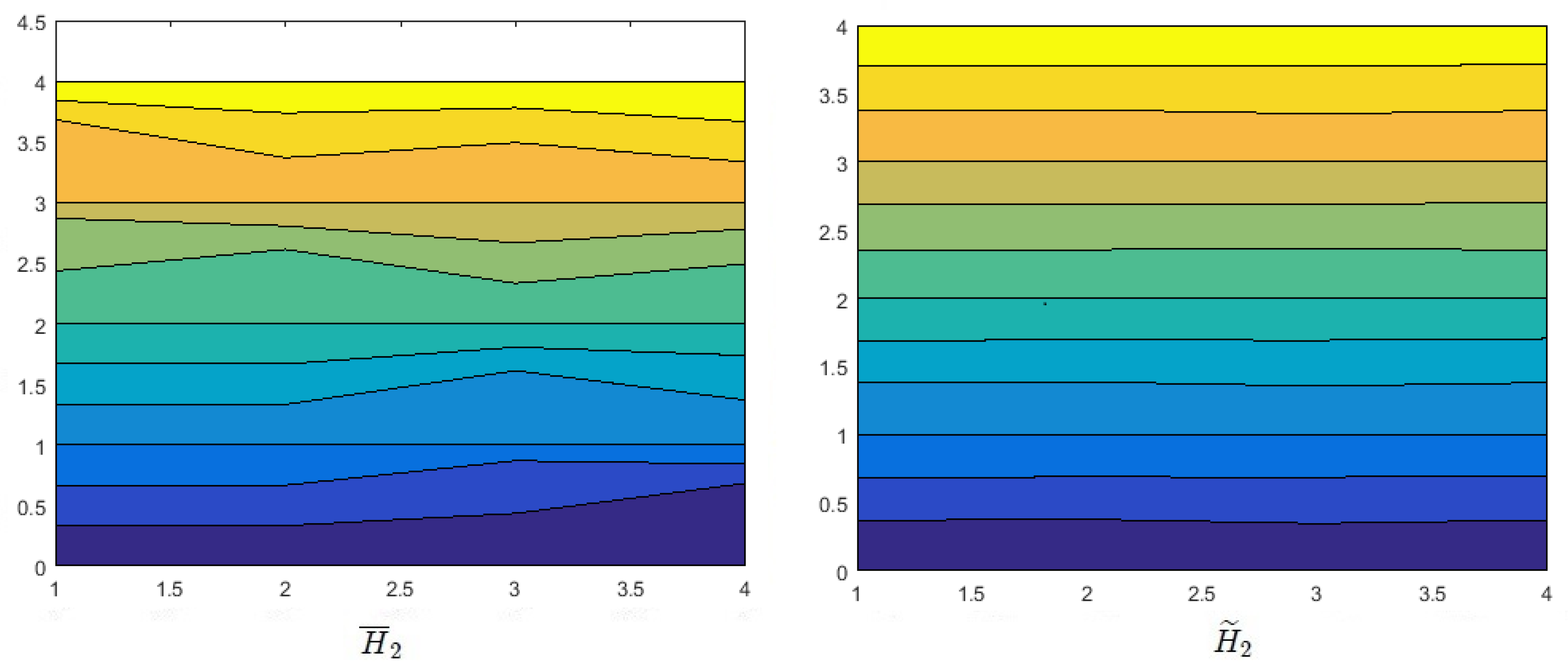
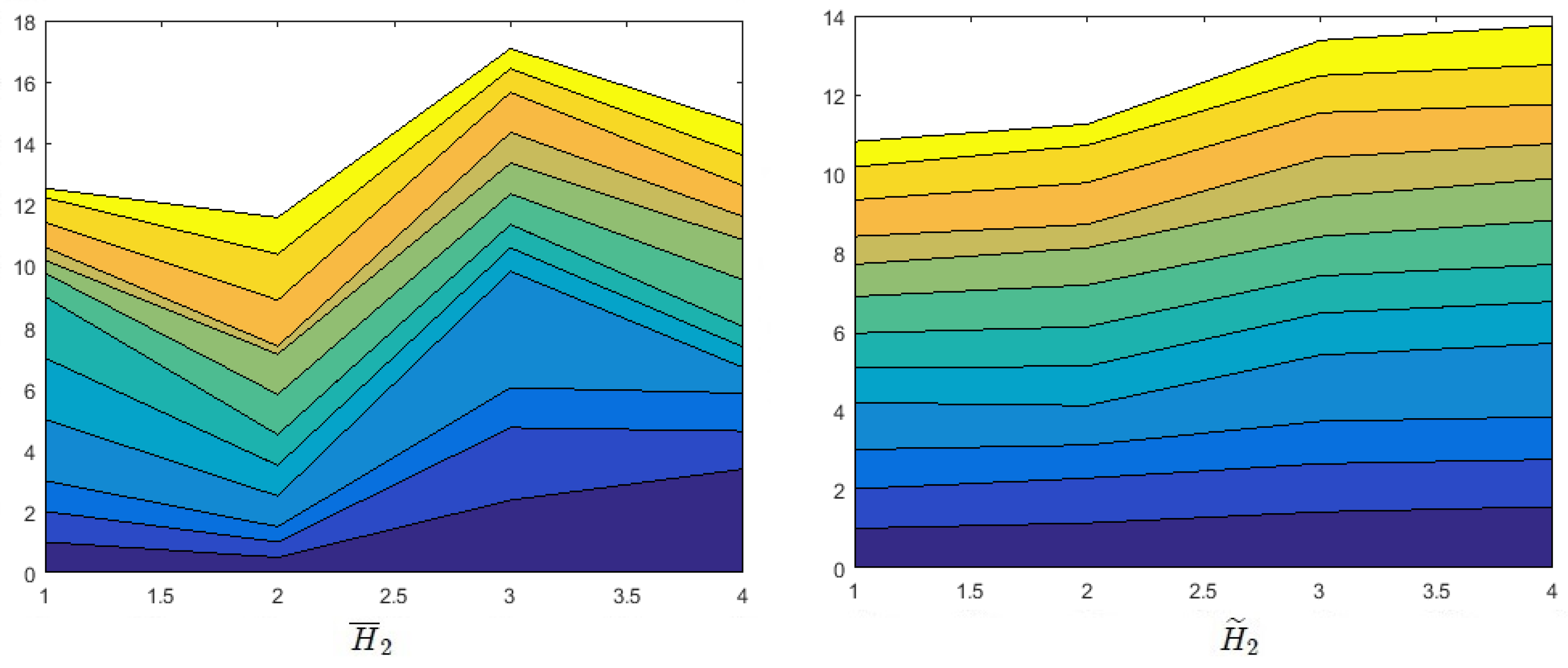
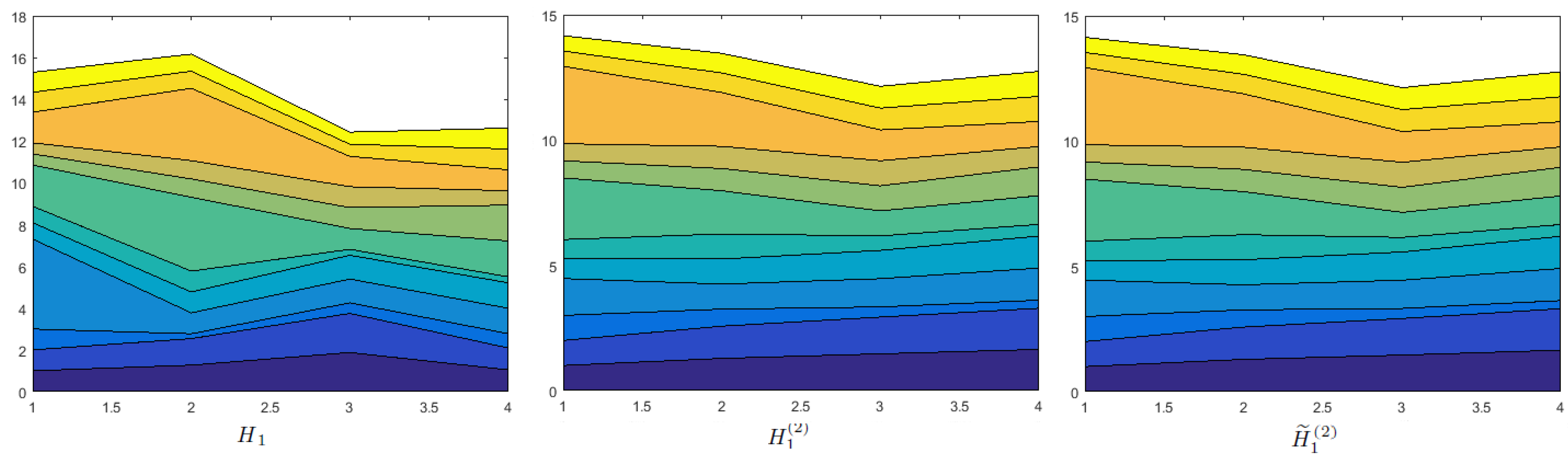
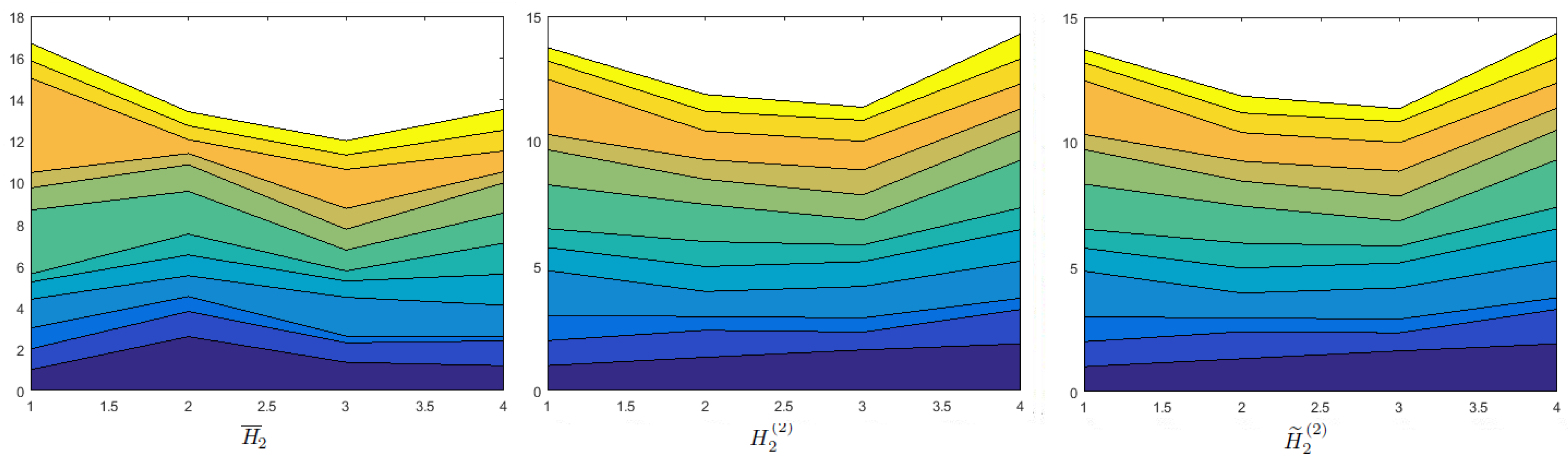
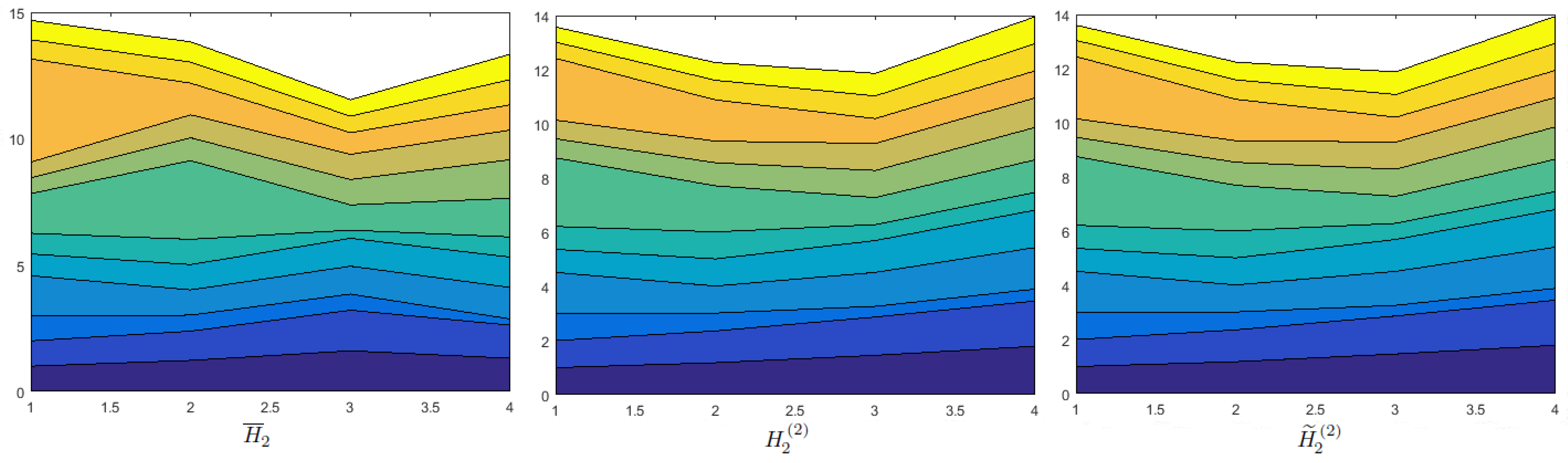
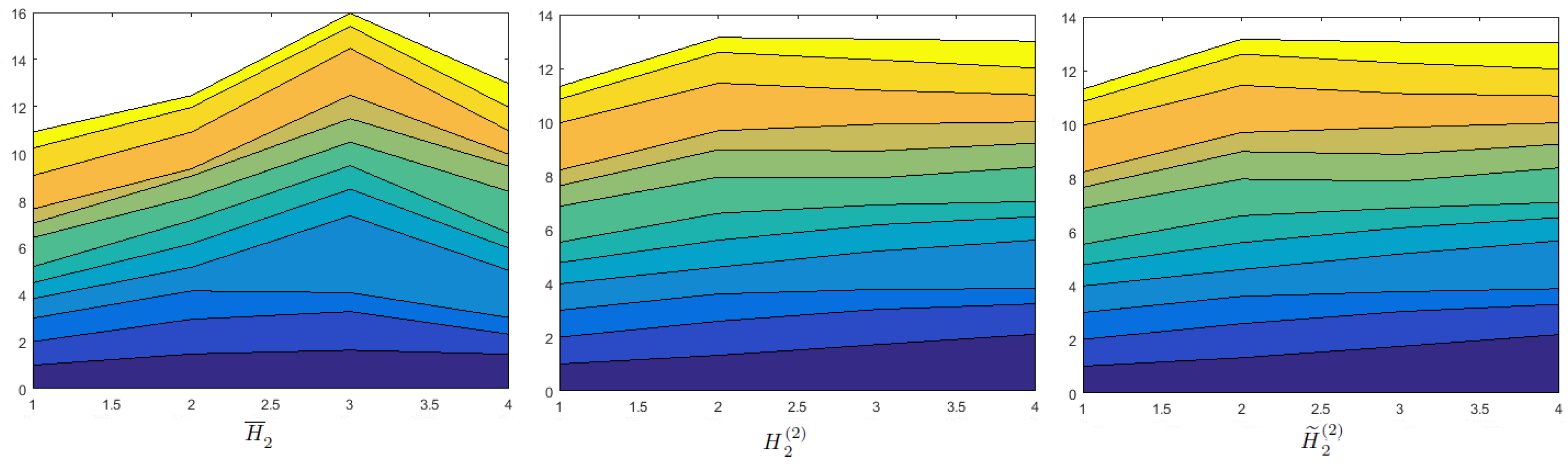
Effects of Probability on Decision Making
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision Making with Uncertainty Using Hesitant Fuzzy Sets. Int. J. Fuzzy Syst. 2018, 20, 99–103. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, W.S.T.; Wątróbski, J.; Zafar, S. Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Lu, N.; Liang, L. Correlation Coefficients of Extended Hesitant Fuzzy Sets and Their Applications to Decision Making. Symmetry 2017, 9, 47. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2017, 48, 557–571. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Ideal solutions for hesitant fuzzy soft sets. J. Intell. Fuzzy Syst. 2016, 30, 143–150. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Hesitant 2-tuple linguistic information in multiple attributes group decision-making. J. Intell. Fuzzy Syst. 2016, 30, 109–116. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.S.; Xia, M.M. Interval-valued hesitant preference relations and their applications to group decision-making. Knowl. Based Syst. 2013, 37, 528–540. [Google Scholar] [CrossRef]
- Qian, G.; Wang, H.; Feng, X. Generalized hesitant fuzzy sets and their application in decision support system. Knowl. Based Syst. 2013, 37, 357–365. [Google Scholar] [CrossRef]
- Rashid, T.; Beg, I. Convex hesitant fuzzy sets. J. Intell. Fuzzy Syst. 2016, 30, 2791–2796. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision-making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.; Xia, M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, W. Consensus building with a group of decision makers under the probabilistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2016. [Google Scholar] [CrossRef]
- Zhai, Y.; Xu, Z.; Liao, H. Probabilistic linguistic vector-term set and its application in group decision-making with multi-granular linguistic information. Appl. Soft Comput. 2016. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.; He, Y. Operations and Integrations of Probabilistic Hesitant Fuzzy Information in Decision Making. Inf. Fusion 2017. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic linguistic term sets in multi-attribute group decision-making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytical Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Uncertainty and rank order in the analytic hierarchy process. Eur. J. Oper. Res. 1987, 32, 107–117. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Managing hesitant information in GDM problems under fuzzy and multiplicative preference relations. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2013, 21, 865–897. [Google Scholar] [CrossRef]
- Wu, Z.B.; Xu, J.P. A consistency and consensus based decision support model for group decision-making with multiplicative preference relations. Decis. Support Syst. 2012, 52, 757–767. [Google Scholar] [CrossRef]
- Orlovsky, S.A. Decision-making with a fuzzy preference relation. Fuzzy Sets Syst. 1978, 1, 155–167. [Google Scholar] [CrossRef]
- Chiclana, F.; Herrera, F.; Herrera-Viedma, E. Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets Syst. 2001, 122, 277–291. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Alonso, S.; Chiclana, F.; Herrera, F. A consensus model for group decision-making with incomplete fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2007, 15, 863–877. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. Group decision-making procedure based on incomplete reciprocal relations. Soft Comput. 2008, 12, 515–521. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, Y.; Li, H. On consistency measures of linguistic preference relations. Eur. J. Oper. Res. 2008, 189, 430–444. [Google Scholar] [CrossRef]
- Herrera, F. A sequential selection process in group decision making with linguistic assessment. Inf. Sci. 1995, 85, 223–239. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E. Linguistic decision analysis: steps for solving decision problems under linguistic information. Fuzzy Sets Syst. 2000, 115, 67–82. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Liao, H.C. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 21, 113–133. [Google Scholar]
- Xu, Z.S. Priority weight intervals derived from intuitionistic multiplicative preference relations. IEEE Trans. Fuzzy Syst. 2013, 21, 642–654. [Google Scholar]
- Xu, Z.S. On compatibility of interval fuzzy preference matrices. Fuzzy Optim. Decis. Mak. 2004, 3, 217–225. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic preference relations and their application in group decision-making. Inf. Sci. 2007, 177, 2363–2379. [Google Scholar] [CrossRef]
- Xu, Z.S. Generalized fuzzy consistency matrix and its priority method. J. PLA Univ. Sci. Technol. 2000, 1, 97–99. [Google Scholar]
- Zhang, Z.; Wang, C.; Tian, X. A decision support model for group decision-making with hesitant fuzzy preference relations. Knowl. Based Syst. 2015, 86, 77–101. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S. Regression methods for hesitant fuzzy preference relations. Technol. Econ. Dev. Econ. 2013, 19, 214–227. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.; Xu, J.P. Deriving a ranking from hesitant fuzzy preference relations under Group Decision Making. IEEE Trans. Cybern. 2014, 44, 1328–1337. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, C. A decision support model for group decision making with hesitant multiplicative preference relations. Inf. Sci. 2014, 282, 136–166. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C. Deriving the priority weights from hesitant multiplicative preference relations in group decision-making. Appl. Soft Comput. 2014, 25, 107–117. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z.S. Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision-making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. Direct approach processes in group decision-making using linguistic OWA operators. Fuzzy Sets Syst. 1996, 79, 175–190. [Google Scholar] [CrossRef]
- Kacprzyk, J. Group decision-making with a fuzzy linguistic majority. Fuzzy Sets Syst. 1986, 18, 105–118. [Google Scholar] [CrossRef]
- Tanino, T. Fuzzy preference orderings in group decision-making. Fuzzy Sets Syst. 1984, 12, 117–131. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Chiclana, F.; Herrera, F.; Alonso, S. Group decision-making model with incomplete fuzzy preference relations based on additive consistency. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 176–189. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. Some issues on consistency of fuzzy preference relations. Eur. J. Oper. Res. 2004, 154, 98–109. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Chen, J. Algorithms for improving consistency or consensus of reciprocal [0, 1]-valued preference relations. Fuzzy Sets Syst. 2013, 216, 108–133. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, G.; Hong, W.-H.; Xu, Y. Consensus models for AHP group decision-making under row geometric mean prioritization method. Decis. Support Syst. 2010, 49, 281–289. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. A consensus model for multiperson decision-making with different preference structures. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2002, 34, 394–402. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M.M. Distance and similarity measures for hesitant fuzzy sets. Inf. Sci. 2011, 181, 2128–2138. [Google Scholar] [CrossRef]
- Bossuyt, P. A Comparison of Probabilistic Unfolding Theories for Paired Comparisons Data; Springer: Berlin, Germany, 1990. [Google Scholar]
- Xu, Z.S. On consistency of the weighted geometric mean complex judgment matrix in AHP. Eur. J. Oper. Res. 2000, 126, 683–687. [Google Scholar] [CrossRef]
| n | d | ||
|---|---|---|---|
| 4 | 4 | 1.0380 | 1.036 |
| 3 | 1.19 | 1.201 | |
| 2 | 2.228 | 2.222 | |
| 5 | 5 | 1.002 | 1.004 |
| 4 | 1.022 | 1.024 | |
| 3 | 1.188 | 1.162 | |
| 6 | 6 | 1.002 | 1.002 |
| 5 | 1.007 | 1.004 | |
| 4 | 1.025 | 1.013 | |
| 7 | 7 | 1.001 | 1 |
| 6 | 1 | 1.001 | |
| 5 | 1.003 | 1.001 | |
| 8 | 8 | 1 | 1 |
| 7 | 1 | 1 | |
| 6 | 1 | 1 | |
| 9 | 9 | 1 | 1 |
| 8 | 1 | 1 | |
| 7 | 1 | 1 | |
| 10 | 10 | 1 | 1 |
| 9 | 1 | 1 | |
| 8 | 1 | 1 |
| n | d | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.3 | 0.6 | 0.8 | |||
| 4 | 4 | 1.05 | 1 | 1.237 | 2.53 | 5.177 |
| 1.1 | 0.989 | 0.991 | 1.683 | 3.125 | ||
| 1.15 | 0.931 | 0.945 | 1.164 | 2.044 | ||
| 3 | 1.05 | 1.003 | 1.297 | 2.598 | 5.29 | |
| 1.1 | 0.99 | 0.993 | 1.687 | 3.306 | ||
| 1.15 | 0.941 | 0.935 | 1.246 | 2.241 | ||
| 2 | 1.05 | 0.996 | 1.344 | 2.597 | 5.343 | |
| 1.1 | 0.978 | 0.979 | 1.734 | 3.309 | ||
| 1.15 | 0.922 | 0.907 | 1.198 | 2.241 | ||
| 5 | 5 | 1.05 | 1 | 1.333 | 2.786 | 5.625 |
| 1.1 | 0.999 | 1 | 1.924 | 3.674 | ||
| 1.15 | 0.998 | 0.999 | 1.385 | 2.573 | ||
| 4 | 1.05 | 1 | 1.452 | 2.838 | 5.706 | |
| 1.1 | 1 | 1 | 1.93 | 3.789 | ||
| 1.15 | 0.998 | 0.999 | 1.439 | 2.698 | ||
| 3 | 1.05 | 1 | 1.546 | 2.86 | 5.847 | |
| 1.1 | 1 | 1.002 | 1.953 | 3.843 | ||
| 1.15 | 0.991 | 0.995 | 1.502 | 2.81 | ||
| 6 | 6 | 1.05 | 1 | 1.456 | 2.928 | 5.805 |
| 1.1 | 1 | 1 | 1.995 | 3.874 | ||
| 1.15 | 1 | 1 | 1.563 | 2.827 | ||
| 5 | 1.05 | 1 | 1.516 | 2.954 | 5.908 | |
| 1.1 | 1 | 1 | 1.997 | 4.012 | ||
| 1.15 | 1 | 1 | 1.605 | 2.95 | ||
| 4 | 1.05 | 1 | 1.632 | 2.962 | 6.053 | |
| 1.1 | 1 | 1 | 2.022 | 4.095 | ||
| 1.15 | 1 | 1 | 1.692 | 3.002 | ||
| 7 | 7 | 1.05 | 1 | 1.524 | 2.987 | 5.889 |
| 1.1 | 1 | 1 | 2.01 | 4.055 | ||
| 1.15 | 1 | 1 | 1.708 | 3.016 | ||
| 6 | 1.05 | 1 | 1.63 | 2.985 | 6.015 | |
| 1.1 | 1 | 1 | 2.007 | 4.095 | ||
| 1.15 | 1 | 1 | 1.745 | 3.095 | ||
| 4 | 1.05 | 1 | 1.83 | 2.999 | 6.275 | |
| 1.1 | 1 | 1 | 2.053 | 4.31 | ||
| 1.15 | 1 | 1 | 1.862 | 3.249 | ||
| 8 | 8 | 1.05 | 1 | 1.619 | 2.996 | 5.935 |
| 1.1 | 1 | 1 | 2.002 | 4.111 | ||
| 1.15 | 1 | 1 | 1.806 | 3.09 | ||
| 7 | 1.05 | 1 | 1.725 | 2.996 | 6.032 | |
| 1.1 | 1 | 1 | 2.007 | 4.168 | ||
| 1.15 | 1 | 1 | 1.858 | 3.168 | ||
| 6 | 1.05 | 1 | 1.788 | 2.998 | 6.13 | |
| 1.1 | 1 | 1 | 2.017 | 4.239 | ||
| 1.15 | 1 | 1 | 1.897 | 3.223 | ||
| 9 | 9 | 1.05 | 1 | 1.648 | 2.999 | 5.991 |
| 1.1 | 1 | 1 | 2.001 | 4.128 | ||
| 1.15 | 1 | 1 | 1.885 | 3.16 | ||
| 8 | 1.05 | 1 | 1.749 | 2.999 | 6.038 | |
| 1.1 | 1 | 1 | 2.006 | 4.199 | ||
| 1.15 | 1 | 1 | 1.919 | 3.204 | ||
| 7 | 1.05 | 1 | 1.845 | 3 | 6.116 | |
| 1.1 | 1 | 1 | 2.005 | 4.266 | ||
| 1.15 | 1 | 1 | 1.946 | 3.257 | ||
| 10 | 10 | 1.05 | 1 | 1.682 | 3 | 6.007 |
| 1.1 | 1 | 1 | 2 | 4.155 | ||
| 1.15 | 1 | 1 | 1.951 | 3.179 | ||
| 9 | 1.05 | 1 | 1.796 | 3 | 6.035 | |
| 1.1 | 1 | 1 | 2.003 | 4.192 | ||
| 1.15 | 1 | 1 | 1.964 | 3.232 | ||
| 8 | 1.05 | 1 | 1.882 | 3 | 6.1 | |
| 1.1 | 1 | 1 | 2.003 | 4.272 | ||
| 1.15 | 1 | 1 | 1.969 | 3.269 | ||
| n | m | d | |||||
|---|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.7 | 0.9 | ||||
| 4 | 4 | 4 | 1.01 | 1.967 | 2.715 | 5.969 | 18.828 |
| 1.05 | 1 | 1.271 | 2.747 | 8.101 | |||
| 1.1 | 0.97 | 0.998 | 1.692 | 4.61 | |||
| 3 | 3 | 1.01 | 1.878 | 2.574 | 5.75 | 18.261 | |
| 1.05 | 0.999 | 1.296 | 2.773 | 8.116 | |||
| 1.1 | 0.938 | 0.967 | 1.589 | 4.311 | |||
| 2 | 2 | 1.01 | 1.759 | 2.525 | 5.756 | 18.47 | |
| 1.05 | 0.884 | 0.927 | 1.552 | 4.394 | |||
| 1.1 | 0.793 | 0.771 | 1.248 | 3.292 | |||
| 5 | 4 | 5 | 1.01 | 1.892 | 2.393 | 5.471 | 17.564 |
| 1.05 | 1 | 1.165 | 2.616 | 7.644 | |||
| 1.1 | 0.99 | 0.998 | 1.714 | 4.569 | |||
| 3 | 4 | 1.01 | 1.896 | 2.512 | 5.652 | 17.993 | |
| 1.05 | 1 | 1.611 | 3.203 | 9.615 | |||
| 1.1 | 0.89 | 0.868 | 1.235 | 2.911 | |||
| 3 | 3 | 1.01 | 1.964 | 2.759 | 6.044 | 19.299 | |
| 1.05 | 0.999 | 1.057 | 2.278 | 6.513 | |||
| 1.1 | 0.86 | 0.871 | 1.133 | 2.655 | |||
| 6 | 5 | 6 | 1.01 | 1.946 | 2.342 | 5.529 | 17.46 |
| 1.05 | 1 | 1.121 | 2.563 | 7.507 | |||
| 1.1 | 0.995 | 0.994 | 1.5 | 3.896 | |||
| 5 | 5 | 1.01 | 1.932 | 2.457 | 5.723 | 17.95 | |
| 1.05 | 1 | 1.213 | 2.642 | 7.891 | |||
| 1.1 | 0.999 | 0.999 | 1.523 | 3.994 | |||
| 4 | 4 | 1.01 | 1.959 | 2.548 | 5.897 | 18.231 | |
| 1.05 | 1.01 | 1.254 | 2.742 | 7.982 | |||
| 1.1 | 0.891 | 1.212 | 2.745 | 4.121 | |||
| 7 | 7 | 7 | 1.01 | 1.891 | 2.21 | 5.123 | 16.213 |
| 1.05 | 0.997 | 1.012 | 2.213 | 7.211 | |||
| 1.1 | 0.995 | 0.985 | 1.213 | 3.456 | |||
| 7 | 6 | 1.01 | 1.893 | 2.225 | 5.54 | 16.523 | |
| 1.05 | 0.995 | 1.12 | 2.241 | 7.543 | |||
| 1.1 | 0.994 | 0.994 | 1.223 | 3.672 | |||
| 8 | 4 | 1.01 | 1.674 | 2.123 | 5.112 | 16.254 | |
| 1.05 | 0.992 | 1.111 | 2.213 | 7.654 | |||
| 1.1 | 0.992 | 0.991 | 1.211 | 3.254 | |||
| 8 | 9 | 8 | 1.01 | 1.259 | 2.004 | 4.951 | 15.319 |
| 1.05 | 0.991 | 1.101 | 2.121 | 7.545 | |||
| 1.1 | 0.991 | 0.989 | 1.221 | 3.224 | |||
| 8 | 7 | 1.01 | 1.261 | 2.112 | 4.998 | 15.119 | |
| 1.05 | 0.991 | 1.104 | 2.132 | 7.614 | |||
| 1.1 | 0.992 | 0.992 | 1.225 | 3.514 | |||
| 8 | 6 | 1.01 | 1.271 | 2.151 | 4.997 | 15.211 | |
| 1.05 | 0.993 | 1.112 | 2.135 | 7.664 | |||
| 1.1 | 0.994 | 0.995 | 1.231 | 3.612 | |||
| 9 | 10 | 9 | 1.01 | 1.101 | 1.121 | 4.121 | 10.123 |
| 1.05 | 0.998 | 1 | 1.857 | 6.345 | |||
| 1.1 | 0.992 | 0.995 | 1.235 | 2.986 | |||
| 7 | 8 | 1.01 | 1.211 | 1.225 | 4.234 | 10.512 | |
| 1.05 | 0.999 | 1 | 1.978 | 6.546 | |||
| 1.1 | 0.999 | 0.999 | 1.435 | 3.102 | |||
| 9 | 7 | 1.01 | 1.112 | 1.235 | 4.225 | 10.562 | |
| 1.05 | 0.999 | 0.999 | 1.898 | 6.658 | |||
| 1.1 | 0.999 | 1 | 1.452 | 3.21 | |||
| 10 | 9 | 10 | 1.01 | 1 | 1 | 2.1 | 7.152 |
| 1.05 | 1 | 1 | 1.21 | 4.231 | |||
| 1.1 | 1 | 1 | 1.102 | 2.147 | |||
| 8 | 9 | 1.01 | 1 | 1 | 2.211 | 7.236 | |
| 1.05 | 1 | 1 | 1.223 | 4.542 | |||
| 1.1 | 1 | 1 | 1.113 | 2.231 | |||
| 8 | 8 | 1.01 | 1 | 1 | 2.321 | 7.325 | |
| 1.05 | 1 | 1 | 1.341 | 4.653 | |||
| 1.1 | 1 | 1 | 1.231 | 2.251 | |||
| HPMPRs | Ranking of Alternatives | Best Commodity |
|---|---|---|
| Copper | ||
| Oil | ||
| Gold |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, Z.; Rashid, T.; Wątróbski, J.; Sałabun, W.; Malik, A. Hesitant Probabilistic Multiplicative Preference Relations in Group Decision Making. Appl. Sci. 2018, 8, 398. https://doi.org/10.3390/app8030398
Bashir Z, Rashid T, Wątróbski J, Sałabun W, Malik A. Hesitant Probabilistic Multiplicative Preference Relations in Group Decision Making. Applied Sciences. 2018; 8(3):398. https://doi.org/10.3390/app8030398
Chicago/Turabian StyleBashir, Zia, Tabasam Rashid, Jarosław Wątróbski, Wojciech Sałabun, and Abbas Malik. 2018. "Hesitant Probabilistic Multiplicative Preference Relations in Group Decision Making" Applied Sciences 8, no. 3: 398. https://doi.org/10.3390/app8030398
APA StyleBashir, Z., Rashid, T., Wątróbski, J., Sałabun, W., & Malik, A. (2018). Hesitant Probabilistic Multiplicative Preference Relations in Group Decision Making. Applied Sciences, 8(3), 398. https://doi.org/10.3390/app8030398





