Effects of Shot-Peening and Stress Ratio on the Fatigue Crack Propagation of AL 7475-T7351 Specimens
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Experimental Procedures
2.1. Materials and Samples
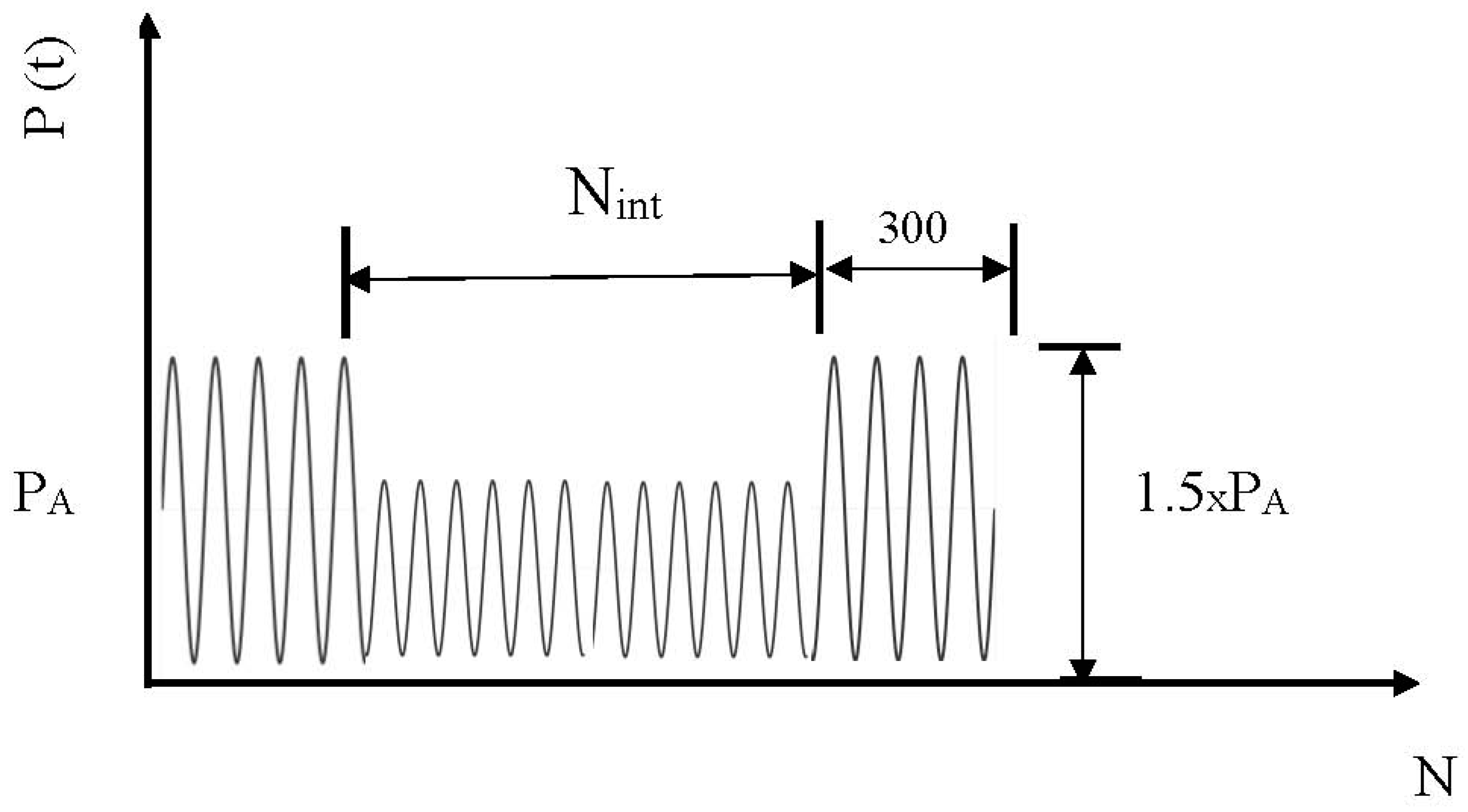
2.2. Fatigue Tests
3. Results and Discussion
4. Conclusions
- -
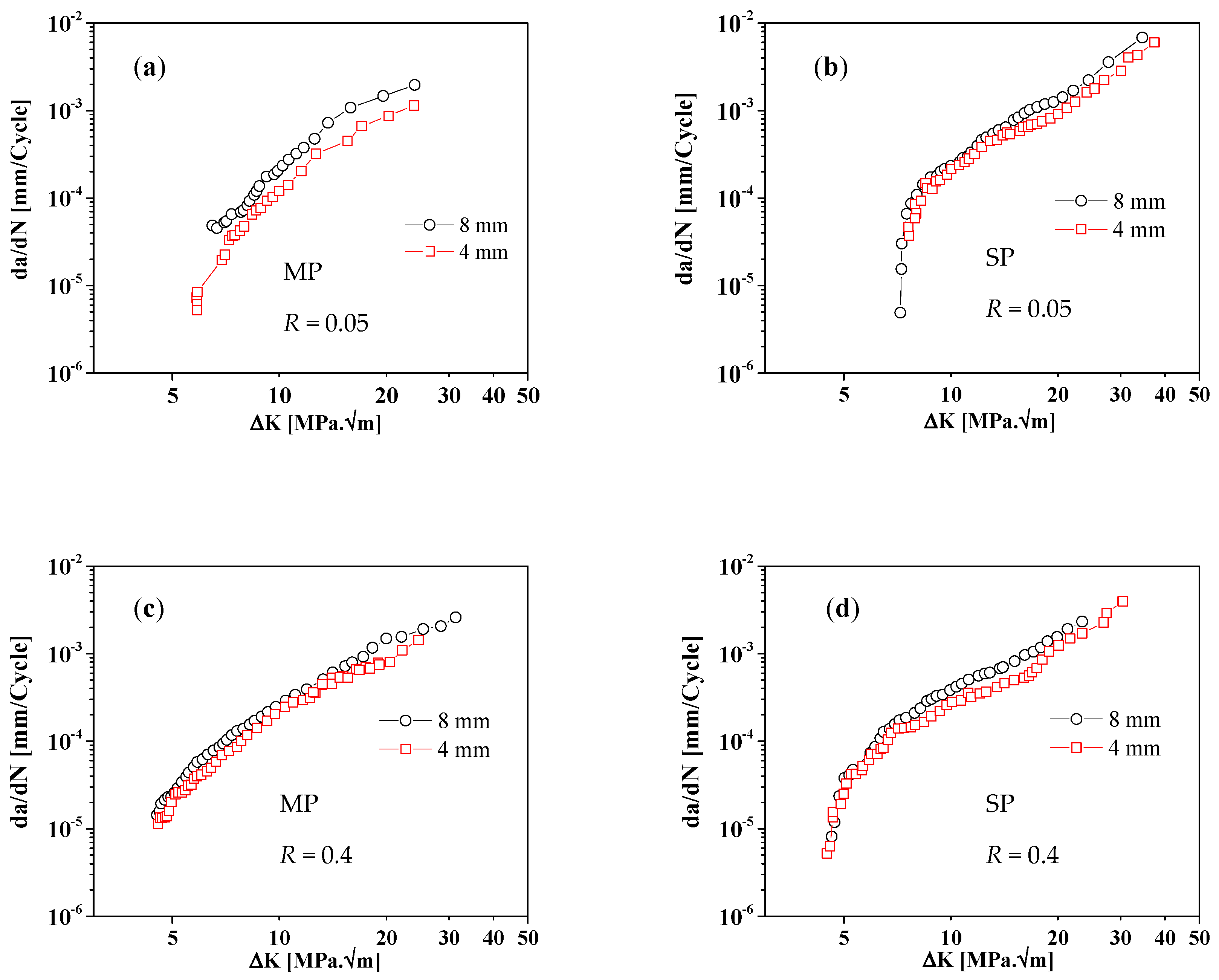
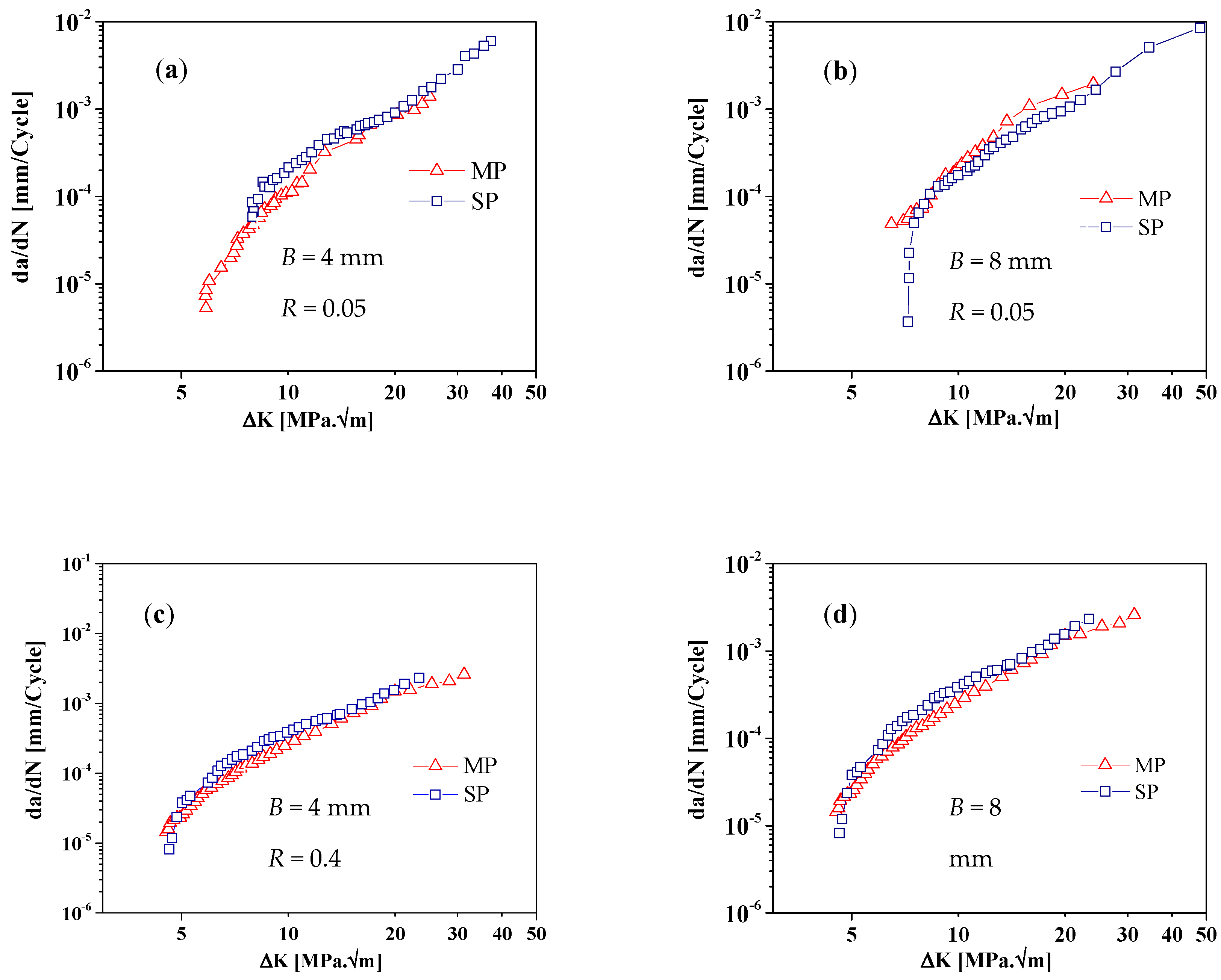
- As a result of its small influence depth, the beneficial effect of shot peening on da/dN-ΔK curves is negligible, particularly for R = 0.4. However, this effect seems to increase near the threshold condition.
- -
- For both mechanically polished and shot-peened samples, a specimen’s thickness has only marginal influence on the stable crack propagation regime.
- -
- A significant effect of the mean stress was observed, particularly in near- threshold region.
- -
- Periodic overload blocks promote a reduction of the fatigue crack growth rate. For MP specimens, the reduction reaches the maximum value for the interval between blocks of 7500 cycles, while, for SP specimens, the crack growth rate continues to decrease for intervals of 15,000 cycles.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fathallah, R.; Laamouri, A.; Sidhom, H.; Braham, C. High cycle fatigue behavior prediction of shot-peened parts. Int. J. Fatigue 2004, 26, 1053–1067. [Google Scholar] [CrossRef]
- Miková, K.; Bagherifard, S.; Bokůvka, O.; Guagliano, M.; Trško, L. Fatigue behavior of X70 microalloyed steel after severe shot peening. Int. J. Fatigue 2013, 55, 33–42. [Google Scholar] [CrossRef]
- Bagherifard, S.; Guagliano, M. Fatigue behavior of a low alloy steel with nanostructured surface obtained by severe shot peening. Eng. Fract. Mech. 2012, 81, 56–68. [Google Scholar] [CrossRef]
- Zhang, P.; Lindemann, J.; Leyens, L. Shot peening on the high-strength magnesium alloy AZ80—effect of peening media. J. Mater. Process. Technol. 2010, 210, 445–450. [Google Scholar] [CrossRef]
- Petit, J.; Mendez, J. Some aspects of the influence of microstructure on fatigue resistance. In Fatigue 96, Proceedings of the Sixth International Fatigue Congress, Berlin, Germany, 6–10 May 1996; Lutjering, G., Nowack, H., Eds.; Pergamon: Oxford, UK, 1996; Volume I, pp. 15–26. [Google Scholar]
- Bergner, F.; Zouhar, G. A new approach to the correlation between the coefficient and the exponent in the power law equation of fatigue crack growth. Int. J. Fatigue 2000, 22, 229–239. [Google Scholar] [CrossRef]
- Bergner, F.; Zouhar, G.; Tempus, G. The material-dependent variability of fatigue crack growth rates of aluminium alloys in the Paris regime. Int. J. Fatigue 2001, 23, 383–394. [Google Scholar] [CrossRef]
- Sunder, R.; Dash, P.K. Measurement of fatigue crack closure through electron microscopy. Int. J. Fatigue 1982, 4, 97–105. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Huang, S.; Sheng, J.; Lu, J.Z.; Wang, C.D.; Chen, K.M.; Ruan, H.Y.; Chen, H.S. Effect of repeated impacts on mechanical properties and fatigue fracture morphologies of 6061-T6 aluminium subject to laser peening. Mater. Sci. Eng. A 2012, 539, 360–368. [Google Scholar] [CrossRef]
- Pant, B.K.; Pavan, A.H.V.; Prakash, R.V.; Kamaraj, M. Effect of laser peening and shot peening on fatigue striations during FCGR study of Ti6Al4V. Int. J. Fatigue 2016, 93, 38–50. [Google Scholar] [CrossRef]
- Vecchio, R.S.; Hertzberg, R.W.; Jaccard, R. On the overload induced fatigue crack propagation behavior in aluminium and steel alloys. Fatigue Fract. Eng. Mater. Struct. 1984, 7, 181–194. [Google Scholar] [CrossRef]
- Ward-Close, C.M.; Blom, A.F.; Richie, R.O. Mechanisms associated with transient fatigue crack growth under variable amplitude loading: An experimental and numerical study. Eng. Fract. Mech. 1989, 32, 613–638. [Google Scholar] [CrossRef]
- Krumar, R.; Garg, S.B.L. Effect of yield strength and single overload cycles on effective stress intensity range ratio in 6061-T6 Alalloy. Eng. Fract. Mech. 1989, 34, 403–412. [Google Scholar] [CrossRef]
- Ling, M.R.; Schijve, J. The effect of intermediate heat treatments on overload induced retardations during fatigue crack growth in an Al-alloy. Fatigue Fract. Eng. Mater. Struct. 1992, 15, 421–430. [Google Scholar] [CrossRef]
- Damri, D.; Knott, J.F. Fracture modes encountered following the application of a major tensile overload cycle. Int. J. Fatigue 1993, 15, 53–60. [Google Scholar] [CrossRef]
- Shuter, D.M.; Geary, W. Some aspects of fatigue crack growth retardation behaviour following tensile overloads in a structural steel. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 185–199. [Google Scholar] [CrossRef]
- Robin, C.; Louah, M.; Pluvinage, G. Influence of the overload on the fatigue crack growth in steels. Fatigue Fract. Eng. Mater. Struct. 1983, 6, 1–13. [Google Scholar] [CrossRef]
- Shercliff, H.R.; Fleck, N.A. Effect of specimen geometry on fatigue crack growth in plane strain—II. Overload response. Fatigue Fract. Eng. Mater. Struct. 1990, 13, 297–310. [Google Scholar] [CrossRef]
- Shin, C.S.; Hsu, S.H. On the mechanisms and behaviour of overload retardation in AISI 304 stainless steel. Int. J. Fatigue 1993, 15, 181–192. [Google Scholar] [CrossRef]
- Dexter, R.J.; Hudak, S.J.; Davidson, D.L. Modelling and measurement of crack closure and crack growth following overloads and underloads. Eng. Fract. Mech. 1989, 33, 855–870. [Google Scholar] [CrossRef]
- Tsukuda, H.; Ogiyama, H.; Shiraishi, T. Transient fatigue crack growth behaviour following single overloads at high stress ratios. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 879–891. [Google Scholar] [CrossRef]
- Borrego, L.P.; Ferreira, J.M.; Pinho da Cruz, J.M.; Costa, J.M. Evaluation of overload effects on fatigue crack growth and closure. Eng. Fract. Mech. 2003, 70, 1379–1397. [Google Scholar] [CrossRef]
- Donald, K.; Paris, P.C. An evaluation of DKeff estimation procedures on 6061-T6 and 2024-T3 aluminium alloys. Int. J. Fatigue 1999, 21, S47–S57. [Google Scholar] [CrossRef]
- Paris, P.C.; Tada, H.; Donald, J.K. Service load fatigue damage––A historical perspective. Int. J. Fatigue 1999, 21, S35–S46. [Google Scholar] [CrossRef]
- Borrego, L.P.; Ferreira, J.M.; Costa, J.M. Fatigue crack growth and crack closure in an AlMgSi alloy. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 255–265. [Google Scholar] [CrossRef]
- The American Standard SAE J443. Procedures for Using Standard Shot Peening Test Strip; American Standard: Piscataway Township, NJ, USA, 1968. [Google Scholar]
- The American Standard. Aerospace Materials Division; SAE, Shot Peening, SAE AMS 2430; American Standard: Piscataway Township, NJ, USA, 2009. [Google Scholar]
- American Society for Testing and Materials. Standard Test Method for Microhardness of Materials. In Annual Book of ASTM Standards; ASTM: West Conshohocken, PA, USA, 2000; Volume 03.01, p. E647. [Google Scholar]
- International Organization for Standardization. DIN EN ISO 4288: Geometrical Product Specifications (GPS). Surface Texture: Profile Method: Rules and Procedures for the Assessment of Surface Texture; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- American Society for Testing and Materials. Standard Test Method for Vickers Indentation Hardness of Advanced Ceramics; ASTM: West Conshohocken, PA, USA, 2015; p. C1327. [Google Scholar]
- Borrego, L.P.; Costa, J.D.M.; Silva, S.; Ferreira, J.M. Microstructure dependent fatigue crack growth in aged hardened aluminium alloys. Int. J. Fatigue 2004, 26, 1321–1331. [Google Scholar] [CrossRef]
- Antunes, F.V.; Chegini, A.G.; Branco, R.; Camas, D. A numerical study of plasticity induced crack closure under plane strain conditions. Int. J. Fatigue 2015, 71, 75–86. [Google Scholar] [CrossRef]
- Antunes, F.V.; Ramalho, A.L.; Ferreira, J.A.M. Identification of Fatigue Crack Propagation Modes with Roughness Measurements. Int. J. Fatigue 2000, 22, 781–788. [Google Scholar] [CrossRef]
- Lin, X.B.; Smith, R.A. Fatigue shape analysis for corner cracks at fastener holes. Eng. Fract. Mech. 1998, 59, 73–87. [Google Scholar] [CrossRef]
- Branco, R. Numerical Study of Fatigue Crack Growth in MT Specimens. Master’s Thesis, Department of Mechanical Engineering, University of Coimbra, Coimbra, Portugal, 2006. [Google Scholar]
- He, B.Y.; Soady, K.A.; Mellor, B.G.; Harrison, G.; Reed, P.A.S. Fatigue crack growth behaviour in the LCF regime in a shot peened steam turbine blade material. Int. J. Fatigue 2016, 82, 280–291. [Google Scholar] [CrossRef]
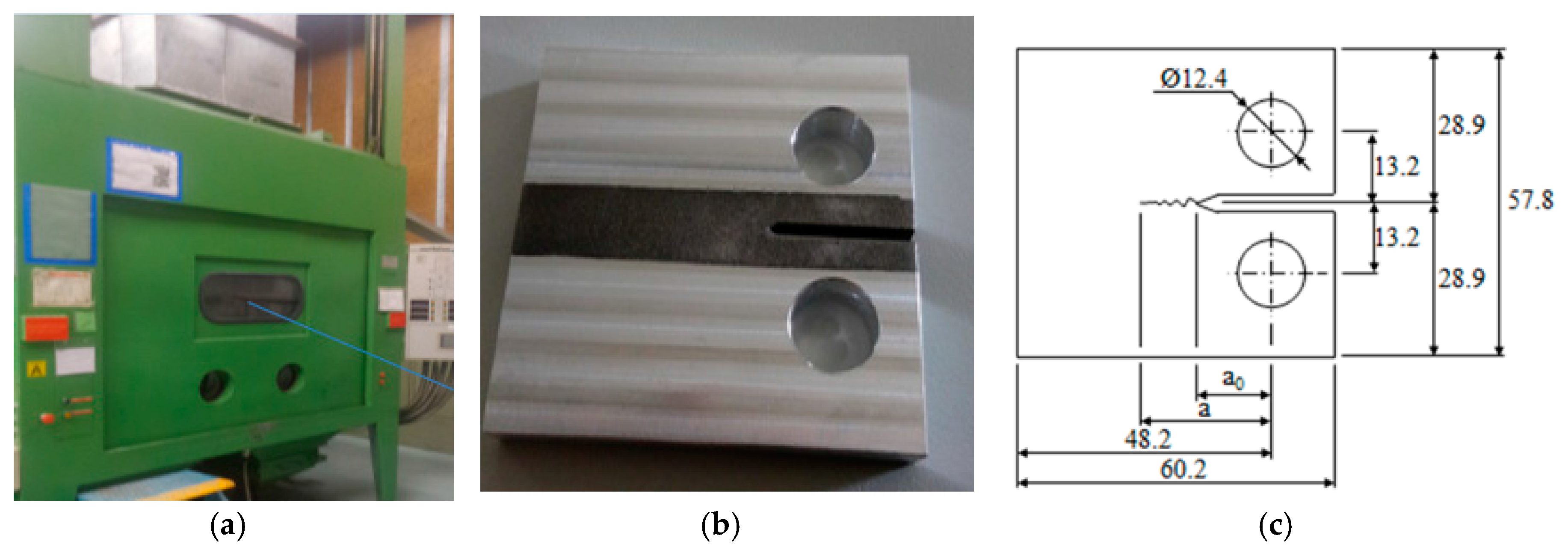


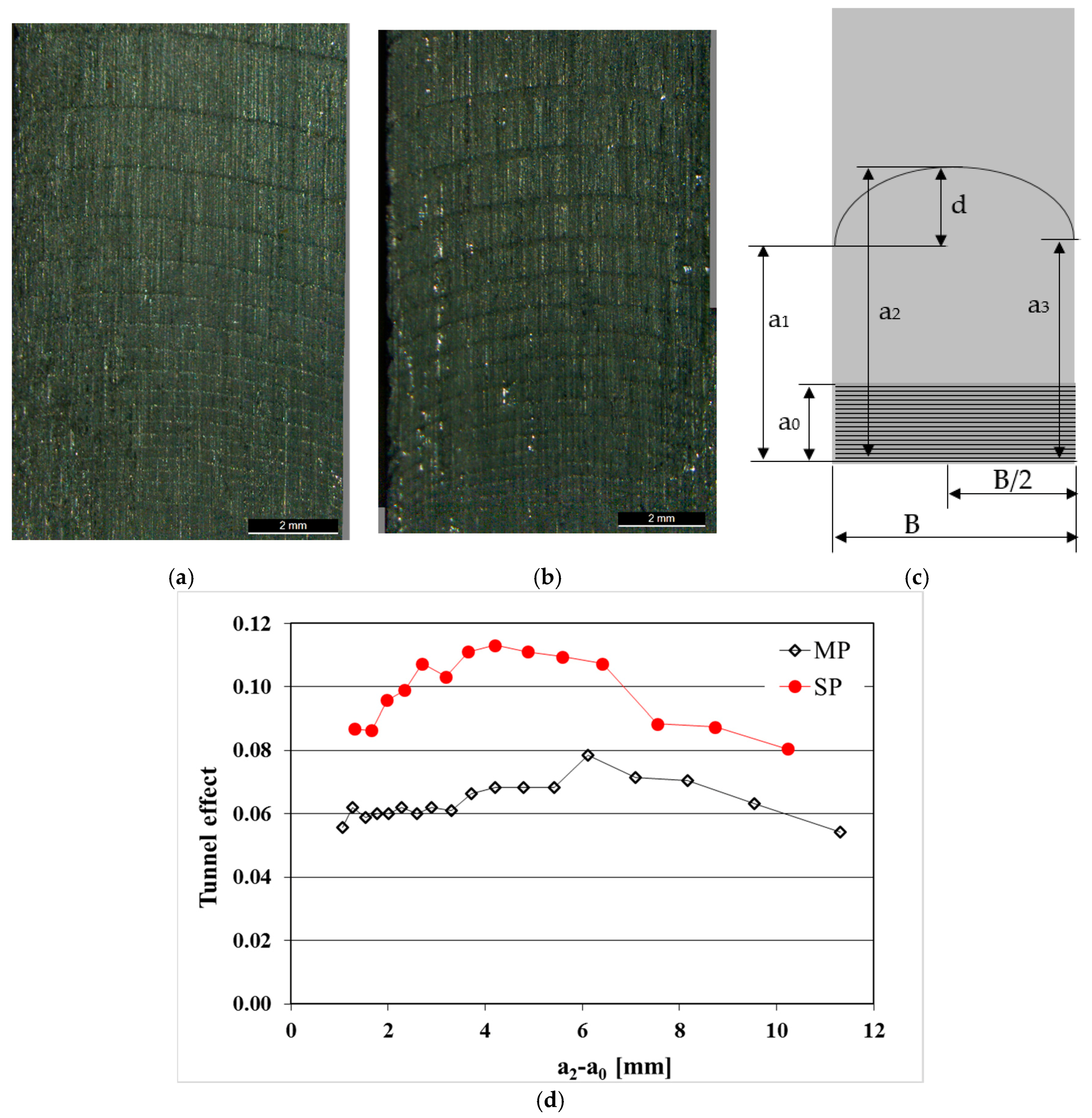
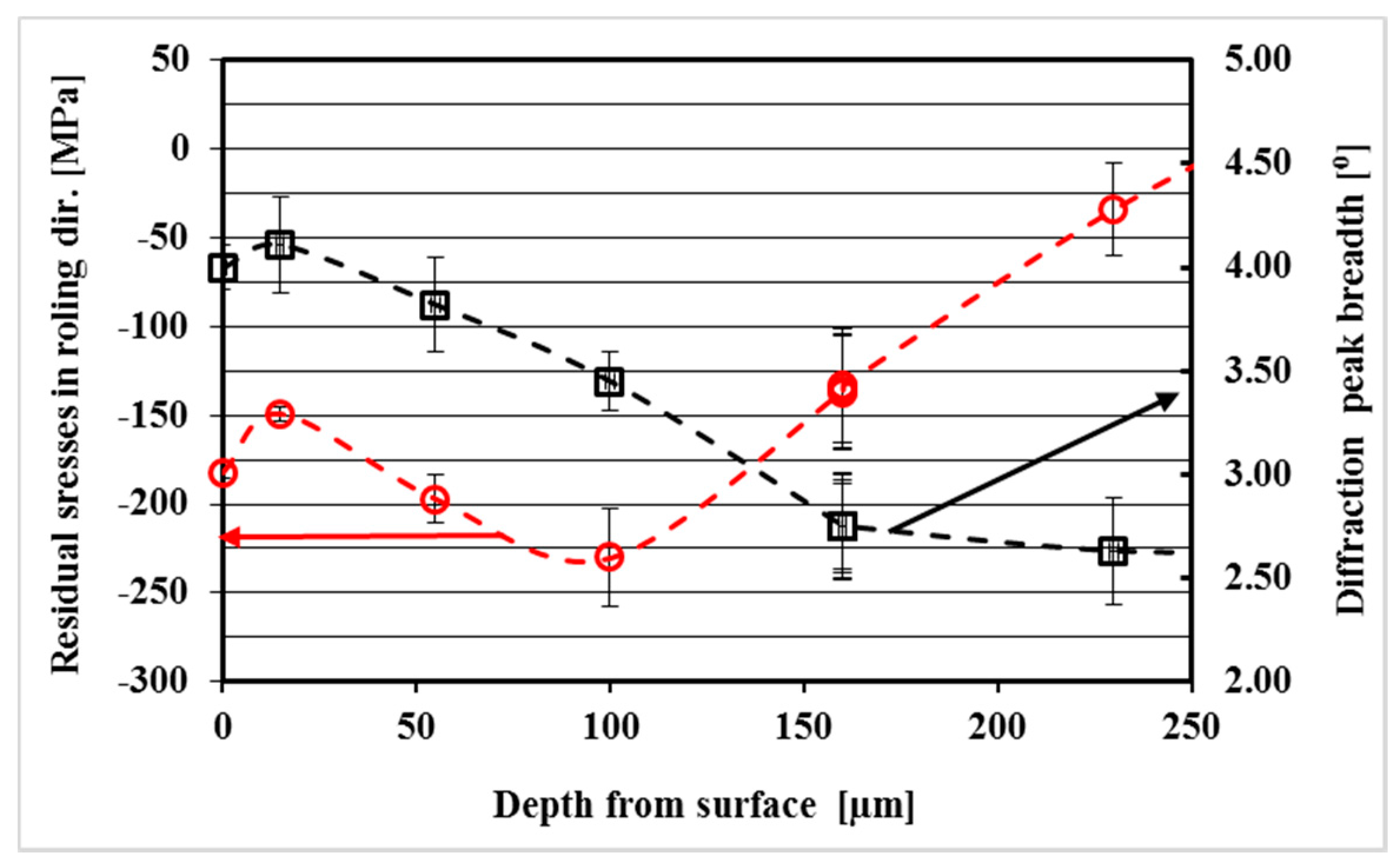
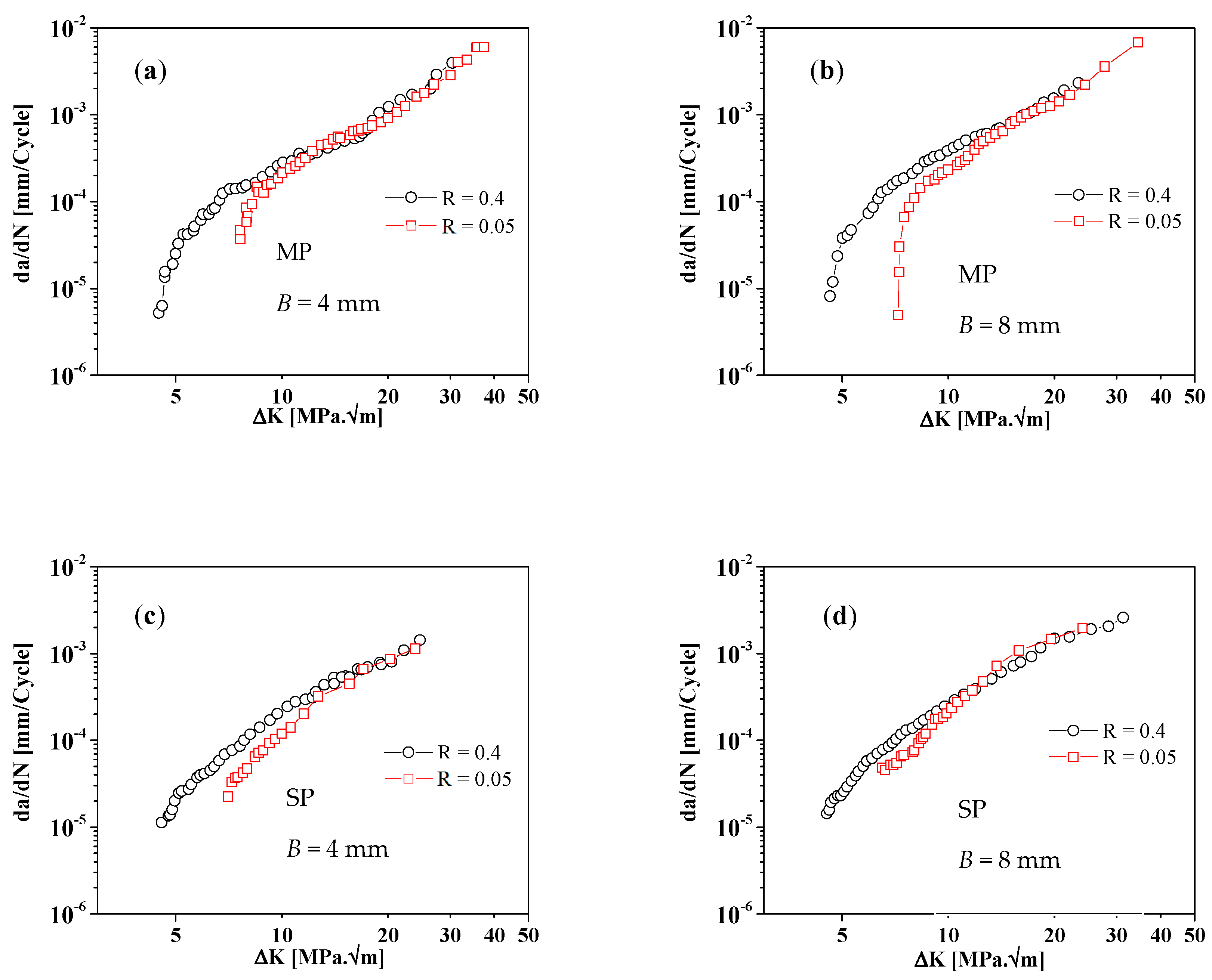
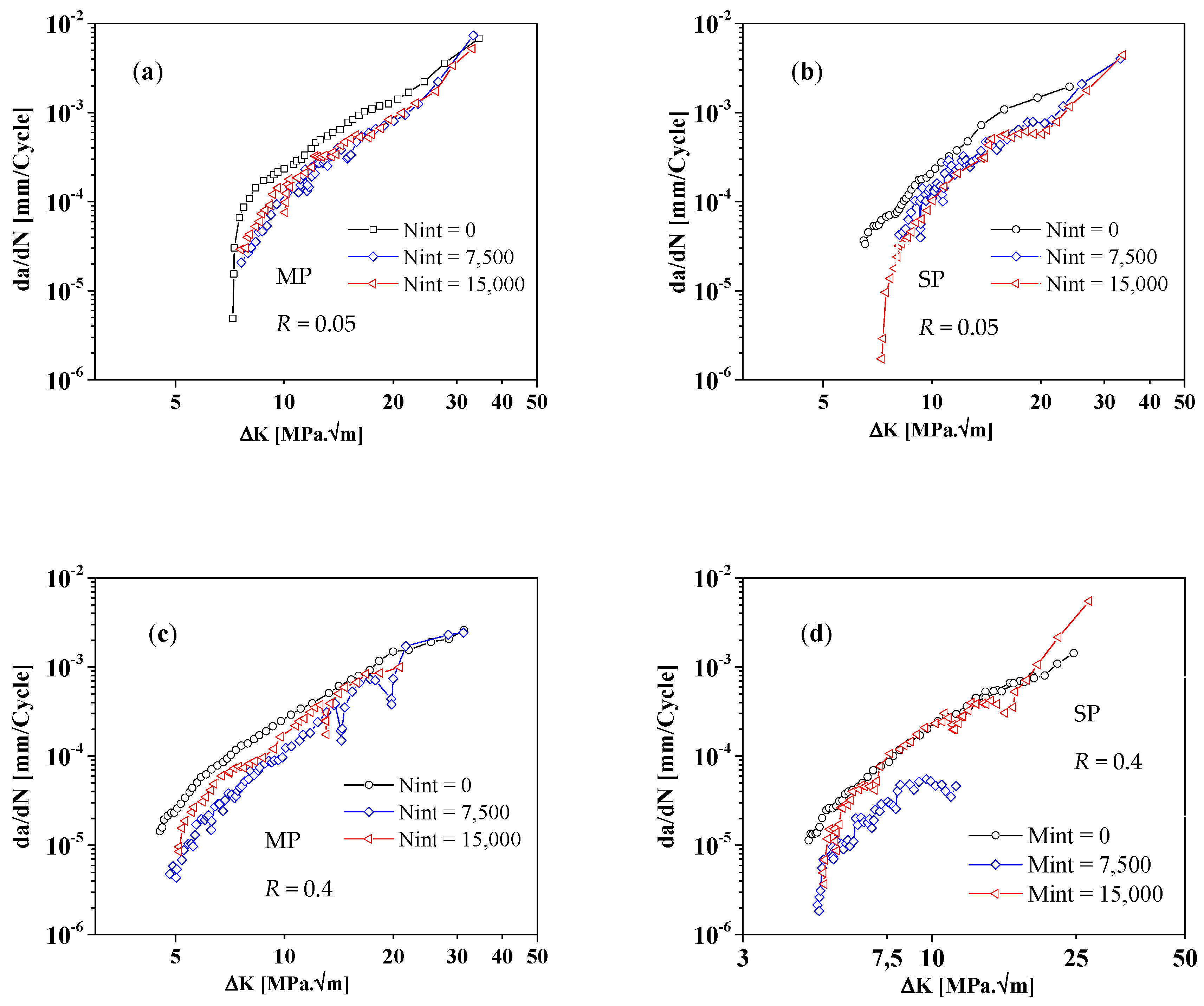

| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Others | Al |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.12 | 1.2–1.9 | 0.06 | 1.9–2.6 | 0.18–0.25 | 5.2–6.2 | 0.06 | 0.15 | Remaining |
| Specimen | Parameter | Mean Value ± Standard Deviation (μm) |
|---|---|---|
| MP | Ra | 1.22 ± 0.02 |
| Rq | 1.50 ± 0.02 | |
| Rz | 7.74 ± 0.13 | |
| SP | Ra | 3.70 ± 0.17 |
| Rq | 4.60 ± 0.21 | |
| Rz | 23.50 ± 2.00 |
| B [mm] | Specimen | R | C | m | Validity [MPa m1/2] | Correlation Factor |
|---|---|---|---|---|---|---|
| 4 | MP | 0.05 | 1.41 × 10−8 | 3.94 | 7–13 | 0.995 |
| 4 | MP | 0.4 | 2.42 × 10−6 | 2.04 | 12–24 | 0.996 |
| 4 | SP | 0.05 | 2.95 × 10−7 | 2.94 | 8–14 | 0.970 |
| 4 | SP | 0.4 | 2.70 × 10−7 | 3.05 | 5–10 | 0.982 |
| 8 | MP | 0.05 | 2.72 × 10−8 | 3.89 | 7–12 | 0.996 |
| 8 | MP | 0.4 | 1.96 × 10−6 | 2.16 | 13–22 | 0.998 |
| 8 | SP | 0.05 | 2.53 × 10−7 | 2.97 | 9–16 | 0.991 |
| 8 | SP | 0.4 | 2.63 × 10−7 | 3.25 | 5–17 | 0.973 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, N.; Antunes, P.V.; Ferreira, J.A.M.; D. M. Costa, J.; Capela, C. Effects of Shot-Peening and Stress Ratio on the Fatigue Crack Propagation of AL 7475-T7351 Specimens. Appl. Sci. 2018, 8, 375. https://doi.org/10.3390/app8030375
Ferreira N, Antunes PV, Ferreira JAM, D. M. Costa J, Capela C. Effects of Shot-Peening and Stress Ratio on the Fatigue Crack Propagation of AL 7475-T7351 Specimens. Applied Sciences. 2018; 8(3):375. https://doi.org/10.3390/app8030375
Chicago/Turabian StyleFerreira, Natália, Pedro V. Antunes, José A. M. Ferreira, José D. M. Costa, and Carlos Capela. 2018. "Effects of Shot-Peening and Stress Ratio on the Fatigue Crack Propagation of AL 7475-T7351 Specimens" Applied Sciences 8, no. 3: 375. https://doi.org/10.3390/app8030375
APA StyleFerreira, N., Antunes, P. V., Ferreira, J. A. M., D. M. Costa, J., & Capela, C. (2018). Effects of Shot-Peening and Stress Ratio on the Fatigue Crack Propagation of AL 7475-T7351 Specimens. Applied Sciences, 8(3), 375. https://doi.org/10.3390/app8030375






