Characterization of Control-Dependent Variable Stiffness Behavior in Discrete Muscle-Like Actuators
Abstract
:1. Introduction
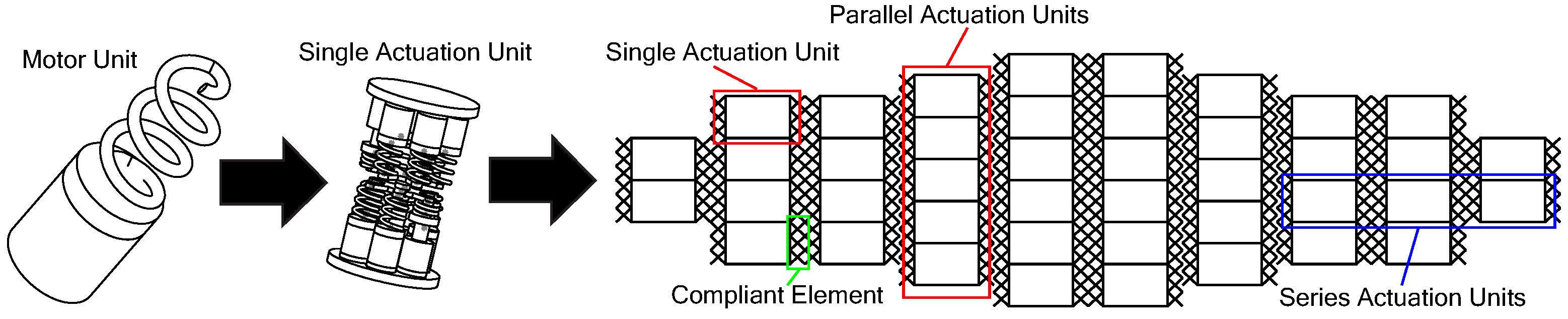
2. Muscle-Like Actuators Composed of Discrete Building Blocks
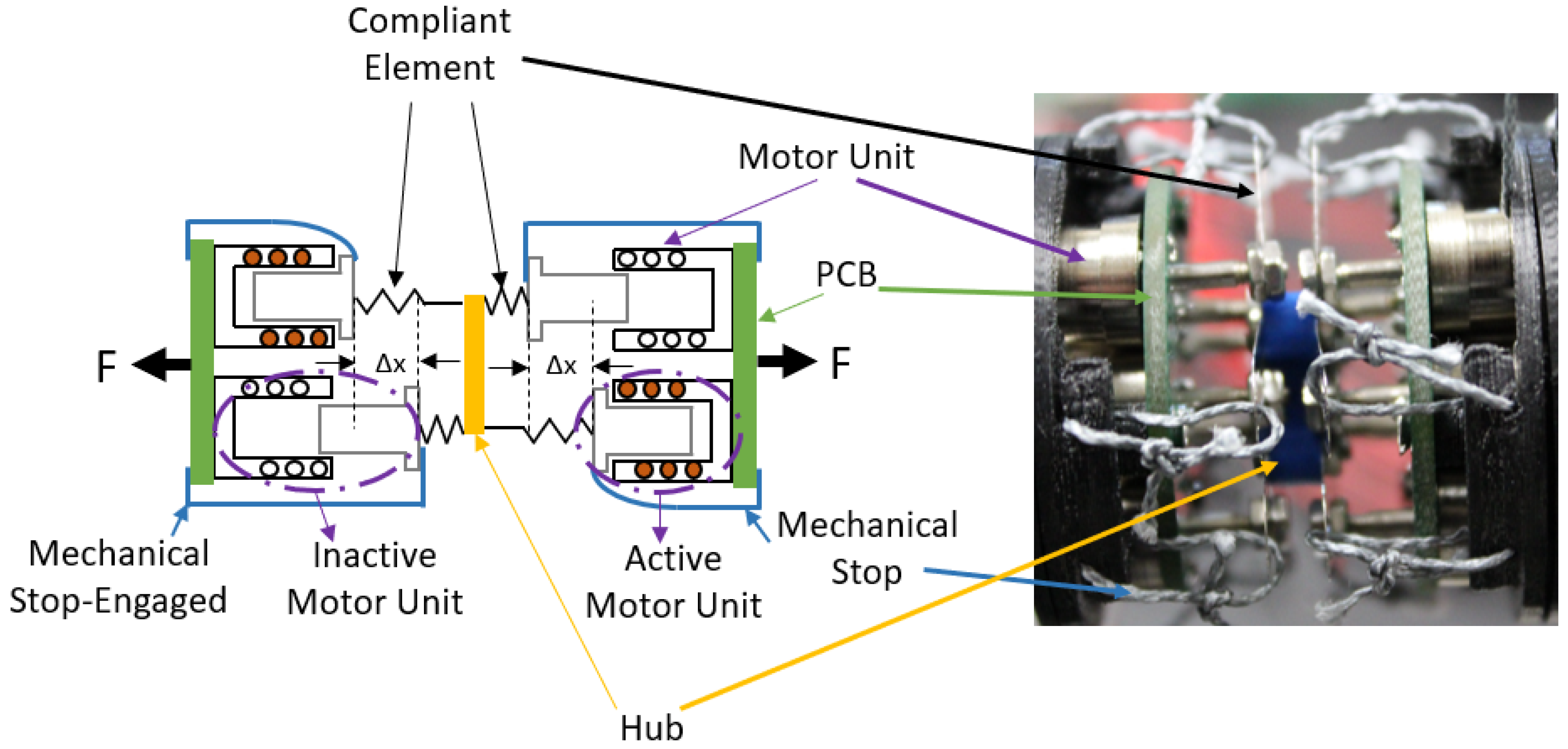
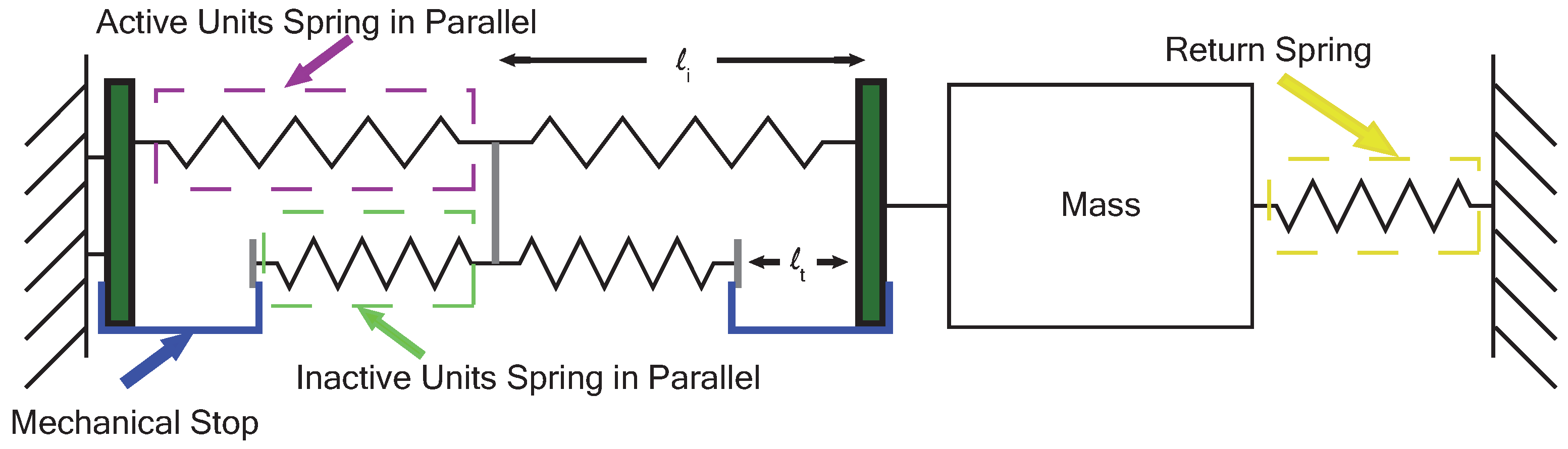
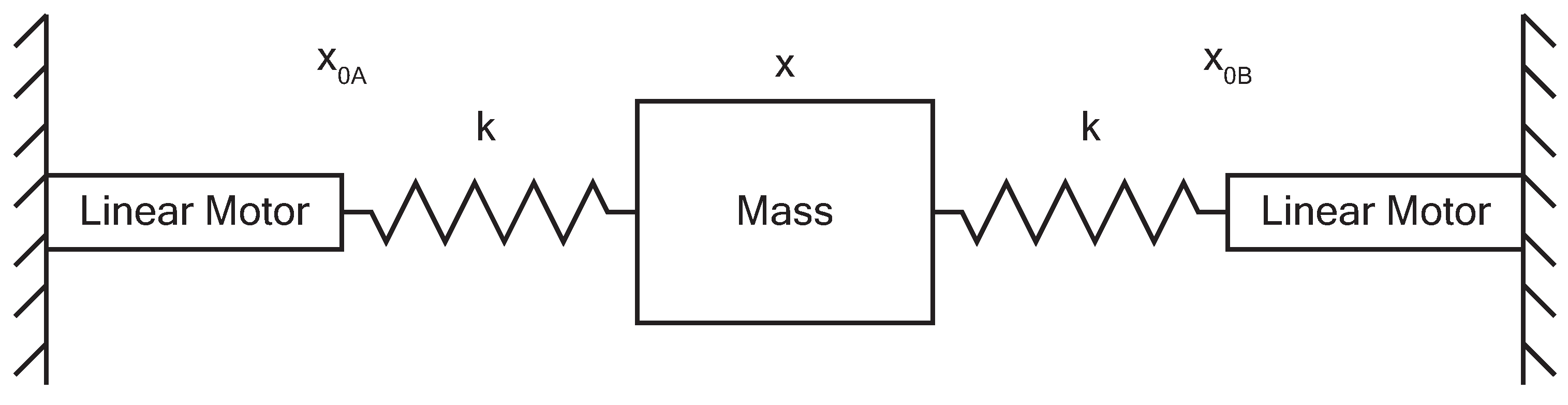
2.1. Actuation Unit Design and Definition
2.2. The Mechanical Stop and Limiting Condition
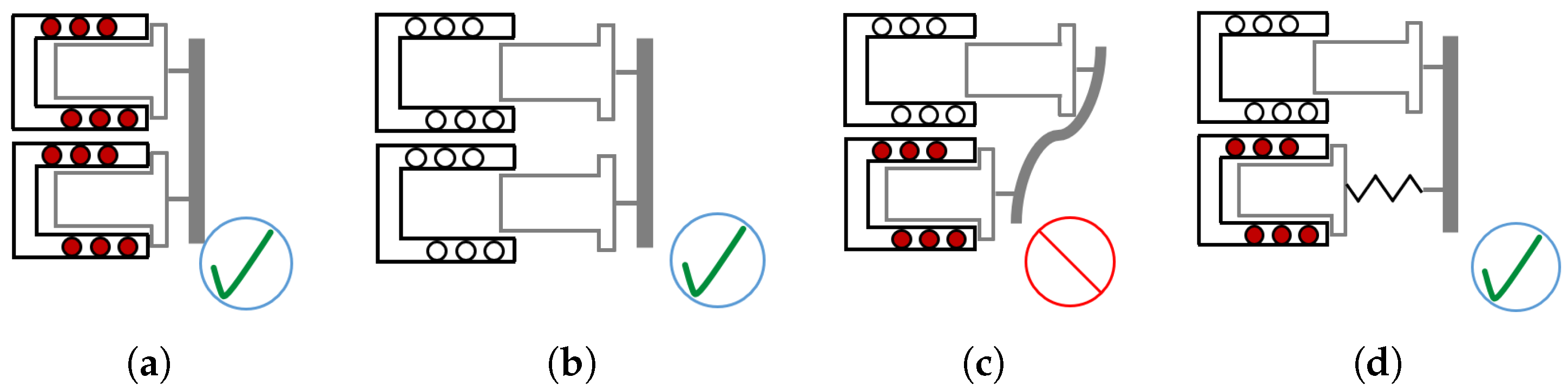
2.3. Class Structure
2.3.1. Class 0
2.3.2. Class I
2.3.3. Class II
2.3.4. Class III
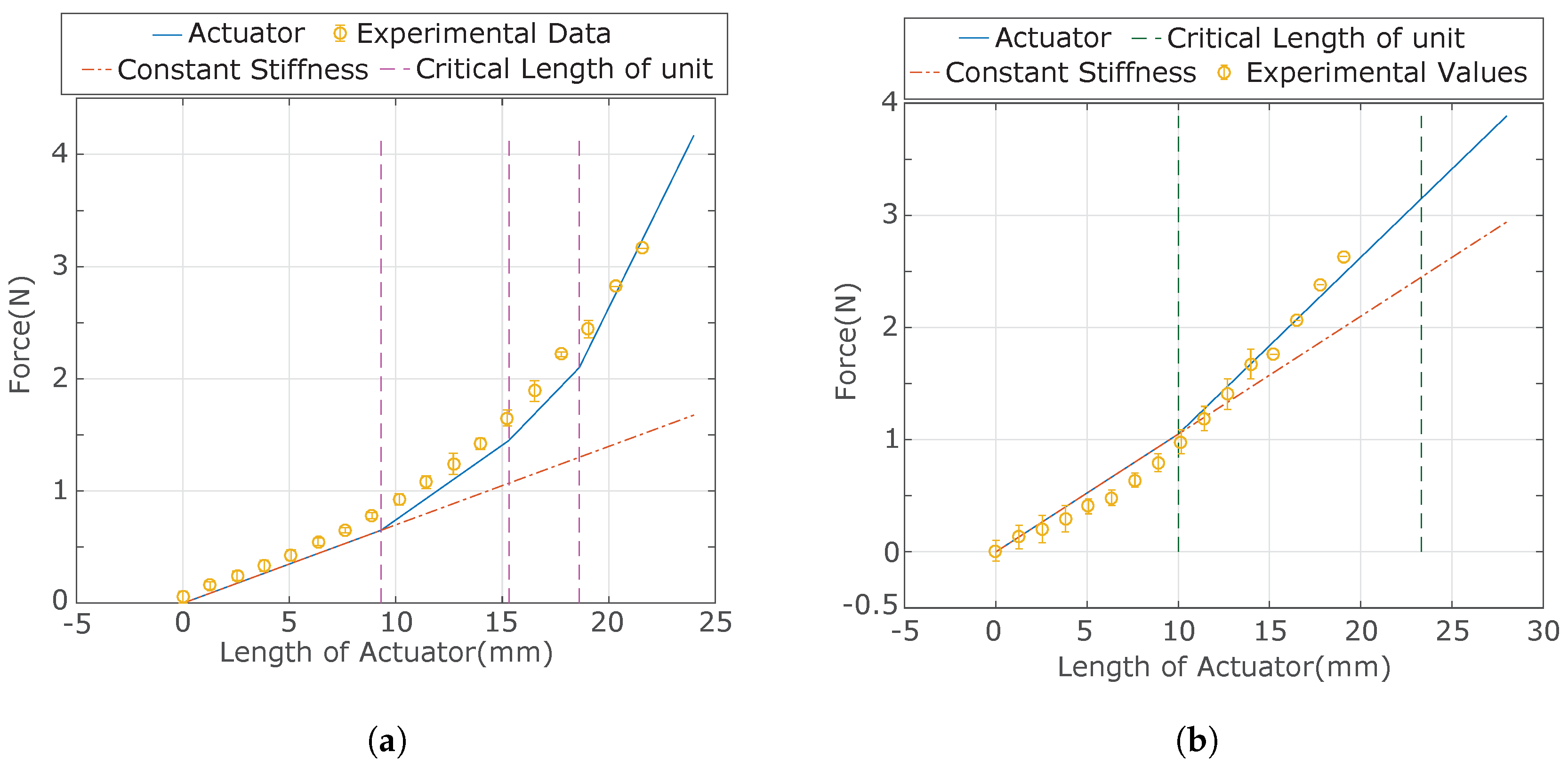
2.3.5. Critical Length
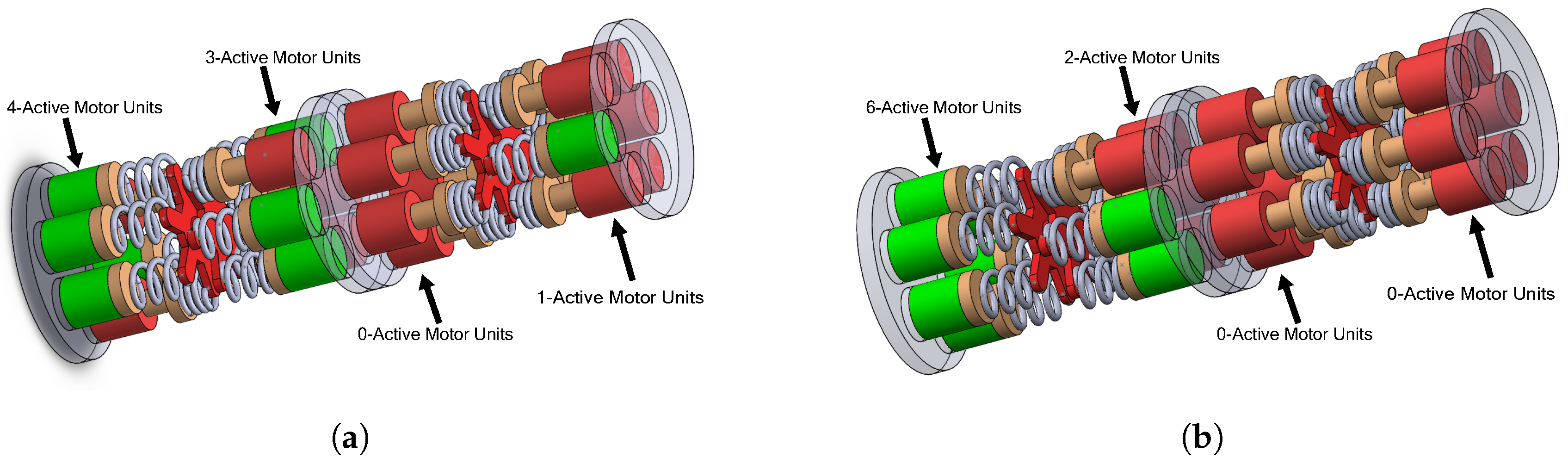
2.4. Activation Patterns and Activation Levels
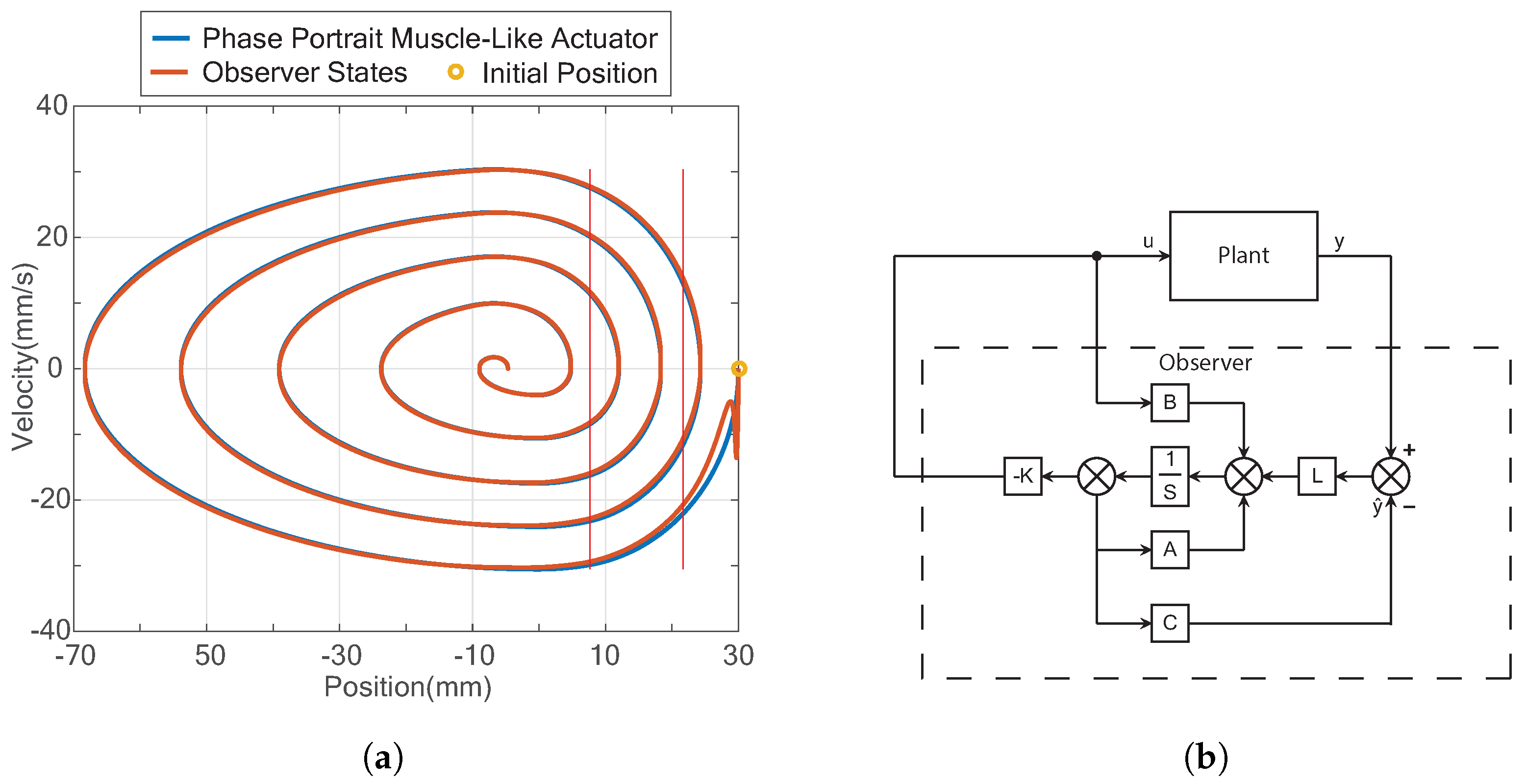
3. Complex System Dynamics of a Variable Impedance Discrete Actuator with a Simple SEA Observer Model
- A typical continuously variable signal will not be sufficient for driving a discrete actuator.
- The control signal must be transformed into an integer number of motor units “on”.
- This number of motor units “on” must be selected based upon the closest value to the control signal that is possible.
- One must decide which units will lead to the most desired affect on the system dynamics.
- These steps are symplified by treating the entire actuator as an SEA.
- The contraction of the motor units is frictionless.
- The mass of the actuation units is negligible as compared to the driven inertial mass.
- The mechanical stops at each spring lobe engage at same length.
3.1. Mathematica Formulation
3.2. Simulations and Illustrative Examples of Discrete Muscle-Like Actuator Dynamics
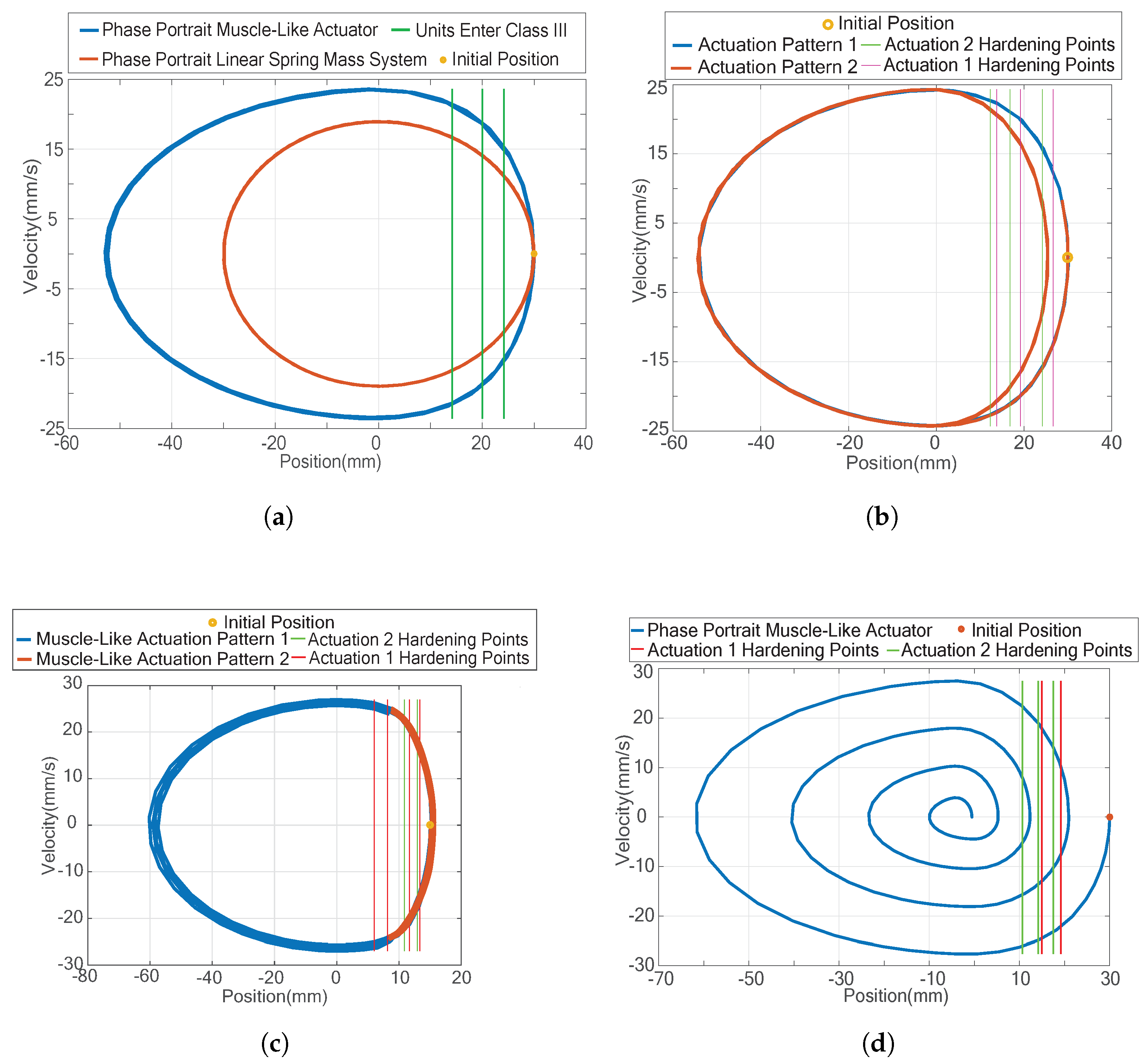
- Figure 8a shows the phase portrait of the natural response of the muscle-like actuator due to an initial condition (blue), contrasting a linear spring setup showing the familiar symmetrical ellipse pattern. The “D” shape curve clearly shows the hardening behavior. The three vertical lines show the points at which the actuation units move from Class II to Class III, the first vertical line closest to the origin being the Critical Length of the actuator.
- Figure 8b looks at the phase portrait in which the actuator switches between two different activation patterns halfway through the simulation time. It is evident the phase portrait changes shape, and is easy to tell that the second pattern has a higher stiffness than the first.
- Figure 8c displays a switching pattern that changes the activation pattern at equilibrium position. It is evident that this switching pattern does not offer the stark difference between activation patterns, and thus it should be noted that as long as the actuator is in Class Zero it has no hardening behavior, this also means that as long as the oscillation has a negative position on the phase portrait it is only affected by the return spring and carries none of the aspects of the variable stiffness muscle-like actuator.
- Figure 8d shows a switching condition based upon the velocity of the load mass, which can easily be measured in practice. Velocity switching occurs by moving from an actuation pattern that is less “stiff” to an actuation pattern that is more “stiff” at the point when the velocity sign changes; it can be noted that this can be done with the same total number of motor units active across the actuation units (but changing the distribution) or by increasing the number of total active motor units. The results from this simulation, see Figure 8d, are quite interesting. For the mass fixed to the end of this actuator and a return spring it exhibits damping-like behavior without there being any damping modeled in the system.
3.3. SEA Model Implementation
3.3.1. Quantization of the Observer Control Signal to Discrete Control Signal
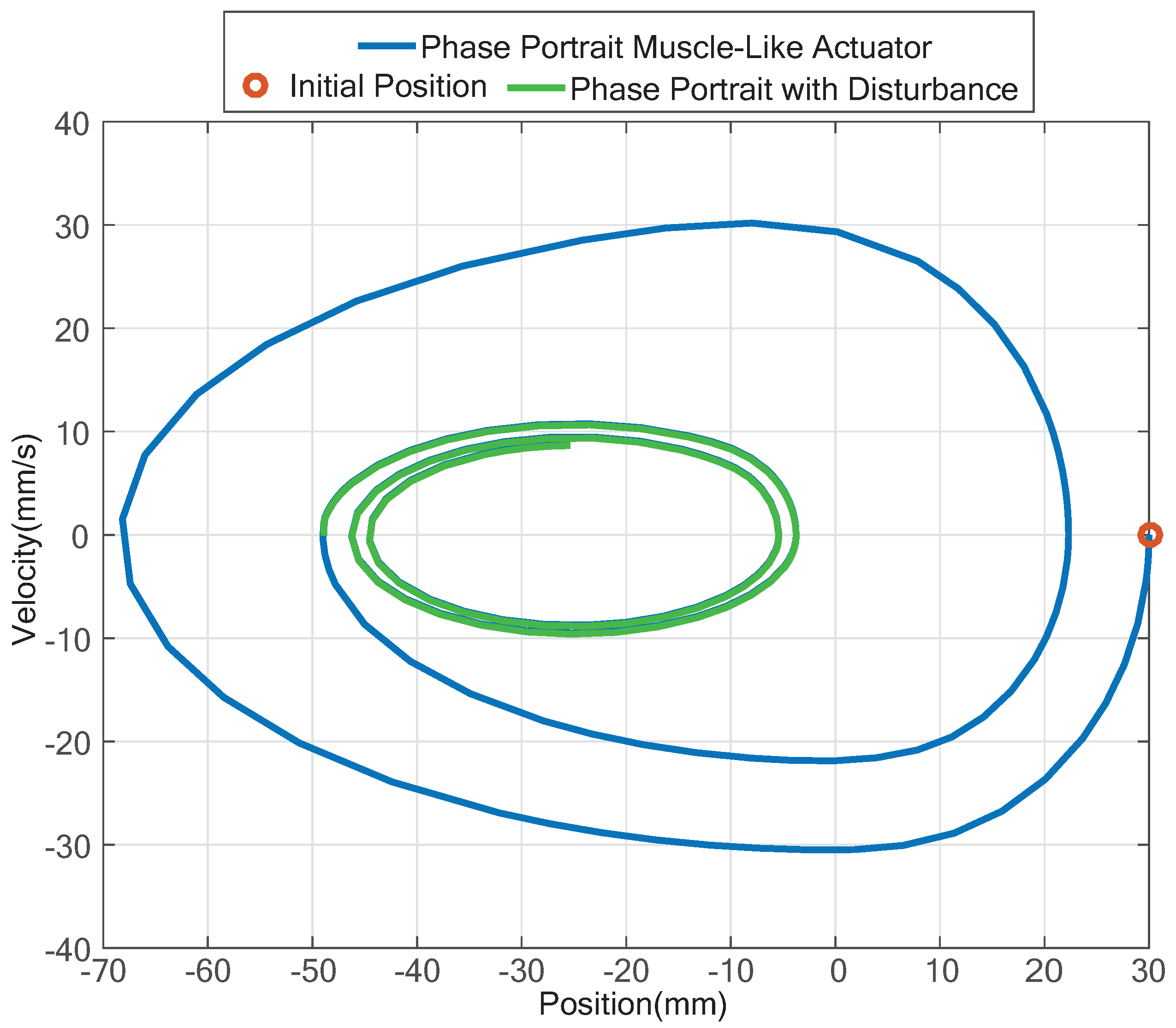
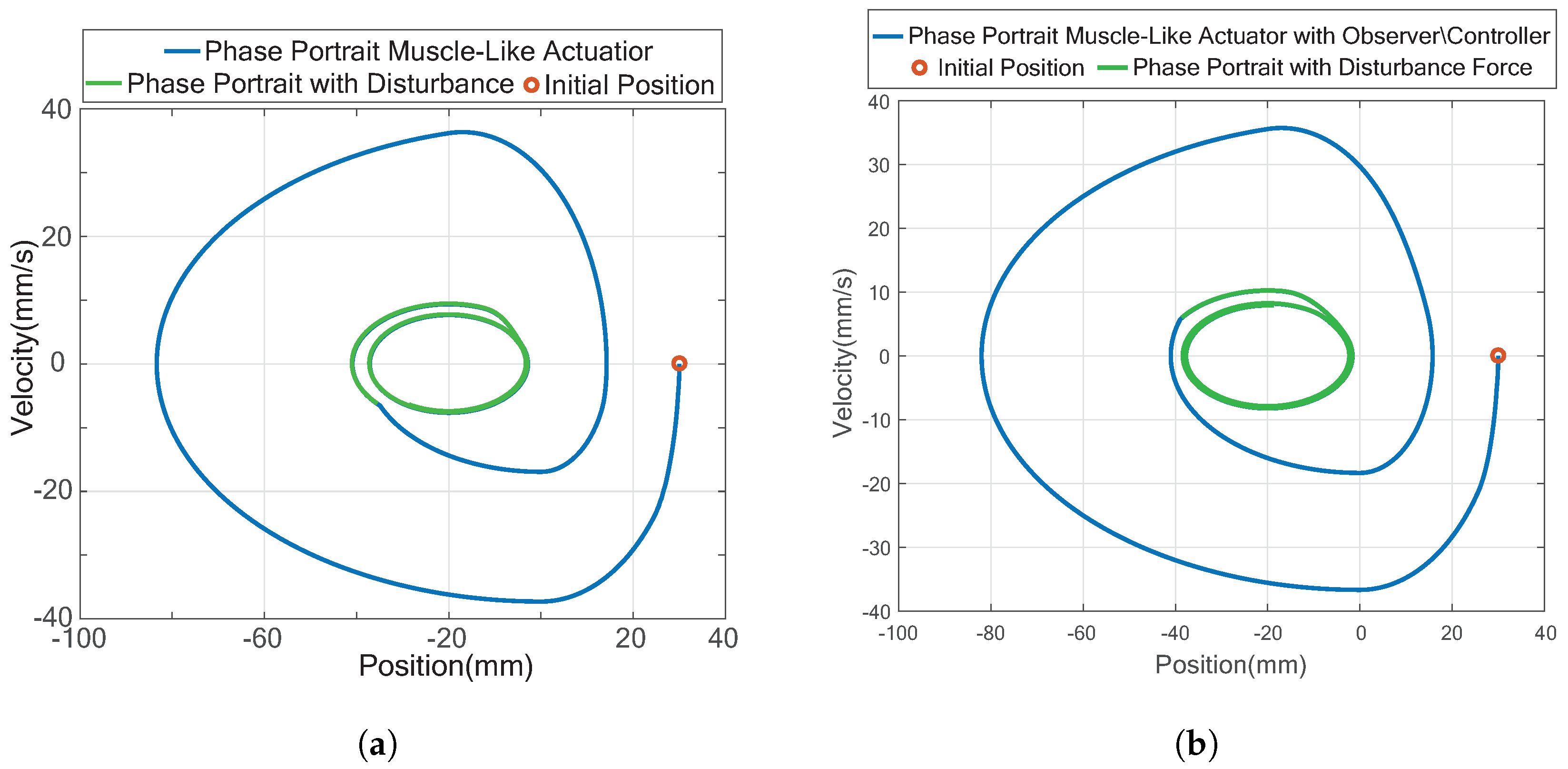
3.3.2. Introducing a Disturbance
3.3.3. Muscle-Like Actuator in Antagonistic Setup
4. Experimental Verification of Length-Based Hardening
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Enoka, C. Motor Unit. Compr. Physiol. 2012, 2, 2629–2682. [Google Scholar]
- Mathijssen, G.; Schultz, J.; Vanderborght, B.; Bicchi, A. A muscle-like recruitment actuator with modular redundant actuation units for soft robotics. Robot. Auton. Syst. 2015, 74, 40–50. [Google Scholar] [CrossRef]
- Gere, J.; Goodno, B. Mechanics of Materials; Cengage Learning: Boston, MA, USA, 2008. [Google Scholar]
- Pratt, G.A.; Williamson, M.M. Series elastic actuators. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems 95. “Human Robot Interaction and Cooperative Robots”, Pittsburgh, PA, USA, 5–9 August 1995; Volume 1, pp. 399–406. [Google Scholar]
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Tonietti, G.; Schiavi, R.; Bicchi, A. Design and Control of a Variable Stiffness Actuator for Safe and Fast Physical Human/Robot Interaction. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Schultz, J.; Mathijssen, G.; Vanderborght, B.; Bicchi, A. A selective recruitment strategy for exploiting muscle-like actuator impedance properties. In Proceedings of the 2015 IEEE/RSJ Intelligent Robots and Systems Conference, Hamburg, Germany, 28 September–2 October 2015; pp. 40–50. [Google Scholar]
- Corr, L.R.; Clark, W.W. Comparison of low-frequency piezoelectric switching shunt techniques for structural damping. Smart Mater. Struct. 2002, 11, 307. [Google Scholar] [CrossRef]
- Gasparri, G.M.; Garabini, M.; Pallottino, L.; Malagia, L.; Catalano, M.; Grioli, G.; Bicchi, A. Variable Stiffness Control for Oscillation Damping. In Proceedings of the 2015 IEEE/RSJ Intelligent Robots and Systems Conference, Hamburg, Germany, 28 September–2 October 2015; pp. 6543–6550. [Google Scholar]
- Rahman, S.M.M. A novel variable impedance compact compliant series elastic actuator for human-friendly soft robotics applications. In Proceedings of the IEEE International Workshop on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 19–24. [Google Scholar]
- Braun, D.J.; Petit, F.; Huber, F.; Haddadin, S.; Van Der Smagt, P.; Albu-Schaffer, A.; Vijayakumar, S. Robots driven by compliant actuators: Optimal control under actuation constraints. IEEE Trans. Robot. 2013, 29, 1085–1101. [Google Scholar] [CrossRef]
- Brogan, W. Modern Control Theory, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1991; pp. 532–533. [Google Scholar]
- Sinha, A. Linear Systems: Optimal and Robust Control; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Schultz, J.A.; Ueda, J. Intersample discretization of control inputs for flexible systems with quantized cellular actuation. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 421–428. [Google Scholar]
- Corradini, M.L.; Orlando, G. Robust quantized feedback stabilization of linear systems. Automatica 2008, 44, 2458–2462. [Google Scholar] [CrossRef]
- Van Ham, R.; Thomas, S.; Vanderborght, B.; Hollander, K.; Lefeber, D. Review of Actuators with Passive Adjustable Compliance/Controllable Stiffness for Robotic Applications. IEEE Robot. Autom. Mag. 2009. [Google Scholar] [CrossRef]






| Term | Description |
|---|---|
| spring constant active motor units in parallel | |
| spring constant active motor units in parallel for next node in chain | |
| spring constant inactive motor units in parallel | |
| spring constant inactive motor units in parallel for next node in chain | |
| length of actuation unit | |
| length of next actuation unit in chain | |
| resting length of active actuation unit | |
| resting length of next active actuation unit in chain | |
| resting length of inactive actuation unit | |
| resting length of next inactive actuation unit in chain |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuller, C.; Schultz, J. Characterization of Control-Dependent Variable Stiffness Behavior in Discrete Muscle-Like Actuators. Appl. Sci. 2018, 8, 346. https://doi.org/10.3390/app8030346
Fuller C, Schultz J. Characterization of Control-Dependent Variable Stiffness Behavior in Discrete Muscle-Like Actuators. Applied Sciences. 2018; 8(3):346. https://doi.org/10.3390/app8030346
Chicago/Turabian StyleFuller, Caleb, and Joshua Schultz. 2018. "Characterization of Control-Dependent Variable Stiffness Behavior in Discrete Muscle-Like Actuators" Applied Sciences 8, no. 3: 346. https://doi.org/10.3390/app8030346
APA StyleFuller, C., & Schultz, J. (2018). Characterization of Control-Dependent Variable Stiffness Behavior in Discrete Muscle-Like Actuators. Applied Sciences, 8(3), 346. https://doi.org/10.3390/app8030346





