Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens
Abstract
1. Introduction
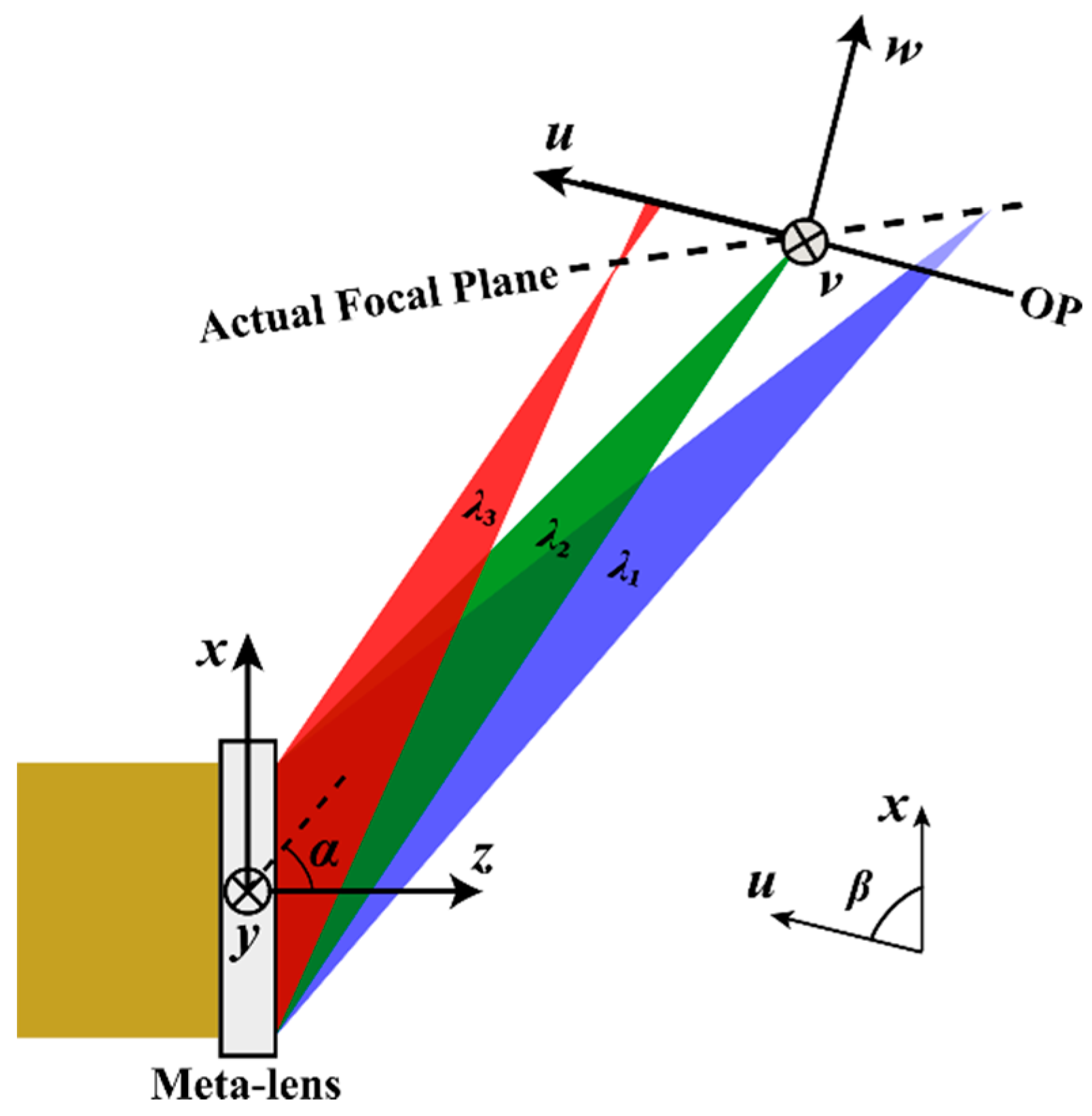
2. Design Principle of Spectrometer Based on Off-Axis Meta-Lens
3. Results and Discussion
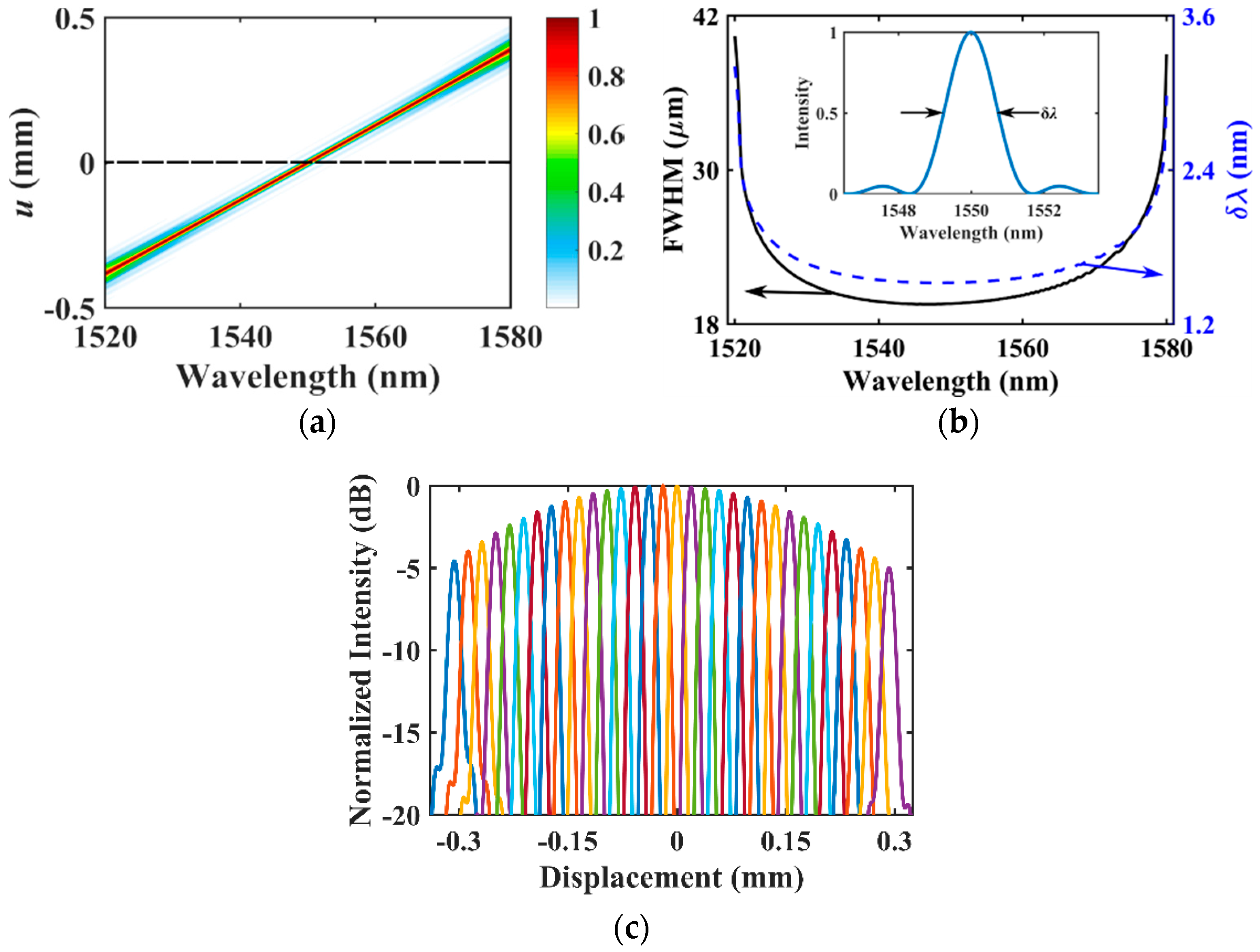
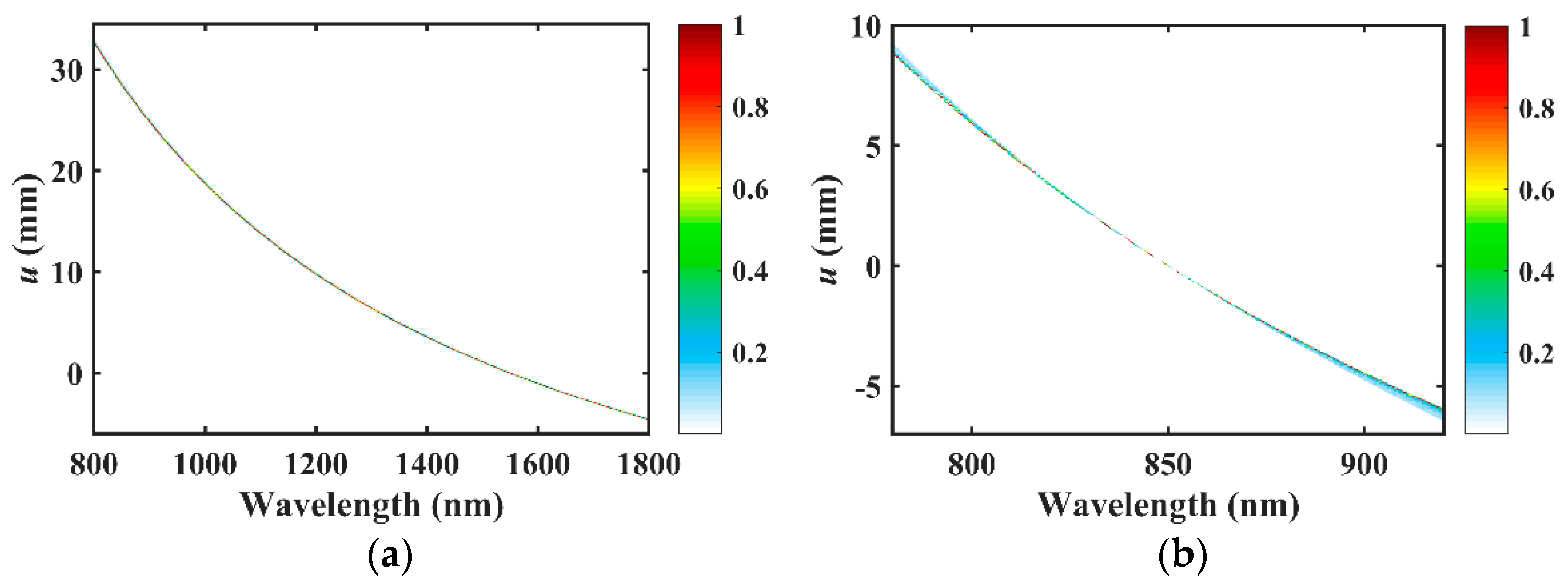
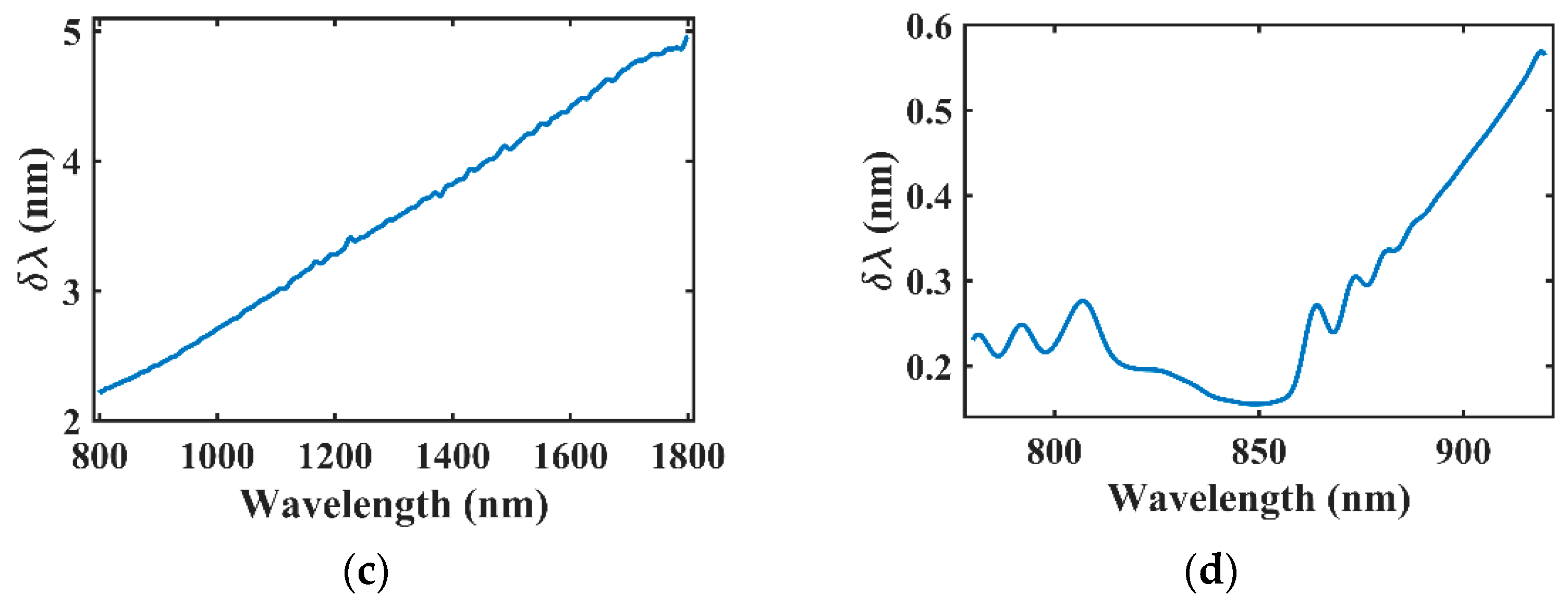
3.1. Simulation Results of a Typical Meta-Lens-Based Spectrometer
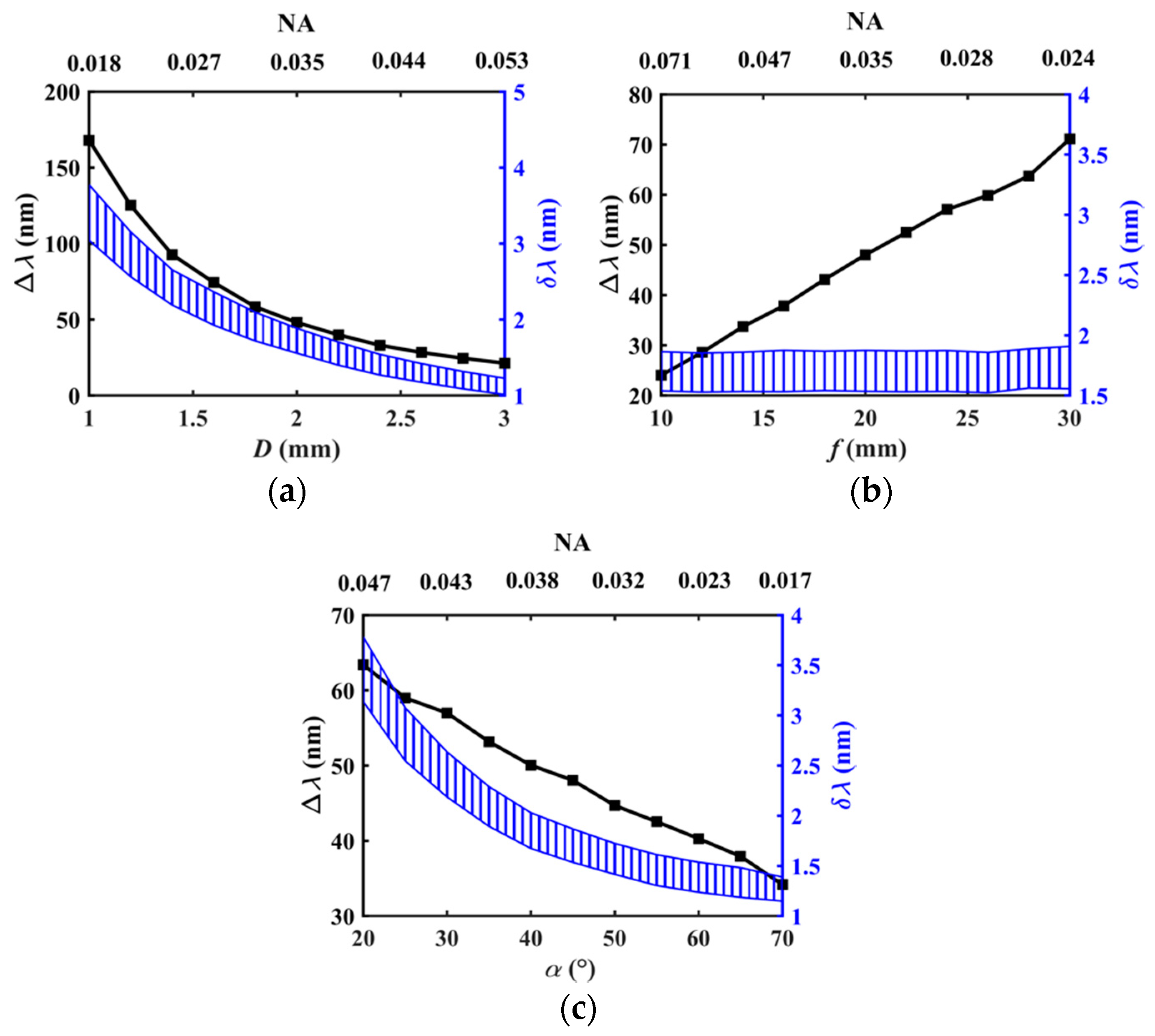
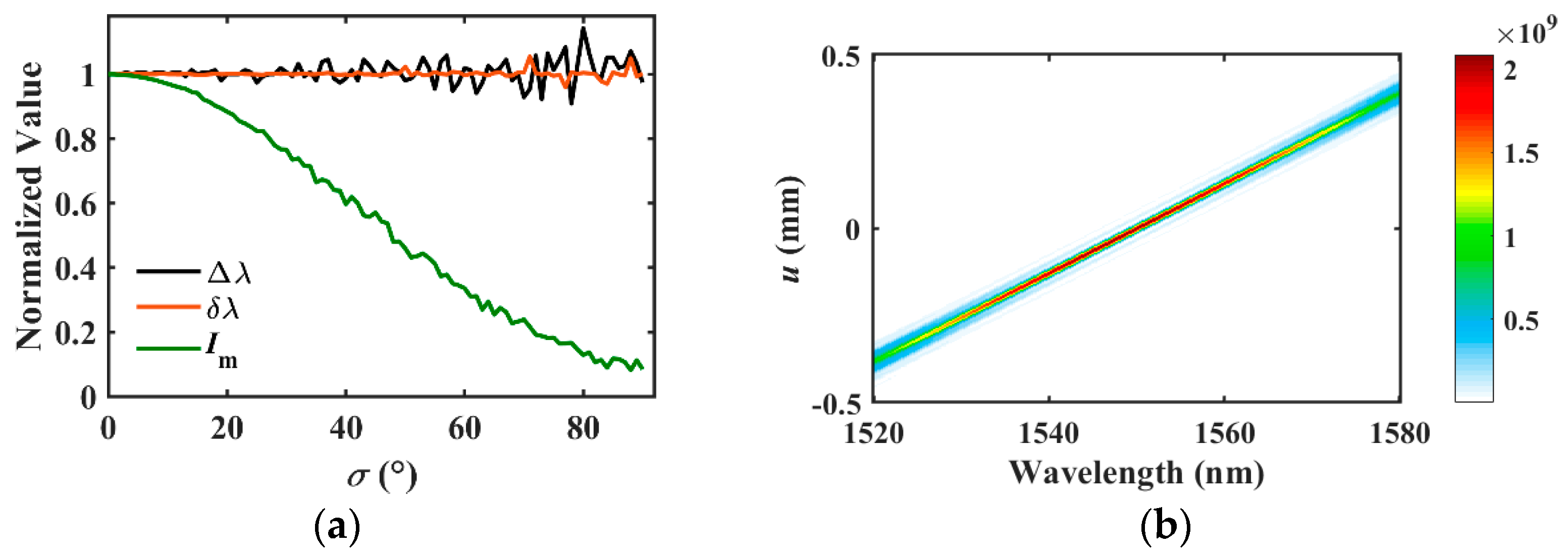
3.2. Relationship between Structural Parameters and Evaluation Indexes of Spectrometer
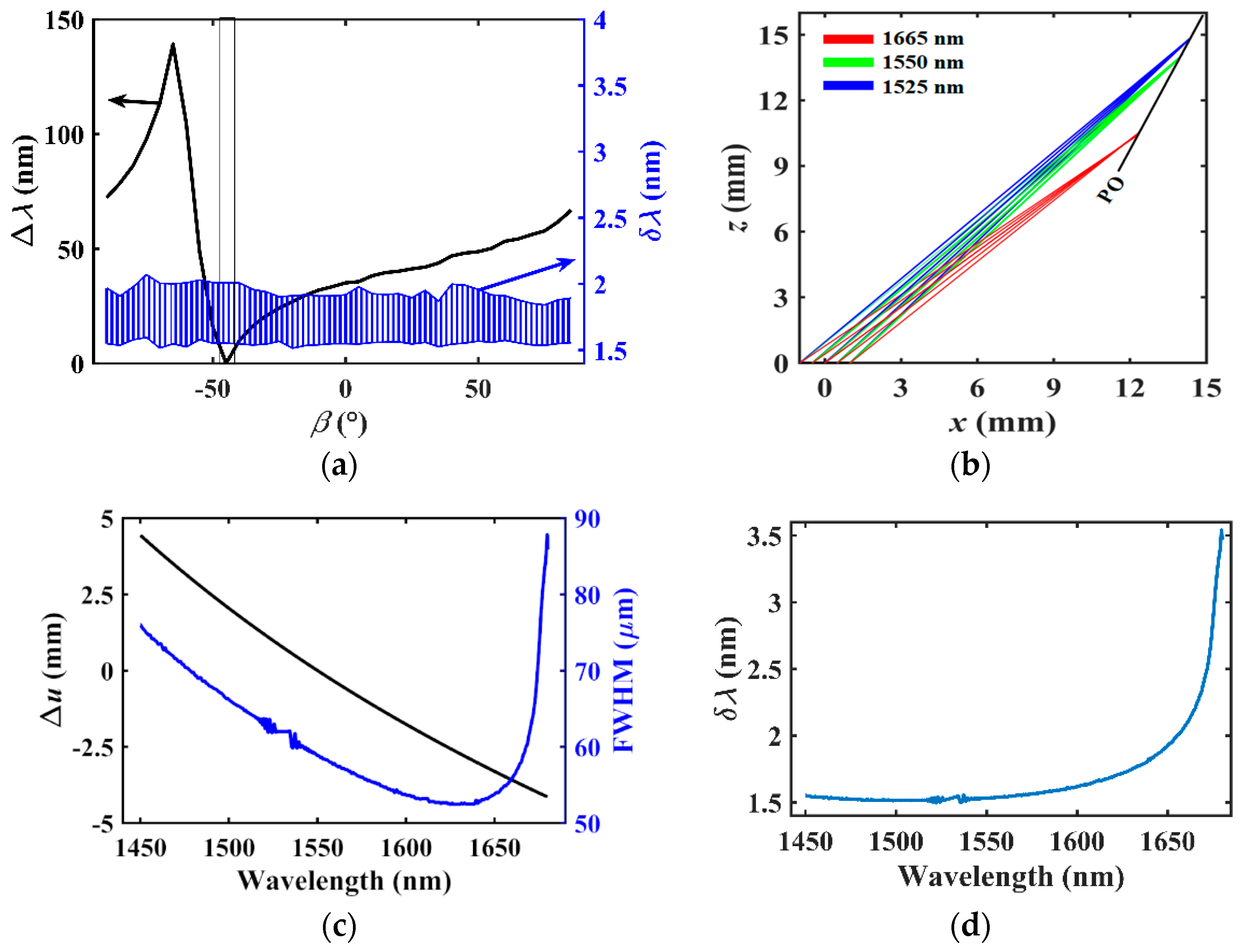
3.3. Two Practical Device for Different Applications
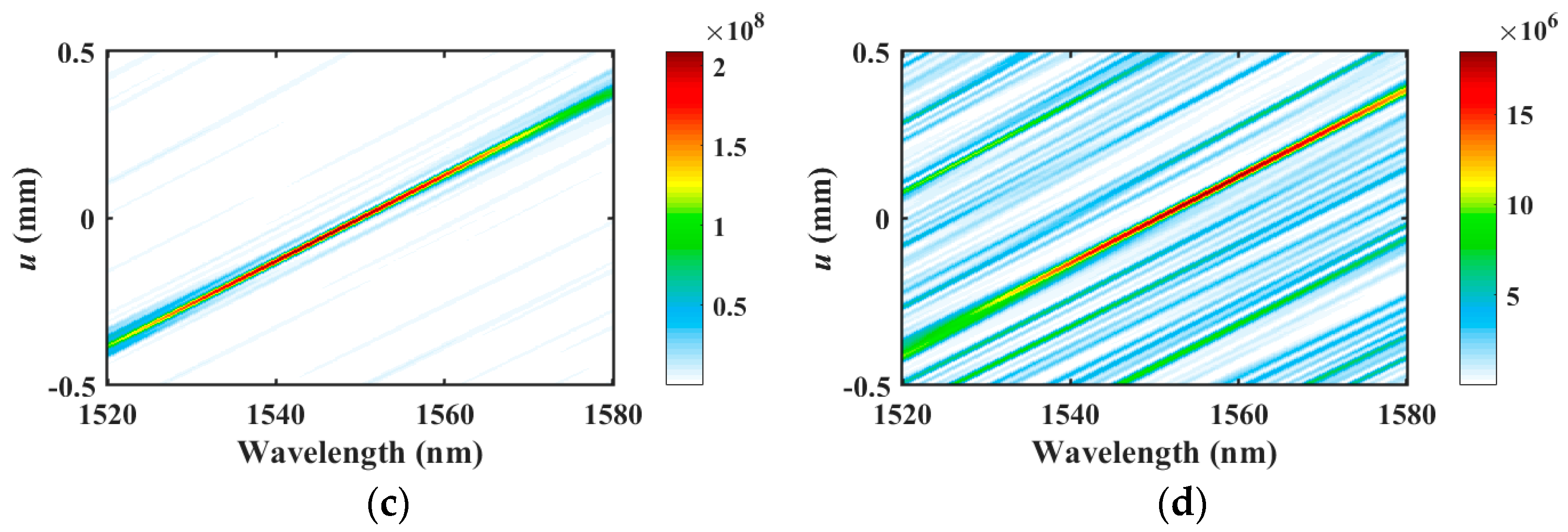
3.4. Influence of the Fabrication Error Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Staude, I.; Schilling, J. Metamaterial-Inspired Silicon Nanophotonics. Nat. Photonics 2017, 11, 274–284. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband Light Bending with Plasmonic Nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Nielsen, M.G.; Eriksen, R.L.; Bozhevolnyi, S.I. Broadband Focusing Flat Mirrors Based on Plasmonic Gradient Metasurfaces. Nano Lett. 2013, 13, 829–834. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric Metasurfaces for Complete Control of Phase and Polarization with Subwavelength Spatial Resolution and High Transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Balthasar Mueller, J.P.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Crozier, K.B. Silicon Nanofin Grating as a Miniature Chirality-Distinguishing Beam-Splitter. Nat. Commun. 2014, 5, 5386. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature Optical Planar Camera Based on a Wide-Angle Metasurface Doublet Corrected for Monochromatic Aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Ardron, M.; Chen, X. Multifunctional Metasurface Lens for Imaging and Fourier Transform. Sci. Rep. 2016, 6, 27628. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Li, G.; Su, X.; Cao, G.; Zhao, Z.; Chen, X.; Lu, W. Reflective Metalens with Sub-Diffraction-Limited and Multifunctional Focusing. Sci. Rep. 2017, 7, 12632. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral Chiral Imaging with a Metalens. Nano Lett. 2016, 16, 4595–6000. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Khorasaninejad, M.; Shi, Z.; Sanjeev, V.; Capasso, F. Immersion Meta-Lenses at Visible Wavelengths for Nanoscale Imaging. Nano Lett. 2017, 17, 3188–3194. [Google Scholar] [CrossRef] [PubMed]
- Groever, B.; Chen, W.T.; Capasso, F. Meta-Lens Doublet in the Visible Region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface Holograms for Visible Light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Chen, W.T.; Yang, K.Y.; Wang, C.M.; Huang, Y.W.; Sun, G.; Chiang, I.D.; Liao, C.Y.; Hsu, W.L.; Lin, H.T.; Sun, S.; et al. High-Efficiency Broadband Meta-Hologram with Polarization-Controlled Dual Images. Nano Lett. 2014, 14, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity Multiplexed Broadband Metasurface Holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface Holograms Reaching 80% Efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yue, F.; Wen, D.; Chen, M.; Zhang, Z.; Wang, W.; Chen, X. Multichannel Metasurface for Simultaneous Control of Holograms and Twisted Light Beams. ACS Photonics 2017, 4, 1906–1912. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Oh, J.; Capasso, F. Super-Dispersive Off-Axis Meta-Lenses for Compact High Resolution Spectroscopy. Nano Lett. 2016, 16, 3732–3737. [Google Scholar] [CrossRef] [PubMed]
- Zhu, A.Y.; Chen, W.T.; Khorasaninejad, M.; Oh, J.; Zaidi, A.; Mishra, I.; Devlin, R.C.; Capasso, F. Ultra-Compact Visible Chiral Spectrometer with Meta-Lenses. APL Photonics 2017, 2, 036103. [Google Scholar] [CrossRef]
- Minovich, A.E.; Miroshnichenko, A.E.; Bykov, A.Y.; Murzina, T.V.; Neshev, D.N.; Kivshar, Y.S. Functional and Nonlinear Optical Metasurfaces. Laser Photonics Rev. 2015, 9, 195–213. [Google Scholar] [CrossRef]
- Walter, F.; Li, G.; Meier, C.; Zhang, S.; Zentgraf, T. Ultrathin Nonlinear Metasurface for Optical Image Encoding. Nano Lett. 2017, 17, 3171–3175. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mei, Z.L.; Zhang, M.R.; Yang, F.; Cui, T.J. An Ultrathin Directional Carpet Cloak Based on Generalized Snell’s Law. Appl. Phys. Lett. 2013, 103, 151115. [Google Scholar] [CrossRef]
- Ni, X.; Wong, Z.J.; Mrejen, M.; Wang, Y.; Zhang, X. An Ultrathin Invisibility Skin Cloak for Visible Light. Science 2015, 349, 1310–1314. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Jing, L.; Zheng, B.; Hao, R.; Yin, W.; Li, E.; Soukoulis, C.M.; Chen, H. Full-Polarization 3D Metasurface Cloak with Preserved Amplitude and Phase. Adv. Mater. 2016, 28, 6866–6871. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-0-521-64222-4. [Google Scholar]
- Bao, J.; Bawendi, M.G. A Colloidal Quantum Dot Spectrometer. Nature 2015, 523, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Henstridge, M.; Zhou, J.; Guo, L.J.; Merlin, R. Wavelength Scale Terahertz Spectrometer Based on Extraordinary Transmission. Appl. Phys. Lett. 2017, 111, 063503. [Google Scholar] [CrossRef]
- Yuan, L.; He, Z.; Lv, G.; Wang, Y.; Li, C.; Xie, J.; Wang, J. Optical Design, Laboratory Test, and Calibration of Airborne Long Wave Infrared Imaging Spectrometer. Opt. Express 2017, 25, 22440–22454. [Google Scholar] [CrossRef] [PubMed]
- Cook, T. Anamorphic Integral Field Spectrometer for Diffuse Ultraviolet Astronomy. Appl. Opt. 2013, 52, 8765–8770. [Google Scholar] [CrossRef] [PubMed]
- Cataldo, G.; Hsieh, W.-T.; Huang, W.-C.; Moseley, S.H.; Stevenson, T.R.; Wollack, E.J. Micro-Spec: An Ultracompact, High-Sensitivity Spectrometer for Far-Infrared and Submillimeter Astronomy. Appl. Opt. 2014, 53, 1094–1102. [Google Scholar] [CrossRef] [PubMed]
- Zavvari, A.; Islam, M.T.; Anwar, R.; Abidin, Z.Z.; Asillam, M.F.; Monstein, C. Analysis of Radio Astronomy Bands Using CALLISTO Spectrometer at Malaysia-UKM Station. Exp. Astron. 2016, 41, 185–195. [Google Scholar] [CrossRef]
- Udeigwe, T.K.; Young, J.; Kandakji, T.; Weindorf, D.C.; Mahmoud, M.A.; Stietiya, M.H. Elemental Quantification, Chemistry, and Source Apportionment in Golf Course Facilities in a Semi-Arid Urban Landscape Using a Portable X-Ray Fluorescence Spectrometer. Solid Earth 2015, 6, 415–424. [Google Scholar] [CrossRef][Green Version]
- Buzan, E.M.; Beale, C.A.; Boone, C.D.; Bernath, P.F. Global Stratospheric Measurements of the Isotopologues of Methane from the Atmospheric Chemistry Experiment Fourier Transform Spectrometer. Atmos. Meas. Tech. 2016, 9, 1095–1111. [Google Scholar] [CrossRef]
- Mantouvalou, I.; Lachmann, T.; Singh, S.P.; Vogel-Mikuš, K.; Kanngießer, B. Advanced Absorption Correction for 3D Elemental Images Applied to the Analysis of Pearl Millet Seeds Obtained with a Laboratory Confocal Micro X-ray Fluorescence Spectrometer. Anal. Chem. 2017, 89, 5453–5460. [Google Scholar] [CrossRef] [PubMed]
- Shaltout, A.; Liu, J.; Kildishev, A.; Shalaev, V. Photonic Spin Hall Effect in Gap Plasmon Metasurfaces for On-Chip Chiroptical Spectroscopy. Optica 2015, 2, 860–863. [Google Scholar] [CrossRef]
- Maguid, E.; Yulevich, I.; Veksler, D.; Kleiner, V.; Brongersma, M.L.; Hasman, E. Photonic Spin-Controlled Multifunctional Shared-Aperture Antenna Array. Science 2016, 352, 1202–1206. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Pors, A.; Chen, Y.; Zenin, V.A.; Bozhevolnyi, S.I. Beam-Size-Invariant Spectropolarimeters Using Gap-Plasmon Metasurfaces. ACS Photonics 2017, 4, 943–949. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, R.; Ma, Y. Design of Optical Wavelength Demultiplexer Based on Off-Axis Meta-Lens. Opt. Lett. 2017, 42, 4716–4719. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Company Publishers: Englewood, IL, USA, 2005; ISBN 978-0-9747077-2-3. [Google Scholar]
- Noll, R.J. Zernike Polynomials and Atmospheric Turbulence. J. Opt. Soc. Am. A 1976, 66, 201–211. [Google Scholar] [CrossRef]
- Welford, W.T. Aberrations of Optical Systems, 1st ed.; IOP Publishing: Bristol, UK, 1986; ISBN 978-0-85274-564-9. [Google Scholar]
- Hamamatsu Mini-Spectrometers Product Page. Available online: http://www.hamamatsu.com/eu/en/product/category/5001/4016/index.html (accessed on 29 November 2017).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Chen, R.; Ma, Y. Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens. Appl. Sci. 2018, 8, 321. https://doi.org/10.3390/app8030321
Zhou Y, Chen R, Ma Y. Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens. Applied Sciences. 2018; 8(3):321. https://doi.org/10.3390/app8030321
Chicago/Turabian StyleZhou, Yi, Rui Chen, and Yungui Ma. 2018. "Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens" Applied Sciences 8, no. 3: 321. https://doi.org/10.3390/app8030321
APA StyleZhou, Y., Chen, R., & Ma, Y. (2018). Characteristic Analysis of Compact Spectrometer Based on Off-Axis Meta-Lens. Applied Sciences, 8(3), 321. https://doi.org/10.3390/app8030321



