Joint Image Compression and Encryption Using IWT with SPIHT, Kd-Tree and Chaotic Maps
Abstract
1. Introduction
2. Related Works
2.1. SPIHT-Based Image Compression
2.2. Image Encryption with Chaotic Maps
2.3. Joint Image Compression and Encryption
3. Compact Data Structures
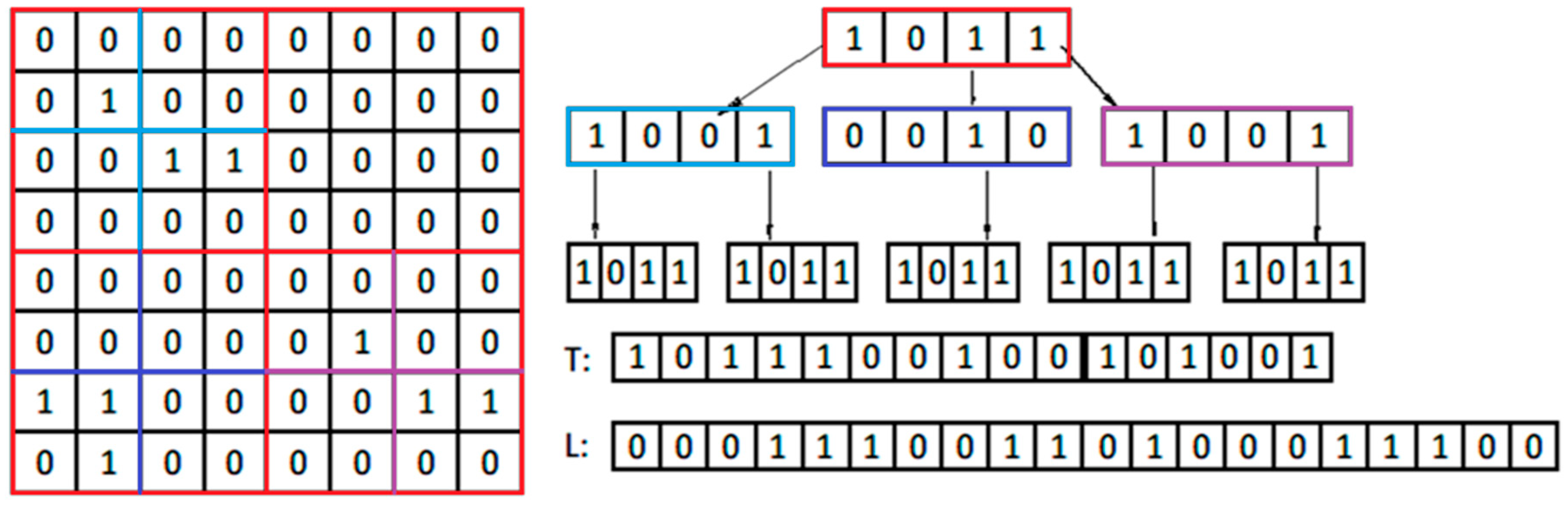
3.1. Kd-Tree
- T (tree): stores all the level-wise traversal bits, except the last-level values when the original matrix values have been reached. The bits in the T tree are placed level-wise.
- L (last-level leaves): stores leave values of the original binary matrix after recursive subdivisions with replacement of consecutive zeros and ones (more than three).
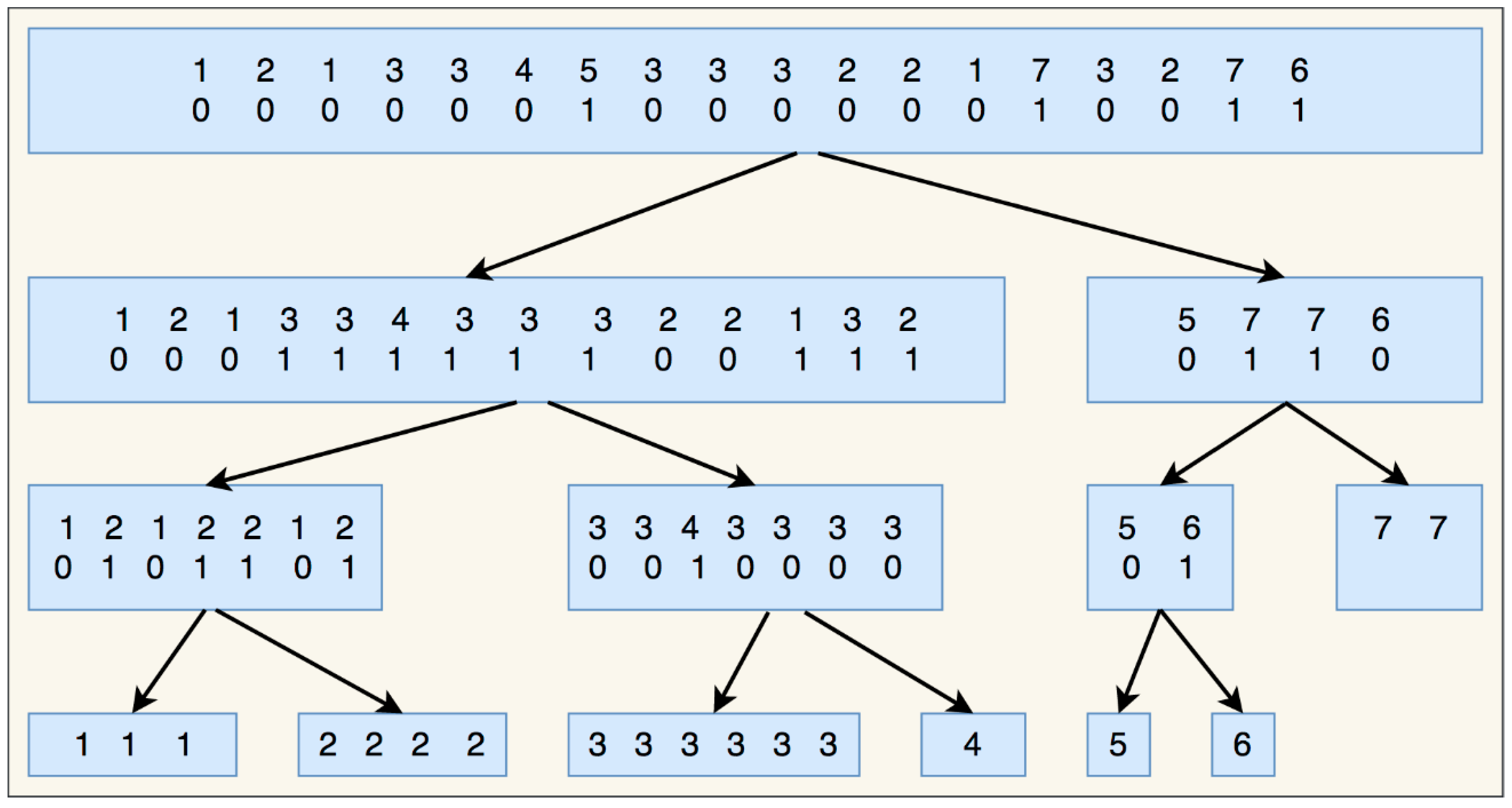
3.2. Wavelet Tree
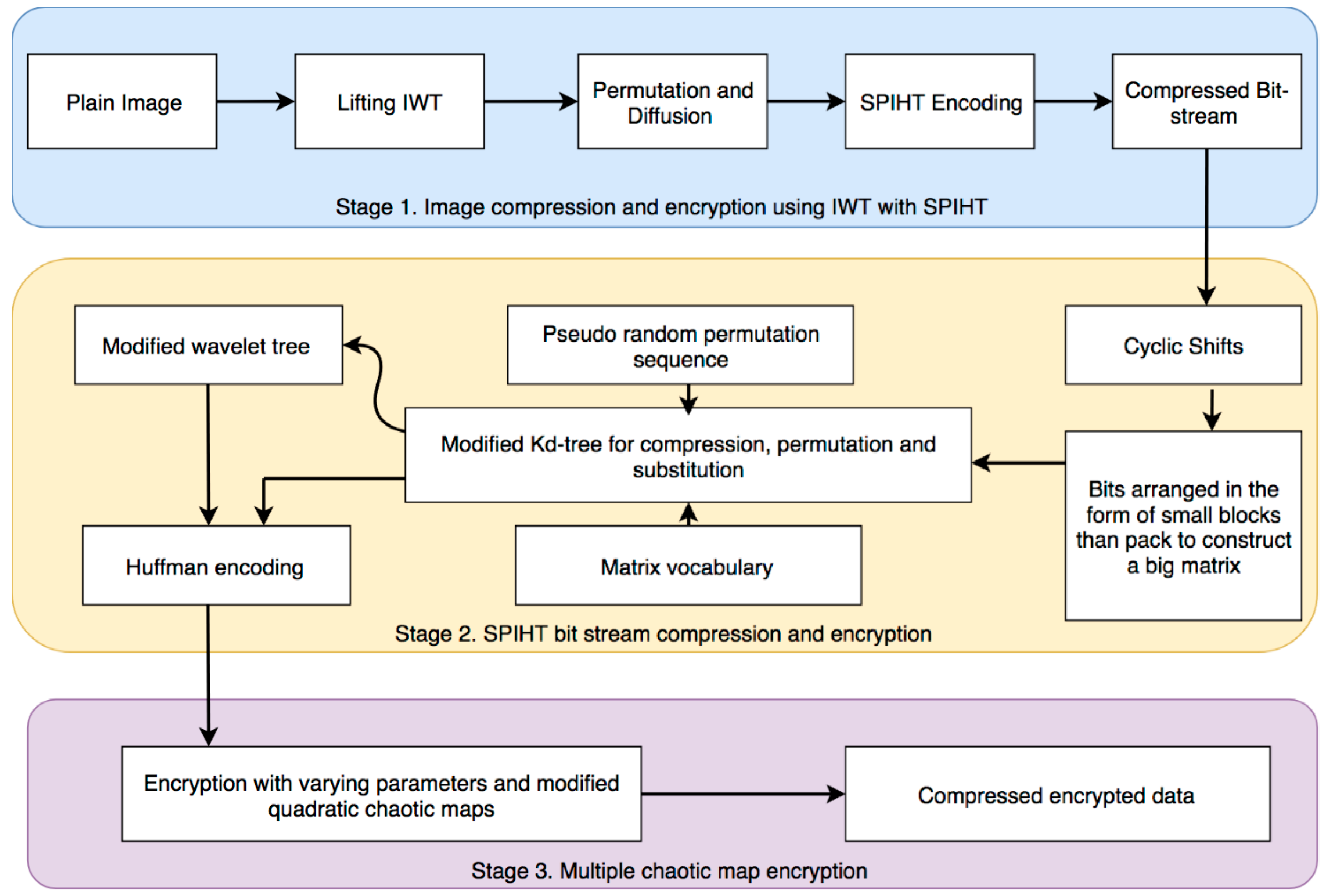
4. Proposed Image Compression and Encryption Algorithm
4.1. Compression and Encryption Based on IWT and SPIHT
4.2. Compression with Confusion-Diffusion through Kd-Tree, Wavelet Tree and Huffman Coding
4.2.1. Confusion-Diffusion and Compression with K2-Tree
4.2.2. Diffusion and Compression with Wavelet Tree
4.2.3. Huffman Coding
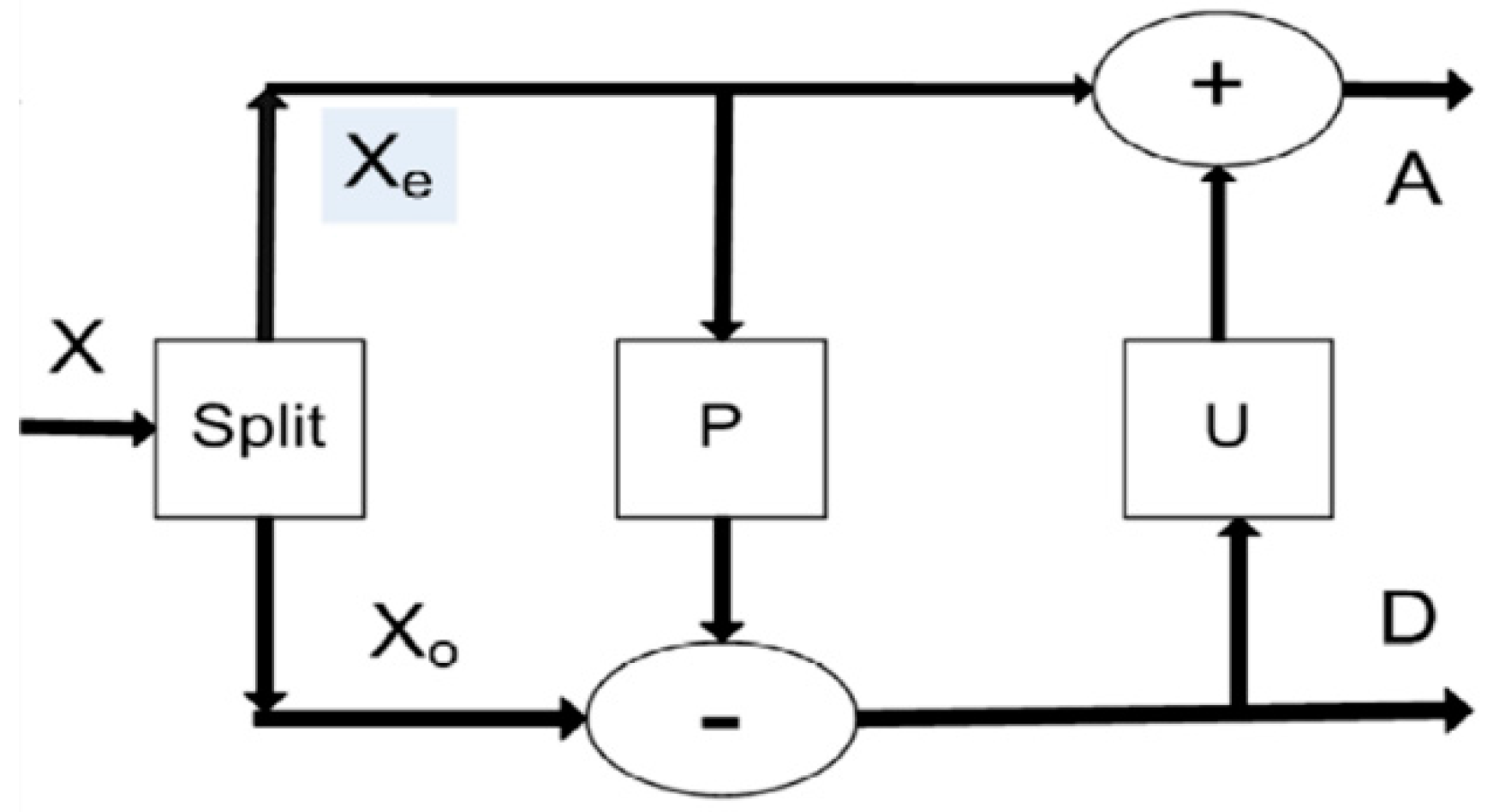
4.3. Chaotic-Map-Based Encryption

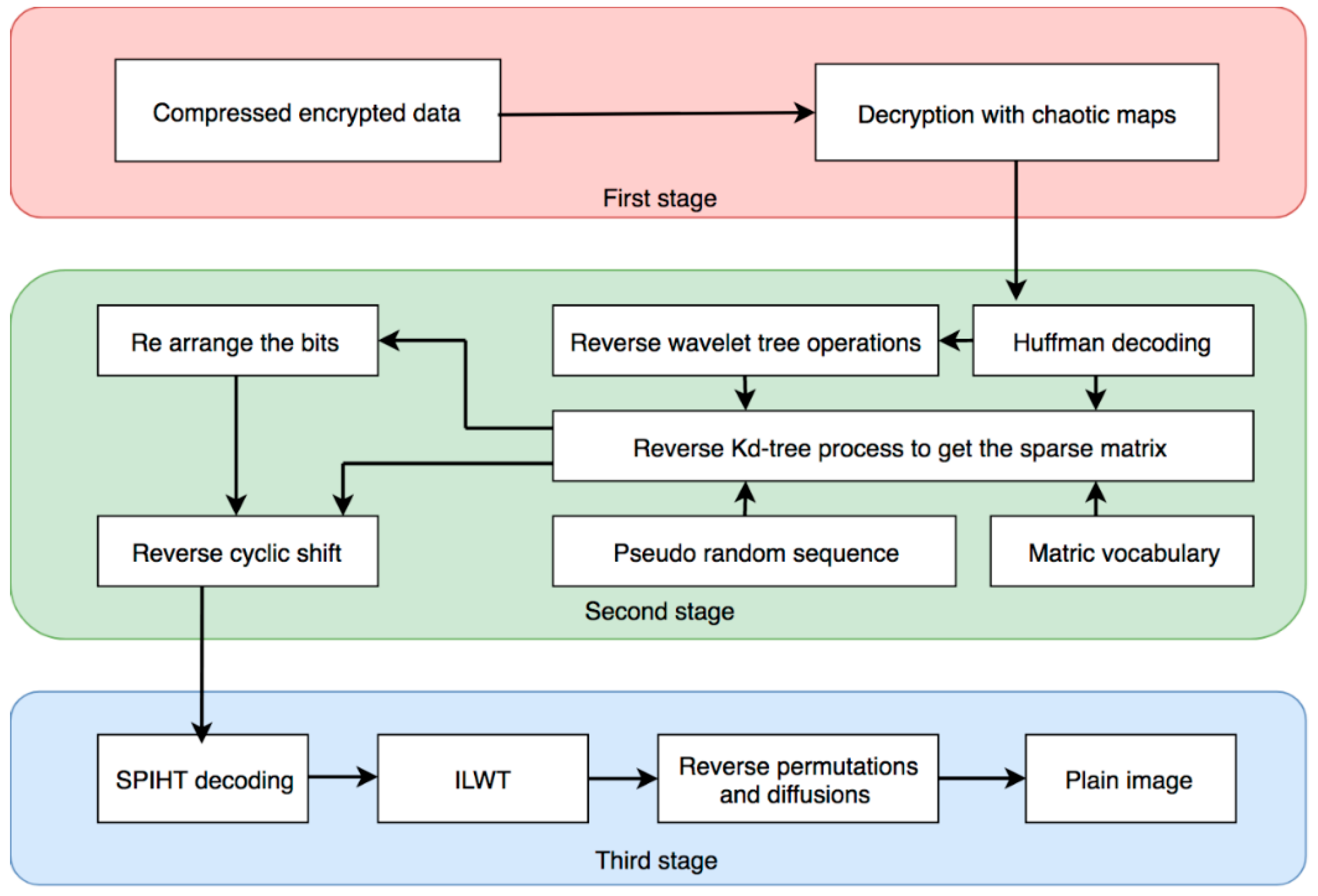
4.4. Reverse Process of Compression and Encryption
5. Experimental Results and Discussion
5.1. Experimental Results
5.2. Compression Performance
5.3. Key-Space Analysis
5.4. Key Sensitivity
5.5. Resistance to Statistical Attacks
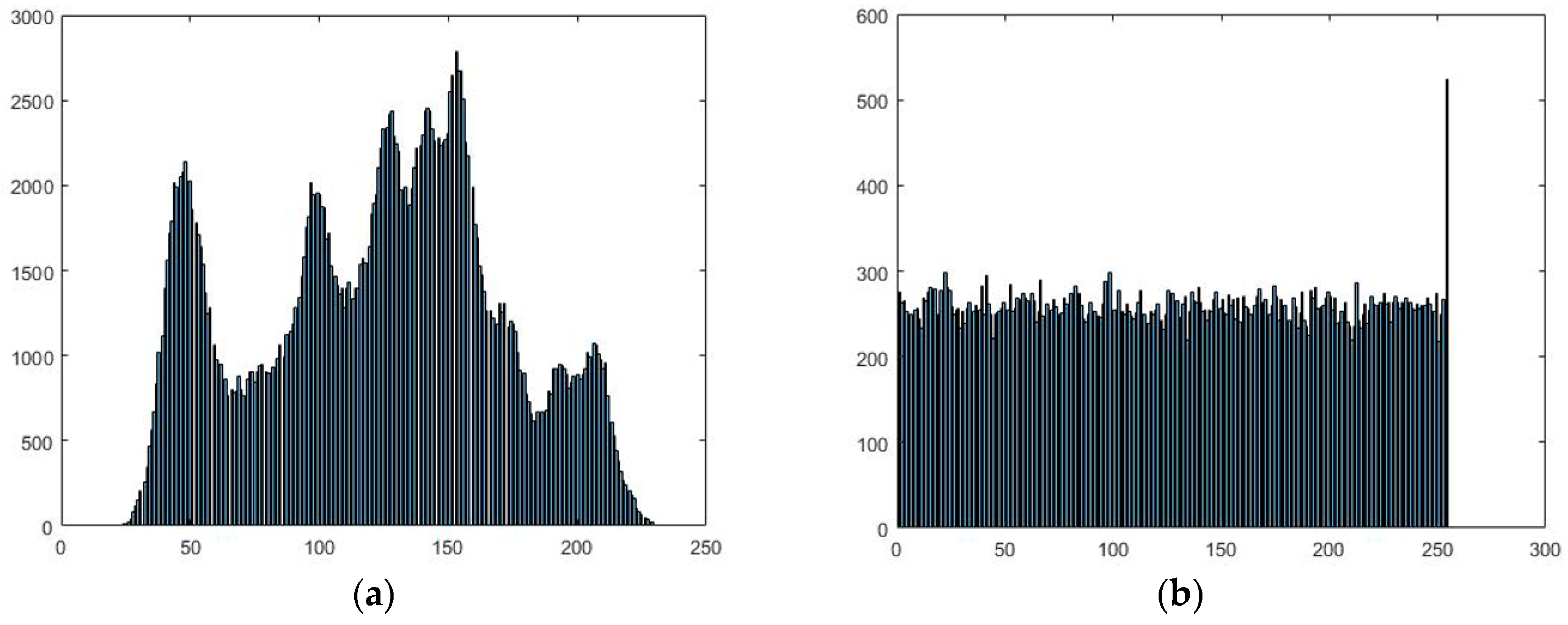
5.5.1. Histogram Analysis
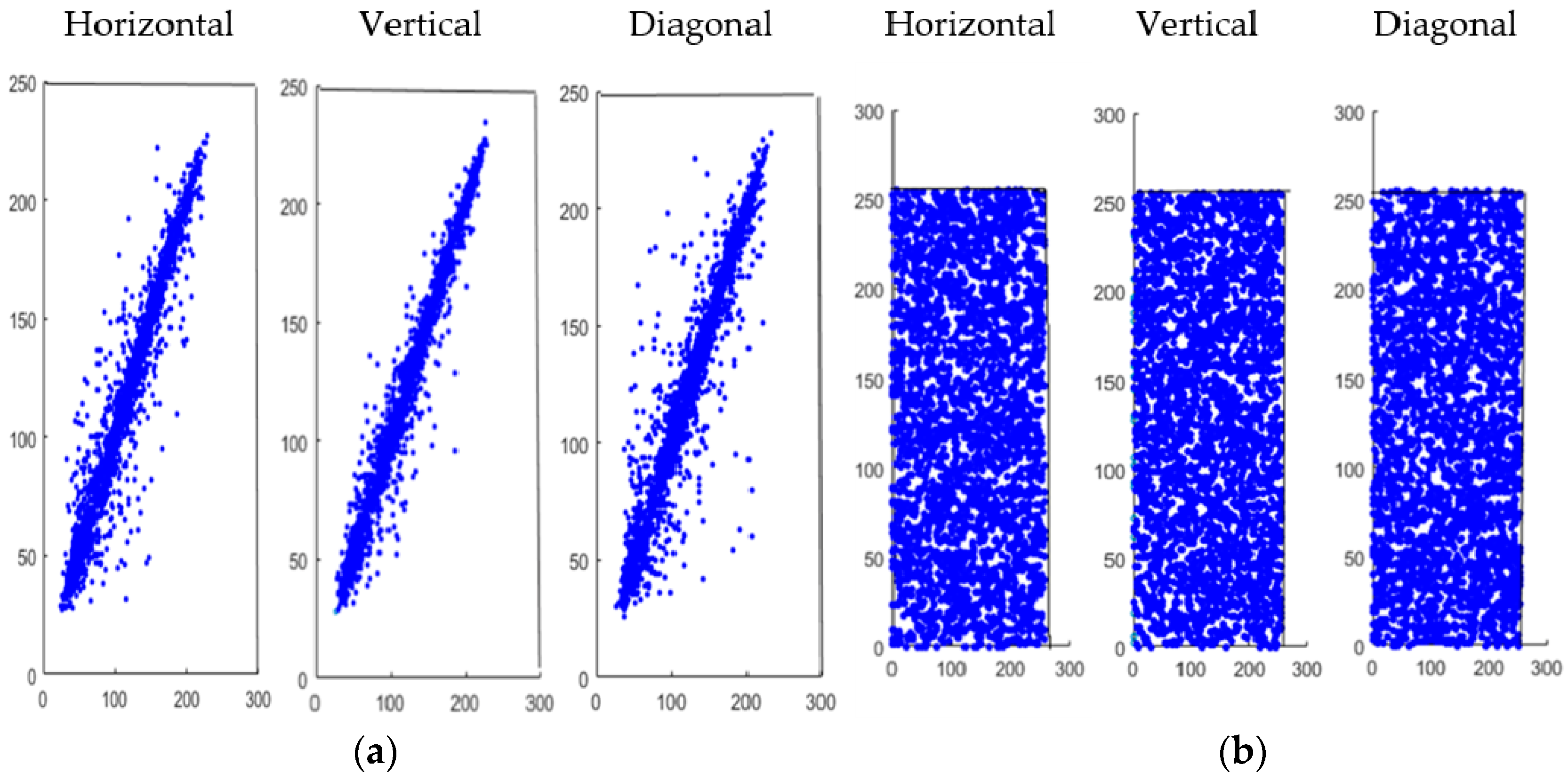
5.5.2. Correlation of Two Adjacent Pixels
5.5.3. Information Entropy Analysis
5.5.4. NIST SP800-22 Tests of Encrypted Bit Stream
5.6. Resistance to Linear and Differential Attacks
5.7. Computational Compexity and Encryption Speed
5.8. Joint Compression and Encryption for the Worst Case Images
5.9. Performance Comparison with Related Methods
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yuen, C.-H.; Wong, K.-W. A chaos-based joint image compression and encryption scheme using DCT and SHA-1. Appl. Soft Comput. 2011, 11, 5092–5098. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, X.; Zhou, S.; Xhou, C.; Wei, X.; Zhang, Q.; Che, C. Encrypting the compressed image by chaotic map and arithmetic coding. Opt. Int. J. Light Electron Opt. 2014, 125, 6117–6122. [Google Scholar] [CrossRef]
- Lian, S. Efficient image or video encryption based on spatiotemporal chaos system. Chaos Solitons Fractals 2009, 40, 2509–2519. [Google Scholar] [CrossRef]
- Li, S.; Mou, X.; Cai, Y.; Ji, Z.; Zhang, J. On the security of a chaotic encryption scheme: Problems with computerized chaos in finite computing precision. Comput. Phys. Commun. 2003, 153, 52–58. [Google Scholar] [CrossRef]
- Gong, L.; Deng, C.; Pan, S.; Zhou, N. Image compression-encryption algorithms by combining hyper-chaotic system with discrete fractional random transform. Opt. Laser Technol. 2018, 103, 48–58. [Google Scholar] [CrossRef]
- Singh, R.K.; Kumar, B.; Shaw, D.K.; Khan, D.A. Level by level image compression-encryption algorithm based on quantum chaos map. J. King Saud Univ. Comput. Inf. Sci. 2018. [CrossRef]
- Wang, Q.; Wei, M.; Chen, X.; Miao, Z. Joint encryption and compression of 3D images based on tensor compressive sensing with non-autonomous 3D chaotic system. Multimed. Tools Appl. 2018, 77, 1715–1734. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Novel secure pseudo-random number generation scheme based on two tinkerbell maps. Adv. Stud. Theor. Phys. 2015, 9, 411–421. [Google Scholar] [CrossRef]
- Tong, X.; Liu, Y.; Zhang, M.; Xu, H.; Wang, Z. An image encryption scheme based on hyperchaotic Rabinovich and exponential chaos maps. Entropy 2015, 17, 181–196. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. A novel pseudorandom bit generator based on Chirikov standard map filtered with shrinking rule. Math. Prob. Eng. 2014, 2014, 986174. [Google Scholar] [CrossRef]
- Stoyanov, B.P. Chaotic cryptographic scheme and its randomness evaluation. AIP Conf. Proc. 2012, 1487, 397–404. [Google Scholar]
- Liu, Y.; Tong, X. Hyperchaotic system-based pseudorandom number generator. IET Inf. Secur. 2016, 10, 433–441. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Yang, G.; Jin, H. Image encryption using the two-dimensional logistic chaotic map. J. Electron. Imaging 2012, 21, 013014. [Google Scholar] [CrossRef]
- Zhang, M.; Tong, X. Joint image encryption and compression scheme based on IWT and SPIHT. Opt. Lasers Eng. 2017, 90, 254–274. [Google Scholar] [CrossRef]
- Hamdi, M.; Rhouma, R.; Belghith, S. A selective compression-encryption of images based on SPIHT coding and Chirikov Standard Map. Signal Proc. 2017, 131, 514–526. [Google Scholar] [CrossRef]
- Xiang, T.; Qu, J.; Xiao, D. Joint SPIHT compression and selective encryption. Appl. Soft Comput. 2014, 21, 159–170. [Google Scholar] [CrossRef]
- Said, A.; Pearlman, W.A. A new, fast, and efficient image codec based on set partitioning in hierarchical trees. IEEE Trans. Circuits Syst. Video Technol. 1996, 6, 243–250. [Google Scholar] [CrossRef]
- Daubechies, I.; Sweldens, W. Factoring wavelet transforms into lifting steps. J. Fourier Anal. Appl. 1998, 4, 247–269. [Google Scholar] [CrossRef]
- Rhouma, R.; Belghith, S. Cryptanalysis of a spatiotemporal chaotic image/video cryptosystem. Phys. Lett. A 2008, 372, 5790–5794. [Google Scholar] [CrossRef]
- Rhouma, R.; Belghith, S. Cryptanalysis of a new image encryption algorithm based on hyper-chaos. Phys. Lett. A 2008, 372, 5973–5978. [Google Scholar] [CrossRef]
- Alvarez, G.; Amigó, J.M.; Arroyo, D.; Li, S. Lessons learnt from the cryptanalysis of chaos-based ciphers. In Chaos-Based Cryptography: Theory, Algorithms and Applications; Springer: Cham, Switzerland, 2011; Volume 354, pp. 257–295. [Google Scholar]
- Alvarez, G.; Li, S. Cryptanalyzing a nonlinear chaotic algorithm (NCA) for image encryption. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3743–3749. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Lo, K.-T. Breaking a modified substitution–diffusion image cipher based on chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 837–843. [Google Scholar] [CrossRef]
- Li, C.; Xie, T.; Liu, Q.; Cheng, G. Cryptanalyzing image encryption using chaotic logistic map. Nonlinear Dyn. 2014, 78, 1545–1551. [Google Scholar] [CrossRef]
- Memon, Q.A. Synchronized choas for network security. Comput. Commun. 2003, 26, 498–505. [Google Scholar] [CrossRef]
- Ravichandran, D.; Praveenkumar, P.; Rayappan, J.B.B.; Amirtharajan, R. Chaos based crossover and mutation for securing DICOM image. Comput. Biol. Med. 2016, 72, 170–184. [Google Scholar] [CrossRef] [PubMed]
- El-Latif, A.A.A.; Li, L.; Zhang, T.; Wang, N.; Song, X.; Niu, X. Digital image encryption scheme based on multiple chaotic systems. Sens. Imaging Int. J. 2012, 13, 67–88. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S.; Hernandez, L. Analysis of security problems in a medical image encryption system. Comput. Biol. Med. 2007, 37, 424–427. [Google Scholar] [CrossRef] [PubMed]
- Ravichandran, D.; Praveenkumar, P.; Rayappan, J.B.B.; Amirtharajan, R. DNA chaos blend to secure medical privacy. IEEE Trans. Nanobiosci. 2017, 16, 850–858. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Nie, W.; MA, Y.; Tian, Q. Cryptanalysis and improvement of an image encryption algorithm based on hyper-chaotic system and dynamic S-box. Multimed. Tools Appl. 2017, 76, 15641–15659. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. An image encryption algorithm based on Baker map with varying parameter. Multimed. Tools Appl. 2017, 76, 16511–16527. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new image encryption algorithm based on logistic chaotic map with varying parameter. SpringerPlus 2016, 5, 289. [Google Scholar] [CrossRef] [PubMed]
- Maqbool, S.; Ahmad, N.; Muhammad, A.; Enriquez, A.M.M. Simultaneous Encryption and Compression of Digital Images Based on Secure-JPEG Encoding. In Mexican Conference on Pattern Recognition; Springer: Cham, Switzerland, 2016; pp. 145–154. [Google Scholar]
- Ji, X.; Bai, S.; Zhu, G.; Yan, B. Image encryption and compression based on the generalized knight’s tour, discrete cosine transform and chaotic maps. Multimed. Tools Appl. 2017, 76, 12965–12979. [Google Scholar]
- Tong, X.-J.; Chen, P.; Zhang, M. A joint image lossless compression and encryption method based on chaotic map. Multimed. Tools Appl. 2017, 76, 13995–14020. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Chaos-based partial encryption of SPIHT coded color images. Signal Proc. 2013, 93, 2422–2431. [Google Scholar] [CrossRef]
- Zhang, M.; Tong, X. A new algorithm of image compression and encryption based on spatiotemporal cross chaotic system. Multimed. Tools Appl. 2015, 74, 11255–11279. [Google Scholar] [CrossRef]
- Li, P.; Lo, K.-T.A. Content-Adaptive Joint Image Compression and Encryption Scheme. IEEE Trans. Multimed. 2018, 20, 1960–1972. [Google Scholar] [CrossRef]
- De Bernardo, G.; Álvarez-García, S.; Brisaboa, N.R.; Navarro, G.; Pedreira, O. Compact querieable representations of raster data. In International Symposium on String Processing and Information Retrieval; Springer: Cham, Switzerland, 2013; pp. 96–108. [Google Scholar]
- Navarro, G. Wavelet trees for all. In Annual Symposium on Combinatorial Pattern Matching; Springer: Cham, Switzerland, 2012; pp. 2–26. [Google Scholar]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Bassham, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. Sp 800-822 rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010.
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber journals: Multidisciplinary journals in science and technology. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]


| Image | PSNR/dB | CR/bpp | ||||||
|---|---|---|---|---|---|---|---|---|
| Our Approach | Ref. [37] | Ref. [38] | Our Approach | Ref. [14] CR | Ref. [35] CR | Ref. [37] CR | Ref. [38] QF = 80/bpp | |
| Lena (grayscale) | 39.85 | 42.23 | ----- | 8.19/0.97 | 6.222713 | 10.426 | 4 | - |
| Baboon (grayscale) | 36.37 | 35.15 | 32.5956 | 8.20/0.97 | 7.569092 | 4.977 | 4 | 2.4414 |
| Peppers (grayscale) | 37.81 | 41.3 | - | 8.26/0.96 | 6.698654 | - | 4 | - |
| Airplane (grayscale) | 40.68 | - | - | 8.49/0.94 | 6.388039 | 5.313 | - | - |
| House (grayscale) | 40.41 | - | - | 8.13/0.98 | 6.671848 | - | - | - |
| Lake (grayscale) | 34.54 | - | - | 8.39 | - | - | - | - |
| Proposed Method | Ref. [8] | Ref. [9] | Ref. [10] | Ref. [11] |
|---|---|---|---|---|
| 21024 | 2183 | 2776 | 2320 | 296 |
| Image | Decryption with 1-bit Key Difference in the Permutations of Lower 64 × 64 Wavelet Coefficients | Decryption with 1-bit Key Difference in the Permutations of SPIHT Output with Kd-Tree | Decryption with 1-bit Key Difference in Logistic Chaotic Map | Decryption with 1-bit Key Difference in Quadratic Chaotic Map | |
|---|---|---|---|---|---|
| Lena | PSNR MSSIM | 9.5241 0.1472 | 3.0214 0.0128 | 2.0135 0.0214 | 2.8742 0.1251 |
| Baboon | PSNR MSSIM | 7.3254 0.0713 | 4.5210 0.0843 | 2.0176 0.0421 | 2.6522 0.2414 |
| Pepper | PSNR MSSIM | 7.3617 0.1382 | 3.2412 0.0421 | 2.0187 0.0342 | 2.6415 0.1453 |
| Airplane | PSNR MSSIM | 8.3692 0.1426 | 3.0124 0.0621 | 2.0873 0.0462 | 2.3541 0.3524 |
| House | PSNR MSSIM | 7.3641 0.1536 | 2.0146 0.0143 | 3.5214 0.0517 | 2.6521 0.3245 |
| Lake | PSNR MSSIM | 0.7125 0.1285 | 3.0241 0.0142 | 2.0364 0.0394 | 2.6521 0.0124 |
| Image | -Text | |
|---|---|---|
| Plain Image | Encrypted Image | |
| Lena (grayscale) | 158360 | 270 |
| Baboon (grayscale) | 211370 | 281 |
| Peppers (grayscale) | 549150 | 276 |
| Airplane (grayscale) | 728690 | 286 |
| House (grayscale) | 880954 | 291 |
| Lake (grayscale) | 181220 | 273 |
| Image | Orientation | ||
|---|---|---|---|
| Horizontal | Vertical | Diagonal | |
| Lena (plain) | 0.9719 | 0.9850 | 0.9593 |
| Lena (encrypted) | 0.00051 | −0.0043 | 0.00031 |
| Baboon (plain) | 0.9337 | 0.9123 | 0.8669 |
| Baboon (encrypted) | −0.00245 | −0.00314 | 0.00137 |
| Peppers (plain) | 0.9802 | 0.9803 | 0.9706 |
| Peppers (encrypted) | −0.00178 | 0.00812 | −0.00031 |
| Airplane (plain) | 0.9676 | 0.9628 | 0.9371 |
| Airplane (encrypted) | 0.00519 | −0.00362 | −0.00039 |
| House (plain) | 0.9401 | 0.9372 | 0.8952 |
| House (encrypted) | −0.00238 | −0.00497 | 0.00847 |
| Lake (plain) | 0.9761 | 0.9764 | 0.9616 |
| Lake (encrypted) | 0.00874 | 0.00812 | 0.00038 |
| Image (Encrypted) | Information Entropy |
|---|---|
| Lena | 7.99642 |
| Baboon | 7.99645 |
| Pepper | 7.98953 |
| Airplane | 7.99231 |
| House | 7.99483 |
| Lake | 7.99681 |
| Image (Encrypted) | Information Entropy | Result |
|---|---|---|
| Lena | 7.90642 | Pass |
| Baboon | 7.90382 | Pass |
| Pepper | 7.91124 | Pass |
| Airplane | 7.90235 | Pass |
| House | 7.90321 | Pass |
| Lake | 7.91156 | Pass |
| Mean ± Std. | 7.90643 ± 0.0040 |
| Test | p-Value | Pass Rate |
|---|---|---|
| Monobit test | 0.231475 | Pass |
| Frequency within block test | 0.754126 | Pass |
| Runs test | 0.632514 | Pass |
| Longest run ones in a block test | 0.641258 | Pass |
| Binary matrix rank test | 0.412572 | Pass |
| DFT test | 0.754163 | Pass |
| Non overlapping template matching test | 0.425712 | Pass |
| Overlapping template matching test | 0.912458 | Pass |
| Universal test | 0.952413 | Pass |
| Linear complexity test | 0.342587 | Pass |
| Serial test | 0.765812 | Pass |
| Approximate entropy test | 0.672541 | Pass |
| Cumulative sum test | 0.192745 | Pass |
| Random excursion test | 0.256312 | Pass |
| Random excursion variant test | 0.028735 | Pass |
| Images/Tests | Lena | Baboon | Pepper | Airplane | House | Lake |
|---|---|---|---|---|---|---|
| NPCR | 99.47% | 99.36% | 99.52% | 99.38% | 99.25% | 99.46% |
| UACI | 33.23% | 33.21% | 33.34% | 33.46% | 33.14% | 33.18% |
| Joint Compression and Encryption | Diffusion and Permutations of Wavelet Coefficients | SPIHT Encoding and Bits Packing | Permutations with Kd-Tree and Chaotic Bit Stream Encryption |
|---|---|---|---|
| Computational complexity |
| Image | Wavelet Coefficient Encryption Time | SPIHT Compression Time | Compression and Encryption with Kd-Tree | Compression with Wavelet Tree and Huffman Coding | Total Compression and Encryption Time |
|---|---|---|---|---|---|
| Lena | 3.3 s | 2.4 s | 12.3 s | 1.2 s | 19.2 s |
| Baboon | 3.1 s | 2.1 s | 12.1 s | 1.4 s | 18.7 s |
| Peppers | 3.4 s | 2.3 s | 12.5 s | 1.3 s | 19.5 s |
| Airplane | 3.0 s | 2.1 s | 12.3 s | 1.2 s | 18.6 s |
| House | 3.1 s | 2.2 s | 12.4 s | 1.4 s | 19.1 s |
| Lake | 3.2 s | 2.3 s | 12.2 s | 1.3 s | 19.0 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasrullah; Sang, J.; Akbar, M.A.; Cai, B.; Xiang, H.; Hu, H. Joint Image Compression and Encryption Using IWT with SPIHT, Kd-Tree and Chaotic Maps. Appl. Sci. 2018, 8, 1963. https://doi.org/10.3390/app8101963
Nasrullah, Sang J, Akbar MA, Cai B, Xiang H, Hu H. Joint Image Compression and Encryption Using IWT with SPIHT, Kd-Tree and Chaotic Maps. Applied Sciences. 2018; 8(10):1963. https://doi.org/10.3390/app8101963
Chicago/Turabian StyleNasrullah, Jun Sang, Muhammad Azeem Akbar, Bin Cai, Hong Xiang, and Haibo Hu. 2018. "Joint Image Compression and Encryption Using IWT with SPIHT, Kd-Tree and Chaotic Maps" Applied Sciences 8, no. 10: 1963. https://doi.org/10.3390/app8101963
APA StyleNasrullah, Sang, J., Akbar, M. A., Cai, B., Xiang, H., & Hu, H. (2018). Joint Image Compression and Encryption Using IWT with SPIHT, Kd-Tree and Chaotic Maps. Applied Sciences, 8(10), 1963. https://doi.org/10.3390/app8101963





