Context-Aware Caching Distribution and UAV Deployment: A Game-Theoretic Approach
Abstract
:1. Introduction
- We first investigate the problem of joint optimization of UAVs’ caching contents and service locations with the goal of balancing the tradeoff between user’s service probability and transmission overhead under the consideration of the share of neighbor UAVs’ caching contents.
- The problem is modeled as a UAV caching game, which intends to find the optimal solution that maximizes UAVs’ performance indicators, i.e., the ratio of user’s service probability and transmission overhead. In addition, the proposed game is proved to be a potential game with at least one pure-strategy NE. Meanwhile, the optimal solution can be achieved by its optimal NE.
- The log-linear caching algorithm is proposed to achieve the desirable solution in joint caching contents and service locations optimization problem. The simulation results show that the proposed algorithm can converge to a great NE solution and guarantee the great performance of UAV-assisted networks, which demonstrates the algorithm’s validity and effectiveness.
2. System Model and Problem Formulation
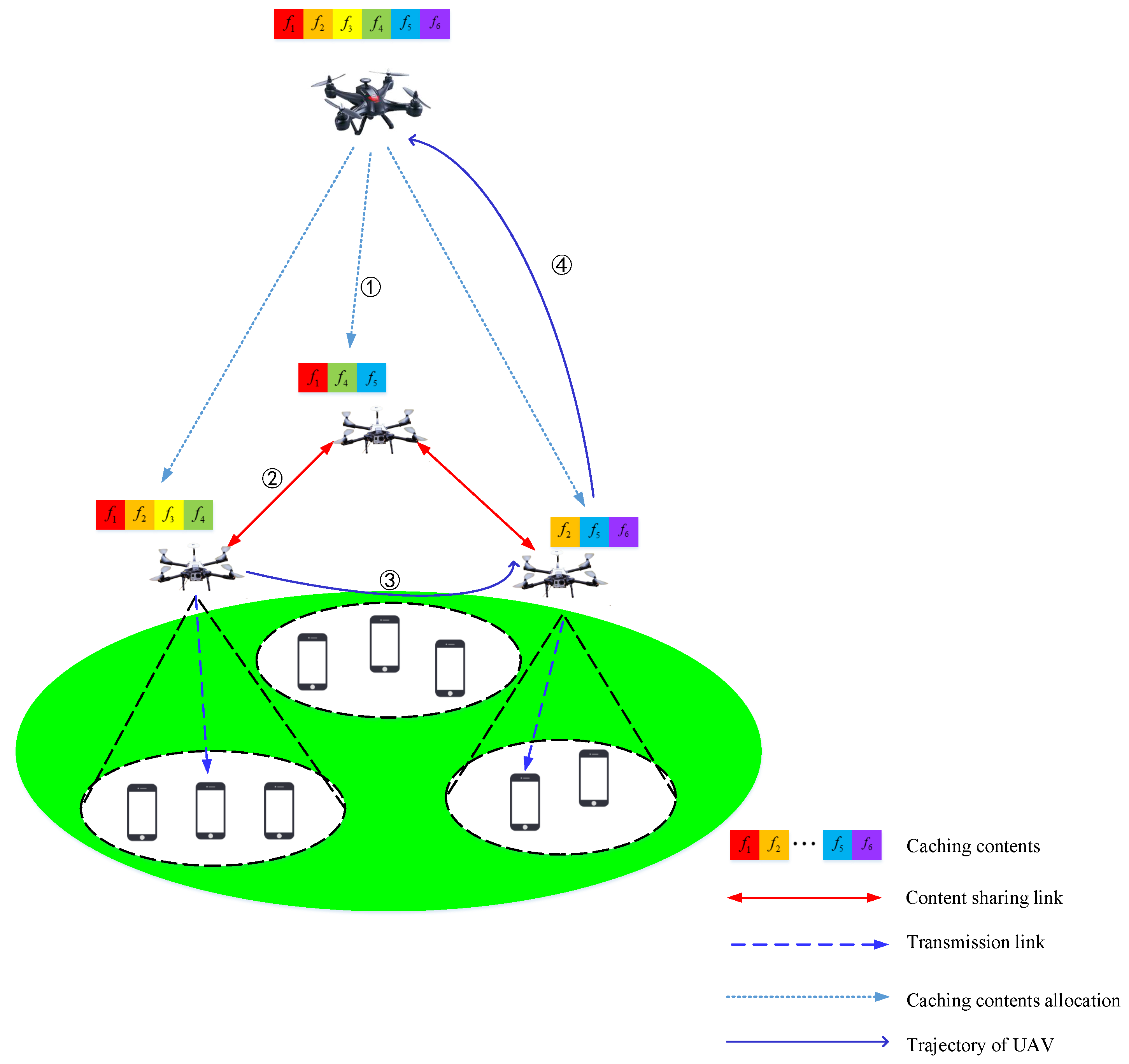
2.1. System Model
2.2. Problem Formulation
2.3. Summary
3. UAV-Assisted Caching Game
3.1. Game Model
3.2. Analysis of NE
- The potential game has one pure strategy NE at least.
- Local or global maxima of potential function constitutes a pure strategy NE.
3.3. Log-Linear Caching Algorithm
| Algorithm 1: Log-linear caching algorithm (LCA) |
| 1. Initialization (1) Initialize randomly users’ locations, file popularity and file requests , . Initialize randomly and , satisfying to and . (2) Moreover, set k = 0 as the round count and as the maximum round. 2. Repeat Round k = k + 1 Choose UAV n randomly. Repeat iterations:: (1) Calculate by taking the action . (2) Generate randomly from its strategy space (3) Calculate by taking the action and keep other UAVs’ actions. (4) Update strategy: where , and is the learning parameter. Meanwhile, all other UAVs keep their actions, and . (5) until or , End iterations Output: 3. End rounds |
4. Simulation and Numerical Results and Discussion
4.1. Simulation Scenario
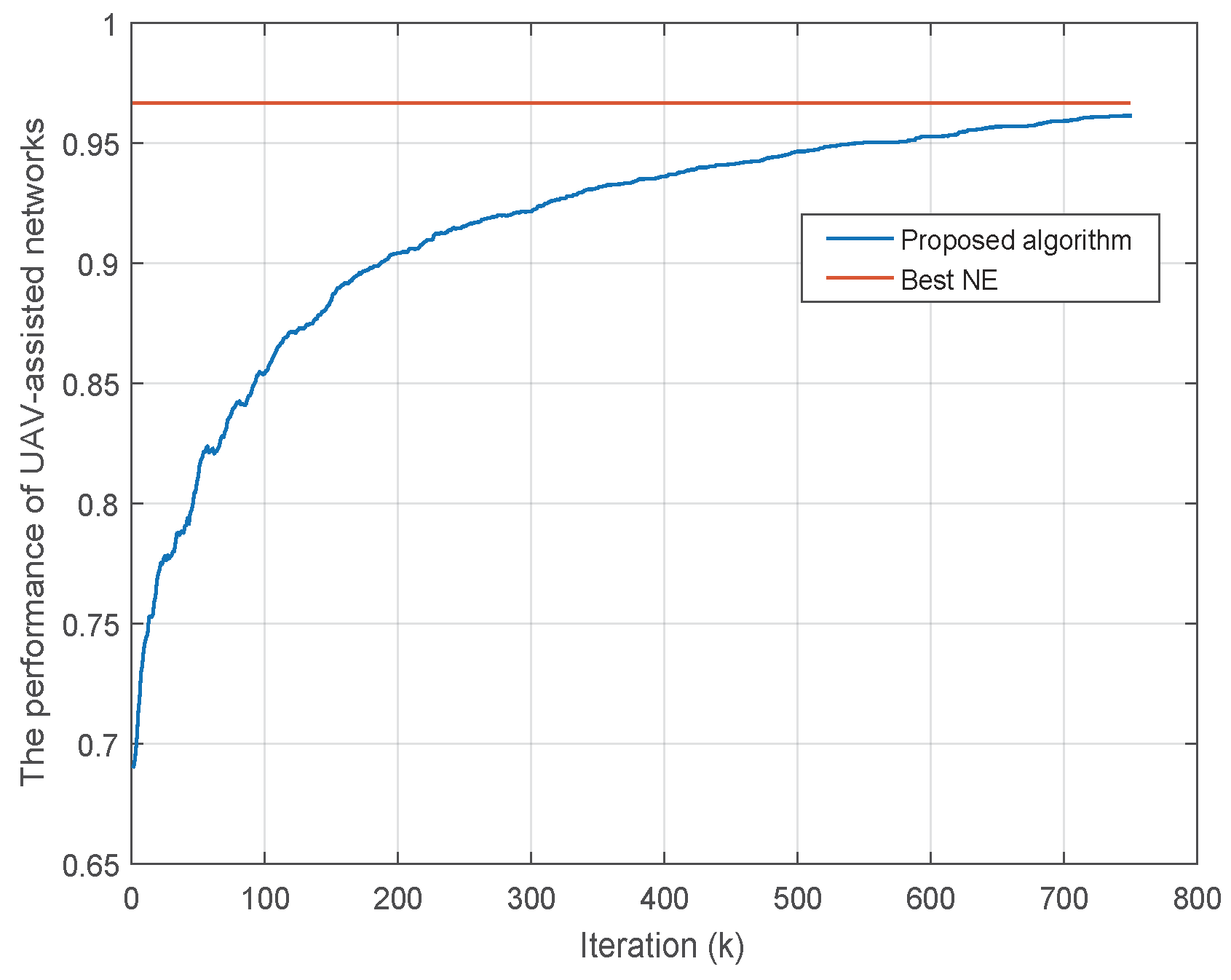
4.2. Convergence Behavior
4.3. Performance Analysis
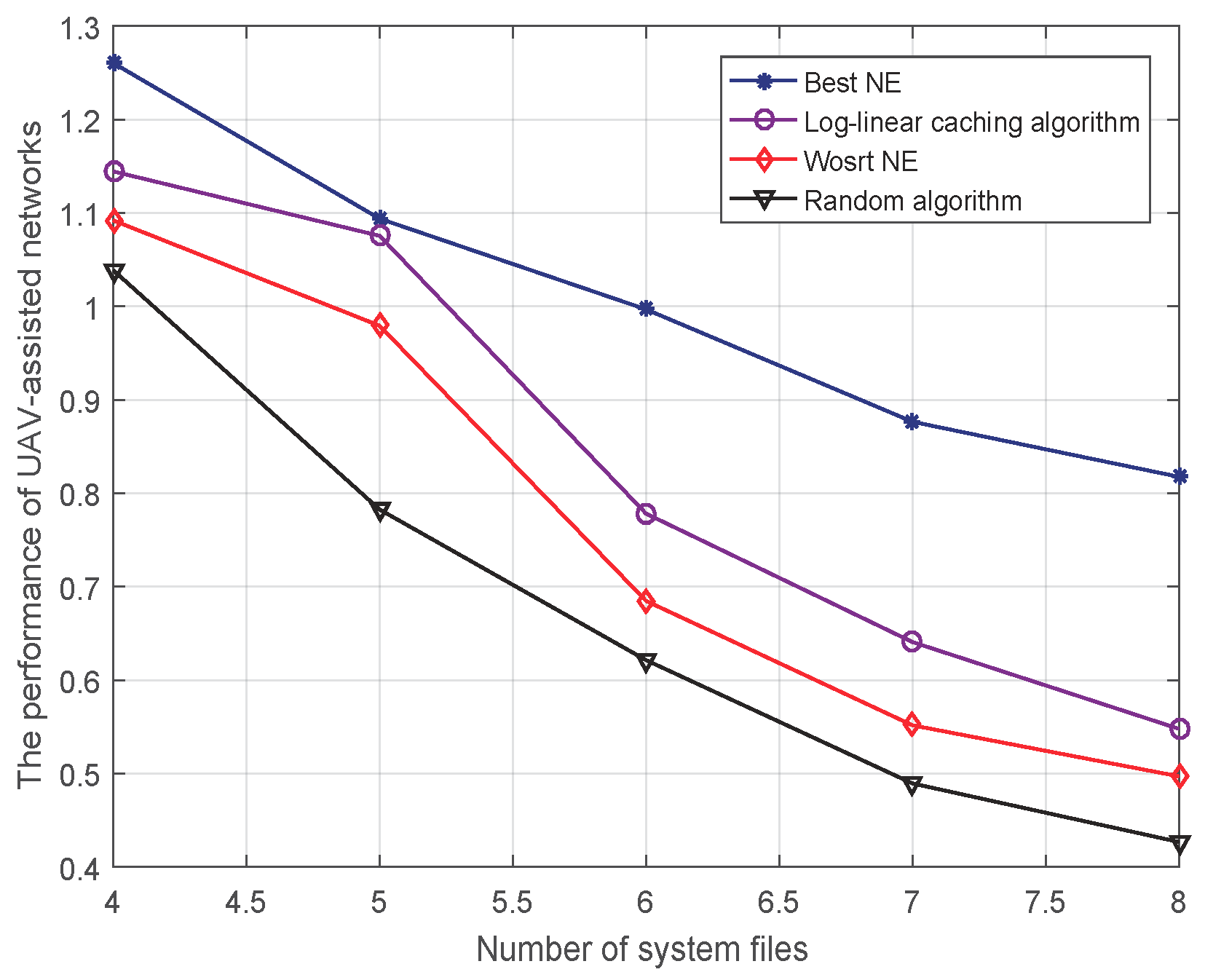
4.3.1. Performance of UAV-Assisted Networks versus the Number of System Files
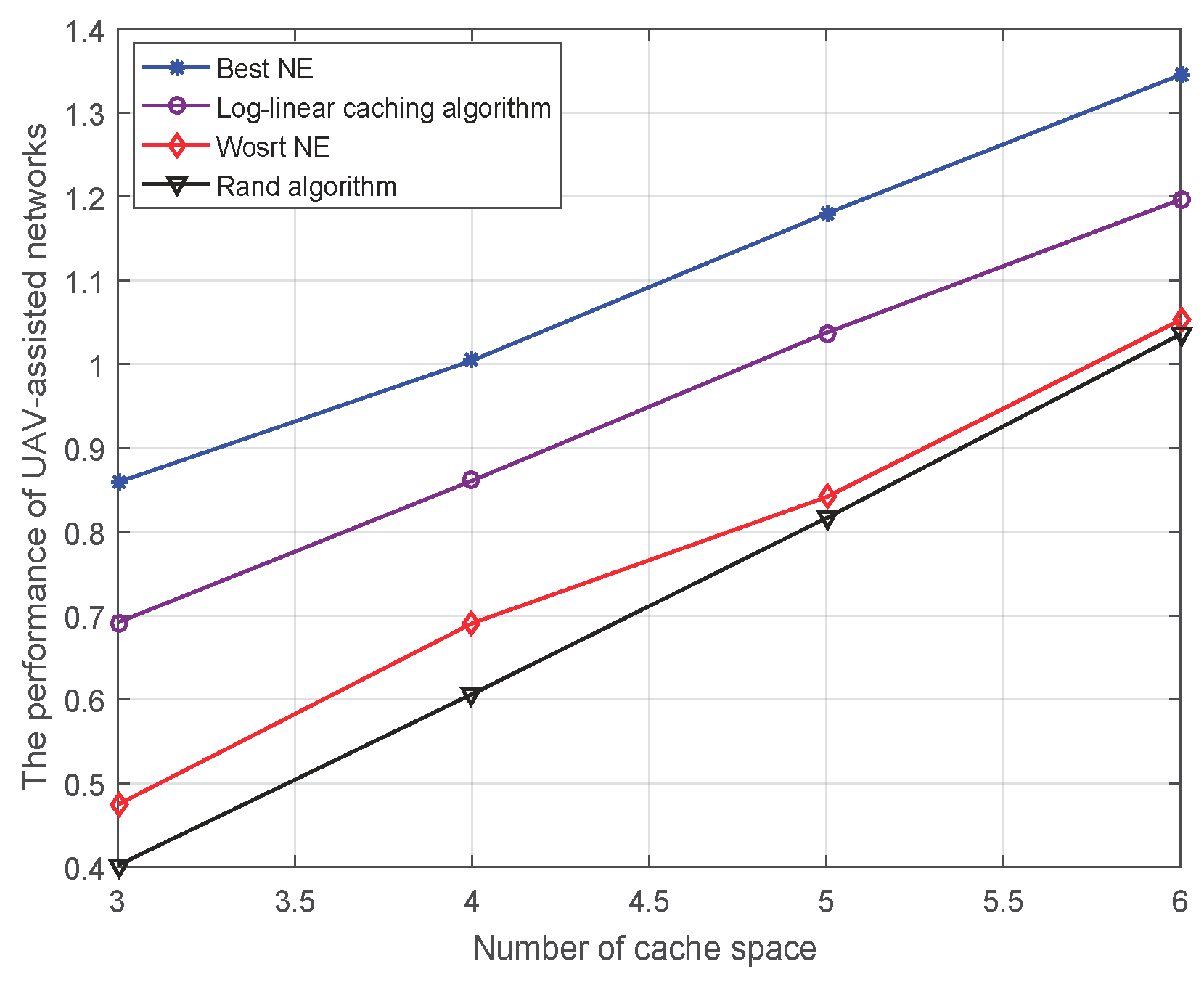
4.3.2. Performance of UAV-Assisted Networks versus the Number of Cache Space
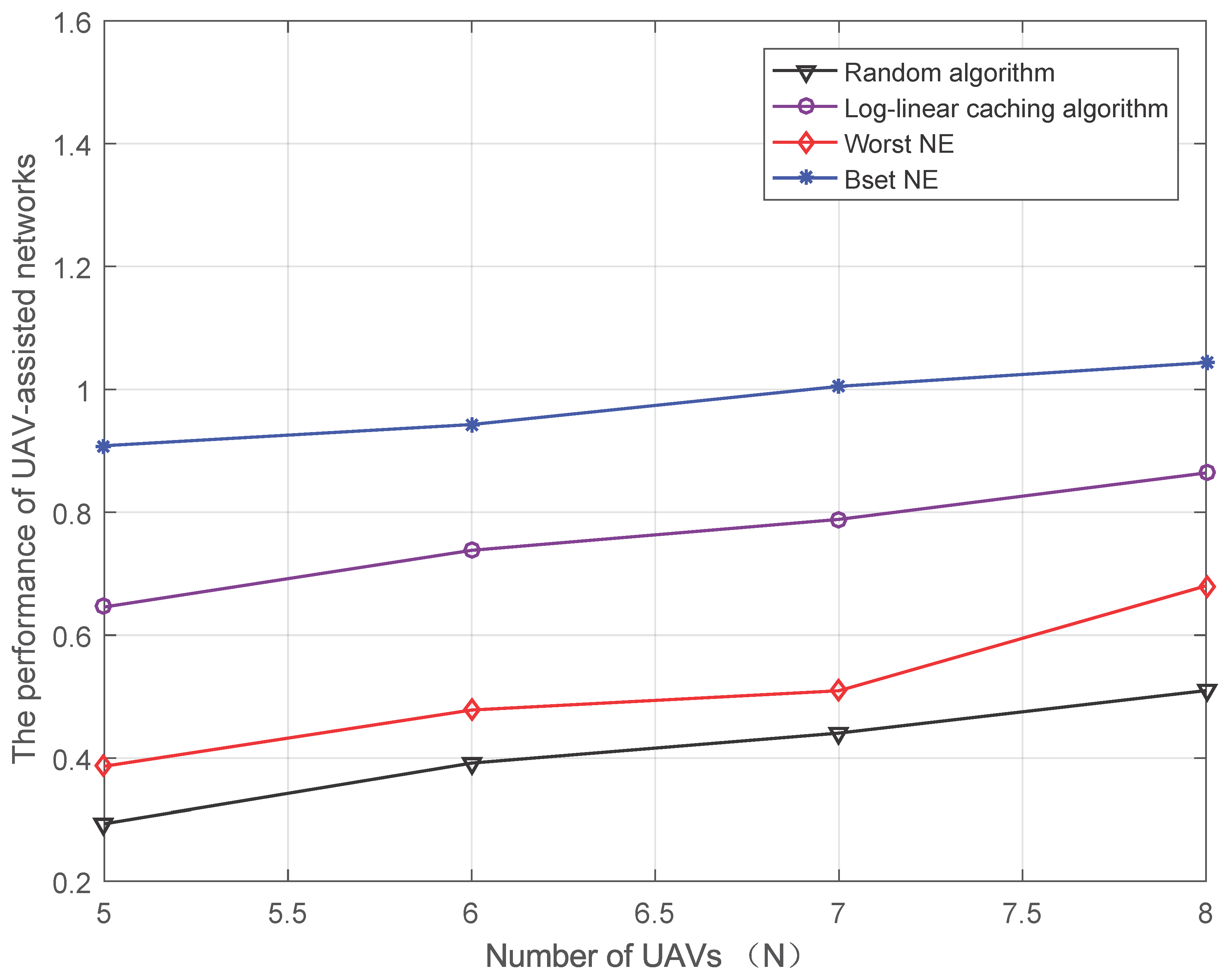
4.3.3. Performance of UAV-Assisted Networks versus the Number of UAVs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Orfanus, D.; de Freitas, E.P.; Eliassen, F. Self-organization as a supporting paradigm for military UAV relay networks. IEEE Commun. Lett. 2016, 20, 804–807. [Google Scholar] [CrossRef]
- Ma’sum, M.A.; Arrofi, M.K.; Jati, G.; Arifin, F.; Kurniawan, M.N.; Mursanto, P.; Jatmiko, W. Simulation of intelligent unmanned aerial vehicle (UAV) for military surveillance. In Proceedings of the 2013 International Conference on Advanced Computer Science and Information Systems, Bali, Indonesia, 28–29 September 2013; pp. 161–166. [Google Scholar]
- Giese, S.; Carr, D.; Chahl, J. Implications for unmanned systems research of military UAV mishap statistics. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium, Gold Coast, QLD, Australia, 23–26 June 2013; pp. 1191–1196. [Google Scholar]
- Johnson, C.W. Military risk assessment in counter insurgency operations: Case study in the retrieval of a UAV, Nr Sangin, Afghanistan, 11 June 2006. In Proceedings of the 2008 3rd IET International Conference on System Safety, Birmingham, UK, 20–22 October 2008; pp. 1–6. [Google Scholar]
- Chen, Z.; Luo, J.; Jiang, H.; Shi, W. Design & application of MIS on UAV quality & reliability for total life span. In Proceedings of the 2009 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009; pp. 1290–1292. [Google Scholar]
- Cecil, J. A conceptual framework for supporting UAV based cyber physical weather monitoring activities. In Proceedings of the 2018 Annual IEEE International Systems Conference, Vancouver, BC, Canada, 23–26 April 2018; pp. 1–8. [Google Scholar]
- Zhou, S.; Wang, Y.; Ye, S.; Zhu, G.; Cheng, L. The intelligent wind detection system of weather UAV based on the multi-mode variable structure. In Proceedings of the 2011 Fourth International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; pp. 765–768. [Google Scholar]
- Zhang, W.; Yu, H.; Yan, Z.; Xu, J. Study on disaster monitoring technology of mountain fire based on UAV transmission line inspection. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems, Beijing, China, 27–29 October 2017; pp. 400–403. [Google Scholar]
- Yuan, C.; Liu, Z.; Zhang, Y. UAV-based forest fire detection and tracking using image processing techniques. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems, Denver, CO, USA, 9–12 June 2015; pp. 639–643. [Google Scholar]
- Ji, X.; Hua, Q.; Li, C.; Tang, J.; Wang, A.; Chen, X.; Fang, D. 2-OptACO: An improvement of ant colony optimization for UAV path in disaster rescue. In Proceedings of the 2017 International Conference on Networking and Network Applications, Kathmandu, Nepal, 16–19 October 2017; pp. 225–231. [Google Scholar]
- Nakadai, K.; Kumon, M.; Okuno, H.G.; Hoshiba, K.; Wakabayashi, M.; Washizaki, K.; Ishiki, T.; Gabriel, D.; Bando, Y.; Morito, T.; et al. Development of microphone-array-embedded UAV for search and rescue task. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 5985–5990. [Google Scholar]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, Y.; Guan, Y.L.; Zhang, R. Overcoming Endurance Issue: UAV-Enabled Communications with Proactive Caching. IEEE J. Sel. Areas Commun. 2018, 36, 1231–1244. [Google Scholar] [CrossRef]
- Chen, M.; Mozaffari, M.; Saad, W.; Yin, C.; Debbah, M.; Hong, C.S. Caching in the sky: Proactive deployment of cache-enabled unmanned aerial vehicles for optimized quality-of-experience. IEEE J. Sel. Areas Commun. 2017, 35, 1046–1061. [Google Scholar] [CrossRef]
- Fang, T.; Tian, H.; Yang, Y.; Liu, X.; Wu, D.; Chen, X. An influence factor based caching node selection algorithm in D2D networks. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 805–809. [Google Scholar]
- Zhang, Y.; Xu, Y.; Wu, Q.; Liu, X.; Yao, K.; Anpalagan, A. A game-theoretic approach for optimal distributed cooperative hybrid caching in D2D networks. IEEE Wirel. Commun. Lett. 2018, 7, 324–327. [Google Scholar] [CrossRef]
- Zhao, N.; Cheng, F.; Yu, F.R.; Tang, J.; Chen, Y.; Gui, G.; Sari, H. Caching UAV assisted secure transmission in hyper-dense networks based on interference alignment. IEEE Trans. Commun. 2018, 66, 2281–2294. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C. Liquid state machine learning for resource allocation in a network of cache-enabled LTE-U UAVs. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Fang, T.; Tian, H.; Yang, Y.; Zhang, X.; Zhang, Y.; Xu, Y. Location-aware emergency content delivery in UAV-assisted networks: A game-theoretic approach. IEEE Access 2018. submitted. [Google Scholar]
- Cha, M.; Kwak, H.; Rodriguez, P.; Ahn, Y.Y.; Moon, S. I tube, you tube, everybody tubes: Analyzing the world’s largest user generated content video system. In Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement, San Diego, CA, USA, 24–26 October 2007. [Google Scholar]
- UMassTraceRepository. Available online: http://traces.cs.umass.edu/index.php/network/network (accessed on 17 April 2013).
- Xu, Y.; Wang, J.; Wu, Q.; Anpalagan, A.; Yao, Y.D. Opportunistic spectrum access in cognitive radio networks: Global optimization using local interaction games. IEEE J. Sel. Top. Signal Process. 2012, 6, 180–194. [Google Scholar] [CrossRef]
- Emara, M.; Elsawy, H.; Sorour, S.; Al-Ghadhban, S.; Alouini, M.; Al-Naffouri, T.Y. Optimal caching in 5G networks with opportunistic spectrum access. IEEE Trans. Wirel. Commun. 2018, 17, 4447–4461. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP altitude for maximum coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, G.; Chen, J.; Luo, Y.; Jia, L.; Liu, X.; Yang, Y.; Xu, Y. A one-leader multi-follower bayesian-stackelberg game for anti-jamming transmission in UAV communication networks. IEEE Access 2018, 6, 21697–21709. [Google Scholar] [CrossRef]
- Jia, L.; Xu, Y.; Sun, Y.; Feng, S.; Anpalagan, A. Stackelberg game approaches for anti-jamming defence in wireless networks. arXiv. 2018. Available online: https://arxiv.org/abs/1805.12308 (accessed on 31 May 2018).
- Xu, Y.; Wang, J.; Wu, Q.; Zheng, J.; Shen, L.; Anpalagan, A. Dynamic spectrum access in time-varying environment: Distributed learning beyond expectation optimization. IEEE Trans. Commun. 2017, 65, 5305–5318. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Q.; Xu, Y.; Zhang, Y.; Yang, Y. Distributed demand- aware channel-slot selection for multi-UAV networks: A game-theoretic learning approach. IEEE Access 2018, 6, 14799–14811. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wang, J.; Xu, Y.; Anpalagan, A.; Wu, Q.; Wang, H.; Shen, L. Self-organizing relay selection in UAV communication networks: A matching game perspective. arXiv, 2018; arXiv:1805.09257. [Google Scholar]
- Zhang, Y.; Xu, Y.; Anpalagan, A.; Wu, Q.; Xu, Y.; Sun, Y.; Feng, S.; Luo, Y. Context-aware group buying in ultra-dense small cell networks: Unity is strength. IEEE Wirel. Commun. 2018, in press. [Google Scholar]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, D.; Xu, Y.; Wang, J. Demand-aware multichannel opportunistic spectrum access: A local interaction game approach With reduced information exchange. IEEE Trans. Veh. Technol. 2015, 64, 4899–4904. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Q.; Wang, J.; Shen, L.; Anpalagan, A. Opportunistic spectrum access using partially overlapping channels: Graphical game and uncoupled learning. IEEE Trans. Commun. 2013, 61, 3906–3918. [Google Scholar] [CrossRef]
| Variables | Explanation |
|---|---|
| M | Number of ground users |
| N | Number of unmanned aerial vehicles (UAVs) |
| f | Set of system files |
| i-th requested file | |
| Probability of requesting the i-th file | |
| Parameter of a Zipf Distribution | |
| Overhead of user m to obtain files | |
| Set of user m’s interested files | |
| Action of UAV n | |
| Location of UAV n | |
| Caching contents of UAV n | |
| Communication thresholds between UAVs | |
| Physical distance from UAV i to j | |
| Neighbor UAVs by one hop | |
| Overhead that User m gets file k | |
| UAV that is serving for User m | |
| UAV that caches file k | |
| Overhead per file per distance from UAV to user m | |
| Successful communication probability from UAV n to user m | |
| Communication threshold | |
| Channel power gain from UAV to user m | |
| h | Nakagami fading |
| Distance from UAV to user m | |
| Set of files that UAV caches | |
| I | Indicator function |
| Transmit power of UAV n | |
| Path loss exponent | |
| Background noise | |
| Additional attenuation factor due to the non-line-of-sight (NLOS) link | |
| h | Nakagami fading |
| Shape parameter | |
| Scale parameter | |
| Elevation angle | |
| Height of UAV | |
| Set of ground users that UAV n serves | |
| Strategy space of player n | |
| Utility function of player n | |
| R | Overhead of all ground users |
| Potential function |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, T.; Tian, H.; Zhang, X.; Chen, X.; Shao, X.; Zhang, Y. Context-Aware Caching Distribution and UAV Deployment: A Game-Theoretic Approach. Appl. Sci. 2018, 8, 1959. https://doi.org/10.3390/app8101959
Fang T, Tian H, Zhang X, Chen X, Shao X, Zhang Y. Context-Aware Caching Distribution and UAV Deployment: A Game-Theoretic Approach. Applied Sciences. 2018; 8(10):1959. https://doi.org/10.3390/app8101959
Chicago/Turabian StyleFang, Tao, Hua Tian, Xiaobo Zhang, Xueqiang Chen, Xinhong Shao, and Yuli Zhang. 2018. "Context-Aware Caching Distribution and UAV Deployment: A Game-Theoretic Approach" Applied Sciences 8, no. 10: 1959. https://doi.org/10.3390/app8101959
APA StyleFang, T., Tian, H., Zhang, X., Chen, X., Shao, X., & Zhang, Y. (2018). Context-Aware Caching Distribution and UAV Deployment: A Game-Theoretic Approach. Applied Sciences, 8(10), 1959. https://doi.org/10.3390/app8101959




