Development of Efficient and Accurate Parallel Computation Algorithm Using Moving Overset Grids on Background Multi-Domains for Complex Two-Phase Flows
Abstract
1. Introduction
2. Governing Equations and Numerical Methods
2.1. Governing Equations
2.2. Preconditioning System and Dual-Time Stepping
2.3. Cavitation Model
2.4. Turbulence Model
2.5. Numerical Scheme
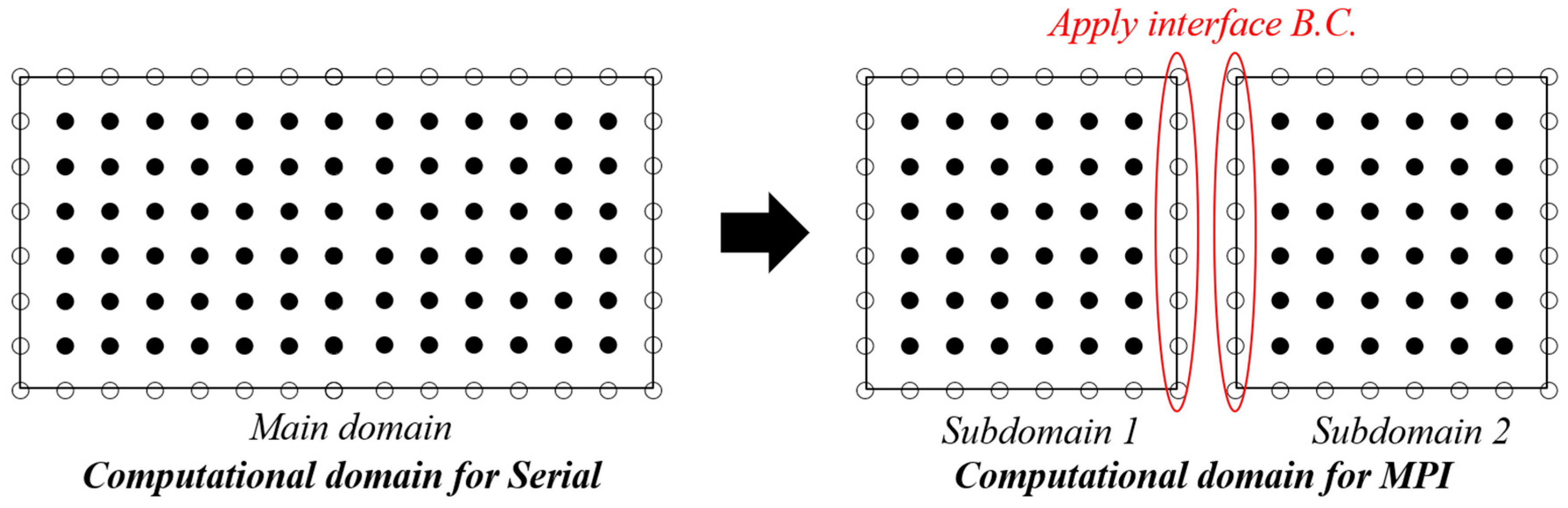
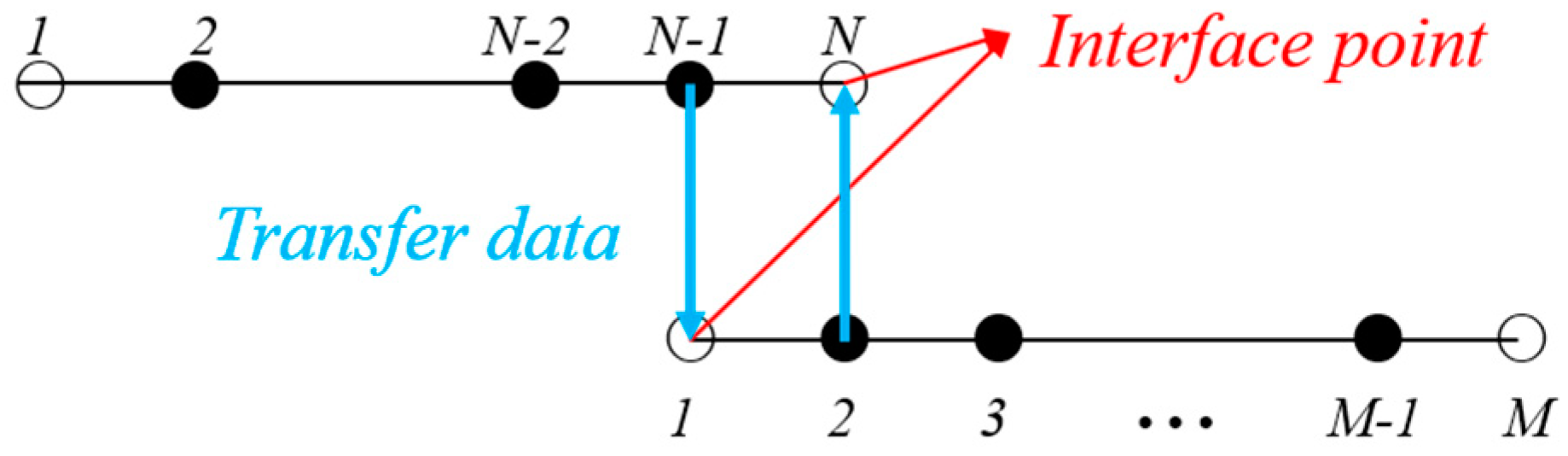
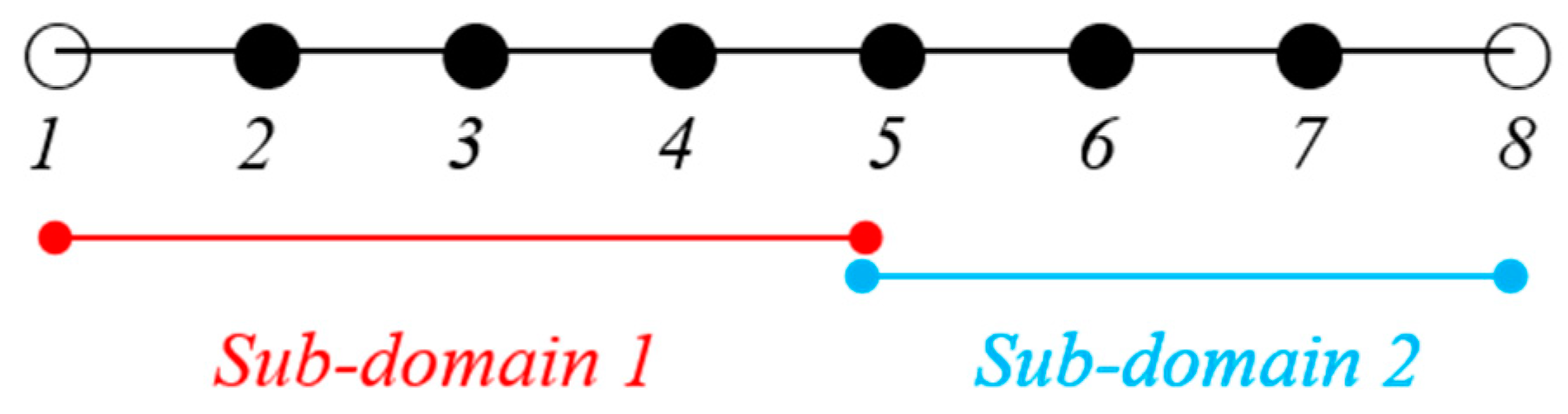
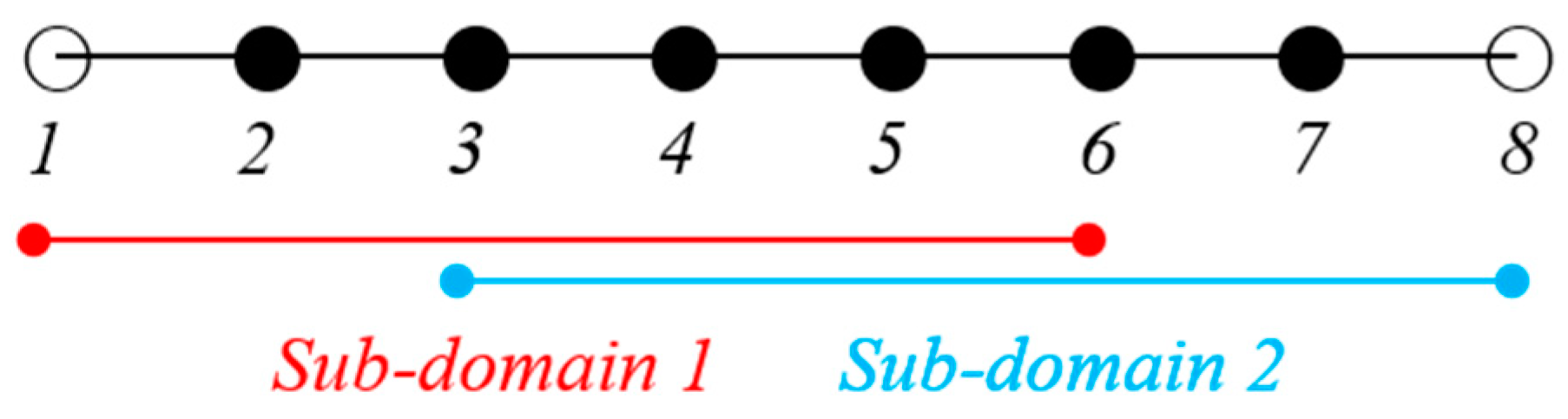
3. Parallel Computation and Grid-Overlapping Interface
3.1. Domain Decomposition Strategy
3.2. Grid-Overlapping Interface
4. Cavitation Flow over the Hemispherical Head Form
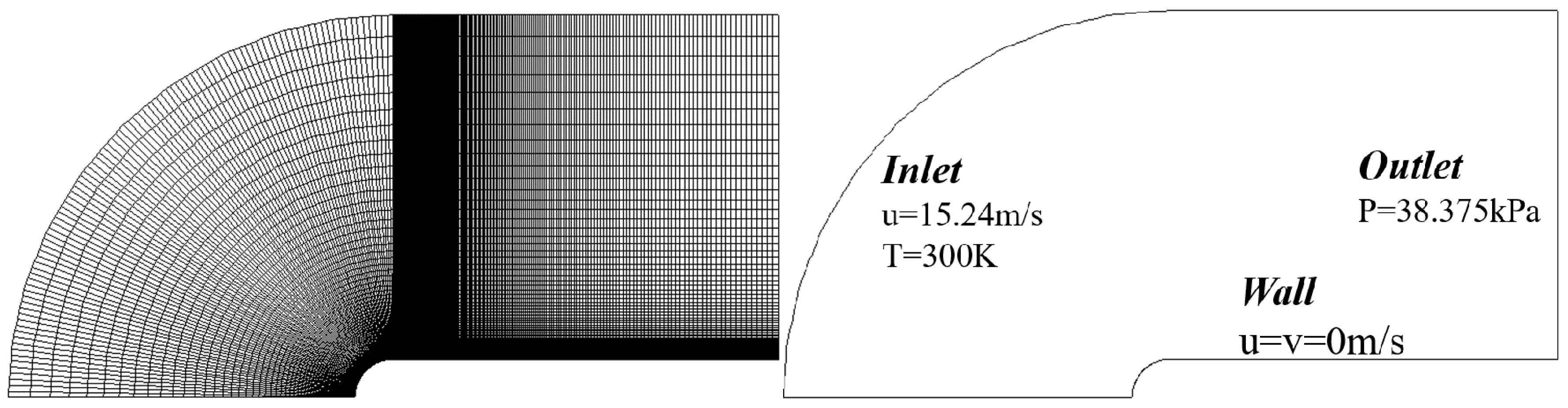
4.1. Computational Domain
4.2. Interface Boundary Condition
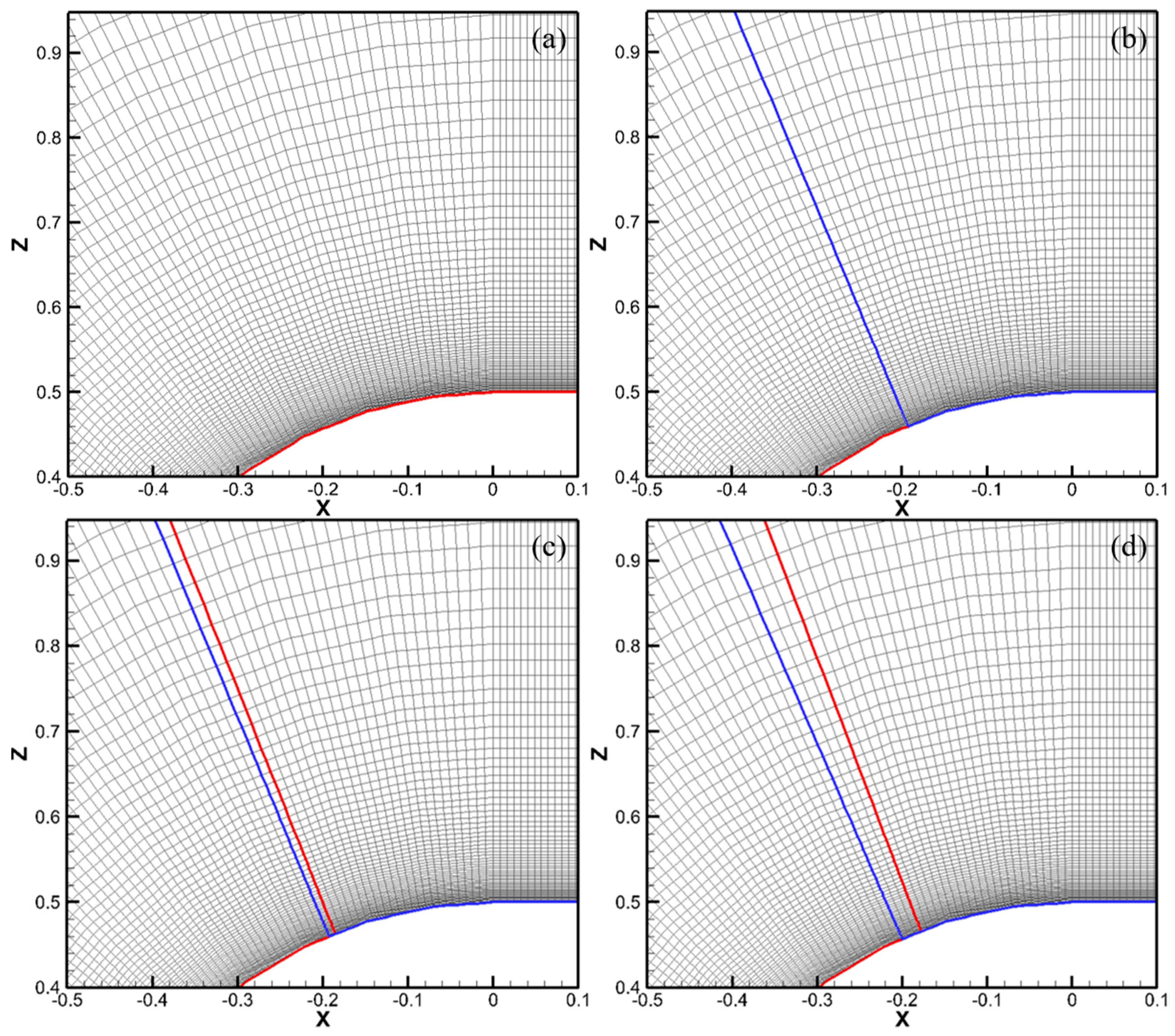
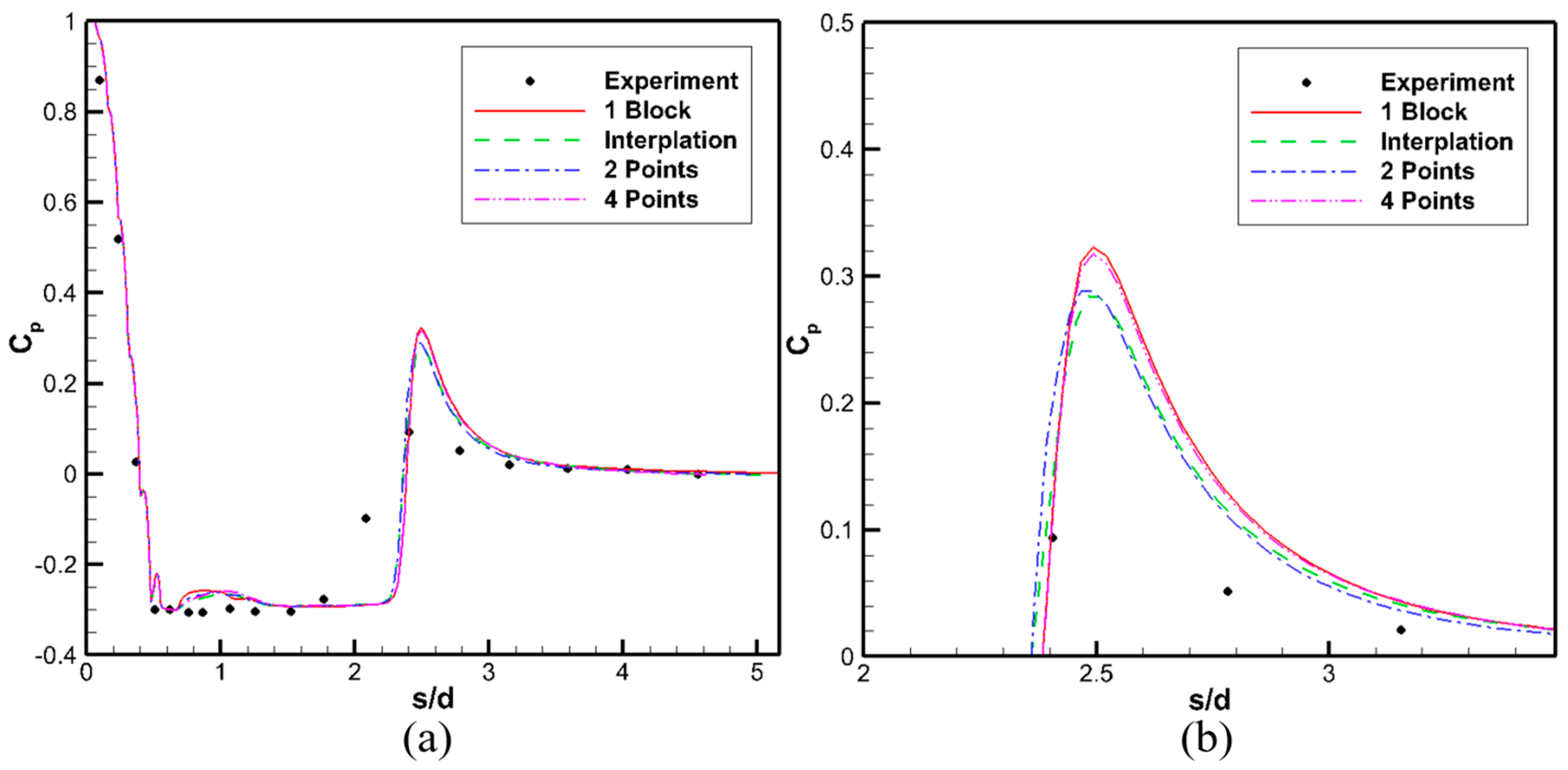
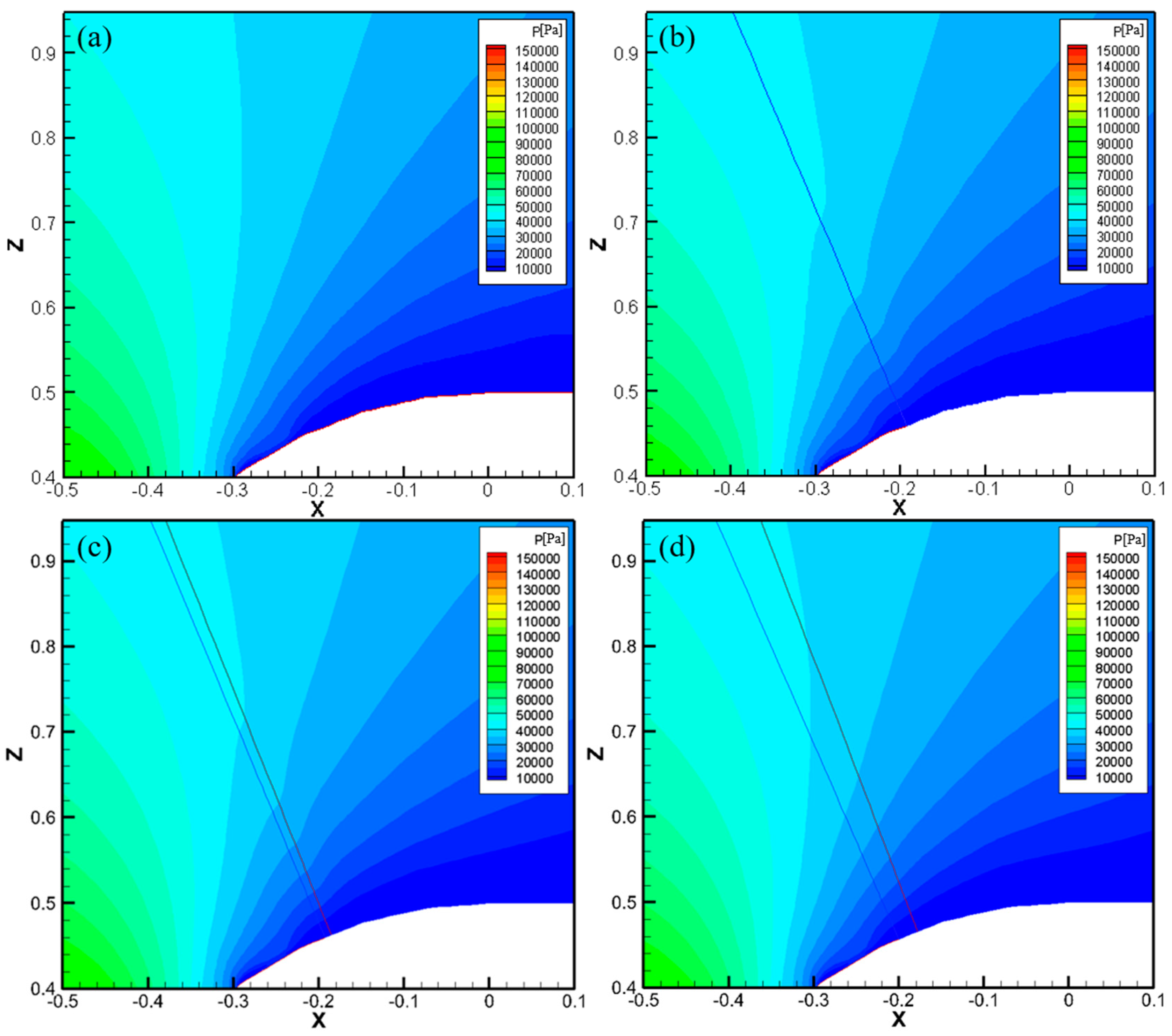
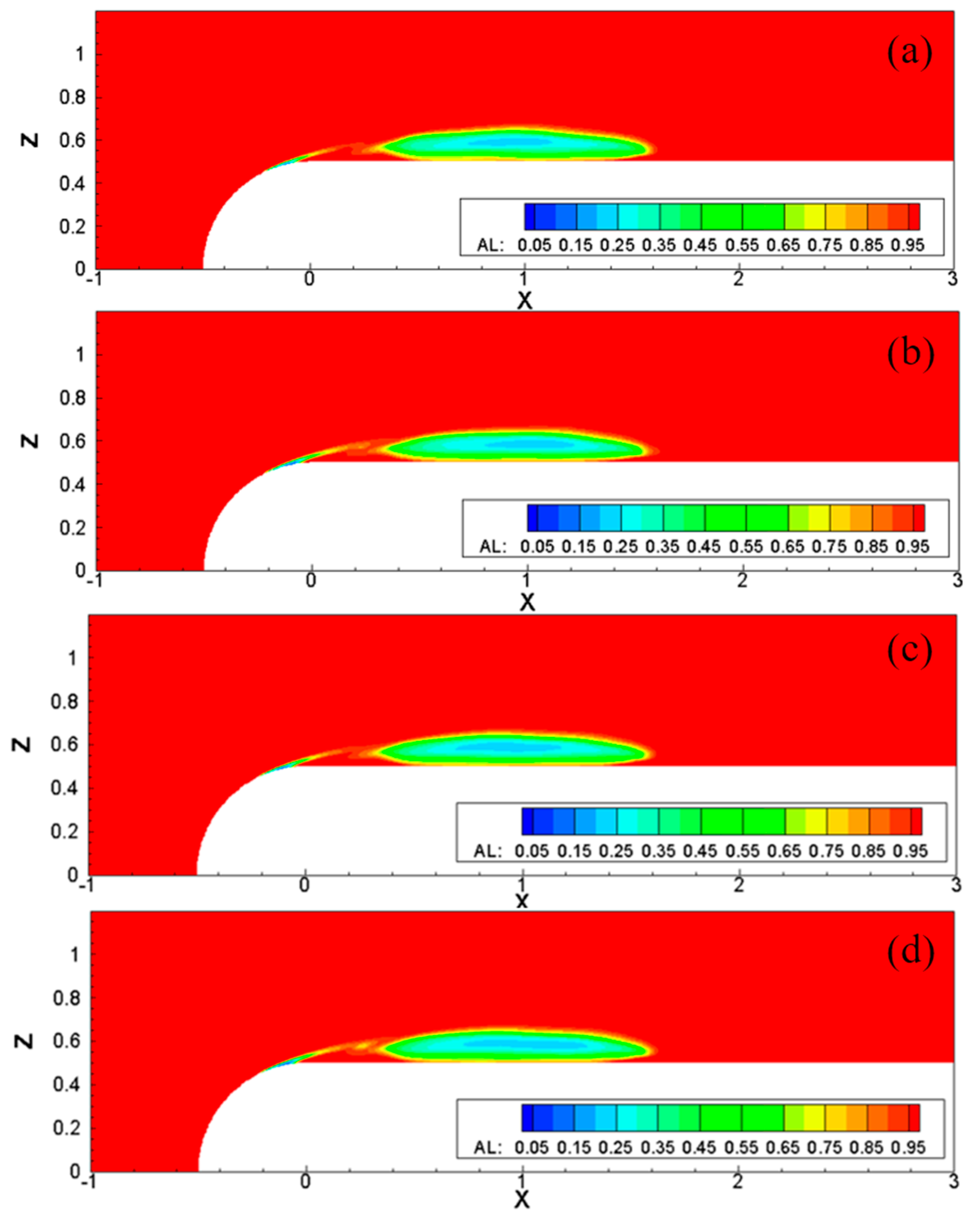
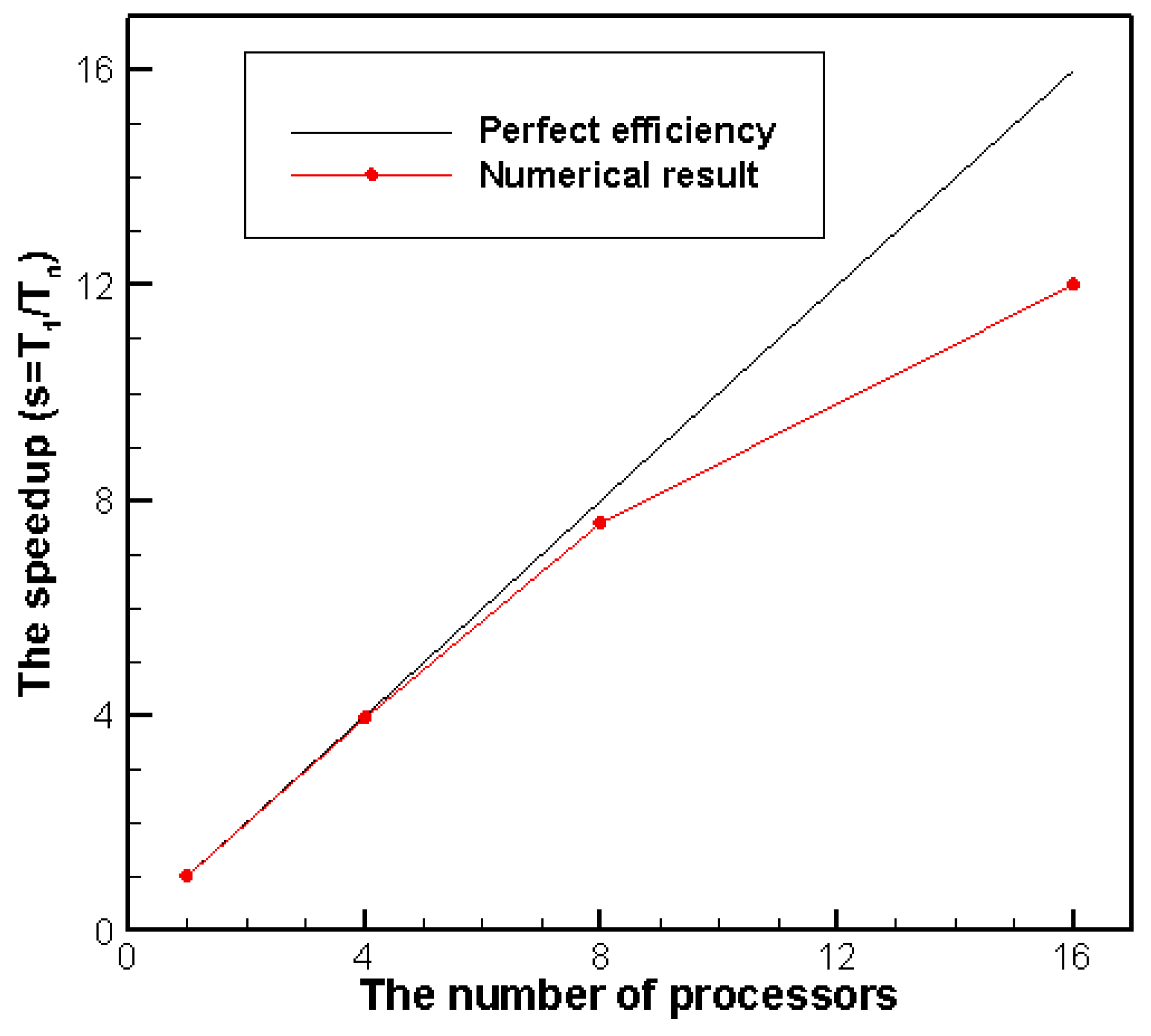
4.3. Number of Subgrid Blocks (or Processors)
5. Moving Overset Grid Method
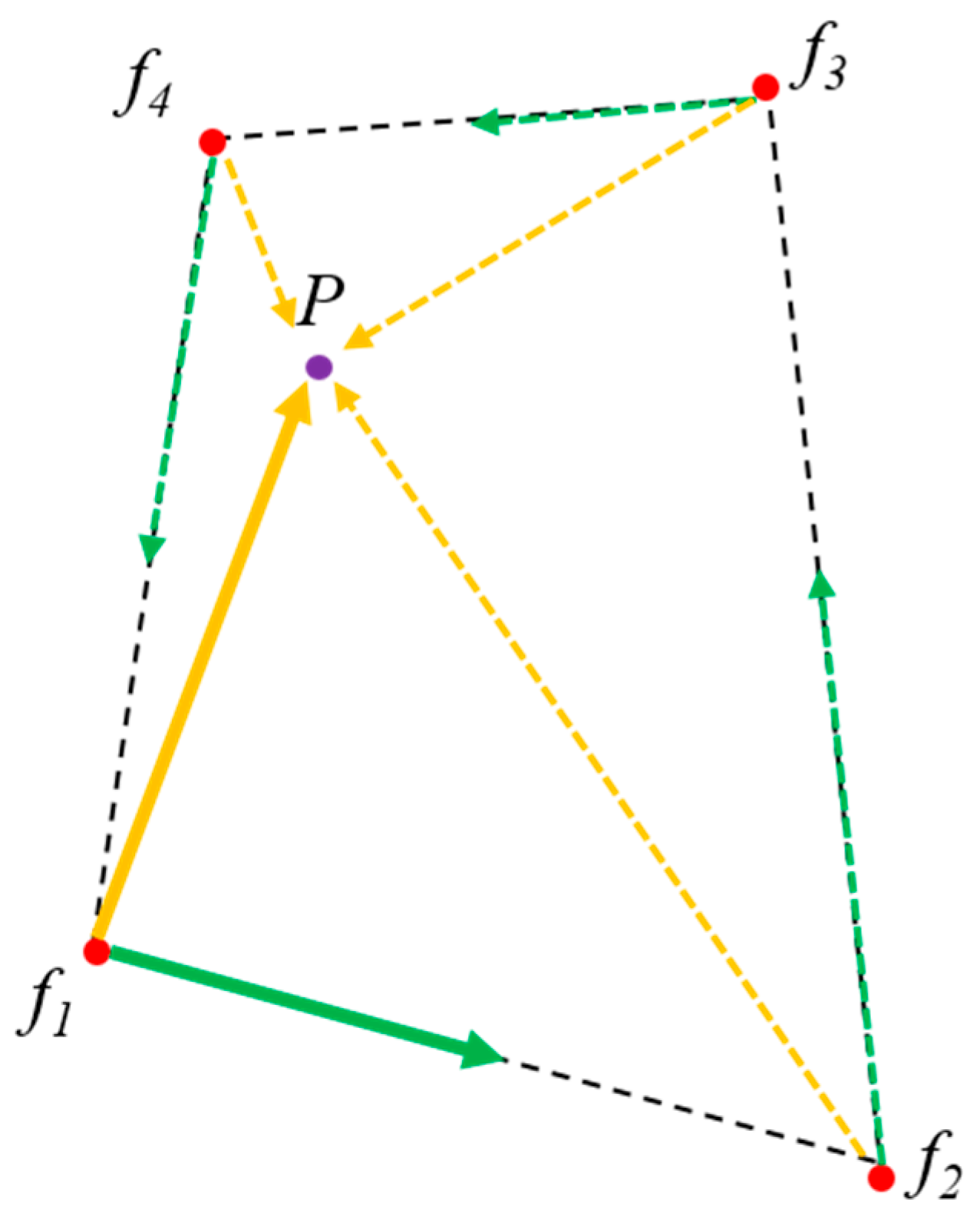
5.1. Hole Cutting
5.2. Donor Cell
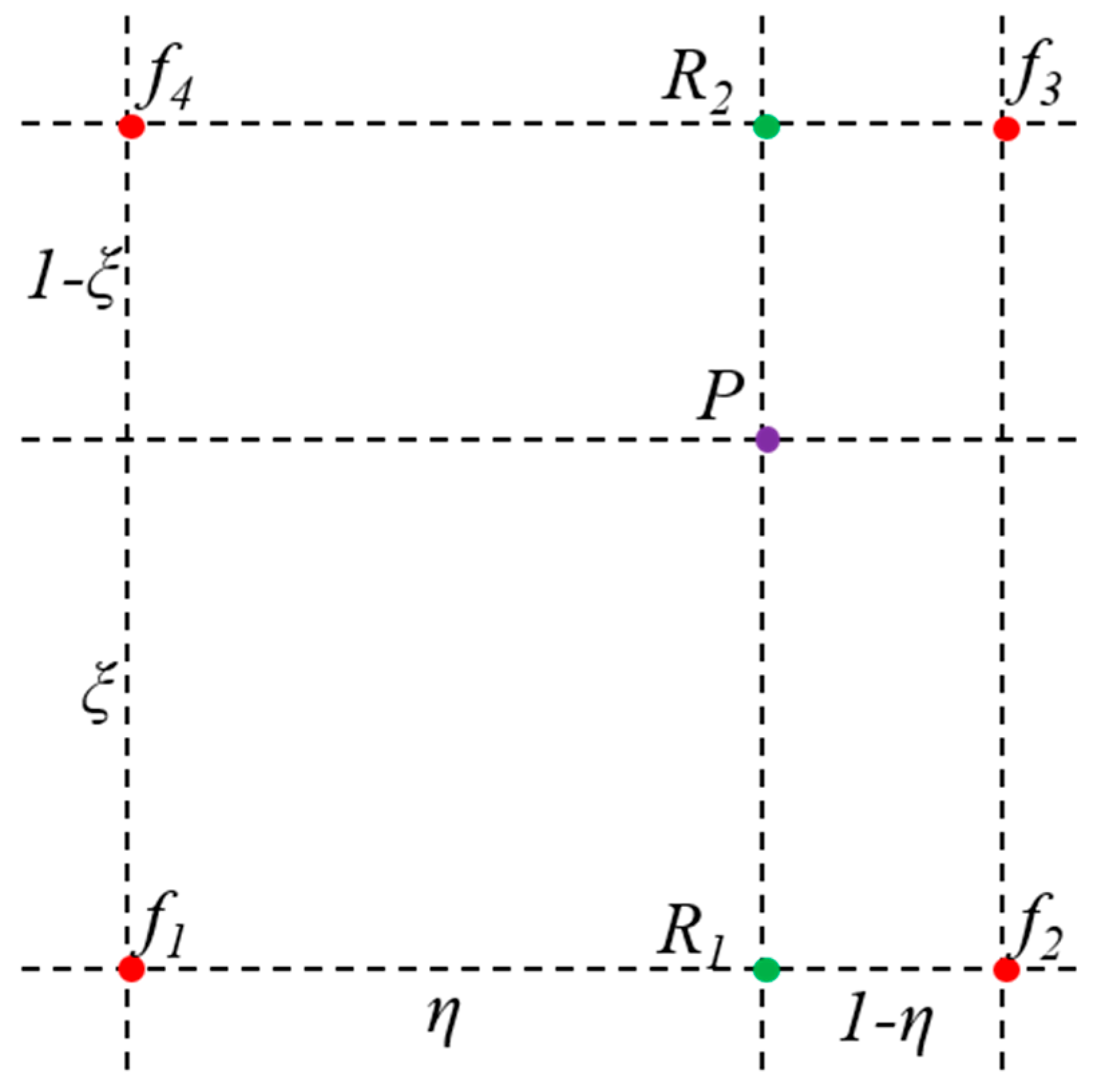
5.3. Bilinear Interpolation
6. Gust Flow by Two Pitching Hydrofoils
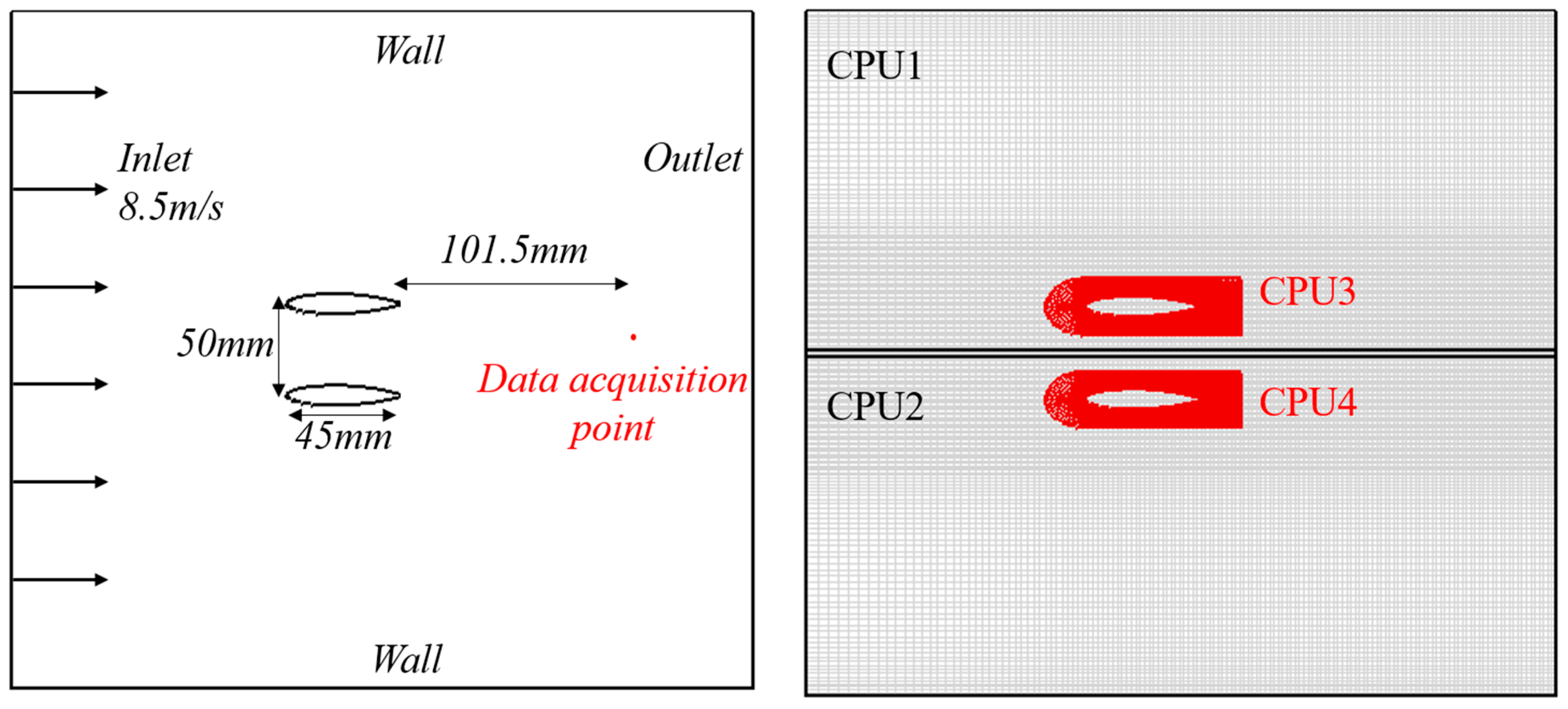
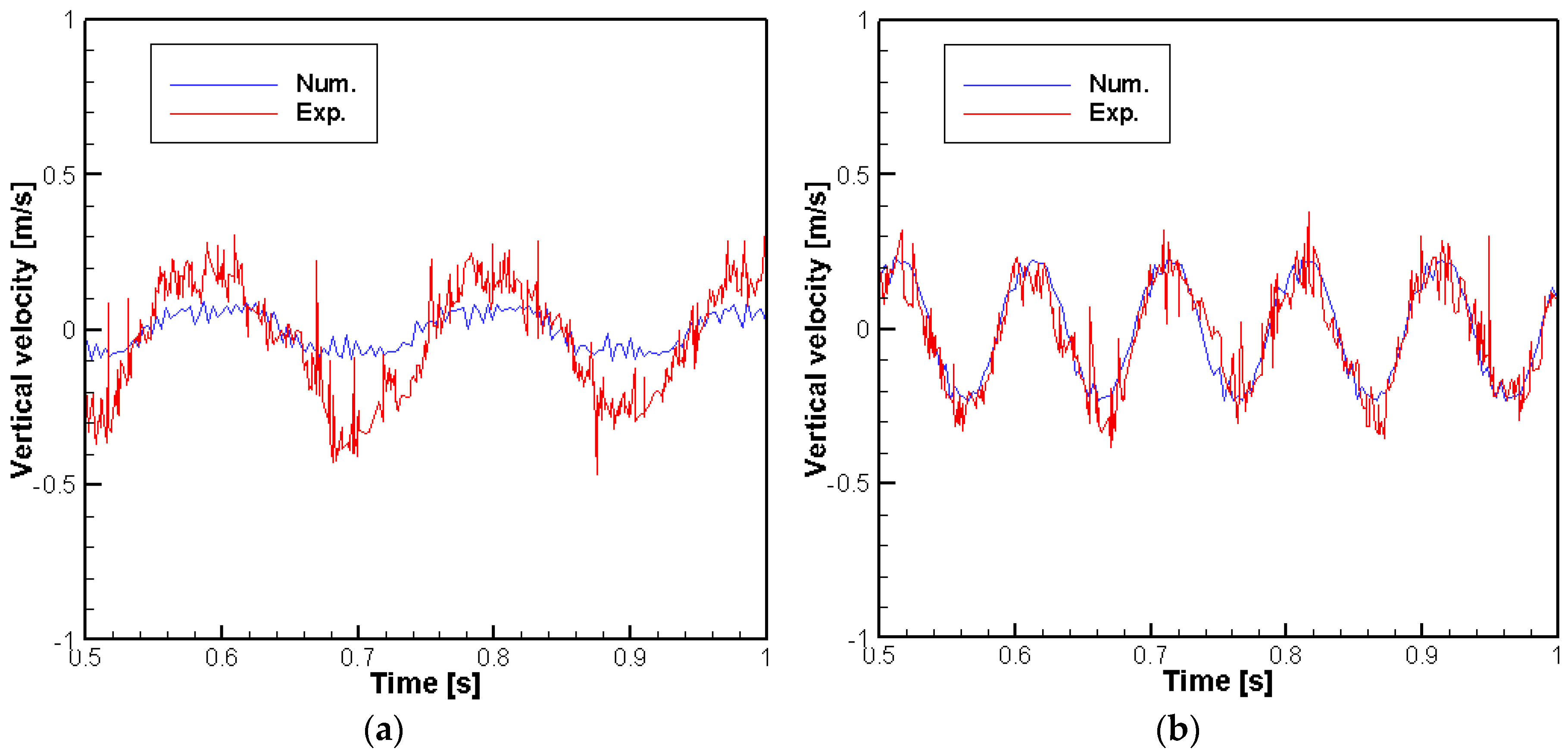
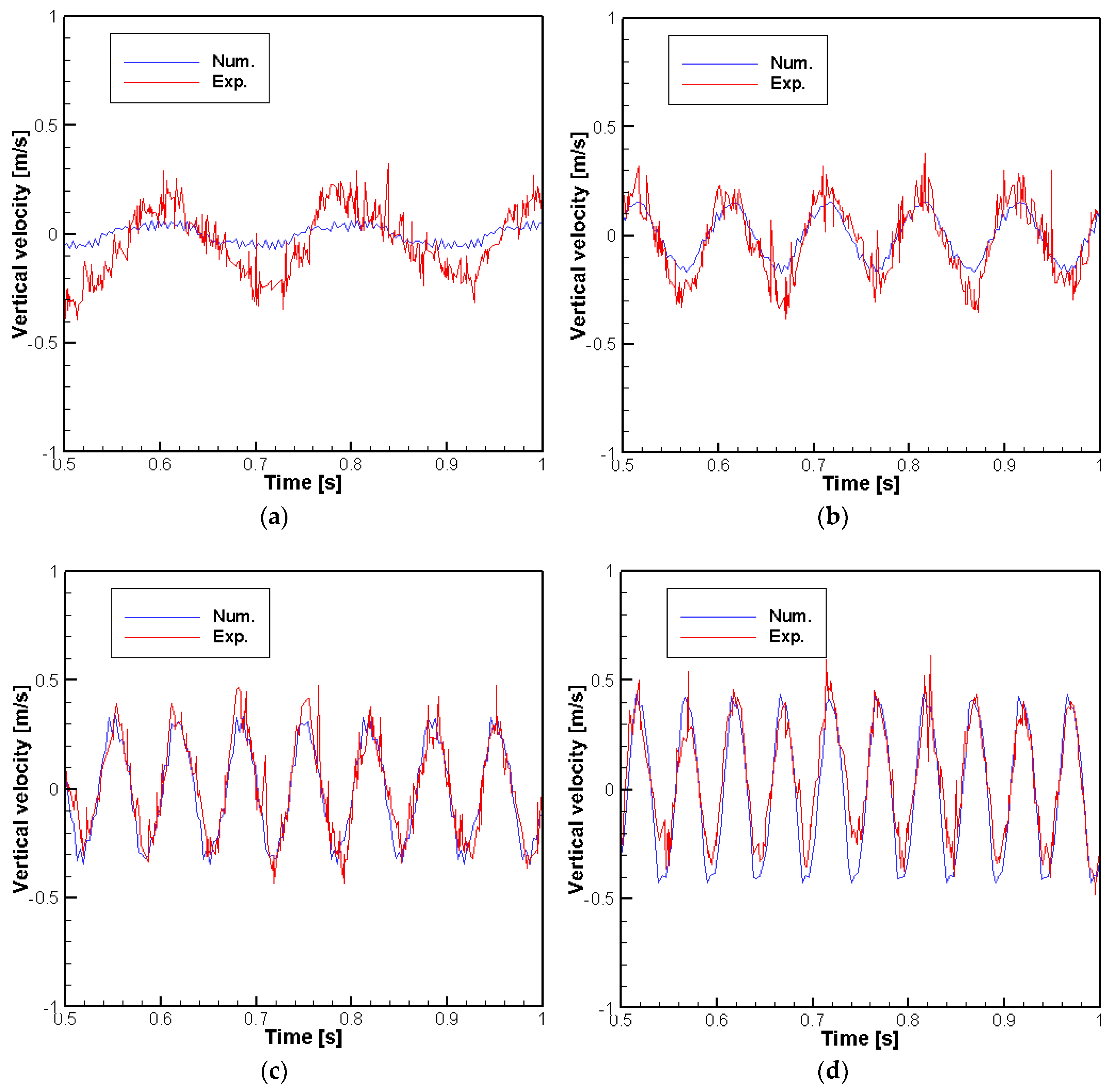
6.1. Experimental Setup and Computational Domain
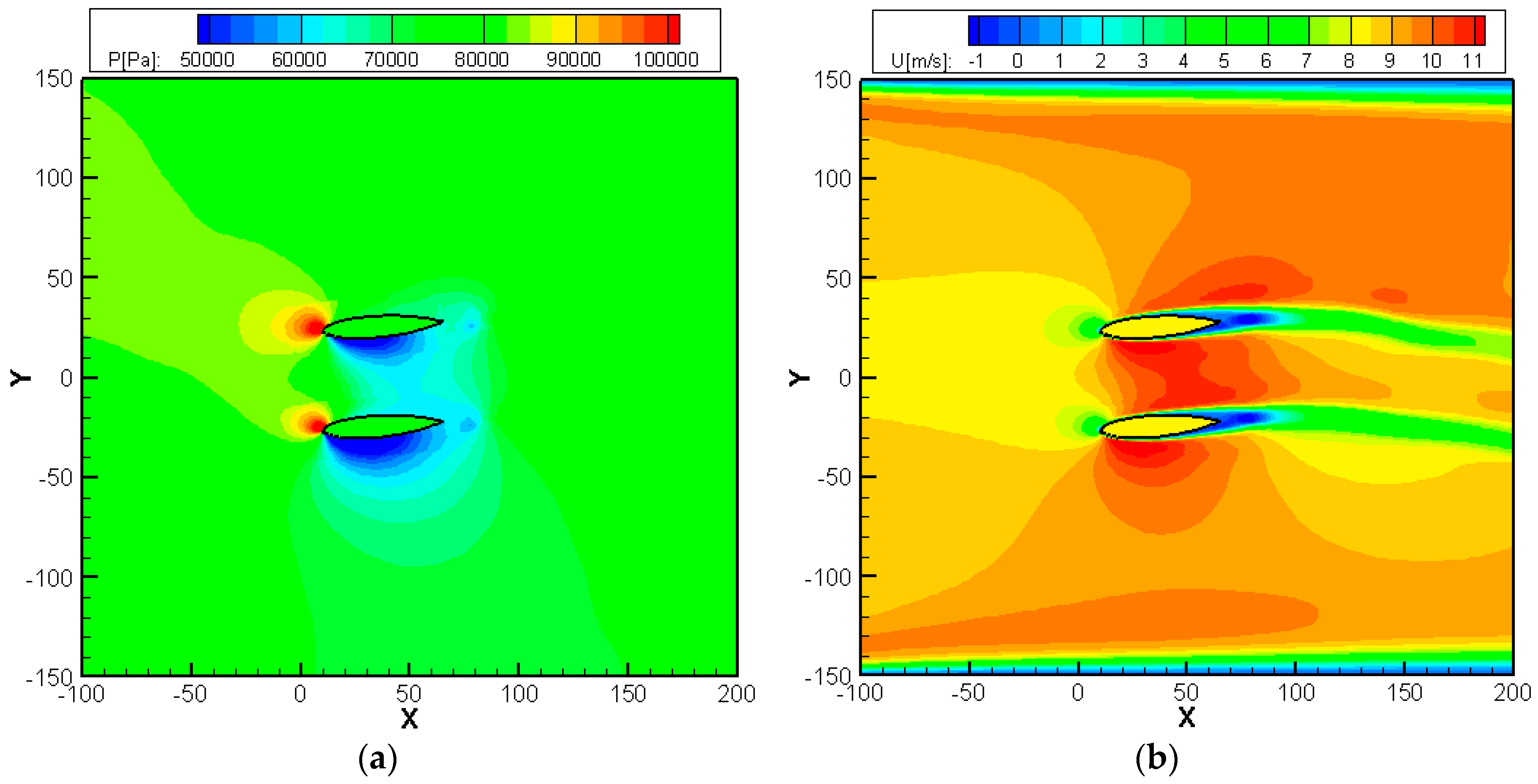
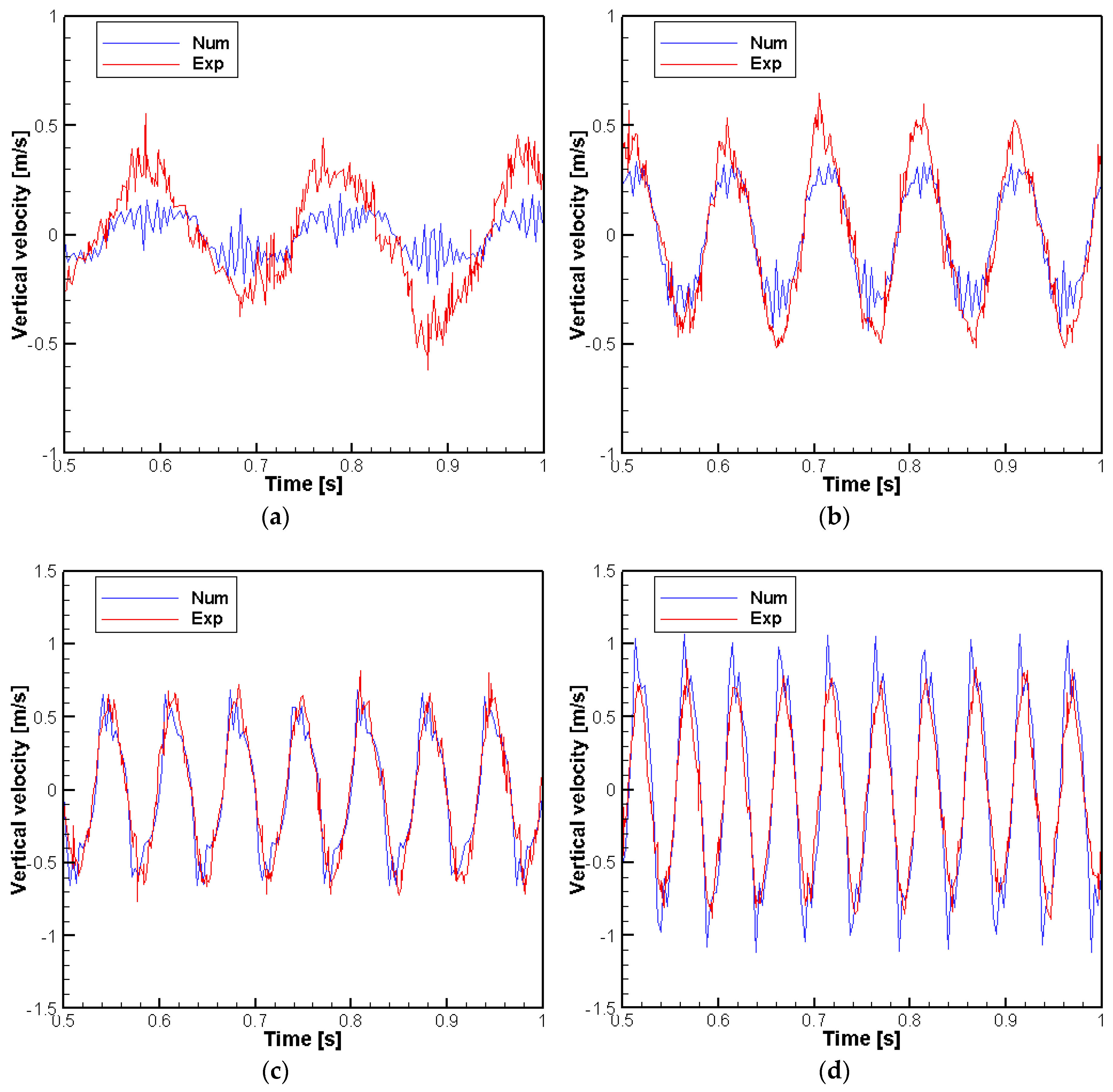
6.2. Numerical Results with Measured Data
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kopriva, J.; Arndt, R.E.A.; Amromin, E.L. Improvement of hydrofoil performance by partial ventilated cavitation in steady flow and periodic gusts. J. Fluid Eng. 2008, 130, 031301. [Google Scholar] [CrossRef]
- Lee, S.J.; Kawakami, E.; Arndt, R.E.A. Investigation of the Behavior of Ventilated Supercavities in a Periodic Gust Flow. J. Fluids Eng. 2013, 135, 081301. [Google Scholar] [CrossRef]
- Lee, S.J.; Kawakami, E.; Karn, A.; Arndt, R.E.A. A comparative study of behaviors of ventilated supercavities between experimental models with different mounting configurations. Fluid Dyn. Res. 2016, 48, 045506. [Google Scholar] [CrossRef]
- Karn, A.; Arndt, R.E.A.; Hong, J. Dependence of supercavity closure upon flow unsteadiness. Exp. Therm. Fluid Sci. 2015, 68, 493–498. [Google Scholar] [CrossRef]
- Toumi, I.; Kumbaro, A.; Paillere, H. Approximate Riemann Solvers and Flux Vector Splitting Schemes for Two-Phase Flow; CEA Saclay, Direction de L’information Scientifique et Technique: Gif-sur-Yvette, France, 1999. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics - Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Merkle, C.L.; Feng, J.; Buelow, P.E.O. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the Third International Symposium on Cavitation, Grenoble, France, 7–10 April 1998; pp. 307–311. [Google Scholar]
- Turkel, E. Preconditioned methods for solving the incompressible and low speed compressible equations. J. Comput. Phys. 1987, 72, 277–298. [Google Scholar] [CrossRef]
- Choi, Y.-H.; Merkle, C.L. The application of preconditioning in viscous flows. J. Comput. Phys. 1993, 105, 207–223. [Google Scholar] [CrossRef]
- Venkateswaran, S.; Merkle, C.L. Dual Time Stepping and Preconditioning for Unsteady Computations. In Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995; p. 78. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Chyczewski, T.S.; Stinebring, D.; Gibeling, H.; Govindan, T.R. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies. In Proceedings of the 3rd ASME/JSME Joint Fluids Engineering Conference, FEDAM’99, San Francisco, CA, USA, 18–23 July 1999; Volume 99, p. 1. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Lindau, J.; Kunz, R.; Boger, D.; Stinebring, D.; Gibeling, H. Validation of high Reynolds number, unsteady multi-phase cfd modeling for naval applications. In Proceedings of the Twenty-Third Symposium on Naval Hydrodynamics, Val de Reuil, France, 17–22 September 2000. [Google Scholar]
- Lindau, J.W.; Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Gibeling, H.J. High Reynolds number, unsteady, multiphase CFD modeling of cavitating flows. J. Fluids Eng. 2002, 124, 607–616. [Google Scholar] [CrossRef]
- Owis, F.M.; Nayfeh, A.H. Numerical simulation of super-and partially-cavitating flows over an axisymmetric projectile. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, NV, USA, 8–11 January 2001; p. 1042. [Google Scholar]
- Owis, F.M.; Nayfeh, A.H. Numerical simulation of 3-D incompressible, multi-phase flows over cavitating projectiles. Eur. J. Mech. B Fluids 2004, 23, 339–351. [Google Scholar] [CrossRef]
- Rouse, H.; McNown, J.S. Cavitation and Pressure Distribution: Head Forms at Zero Angle of Yaw; State University of Iowa: Iowa, CA, USA, 1948; p. 51. [Google Scholar]
- Lindau, J.W.; Kunz, R.F.; Mulherin, J.M.; Dreyer, J.J.; Stinebring, D.R. Fully coupled, 6-DOF to URANS, modeling of cavitating flows around a supercavitating vehicle. In Proceedings of the 5th international symposium on cavitation, Osaka, Japan, 1–4 November 2003; pp. 1–4. [Google Scholar]
- Venkateswaran, S.; Lindau, J.W.; Kunz, R.F.; Merkle, C.L. Preconditioning algorithms for the computation of multi-phase mixture flows. In Proceeding of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 279. [Google Scholar]
- Venkateswaran, S.; Lindau, J.W.; Kunz, R.F.; Merkle, C.L. Computation of multiphase mixture flows with compressibility effects. J. Comput. Phys. 2002, 180, 54–77. [Google Scholar] [CrossRef]
- Ahuja, V.; Hosangadi, A.; Arunajatesan, S. Simulations of cavitating flows using hybrid unstructured meshes. J. Fluids Eng. 2001, 123, 331–340. [Google Scholar] [CrossRef]
- Senocak, I.; Shyy, W. A pressure-based method for turbulent cavitating flow computations. J. Comput. Phys. 2002, 176, 363–383. [Google Scholar] [CrossRef]
- Kunz, R.F.; Lindau, J.W.; Billet, M.L.; Stinebring, D.R. Multiphase CFD Modeling of Developed and Supercavitating Flows; Pennsylvania State University Applied Research Laboratory: Arlington, VA, USA, 2001. [Google Scholar]
- Kunz, R.F.; Lindau, J.W.; Gibeling, H.J.; Mulherin, J.M.; Bieryla, D.J.; Reese, E.A. Unsteady, three-dimensional multiphase CFD analysis of maneuvering high speed supercavitating vehicles. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 841. [Google Scholar]
- Lindau, J.W.; Venkateswaran, S.; Kunz, R.F.; Merkle, C.L. Development of a fully-compressible multi-phase Reynolds-averaged Navier-Stokes model. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2648. [Google Scholar]
- Lindau, J.W.; Venkateswaran, S.; Kunz, R.F.; Merkle, C.L. Computation of compressible multiphase flows. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, NV, USA, 6–9 January 2003; p. 1285. [Google Scholar]
- Lindau, J.W.; Venkateswaran, S.; Kunz, R.F.; Merkle, C.L. Multiphase computations for underwater propulsive flows. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 4105. [Google Scholar]
- Owis, F.M.; Nayfeh, A.H. Computations of the compressible multiphase flow over the cavitating high-speed torpedo. J. Fluids Eng. 2003, 125, 459–468. [Google Scholar] [CrossRef]
- Kim, S.; Cheong, C.; Park, W.G. Numerical investigation on cavitation flow of hydrofoil and its flow noise with emphasis on turbulence models. AIP Adv. 2017, 7, 065114. [Google Scholar] [CrossRef]
- Kim, S.; Cheong, C.; Park, W.-G. Numerical Investigation into Effects of Viscous Flux Vectors on Hydrofoil Cavitation Flow and Its Radiated Flow Noise. Appl. Sci. 2018, 8, 289. [Google Scholar]
- Prewitt, N.C.; Belk, D.M.; Shyy, W. Parallel computing of overset grids for aerodynamic problems with moving objects. Prog. Aerosp. Sci. 2000, 36, 117–172. [Google Scholar] [CrossRef]
- Stagg, A.K.; Carey, G.F.; Cline, D.D.; Shadid, J.N. Massively parallel MIMD solution of the parabolized Navier-Stokes equations. In Proceedings of the Scalable High Performance Computing Conference SHPCC-92, Williamsburg, VA, USA, 26–29 April 1992; pp. 328–335. [Google Scholar]
- Ha, C.T.; Park, W.G. Evaluation of a new scaling term in preconditioning schemes for computations of compressible cavitating and ventilated flow. Ocean Eng. 2016, 126, 432–466. [Google Scholar] [CrossRef]
- Ha, C.T.; Kim, D.H.; Park, W.G.; Jung, C.M. A compressive interface-capturing scheme for computation of compressible multi-fluid flows. Comput. Fluids 2017, 152, 164–181. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]
- Johansen, S.T.; Wu, J.; Shyy, W. Filter-based unsteady RANS computations. Int. J. Heat Fluid Flow 2004, 25, 10–21. [Google Scholar] [CrossRef]
- Beam, R.M.; Warming, R.F. An implicit finite-difference algorithm for hyperbolic systems in conservation-law form. J. Comput. Phys. 1976, 22, 87–110. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Vu, D.T.; Park, W.G.; Jung, C.M. Navier-Stokes solver for water entry bodies with moving Chimera grid method in 6DOF motions. Comput. Fluids 2016, 140, 19–38. [Google Scholar] [CrossRef]
- Shen, Z.; Wan, D.; Carrica, P.M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering. Ocean Eng. 2015, 108, 287–306. [Google Scholar] [CrossRef]
- Li, Y.; Paik, K.J.; Xing, T.; Carrica, P.M. Dynamic overset CFD simulations of wind turbine aerodynamics. Renewable Energy 2012, 37, 285–298. [Google Scholar] [CrossRef]
- Carrica, P.M.; Wilson, R.V.; Noack, R.W.; Stern, F. Ship motions using single-phase level set with dynamic overset grids. Comput. Fluids 2007, 36, 1415–1433. [Google Scholar] [CrossRef]
- Hsiao, C.T.; Chahine, G. Prediction of tip vortex cavitation inception using coupled spherical and nonspherical bubble models and Navier–Stokes computations. J. Mar. Sci. Technol. 2004, 8, 99–108. [Google Scholar] [CrossRef]
- Graham, R.L. An efficient algorithm for determining the convex hull of a finite planar set. Inf. Process. Lett. 1972, 1, 132–133. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in FORTRAN, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; Chapter 3; pp. 116–117. [Google Scholar]
- Paik, B.G.; Park, I.R.; Kim, K.S.; Lee, K.C.; Kim, M.J.; Kim, K.Y. Design of a bubble collecting section in a high speed water tunnel for ventilated supercavitation experiments. J. Mech. Sci. Technol. 2017, 31, 4227–4235. [Google Scholar] [CrossRef]
- Lee, S.J.; Paik, B.G.; Kim, K.Y.; Jung, Y.R.; Kim, M.J.; Arndt, R.E.A. On axial deformation of ventilated supercavities in closed-wall tunnel experiments. Exp. Therm. Fluid Sci. 2018, 96, 321–328. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Webb, J.C. Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys. 1993, 107, 262–281. [Google Scholar] [CrossRef]
- Cheong, C.; Lee, S. The effects of discontinuous boundary conditions on the directivity of sound from a piston. J. Sound Vib. 2001, 239, 423–443. [Google Scholar] [CrossRef]
- Cheong, C.; Lee, S. Grid-optimized dispersion-relation-preserving schemes on general geometries for computational aeroacoustics. J. Com. Phys. 2001, 174, 248–276. [Google Scholar] [CrossRef]
- Kim, D.; Cheong, C. Time- and frequency-domain computations of broadband noise due to interaction between incident turbulence and rectilinear cascade of fat plates. J. Sound Vib. 2012, 331, 4729–4753. [Google Scholar] [CrossRef]
- Kim, D.; Heo, S.; Cheong, C. Time-domain inflow boundary condition for turbulence-airfoil interaction noise prediction using synthetic turbulence modeling. J. Sound Vib. 2015, 340, 138–151. [Google Scholar] [CrossRef]
- Kim, D.; Lee, G.-S.; Cheong, C. Inflow broadband noise from an isolated symmetric airfoil interacting with incident turbulence. J. Fluids Struct. 2015, 55, 428–450. [Google Scholar] [CrossRef]
- Kim, S.; Cheong, C.; Park, J.; Kim, H.; Lee, H. Investigation of flow and acoustic performances of suction mufflers in hermetic reciprocating compressor. Int. J. Refrig. 2016, 69, 74–84. [Google Scholar] [CrossRef]






| u, v | Velocity | Y | Mass fraction | τ | Viscous stress |
| p | Static pressure | ht | Total enthalpy | Mass transfer rate | |
| t | Physical time | ρ | Density | q | Heat flux |
| U, V | Contravariant Velocity | g | Acceleration of Gravity | ca | 1: Axisymmetric flow 0: Planar flow |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, M.; Cheong, C.; Seol, H.; Paik, B.-G.; Kim, M.-J.; Jung, Y.-R. Development of Efficient and Accurate Parallel Computation Algorithm Using Moving Overset Grids on Background Multi-Domains for Complex Two-Phase Flows. Appl. Sci. 2018, 8, 1937. https://doi.org/10.3390/app8101937
Ha M, Cheong C, Seol H, Paik B-G, Kim M-J, Jung Y-R. Development of Efficient and Accurate Parallel Computation Algorithm Using Moving Overset Grids on Background Multi-Domains for Complex Two-Phase Flows. Applied Sciences. 2018; 8(10):1937. https://doi.org/10.3390/app8101937
Chicago/Turabian StyleHa, Minho, Cheolung Cheong, Hanshin Seol, Bu-Geun Paik, Min-Jae Kim, and Young-Rae Jung. 2018. "Development of Efficient and Accurate Parallel Computation Algorithm Using Moving Overset Grids on Background Multi-Domains for Complex Two-Phase Flows" Applied Sciences 8, no. 10: 1937. https://doi.org/10.3390/app8101937
APA StyleHa, M., Cheong, C., Seol, H., Paik, B.-G., Kim, M.-J., & Jung, Y.-R. (2018). Development of Efficient and Accurate Parallel Computation Algorithm Using Moving Overset Grids on Background Multi-Domains for Complex Two-Phase Flows. Applied Sciences, 8(10), 1937. https://doi.org/10.3390/app8101937






