Abstract
Various electronic devices are increasingly being connected to the Internet. Meanwhile, security problems, such as fake silicon chips, still exist. The significance of verifying the authenticity of these devices has led to the proposal of side-channel authentication. Side-channel authentication is a promising technique for enriching digital authentication schemes. Motivated by the fact that each cryptographic device leaks side-channel information depending on its used secret keys, cryptographic devices with different keys can be distinguished by analyzing the side-channel information leaked during their calculation. Based on the original side-channel authentication scheme, this paper adapts an ID-based authentication scheme that can significantly increase the authentication speed compared to conventional schemes. A comprehensive study is also conducted on the proposed ID-based side-channel authentication scheme. The performance of the proposed authentication scheme is evaluated in terms of speed and accuracy based on an FPGA-based AES implementation. With the proposed scheme, our experimental setup can verify the authenticity of a prover among different provers within s; this could not be handled effectively using previous schemes.
1. Introduction
Nowadays, wearable embedded technology is being increasingly used under the rapid development of electronic devices. The users and the embedded computing systems are connected to the Internet and exposed to various security threats, such as fake silicon chips. As a fundamental method against these security threats, the authenticity of these electronic devices has to be verified carefully. As a typical authentication scenario, we focus on the case where the identity of the prover is verified based on shared secret information between the prover and the verifier.
In [1], side-channel authentication was proposed as a new authentication scheme. Side-channel leakage, e.g., power consumption and electromagnetic (EM) radiation, is the unintentional information leakage that generally exists along the device’s computation. Side-channel leakage has received much attention since it can be used to perform key-recovery attacks against cryptographic implementations [2,3]. In side-channel authentication, side-channel information is constructively used as a communication channel through which certain characteristics of the performed calculation can be observed. Cryptographic hardware with a unique secret key leaks unique key-dependent side-channel information under a given challenge. The idea of side-channel authentication is to measure and analyze this side-channel information to verify whether the used secret key is the pre-shared one.
Side-channel authentication has several positive features that make it valuable to be further researched. First, the measurement of side-channel information usually requires another measurement setup which is different from the main communication. Thus, the executions of relay attacks and reply attacks are expected to become difficult. Second, side-channel information such as time, power consumption, and electromagnetic radiation generally exists during the cryptographic calculation. This side-channel information contains information about the processed data including the key-related information; this can be measured and used in the authentication. As the minimal requirement for side-channel authentication, each prover device runs a computation module that uses a pre-share key with the verifier which has measurable side-channel information during the calculation. Thus, the modification of existing prover devices could be minimal for side-channel authentication. For devices that do not have a general communication capability, side-channel authentication could still be applied by using pre-defined challenges. For example, side-channel authentication could be used for a Machine-to-Machine (M2M) authentication scenario in which the resource-restricted prover device has symmetric-key cryptographic primitives implemented. Specifically, the smart cards used in public transportation systems and the keyless entry system of vehicles could be considered to use side-channel authentication.
As the first proposed side-channel authentication scheme from [1], the 128-bit Advanced Encryption Standard (AES-128) is a cryptographic module. In order to simplify the system, a modified AES that has increased rounds is used in side-channel authentication so that a single trace of the side-channel measurement is enough for authentication. In [1], several protocols for side-channel authentication were proposed as well. According to the originally proposed side-channel authentication system in [1], the prover can be identified only with side-channel information, i.e., by deriving correlation coefficients for all of the registered devices to identify the legitimate prover. Therefore, authentication is time-consuming. The authors of [4] provided a quantitative discussion about side-channel information according to the number of distinguishable provers. However, the aspects related to the accuracy of authentication, such as the false acceptance rate and the false rejection rate, have not been discussed.
As the contribution of this paper, we propose an identification-based (ID-based) authentication scheme and perform a comprehensive evaluation with regard to the authentication speed, the authentication accuracy, and the used leakage models. The detailed contributions of this paper are summarized as follows.
- This paper proposes the ID-based authentication scheme to mitigate the speed problem of the side-channel authentication scheme proposed in [1]. To demonstrate the advantage of the ID system for acceleration, the authentication speed and authentication accuracy are evaluated for the ID-based authentication system. We overview the technical choices for side-channel authentication schemes and compare their effectiveness based on both theoretical analysis and experiments based on field-programmable gate array (FPGA).
- This paper evaluates the error-rate of ID-based side channel authentication in a laboratory environment. The authentication accuracy is quantitatively estimated as the false acceptance rate and the false rejection rate. First, a quantitative discussion of the side-channel information is performed according to the number of distinguishable provers. The side-channel information of the provers is experimentally obtained from AES implementations on FPGA. The histograms for rejection and acceptance trials are both approximated to a normal distribution. Based on the principle that the false rejection rate and false acceptance rate are set to be equal, the parameters in the authentication can be determined. As a result, the authentication accuracy can be determined. This part of the contribution has been partially discussed by us in [4].
- In our evaluation, both a non-profiling leakage model and a profiling leakage model are considered for different scenarios. Similar to side-channel attacks, the leakage model describes the relations between the side-channel leakage and the processed data. Generally speaking, one can expect side-channel attacks to have a reduced data complexity with a more accurate leakage model. Specifically, we use a Hamming distance (HD) model as the non-profiling leakage model and the XOR (exclusive-or) model proposed in [5] as the representative of the profiling leakage model. It is expected that the profiling model will improve the authentication accuracy of the system. The experiments show that the XOR model leads to a larger mean and smaller variance for the histogram of the correlation coefficients compared to that of the HD model. The authentication accuracy and the authentication time are compared between the HD model and the XOR model.
The rest of the paper is organized as follows. Section 2 reviews the previously proposed scheme for side-channel authentication. Section 3 presents the idea of an ID-based authentication system for side-channel authentication. Section 4 explains the setup for the evaluation of ID-based side-channel authentication. In Section 5 and Section 6, the evaluation of the ID-based side-channel authentication system with regard to the authentication speed and the authentication accuracy is presented. Section 7 concludes this paper.
2. Preliminaries
In this section, the first side-channel authentication proposal in [1] is briefly reviewed.
2.1. n-Round AES
AES-128 has 10 rounds of operation, which usually takes 10 clock cycles to calculate in hardware implementation. Using AES-128 in side-channel authentication requires multiple traces to ensure authentication accuracy. Each execution requires a fresh plaintext. Furthermore, only the middle round of each trace is used in the authentication to prevent the security threat from conventional side-channel key recovery attacks.
An easy alternative option is to use a modified AES that has more than 10 round operations, which is called a n-round AES. Here, n should be larger than 10 and big enough, e.g., , so that a single side-channel trace is enough to perform the authentication. A n-round AES could simplify the system and the modification of the AES hardware could be minimized as well. To prevent security threats from conventional side-channel key recovery attacks, several rounds, e.g., 4 rounds, near the public data are not used in the r-round AES authentication.
An illustration of 10-round AES and n-round AES is shown in Figure 1.
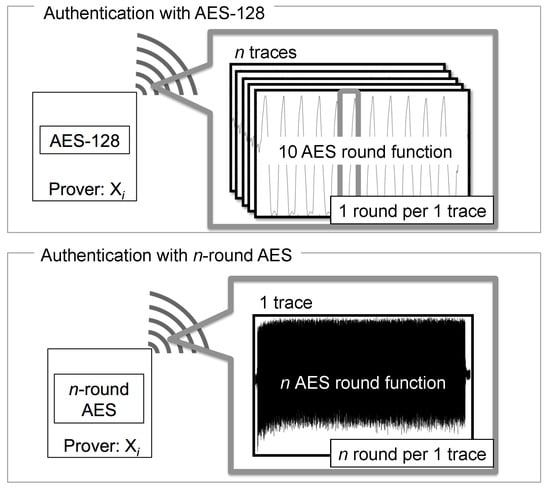
Figure 1.
Two types of side-channel data with Advanced Encryption Standard (AES).
2.2. Protocol in Side-Channel Authentication
The possible protocols for side-channel authentication were discussed in [1]. In this paper, we only discuss the Challenge-S-Response authentication and the Challenge-S authentication, as shown in Figure 2a,b. Here, challenge c and response r are the same with conventional authentication schemes, and S denotes the side-channel information.
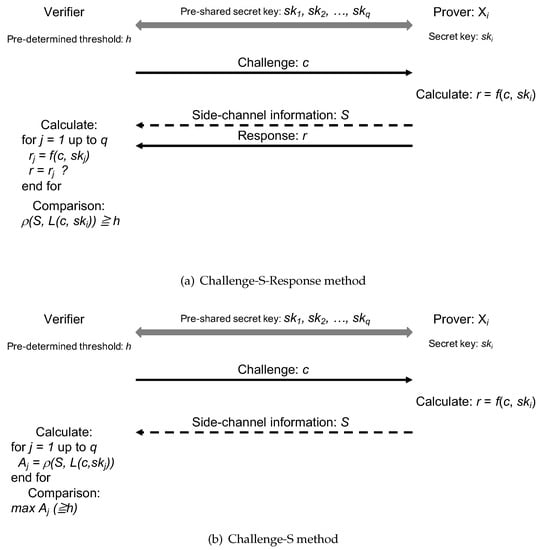
Figure 2.
Two types of authentication methods proposed in [1]. (a) Challenge-S-Response method; (b) Challenge-S method.
For both schemes, prover registers its secret key in the verifier before the authentication. The authentication starts when the verifier sends a challenge c to a prover . Prover calculates using its secret key , where is a cryptographic calculation. The verifier measures the side-channel information S during the encryption process.
The major difference between these two schemes is whether the response r is sent back from the prover to the verifier to be used in the verification.
For Challenge-S-Response authentication, the response r is sent to the verifier. The identification of the prover is performed using both side-channel information S and the conventional challenge-response verification. First, the verifier searches the secret key to find the such that . Then, the found is used with c and a leakage model to estimate the side-channel information as . After that, Pearson’s correlation coefficient between the measurement of real side-channel information S and the estimation is calculated and compared with a pre-determined threshold h. The authentication is passed only when both the response and the side-channel information match the expectation. This scheme is similar to conventional challenge-response authentication.
For Challenge-S authentication, only the side-channel information S is used in the authentication. The response of the encryption process is not returned to the verifier. The verifier is required to calculate the expected leakage for all registered keys as . Then, for each registered key, a correlation calculation is conducted. The key with the largest correlation among all possible keys is compared with a pre-determined threshold h. Only when the maximal correlation is larger than the threshold, is the prover considered to be a legitimate prover. The comparison with the threshold is done to prevent a situation where the invalid keys can pass the authentication.
For Challenge-S authentication, the response r is not transmitted in the communication channel. The benefits of omitting r transmission are two-fold. First, the response r is not available for the attacker for any key recovery attack. Second, the communication for the authentication in the main channel can be reduced. Furthermore, the communication can be omitted entirely if the challenge c is predefined between the prover device and the verifier.
For the Challenge-S authentication scheme in conventional side-channel authentication [1], the correlation coefficients are calculated for all the pre-registered keys. Thus, it is expected to be time consuming when the number of registered provers is large. In this paper, we want to accelerate the Challenge-S authentication scheme of the side-channel authentication.
3. ID-Based Side-Channel Authentication System
To accelerate the authentication, we adapt a well-known ID system to the Challenge-S authentication. The idea is to reduce the amount of computation by sending an ID to the verifier before challenge-response authentication. The ID helps the verifier to quickly identify the corresponding registered key.
3.1. ID-Based Side-Channel Authentication Scheme
As shown in Figure 3, the pairs of ID and secret key of q provers, (ID, ), (ID, ), …, (ID, ) are registered in the verifier. The verifier initiates the authentication by sending an ID query to the prover, and then the verifier receives the prover’s ID as ID. The verifier searches for the corresponding secret key and creates the corresponding leakage profile for the n-round AES. Then, Pearson’s correlation coefficient is calculated between the measured estimated side-channel information. Finally, the verifier confirms whether the correlation coefficient is larger than the pre-determined threshold h to decide the authentication result. If the derived is larger than the pre-determined threshold h, the authentication is successful.
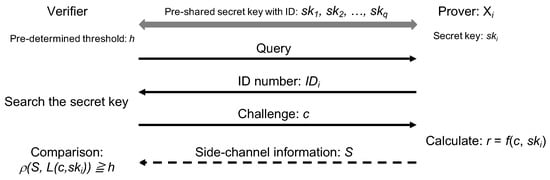
Figure 3.
Proposed Authentication Method Using ID Query.
Figure 4 shows the frameworks of the conventional and the ID-based side-channel authentication systems. The major difference between the two authentication schemes is the number of correlation coefficient calculations. In previous work [1], the leakage profile and the correlation were calculated for all registered secret keys. Meanwhile, the calculation of the model and correlation coefficient is performed only once in the proposed authentication scheme as the secret key is identified using the ID sent from prover. Therefore, it is possible to authenticate much faster compared to the conventional scheme.
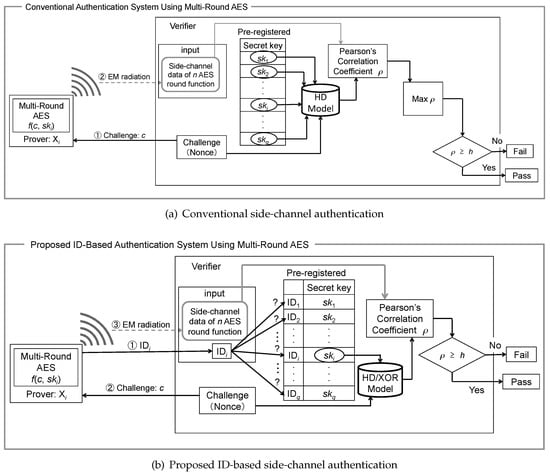
Figure 4.
Comparison of frameworks of the conventional (a) and proposed (b) ID-based side-channel authentication.
3.1.1. Comparison of Expected Authentication Speed
Table 1 shows the comparison of the expected authentication speed between a straightforward Challenge-S approach using normal AES and the ID-based Challenge-S using n-round AES. By denoting the clock period as , the acquisition time of the side-channel information for each method is and , respectively. Denote the data processing time of each AES round to obtain the intermediate values as ; then, the total data processing time can be calculated. For the straightforward Challenge-S approach, the data processing time can be represented by since only 5 rounds of intermediate values are calculated. For the ID-based n-round Challenge-S approach, the data processing time is . The total time for authentication consists of the acquisition time and the data processing time. It can be seen that ID-based n-round approach is much more efficient.

Table 1.
Comparison between two side-channel authentication schemes.
3.1.2. Resistance against Side-Channel Attacks
One big concern for side-channel authentication is that the shared secret key can be extracted by the attackers using the side-channel leakage. To mitigate the risk of such attacks, the system can apply the following changes. First, the side-channel information near the public data should be protected by side-channel countermeasures such as masking. Second, only the side-channel information that is far from the public data is used in the authentication. For normal AES, we only use the middle round in the authentication. Similarly, for n-round AES, several rounds near the public data are not used in the authentication.
3.1.3. Trade-Off for the ID-Based System
As for the trade-off, in conventional side-channel authentication, the verifier is pre-registered only with the secret keys. In ID-based authentication, the secret key and ID number pairs are pre-shared between the verifier and the prover. In this system, we consider a case where the ID does not contain any secret information related to the secret key. The ID works as a tag to help the verifier quickly identify the claimed secret key of the verifier. A privacy problem could also exist for the ID-based authentication system since the ID information is transmitted in air. It is possible to trace the holder of a device by tracing the ID of the device. A possible mitigation of this problem is to introduce a periodical update of the ID.
Regarding the secret of the ID and secret key, it is assumed that the registration of the ID/secret key is performed in a secure environment. As for other possible leakages of the ID and secret key, if only the ID is intercepted by a non-legitimate source, the attacker can pretend to be a certain device by using the leaked ID. However, since the secret key is unknown to the attacker, the fake device cannot pass the authentication. In the case that both the ID and secret key are intercepted and used by an attacker, the attackers can pass the authentication without any problem. As long as the verifier realizes this situation, a possible mitigation is to register the legitimate users again with new keys.
4. Evaluation Setup of ID-Based Authentication
In this work, we performed experimental evaluations of ID-based authentication using a hardware AES implemented on FPGA. This section mainly focuses on the experiment setup and leakage models used in the evaluation.
4.1. Experimental Setup on n-Round AES
In the experiment, we used ALTERA CycloneIV (FPGA) on Terasic DE0-nano (FPGA board) [6] as the prover device. A 1000-round AES modified from the 128-bit AES [7] was used as the calculation to generate side-channel information. The AES implementation uses a 128-bit data path and the composite-field S-box, which runs at 50 MHz on the DE0-nano board. The side-channel information was measured as the electro-magnetic radiation near the FPGA by the EM probe (Langer-EMV RF-U 5-2). The signal captured by the probe was recorded using an oscilloscope (Agilent Technology DSO7032A), which recorded at 1 GSa/s. Each measurement included about 21,000 samples. A photo of the experimental setup is shown in Figure 5. Note that, the measurement of side-channel information can be performed without modifying the hardware, but the probe still needs to be close to the FPGA to ensure the quality of measurements is sufficient [8,9].

Figure 5.
Experimental Environment for Side-Channel Authentication.
On the verifier side, we used a normal PC to process the data. The correlation calculation was performed with both non-profile leakage models and leakage profiles.
4.2. Leakage Model in Authentication
In this work, for both the profiling model and the general leakage model, the side-channel authentication performance was evaluated. For side-channel attacks, the leakage model describes the relations between the side-channel leakage and the processed data. An accurate leakage model could lead to better attack efficiency by side-channel attacks. Similarly, an accurate leakage model could lead to better side-channel authentication authentication efficiency. Generally speaking, a general leakage model has wide applicability but less accuracy. In contrast, a device-specific leakage model or leakage profile has better accuracy but less generality. It is well-known that side-channel attacks can be categorized into two types: non-profiling attacks and profiling attacks. In profiling attacks, the attackers have an identical device that is used to learn the leakage profile of the device so that the data complexity of the key recovery attack is reduced compared with the non-profiling attack that uses a general leakage model. Other side-channel attack techniques can be applied to side-channel authentication as well. The usage of Pearson’s correlation coefficient as the distinguisher is one such example.
4.2.1. Non-Profiled Model: HD Model
As for the non-profile model, we used the well-known Hamming distance model. Since the key is known to the verifier, the Hamming distance of the 128-bit intermediate value rather than a single byte was used. For the Hamming distance model proposed in [2], side-channel information, denoted by W, is modeled as
where is the Hamming distance between D and E, which are intermediate values for an AES round, and k and b are constants. For the HD model, the intermediate values are the ones stored in registers, i.e., D is stored in a register and is replaced with E after a round operation. The HD model assumes that there is a linear dependency between the side-channel leakage W and the Hamming distance value .
In [1], it was shown that the 128-bit intermediate values can be used in the HD model because AES-comp implementation [7] performs each AES round in 1 cycle. In this work, we also considered the authentication using n-round AES, which is modified from the AES-comp implementation. The i-th round leakage model and measured side-channel information are denoted as , and , respectively. Here, N is the number of total plaintexts. The correlation coefficients are derived by and classified into acceptance trials and rejection trials. In the acceptance trial, it is assumed that the prover who registered the pre-shared secret key in the verifier is authenticated, i.e., legitimate prover authentication. On the other hand, if it is authenticated using the unregistered secret key, it is considered to be the rejection trial.
4.2.2. Profiling Model: XOR Model
As a profiling model, we used the XOR model that was proposed in [5]. In [5], the advantage of the XOR model in correctly profiling the leakage of AES-comp implementation was shown. The XOR model leads to successful key recovery with reduced power traces compared to the HD model. In the HD model, it is assumed that the amount of bit-flipped information, i.e., the Hamming distance, is proportional to the physical information, e.g., the power consumption and the amount of EM radiation. Since the Hamming distance does not distinguish between bits, the HD model for the 8-bit intermediate value classifies the leakage into nine classes from 0 to 8. Meanwhile, in the XOR model, it is assumed that the bit reversed position affects the amount of side-channel leakage. Specifically, the XOR model classifies the side-channel leakage for 8-bit intermediate values into 256 classes ranging from 0 to 255.
The side-channel authentication is classified into a profiling phase and an authentication phase. In the profiling phase, the properties of each device are investigated in pre-processing. Specifically, the amount of EM radiation for an XORed value that changes with each product, called a model value , is derived using the side-channel information whose intermediate value is known. When authenticating using the XOR model for 16-byte AES, the XOR model is classified into 256 × 16 classes. Therefore, the model value is expressed as
where is the amount of EM radiation when the XORed value of the t-th byte is r.
In the authentication phase, the correlation coefficient is calculated using the model value derived in the profiling phase. Based on the intermediate value derived from the challenge and a secret key, the amount of EM radiation is estimated using the model value . The process is exactly the same as that using HD model, except that the Hamming distance model is replaced with the profiling model . After that, the correlation coefficient is calculated between the acquired EM radiation and the estimated EM radiation. The leakage profiles for 256 classes for 16 s-boxes are obtained by solving the system of equations with the profiling measurement. Note that the authentication scheme using the XOR model was first discussed by us in [10].
5. Evaluation of the Authentication Speed
In this section, we describe the evaluation of the authentication speed using our experiment setup. Table 2 represents the difference in authentication time between the straightforward Challenge-S approach [1] and the ID-based n-round Challenge-S approach. As for the acquisition time, our setup takes 43 s to measure 1000 EM traces and s to measure a 1000-round EM trace. This shows that the n-round approach could largely reduce the data acquisition time.

Table 2.
The difference in authentication time in seconds.
As for the data processing time, both the n-round AES and the ID system have advantages. In the data processing of the straightforward Challenge-S approach, 5 AES rounds have to be calculated for each EM trace to estimate the side-channel information. Since there are, in total, 1000 traces, 5000 AES rounds must be calculated using 1000 different plaintexts. In contrast, the 1000-round AES calculates 1000 intermediate values in total. Moreover, the 5000 AES rounds of calculation need to be performed for each register key without the ID system. Using the ID system, only the claimed register key is compared with the observed side-channel information. As shown in Table 2, the data processing time is for the straightforward Challenge-S approach, while the ID-based n-round Challenge-S approach requires less than s. For both the HD model and the XOR model, the leakage profile is prepared before the processing the measurement. Therefore, both models will be able to authenticate in a short time period.
It is reasonable to expect the acceleration of authentication when the ID system is applied to side-channel authentication. With the performed experiments and the time measurements, the acceleration can be understood more clearly since both the decomposition of the consumed time and the contributions of each techniques are clear.
Note that, the time required for the pre-authentication processes is similar for both authentication schemes. The pre-authentication processes consist of the key registration part and the leakage profiling part. As for the key registration part, the ID-based side-channel authentication scheme is the same as the conventional scheme except that a device ID is additionally registered together with the secret key. For the leakage profiling part, only the scheme using the XOR model requires the leakage profiling, which has negligible time consumption, since the profile only needs to be performed once for each type of prover device.
6. Evaluation of Authentication Accuracy
In this section, the parameters and the performance of the side-channel authentication are discussed. First, we define several parameters that are related to the perforation evaluation. Then, we discuss how to obtain reasonable choices for these parameters. Then, based on our laboratory setup, we calculate the optimal parameters for both the non-profiling model and profiling model. Finally, we apply these parameters and evaluate the error rate for several variations.
6.1. Accuracy-Related Parameters
As for the authentication accuracy, we refer to the error rate as the false acceptation rate and false rejection rate. After the setup is fixed, we consider that there are two related system parameters: the number of the total provers M and the threshold h. We consider parameter M to be the maximum number of authentication trials that enables an authentication system to operate without producing false errors. M is the number of devices that can be used in the system. The error rate is likely to be increased along the increase in M.
6.2. Relationship Among M, n, and False Errors
Following the approach in [4], the relationship between M, n, and the false acceptance and false rejection errors and can be visualized when changing h, as shown in Figure 6. The threshold h was set in the range from to 1.
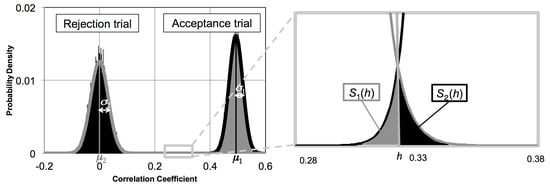
Figure 6.
Conceptual diagram of the normal distribution derived from the correlation coefficients.
There are two major differences between the work of [4] and the proposed scheme. One is that the parameter M is regarded as the number of authentication trials in this paper, although it was previously taken to mean the number of provers in [4] by assuming that each prover was only accessed once. That is, M corresponded to the number of distinguishable provers. In contrast, in this study, it is assumed that M fake provers access the authentication system as well as M legitimate provers. In total, trials are assumed when estimating the false errors, whereas trials were used in [4]. This assumption affects the variance parameter and the mean values of approximated normal distributions because the number of samples is different. The other difference relates to the parameter n, which is defined as the number of rounds of 128-bit AES in this paper, whereas it was defined as the number of traces of 128-bit AES encryption in [4].
To derive the histogram of acceptance and rejection trials, Fisher z-transformation was applied to achieve approximation. After that, we verified the validity with the Jarque–Bera test. Since the histogram can approximate a normal distribution, it was found that the correlation coefficients dependent on secret keys and plaintext were not derived. Then, the histograms of the acceptance and rejection trials were approximated to follow normal distributions (see Figure 6), respectively, as and where the variances and are described with n as
where and are constants that are experimentally determined with the correlation coefficients between the observed n-round side-channel information and the leakage model. Therefore, with the threshold, defined as h, the probability of a false rejection ratio and false acceptance ratio are represented by
As the total number of false errors should be equal to or less than one for trials, we have
Therefore, the total number of trials M can be derived from
By increasing the number of rounds, the system is capable of distinguishing many provers.
6.3. Formulation of n under Equal Error Rate
In our method, h is determined such that the probabilities of false acceptance and false rejection rates occurring are equal, i.e., the error rate was required to be equal. Thus, the equal error rate adopted in our authentication system assumes that false acceptance and false rejection occur with the same probability. Therefore, in the case of , the threshold h is expressed as
Hence, the maximum number of total trials is expressed as
where the constant is
Accordingly, the number of AES round function calls is represented using M as
6.4. Parameters with Different Settings
We derived the relationship between n and M using two datasets corresponding to two authentication schemes discussed throughout this work.
- Dataset A: n EM traces of AES-128
- Dataset B: one trace for n-rounds of AES
Table 3 summarizes the parameters that were experimentally obtained, which are necessary for approximating a normal distribution.

Table 3.
Experimentally obtained parameters: mean values and and constants of proportionality and ; , and h.
6.5. Experimental Results
Figure 7a shows the relationship between the number of EM traces and the number of distinguishable provers when the previous authentication scheme was used with Dataset A. In the case of , i.e., using 1171 EM traces, , which indicates that provers were distinguishable from the previous authentication scheme. Contrary to the above result, the results obtained with the proposed scheme using Dataset B show that when , i.e., 908-round AES, was obtained (see Figure 7b) which means that false errors do not occur even if 10 million provers are authenticated twice a day for 100 years. Furthermore, it should be noted that the authentication time was 0.58 s. In addition, Figure 7c shows that was obtained with 759-rounds of AES. The summaries of these figures are listed in Table 4.
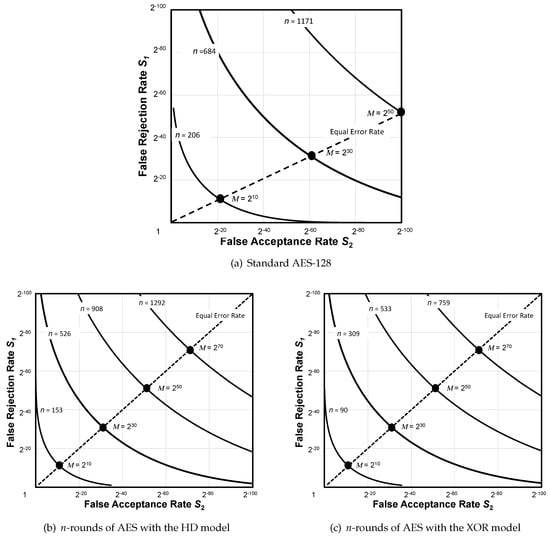
Figure 7.
Relationship between the number of rounds and the number of distinguishable provers for Datasets A and B.

7. Conclusions
In this work, an ID-based authentication scheme was adopted for side-channel authentication. In addition, the performance of the side-channel authentication was evaluated in terms of the authentication speed and authentication accuracy. In the performance evaluation, this work overviewed several technical choices for side-channel authentication to compare them. Based on both theoretical analysis and FPGA-based experiments, it is clear the ID-based scheme can accelerate the authentication speed, and the profiling model leads to better data complexity. The results showed that our experimental setup is a possible way to check the authenticity of a prover among different provers within s using 759 AES round function calls, which demonstrates the feasibility for side-channel authentication to be used as a future practice. In order to apply the side-channel authentication in a specific scenario, further optimization and field tests are considered as future works.
Author Contributions
Conceptualization, M.K. and K.S.; Investigation, M.K.; Supervision, K.S.; Writing–original draft, M.K.; Writing–review & editing, Y.L.
Funding
This research was funded by Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) grant number 15K12035.
Acknowledgments
We are grateful to the editor and the anonymous reviewers for various constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sakiyama, K.; Kasuya, M.; Machida, T.; Matsubara, A.; Kuai, Y.; Hayashi, Y.I.; Mizuki, T.; Miura, N.; Nagata, M. Physical Authentication Using Side-Channel Information. In Proceedings of the 2016 4th International Conference on Information and Communication Technology (ICoICT), Bandung, Indonesia, 25–27 May 2016. [Google Scholar]
- Brier, E.; Clavier, C.; Olivier, F. Correlation Power Analysis with a Leakage Model. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2004, Cambridge, MA, USA, 11–13 August 2004; pp. 16–29. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential Power Analysis. In Proceedings of the Advances in Cryptology—CRYPTO’ 99, 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; pp. 388–397. [Google Scholar]
- Kasuya, M.; Machida, T.; Sakiyama, K. New Metric for Side-Channel Information Leakage: Case Study on EM Radiation from AES Hardware. In Proceedings of the 2016 URSI Asia-Pacific Radio Science Conference (URSI AP-RASC), Seoul, South Korea, 21–25 August 2016. [Google Scholar]
- Clavier, C.; Danger, J.L.; Duc, G.; Elaabid, M.A.; Gérard, B.; Guilley, S.; Heuser, A.; Kasper, M.; Li, Y.; Lomné, V.; et al. Practical improvements of side-channel attacks on AES: Feedback from the 2nd DPA contest. J. Cryptogr. Eng. 2014, 4, 259–274. [Google Scholar] [CrossRef]
- Terasic Inc. DE0-Nano Development and Education Board. Available online: http://www.terasic.com.tw/en (accessed on 29 March 2018).
- Tohoku University. Cryptographic Hardware Project. Available online: http://www.aoki.ecei.tohoku.ac.jp/crypto/ (accessed on 29 March 2018).
- Gandolfi, K.; Mourtel, C.; Olivier, F. Electromagnetic Analysis: Concrete Results. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2001, Paris, France, 14–16 May 2001; pp. 251–261. [Google Scholar]
- De Mulder, E.; Örs, S.B.; Preneel, B.; Verbauwhede, I. Differential Power and Electromagnetic Attacks on a FPGA Implementation of Elliptic Curve Cryptosystems. Comput. Electr. Eng. 2007, 33, 367–382. [Google Scholar] [CrossRef]
- Kasuya, M.; Sakiyama, K. Improved EM Side-Channel Authentication Using Profile-Based XOR Model. In Proceedings of the International Workshop on Information Security Applications (WISA 2017), Jeju Island, Korea, 24–26 August 2017. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).