Elucidating the Energetics and Effects of Solvents on Cellulose Hydrolysis Using a Polymeric Acid Catalyst
Abstract
Featured Application
Abstract
1. Introduction
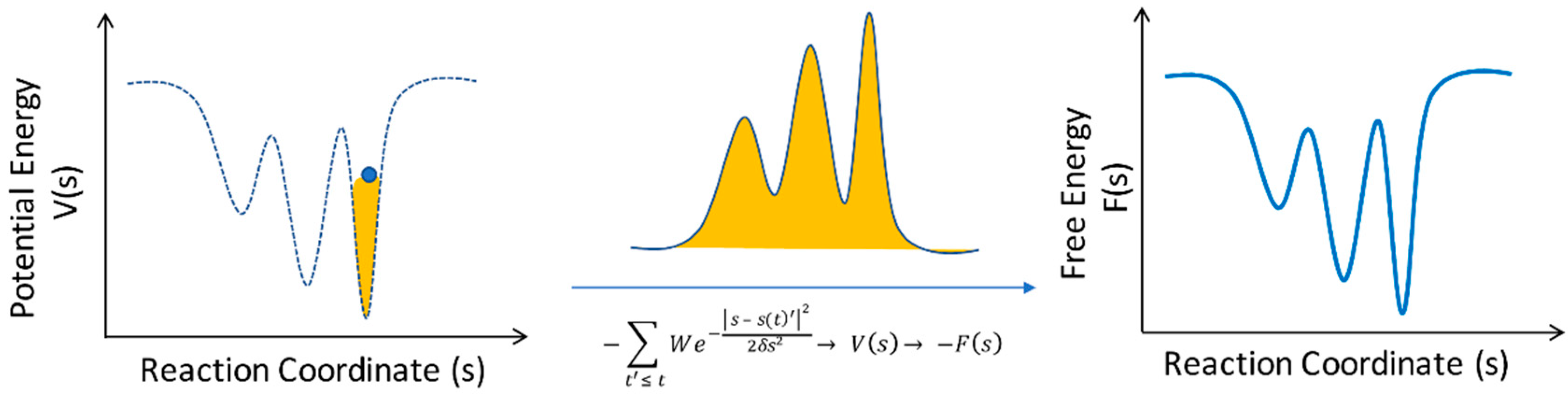
2. Computational Methods
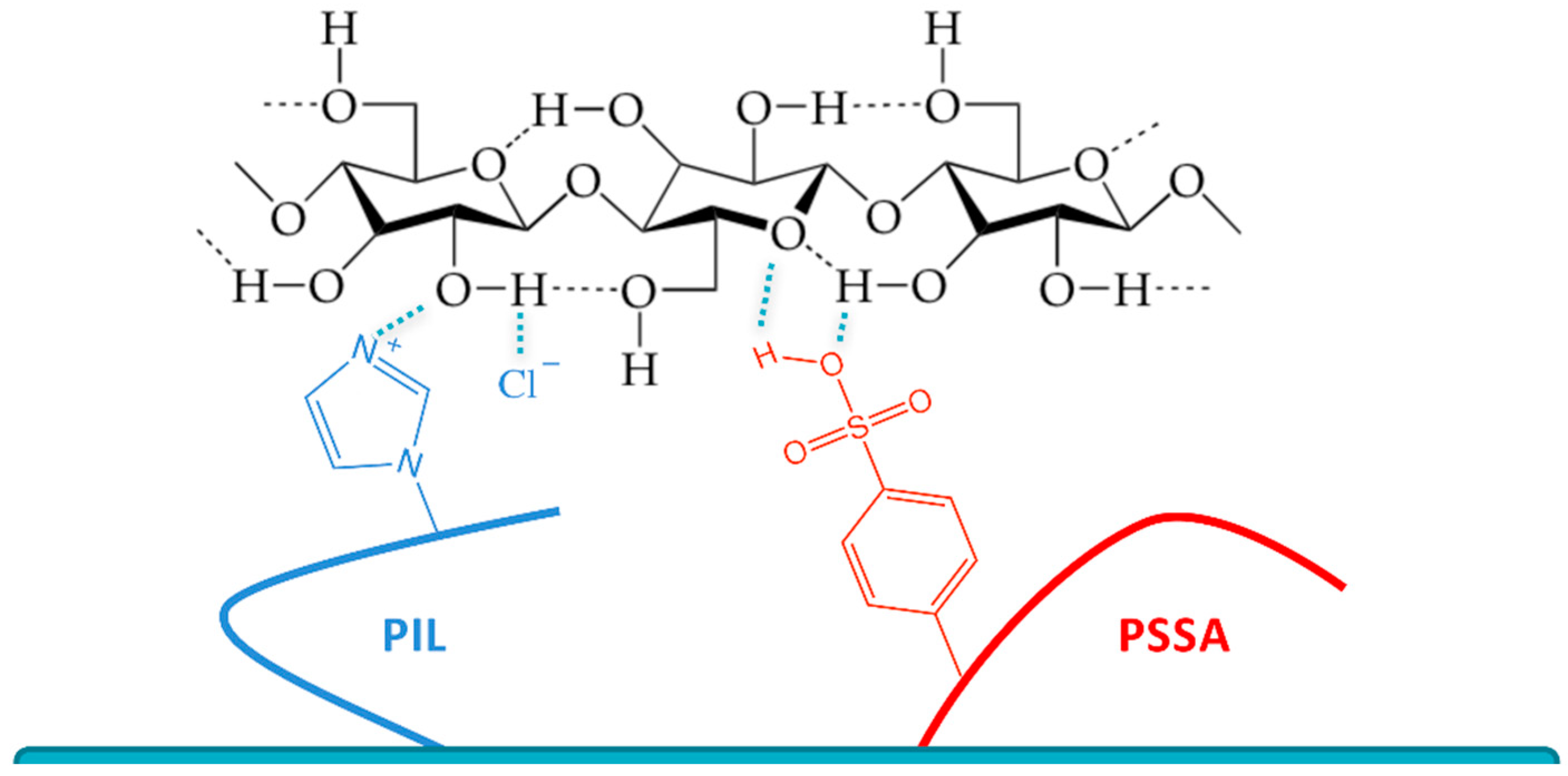
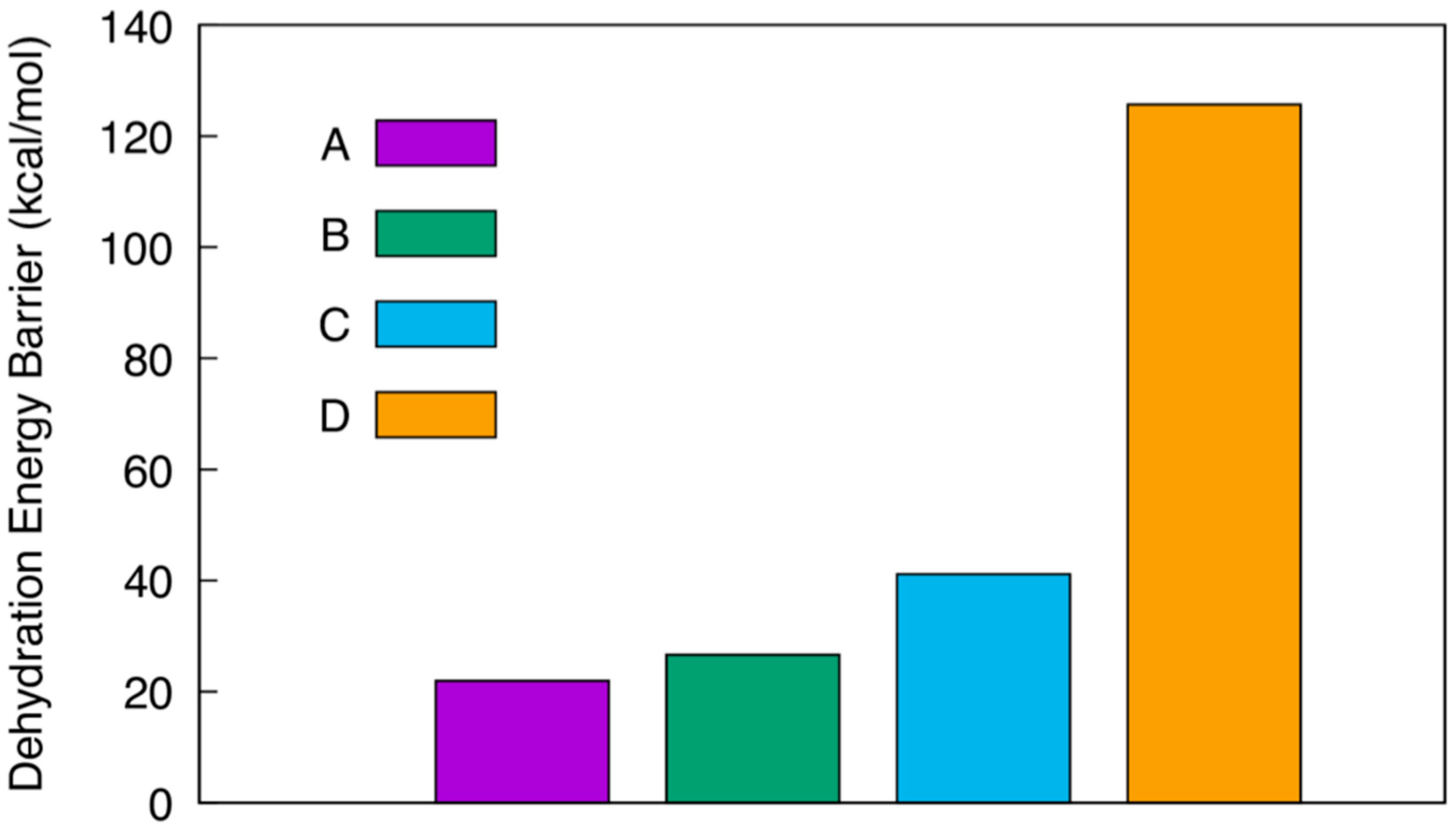
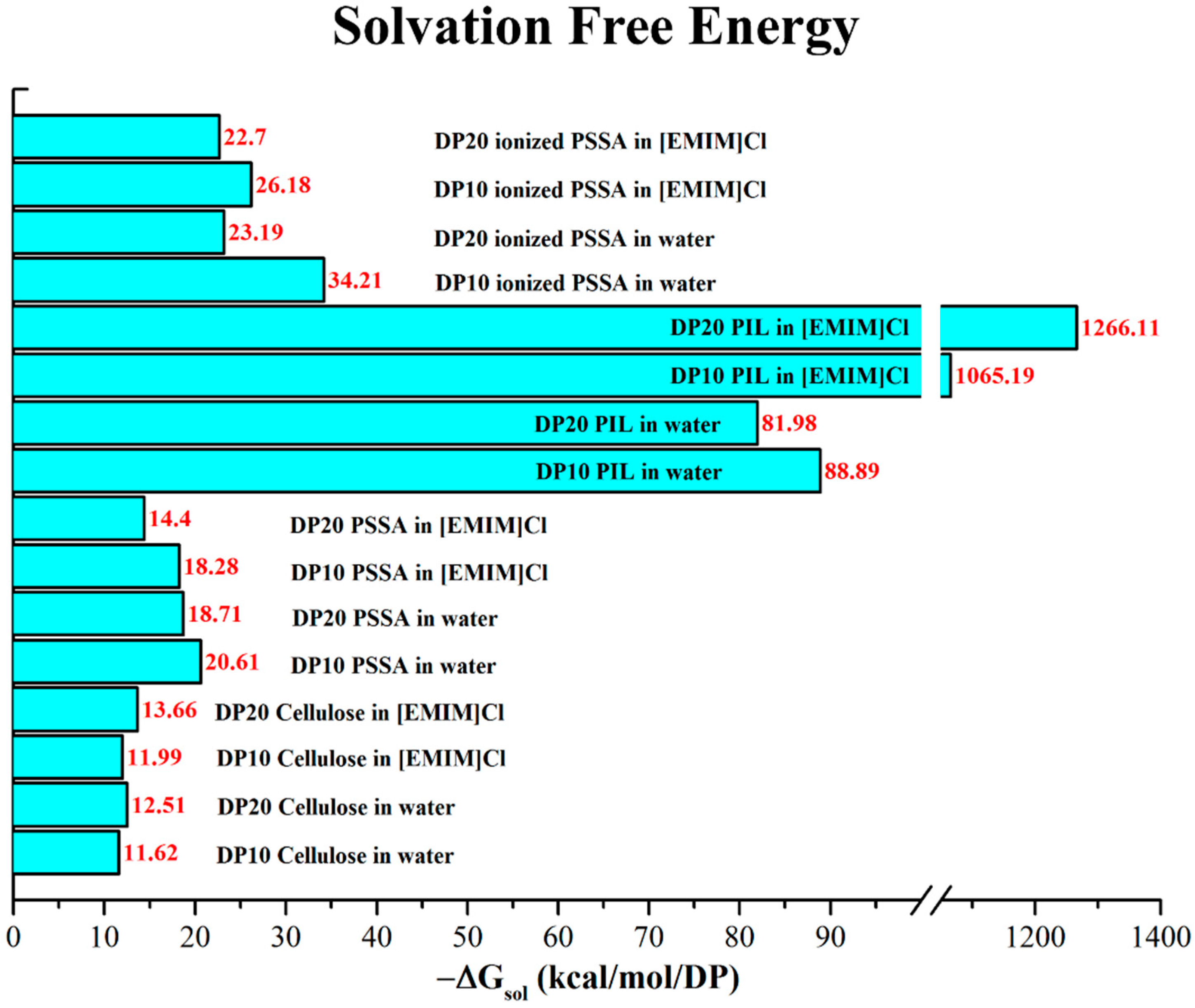
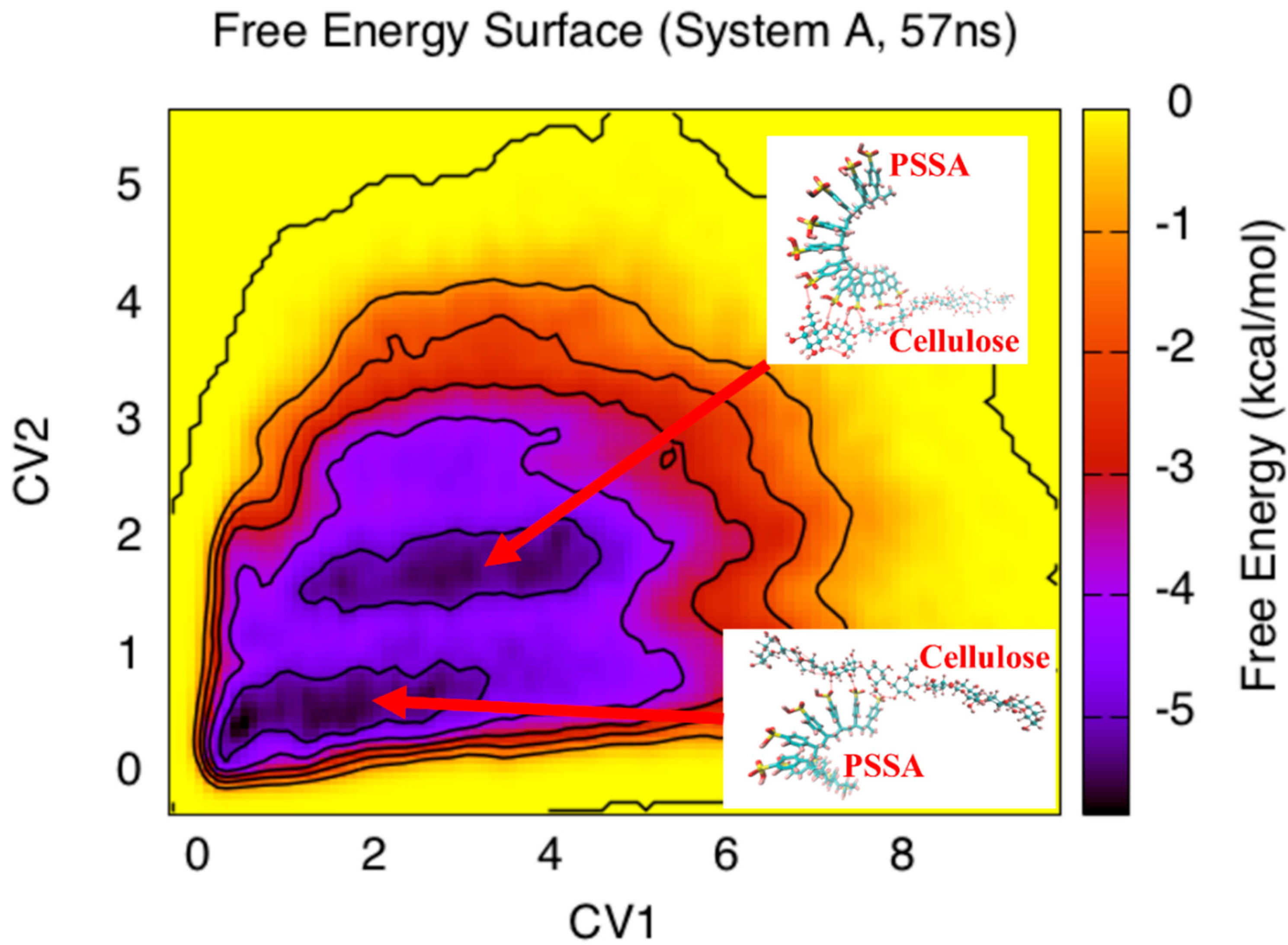
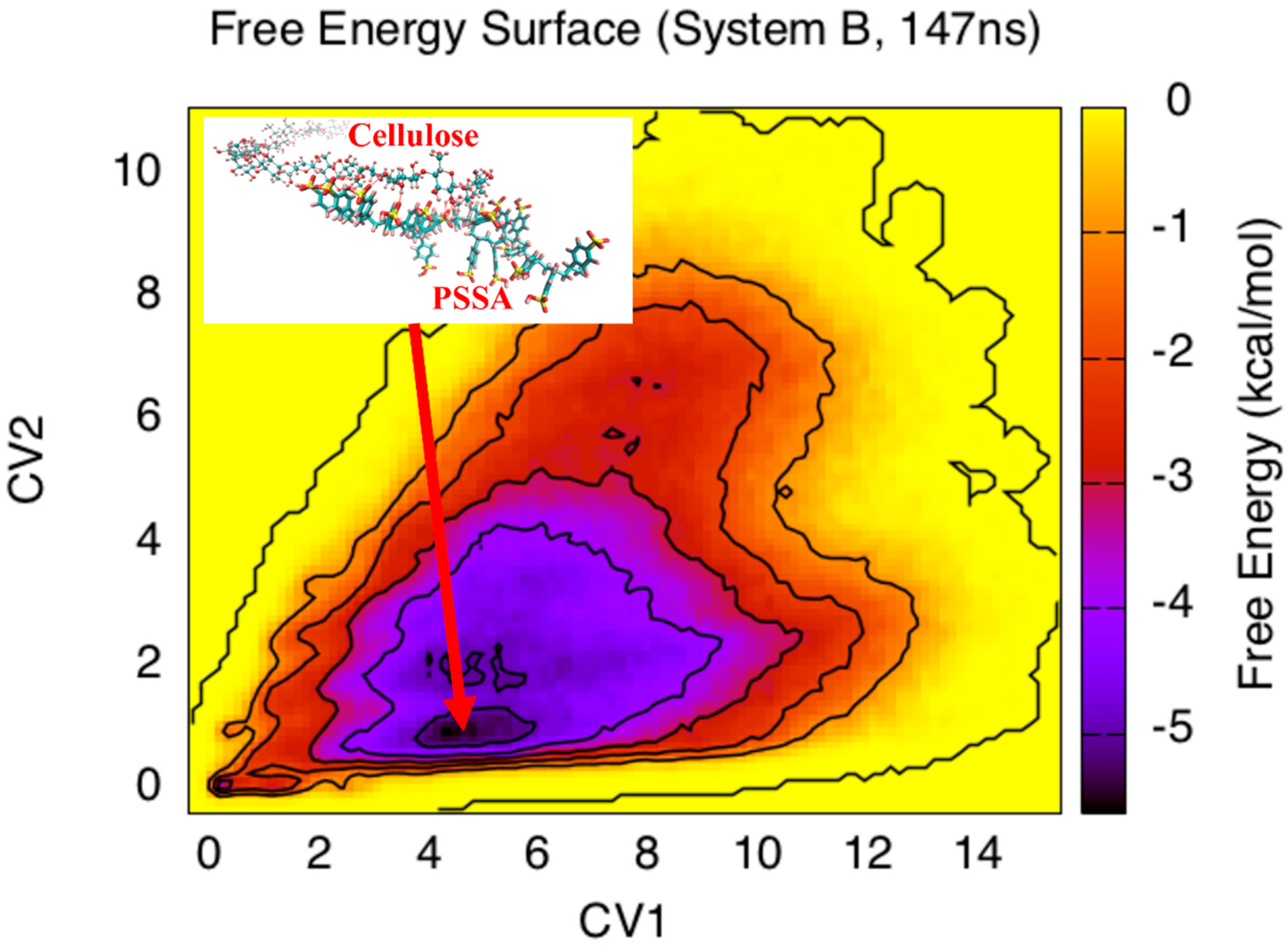
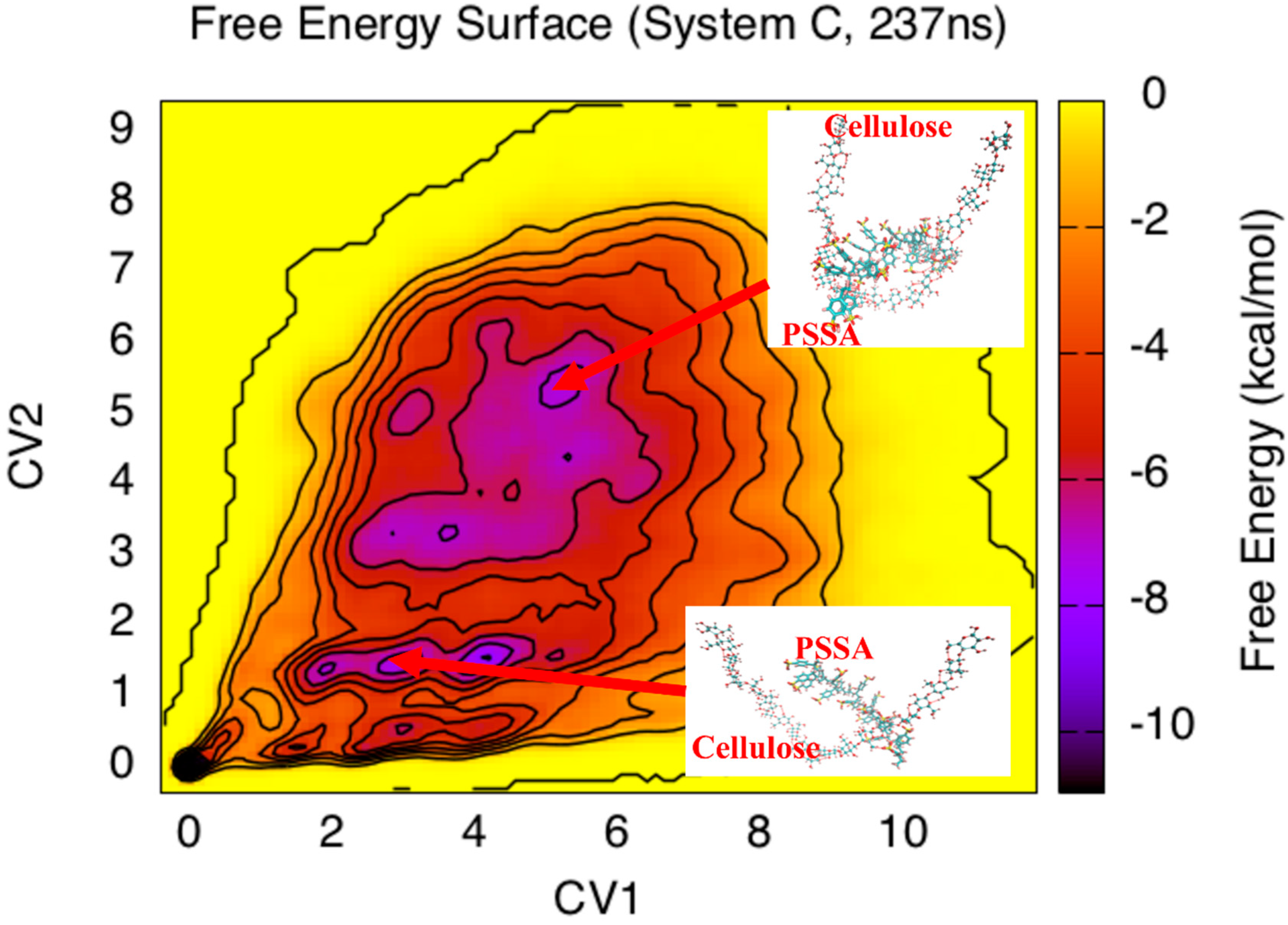
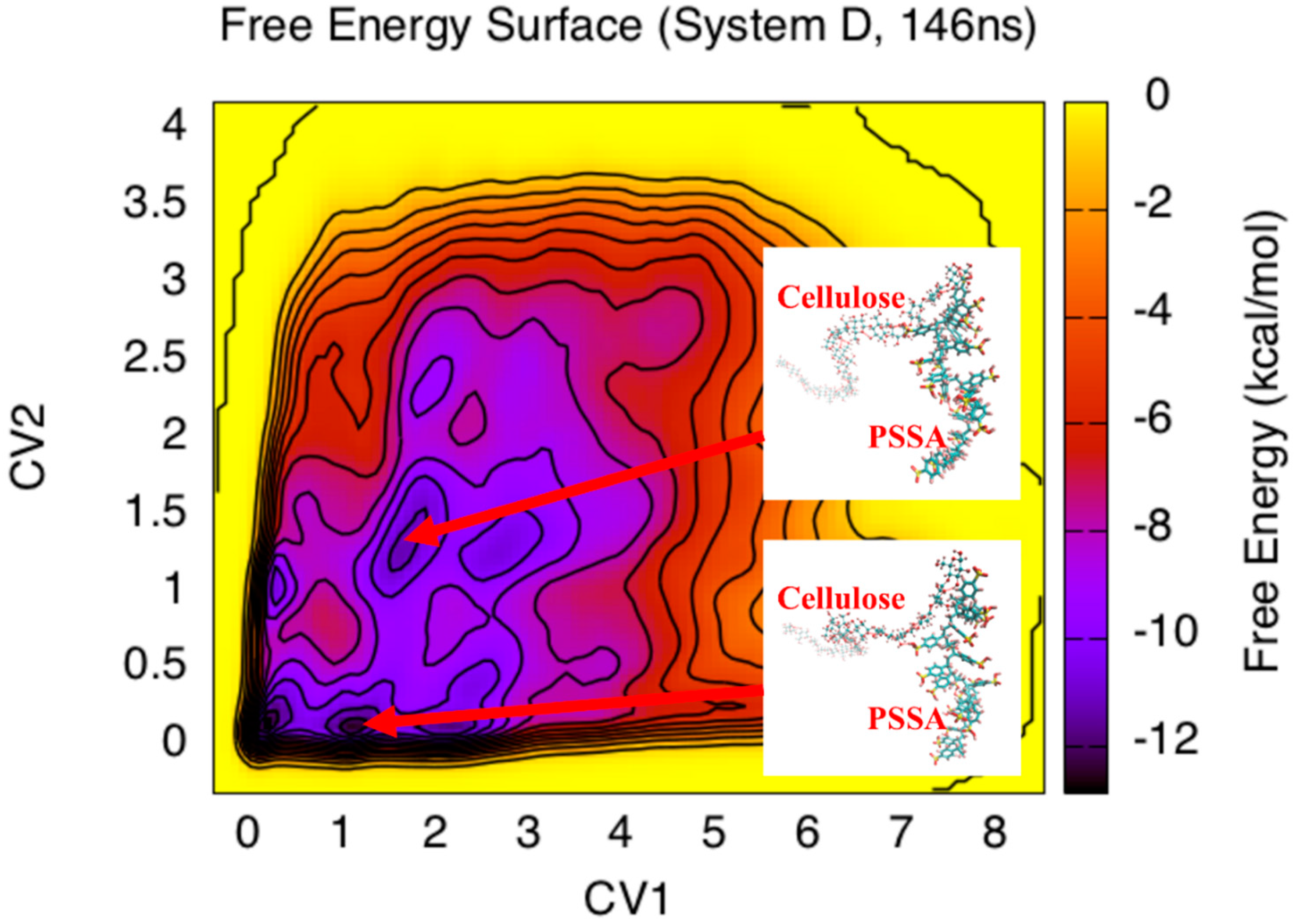
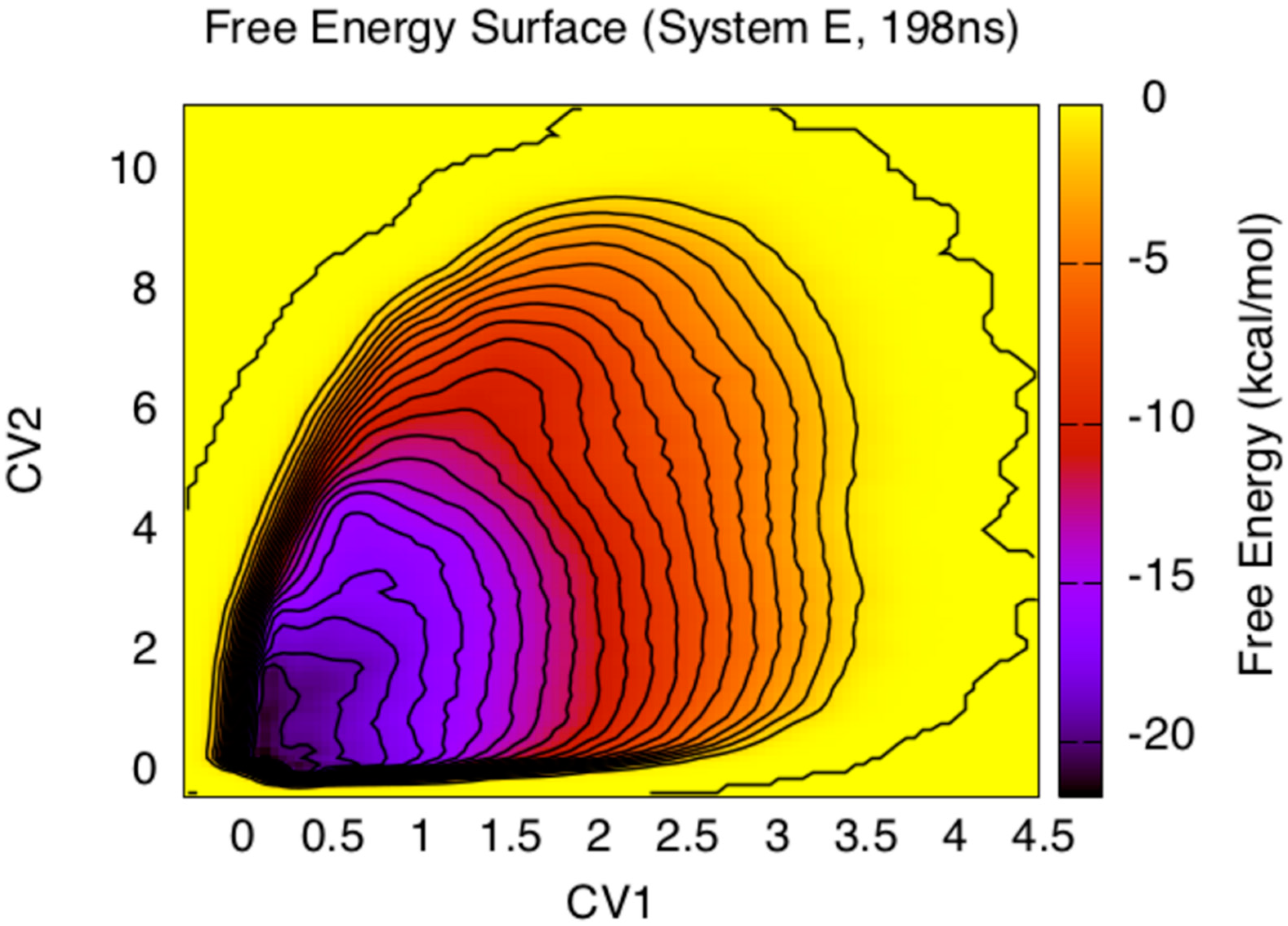
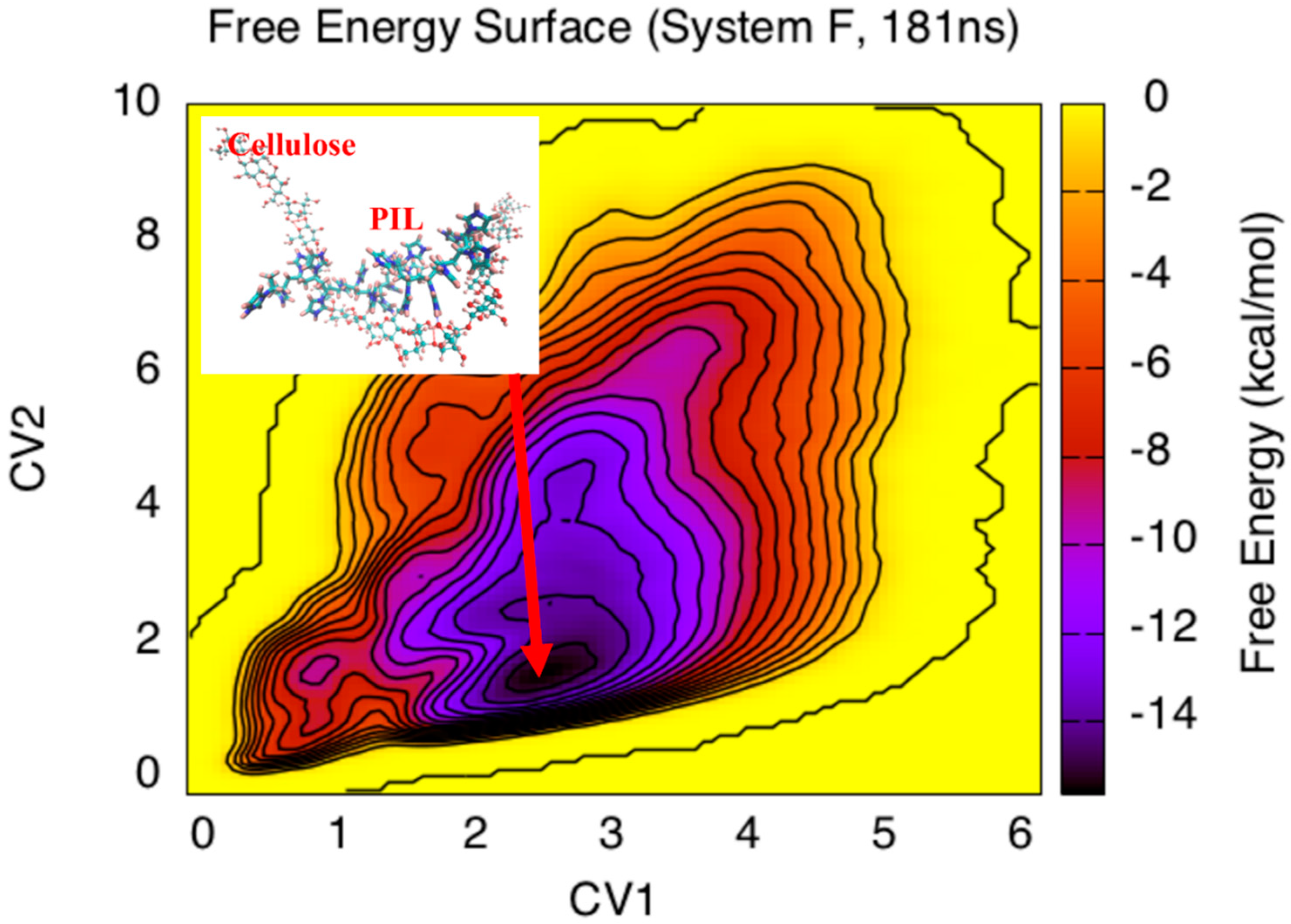
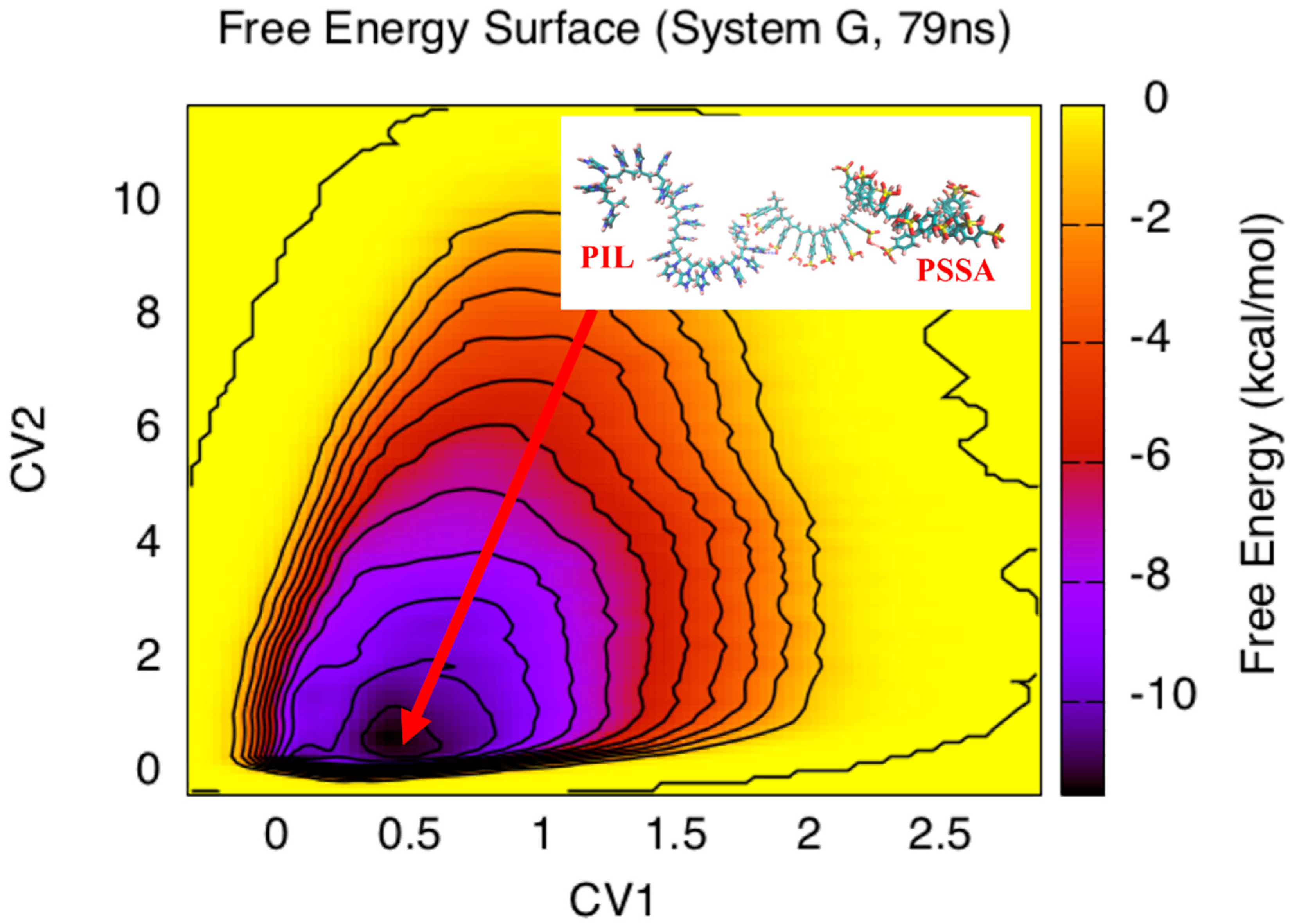
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agarwal, A.K. Biofuels (alcohols and biodiesel) applications as fuels for internal combustion engines. Prog. Energy Combust. Sci. 2007, 33, 233–271. [Google Scholar] [CrossRef]
- Greene, N.; Celik, F.E.; Dale, B.; Jackson, M.; Jayawardhana, K.; Jin, H.; Larson, E.D.; Laser, M.; Lynd, L.; MacKenzie, D. Growing Energy. How Biofuels Can Help End America’s Oil Dependence; Natural Resources Defense Council: New York, NY, USA, 2004. [Google Scholar]
- Guo, M.; Song, W.; Buhain, J. Bioenergy and biofuels: History, status, and perspective. Renew. Sustain. Energy Rev. 2015, 42, 712–725. [Google Scholar] [CrossRef]
- Ho, D.P.; Ngo, H.H.; Guo, W. A mini review on renewable sources for biofuel. Bioresour. Technol. 2014, 169, 742–749. [Google Scholar] [CrossRef] [PubMed]
- Liew, W.H.; Hassim, M.H.; Ng, D.K.S. Review of evolution, technology and sustainability assessments of biofuel production. J. Clean. Prod. 2014, 71, 11–29. [Google Scholar] [CrossRef]
- Naik, S.N.; Goud, V.V.; Rout, P.K.; Dalai, A.K. Production of first and second generation biofuels: A comprehensive review. Renew. Sustain. Energy Rev. 2010, 14, 578–597. [Google Scholar] [CrossRef]
- Dragone, G.; Fernandes, B.D.; Vicente, A.A.; Teixeira, J.A. Third generation biofuels from microalgae. Curr. Res. Technol. Educ. Top. Appl. Microbiol. Microb. Biotechnol. 2010, 2, 1355–1366. [Google Scholar]
- Agbor, V.B.; Cicek, N.; Sparling, R.; Berlin, A.; Levin, D.B. Biomass pretreatment: Fundamentals toward application. Biotechnol. Adv. 2011, 29, 675–685. [Google Scholar] [CrossRef] [PubMed]
- Bajpai, P. Summary of Biomass Pretreatment Methods, Pretreatment of Lignocellulosic Biomass for Biofuel Production; Springer: Singapore, 2016; pp. 71–75. [Google Scholar]
- Kumar, A.K.; Sharma, S. Recent updates on different methods of pretreatment of lignocellulosic feedstocks: A review. Bioresour. Bioprocess. 2017, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Barrett, D.M.; Delwiche, M.J.; Stroeve, P. Methods for Pretreatment of Lignocellulosic Biomass for Efficient Hydrolysis and Biofuel Production. Ind. Eng. Chem. Res. 2009, 48, 3713–3729. [Google Scholar] [CrossRef]
- Harris, E.E.; Kline, A.A. Hydrolysis of Wood Cellulose with Hydrochloric Acid and Sulfur Dioxide and the Decomposition of its Hydrolytic Products. J. Phys. Chem. 1949, 53, 344–351. [Google Scholar] [CrossRef]
- Segal, L.; Nelson, M.L. The Effect of Aqueous Hydrochloric Acid on the Cotton Cellulose III Lattice and Its Implications Concerning the Determinations of Crystallinity and Leveling-off Degree of Polymerization 2. J. Am. Chem. Soc. 1954, 76, 4626–4630. [Google Scholar] [CrossRef]
- Lin, J.-H.; Chang, Y.-H.; Hsu, Y.-H. Degradation of cotton cellulose treated with hydrochloric acid either in water or in ethanol. Food Hydrocoll. 2009, 23, 1548–1553. [Google Scholar] [CrossRef]
- Béguin, P.; Aubert, J.-P. The biological degradation of cellulose. FEMS Microbiol. Rev. 1994, 13, 25–58. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Cheng, J. Hydrolysis of lignocellulosic materials for ethanol production: A review. Bioresour. Technol. 2002, 83, 1–11. [Google Scholar] [CrossRef]
- Lee, J. Biological conversion of lignocellulosic biomass to ethanol. J. Biotechnol. 1997, 56, 1–24. [Google Scholar] [CrossRef]
- Vital de Oliveira, O. Molecular Dynamics and Metadynamics Simulations of the Cellulase Cel48F. Enzyme Res. 2014, 2014, 692738. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, J.-L.; Sun, L.; Niu, X.-D.; Wang, S.; Shan, Y.-M. Molecular dynamics simulation of the processive endocellulase Cel48F from Clostridium cellulolyticum: A novel “water-control mechanism” in enzymatic hydrolysis of cellulose. J. Mol. Recognit. JMR 2014, 27, 438–447. [Google Scholar] [CrossRef] [PubMed]
- Lian, P.; Guo, H.-B.; Smith, J.C.; Wei, D.-Q.; Guo, H. Catalytic mechanism and origin of high activity of cellulase TmCel12A at high temperature: A quantum mechanical/molecular mechanical study. Cellulose 2013, 21, 937–949. [Google Scholar] [CrossRef]
- Alekozai, E.M.; GhattyVenkataKrishna, P.K.; Uberbacher, E.C.; Crowley, M.F.; Smith, J.C.; Cheng, X. Simulation analysis of the cellulase Cel7A carbohydrate binding module on the surface of the cellulose Iβ. Cellulose 2013, 21, 951–971. [Google Scholar] [CrossRef]
- Qian, X.; Nimlos, M.R.; Davis, M.; Johnson, D.K.; Himmel, M.E. Ab initio molecular dynamics simulations of β-d-glucose and β-d-xylose degradation mechanisms in acidic aqueous solution. Carbohydr. Res. 2005, 340, 2319–2327. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Nimlos, M.R.; Johnson, D.K.; Himmel, M.E. Acidic Sugar Degradation Pathways, Twenty-Sixth Symposium on Biotechnology for Fuels and Chemicals; Humana Press: New York, NY, USA, 2005; pp. 989–997. [Google Scholar]
- Dong, H.; Nimlos, M.R.; Himmel, M.E.; Johnson, D.K.; Qian, X. The Effects of Water on β-d-Xylose Condensation Reactions. J. Phys. Chem. A 2009, 113, 8577–8585. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Nimlos, M.R.; Johnson, D.K.; Himmel, M.E.; Qian, X. Free Energy Landscape for Glucose Condensation Reactions. J. Phys. Chem. A 2010, 114, 12936–12944. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Johnson, D.K.; Himmel, M.E.; Nimlos, M.R. The role of hydrogen-bonding interactions in acidic sugar reaction pathways. Carbohydr. Res. 2010, 345, 1945–1951. [Google Scholar] [CrossRef] [PubMed]
- Qian, X. Mechanisms and Energetics for Acid Catalyzed β-d-Glucose Conversion to 5-Hydroxymethylfurfurl. J. Phys. Chem. A 2011, 115, 11740–11748. [Google Scholar] [CrossRef] [PubMed]
- Qian, X. Mechanisms and Energetics for Brønsted Acid-Catalyzed Glucose Condensation, Dehydration and Isomerization Reactions. Top. Catal. 2012, 55, 218–226. [Google Scholar] [CrossRef]
- Qian, X.; Wei, X. Glucose Isomerization to Fructose from ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2012, 116, 10898–10904. [Google Scholar] [CrossRef] [PubMed]
- Qian, X. Free Energy Surface for Brønsted Acid-Catalyzed Glucose Ring-Opening in Aqueous Solution. J. Phys. Chem. B 2013, 117, 11460–11465. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Liu, D. Free energy landscape for glucose condensation and dehydration reactions in dimethyl sulfoxide and the effects of solvent. Carbohydr. Res. 2014, 388, 50–60. [Google Scholar] [CrossRef] [PubMed]
- Breslow, R. Biomimetic Chemistry and Artificial Enzymes: Catalysis by Design. Acc. Chem. Res. 1995, 28, 146–153. [Google Scholar] [CrossRef]
- Simmons, T.R.; Berggren, G.; Bacchi, M.; Fontecave, M.; Artero, V. Mimicking hydrogenases: From biomimetics to artificial enzymes. Coord. Chem. Rev. 2014, 270–271, 127–150. [Google Scholar] [CrossRef]
- Qian, X.; Lei, J.; Wickramasinghe, S.R. Novel polymeric solid acid catalysts for cellulose hydrolysis. RSC Adv. 2013, 3, 24280–24287. [Google Scholar] [CrossRef]
- Vu, A.; Wickramasinghe, S.R.; Qian, X. Polymeric Solid Acid Catalysts for Lignocellulosic Biomass Fractionation. Ind. Eng. Chem. Res. 2018, 57, 4514–4525. [Google Scholar] [CrossRef]
- Qi, B.; Vu, A.; Wickramasinghe, S.R.; Qian, X. Glucose production from lignocellulosic biomass using a membrane-based polymeric solid acid catalyst. Biomass Bioenergy 2018, 117, 137–145. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. PNAS 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed]
- Ensing, B.; de Vivo, M.; Liu, Z.; Moore, P.; Klein, M.L. Metadynamics as a Tool for Exploring Free Energy Landscapes of Chemical Reactions. Acc. Chem. Res. 2006, 39, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. WIREs Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Lopes, J.N.C.; Deschamps, J.; Pádua, A.A.H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar] [CrossRef]
- Sunda, A.P.; Venkatnathan, A. Molecular dynamics simulations of triflic acid and triflate ion/water mixtures: A proton conducting electrolytic component in fuel cells. J. Comput. Chem. 2011, 32, 3319–3328. [Google Scholar] [CrossRef] [PubMed]
- Dommert, F.; Holm, C. Refining classical force fields for ionic liquids: Theory and application to [MMIM][Cl]. Phys. Chem. Chem. Phys. 2013, 15, 2037–2049. [Google Scholar] [CrossRef] [PubMed]
- Dommert, F.; Wendler, K.; Qiao, B.; Site, L.D.; Holm, C. Generic force fields for ionic liquids. J. Mol. Liquids 2014, 192, 34–37. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.H.; et al. Fox, Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollmann, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Cieplak, P.; Cornell, W.D.; Bayly, C.; Kollman, P.A. Application of the multimolecule and multiconformational RESP methodology to biopolymers: Charge derivation for DNA, RNA, and proteins. J. Comput. Chem. 1995, 16, 1357–1377. [Google Scholar] [CrossRef]
- Fox, T.; Kollman, P.A. Application of the RESP Methodology in the Parametrization of Organic Solvents. J. Phys. Chem. B 1998, 102, 8070–8079. [Google Scholar] [CrossRef]
- Sun, X. Structure and Property of Polymers and Biopolymers from Molecular Dynamic Simulations; University of Arkansas: Fayetteville, AR, USA, 2018. [Google Scholar]
- Case, D.; Darden, T.A.; Cheatham, T.E.; Simmerling, C.; Wang, J.; Duke, R.; Luo, R.; Crowley, M.; Walker, R.; Zhang, W.; et al. Amber 11; University of California, San Francisco: San Francisco, CA, USA, 2010. [Google Scholar]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, K.N.; Yongye, A.B.; Tschampel, S.M.; González-Outeiriño, J.; Daniels, C.R.; Foley, B.L.; Woods, R.J. GLYCAM06: A generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Joung, I.S. Cheatham, Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Binder, J.B.; Raines, R.T. Fermentable sugars by chemical hydrolysis of biomass. PNAS 2010, 107, 4516–4521. [Google Scholar] [CrossRef] [PubMed]
- Dee, S.J.; Bell, A.T. A study of the acid-catalyzed hydrolysis of cellulose dissolved in ionic liquids and the factors influencing the dehydration of glucose and the formation of humins. ChemSusChem 2011, 4, 1166–1173. [Google Scholar] [CrossRef] [PubMed]
- Mora-Pale, M.; Meli, L.; Doherty, T.V.; Linhardt, R.J.; Dordick, J.S. Room temperature ionic liquids as emerging solvents for the pretreatment of lignocellulosic biomass. Biotechnol. Bioeng. 2011, 108, 1229–1245. [Google Scholar] [CrossRef] [PubMed]
- Sen, S.M.; Binder, J.B.; Raines, R.T.; Maravelias, C.T. Conversion of biomass to sugars via ionic liquid hydrolysis: Process synthesis and economic evaluation, Biofuels. Bioprod. Biorefin. 2012, 6, 444–452. [Google Scholar] [CrossRef]
- Strachan, J. Solubility of Cellulose in Water. Nature 1938, 141, 332. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Qian, X. Elucidating the Energetics and Effects of Solvents on Cellulose Hydrolysis Using a Polymeric Acid Catalyst. Appl. Sci. 2018, 8, 1767. https://doi.org/10.3390/app8101767
Sun X, Qian X. Elucidating the Energetics and Effects of Solvents on Cellulose Hydrolysis Using a Polymeric Acid Catalyst. Applied Sciences. 2018; 8(10):1767. https://doi.org/10.3390/app8101767
Chicago/Turabian StyleSun, Xiaoquan, and Xianghong Qian. 2018. "Elucidating the Energetics and Effects of Solvents on Cellulose Hydrolysis Using a Polymeric Acid Catalyst" Applied Sciences 8, no. 10: 1767. https://doi.org/10.3390/app8101767
APA StyleSun, X., & Qian, X. (2018). Elucidating the Energetics and Effects of Solvents on Cellulose Hydrolysis Using a Polymeric Acid Catalyst. Applied Sciences, 8(10), 1767. https://doi.org/10.3390/app8101767



