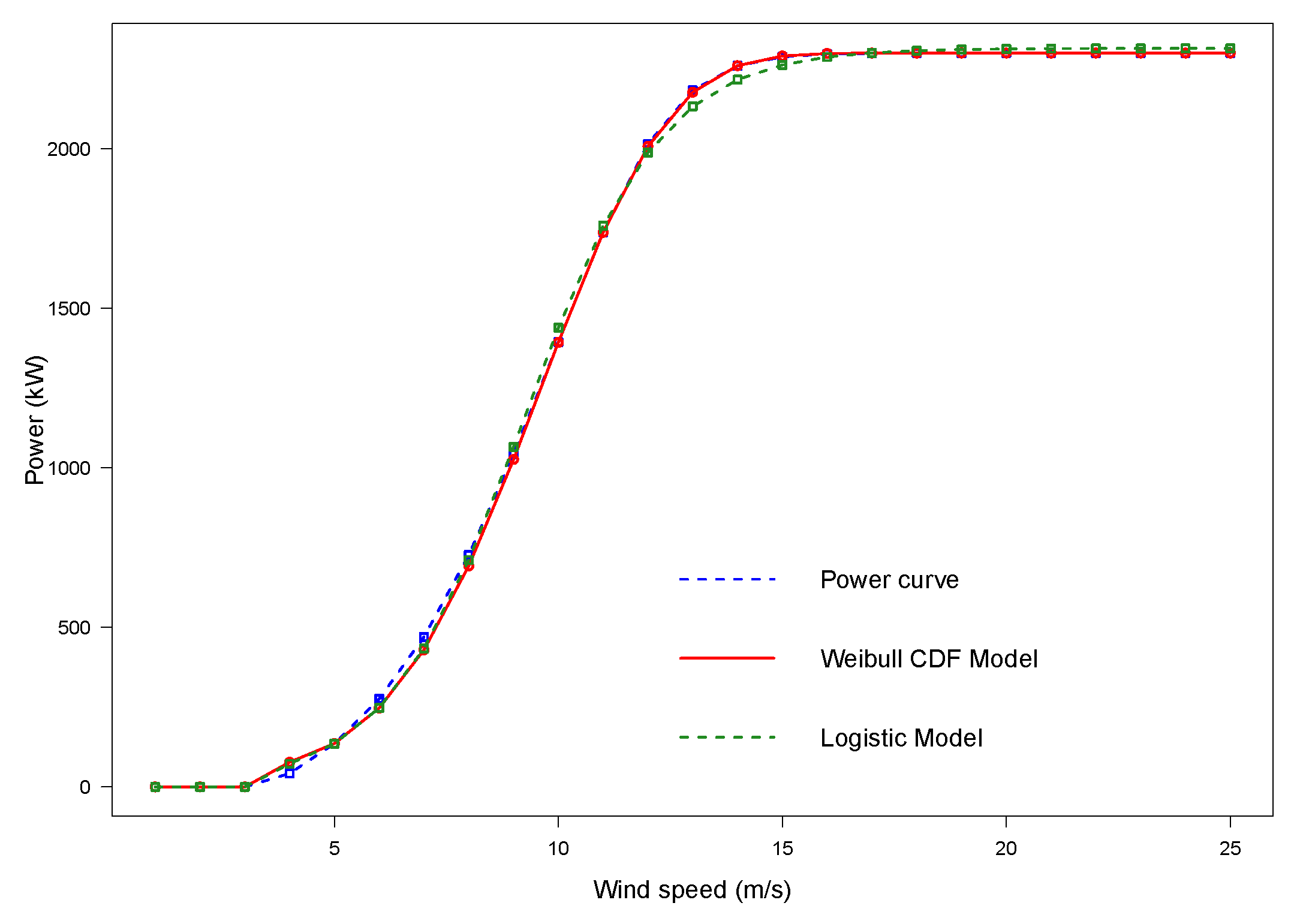
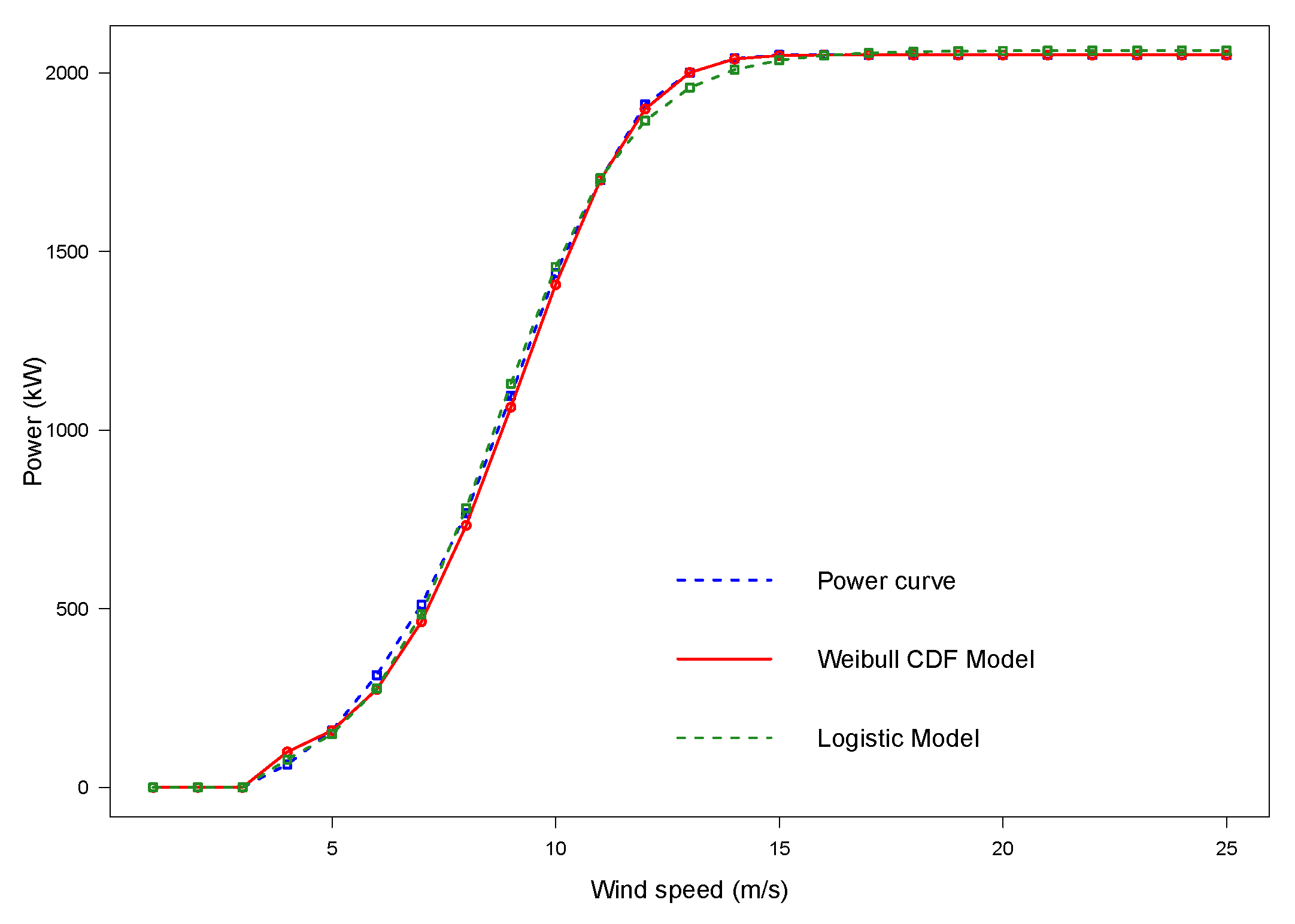
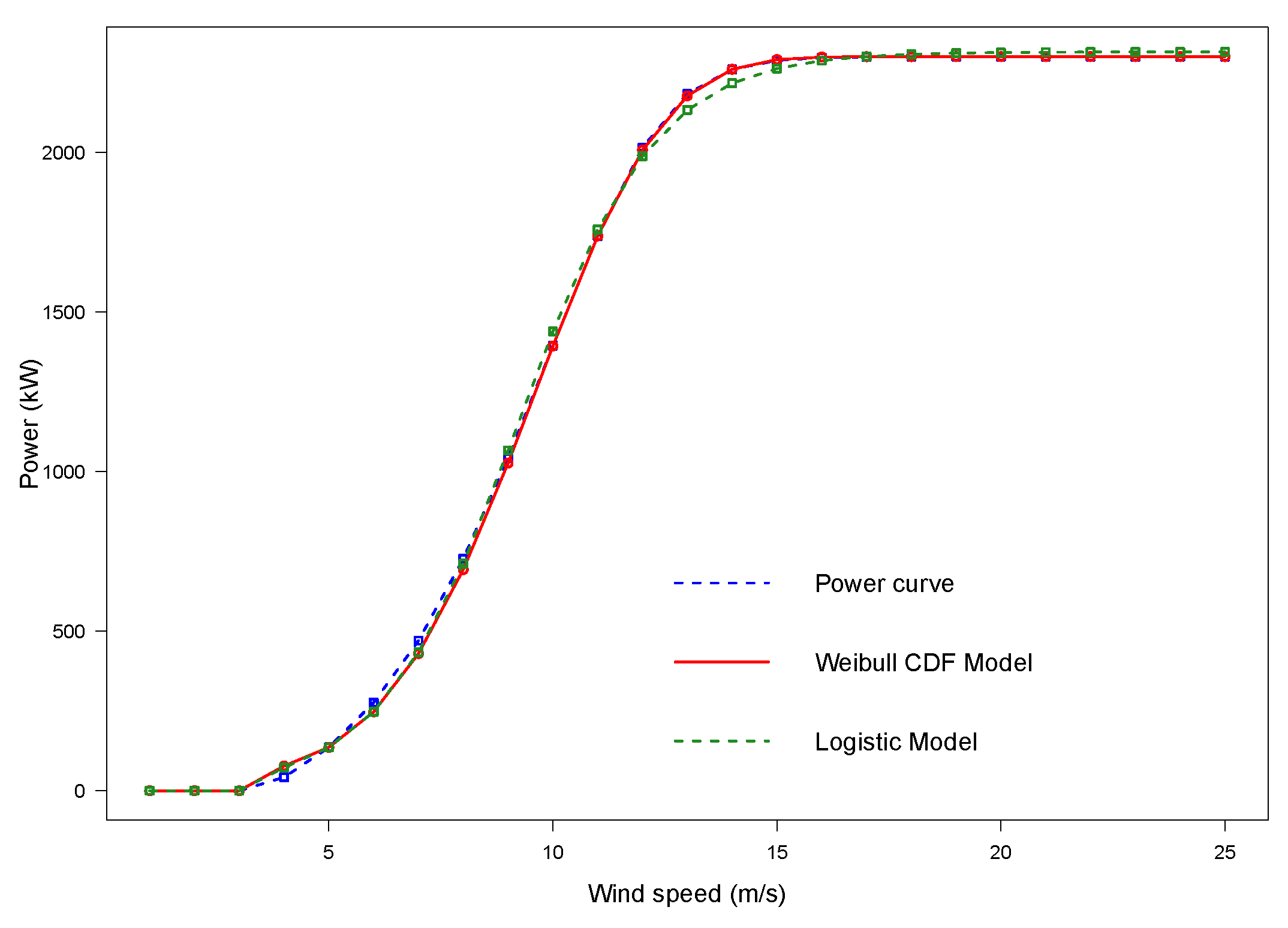
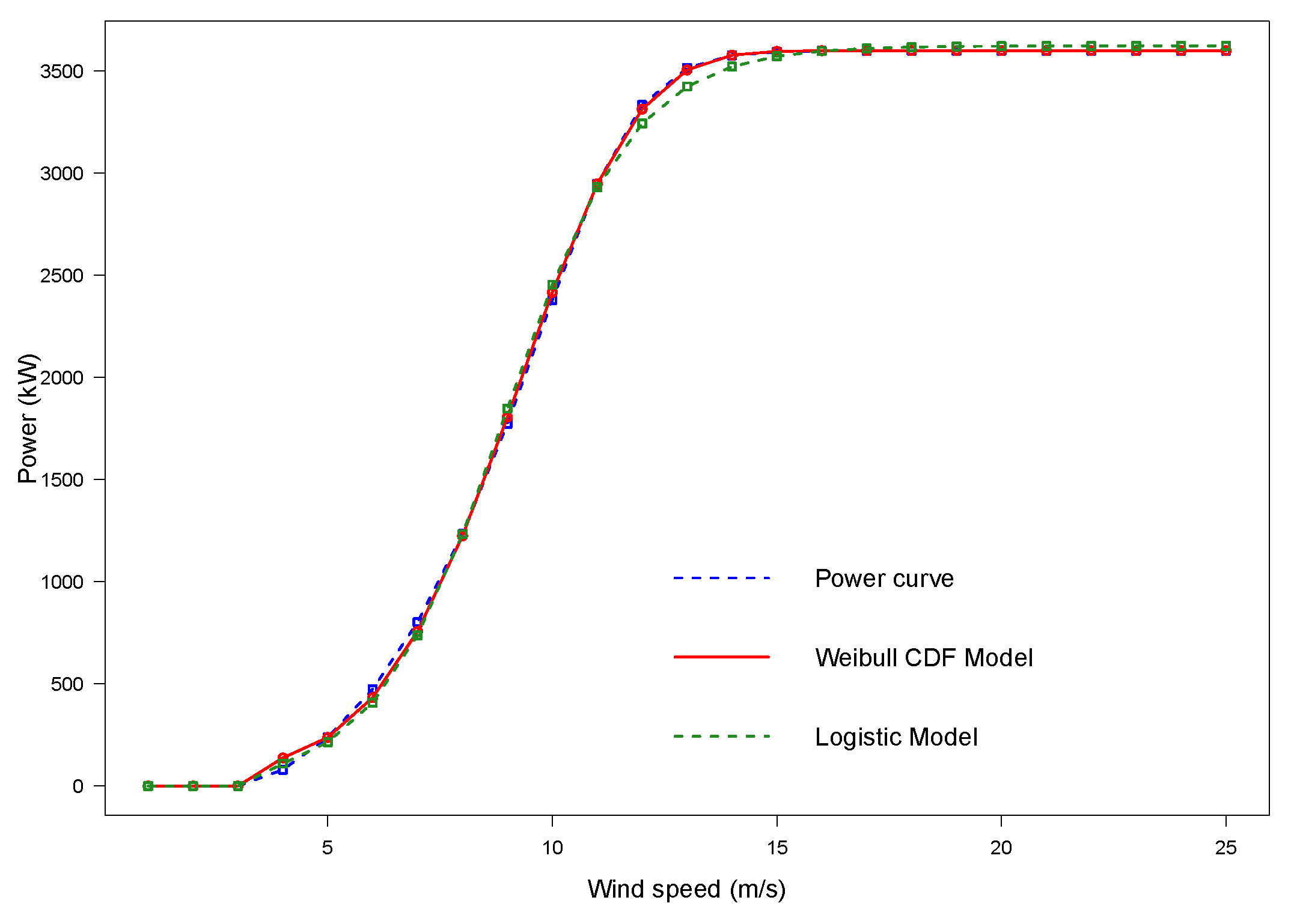
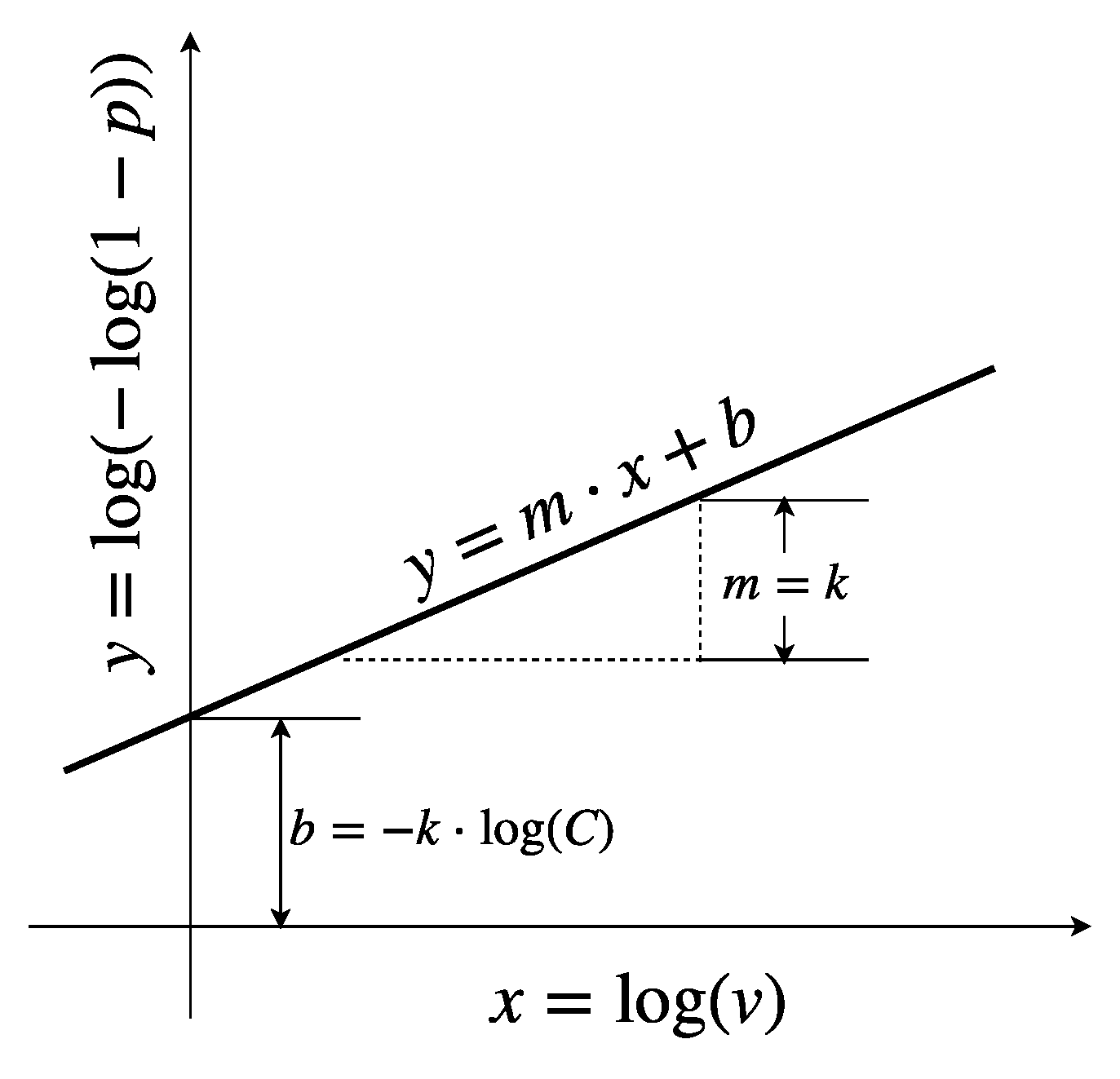Appendix A.2. Overview of WindCurves
WindCurves [
25] is used as a tool to fit WT power curves. As mentioned in the previous section, it can be useful for researchers, data analysts/scientists, practitioners, statisticians and students working on WT power curves. The most salient features of
WindCurves are the following:
It facilitates fitting the WT power curve with the Weibull CDF, the logistic function [
7] and user-defined techniques. The user-defined techniques include a power curve fitting technique that has to be compared with the performance of the above-mentioned default methods. In other words, this tool can be utilized as a test bench on a similar principle as ‘
imputetTestbench’ [
26,
27] to compare the performance of distinct WT power curve fitting techniques.
It provides the visualization, information in the form of parametric equations and a comparison of fitted WT power curves in term of various error measures including RMSE, MAE and MAPE. Other user-defined error measures can be added in the comparison.
Datasets [
21] on the power curves of the WT from four major manufacturers are available in the package: Siemens, Vestas, REpower and Nordex. The use of such datasets ensures the comparison study within an industry standard. These datasets represent wind WT power output in ‘kW’ against wind speed in ‘m/s’.
It provides a feature to extract/capture wind speed versus generated wind power discrete points from power curve images. It works on a similar principle as the ‘
digitize’ package [
28], but in updated form, more precisely for wind power curves along with a few additional features.
The primary function is ‘
fitcurve()’, which is used to fit the power curve with various curve fitting techniques. The ‘
validatecurve()’ function is used to compare the performance of curve fitting techniques operated in the ‘
fitcurve()’ function, and ‘
fitcurve_plot()’ (an S3method function) provides a plotting option to demonstrate how accurately the power curves are fitted. The above-mentioned sample dataset [
21] of the WT power curve is in the ‘
pcurves()’ function. The remaining function, ‘
img2points()’, is used to extract discrete values of wind speed (in m/s) and corresponding generated wind power (in kW) from a power curve image. The dependencies include additional packages for graphing (
grid [
29],
grDevices [
29],
graphics [
29] and
readbitmap [
30]), statistical analysis (
stats [
29]) and the standard tool (
methods [
29]). The details of these functions are described below.
Appendix A.2.1. The ‘fitcurve()’ Function
The ‘
fitcurve()’ function fits the power curves for given discrete values of wind speed and corresponding generated power. These values are accepted in the form of the data frame object having two columns, wind speed and generated power, respectively. The default methods of wind curve fitting included in ‘
fitcurve()’ are the Weibull CDF and logistic function [
7] methods. These methods have shown better accuracy in fitting the power curves in comparison to various piece-wise and other contemporary methods. The shape of a WT power curve is very similar to the shape of some CDFs. When using the Weibull CDF, a good approach is obtained by estimating two of the three parameters of a Weibull distribution, i.e., shape and scale parameters, to fit a WT power curve by means of such a function; whereas, in the logistic function, a three-parameter function obtained with the ‘
stats’ [
29] package is used. Although only two methods are used in the function, these default methods are very efficient in fitting WT power curves. As noted below, the additional method can be added as needed. The ‘
fitcurve()’ function has the following arguments:
fitcurve(data, MethodPath, MethodName)
- data:
A data frame object that will be evaluated. The input object is a dataset in the form of data frame having two columns, wind speed and its corresponding generated power. The example in the documentation uses the wind speed and wind power generated by the ‘Nordex N90’ WT [
21], which is also available in ‘
WindCurves’ in the ‘
pcurves’ dataset.
- MethodPath:
A character string for the sourced path of the user-defined function that includes a function passed to methods. This path can be absolute or relative within the working directory for the current R session. The ‘fitcurve()’ function uses the sourced path and adds the user-defined curve fitting function to the global environment.
- MethodName:
A character string that represents the name for the user-defined function, which is added in the ‘fitcurve()’ function through the ‘MethodPath’ argument.
Considering the default values of the above arguments, the ‘fitcurve()’ function returns the fitted model of the Weibull CDF and logistic functions with the corresponding calculated parameters and the fitted WT power curve values.
library(WindCurves)
data(pcurves)
s <- pcurves$Speed
p <- pcurves$‘Nordex N90‘
da <- data.frame(s,p)
x <- fitcurve(da)
#> Weibull CDF model
#> -----------------
#> P = 1 - exp[-(S/C)^k]
#> where P -> Power and S -> Speed
#>
#> Shape (k) = 4.242446
#> Scale (C) = 9.564993
#> ===================================
#>
#> Logistic Function model
#> -----------------------
#> P = phi1/(1+exp((phi2-S)/phi3))
#> where P -> Power and S -> Speed
#>
#> phi 1 = 2318.242
#> phi 2 = 8.65861
#> phi 3 = 1.366053
#> ===================================
x
#> $Speed
#> [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
#> [24] 24 25
#>
#> Power
#> [1] 0 0 0 35 175 352 580 870 1237 1623 2012 2230 2300 2300
#> [15] 2300 2300 2300 2300 2300 2300 2300 2300 2300 2300 2300
#>
#> ‘Weibull CDF‘
#> [1] 0.0000 0.0000 0.0000 90.3871 175.0000 327.5161 563.9085
#> [8] 882.3965 1253.7489 1623.0000 1929.1254 2134.6685 2242.6251 2285.2438
#> [15] 2297.3355 2299.6816 2299.9764 2299.9990 2300.0000 2300.0000 2300.0000
#> [22] 2300.0000 2300.0000 2300.0000 2300.0000
#>
#> ‘Logistic Function‘
#> [1] 0.00000 0.00000 0.00000 74.12813 148.99331 289.70713
#> [7] 530.79720 884.98933 1303.20985 1686.50765 1964.36723 2133.40810
#> [13] 2225.51236 2272.70005 2296.11389 2307.54694 2313.08606 2315.75946
#> [19] 2317.04738 2317.66729 2317.96554 2318.10900 2318.17801 2318.21119
#> [25] 2318.22715
#>
#> attr(,"row.names")
#> [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
#> [24] 24 25
#> attr(,"class")
#> [1] "fitcurve"$
Appendix A.2.2. Analyzing Results from ‘fitcurve()’
Apart from this, the ‘validatecurve()’ function presents the accuracy of curve fitting methods compared to the object generated by the ‘fitcurve()’ function. This function returns the comparison of different curve fitting methods with various error metrics. The default error metrics available in the ‘validatecurve()’ function are root-mean-squared error (RMSE), mean absolute error (MAE), mean absolute percent error (MAPE), R squared values (R2) and correlation coefficients (COR). Apart from these, the additional error metrics can be added in the ‘validatecurve()’ analysis as user-supplied functions using the ‘MethodPath’ and ‘MethodName’ arguments. These arguments are similar to the ‘MethodPath’ and ‘MethodName’ arguments used in the ‘fitcurve()’ function, except for their intention to include new error metrics in the analysis. Considering the default values for the input arguments, the ‘validatecurve()’ function returns the comparison of the fitted wind curve in terms of distinct error metrics as follows.
validate.curve(x)
#> Metrics Weibull CDF Logistic Function
#> 1 RMSE 30.8761687 38.8753476
#> 2 MAE 15.1381094 29.3213484
#> 3 MAPE 3.9292946 5.9183795
#> 4 R2 0.9989322 0.9983073
#> 5 COR 0.9995413 0.9991591
Appendix A.2.3. Extracting Discrete WT Power Curve Points from a Power Curve Image
Generally, WT manufacturers provide the power curves in the form of graphs, and manual ruler-based approach has been used to extract the wind speed and corresponding power values from the curve. A similar approach is exercised while replicating the power curves from research articles, books or digital manuals. In order to minimize these efforts, ‘
WindCurves’ provides the ‘
img2points()’ function, which eases the process of extracting discrete WT power curve points from a power curve image. The ‘
img2points()’ function works on a similar principal of the ‘
digitize’ package [
28], but designed more specifically for WT power curves fitting with additional features. The ‘
img2points()’ function has the following arguments:
img2points(imagePath, n)
- imagePath’:
A character string for the path of an image of a power curve from which discrete values have to be extracted. This path can be absolute or relative within the working directory for the current R session. The ‘img2points()’ function uses this path and allows the user to select the desired points on the curve image.
- n:
An integer that represents the number of points to be captured on the curve image. The default value of the argument is fixed to 15.
The procedure to use the ‘img2points()’ function is as follows:
img2points(“image.jpeg”)
This function will import the desired image in the viewer panel and ask the user to locate two points on the X-axis and Y-axis of each of power curve image. Furthermore, it will ask the user to provide the actual values of the located four points on the image. The selection of any two points on each axis will work, but it is desired to select the extreme endpoints (with known values) of the curve image.
With these values, the ‘img2points()’ function maps the curve image and asks the user to point to ‘n’ points on the mapped image. Eventually, this function returns a data frame with two columns, wind speed, and generated power, that can be directly processed with the ‘fitcurve()’ function.
The ‘
img2points()’ function operates similarly and as accurately as the ‘
digitize’ package [
28]. As discussed in [
28], the performance of the ‘
digitize’ package gets deflected for the inclined input images. For such an inclined image, the points extracted from the curve are found to be deflected from its expected positions. The ‘
img2points()’ function tackles such situations internally and retains the image with zero inclination in the X- and Y-axes. Eventually, this provides higher accuracy in extracting the discrete power curve points. Furthermore, in several cases, when the image is highly inclined and after relocating it to zero inclination of axes, the initial mapping of extreme ends of axes varies slightly and may produce a minute error in the system. Hence, in such cases, the ‘
img2points()’ function asks the user to make the decision whether to map the extreme ends of axes again. The user can observe the deviation in mapping and accordingly decide whether to map the axes’ points again.
Appendix A.3. Demonstration of ‘WindCurves’
This example demonstrates how ‘
WindCurves’ can be used as a useful tool for analyzing and fitting the WT power curves. The objective of this demonstration is to become aware of the procedures to be followed when using the ‘
WindCurves’ package to fit the WT power curves. In an earlier section, the ‘Nordex N90’ dataset was fitted, whereas in this section, the discrete values of the power curve were extracted from the curve image shown in
Figure A1.
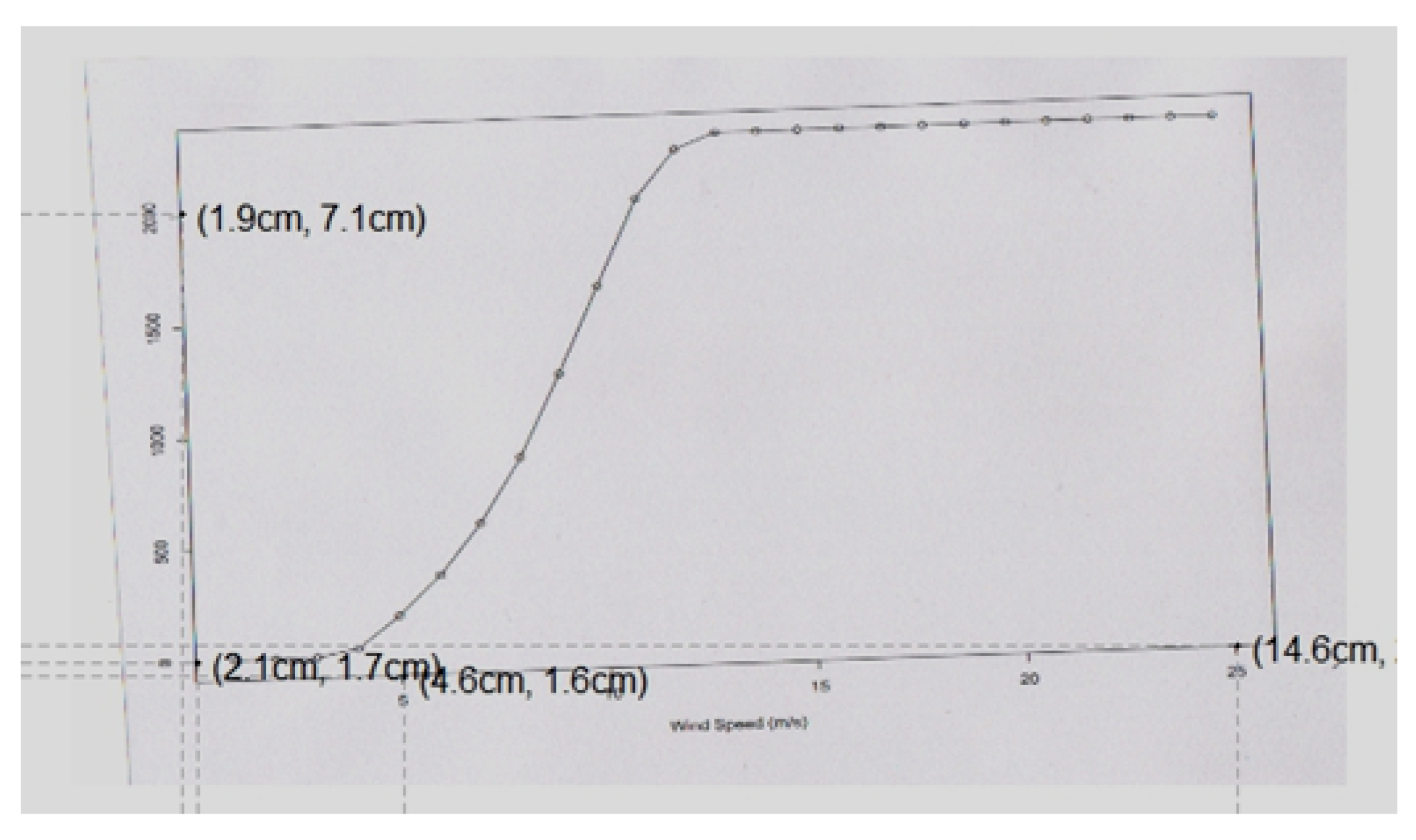
Figure A1.
The WT power curve image to be supplied to ‘img2points()’ function.
Figure A1.
The WT power curve image to be supplied to ‘img2points()’ function.
Appendix A.3.1. Step 1: Extract Discrete Values of the Power Curve
This step involves two actions:
- 1.
Select two extreme points on each X- and Y-axes (
Figure A2).
In this state, the inclination angle of the image (if there is one) is informed to the user who is asked to decide whether to re-map the X- and Y-axes’ points in the image. Furthermore, it transforms the inclined image with a new and non-inclined image. If the user permits character “Y”, the ‘img2points()’ function will ask again to map the axes’ points, and a more accurate mapping is achieved. Otherwise, the following action is activated.
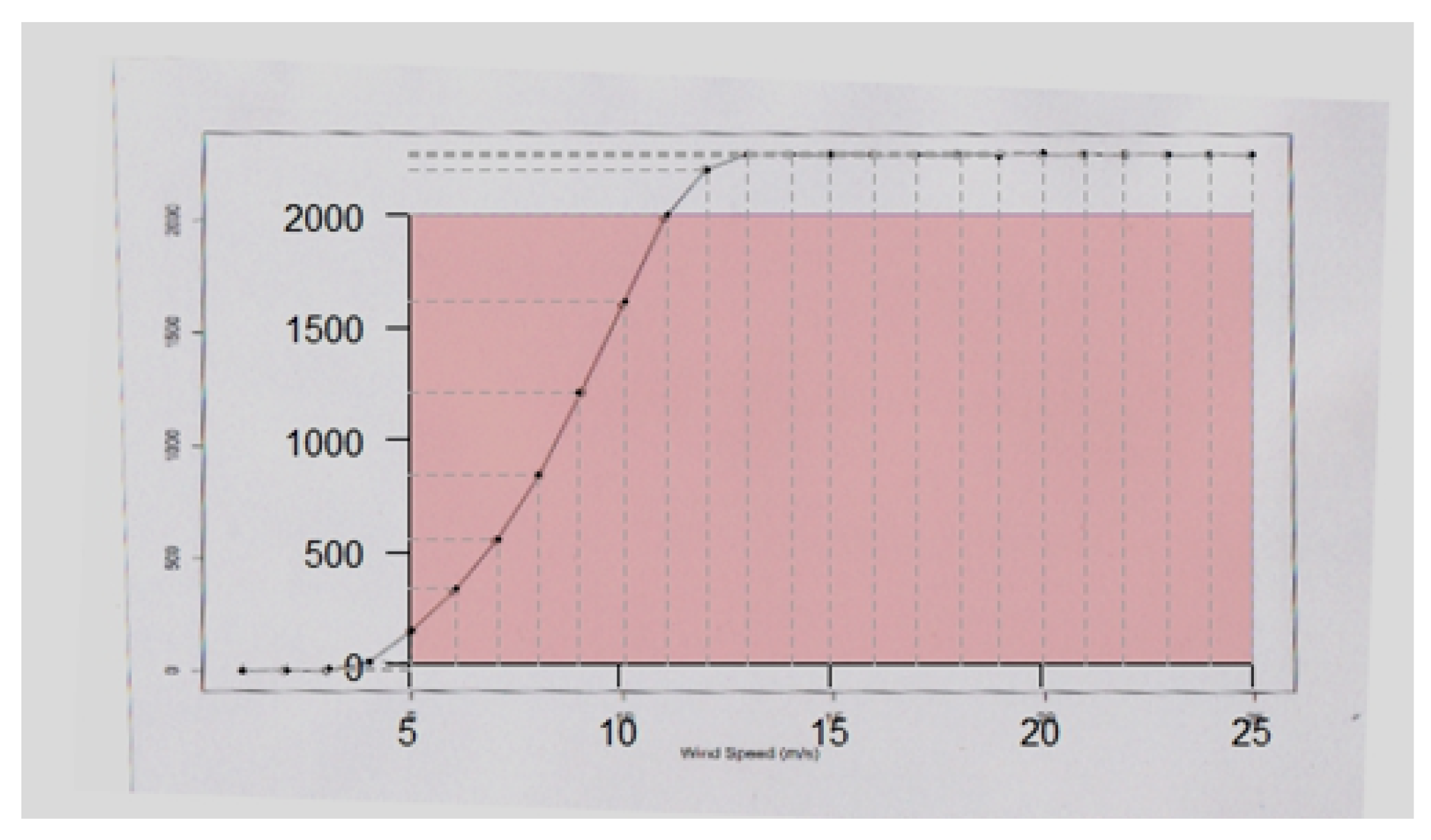
Figure A2.
Selection and mapping of two points on each X- and Y-axes.
Figure A2.
Selection and mapping of two points on each X- and Y-axes.
- 2.
Point to ‘
n’ numbers of points on the power curve image. (
Figure A3).
a <- img2points(“scanned_image.jpeg”, n = 25)
#> Click on leftmost point on X axis and then enter the value of the point:
#> Enter the value: 5
#> Click on rightmost point on X axis and then enter the value of the point:
#> Enter the value: 25
#> Click on lowermost point on Y axis and then enter the value of the point:
#> Enter the value: 0
#> Click on uppermost point on Y axis and then enter the value of the point:
#> Enter the value: 2000
#>
#> The image was tilted by -2.11550492800417 Degrees.
#> Do you wish to resize the Scale?(Y/N)
#> N
#>
#> Select desired 25 points on the curve:
#>
a
#> Speed Power
#> 1 1.033058 0.00000
#> 2 2.079890 0.00000
#> 3 3.016529 29.62963
#> 4 4.118457 44.44444
#> 5 5.000000 177.77778
#> 6 5.936639 370.37037
#> 7 6.983471 562.96296
#> 8 8.030303 874.07407
#> 9 9.022039 1244.44444
#> 10 10.068871 1644.44444
#> 11 11.060606 2014.81481
#> 12 11.997245 2222.22222
#> 13 12.988981 2311.11111
#> 14 14.035813 2311.11111
#> 15 15.027548 2311.11111
#> 16 16.019284 2311.11111
#> 17 17.011019 2311.11111
#> 18 18.002755 2311.11111
#> 19 18.994490 2325.92593
#> 20 20.041322 2311.11111
#> 21 20.977961 2325.92593
#> 22 22.024793 2325.92593
#> 23 23.016529 2325.92593
#> 24 24.008264 2325.92593
#> 25 25.000000 2325.92593
Figure A3.
Extraction of discrete points from the WT power curve.
Figure A3.
Extraction of discrete points from the WT power curve.
Appendix A.3.2. Step 2: Fit the Curve for Discrete Values Extracted in Step 1 with the ‘fitcurve()’ Function
The default syntax for the ‘fitcurve()’ function is as follows.
b <- fitcurve(data = a)
In this example, the following sample curve fitting method ‘random()’ is added in the study.
random <- function(x)
{
data_y <- sort(sample(1:1500, size = 25, replace = TRUE))
d <- data.frame(data_y)
return(d)
}
b <- fitcurve(data = a,
MethodPath = "source(’~/curves/random.R’)",
MethodName = "Random Method")
#> Weibull CDF model
#> -----------------
#> P = 1 - exp[-(S/C)^k]
#> where P -> Power and S -> Speed
#>
#> Shape (k) = 4.292249
#> Scale (C) = 9.713117
#> ===================================
#>
#> Logistic Function model
#> -----------------------
#> P = phi1/(1+exp((phi2-S)/phi3))
#> where P -> Power and S -> Speed
#>
#> phi 1 = 2325.242
#> phi 2 = 8.690274
#> phi 3 = 1.39292
#> ===================================
b
#> $Speed
#> [1] 0.9668508 2.0718232 3.0662983 4.0607735 5.0552486 6.0497238 6.9889503
#> [8] 8.0386740 8.9779006 10.1381215 11.0220994 12.0165746 13.0662983 14.0607735
#> [15] 15.0000000 16.1049724 17.0441989 18.0386740 19.0331492 20.1381215 21.0220994
#> [22] 22.0165746 23.0110497 24.0607735 25.0000000
#>
#> Power
#> [1] 0.00000 0.00000 0.00000 44.44444 177.77778 355.55556 577.77778
#> [8] 888.88889 1229.62963 1629.62963 2000.00000 2237.03704 2296.29630 2311.11111
#> [15] 2311.11111 2311.11111 2311.11111 2311.11111 2311.11111 2296.29630 2311.11111
#> [22] 2311.11111 2311.11111 2296.29630 2296.29630
#>
#> ‘Weibull CDF‘
#> [1] 0.00000 0.00000 0.00000 97.48009 177.77778 322.83674 534.25616
#> [8] 856.98139 1200.39308 1629.62963 1905.45360 2123.71918 2247.36848 2294.10923
#> [15] 2307.55658 2310.75608 2311.07933 2311.10965 2311.11107 2311.11111 2311.11111
#> [22] 2311.11111 2311.11111 2311.11111 2311.11111
#>
#> ‘Logistic Function‘
#> [1] 0.00000 0.00000 0.00000 80.85006 159.32640 303.66882 529.43169
#> [8] 895.54047 1282.23262 1717.75136 1958.12353 2129.70846 2228.92454 2277.05646
#> [15] 2300.43863 2313.95630 2319.47823 2322.41612 2323.85754 2324.61579 2324.91021
#> [22] 2325.07976 2325.16280 2325.20498 2325.22338
#>
#> ‘Random Method‘
#> [1] 52 73 84 176 212 230 306 323 345 357 481 723 753 813 862
#> [16] 954 963 1114 1159 1206 1302 1379 1379 1384 1483
#>
#> attr(,"row.names")
#> [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
#> attr(,"class")
#> [1] "fitcurve"$
Appendix A.3.3. Step 3: Compare the Fitted Curves
The default syntax for the ‘validate.curve()’ function is as follows.
validate.curve(x = b)
In this example, the following addition sample error metric ‘
error()’ (which returns the RSME values) is added in the study, and corresponding fitted curves can be plotted as shown in
Figure A4.
library(imputeTestbench)
error <- function(a,b)
{
c <- rmse(a,b)
return(c)
}
validate.curve(x = b,
MethodPath = "source(’~/curves/error.R’)", MethodName = "New Error")
#> Metrics Weibull CDF Logistic Function Random Method
#> 1 RMSE 36.2129522 39.8916751 1020.3785758
#> 2 MAE 20.5040548 29.0803404 870.4992593
#> 3 MAPE 4.2798325 5.0902950 132.7159241
#> 4 R2 0.9985355 0.9982228 -0.1627775
#> 5 COR 0.9993632 0.9991146 0.8734492
#> 6 New Error 36.2129522 39.8916751 1020.3785758
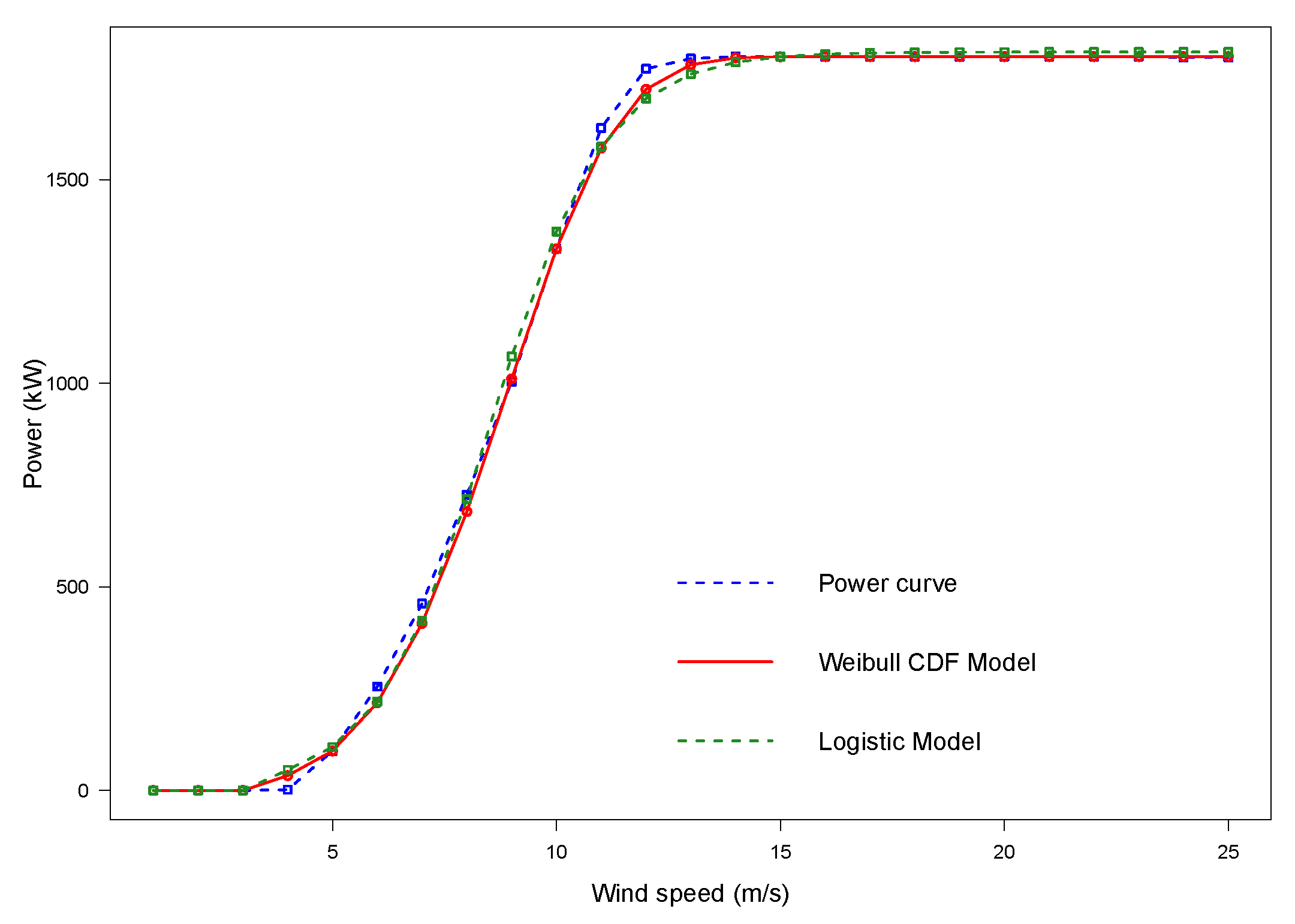
plot(b)
Figure A4.
The plot of the WT power curve fitted with the ‘fitcurve()’ function.
Figure A4.
The plot of the WT power curve fitted with the ‘fitcurve()’ function.