A Review of Mixture Theory for Deformable Porous Media and Applications
Abstract
:1. Introduction
2. Mixture Theory: General Framework
3. Applications of Mixture Theory
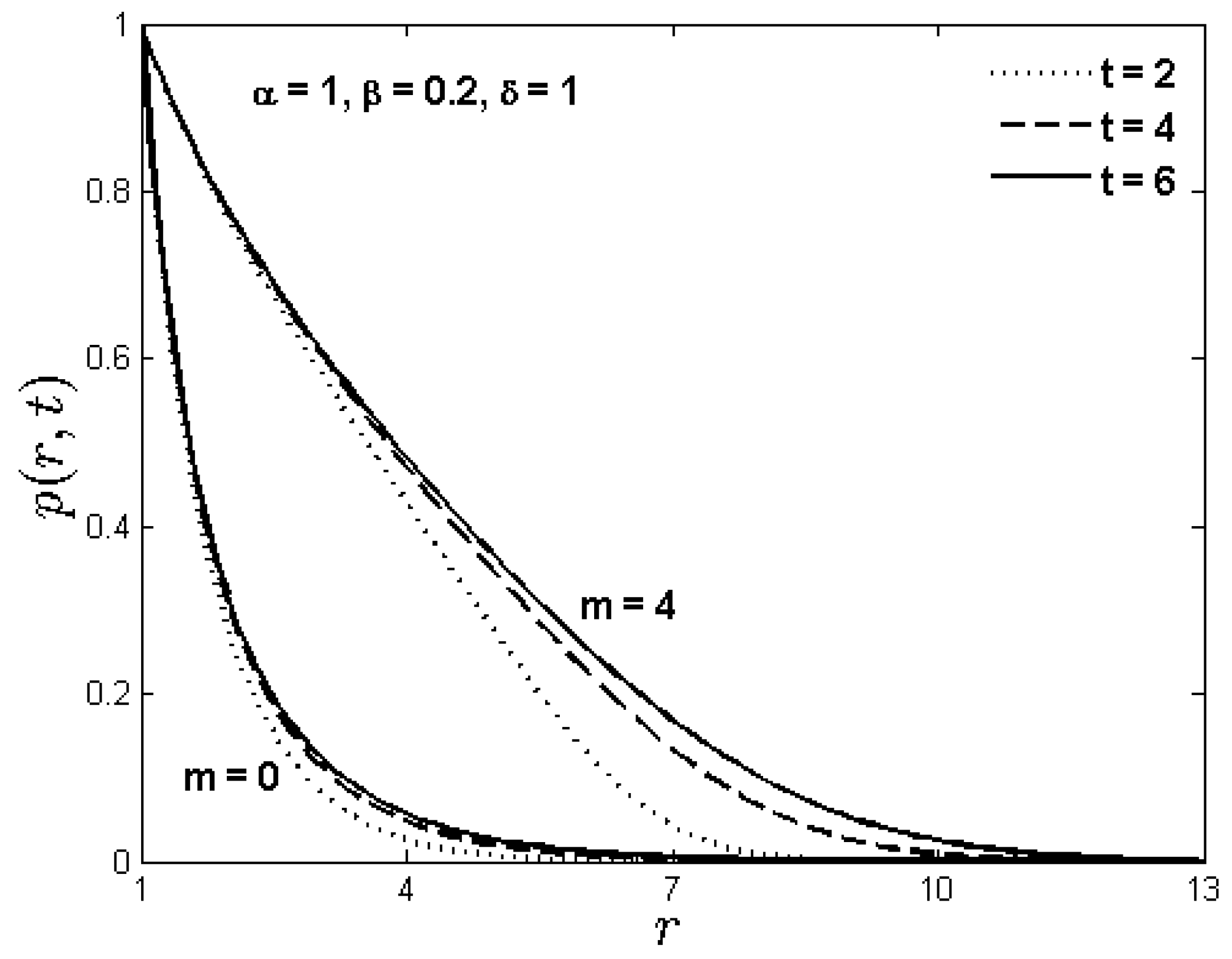
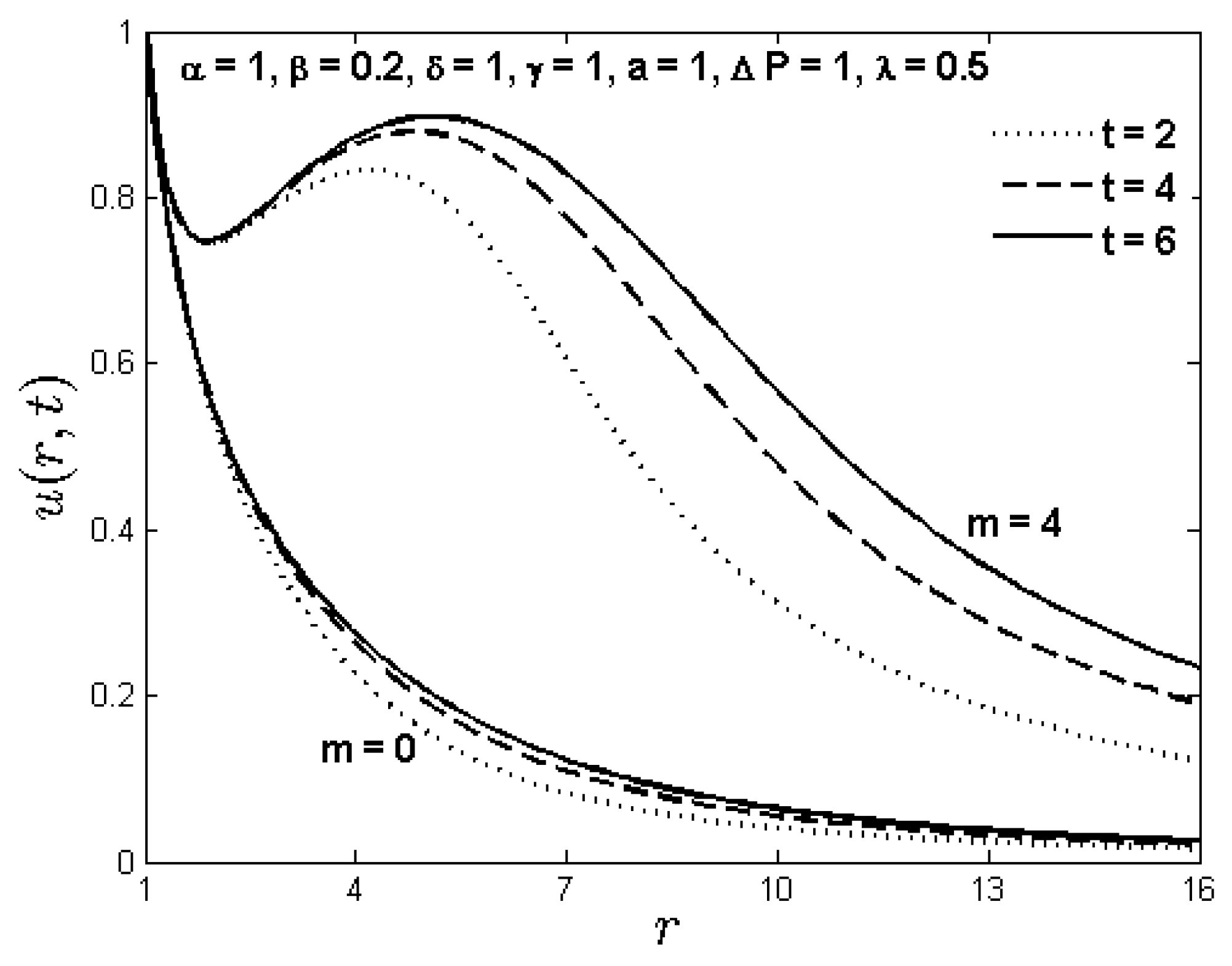
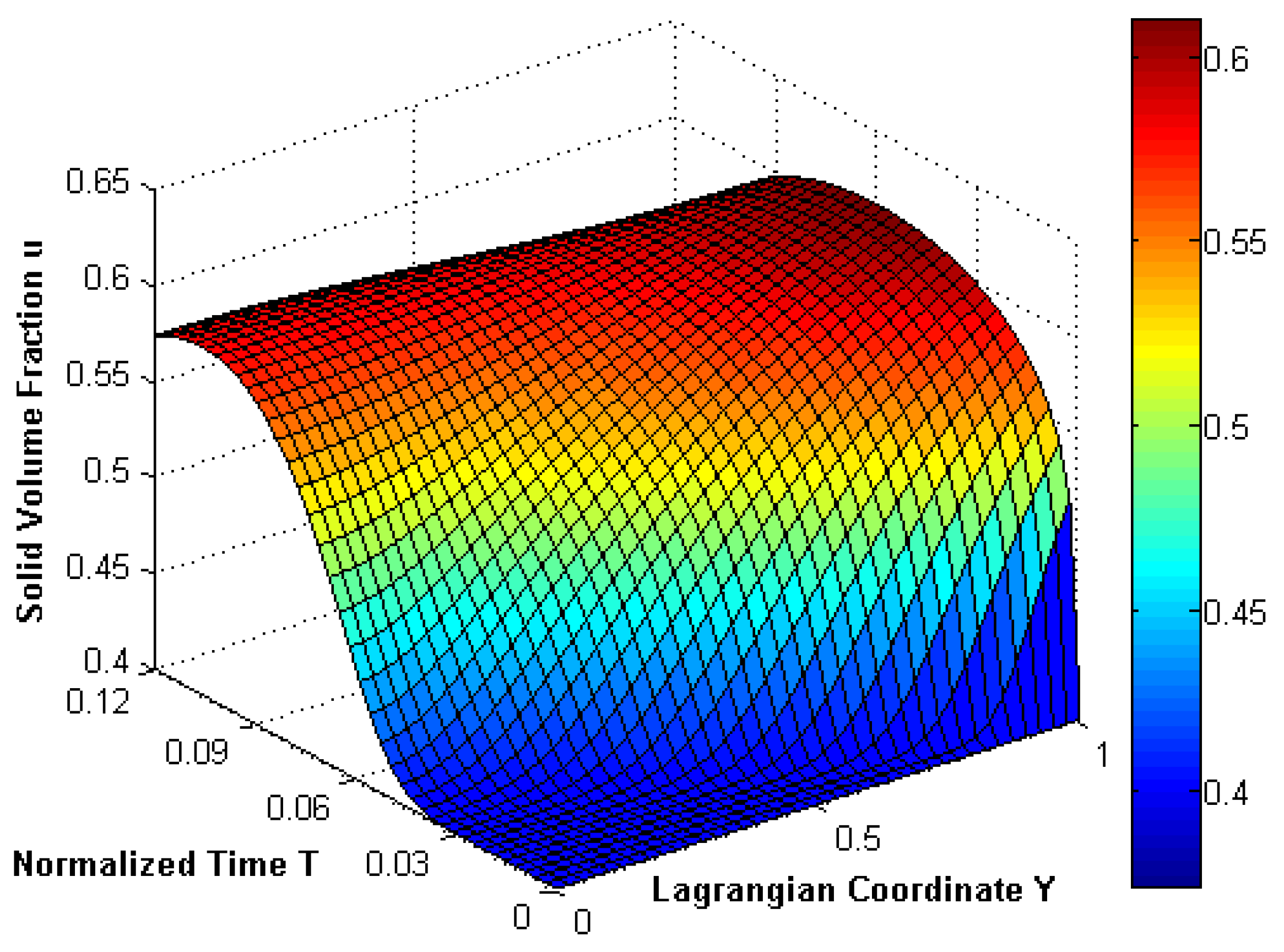
3.1. Flow Induced Deformation of Porous Biological Tissues
- tissue to be deformable fully fluid saturated of infinite extent
- initially tissue is homogeneous and isotropic
- capillaries and lymphatics are distributed uniformly through the porous tissue
- tissue has ability to absorb the fluid at a rate proportional to local pressure.
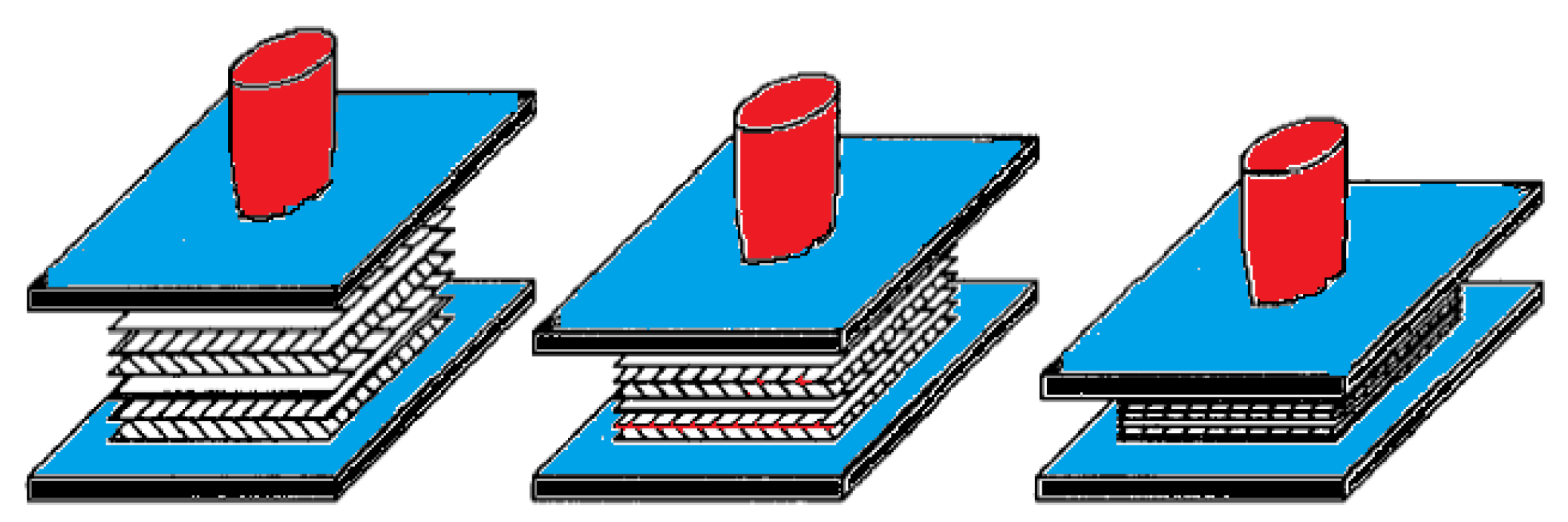
3.2. Mixture Theory Based Modelling and Simulation of Composite Manufacturing Processes
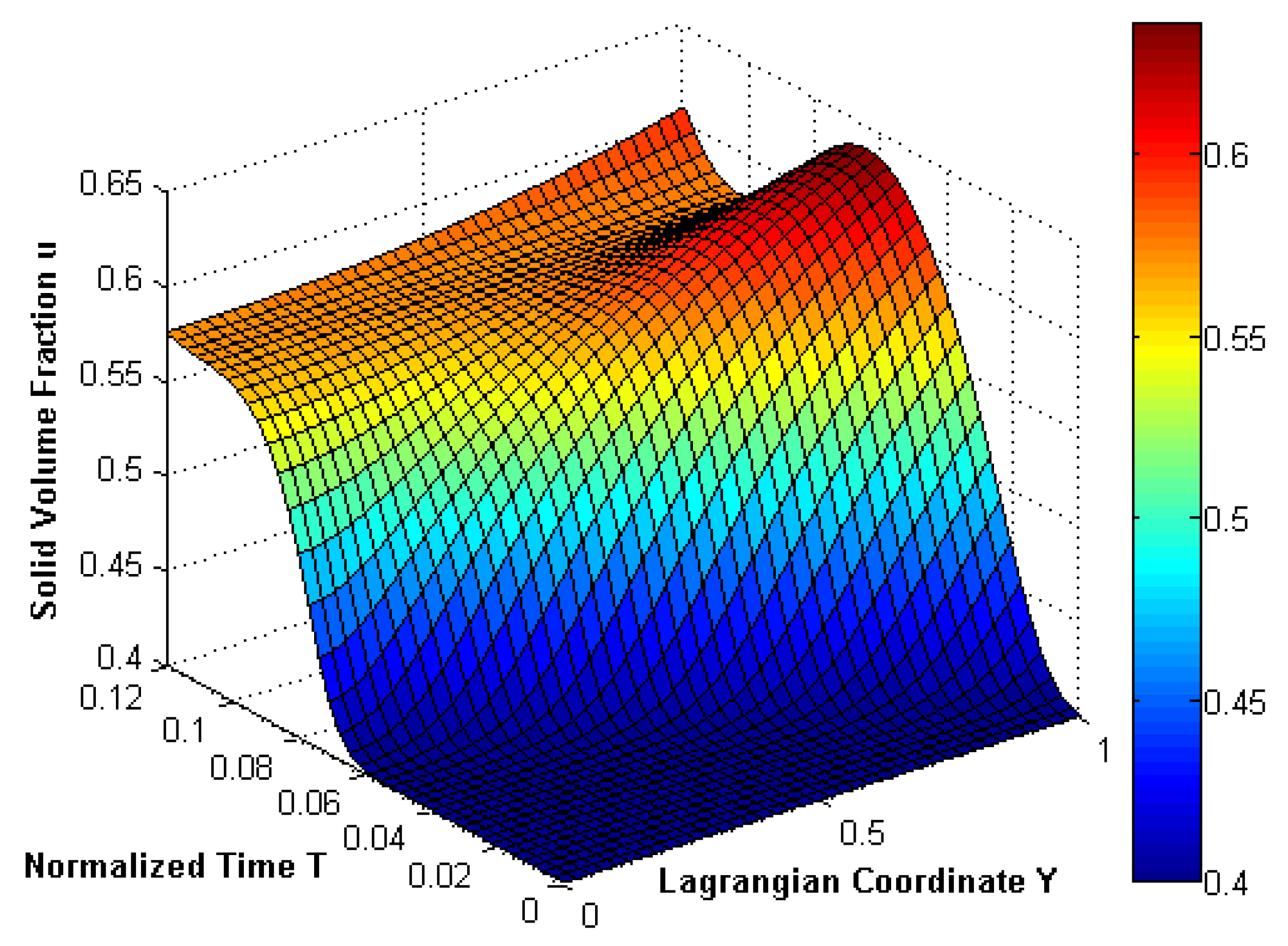
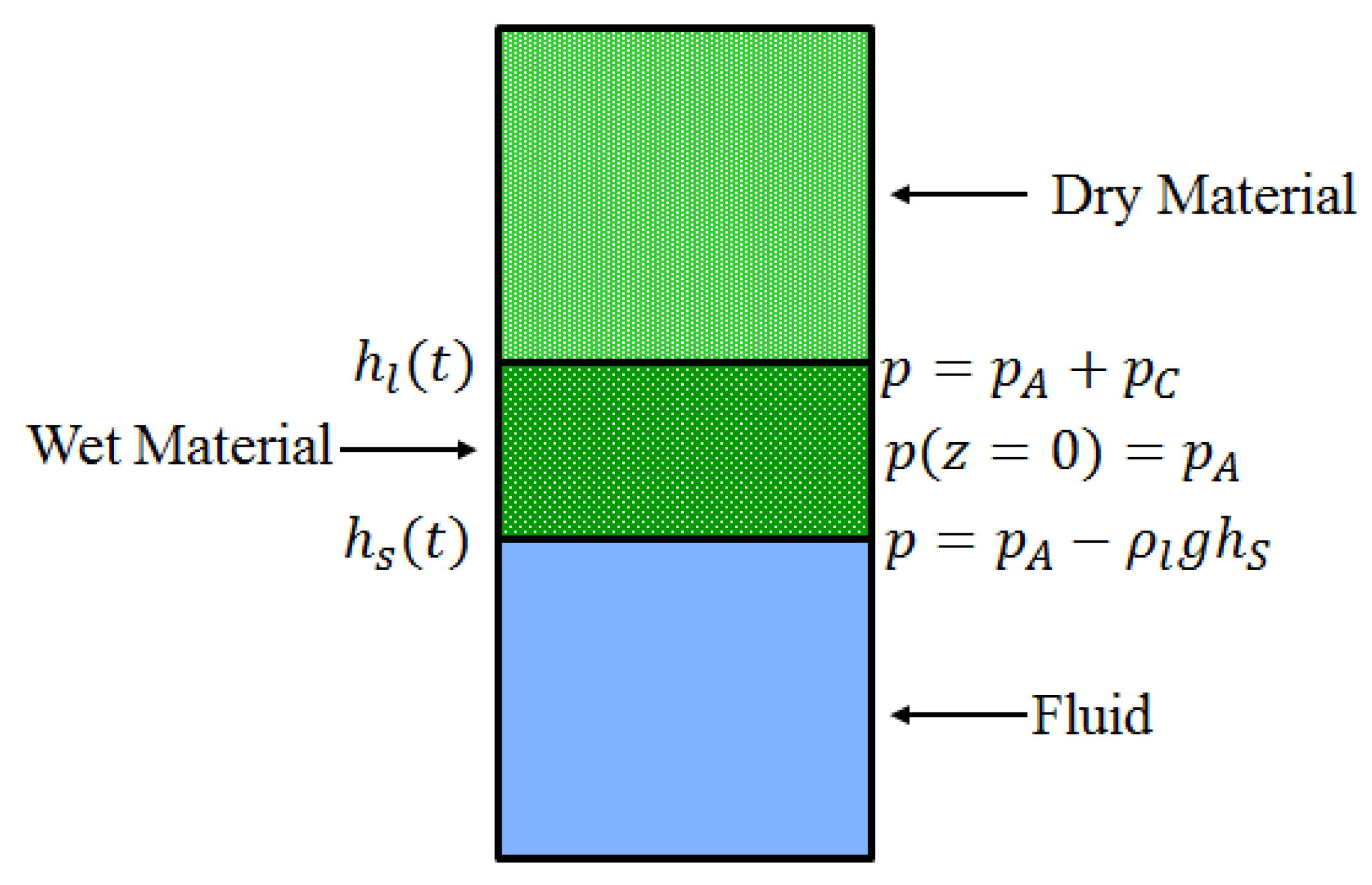
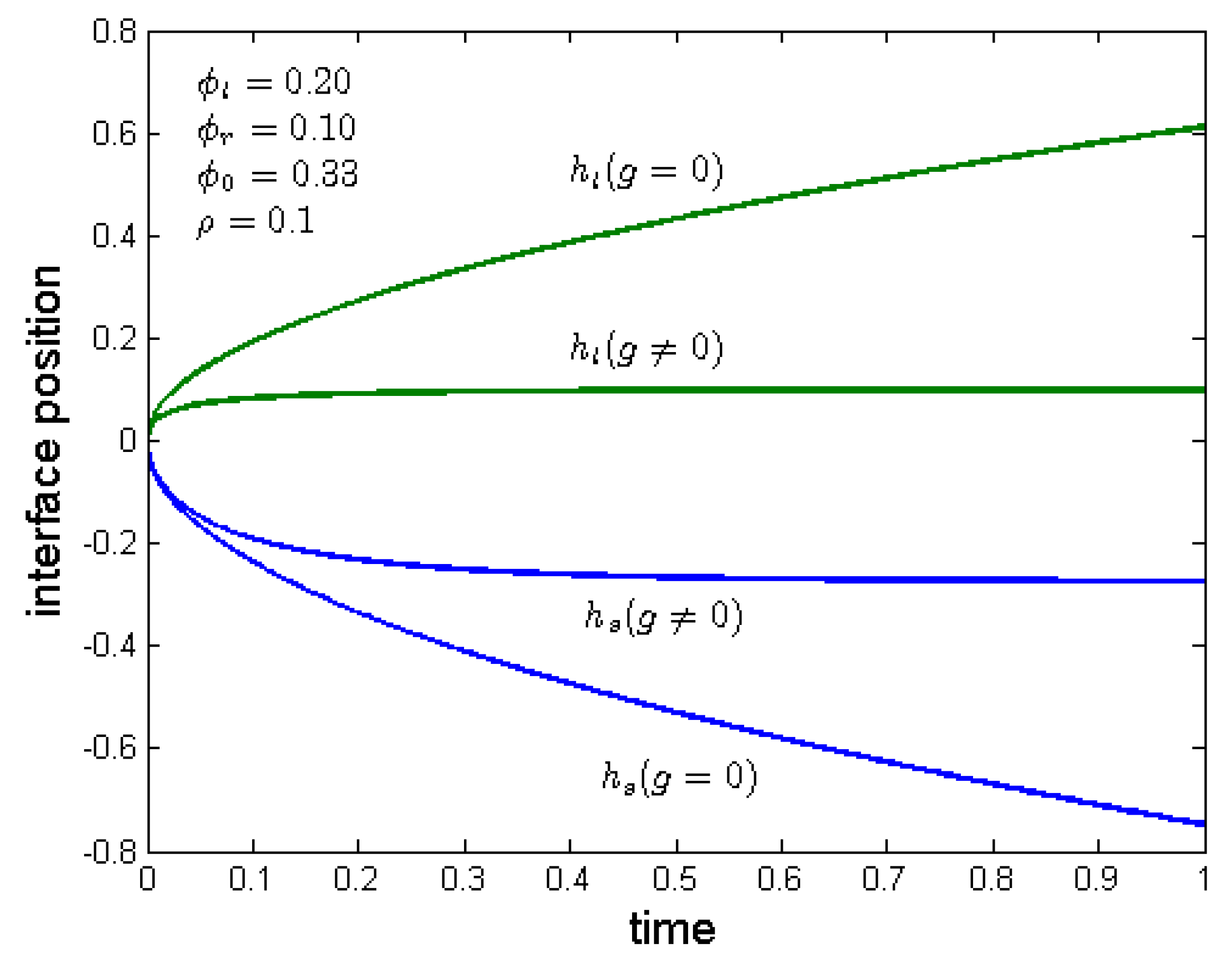
3.3. Unidirectional Capillary Rise into Deformable Porous Material
4. Further Applications of Mixture Theory
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bedford, A.; Drumheller, D.S. Theories of immiscible and structured mixtures. Int. J. Eng. Sci. 1983, 21, 863–960. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R.A. The classical field theories of mechanics. In Hand Book of Physics; Springer: New York, NY, USA, 1960; Volume 3. [Google Scholar]
- Truesdell, C. Sulle basi de la termomecanica. Rend. Acad. Lincei 1957, 22, 33–88. (In Italian) [Google Scholar]
- Truesdell, C. Rational Thermodynamics, 2nd ed.; Springer: New York, NY, USA, 1984. [Google Scholar]
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In The Non-Linear Field Theories of Mechanics; Springer: New York, NY, USA, 2004; pp. 1–579. [Google Scholar]
- Atkin, R.J.; Craine, R.E. Continuum theories of mixtures: Basic theory and historical development. Q. J. Mech. Appl. Math. 1976, 29, 209–244. [Google Scholar] [CrossRef]
- Terzaghi, K. Erdbaumechanik auf Bodenphysikalischer Grundlage; Franz Deuticke: Leipzig, Germany, 1925. (In German) [Google Scholar]
- Biot, M.A. General theory of three dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 1955, 26, 182–185. [Google Scholar] [CrossRef]
- Biot, M.A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Mow, V.C.; Lai, W.M. Mechanics of animal joints. Annu. Rev. Fluid Mech. 1979, 11, 247–288. [Google Scholar] [CrossRef]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic creep and stress relaxation of articular cartilage in compression: Theory and experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Mow, V.C.; Holmes, M.H.; Lai, W.M. Fluid transport and mechanical properties of articular cartilage: A review. J. Biomech. 1984, 17, 377–394. [Google Scholar] [CrossRef]
- Bowen, R.M. Incompressible porous media Models by use of the theory of mixtures. Int. J. Eng. Sci. 1980, 18, 1129–1148. [Google Scholar] [CrossRef]
- Ambrosi, D.; Preziosi, L. Modeling injection molding processes with deformable porous preforms. SIAM J. Appl. Math. 2000, 61, 22–42. [Google Scholar] [CrossRef]
- Barry, S.I.; Aldis, G.K. Flow-induced deformation from pressurized cavities in absorbing porous tissues. Bull. Math. Biol. 1992, 54, 977–997. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.M.; Siddique, J.I. Modeling wicking in deformable porous media using mixture theory. In Wicking in Porous Materials: Traditional and Modern Modeling Approaches; CRC Press: Boca Raton, FL, USA, 2012; p. 295. [Google Scholar]
- Barry, S.I.; Aldis, G.K. Comparison of models for flow induced deformation of soft biological tissue. J. Biomech. 1990, 23, 647–654. [Google Scholar] [CrossRef]
- Siddique, J.I.; Anderson, D.M. Capillary rise of a non-Newtonian liquid into a deformable porous material. J. Porous Media 2011, 14, 1087–1102. [Google Scholar] [CrossRef]
- Siddique, J.I.; Anderson, D.M.; Bondarev, A. Capillary rise of a liquid into a deformable porous material. Phys. Fluids 2009, 21, 013106. [Google Scholar] [CrossRef]
- Klanchar, M.; Tarbell, J.M. Modeling water flow through arterial tissue. Bull. Math. Biol. 1987, 49, 651–669. [Google Scholar] [CrossRef] [PubMed]
- Farina, A.; Cocito, P.; Boretto, G. Flow in deformable porous media: modelling and simulations of compression moulding processes. Math. Comput. Model. 1997, 26, 1–15. [Google Scholar] [CrossRef]
- Barry, S.I.; Aldis, G.K. Radial flow through deformable porous shells. J. Aust. Math. Soc. Ser. B 1993, 34, 333–354. [Google Scholar] [CrossRef]
- Barry, S.I.; Aldis, G.K. Unsteady flow induced deformation of porous materials. Int. J. Non-Linear Mech. 1991, 26, 687–699. [Google Scholar] [CrossRef]
- Barry, S.I.; Parkerf, K.H.; Aldis, G.K. Fluid flow over a thin deformable porous layer. Z. Angew. Math. Phys. 1991, 42, 633–648. [Google Scholar] [CrossRef]
- Preziosi, L.; Joseph, D.D.; Beavers, G.S. Infiltration of initially dry, deformable porous media. Int. J. Multiph. Flow 1996, 22, 1205–1222. [Google Scholar] [CrossRef]
- Billi, L.; Farina, A. Unidirectional infiltration in deformable porous media: Mathematical modeling and self-similar solution. Q. Appl. Math. 2000, 58, 85–101. [Google Scholar] [CrossRef]
- Preziosi, L. The theory of deformable porous media and its application to composite materials manufacturing. Surv. Math. Ind. 1996, 6, 167–214. [Google Scholar]
- Anderson, D.M. Imbibition of a liquid droplet on a deformable porous substrate. Phys. Fluids 2005, 17, 087104. [Google Scholar] [CrossRef]
- Siddique, J.I.; Kara, A. Capillary rise of magnetohydrodynamics liquid into deformable porous material. J. Appl. Fluid Mech. 2016, 9, 2837–2843. [Google Scholar]
- Sommer, J.L.; Mortensen, A. Forced unidirectional infiltration of deformable porous media. J. Fluid Mech. 1996, 311, 193–217. [Google Scholar] [CrossRef]
- Humphrey, J.D. Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2003, 459, 3–46. [Google Scholar] [CrossRef]
- Lai, W.M. Drag induced compression of articular cartilage during a permeation experiment. J. Biorheol. 1980, 17, 111–123. [Google Scholar]
- Mow, V.C.; Kwan, M.K.; Lai, W.M.; Holmes, M.H. A finite deformation theory for nonlinearly permeable soft hydrated biological tissues. In Frontiers in Biomechanics; Springer: New York, NY, USA, 1986; pp. 153–179. [Google Scholar]
- Lai, W.M.; Hou, J.S.; Mow, V.C. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J. Biomech. Eng. 1991, 113, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Ricken, T.; Schwarz, A.; Bluhm, J. A triphasic theory for growth in biological tissue-basics and applications. Materialwiss. Werkstofftech. 2006, 37, 446–456. [Google Scholar] [CrossRef]
- Myers, T.G.; Aldis, G.K.; Naili, S. Ion induced deformation of soft tissue. Bull. Math. Biol. 1995, 57, 77–98. [Google Scholar] [CrossRef] [PubMed]
- Frijns, A.J.H.; Huyghe, J.M.; Janssen, J.D. A validation of the quadriphasic mixture theory for intervertebral disc tissue. Int. J. Eng. Sci. 1997, 35, 1419–1429. [Google Scholar] [CrossRef]
- Holmes, M.H. A nonlinear diffusion equation arising in the study of soft tissue. Q. Appl. Math. 1983, 41, 209–220. [Google Scholar] [CrossRef]
- Holmes, M.H. Comparison theorems and similarity solution approximations for a nonlinear diffusion equation arising in the study of soft tissue. SIAM J. Appl. Math. 1984, 44, 545–556. [Google Scholar] [CrossRef]
- Lekszycki, T.; Dell’Isola, F. A mixture model with evolving mass densities for describing synthesis and resorption phenomena in bones reconstructed with bio-resorbable materials. Z. Angew. Math. Mech. 2012, 92, 426–444. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; Scerrato, D.; Dell’Isola, F. A visco-poroelastic model of functional adaptation in bones reconstructed with bio-resorbable materials. Biomech. Model. Mechanobiol. 2016, 15, 1325–1343. [Google Scholar] [CrossRef] [PubMed]
- Kenyon, D.E. The theory of an incompressible solid-fluid mixture. Arch. Ration. Mech. Anal. 1976, 62, 131–147. [Google Scholar] [CrossRef]
- Jayaraman, G. Water transport in the arterial wall a theoretical study. J. Biomech. 1983, 16, 833–840. [Google Scholar] [CrossRef]
- Friedman, M.H. General theory of tissue swelling with application to the corneal stroma. J. Theor. Biol. 1971, 30, 93–109. [Google Scholar] [CrossRef]
- Oomens, C.W.J.; van Campen, D.H.; Grootenboer, H.J. A mixture approach to the mechanics of skin. J. Biomech. 1987, 20, 877–885. [Google Scholar] [CrossRef]
- Ford, T.R.; Sachs, J.S.; Grotberg, J.B.; Glucksberg, M.R. Mechanics of the perialveolar interstitium of the lung. In Proceedings of the First World Congress of Biomechanics, La Jolla, CA, USA, 30 August–4 September 1990; Volume 1, p. 31. [Google Scholar]
- Byrne, H.; Preziosi, L. Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 2003, 20, 341–366. [Google Scholar] [CrossRef] [PubMed]
- Ambrosi, D.; Preziosi, L. On the closure of mass balance models for tumor growth. Math. Model. Methods Appl. Sci. 2002, 12, 737–754. [Google Scholar] [CrossRef]
- Preziosi, L.; Tosin, A. Multiphase and multiscale trends in cancer modelling. Math. Model. Nat. Phenom. 2009, 4, 1–11. [Google Scholar] [CrossRef]
- Ambrosi, D.; Preziosi, L.; Vitale, G. The insight of mixtures theory for growth and remodeling. Z. Angew. Math. Phys. 2010, 61, 177–191. [Google Scholar] [CrossRef]
- Cvetković, B.P.; Kuzmanović, D.S.; Cvetković, P.A. An application of continuum theory on the case of one-dimensional sedimentation. FME Trans. 2011, 39, 61–65. [Google Scholar]
- Nayfeh, A.H. A continuum mixture theory of heat conduction in laminated composites. J. Appl. Mech. 1975, 42, 399–404. [Google Scholar] [CrossRef]
- Rosi, G.; Placidi, L.; Dell’Isola, F. Fast and slow pressure waves electrically induced by nonlinear coupling in Biot-type porous medium saturated by a nematic liquid crystal. Z. Angew. Math. Phys. 2017, 68, 51–64. [Google Scholar] [CrossRef]
- Baer, M.R.; Nunziato, J.W. A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Kirwan, A.D. A review of mixture theory with applications in physical oceanography and meteorology. J. Geophys. Res. Oceans 1985, 90, 3265–3283. [Google Scholar] [CrossRef]
- Decker, R. A continuum mixture theory with an application to turbulent snow, air flows and sedimentation. J. Wind Eng. Ind. Aerodyn. 1990, 36, 877–887. [Google Scholar] [CrossRef]
- Del Bufalo, G.; Placidi, L.; Porfiri, M. A mixture theory framework for modeling the mechanical actuation of ionic polymer metal composites. Smart Mater. Struct. 2008, 17, 045010. [Google Scholar] [CrossRef]
- De Boer, R. Trends in Continuum Mechanics of Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Chen, P.J. A coupled solid/fluids mixture theory that suffices for diffusion problems. J. Elast. 1996, 45, 117–134. [Google Scholar] [CrossRef]
- Eringen, A.C. A mixture theory of electromagnetism and superconductivity. Int. J. Eng. Sci. 1998, 36, 525–543. [Google Scholar] [CrossRef]
- Peng, X.; Han, Y.; Huang, S. A mixture theory based constitutive model for SMA. Mech. Res. Commun. 2000, 27, 21–28. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Mohammad, L.; Wang, Y. Application of mixture theory in the evaluation of mechanical properties of asphalt concrete. J. Mater. Civ. Eng. 2004, 16, 167–174. [Google Scholar] [CrossRef]
- Krishnan, J.M.; Rao, C.L. Permeability and bleeding of asphalt concrete using mixture theory. Int. J. Eng. Sci. 2001, 39, 611–627. [Google Scholar] [CrossRef]
- Krishnan, J.M.; Rao, C.L. Mechanics of air voids reduction of asphalt concrete using mixture theory. Int. J. Eng. Sci. 2000, 38, 1331–1354. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Yalamanchili, R.C.; Wineman, A.S. Modeling electro-rheological materials through mixture theory. Int. J. Eng. Sci. 1994, 32, 481–500. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, C.R. The Coupled Theory of Mixtures in Geomechanics with Applications; Springer: New York, NY, USA, 2006. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddique, J.I.; Ahmed, A.; Aziz, A.; Khalique, C.M. A Review of Mixture Theory for Deformable Porous Media and Applications. Appl. Sci. 2017, 7, 917. https://doi.org/10.3390/app7090917
Siddique JI, Ahmed A, Aziz A, Khalique CM. A Review of Mixture Theory for Deformable Porous Media and Applications. Applied Sciences. 2017; 7(9):917. https://doi.org/10.3390/app7090917
Chicago/Turabian StyleSiddique, Javed Iqbal, Aftab Ahmed, Asim Aziz, and Chaudry Masood Khalique. 2017. "A Review of Mixture Theory for Deformable Porous Media and Applications" Applied Sciences 7, no. 9: 917. https://doi.org/10.3390/app7090917
APA StyleSiddique, J. I., Ahmed, A., Aziz, A., & Khalique, C. M. (2017). A Review of Mixture Theory for Deformable Porous Media and Applications. Applied Sciences, 7(9), 917. https://doi.org/10.3390/app7090917




