Ultrashort Free-Electron Laser X-ray Pulses
Abstract
1. Introduction—Laser-Assisted Time-Domain Characterization at Free-Electron Lasers
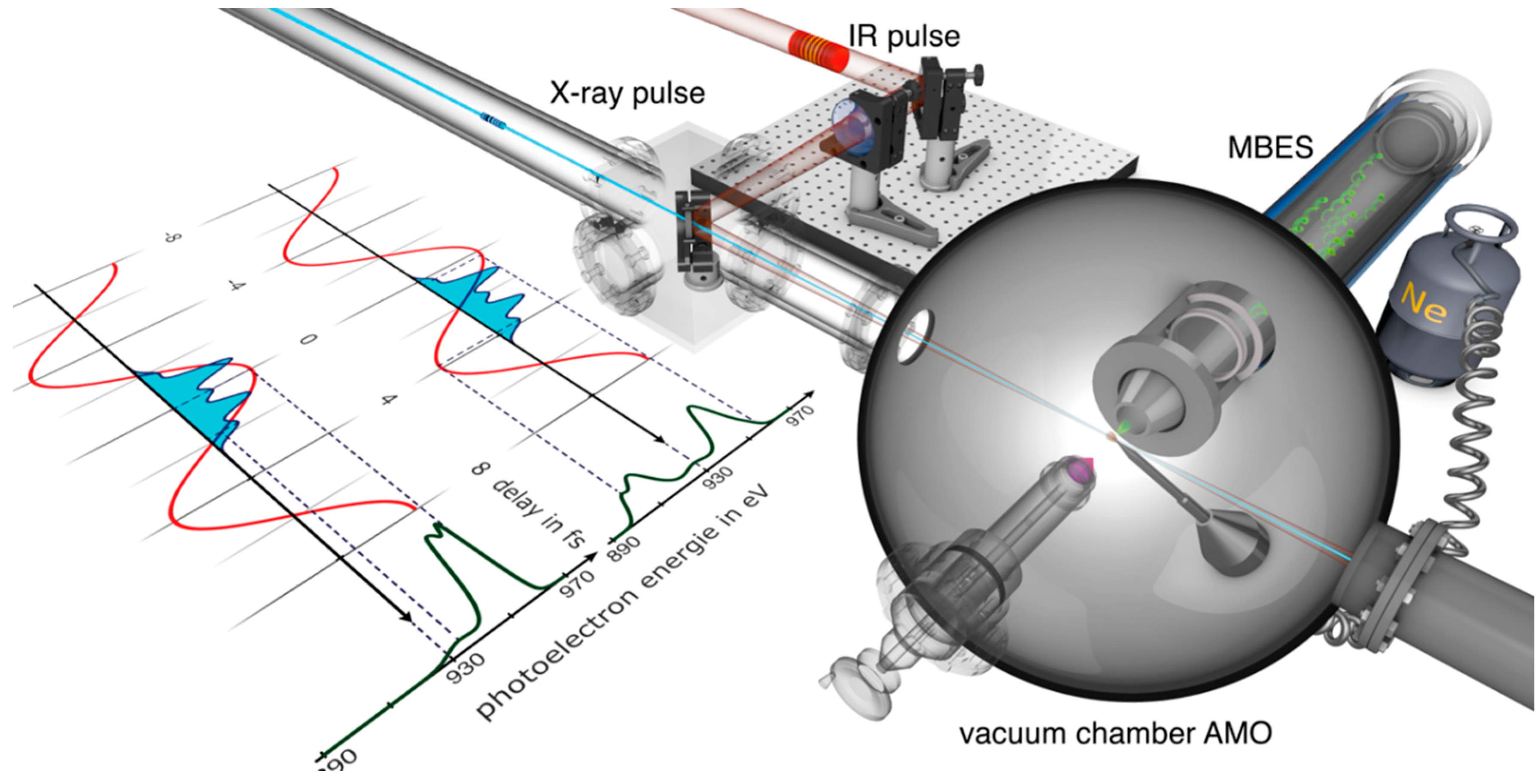
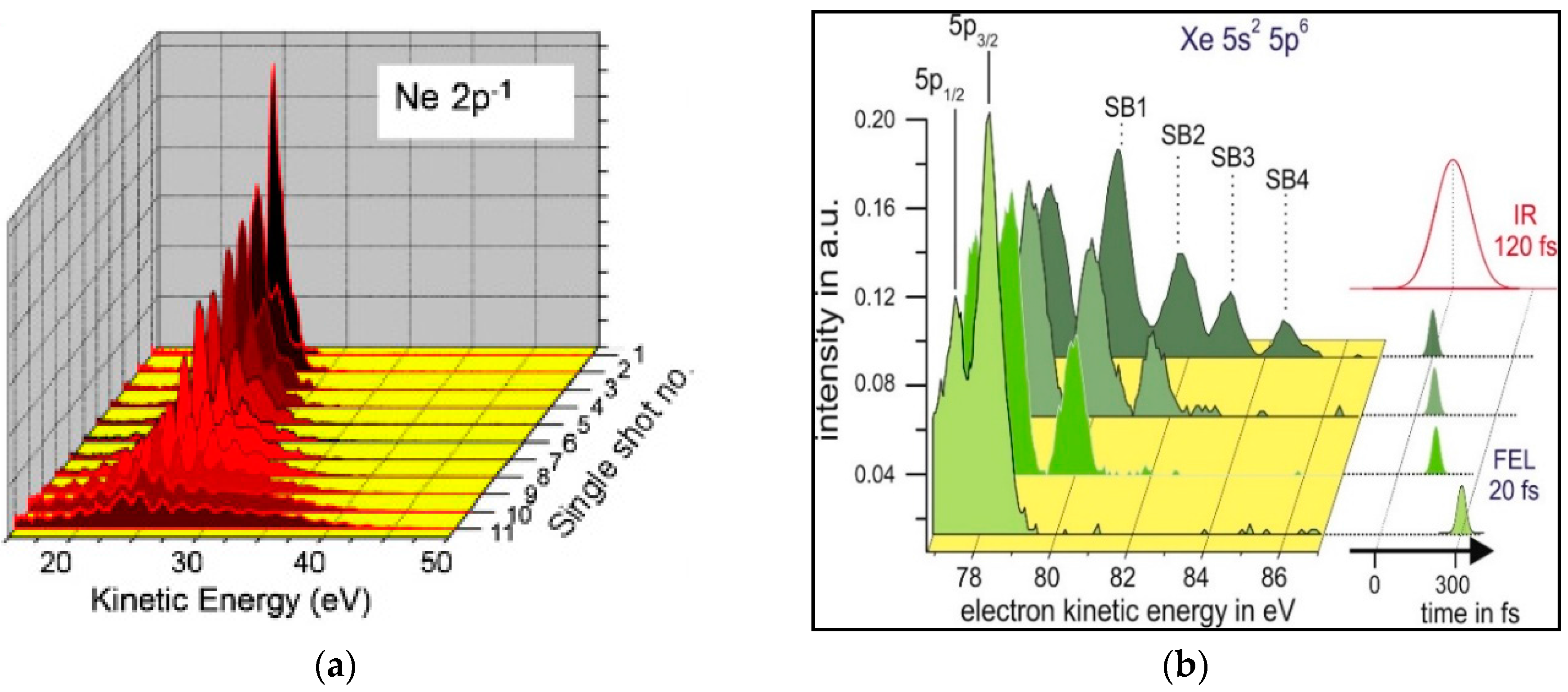
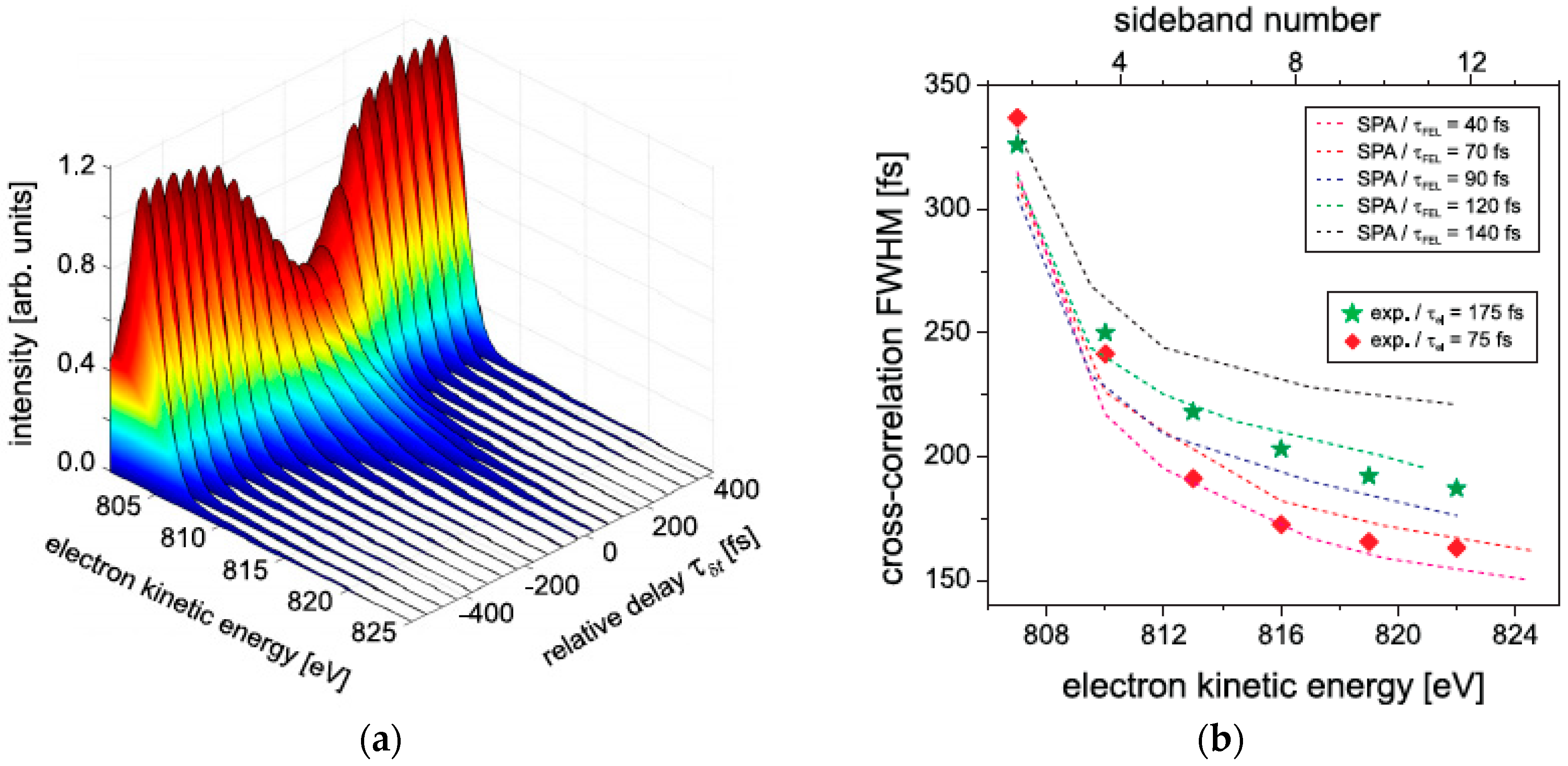
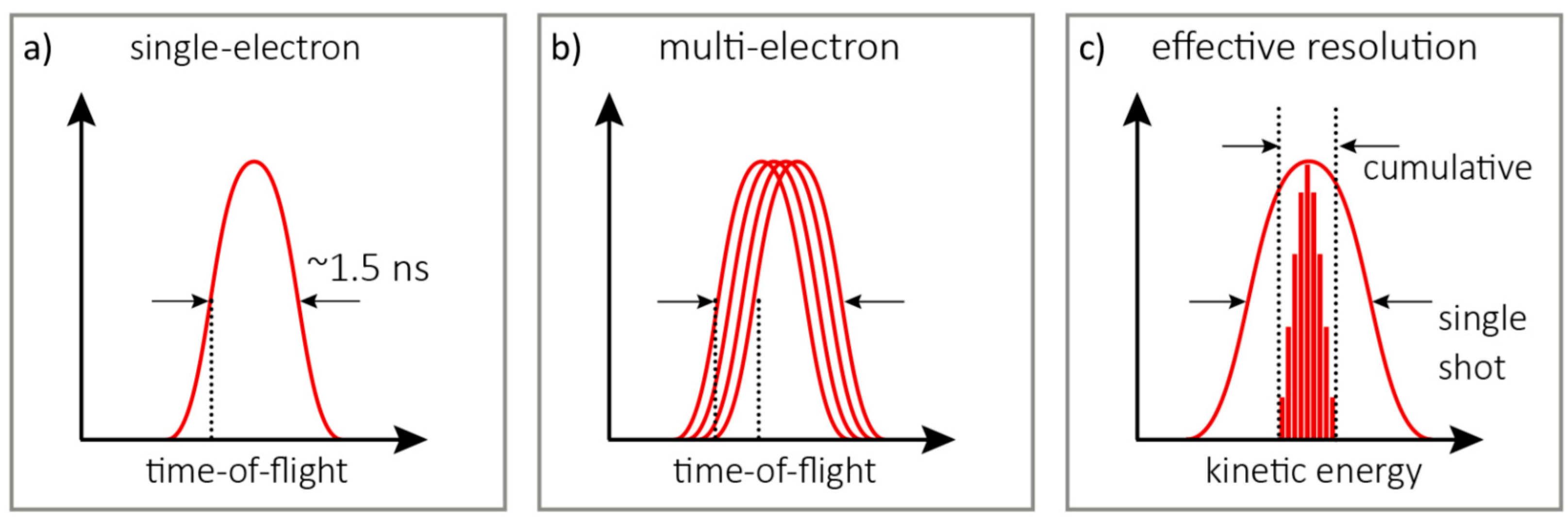
2. Sideband Method for X-ray Pulse Characterization
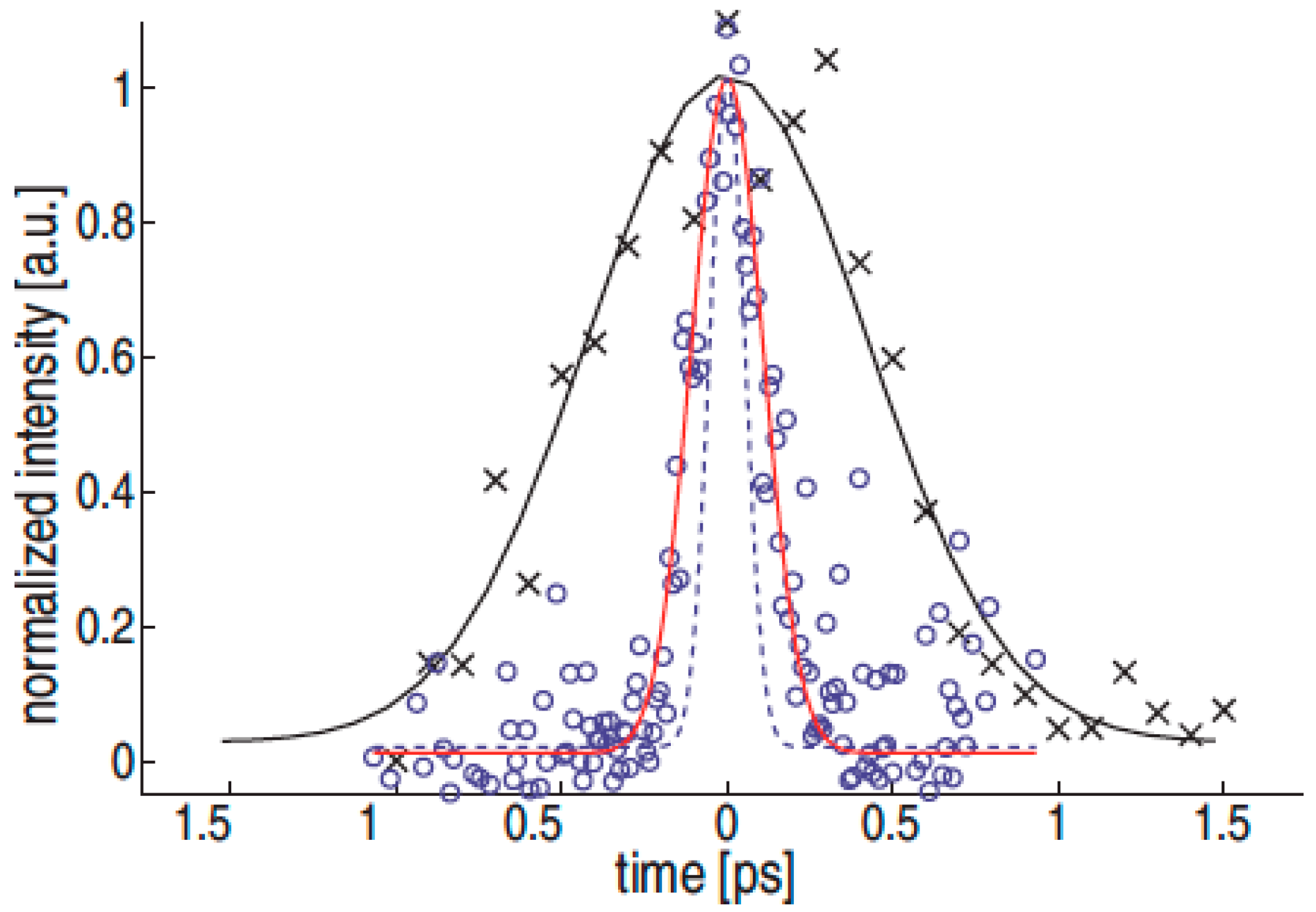
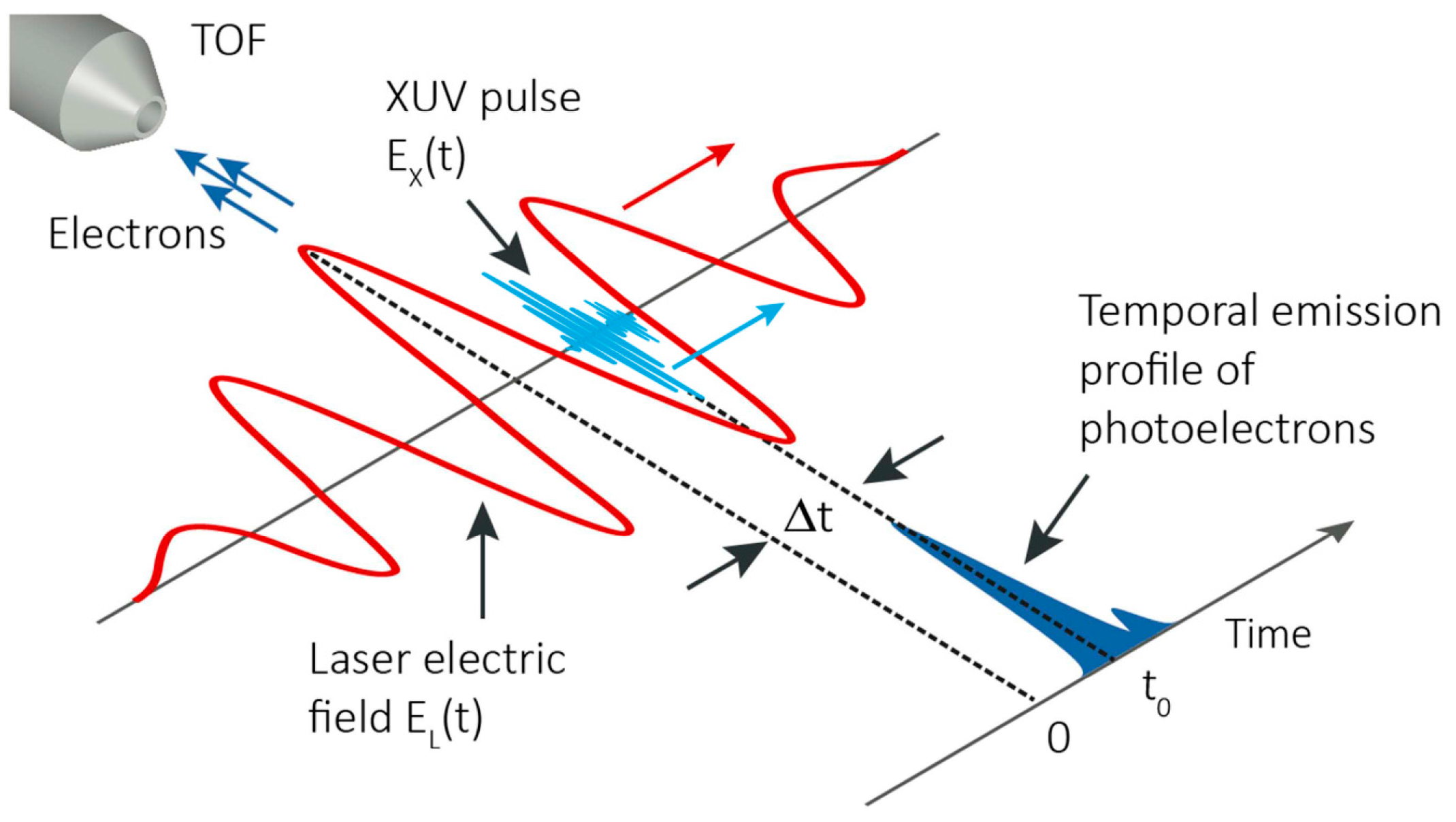
3. Linear Streaking Measurements at Free-Electron Lasers
3.1. Streaking Measurements of Soft X-ray Pulses
3.1.1. Infrared Streaking Experiments at Free-Electron Lasers
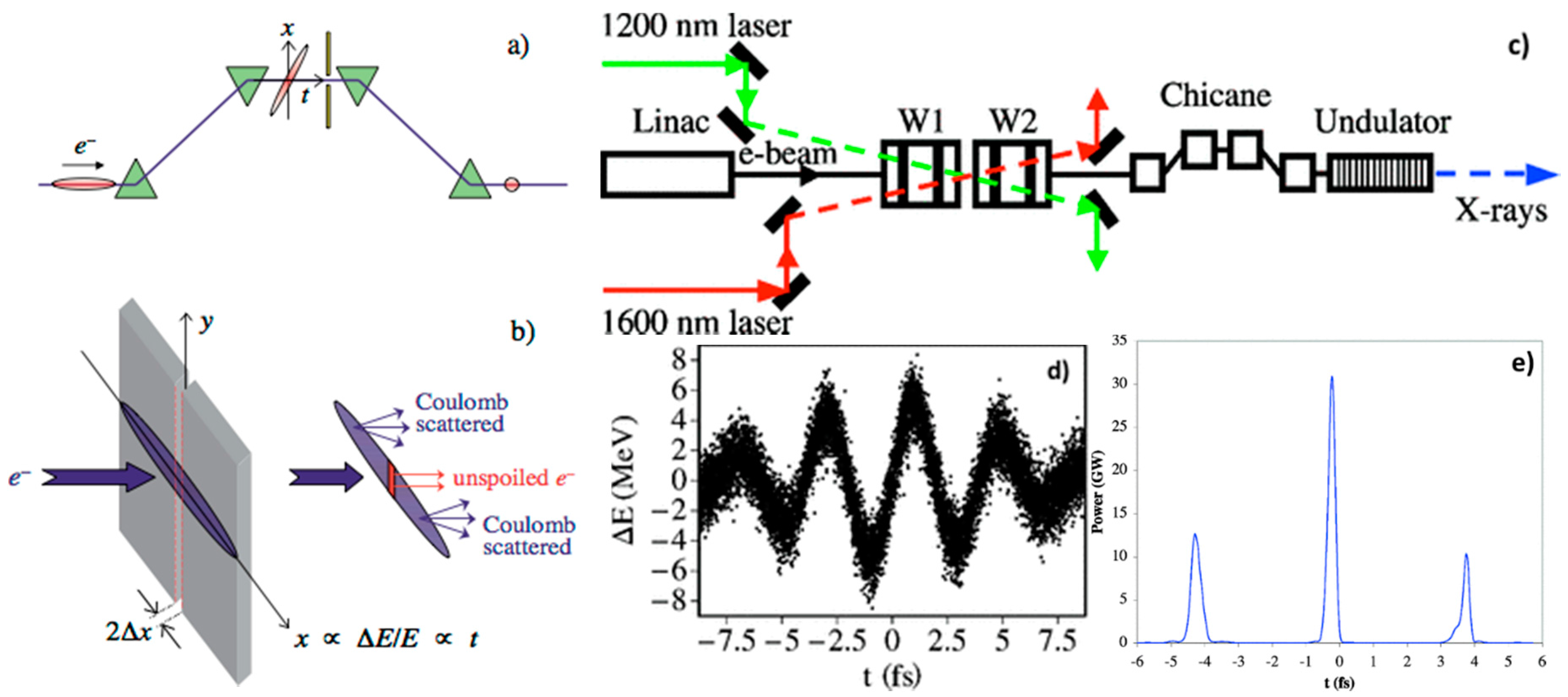
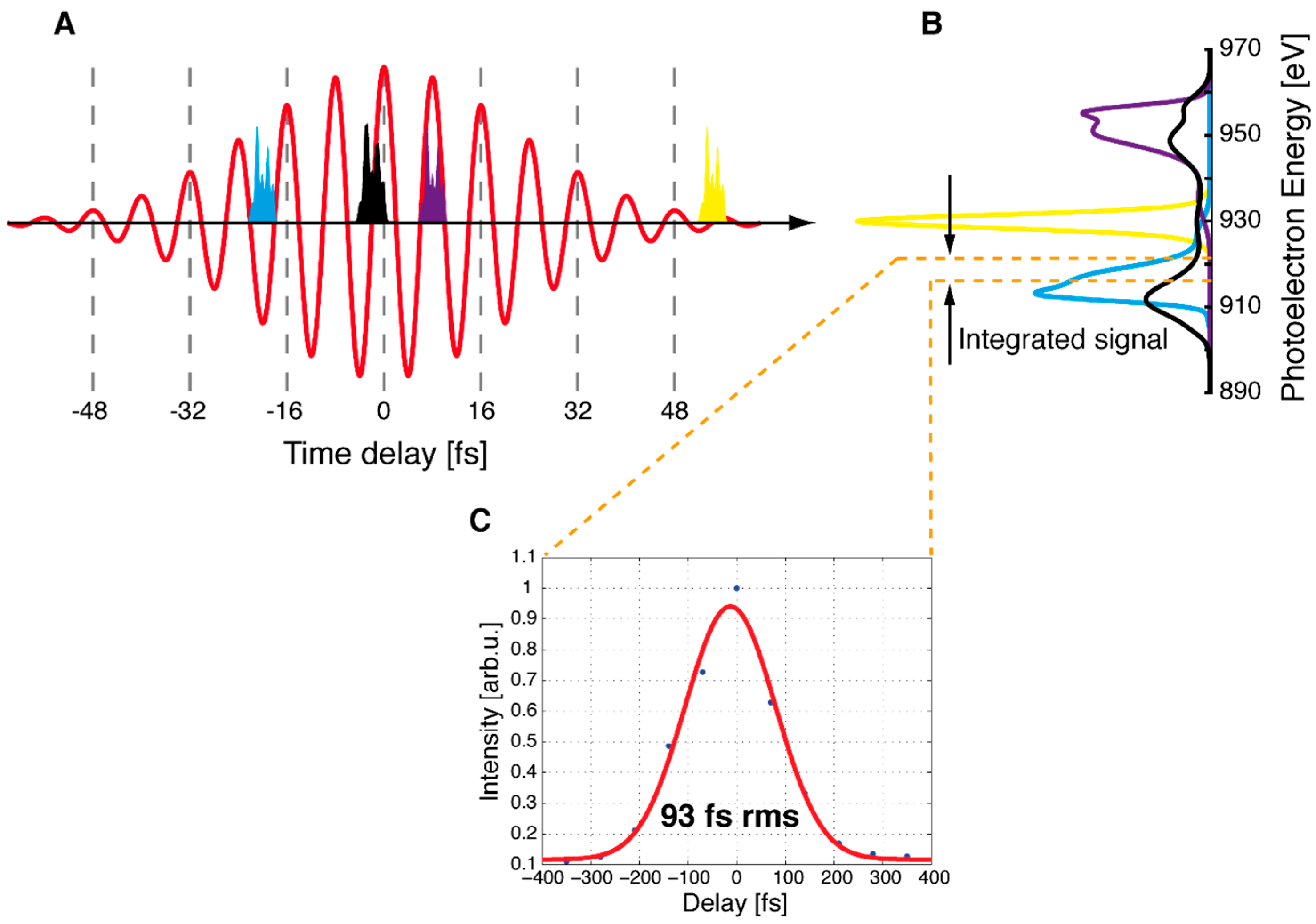
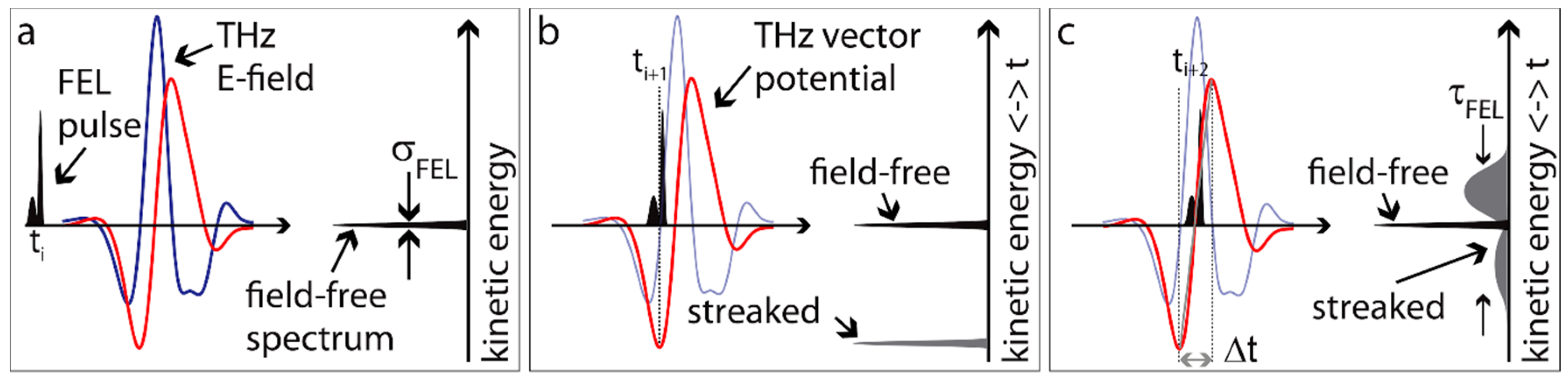
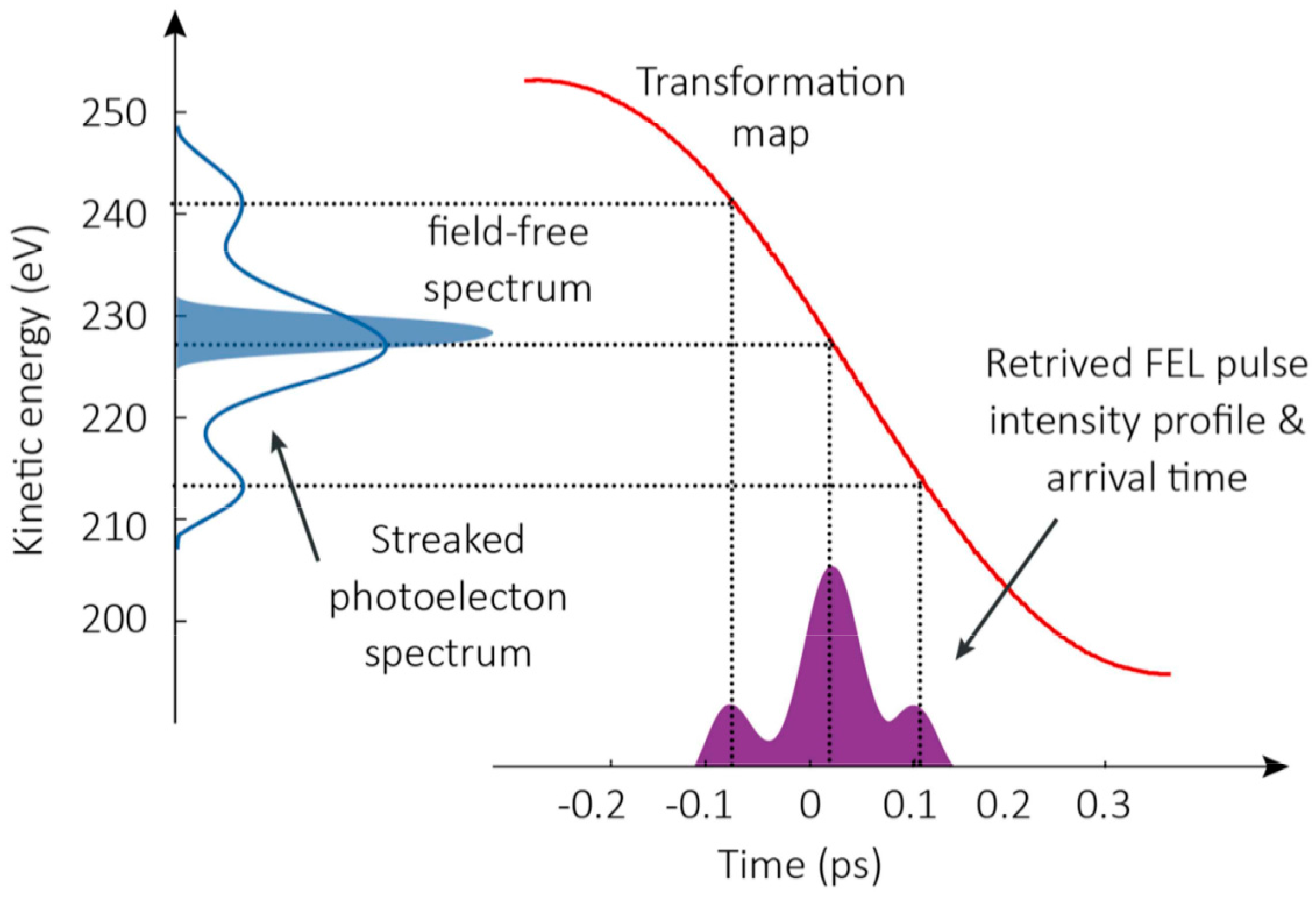
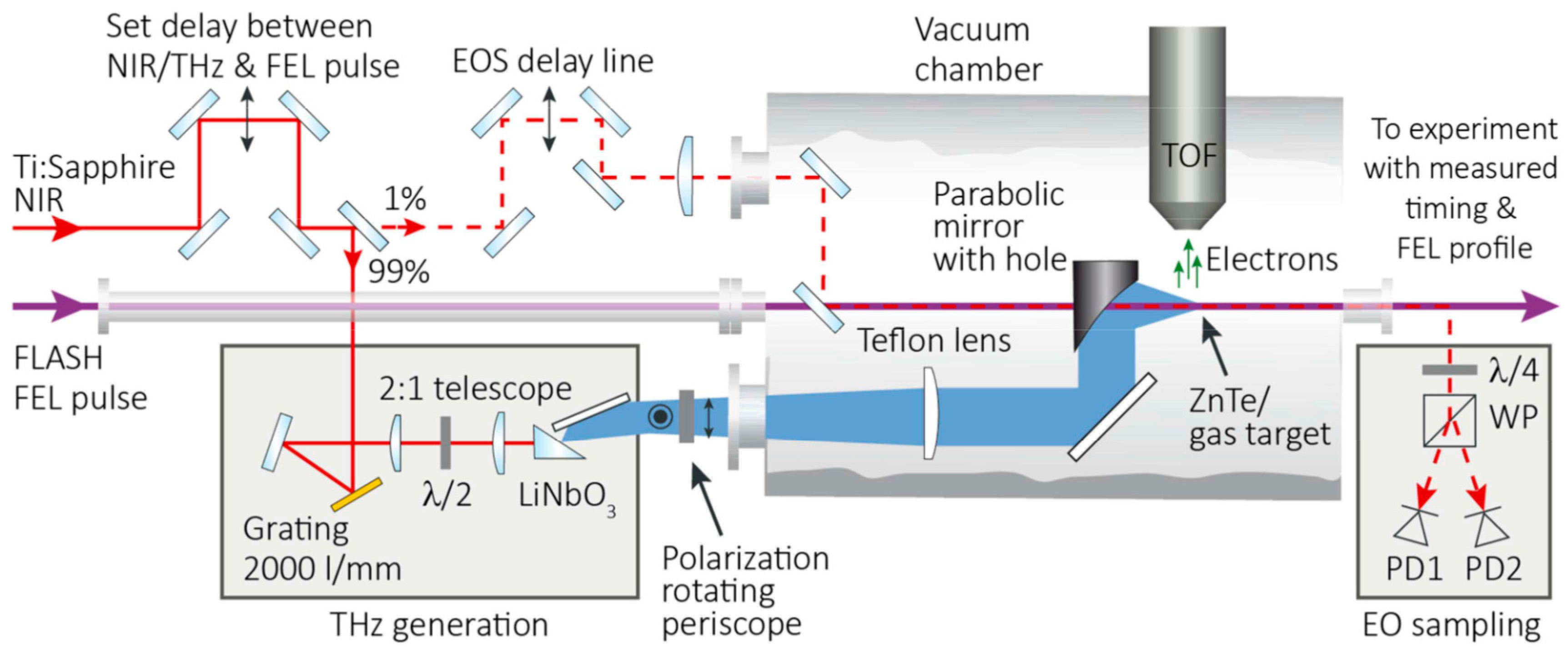
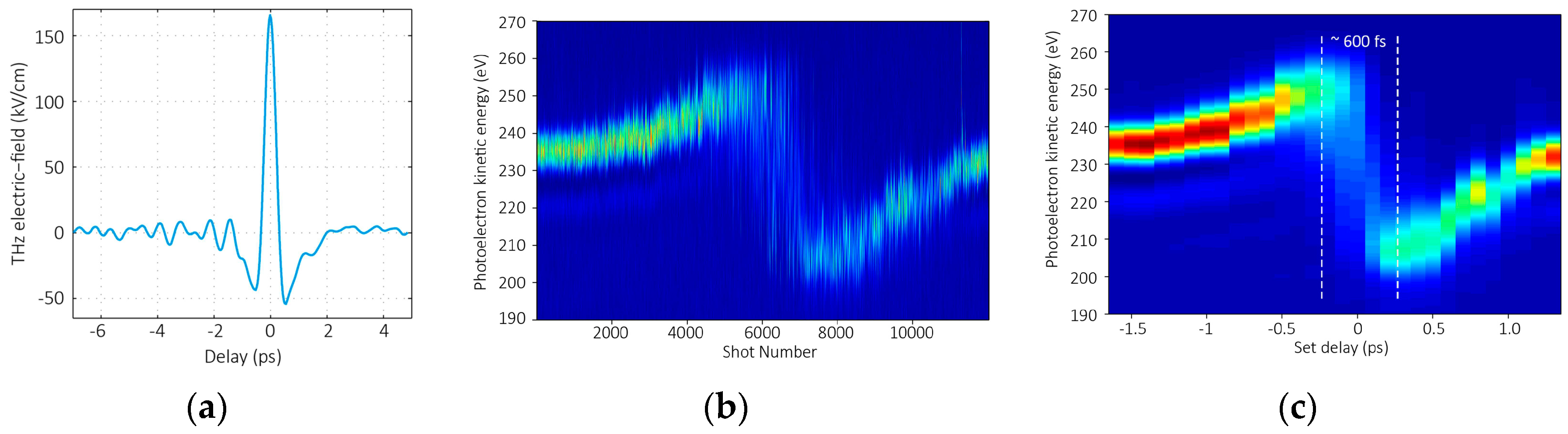
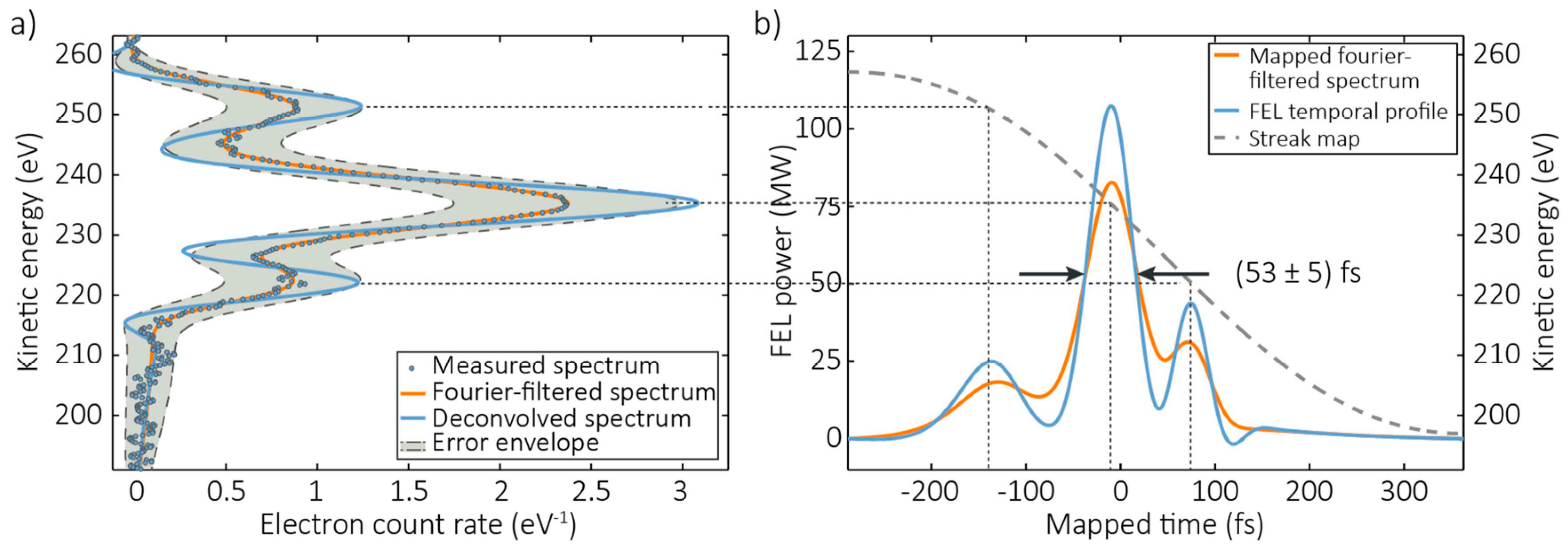
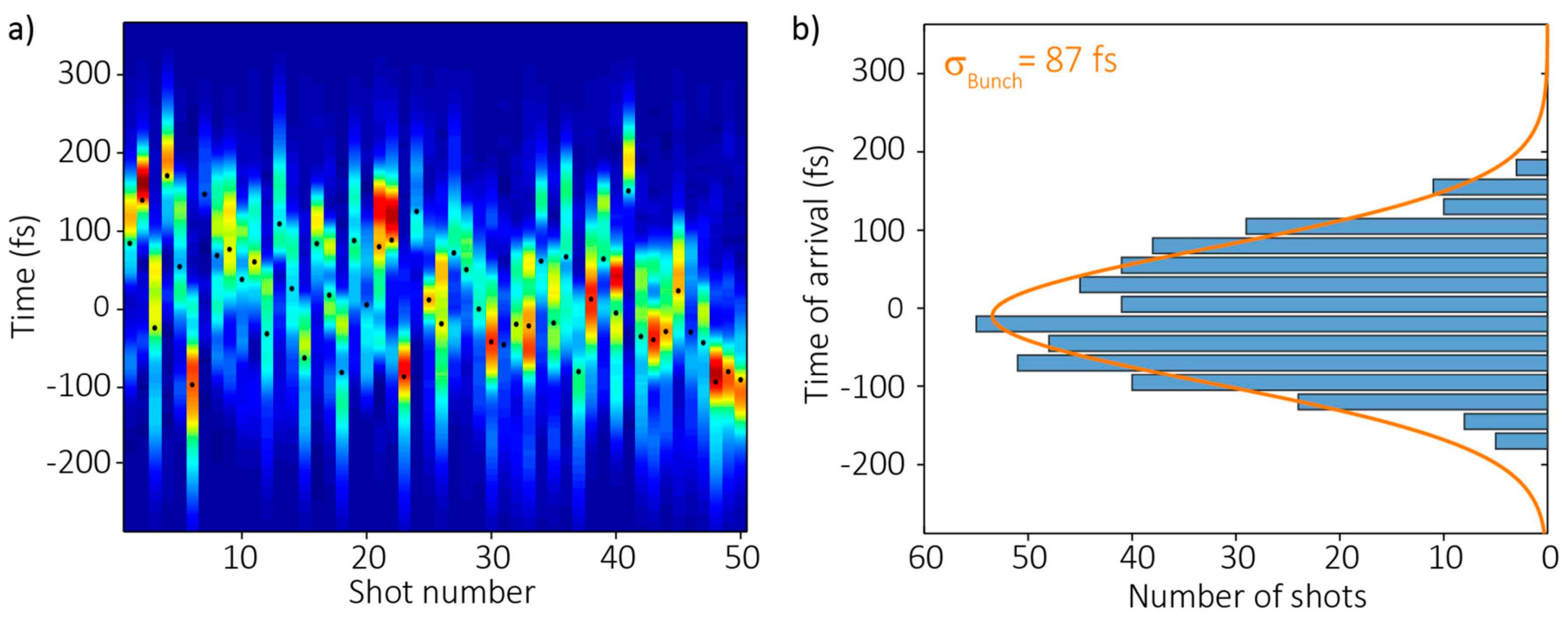
3.1.2. Laser-Driven Terahertz Streaking for Complete Temporal Characterization
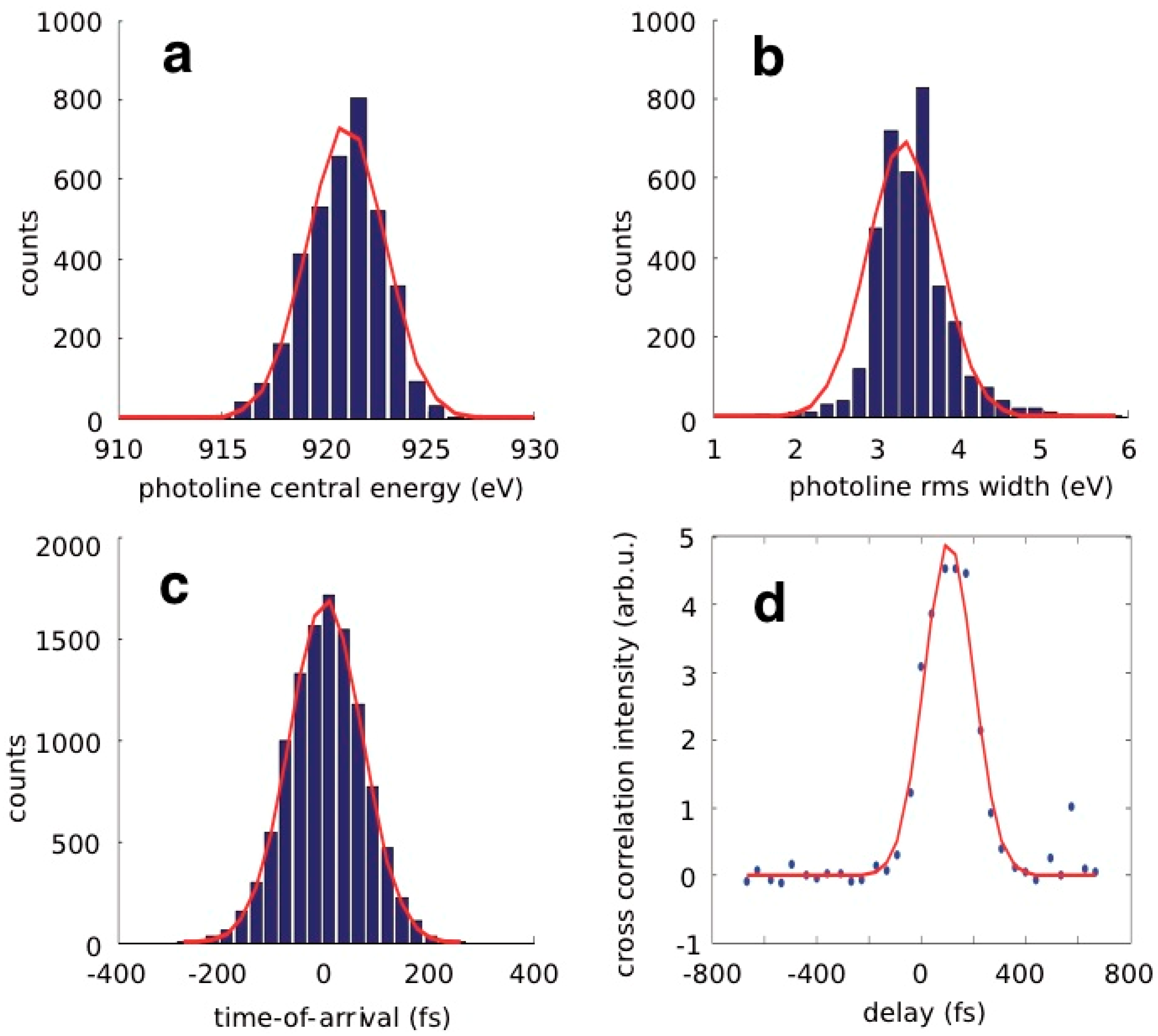
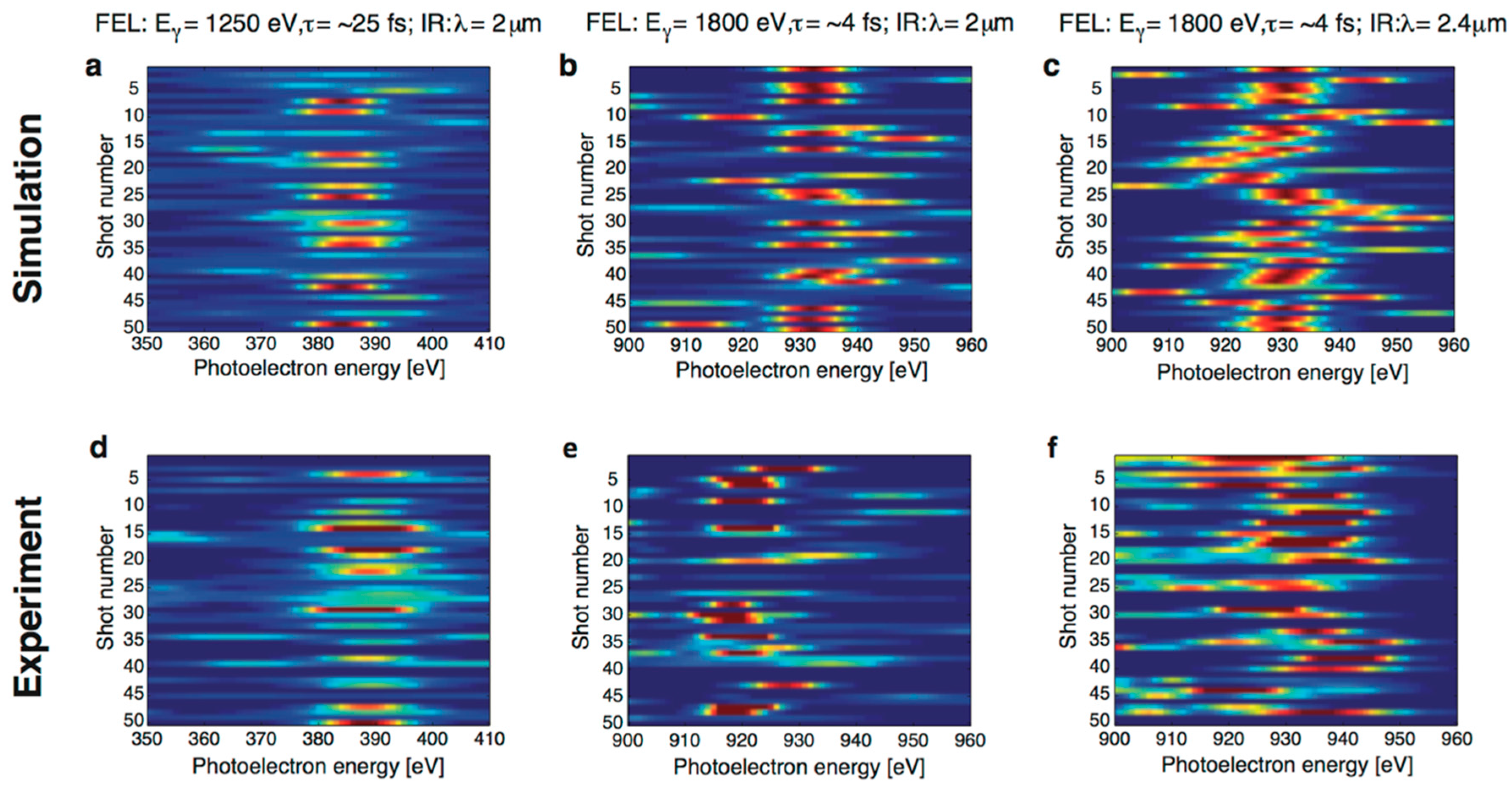
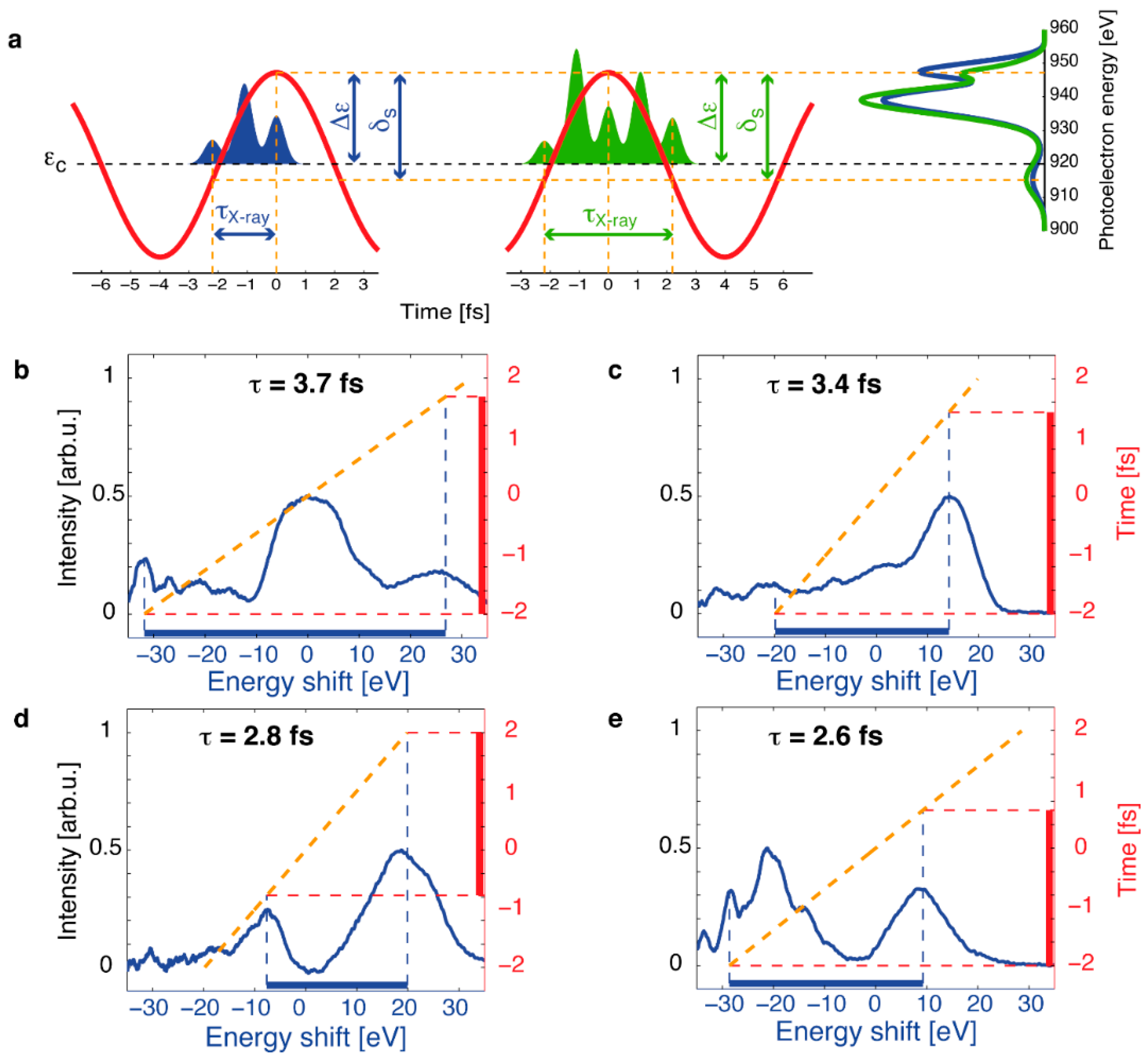
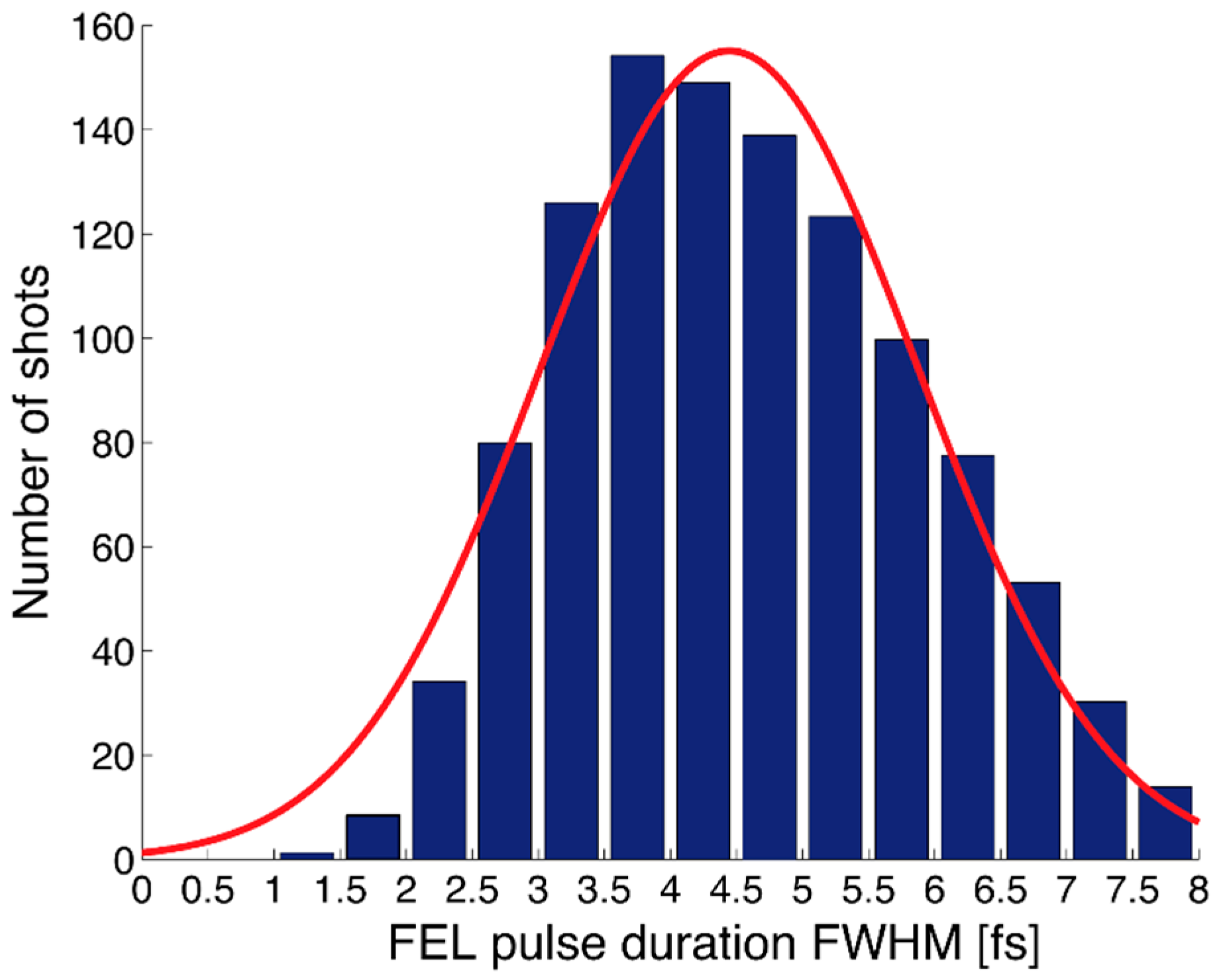
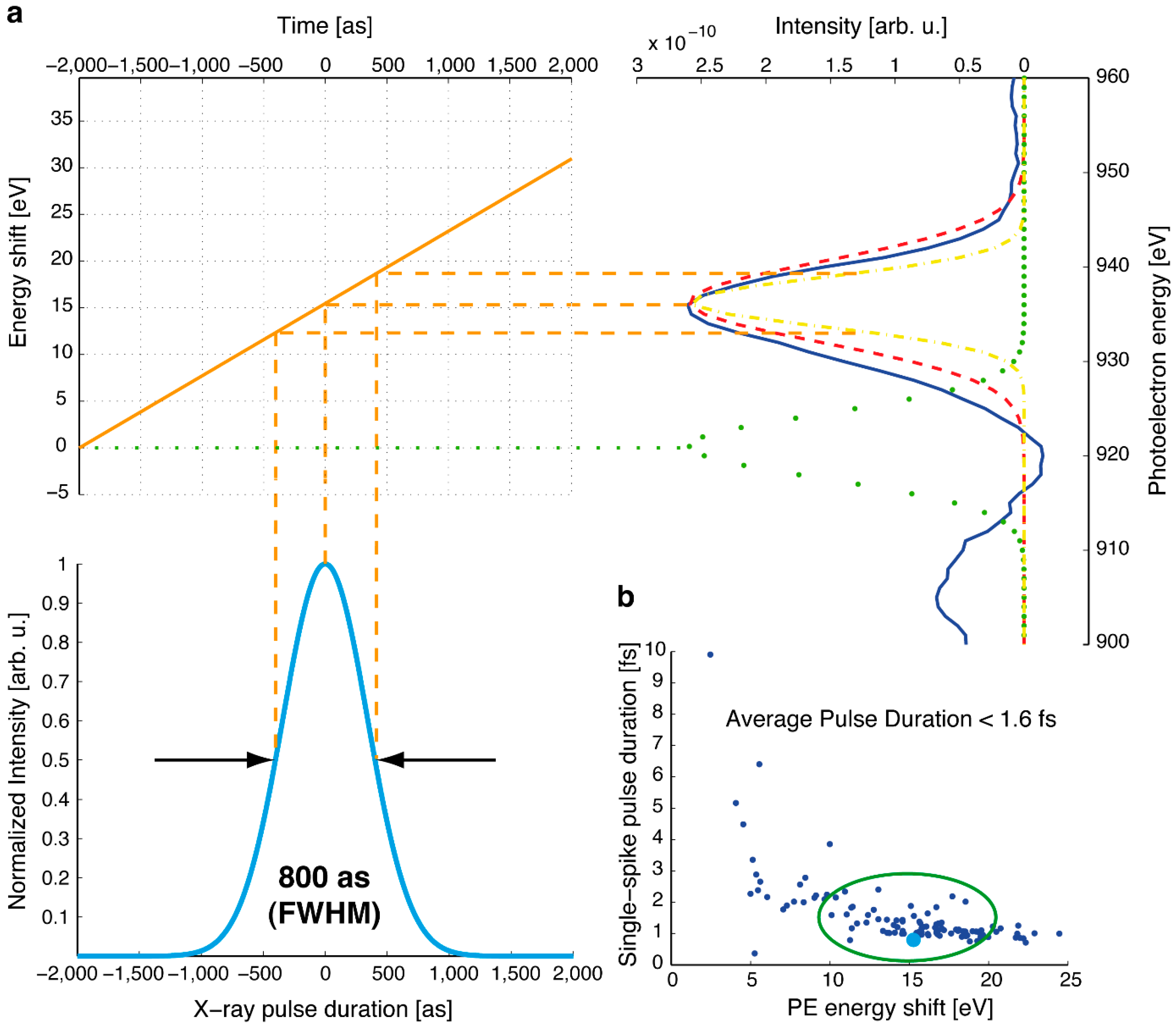
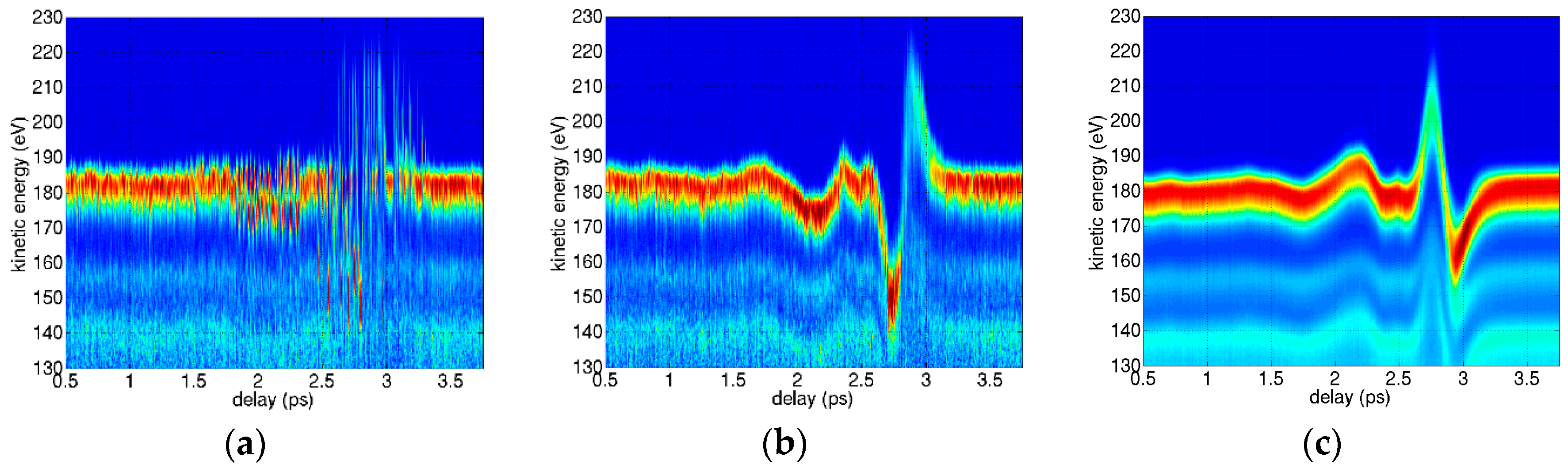
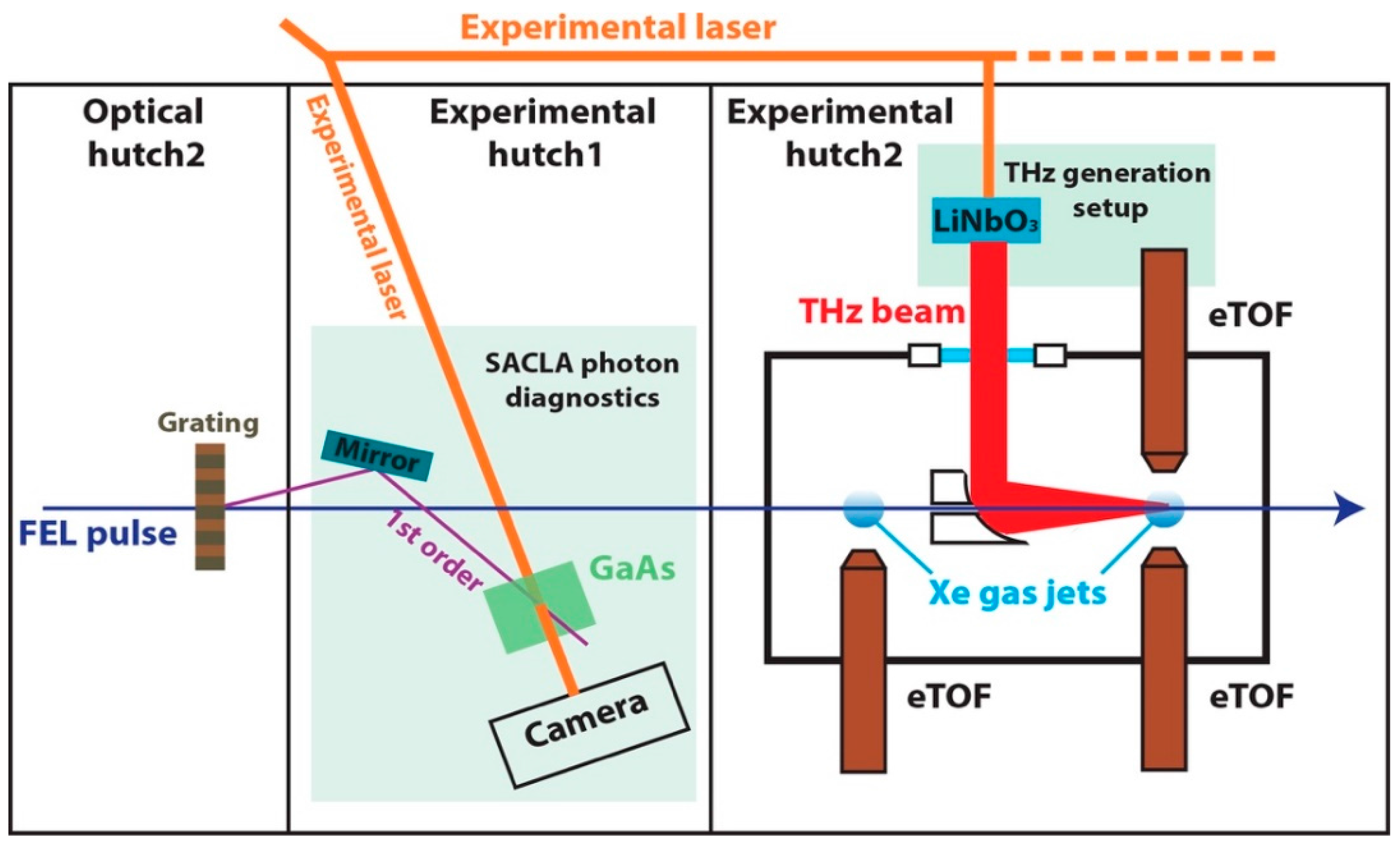
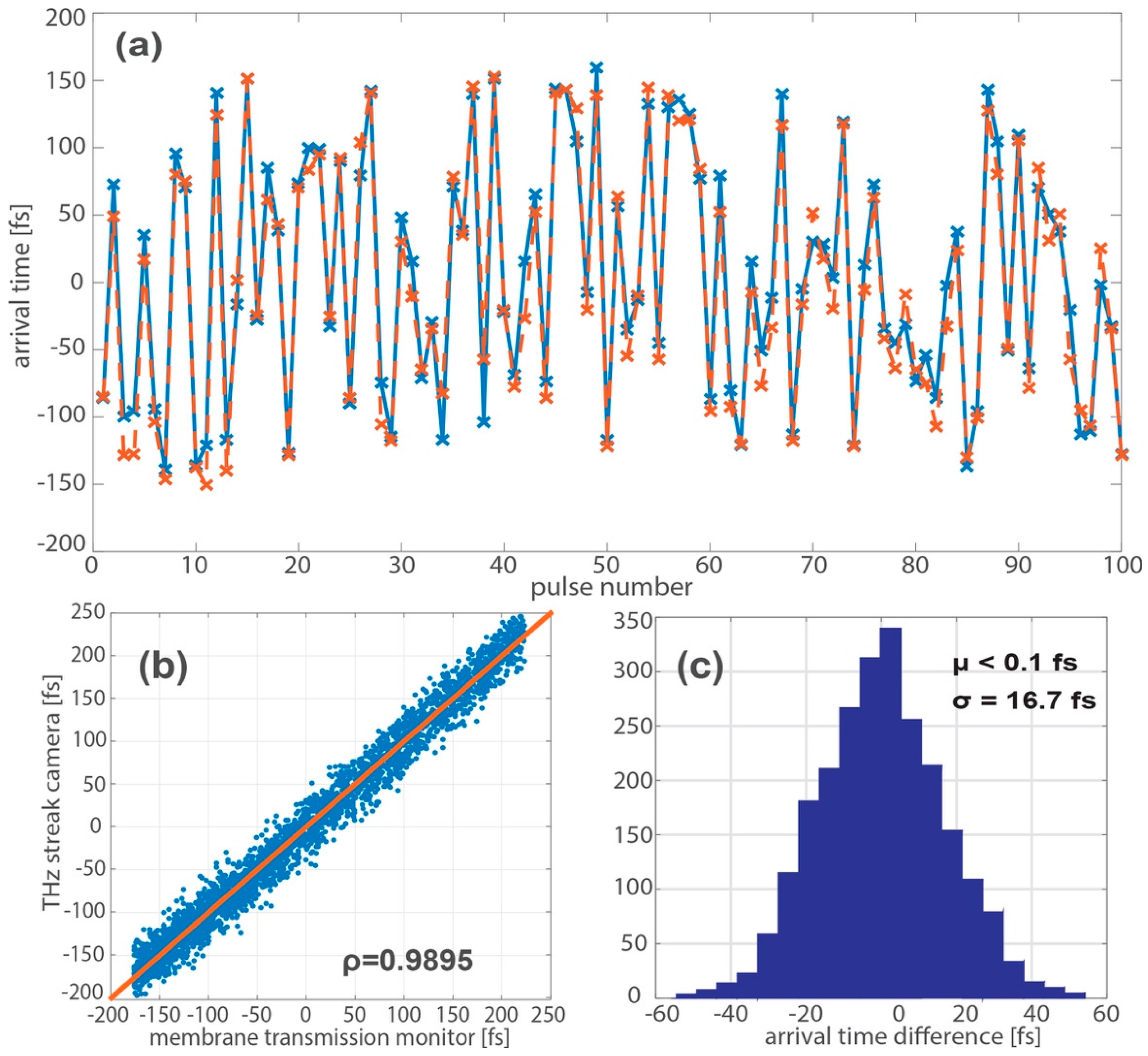
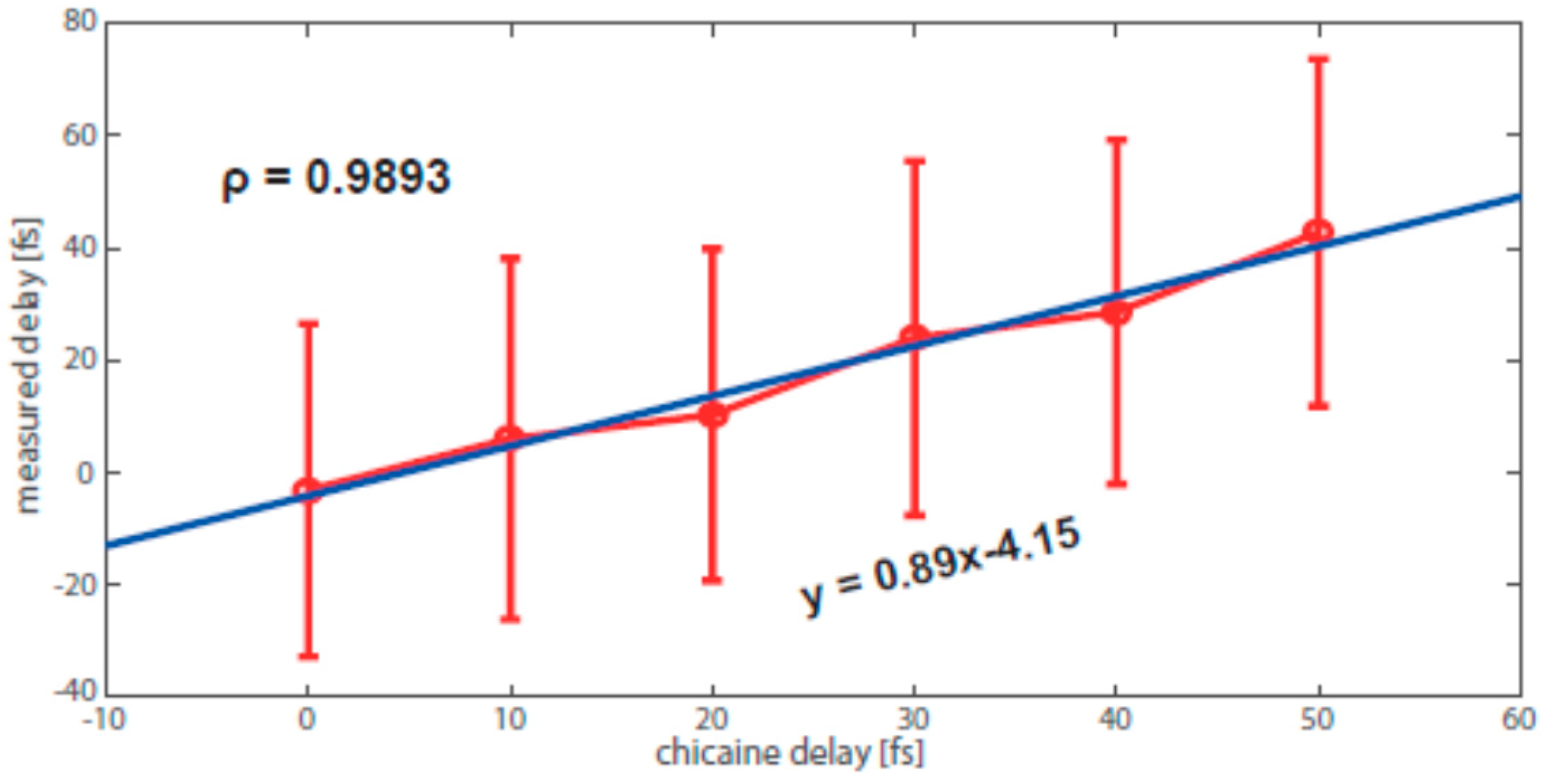
3.2. Terahertz Streaking with Hard X-rays
4. Outlook
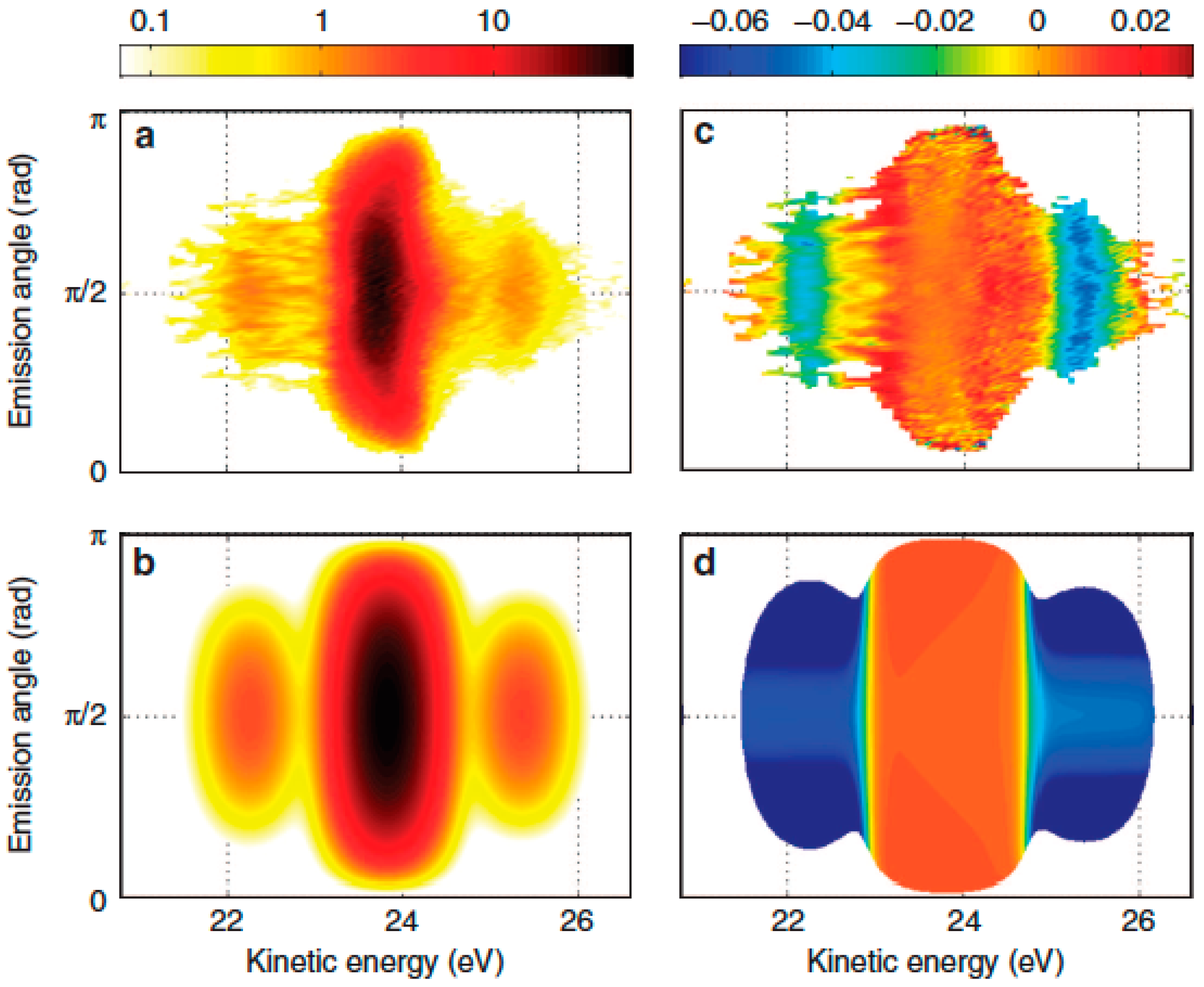
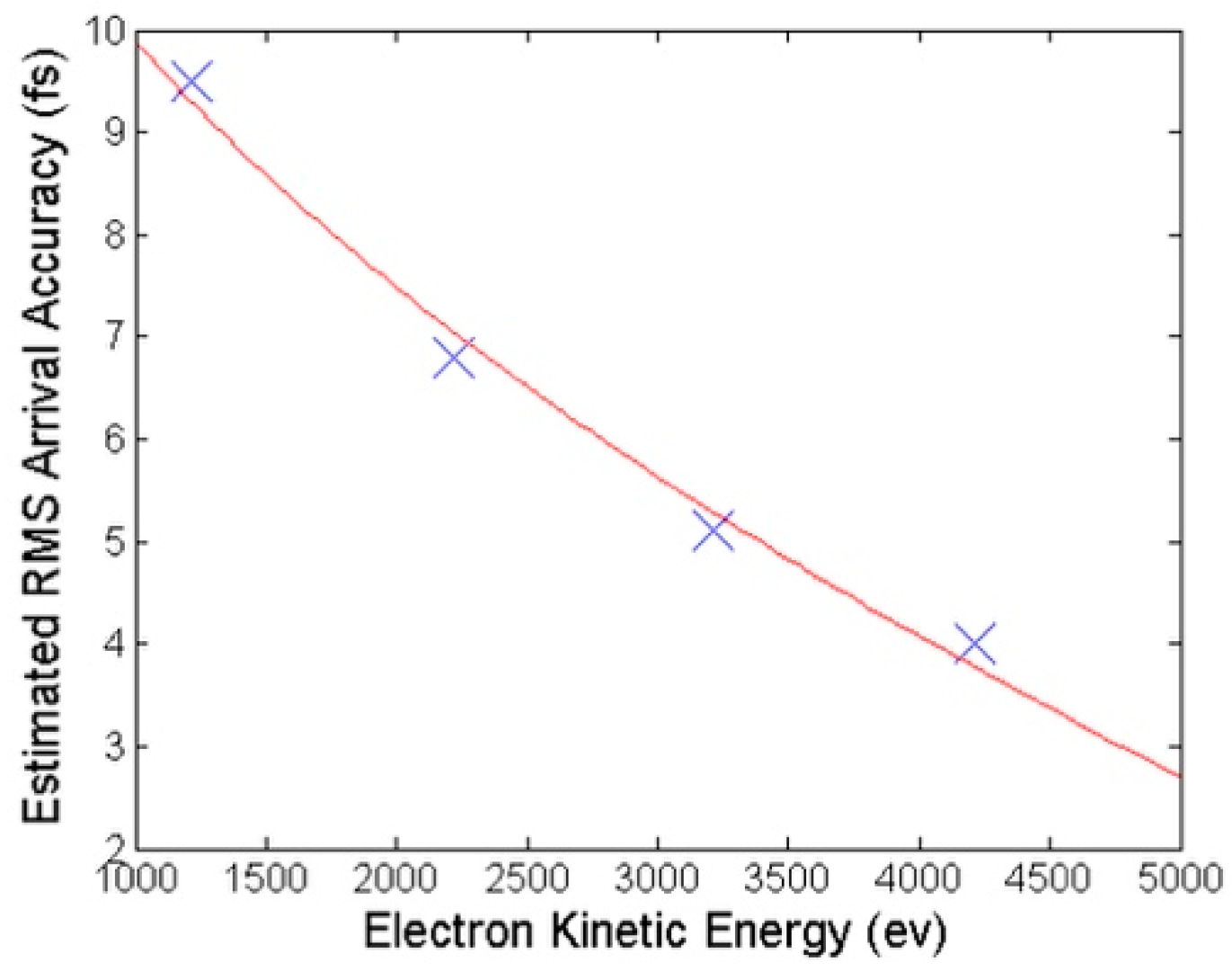
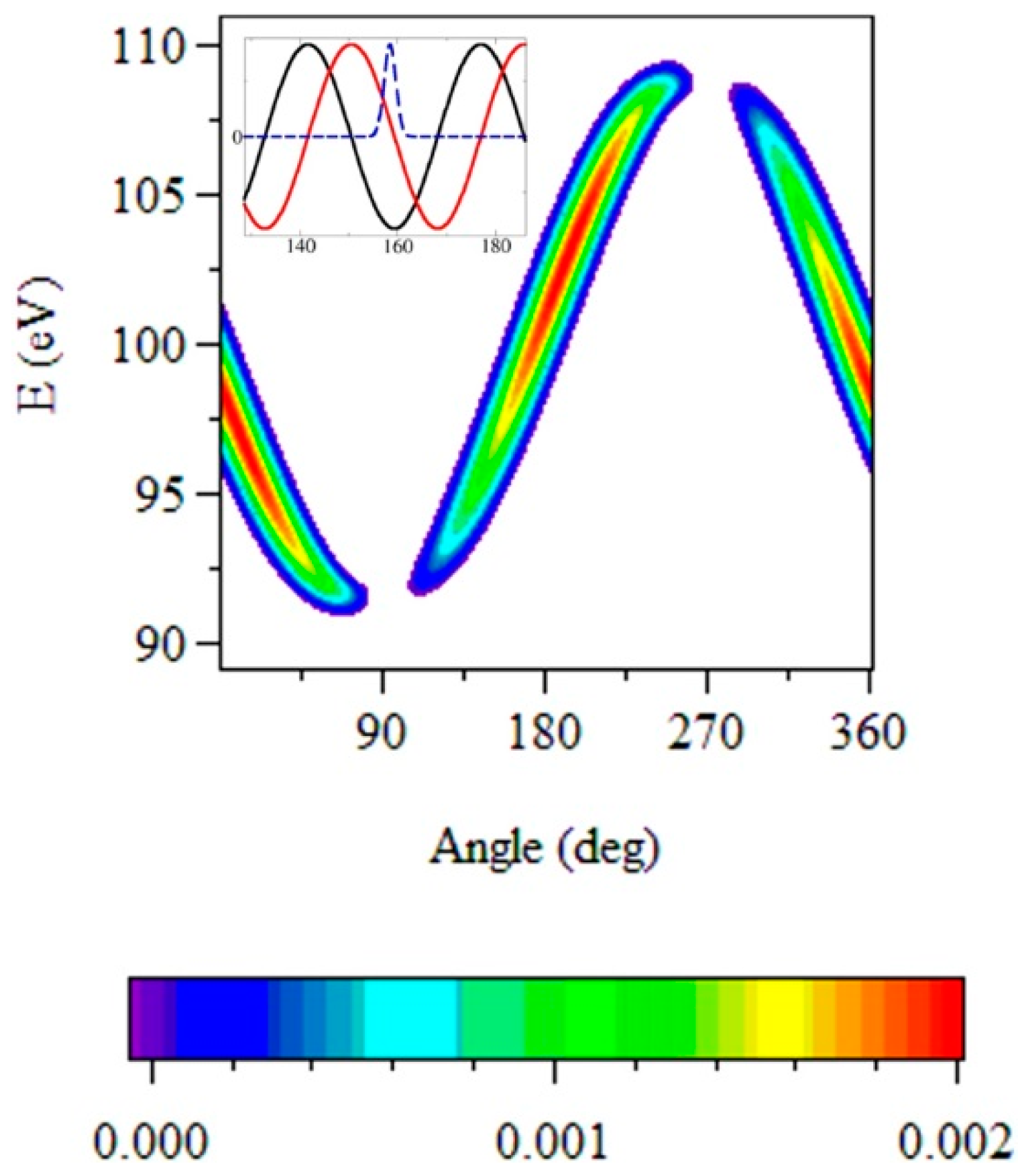
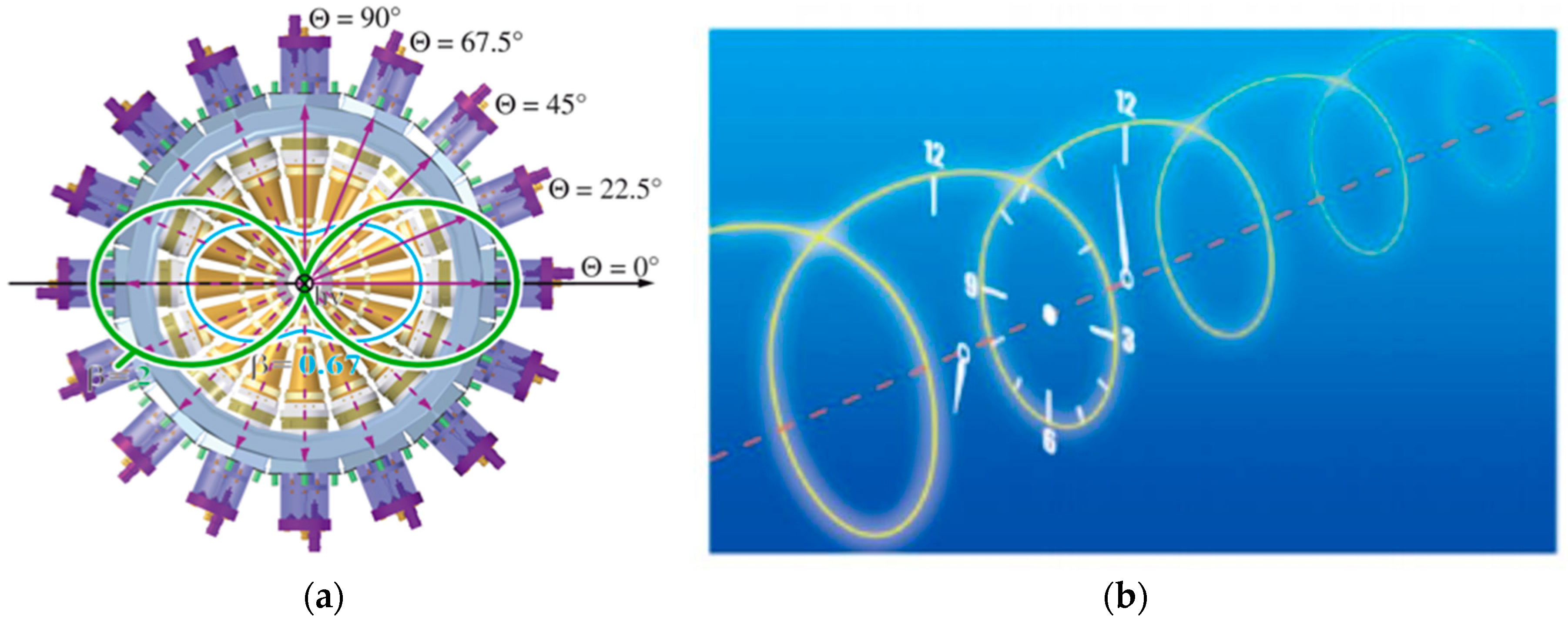
4.1 Angular Streaking—Full Time–Energy SASE Pulse Retrieval
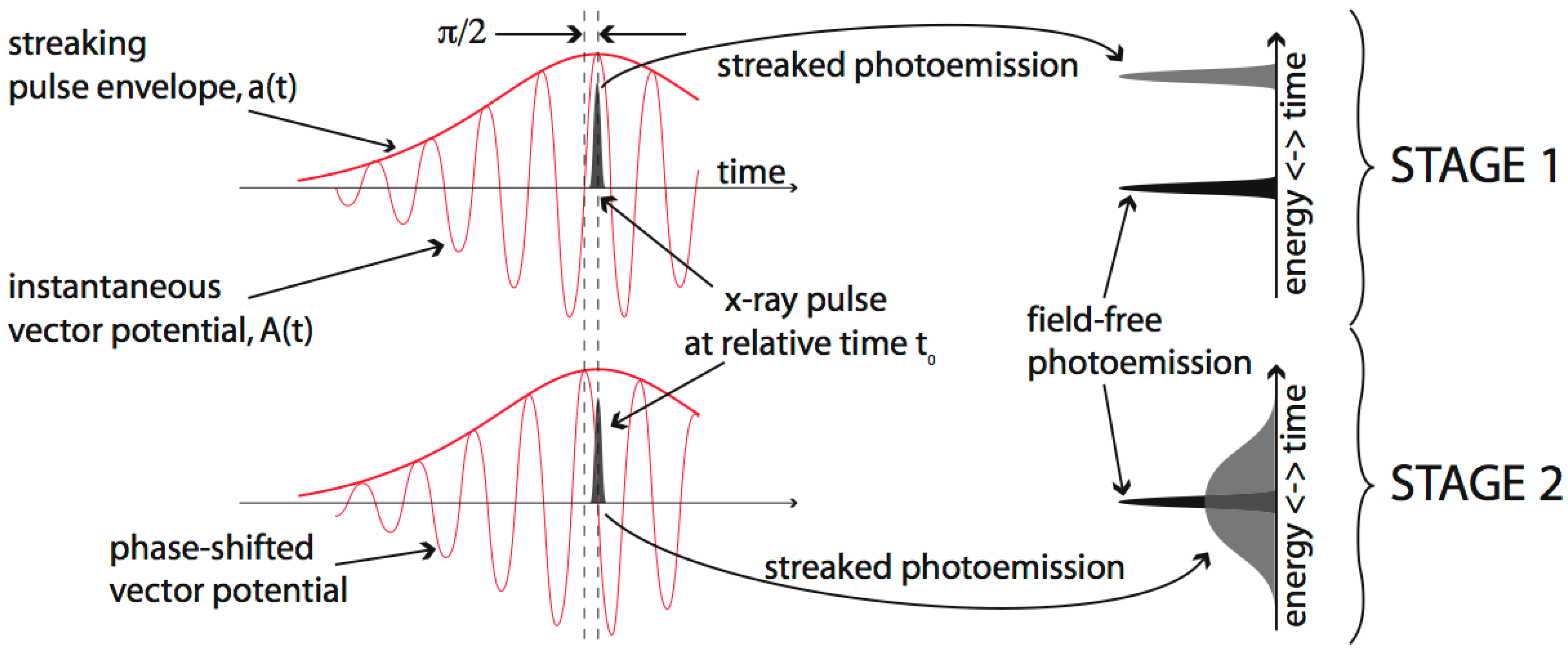
4.2. Tandem Phase-Shifted Geometry for Infrared Streaking and Attosecond Resolution
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Roentgen, W.C. Ueber eine neue Art von Strahlen. Sitzungsberichte der Würzburger Phys.-medic. Ges. 1895, 132. [Google Scholar]
- Elder, F.R.; Gurewitsch, A.M.; Langmuir, R.V.; Pollock, H.C. Radiation from Electrons in a Synchrotron. Phys. Rev. 1947, 71, 829–830. [Google Scholar] [CrossRef]
- Madden, R.P.; Codling, K. New Autoionizing Atomic Energy Levels in He, Ne, and Ar. Phys. Rev. Lett. 1963, 10, 516–518. [Google Scholar] [CrossRef]
- Rowe, E.M.; Mills, F.E. TANTALUS I: A Dedicated Storage Ring Synchrotron Radiation Source. Part. Accel. 1973, 4, 211–227. [Google Scholar]
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nucl. Instrum. Methods 1980, 169, 1–10. [Google Scholar] [CrossRef]
- Christov, I.P.; Murnane, M.M.; Kapteyn, H.C. High-Harmonic Generation of Attosecond Pulses in the “Single-Cycle” Regime. Phys. Rev. Lett. 1997, 78, 1251–1254. [Google Scholar] [CrossRef]
- Deacon, D.; Elias, L.; Madey, J.; Ramian, G.; Schwettman, H.; Smith, T. First Operation of a Free-Electron Laser. Phys. Rev. Lett. 1977, 38, 892–894. [Google Scholar] [CrossRef]
- McNeil, B.W.J.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814–821. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.D.; Brachmann, A.; Bucksbaum, P.H.; Coffee, R.N.; Decker, F.-J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Ganter, R. PSI—SwissFEL Conceptual Design Report. 5232 Villigen PSI, Switzerland. 2012. Available online: https://www.psi.ch/swissfel/CurrentSwissFELPublicationsEN/SwissFEL_CDR_V20_23.04.12_small.pdf (accessed on 1 September 2017).
- Kang, H.-S.; Han, J.H.; Kim, C.; Kim, D.E.; Kim, S.H.; Park, K.-H.; Park, S.-J.; Kang, T.-H.; Ko, I.S. Current status of PAL-XFEL project. In Proceedings of the IPAC2013, Shanghai, China, 12–17 May 2013; pp. 2074–2076. Available online: https://accelconf.web.cern.ch/accelconf/IPAC2013/papers/weodb103.pdf (accessed on 1 September 2017).
- Nakajima, K. Compact X-ray sources: Towards a table-top free-electron laser. Nat. Phys. 2008, 4, 92–93. [Google Scholar] [CrossRef]
- Maier, A.R.; Meseck, A.; Reiche, S.; Schroeder, C.B.; Seggebrock, T.; Grüner, F. Demonstration Scheme for a Laser-Plasma-Driven Free-Electron Laser. Phys. Rev. X 2012, 2, 31019. [Google Scholar] [CrossRef]
- Maier, A.R.; Kirchen, M.; Grüner, F. Brilliant Light Sources driven by Laser-Plasma Accelerators. In Synchrotron Light Sources and Free-Electron Lasers; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–22. [Google Scholar]
- Kärtner, F.X.; Ahr, F.; Calendron, A.-L.; Çankaya, H.; Carbajo, S.; Chang, G.; Cirmi, G.; Dörner, K.; Dorda, U.; Fallahi, A.; et al. AXSIS: Exploring the frontiers in attosecond X-ray science, imaging and spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2016, 829, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Altarelli, M.; Brinkmann, R.; Chergui, M.; Decking, W.; Dobson, B.; Düsterer, S.; Grübel, G.; Graeff, W.; Graafsma, H.; Hajdu, J.; et al. The European X-ray Free-Electron Laser—Technical Design Report; Notkestrasse: Hamburg, Germany, 2007; Available online: http://xfel.desy.de/localfsExplorer_read?currentPath=/afs/desy.de/group/xfel/wof/EPT/TDR/XFEL-TDR-final.pdf (accessed on 1 September 2017).
- Galayda, J. The new LCLS-II project: Status and challenges. In Proceedings of the LINAC2014, Geneva, Switzerland, 31 August–5 September 2014; Available online: https://inspirehep.net/record/1363411 (accessed on 1 September 2017).
- Drescher, M.; Hentschel, M.; Kienberger, R.; Uiberacker, M.; Yakovlev, V.S.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; Krausz, F. Time-resolved atomic inner-shell spectroscopy. Nature 2002, 419, 803–807. [Google Scholar] [CrossRef] [PubMed]
- Uiberacker, M.; Uphues, T.; Schultze, M.; Verhoef, A.J.; Yakovlev, V.S.; Kling, M.F.; Rauschenberger, J.; Kabachnik, N.M.; Schröder, H.; Lezius, M.; et al. Attosecond real-time observation of electron tunnelling in atoms. Nature 2007, 446, 627–632. [Google Scholar] [CrossRef] [PubMed]
- Cavalieri, A.L.; Müller, N.; Uphues, T.; Yakovlev, V.S.; Baltuška, A.; Horvath, B.; Schmidt, B.; Blümel, L.; Holzwarth, R.; Hendel, S.; et al. Attosecond spectroscopy in condensed matter. Nature 2007, 449, 1029–1032. [Google Scholar] [CrossRef] [PubMed]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef] [PubMed]
- Klünder, K.; Dahlström, J.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing Single-Photon Ionization on the Attosecond Time Scale. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Schultze, M.; Ramasesha, K.; Pemmaraju, C.D.; Sato, S.A.; Whitmore, D.; Gandman, A.; Prell, J.S.; Borja, L.J.; Prendergast, D.; Yabana, K.; et al. Attosecond band-gap dynamics in silicon. Science 2014, 346, 1348–1352. [Google Scholar] [CrossRef] [PubMed]
- Neppl, S.; Ernstorfer, R.; Cavalieri, A.L.; Lemell, C.; Wachter, G.; Magerl, E.; Bothschafter, E.M.; Jobst, M.; Hofstetter, M.; Kleineberg, U.; et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 2015, 517, 342–346. [Google Scholar] [CrossRef] [PubMed]
- Sabbar, M.; Heuser, S.; Boge, R.; Lucchini, M.; Carette, T.; Lindroth, E.; Gallmann, L.; Cirelli, C.; Keller, U. Resonance Effects in Photoemission Time Delays. Phys. Rev. Lett. 2015, 115, 133001. [Google Scholar] [CrossRef] [PubMed]
- Kraus, P.M.; Mignolet, B.; Baykusheva, D.; Rupenyan, A.; Horny, L.; Penka, E.F.; Grassi, G.; Tolstikhin, O.I.; Schneider, J.; Jensen, F.; et al. Measurement and laser control of attosecond charge migration in ionized iodoacetylene. Science 2015, 350, 790–795. [Google Scholar] [CrossRef] [PubMed]
- Förg, B.; Schötz, J.; Süßmann, F.; Förster, M.; Krüger, M.; Ahn, B.; Okell, W.A.; Wintersperger, K.; Zherebtsov, S.; Guggenmos, A.; et al. Attosecond nanoscale near-field sampling. Nat. Commun. 2016, 7, 11717. [Google Scholar] [CrossRef] [PubMed]
- Ossiander, M.; Siegrist, F.; Shirvanyan, V.; Pazourek, R.; Sommer, A.; Latka, T.; Guggenmos, A.; Nagele, S.; Feist, J.; Burgdörfer, J.; et al. Attosecond correlation dynamics. Nat. Phys. 2016, 1. [Google Scholar] [CrossRef]
- Emma, P.; Bane, K.; Cornacchia, M.; Huang, Z.; Schlarb, H.; Stupakov, G.; Walz, D. Femtosecond and Subfemtosecond X-ray Pulses from a Self-Amplified Spontaneous-Emission–Based Free-Electron Laser. Phys. Rev. Lett. 2004, 92, 74801. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Behrens, C.; Coffee, R.; Decker, F.-J.; Emma, P.; Field, C.; Helml, W.; Huang, Z.; Krejcik, P.; Krzywinski, J.; et al. Generating femtosecond X-ray pulses using an emittance-spoiling foil in free-electron lasers. Appl. Phys. Lett. 2015, 107, 191104. [Google Scholar] [CrossRef]
- Zholents, A.; Fawley, W. Proposal for Intense Attosecond Radiation from an X-ray Free-Electron Laser. Phys. Rev. Lett. 2004, 92, 224801. [Google Scholar] [CrossRef] [PubMed]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. A new technique to generate 100 GW-level attosecond X-ray pulses from the X-ray SASE FELs. Opt. Commun. 2004, 239, 161–172. [Google Scholar] [CrossRef]
- Prat, E.; Reiche, S. Simple Method to Generate Terawatt-Attosecond X-ray Free-Electron-Laser Pulses. Phys. Rev. Lett. 2015, 114, 244801. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Parc, Y.W.; Landsman, A.S.; Kim, D.E. Temporally-coherent terawatt attosecond XFEL synchronized with a few cycle laser. Sci. Rep. 2016, 6, 37700. [Google Scholar] [CrossRef] [PubMed]
- Zholents, A.A.; Penn, G. Obtaining attosecond X-ray pulses using a self-amplified spontaneous emission free electron laser. Phys. Rev. Spec. Top. Accel. Beams 2005, 8, 50704. [Google Scholar] [CrossRef]
- Picón, A.; Lehmann, C.S.; Bostedt, C.; Rudenko, A.; Marinelli, A.; Osipov, T.; Rolles, D.; Berrah, N.; Bomme, C.; Bucher, M.; et al. Hetero-site-specific X-ray pump-probe spectroscopy for femtosecond intramolecular dynamics. Nat. Commun. 2016, 7, 11652. [Google Scholar] [CrossRef] [PubMed]
- Pande, K.; Hutchison, C.D.M.; Groenhof, G.; Aquila, A.; Robinson, J.S.; Tenboer, J.; Basu, S.; Boutet, S.; DePonte, D.P.; Liang, M.; et al. Femtosecond structural dynamics drives the trans/cis isomerization in photoactive yellow protein. Science 2016, 352, 725–729. [Google Scholar] [CrossRef] [PubMed]
- Yakovlev, V.S.; Stockman, M.I.; Krausz, F.; Baum, P. Atomic-scale diffractive imaging of sub-cycle electron dynamics in condensed matter. Sci. Rep. 2015, 5, 14581. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Guehr, M.; Vecchione, T.; Robinson, M.S.; Li, R.; Hartmann, N.; Shen, X.; Coffee, R.; Corbett, J.; Fry, A.; et al. Diffractive imaging of a rotational wavepacket in nitrogen molecules with femtosecond megaelectronvolt electron pulses. Nat. Commun. 2016, 7, 11232. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Guehr, M.; Shen, X.; Li, R.; Vecchione, T.; Coffee, R.; Corbett, J.; Fry, A.; Hartmann, N.; Hast, C.; et al. Diffractive Imaging of Coherent Nuclear Motion in Isolated Molecules. Phys. Rev. Lett. 2016, 117, 153002. [Google Scholar] [CrossRef] [PubMed]
- Glownia, J.M.; Natan, A.; Cryan, J.P.; Hartsock, R.; Kozina, M.; Minitti, M.P.; Nelson, S.; Robinson, J.; Sato, T.; van Driel, T.; et al. Self-Referenced Coherent Diffraction X-ray Movie of Ångstrom- and Femtosecond-Scale Atomic Motion. Phys. Rev. Lett. 2016, 117, 153003. [Google Scholar] [CrossRef] [PubMed]
- Bostedt, C.; Fritz, D.M.; Huang, Z.; Lee, H.J.; Lemke, H.; Schlotter, W.F.; Turner, J.J.; Williams, G.J. Linac Coherent Light Source: The First Five Years. Rev. Mod. Phys. 2015, 88. [Google Scholar] [CrossRef]
- Milton, S.V.; Gluskin, E.; Arnold, N.D.; Benson, C.; Berg, W.; Biedron, S.G.; Borland, M.; Chae, Y.C.; Dejus, R.J.; Den Hartog, P.K.; et al. Exponential gain and saturation of a self-amplified spontaneous emission free-electron laser. Science 2001, 292, 2037–2041. [Google Scholar] [CrossRef] [PubMed]
- Düsterer, S.; Rehders, M.; Al-Shemmary, A.; Behrens, C.; Brenner, G.; Brovko, O.; DellAngela, M.; Drescher, M.; Faatz, B.; Feldhaus, J.; et al. Development of experimental techniques for the characterization of ultrashort photon pulses of extreme ultraviolet free-electron lasers. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 120702. [Google Scholar] [CrossRef]
- Ding, Y.; Brachmann, A.; Decker, F.-J.; Dowell, D.; Emma, P.; Frisch, J.; Gilevich, S.; Hays, G.; Hering, P.; Huang, Z.; et al. Measurements and Simulations of Ultralow Emittance and Ultrashort Electron Beams in the Linac Coherent Light Source. Phys. Rev. Lett. 2009, 102, 254801. [Google Scholar] [CrossRef] [PubMed]
- Lutman, A.; Ding, Y.; Feng, Y.; Huang, Z.; Messerschmidt, M.; Wu, J.; Krzywinski, J. Femtosecond X-ray free electron laser pulse duration measurement from spectral correlation function. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 1–13. [Google Scholar] [CrossRef]
- Young, L.; Kanter, E.P.; Krässig, B.; Li, Y.; March, A.M.; Pratt, S.T.; Santra, R.; Southworth, S.H.; Rohringer, N.; Dimauro, L.F.; et al. Femtosecond electronic response of atoms to ultra-intense X-rays. Nature 2010, 466, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Düsterer, S.; Radcliffe, P.; Bostedt, C.; Bozek, J.D.; Cavalieri, A.L.; Coffee, R.N.; Costello, J.T.; Cubaynes, D.; DiMauro, L.F.; Ding, Y.; et al. Femtosecond X-ray pulse length characterization at the Linac Coherent Light Source free-electron laser. New J. Phys. 2011, 13, 93024. [Google Scholar] [CrossRef]
- Behrens, C.; Decker, F.-J.; Ding, Y.; Dolgashev, V.A.; Frisch, J.; Huang, Z.; Krejcik, P.; Loos, H.; Lutman, A.; Maxwell, T.J.; et al. Few-femtosecond time-resolved measurements of X-ray free-electron lasers. Nat. Commun. 2014, 5, 3762. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Gonzalez, A.; Micaelli, P.; Olivier, C.; Barillot, T.R.; Ilchen, M.; Lutman, A.A.; Marinelli, A.; Maxwell, T.; Achner, A.; Agåker, M.; et al. Accurate prediction of X-ray pulse properties from a free-electron laser using machine learning. Nat. Commun. 2017, 8, 15461. [Google Scholar] [CrossRef] [PubMed]
- Mitzner, R.; Sorokin, A.A.; Siemer, B.; Roling, S.; Rutkowski, M.; Zacharias, H.; Neeb, M.; Noll, T.; Siewert, F.; Eberhardt, W.; et al. Direct autocorrelation of soft-X-ray free-electron-laser pulses by time-resolved two-photon double ionization of He. Phys. Rev. A 2009, 80, 25402. [Google Scholar] [CrossRef]
- Moshammer, R.; Pfeifer, T.; Rudenko, A.; Jiang, Y.H.; Foucar, L.; Kurka, M.; Kühnel, K.U.; Schröter, C.D.; Ullrich, J.; Herrwerth, O.; et al. Second-order autocorrelation of XUV FEL pulses via time resolved two-photon single ionization of He. Opt. Express 2011, 19, 21698. [Google Scholar] [CrossRef] [PubMed]
- Iaconis, C.; Walmsley, I.A. Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses. Opt. Lett. 1998, 23, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Mahieu, B.; Gauthier, D.; De Ninno, G.; Dacasa, H.; Lozano, M.; Rousseau, J.-P.; Zeitoun, P.; Garzella, D.; Merdji, H. Spectral-phase interferometry for direct electric-field reconstruction applied to seeded extreme-ultraviolet free-electron lasers. Opt. Express 2015, 23, 17665–17674. [Google Scholar] [CrossRef] [PubMed]
- Harmand, M.; Coffee, R.; Bionta, M.R.; Chollet, M.; French, D.; Zhu, D.; Fritz, D.M.; Lemke, H.T.; Medvedev, N.; Ziaja, B.; et al. Achieving few-femtosecond time-sorting at hard X-ray free-electron lasers. Nat. Photonics 2013, 7, 215–218. [Google Scholar] [CrossRef]
- Finetti, P.; Höppner, H.; Allaria, E.; Callegari, C.; Capotondi, F.; Cinquegrana, P.; Coreno, M.; Cucini, R.; Danailov, M.B.; Demidovich, A.; et al. Pulse Duration of Seeded Free-Electron Lasers. Phys. Rev. X 2017, 7, 21043. [Google Scholar] [CrossRef]
- Bencivenga, F.; Cucini, R.; Capotondi, F.; Battistoni, A.; Mincigrucci, R.; Giangrisostomi, E.; Gessini, A.; Manfredda, M.; Nikolov, I.P.; Pedersoli, E.; et al. Four-wave mixing experiments with extreme ultraviolet transient gratings. Nature 2015, 520, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Bencivenga, F.; Masciovecchio, C. Results and Perspectives for Short-Wavelength, Four-Wave-Mixing Experiments with Fully Coherent Free Electron Lasers. Synchrotron Radiat. News 2016, 29, 15–20. [Google Scholar] [CrossRef]
- Mairesse, Y.; Zeidler, D.; Dudovich, N.; Spanner, M.; Levesque, J.; Villeneuve, D.M.; Corkum, P.B. High-order harmonic transient grating spectroscopy in a molecular jet. Phys. Rev. Lett. 2008, 100, 15–18. [Google Scholar] [CrossRef] [PubMed]
- Itatani, J.; Quéré, F.; Yudin, G.; Ivanov, M.; Krausz, F.; Corkum, P. Attosecond Streak Camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef] [PubMed]
- Kitzler, M.; Milosevic, N.; Scrinzi, A.; Krausz, F.; Brabec, T. Quantum Theory of Attosecond XUV Pulse Measurement by Laser Dressed Photoionization. Phys. Rev. Lett. 2002, 88, 173904. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.B.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817–821. [Google Scholar] [CrossRef] [PubMed]
- Goulielmakis, E.; Uiberacker, M.; Kienberger, R.; Baltuška, A.; Yakovlev, V.S.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; Drescher, M.; et al. Direct measurement of light waves. Science 2004, 305, 1267–1269. [Google Scholar] [CrossRef] [PubMed]
- Baumgartner, R.; Byer, R. Optical parametric amplification. IEEE J. Quantum Electron. 1979, 15, 432–444. [Google Scholar] [CrossRef]
- Helml, W.; Maier, A.R.; Schweinberger, W.; Grguraš, I.; Radcliffe, P.; Doumy, G.; Roedig, C.; Gagnon, J.; Messerschmidt, M.; Schorb, S.; et al. Measuring the temporal structure of few-femtosecond free-electron laser X-ray pulses directly in the time domain. Nat. Photonics 2014, 8, 950–957. [Google Scholar] [CrossRef]
- Wuilleumier, F.J.; Meyer, M. Pump–probe experiments in atoms involving laser and synchrotron radiation: An overview. J. Phys. B At. Mol. Opt. Phys. 2006, 39, R425–R477. [Google Scholar] [CrossRef]
- Glover, T.; Schoenlein, R.; Chin, A.; Shank, C. Observation of Laser Assisted Photoelectric Effect and Femtosecond High Order Harmonic Radiation. Phys. Rev. Lett. 1996, 76, 2468–2471. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.; Costello, J.T.; Düsterer, S.; Li, W.B.; Radcliffe, P. Two-colour experiments in the gas phase. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 194006. [Google Scholar] [CrossRef]
- Radcliffe, P.; Arbeiter, M.; Li, W.B.; Düsterer, S.; Redlin, H.; Hayden, P.; Hough, P.; Richardson, V.; Costello, J.T.; Fennel, T.; et al. Atomic photoionization in combined intense XUV free-electron and infrared laser fields. New J. Phys. 2012, 14, 43008. [Google Scholar] [CrossRef]
- O’Keeffe, P.; López-Martens, R.; Mauritsson, J.; Johansson, A.; L’Huillier, A.; Véniard, V.; Taïeb, R.; Maquet, A.; Meyer, M. Polarization effects in two-photon nonresonant ionization of argon with extreme-ultraviolet and infrared femtosecond pulses. Phys. Rev. A 2004, 69, 51401. [Google Scholar] [CrossRef]
- Radcliffe, P.; Düsterer, S.; Azima, A.; Redlin, H.; Feldhaus, J.; Dardis, J.; Kavanagh, K.; Luna, H.; Gutierrez, J.P.; Yeates, P.; et al. Single-shot characterization of independent femtosecond extreme ultraviolet free electron and infrared laser pulses. Appl. Phys. Lett. 2007, 90, 131108. [Google Scholar] [CrossRef]
- Redlin, H.; Al-Shemmary, A.; Azima, A.; Stojanovic, N.; Tavella, F.; Will, I.; Düsterer, S. The FLASH pump-probe laser system: Setup, characterization and optical beamlines. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 635, S88–S93. [Google Scholar] [CrossRef]
- Schulz, S.; Grguraš, I.; Behrens, C.; Bromberger, H.; Costello, J.T.; Czwalinna, M.K.; Felber, M.; Hoffmann, M.C.; Ilchen, M.; Liu, H.Y.; et al. Femtosecond all-optical synchronization of an X-ray free-electron laser. Nat. Commun. 2015, 6, 5938. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.; Cubaynes, D.; O’Keeffe, P.; Luna, H.; Yeates, P.; Kennedy, E.T.; Costello, J.T.; Orr, P.; Taïeb, R.; Maquet, A.; et al. Two-color photoionization in xuv free-electron and visible laser fields. Phys. Rev. A 2006, 74, 11401. [Google Scholar] [CrossRef]
- Maquet, A.; Taïeb, R. Two-colour IR + XUV spectroscopies: the “soft-photon approximation”. J. Mod. Opt. 2007, 54, 1847–1857. [Google Scholar] [CrossRef]
- Meyer, M.; Cubaynes, D.; Glijer, D.; Dardis, J.; Hayden, P.; Hough, P.; Richardson, V.; Kennedy, E.T.; Costello, J.T.; Radcliffe, P.; et al. Polarization Control in Two-Color Above-Threshold Ionization of Atomic Helium. Phys. Rev. Lett. 2008, 101, 193002. [Google Scholar] [CrossRef] [PubMed]
- Hayden, P.; Dardis, J.; Hough, P.; Richardson, V.; Kennedy, E.T.; Costello, J.T.; Düsterer, S.; Redlin, H.; Feldhaus, J.; Li, W.B.; et al. The Laser-assisted photoelectric effect of He, Ne, Ar and Xe in intense extreme ultraviolet and infrared laser fields. J. Mod. Opt. 2016, 63, 358–366. [Google Scholar] [CrossRef]
- Azima, A.; Düsterer, S.; Radcliffe, P.; Redlin, H.; Stojanovic, N.; Li, W.; Schlarb, H.; Feldhaus, J.; Cubaynes, D.; Meyer, M.; et al. Time-resolved pump-probe experiments beyond the jitter limitations at FLASH. Appl. Phys. Lett. 2009, 94, 144102. [Google Scholar] [CrossRef]
- Ayvazyan, V.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bohnet, I.; Bolzmann, A.; Brinkmann, R.; Brovko, O.I.; et al. First operation of a free-electron laser generating GW power radiation at 32 nm wavelength. Eur. Phys. J. D 2006, 37, 297–303. [Google Scholar] [CrossRef]
- Radcliffe, P.; Düsterer, S.; Azima, A.; Li, W.B.; Plönjes, E.; Redlin, H.; Feldhaus, J.; Nicolosi, P.; Poletto, L.; Dardis, J.; et al. An experiment for two-color photoionization using high intensity extreme-UV free electron and near-IR laser pulses. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 583, 516–525. [Google Scholar] [CrossRef]
- Eland, J.H.D.; Vieuxmaire, O.; Kinugawa, T.; Lablanquie, P.; Hall, R.I.; Penent, F. Complete Two-Electron Spectra in Double Photoionization: The Rare Gases Ar, Kr, and Xe. Phys. Rev. Lett. 2003, 90, 53003. [Google Scholar] [CrossRef] [PubMed]
- Mazza, T.; Ilchen, M.; Rafipoor, A.J.; Callegari, C.; Finetti, P.; Plekan, O.; Prince, K.C.; Richter, R.; Demidovich, A.; Grazioli, C.; et al. Angular distribution and circular dichroism in the two-colour XUV + NIR above-threshold ionization of helium. J. Mod. Opt. 2016, 63, 367–382. [Google Scholar] [CrossRef]
- Gauthier, D.; Allaria, E.; Coreno, M.; Cudin, I.; Dacasa, H.; Danailov, M.B.; Demidovich, A.; Di Mitri, S.; Diviacco, B.; Ferrari, E.; et al. Chirped pulse amplification in an extreme-ultraviolet free-electron laser. Nat. Commun. 2016, 7, 13688. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.; Radcliffe, P.; Tschentscher, T.; Costello, J.T.; Cavalieri, A.L.; Grguras, I.; Maier, A.R.; Kienberger, R.; Bozek, J.; Bostedt, C.; et al. Angle-Resolved Electron Spectroscopy of Laser-Assisted Auger Decay Induced by a Few-Femtosecond X-ray Pulse. Phys. Rev. Lett. 2012, 108, 63007. [Google Scholar] [CrossRef] [PubMed]
- Mazza, T.; Ilchen, M.; Rafipoor, A.J.; Callegari, C.; Finetti, P.; Plekan, O.; Prince, K.C.; Richter, R.; Danailov, M.B.; Demidovich, A.; et al. Determining the polarization state of an extreme ultraviolet free-electron laser beam using atomic circular dichroism. Nat. Commun. 2014, 5, 3648. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, G.; Lindahl, A.O.; Knie, A.; Hartmann, N.; Lutman, A.A.; MacArthur, J.P.; Shevchuk, I.; Buck, J.; Galler, A.; Glownia, J.M.; et al. Circular dichroism measurements at an x-ray free-electron laser with polarization control. Rev. Sci. Instrum. 2016, 87, 83113. [Google Scholar] [CrossRef] [PubMed]
- Düsterer, S.; Rading, L.; Johnsson, P.; Rouzée, A.; Hundertmark, A.; Vrakking, M.J.J.; Radcliffe, P.; Meyer, M.; Kazansky, A.K.; Kabachnik, N.M. Interference in the angular distribution of photoelectrons in superimposed XUV and optical laser fields. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 164026. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M.Y. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Yakovlev, V.S.; Gagnon, J.; Karpowicz, N.; Krausz, F. Attosecond Streaking Enables the Measurement of Quantum Phase. Phys. Rev. Lett. 2010, 105, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, J.; Goulielmakis, E.; Yakovlev, V.S. The accurate FROG characterization of attosecond pulses from streaking measurements. Appl. Phys. B 2008, 92, 25–32. [Google Scholar] [CrossRef]
- Grguraš, I. Time Resolved Photoelectron Spectroscopy for Femtosecond Characterization of X-ray Free-Electron Laser Pulses. Ph.D. Thesis, Universität Hamburg, Hamburg, Germany, 2015. Available online: https://www.physnet.uni-amburg.de/services/biblio/dissertation/dissfbPhysik/___Kurzfassungen/Ivanka___Grguras (accessed on 1 September 2017).
- Helml, W. Development & Characterization of Sources for High-Energy, High-Intensity Coherent Radiation. Ph.D. Thesis, Technische Universität München, München, Germany, 2012. Available online: http://nbn-resolving.de/urn/resolver.pl?urn:nbn:de:bvb:91-diss-20120723–1110298–1-6 (accessed on 1 September 2017).
- Bozek, J.D. AMO instrumentation for the LCLS X-ray FEL. Eur. Phys. J. Spec. Top. 2009, 169, 129–132. [Google Scholar] [CrossRef]
- Kruit, P.; Read, F.H. Magnetic field paralleliser for 2π electron-spectrometer and electron-image magnifier. J. Phys. E 1983, 16, 313–324. [Google Scholar] [CrossRef]
- Gagnon, J.; Yakovlev, V.S. The robustness of attosecond streaking measurements. Opt. Express 2009, 17, 17678–17693. [Google Scholar] [CrossRef] [PubMed]
- Krinsky, S.; Gluckstern, R. Analysis of statistical correlations and intensity spiking in the self-amplified spontaneous-emission free-electron laser. Phys. Rev. Spec. Top. Accel. Beams 2003, 6, 50701. [Google Scholar] [CrossRef]
- Frühling, U.; Wieland, M.; Gensch, M.; Gebert, T.; Schütte, B.; Krikunova, M.; Kalms, R.; Budzyn, F.; Grimm, O.; Rossbach, J.; et al. Single-shot terahertz-field-driven X-ray streak camera. Nat. Photonics 2009, 3, 523–528. [Google Scholar] [CrossRef]
- Yeh, K.-L.; Hoffmann, M.C.; Hebling, J.; Nelson, K.A. Generation of 10 µJ ultrashort terahertz pulses by optical rectification. Appl. Phys. Lett. 2007, 90, 171121. [Google Scholar] [CrossRef]
- Grguraš, I.; Maier, A.R.; Behrens, C.; Mazza, T.; Kelly, T.J.; Radcliffe, P.; Düsterer, S.; Kazansky, A.K.; Kabachnik, N.M.; Tschentscher, T.; et al. Ultrafast X-ray pulse characterization at free-electron lasers. Nat. Photonics 2012, 6, 852–857. [Google Scholar] [CrossRef]
- Gagnon, J.; Yakovlev, V.S. The direct evaluation of attosecond chirp from a streaking measurement. Appl. Phys. B Lasers Opt. 2011, 103, 303–309. [Google Scholar] [CrossRef]
- Gouy, L.G. Sur Une Propriete Nouvelle Des Ondes Lumineuses. C. R. Acad. Sci. 1890, 110, 1251–1253. [Google Scholar]
- Wellhöfer, M.; Hoeft, J.T.; Martins, M.; Wurth, W.; Braune, M.; Viefhaus, J.; Tiedtke, K.; Richter, M. Photoelectron spectroscopy as a non-invasive method to monitor SASE-FEL spectra. J. Instrum. 2008, 3, P02003. [Google Scholar] [CrossRef]
- Bionta, M.R.; Lemke, H.T.; Cryan, J.P.; Glownia, J.M.; Bostedt, C.; Cammarata, M.; Castagna, J.-C.; Ding, Y.; Fritz, D.M.; Fry, A.R.; et al. Spectral encoding of X-ray/optical relative delay. Opt. Express 2011, 19, 21855–21865. [Google Scholar] [CrossRef] [PubMed]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Juranić, P.N.; Stepanov, A.; Ischebeck, R.; Schlott, V.; Pradervand, C.; Patthey, L.; Radović, M.; Gorgisyan, I.; Rivkin, L.; Hauri, C.P.; et al. High-precision X-ray FEL pulse arrival time measurements at SACLA by a THz streak camera with Xe clusters. Opt. Express 2014, 22, 30004. [Google Scholar] [CrossRef] [PubMed]
- Gorgisyan, I.; Ischebeck, R.; Erny, C.; Dax, A.; Patthey, L.; Pradervand, C.; Sala, L.; Milne, C.; Lemke, H.T.; Hauri, C.P.; et al. THz streak camera method for synchronous arrival time measurement of two-color hard X-ray FEL pulses. Opt. Express 2017, 25, 2080. [Google Scholar] [CrossRef]
- Irimia, D.; Dobrikov, D.; Kortekaas, R.; Voet, H.; van den Ende, D.A.; Groen, W.A.; Janssen, M.H.M. A short pulse (7 µs FWHM) and high repetition rate (dc-5 kHz) cantilever piezovalve for pulsed atomic and molecular beams. Rev. Sci. Instrum. 2009, 80, 113303. [Google Scholar] [CrossRef] [PubMed]
- Hagena, O.F.; Obert, W. Cluster Formation in Expanding Supersonic Jets: Effect of Pressure, Temperature, Nozzle Size, and Test Gas. J. Chem. Phys. 1972, 56, 1793–1802. [Google Scholar] [CrossRef]
- Juranić, P.N.; Stepanov, A.; Peier, P.; Hauri, C.P.; Ischebeck, R.; Schlott, V.; Radović, M.; Erny, C.; Ardana-Lamas, F.; Monoszlai, B.; et al. A scheme for a shot-to-shot, femtosecond-resolved pulse length and arrival time measurement of free electron laser X-ray pulses that overcomes the time jitter problem between the FEL and the laser. J. Instrum. 2014, 9, P03006. [Google Scholar] [CrossRef]
- Thompson, N.R.; McNeil, B.W.J. Mode Locking in a Free-Electron Laser Amplifier. Phys. Rev. Lett. 2008, 100, 203901. [Google Scholar] [CrossRef] [PubMed]
- Kur, E.; Dunning, D.J.; McNeil, B.W.J.; Wurtele, J.; Zholents, A.A. A wide bandwidth free-electron laser with mode locking using current modulation. New J. Phys. 2011, 13, 63012. [Google Scholar] [CrossRef]
- Xiang, D.; Ding, Y.; Raubenheimer, T.; Wu, J. Mode-locked multichromatic x rays in a seeded free-electron laser for single-shot X-ray spectroscopy. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 50707. [Google Scholar] [CrossRef]
- Ding, Y.; Decker, F.-J.; Emma, P.; Feng, C.; Field, C.; Frisch, J.; Huang, Z.; Krzywinski, J.; Loos, H.; Welch, J.; et al. Femtosecond X-ray Pulse Characterization in Free-Electron Lasers Using a Cross-Correlation Technique. Phys. Rev. Lett. 2012, 109, 254802. [Google Scholar] [CrossRef] [PubMed]
- Riedel, R.; Al-Shemmary, A.; Gensch, M.; Golz, T.; Harmand, M.; Medvedev, N.; Prandolini, M.J.; Sokolowski-Tinten, K.; Toleikis, S.; Wegner, U.; et al. Single-shot pulse duration monitor for extreme ultraviolet and X-ray free-electron lasers. Nat. Commun. 2013, 4, 1731. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, T.J.; Behrens, C.; Ding, Y.; Fisher, A.S.; Frisch, J.; Huang, Z.; Loos, H. Coherent-Radiation Spectroscopy of Few-Femtosecond Electron Bunches Using a Middle-Infrared Prism Spectrometer. Phys. Rev. Lett. 2013, 111, 184801. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, N.; Helml, W.; Galler, A.; Bionta, M.R.; Grünert, J.; Molodtsov, S.L.; Ferguson, K.R.; Schorb, S.; Swiggers, M.L.; Carron, S.; et al. Sub-femtosecond precision measurement of relative X-ray arrival time for free-electron lasers. Nat. Photonics 2014, 8, 706–709. [Google Scholar] [CrossRef]
- Löhl, F.; Arsov, V.; Felber, M.; Hacker, K.; Jalmuzna, W.; Lorbeer, B.; Ludwig, F.; Matthiesen, K.-H.; Schlarb, H.; Schmidt, B.; et al. Electron Bunch Timing with Femtosecond Precision in a Superconducting Free-Electron Laser. Phys. Rev. Lett. 2010, 104, 144801. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Diviacco, B.; Callegari, C.; Finetti, P.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; De Ninno, G.; Lambert, G.; Ferrari, E.; et al. Control of the Polarization of a Vacuum-Ultraviolet, High-Gain, Free-Electron Laser. Phys. Rev. X 2014, 4, 41040. [Google Scholar] [CrossRef]
- Kazansky, A.K.; Bozhevolnov, A.V.; Sazhina, I.P.; Kabachnik, N.M. Interference effects in angular streaking with a rotating terahertz field. Phys. Rev. A 2016, 93, 13407. [Google Scholar] [CrossRef]
- Kazansky, A.K.; Sazhina, I.P.; Nosik, V.L.; Kabachnik, N.M. Angular streaking and sideband formation in rotating terahertz and far-infrared fields. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 105601. [Google Scholar] [CrossRef]
- Constant, E.; Taranukhin, V.; Stolow, A.; Corkum, P. Methods for the measurement of the duration of high-harmonic pulses. Phys. Rev. A 1997, 56, 3870–3878. [Google Scholar] [CrossRef]
- Eckle, P.; Smolarski, M.; Schlup, P.; Biegert, J.; Staudte, A.; Schöffler, M.; Muller, H.G.; Dörner, R.; Keller, U. Attosecond angular streaking. Nat. Phys. 2008, 4, 565–570. [Google Scholar] [CrossRef]
- Ueda, K.; Ishikawa, K.L. Attosecond science: Attoclocks play devil’s advocate. Nat. Phys. 2011, 7, 371–372. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helml, W.; Grguraš, I.; Juranić, P.N.; Düsterer, S.; Mazza, T.; Maier, A.R.; Hartmann, N.; Ilchen, M.; Hartmann, G.; Patthey, L.; et al. Ultrashort Free-Electron Laser X-ray Pulses. Appl. Sci. 2017, 7, 915. https://doi.org/10.3390/app7090915
Helml W, Grguraš I, Juranić PN, Düsterer S, Mazza T, Maier AR, Hartmann N, Ilchen M, Hartmann G, Patthey L, et al. Ultrashort Free-Electron Laser X-ray Pulses. Applied Sciences. 2017; 7(9):915. https://doi.org/10.3390/app7090915
Chicago/Turabian StyleHelml, Wolfram, Ivanka Grguraš, Pavle N. Juranić, Stefan Düsterer, Tommaso Mazza, Andreas R. Maier, Nick Hartmann, Markus Ilchen, Gregor Hartmann, Luc Patthey, and et al. 2017. "Ultrashort Free-Electron Laser X-ray Pulses" Applied Sciences 7, no. 9: 915. https://doi.org/10.3390/app7090915
APA StyleHelml, W., Grguraš, I., Juranić, P. N., Düsterer, S., Mazza, T., Maier, A. R., Hartmann, N., Ilchen, M., Hartmann, G., Patthey, L., Callegari, C., Costello, J. T., Meyer, M., Coffee, R. N., Cavalieri, A. L., & Kienberger, R. (2017). Ultrashort Free-Electron Laser X-ray Pulses. Applied Sciences, 7(9), 915. https://doi.org/10.3390/app7090915







