Abstract
The influence of additive noise, multiplicative noise, and higher-order effects on exploding solitons in the framework of the prototype complex cubic-quintic Ginzburg-Landau equation is studied. Transitions from explosions to filling-in to the noisy spatially homogeneous finite amplitude solution, collapse (zero solution), and periodic exploding dissipative solitons are reported.
1. Introduction
Soliton explosions, fascinating nonlinear phenomena in dissipative systems, have been observed in at least three key experiments. As has been reported by Cundiff et al. [1], a mode-locked laser using a Ti:Sapphire crystal can produce intermittent explosions. More recently, a different medium for explosions was reported by Broderick et al., namely, a passively mode-locked fibre laser [2]. In 2016, Liu et al. showed that in an ultrafast fiber laser, the exploding behavior could operate in a sustained but periodic mode called “successive soliton explosions” [3].
Almost all parts of these exploding objects are unstable, but nevertheless they remain localized. Localized structures in systems far from equilibrium are the result of a delicate balance between injection and dissipation of energy, nonlinearity and dispersion (compare [4] for a recent exposition of the subject). This fact leads to a generalization of the well known conservative soliton to a dissipative soliton DS (Akhmediev et al. [5]). Experimental observation of DSs, apart from explosions, shows a wide spectrum in nature including binary fluid convection, granular systems, chemical surface reactions, nonlinear optics and starch suspensions [6,7,8,9,10,11,12,13,14,15].
Explosions, being chaotic phenomena, are not identical, resulting in a random distribution of times between explosions. Real systems, where explosions were observed, are not continuous, however, explosive behavior was predicted theoretically in the complex cubic-quintic Ginzburg-Landau equation, whose parameters vary continuously [16,17].
The complex cubic-quintic Ginzburg-Landau equation (CQGLE), a prototype envelope equation, derived near the onset of a subcritical instability (inverted Hopf bifurcacion), was first introduced by Brand et al. when modeling binary mixtures [18,19]. However, Thual and Fauve were the first to report explicitly the existence of stable pulse solutions in the CQGLE [20]. In optics, this equation describes laser systems [21,22,23], soliton transmission lines [24], and nonlinear cavities with an external pump [25]. A natural parameter to be varied in this equation is the distance from linear onset. For a large range of parameters, the following sequence was found: stationary pulses, pulses with one and two frequencies, and finally exploding pulses [26]. This fact revealed a quasiperiodic route to chaos for spatially localized solutions [27]. In addition, we have studied the effect of small and large additive noise on the formation of localized patterns [28,29]. We concluded that weak additive noise is enough to induce explosions while the interaction of localization and noise can lead to noisy localized structures. Recently, we have reported that multiplicative noise can reduce and even suppress the existence of explosions in localized solutions [30].
In this article, we study the influence of additive noise, multiplicative noise, and higher-order effects on exploding solitons in the framework of the prototype envelope complex cubic-quintic Ginzburg-Landau equation. Transitions from explosions to filling-in to the noisy spatially homogeneous finite amplitude solution, collapse (zero solution), and periodic exploding dissipative solitons are reported.
2. Influence of Additive and Multiplicative Noise on Exploding Dissipative Solitons
Sources of noise are always present in physical systems, which can be external or internal (as examples, we can mention thermal noise, fluctuations in pressure, temperature or electrical signals, etc.). Ordinary or partial differential equations take account of the behavior of systems under the influence of fluctuations [31,32,33]. Internal noise becomes typically additive [34] while external noise becomes typically multiplicative or both [35].
2.1. Stochastic Equations
The stochastic complex cubic-quintic complex Ginzburg-Landau equation (SCQGLE) under the influence of additive noise reads
Here, is the complex envelope, ; ; ; is the distance from linear onset (real), and the noise strength. and in order to guarantee that we are in the presence of an inverted Hopf bifurcation saturating to quintic order. The complex white noise satisfies (zero mean), and (delta correlated in space and time). Discretization in space and time should not affect quantitative noise features, so that becomes replaced by , where and are uncorrelated random numbers (in space and time) obeying a normal distribution with zero mean and unit variance.
The SCQGLE with multiplicative noise that we investigate here is of the form
where the white noise satisfies (zero mean), and (delta-correlated in time but homogeneous in space), so that is replaced by , where corresponds to uncorrelated random numbers obeying a normal distribution with zero mean and unit variance. Additive noise implies perturbations on short length and time scales. However, homogeneous multiplicative noise leads to a homogeneous enhancement and suppression of the modulus as a function of time. As an example, we can mention electroconvection in nematic liquid crystals by superposing noise on the driving voltage [36].
2.2. Numerical Method
The parameters we used are , , . The complex cubic-quintic Ginzburg-Landau equation has seven parameters. After scaling t, x and A, we can fix , and . Nevertheless, explosions occur as a function of only in a subset of the space . According to our previous experience in explosions [26], we choose , and .
We considered periodic boundary conditions and by varying the box size we made sure that our box is sufficiently large so that none of the results presented in the following are sensitively dependent on the box size.
The bifurcation parameter is varied from −0.26 until −0.16. This range includes values of where deterministically we find stationary solutions and oscillatory solutions (with one and two frequencies) and exploding solitons [28]. Initial conditions are deterministic solutions of the CQGLE.
To numerically solve Equations (1) and (2), we used a pseudo—spectral split—step method, where the derivatives are computed in Fourier space using a fast Fourier transformation and the non-linear part is integrated in time by a fourth order Runge-Kutta method. To perform these operations, we write our equations in the following way
where represents the part of the equation containing the linear and non-linear terms with the exception of the double derivative in x. If we split Equation (3) into two operators, we get and .
We integrate the differential part over a small interval , by performing a Fourier transformation , where is the squared wave vector. After integrating the differential and nonlinear part separately, we obtain
The second integration is performed by a fourth order Runge-Kutta method which gives us a more numerically stable result. Finally, we get the solution for A integrated over a small time step
This numerical method was implemented using a Python code with Fortran subroutines. For the numerical simulations, we used Fourier modes over a discretized grid of length and a time step of size .
2.3. Results
In [28], we studied the effect of weak additive noise on the spatially localized pulses (either stationary or oscillating with one and two frequencies) concluding that small additive noise is enough to induce exploding dissipative solitons, which are mostly chaotic.
Here, we report (Figure 1a) three types of pulses emerging as a function of , including the range where deterministically exploding solitons exist, for varying two decades of (logarithmic scale). For and small values of , we find (in agreement with [28]) noisy non-explosive localized solutions, either chaotic or non-chaotic. Large enough values of noise always induce explosions. Non-chaotic explosions are observed at the border separating non-explosive states from exploding solitons. For sufficiently large noise strength , we observe a transition to filling-in, that is, a noisy spatially homogeneous finite amplitude solution.
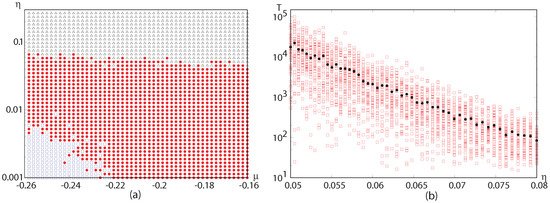
Figure 1.
Phase diagram: Effect of additive noise on exploding solitons for a fixed time scale . (a) Black triangles (Δ) denote filling-in to the spatially homogeneous finite amplitude solution under the influence of additive noise. Red solid circles (•) stand for exploding dissipative solutions and blue squares (□) for noisy non-explosive localized solutions; (b) Filling-in time for the transition from an exploding dissipative soliton to filling-in under the influence of additive noise for . The average time scale T for filling-in is shown as a function of the noise strength . Black solid circles (•) represent an average of over 50 realizations shown as open squares (□).
The phase diagram shown in Figure 1a is rather insensitive to the maximum run time T, as we can notice from Figure 1b. There, the filling-in time for the transition from an exploding dissipative soliton to filling-in under the influence of additive noise for is shown. The average time scale T for filling-in is plotted as a function of the noise strength . Black solid circles represent an average over 50 realizations shown as open squares (□). Inspecting this figure, we see that to decrease T by about one decade, one needs to increase by .
For and , we have a stationary solution. When a small noise () is added to Equation (1), it acts mainly as a perturbation on short length and time scales giving the state a noisy appearance (Figure 2a). When is increased to ∼0.03, a perturbation starts growing in the wings. Once this peak has grown, it interacts with the main pulse forming a wide chaotic localized one (this instant is shown as a snapshot in Figure 2b). After this, rapidly the system collapses to a state, similar to the original starting peak. This is what we call explosion. For large enough noise (), the whole system jumps to a noisy spatially homogeneous finite amplitude solution (Figure 2c).

Figure 2.
Three snapshots for and additive noise for different values of the noise strength . (a) Noisy non-explosive localized solution, ; (b) Exploding dissipative solution, ; (c) Noisy spatially homogeneous finite amplitude solution, .
For spatially homogeneous multiplicative noise, where we observe a collective enhancement and suppression (in space) of the amplitude, we report in Figure 3a three types of patterns, as a function of the bifurcation parameter , and the noise strength: exploding dissipative solitons (red solid circles (•)), oscillating localized states (blue squares (□)). Either they are not explosive or their frequency of explosions is undetectable for . In the range of shown in Figure 3, values of induce collapse (black triangles (Δ)). In a previous article [30], we reported that multiplicative noise can lead to a reduction of the number of explosions and even to the collapse of dissipative solitons.
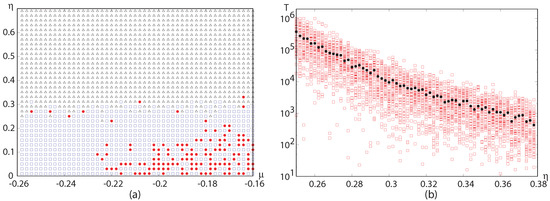
Figure 3.
Phase diagram: Influence of multiplicative noise on exploding solitons for a fixed time scale . (a) Black triangles (Δ) denote collapsed states. Red solid circles (•) stand for exploding dissipative solutions and blue squares (□) for oscillating localized solutions. (b) Collapse time for exploding dissipative solitons under the influence of multiplicative noise for . The average time scale T for collapse is shown as a function of the noise strength . Black solid circles (•) represent an average over 50 realizations shown as open squares (□).
In Figure 3b, collapse time for exploding dissipative solitons under the influence of multiplicative noise is shown for . The average time scale T for collapse is plotted as a function of the noise strength . Black solid circles represent an average of over 50 realizations shown as open squares (□). One can see from the plot that decreasing at the border in 0.03 means to increase T in one decade.
3. Exploding Dissipative Solitons and Higher-Order Effects
The inclusion of higher-order terms to the complex cubic-quintic Ginzburg-Landau equation has a clear physical motivation, namely, modeling the propagation of short pulses along a mode-locked fiber laser. According to Agrawal [37], for short pulses ( ps), where is the width of the pulse, one should include the higher-order effects. Therefore, the generalized pulse-propagation equation reads
where is the envelope (slowly varying function of and T) of the complex electrical field in a comoving frame, g the gain or loss of energy, P the pumping power, stands for the dispersion coefficients, , , where is the effective mode area, is called the nonlinear Kerr parameter, and the carrier frequency. The integral in this equation accounts for the energy transfer resulting from intrapulse Raman scattering.
3.1. Complex Ginzburg-Landau Equation and Short Pulses
For short pulses but wide enough ( ps), expanding in a Taylor-series up to first order in , and considering up to the third-order dispersion , we can deduce from Equation (6) the following non-integrable quation [38]
where is the first moment of the Raman response function and .
One can note that has dimensions of power. Therefore, one can define the dimensionless variable A as . In the same way, using the dispersion length, the dimensionless variable z: , and the dimensionless variable : . Thus, introducing the variables A, z and in Equation (7), we can obtain a dimensionless complex CQGLE including three higher-order effects: third-order dispersion, self-steepening, and intrapulse Raman scattering.
The left side of Equation (8) is nothing but the cubic-quintic non-linear Schrödinger equation, which is conservative. On the right side, the three first terms are related to g, taking account of the linear gain and loss of energy , and for the non-linear gain or absorption of energy . The term associated to plays the role of spectral filtering. The last three terms on the right side are precisely the higher-order effects, which are conservative and whose coefficients , s, and are defined as follows:
3.2. Results
Equation (8) without considering higher-order effects is the optical version for the CQGLE studied in Section 2. Coefficients can easily be converted from Equations (1)–(8): ; ; ; , ; ; and . In optics, to use as a control parameter is meaningful because is related to the pumping power.
As in Section 2, to solve Equation (8), we used a pseudo-spectral split-step numerical method along to Fourier modes, and . Our parameters are: , , , and .
For around 1.02 (and ), the energy exhibits different maxima , which can be plotted in a logistic map (see Figure 4a), giving the aspect of a complex picture, natural consequence of explosive chaotic behavior. While in Figure 5a, one can observe the evolution of the amplitude in a plot for . There, one can notice the random distribution of locations in z between explosions (the analogue of the random distribution of times between explosions in Equation (1)). The distribution of locations in z obeys a narrow distribution centered around a mean value.
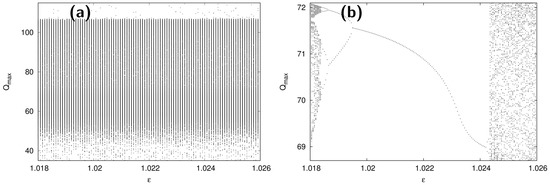
Figure 4.
(a) Logistic map for without including higher-order effects. Complex picture, natural consequence of explosive chaotic behavior; (b) Logistic map for including higher-order effects. One can observe a window without chaos around .
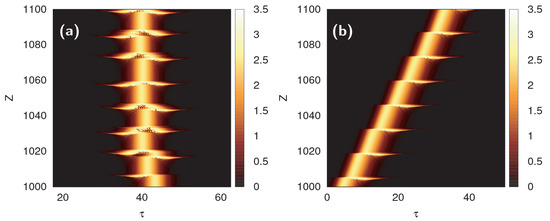
Figure 5.
plot of following the dimensionless complex CQGLE (8) for , (a) without including higher-order effects, showing chaotic explosions, and (b) including higher-order effects, showing periodic explosions.
Considering 3 fs [37] and 0.1 ps, we estimate 0.03, and noticing that (number of cycles tangled by ), s can also be estimated as . Now, following the same above procedure for the CQGLE, but including higher-order nonlinear and dispersive effects (, , ), we notice the appearance of windows corresponding to non-chaotic behaviors (see Figure 4b). Around , one can observe period-halving bifurcations leading to order, and period-doubling bifurcations leading to chaos. Around and , the limit of the ratio of distances between consecutive bifurcation intervals tends to 4.6 (close to the Feigenbaum constant).
Figure 5b shows the evolution of the amplitude in a plot, for , considering higher-order nonlinear and dispersive effects. In contrast to Figure 5a, we see that there is a fixed distance in z between explosions and explosions repeat exactly after a period. We are in the presence of periodic explosions.
4. Conclusions and Discussion
In summary, we have studied the influence of additive noise, multiplicative noise, and higher-order effects on exploding solitons in the framework of the prototype complex cubic-quintic Ginzburg-Landau equation.
For the stochastic CQGLE with enough large additive noise, we report a transition from explosions to filling-in, that is, a noisy spatially finite solution. Under the influence of large multiplicative noise, homogeneous in space, a collapse occurs in the zero amplitude solution.
We show that the phase diagrams for different outcomes under the influence of additive or multiplicative noise are rather insensitive to the choice of the run time. The transitions to filling-in and collapse follow an exponential law for the transition time as a function of the noise strength. This is a typical behavior for a transition between different potential barriers triggered by noise.
For short pulses, we deduced a dimensionless complex CQGLE including three higher-order effects: third-order dispersion, self-steepening, and intrapulse Raman scattering. Periodic exploding dissipative solitons are reported. We notice that a long time ago, but in the context of envelope equations, the effect of nonlinear gradient terms on localized solutions was studied by Deissler and Brand [39].
Acknowledgments
We wish to thank the support of FONDECYT through Project No. 1170728.
Author Contributions
Orazio Descalzi deduced the equations and has partially written the article. Carlos Cartes has carried out the numerical simulations, data analysis and has partially written the article.
Conflicts of Interest
The authors declare no conflict of interest.The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Cundiff, S.; Soto-Crespo, J.; Akhmediev, N. Experimental Evidence for Soliton Explosions. Phys. Rev. Lett. 2002, 88, 073903. [Google Scholar] [CrossRef] [PubMed]
- Runge, A.F.; Broderick, N.G.; Erkintalo, M. Observation of soliton explosions in a passively mode-locked fiber laser. Optica 2015, 2, 36–39. [Google Scholar] [CrossRef]
- Liu, M.; Luo, A.P.; Yan, Y.R.; Hu, S.; Liu, Y.C.; Cui, H.; Luo, Z.C.; Xu, W.C. Successive soliton explosions in an ultrafast fiber laser. Opt. Lett. 2016, 41, 1181–1184. [Google Scholar] [CrossRef] [PubMed]
- Descalzi, O.; Rosso, O.A.; Larrondo, H.A. Localized Structures in Physics and Chemistry. Eur. Phys. J. Spec. Top. 2014, 223, 1–7. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. Dissipative Solitons; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kolodner, P.; Bensimon, D.; Surko, C. Traveling-wave convection in an annulus. Phys. Rev. Lett. 1988, 60, 1723. [Google Scholar] [CrossRef] [PubMed]
- Niemela, J.J.; Ahlers, G.; Cannell, D.S. Localized traveling-wave states in binary-fluid convection. Phys. Rev. Lett. 1990, 64, 1365. [Google Scholar] [CrossRef] [PubMed]
- Kolodner, P. Collisions between pulses of traveling-wave convection. Phys. Rev. A 1991, 44, 6466–6479. [Google Scholar] [CrossRef] [PubMed]
- Rotermund, H.; Jakubith, S.; Von Oertzen, A.; Ertl, G. Solitons in a surface reaction. Phys. Rev. Lett. 1991, 66, 3083. [Google Scholar] [CrossRef] [PubMed]
- Umbanhowar, P.B.; Melo, F.; Swinney, H.L. Localized excitations in a vertically vibrated granular layer. Nature 1996, 382, 793. [Google Scholar] [CrossRef]
- Taranenko, V.; Staliunas, K.; Weiss, C. Spatial soliton laser: Localized structures in a laser with a saturable absorber in a self-imaging resonator. Phys. Rev. A 1997, 56, 1582. [Google Scholar] [CrossRef]
- Lioubashevski, O.; Hamiel, Y.; Agnon, A.; Reches, Z.; Fineberg, J. Oscillons and propagating solitary waves in a vertically vibrated colloidal suspension. Phys. Rev. Lett. 1999, 83, 3190. [Google Scholar] [CrossRef]
- Ultanir, E.A.; Stegeman, G.I.; Michaelis, D.; Lange, C.H.; Lederer, F. Stable dissipative solitons in semiconductor optical amplifiers. Phys. Rev. Lett. 2003, 90, 253903. [Google Scholar] [CrossRef] [PubMed]
- Merkt, F.S.; Deegan, R.D.; Goldman, D.I.; Rericha, E.C.; Swinney, H.L. Persistent holes in a fluid. Phys. Rev. Lett. 2004, 92, 184501. [Google Scholar] [CrossRef] [PubMed]
- Ebata, H.; Sano, M. Self-replicating holes in a vertically vibrated dense suspension. Phys. Rev. Lett. 2011, 107, 088301. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.M.; Akhmediev, N.; Ankiewicz, A. Pulsating, creeping, and erupting solitons in dissipative systems. Phys. Rev. Lett. 2000, 85, 2937–2940. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Soto-Crespo, J.; Town, G. Pulsating solitons, chaotic solitons, period doubling, and pulse coexistence in mode-locked lasers: Complex Ginzburg-Landau equation approach. Phys. Rev. E 2001, 63, 056602. [Google Scholar] [CrossRef] [PubMed]
- Brand, H.R.; Lomdahl, P.S.; Newell, A.C. Evolution of the order parameter in situations with broken rotational symmetry. Phys. Lett. A 1986, 118, 67–73. [Google Scholar] [CrossRef]
- Brand, H.R.; Lomdahl, P.S.; Newell, A.C. Benjamin-Feir turbulence in convective binary fluid mixtures. Physica D 1986, 23, 345–361. [Google Scholar] [CrossRef]
- Thual, O.; Fauve, S. Localized structures generated by subcritical instabilities. J. Phys. France 1988, 49, 1829–1833. [Google Scholar] [CrossRef]
- Haus, H.A. Theory of mode locking with a fast saturable absorber. J. Appl. Phys. 1975, 46, 3049–3058. [Google Scholar] [CrossRef]
- Belanger, P. Coupled-cavity mode locking: A nonlinear model. JOSA B 1991, 8, 2077–2081. [Google Scholar] [CrossRef]
- Weiss, C. Spatio-temporal structures. Part II. Vortices and defects in lasers. Phys. Rep. 1992, 219, 311–338. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Gordon, J.P.; Evangelides, S.G. The sliding-frequency guiding filter: An improved form of soliton jitter control. Opt. Lett. 1992, 17, 1575–1577. [Google Scholar] [CrossRef] [PubMed]
- Firth, W.; Scroggie, A. Optical bullet holes: Robust controllable localized states of a nonlinear cavity. Phys. Rev. Lett. 1996, 76, 1623. [Google Scholar] [CrossRef] [PubMed]
- Descalzi, O.; Brand, H.R. Transition from modulated to exploding dissipative solitons: Hysteresis, dynamics, and analytic aspects. Phys. Rev. E 2010, 82, 026203. [Google Scholar] [CrossRef] [PubMed]
- Descalzi, O.; Cartes, C.; Cisternas, J.; Brand, H.R. Exploding dissipative solitons: The analog of the Ruelle-Takens route for spatially localized solutions. Phys. Rev. E 2011, 83, 056214. [Google Scholar] [CrossRef] [PubMed]
- Cartes, C.; Descalzi, O.; Brand, H.R. Noise can induce explosions for dissipative solitons. Phys. Rev. E 2012, 85, 015205. [Google Scholar] [CrossRef] [PubMed]
- Descalzi, O.; Cartes, C.; Brand, H.R. Noisy localized structures induced by large noise. Phys. Rev. E 2015, 91, 020901. [Google Scholar] [CrossRef] [PubMed]
- Descalzi, O.; Cartes, C.; Brand, H.R. Multiplicative noise can lead to the collapse of dissipative solitons. Phys. Rev. E 2016, 94, 012219. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N. Stochastic Processes in Physics and Chemistry; North-Holland Personal Library; Elsevier Science: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Risken, H.; Haken, H. The Fokker-Planck Equation: Methods of Solution and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Tsimring, L.S. Noise in biology. Rep. Prog. Phys. 2014, 77, 026601. [Google Scholar] [CrossRef] [PubMed]
- Graham, R. Hydrodynamic fluctuations near the convection instability. Phys. Rev. A 1974, 10, 1762. [Google Scholar] [CrossRef]
- Schenzle, A.; Brand, H.R. Multiplicative stochastic processes in statistical physics. Phys. Rev. A 1979, 20, 1628. [Google Scholar] [CrossRef]
- Brand, H.R.; Kai, S.; Wakabayashi, S. External noise can suppress the onset of spatial turbulence. Phys. Rev. Lett. 1985, 54, 555. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G. Nonlinear Fiber Optics; Optics and Photonics Series; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Cartes, C.; Descalzi, O. Periodic exploding dissipative solitons. Phys. Rev. A 2016, 93, 031801. [Google Scholar] [CrossRef]
- Deissler, R.; Brand, H.R. The effect of nonlinear gradient terms on localized states near a weakly inverted bifurcation. Phys. Lett. A 1990, 146, 252. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).