Graphene as a Prototypical Model for Two-Dimensional Continuous Mechanics
Abstract
1. Introduction
2. Mechanical Properties
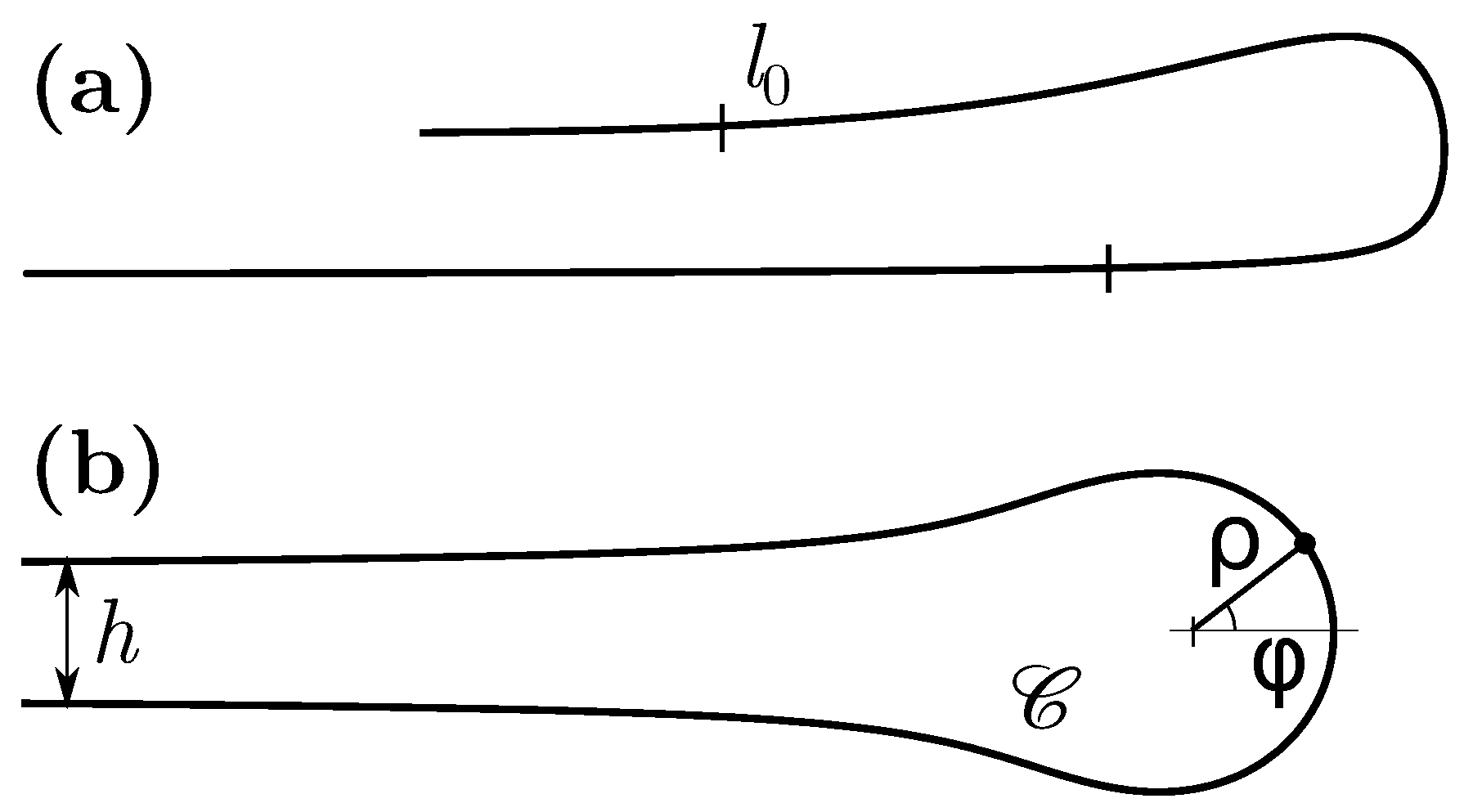
3. Graphene Folding
4. Self - Folding of Graphene
5. Mechanical Tearing
6. Gaussian Curvature
7. Collapse of Nanotubes
8. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
Appendix A. Van der Waals Binding Energy between Few-Layer Graphite Sheets
References
- Ten years in two dimensions. Nat. Nanotechnol. 2014, 10, 725.
- Young, R.J.; Kinloch, I.A.; Gong, L.; Novoselov, K.S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M. Toughening of polymers by graphene. Nanomat. Energy 2013, 2, 265–278. [Google Scholar] [CrossRef]
- Hess, P. Graphene as a model system for 2D fracture behavior of perfect and defective solids. Frattura Integr. Strut. 2015, 34, 341–346. [Google Scholar]
- Lambin, P.H. Elastic properties and stability of physisorbed graphene. Appl. Sci. 2014, 4, 282–304. [Google Scholar] [CrossRef]
- Politano, A.; Chiarello, G. Probing the Young’s modulus and Poisson’s ratio in graphene/metal interfaces and graphite: A comparative study. NanoResearch 2015, 8, 1847–1856. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, B.; Wu, J.; Yang, R.; Dunn, M.L. Bending rigidity and gaussian bending stiffness of single-layered graphene. Nano Lett. 2013, 13, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Torres-Dias, A.C.; Cerqueira, T.F.T.; Cui, W.; Marquesd, M.A.L.; Botti, S.; Machon, D.; Hartmann, M.A.; Sun, Y.; Dunstan, D.J. San-Miguel, Alfonso From mesoscale to nanoscale mechanics in single-wall carbon nanotubes. Carbon 2017, 123, 145–150. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials –Graphene and beyond. Extreme Mech. Lett. 2017, 13, 42–72. [Google Scholar] [CrossRef]
- Liu, F.; Ming, P.; Li, J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B 2007, 76, 1–7. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J.H. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–387. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.H.; Cooper, R.C.; An, S.J.; Lee, S.; van der Zande, A.; Petrone, N.; Hammerberg, A.G.; Lee, C.; Crawford, B.; Oliver, W.; et al. High-strength chemical-vapor deposited graphene and grain boundaries. Science 2013, 340, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Ovidd’ko, I.A. Mechanical properties of graphene. Rev. Adv. Mater. Sci. 2013, 34, 1–11. [Google Scholar]
- Zhang, P.; Ma, L.; Fan, F.; Zeng, Z.; Peng, C.; Loya, P.E.; Liu, Z.; Gong, Y.; Zhang, J.; Zhang, X.; et al. Fracture toughness of graphene. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hwangbo, Y.; Lee, C.K.; Kim, S.M.; Kim, J.H.; Kim, K.S.; Jang, B.; Lee, H.J.; Lee, S.K.; Kim, S.S.; Ahn, J.H.; et al. Fracture characteristics of monolayer CVD-graphene. Sci. Rep. 2014, 4, 4439. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Qi, H.J.; Fan, F.; Zhu, T.; Wang, B.; Wei, Y. Griffith criterion for brittle fracture in graphene. Nano Lett. 2015, 15, 1918–1924. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Kang, S.; Koo, J.; Lee, H.; Kwon, Y.; Kim, J. Cohesion energetics of carbon allotropes: Quantum Monte Carlo study. J. Chem. Phys. 2014, 140, 114702. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Huang, R. Excess energy and deformation along free edges of graphene nanoribbons. Phys. Rev. B 2010, 81, 155410. [Google Scholar] [CrossRef]
- Deng, S.; Berry, V. Wrinkled, rippled and crumpled graphene: An overview of formation mechanism, electronic properties, and applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Nicholl, R.J.T.; Conley, H.J.; Lavrik, N.V.; Vlassiouk, I.; Puzyrev, Y.S.; Sreenivas, V.P.; Pantelides, S.T.; Bolotin, K.I. The effect of intrinsic crumpling on the mechanics of free-standing graphene. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Dewapriya, M.A.N.; Meguid, S.A. Atomistic modeling of out-of-plane deformation of a propagating Griffith crack in graphene. Acta Mech. 2017, 228. [Google Scholar] [CrossRef]
- Song, Z.; Ni, Y.; Xu, Z. Geometrical distortion leads to Griffith strength reduction in graphene membranes. Extreme Mech. Lett. 2017, 14, 31–37. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Ortolani, L.; Cadelano, E.; Veronese, G.P.; Esposti Boschi, C.D.; Snoeck, E.; Colombo, L.; Morandi, V. Folded graphene membranes: Mapping curvature at the nanoscale. Nano Lett. 2012, 12, 5207–5212. [Google Scholar] [CrossRef] [PubMed]
- Morandi, V.; Ortolani, L.; Migliori, A.; Cristian, D.E.B.; Cadelano, E.; Colombo, L. Folds and buckles at the nanoscale: Experimental and theoretical investigation of the bending properties of graphene membranes. In Making and Exploiting Fullerenes, Graphene, and Carbon Nanotubes; Springer: Berlin, Germany, 2013; pp. 205–236. [Google Scholar]
- Zhang, J.; Xiao, J.; Meng, X.; Monroe, C.; Huang, Y.; Zuo, J.M. Free folding of suspended graphene sheets by random mechanical stimulation. Phys. Rev. Lett. 2010, 104, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Dai, S.; Li, X.; Yang, J.; Srolovitz, D.J.; Zheng, Q. Measurement of the cleavage energy of graphite. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Mostaani, E.; Drummond, N.D.; Fal’ko, V.I. Quantum Monte Carlo calculation of the binding energy of bilayer graphene. Phys. Rev. Lett. 2015, 115, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Girifalco, L.A.; Hodak, M. Van der Waals binding energies in graphitic structures. Phys. Rev. B 2002, 65, 1–5. [Google Scholar] [CrossRef]
- Bosak, A.; Krisch, M.; Mohr, M.; Maultzsch, J.; Thomsen, C. Elasticity of single-crystalline graphite: Inelastic x-ray scattering study. Phys. Rev. B 2007, 75, 1–4. [Google Scholar] [CrossRef]
- Rotkin, S.V.; Zarov, I.; Hess, K. Zipping of graphene edge as a mechanism for nanotube nucleation. In Electronic Properties of Molecular Nanostructures; Kuzmany, H., Fink, J., Mehring, M., Roth, S., Eds.; AIP Conference Proceedings 591; American Institute of Physics: New York, NY, USA, 2001; pp. 454–457. [Google Scholar]
- Meng, X.; Li, M.; Kang, Z.; Zhang, X.; Xiao, J. Mechanics of self-folding of single-layer graphene. J. Phys. D 2013, 46, 055308. [Google Scholar] [CrossRef]
- Cox, B.J.; Baowan, D.; Bacsac, W.; Hilld, J.M. Relating elasticity and graphene folding conformation. RSC Adv. 2015, 5, 57515–57520. [Google Scholar] [CrossRef]
- Behfar, K.; Selfi, P.; Naghdabadi, R.; Ghanbar, J. An analytical approach to determination of bending modulus of a multi-layered graphene sheet. Thin Solid Films 2006, 496, 475–480. [Google Scholar] [CrossRef]
- Sen, D.; Novoselov, K.S.; Reis, P.M.; Buehler, M.J. Tearing graphene sheets from adhesive substrates produces tapered nanoribbons. Small 2010, 6, 1108–1116. [Google Scholar] [CrossRef] [PubMed]
- Poot, M.; van der Zant, H.S.J. Nanomechanical properties of few-layer graphene membranes. Appl. Phys. Lett. 2008, 92, 1–3. [Google Scholar] [CrossRef]
- Shen, Y.K.; Wu, H.A. Interlayer shear effect on multilayer graphene subjected to bending. Appl. Phys. Lett. 2012, 100, 1–3. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Zhao, Y.; Wang, X.; Ke, C. Graphene folding on flat substrates. J. Appl. Phys. 2014, 116, 164301. [Google Scholar] [CrossRef]
- Lindahl, N.; Midtvedt, D.; Svensson, J.; Nerushev, O.A.; Lindvall, N.; Isacsson, A.; Campbell, E.E.B. Determination of the bending rigidity of graphene via electrostatic actuation of buckled membranes. Nano Lett. 2012, 12, 3526–3531. [Google Scholar] [CrossRef] [PubMed]
- Koenig, S.P.; Boddeti, N.G.; Dunn, M.L.; Bunch, J.S. Ultra-strong adhesion of graphene membranes. Nat. Nanotechnol. 2011, 6, 543–546. [Google Scholar] [CrossRef] [PubMed]
- Annett, J.; Cross, G.L.W. Self-assembly of graphene ribbons by spontaneous self-tearing and peeling from a substrate. Nature 2016, 535, 271–275. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Ju, L.; Feng, X.; Sun, Y.; Zhou, R.; Liu, K.; Fan, S.; Li, Q. Controlled fabrication of high-quality carbon nanoscrolls from monolayer graphene. Nano Lett. 2009, 9, 2565–2570. [Google Scholar] [CrossRef] [PubMed]
- Yamaletdinov, R.D.; Pershin, Y.V. Finding stable graphene conformations from pull and release experiments with molecular dynamics. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Hamm, E.; Reis, P.; Leblanc, M.; Roman, B.; Cerda, E. Tearing as a test for mechanical characterization of thin adhesive films. Nat. Mater. 2008, 7, 386–390. [Google Scholar] [CrossRef] [PubMed]
- Koskinen, P.; Kit, O.O. Approximate modeling of spherical membranes. Phys. Rev. B 2010, 82, 1–5. [Google Scholar] [CrossRef]
- Zelisko, M.; Ahmadpoor, F.; Gao, H.; Sharma, P. Determining the Gaussian modulus and edge tension of 2D materials from graphene to lipid bilayers. Phys. Rev. Lett. 2017, 119, 068002. [Google Scholar] [CrossRef]
- Davini, C.; Favata, A.; Paroni, R. A new material property of graphene: The bending Poisson cofficient. EPL 2017, 118, 1–6. [Google Scholar] [CrossRef]
- Be aware of the prefactor (1/2) in the definition of the bending energy (line right above Equation (30)) used by Davini, C.; Favata, A.; Paroni, R. The Gaussian stiffness of graphene deduced from a continuum model based on molecular dynamics potentials. J. Mech. Phys. Solids 2017, 104, 96–144. [Google Scholar]
- Tangney, P.; Capaz, R.B.; Spataru, C.D.; Cohen, M.L.; Louie, S.G. Structural Transformations of carbon nanotubes under hydrostatic pressure. Nano Lett. 2005, 5, 2268–2273. [Google Scholar] [CrossRef] [PubMed]
- Tadjbakhsh, I.; Odeh, F. Equilibrium states of elastic rings. J. Math. Anal. Appl. 1967, 18, 59–74. [Google Scholar] [CrossRef]
- López-Polín, G.; Gómez-Navarro, C.; Parente, V.; Guinea, F.; Katsnelson, M.I.; Pérez-Murano, F.; Gómez-Herrero, J. Increasing the elastic modulus of graphene by controlled defect creation. Nat. Phys. 2015, 11, 26–31. [Google Scholar] [CrossRef]
- Gao, W.; Huang, R. Effect of surface roughness on adhesion of graphene membranes. J. Phys. D 2011, 44, 452001. [Google Scholar] [CrossRef]
- Zakharchenko, K.V.; Katsnelson, M.I.; Fasolino, A. Finite Temperature Lattice Properties of Graphene beyond the Quasiharmonic Approximation. Phys. Rev. Lett. 2009, 102, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Tapaszto, L.; Dumitrica, T.; Kim, S.J.; Nemes-Incze, P.; Hwang, C.; Biro, L.P. Breakdown of continuum mechanics for nanometre-wavelength rippling of graphene. Nat. Phys. 2012, 8, 739–742. [Google Scholar] [CrossRef]
- Ahmadpoor, F.; Wang, P.; Huang, R.; Sharma, P. Thermal fluctuations and effective bending stiffness of elastic thin sheets and graphene: A nonlinear analysis. J. Mech. Phys. Solids 2017, 107, 294–319. [Google Scholar] [CrossRef]
- Anastasi, A.A.; Ritos, K.; Cassar, G.; Borg, M.K. Mechanical properties of pristine and nanoporous graphene. Mol. Simul. 2016, 42, 1502–1511. [Google Scholar] [CrossRef]
- Zacharia, R.; Ulbricht, H.; Hertel, T. The interlayer cohesive energy of graphite from thermal desorption of polyaromatic hydrocarbons. Phys. Rev. B 2004, 69, 1–7. [Google Scholar] [CrossRef]
| D (eV) | (J/m) | h (nm) | m | R (nm) | (eV/nm) | ||
|---|---|---|---|---|---|---|---|
| 1.6 | 0.28 | 0.335 | 8.16 | 0.855 | 0.400 | 6.37 | a |
| 1.4 | 0.23 | 0.335 | 8.60 | 0.861 | 0.413 | 5.44 | b |
| 35.5 | 0.35 | 0.67 | 36.2 | 0.944 | 1.95 | 37.72 | c |
| n | 1 | 2 | 3 | ∞ |
|---|---|---|---|---|
| (J/m) | 0.28 | 0.35 | 0.36 | 0.37 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambin, P. Graphene as a Prototypical Model for Two-Dimensional Continuous Mechanics. Appl. Sci. 2017, 7, 830. https://doi.org/10.3390/app7080830
Lambin P. Graphene as a Prototypical Model for Two-Dimensional Continuous Mechanics. Applied Sciences. 2017; 7(8):830. https://doi.org/10.3390/app7080830
Chicago/Turabian StyleLambin, Philippe. 2017. "Graphene as a Prototypical Model for Two-Dimensional Continuous Mechanics" Applied Sciences 7, no. 8: 830. https://doi.org/10.3390/app7080830
APA StyleLambin, P. (2017). Graphene as a Prototypical Model for Two-Dimensional Continuous Mechanics. Applied Sciences, 7(8), 830. https://doi.org/10.3390/app7080830





