Experimental Study on Effectiveness of a Prototype Seismic Isolation System Made of Polymeric Bearings
Abstract
:1. Introduction
- Perform an extensive material testing to determine the basic mechanical properties of the polymer used to construct the PBs;
- Conduct the Dynamic Mechanical Analysis to evaluate the viscoelastic characteristics of the analyzed polymer over a wide range of temperatures for different excitation frequencies;
- Design and construct a prototype base isolation bearing with the use of a specially prepared polymeric material;
- Prepare two experimental models with different dynamic characteristics;
- Investigate the dynamic behaviour of the structure models of both fixed-base and base-isolated during sine sweep testing;
- Conduct an extensive shaking table testing to investigate the dynamic behaviour of the tested models with and without the PBs under various ground motions.
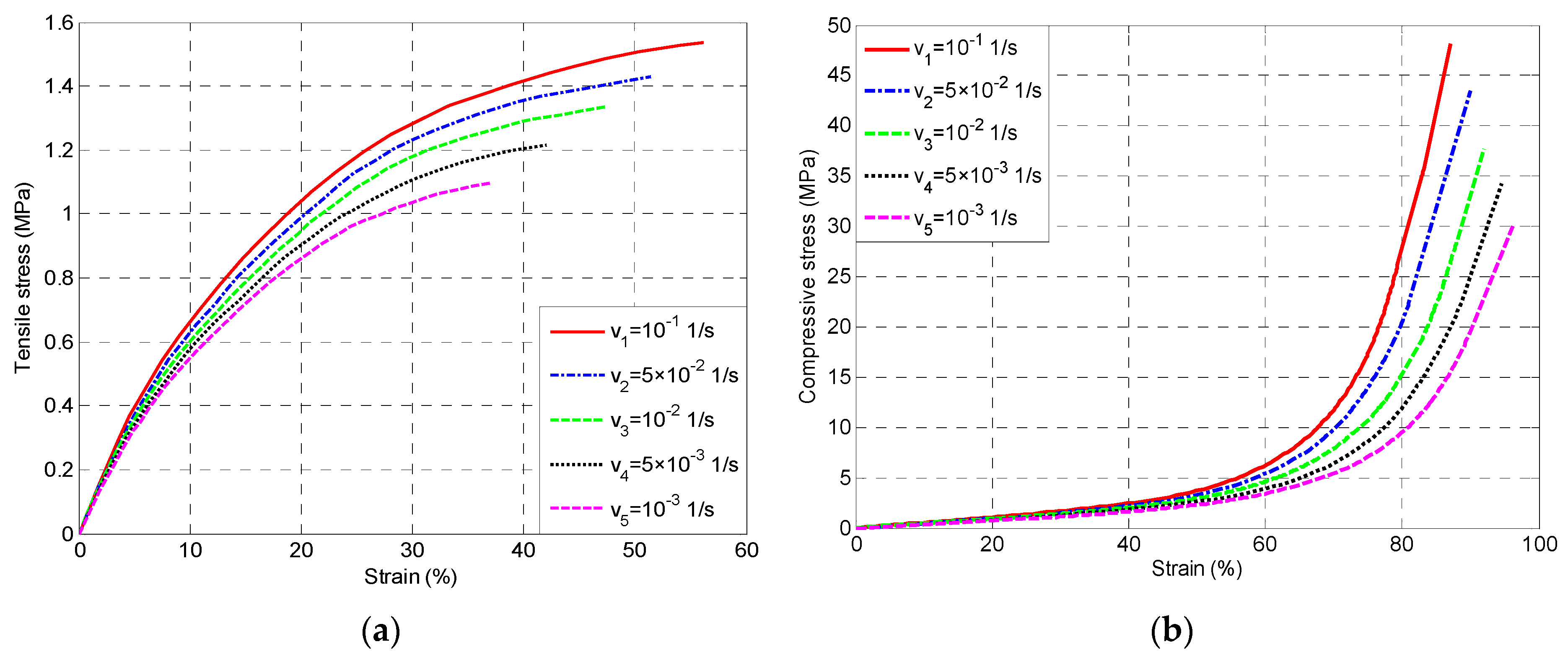
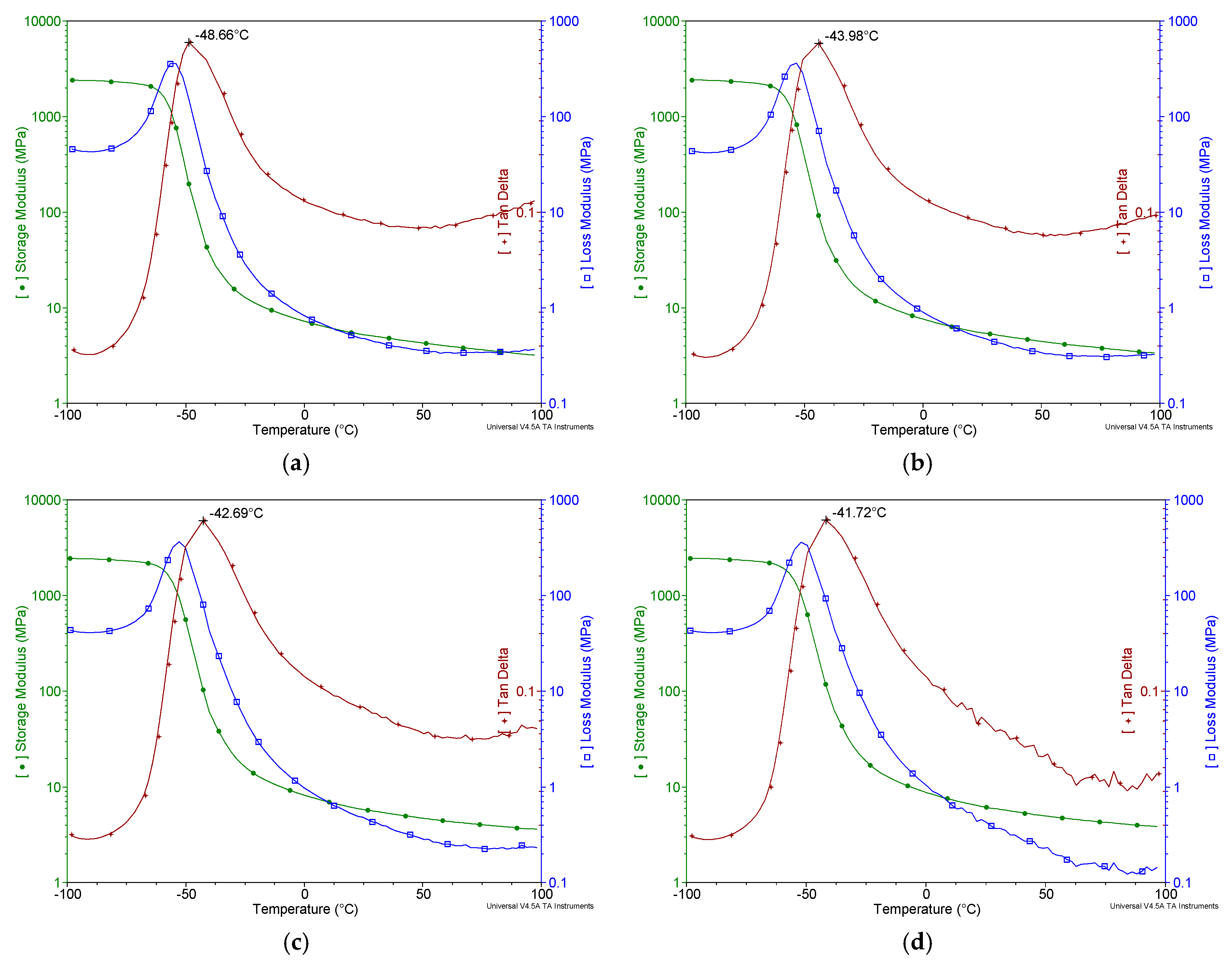
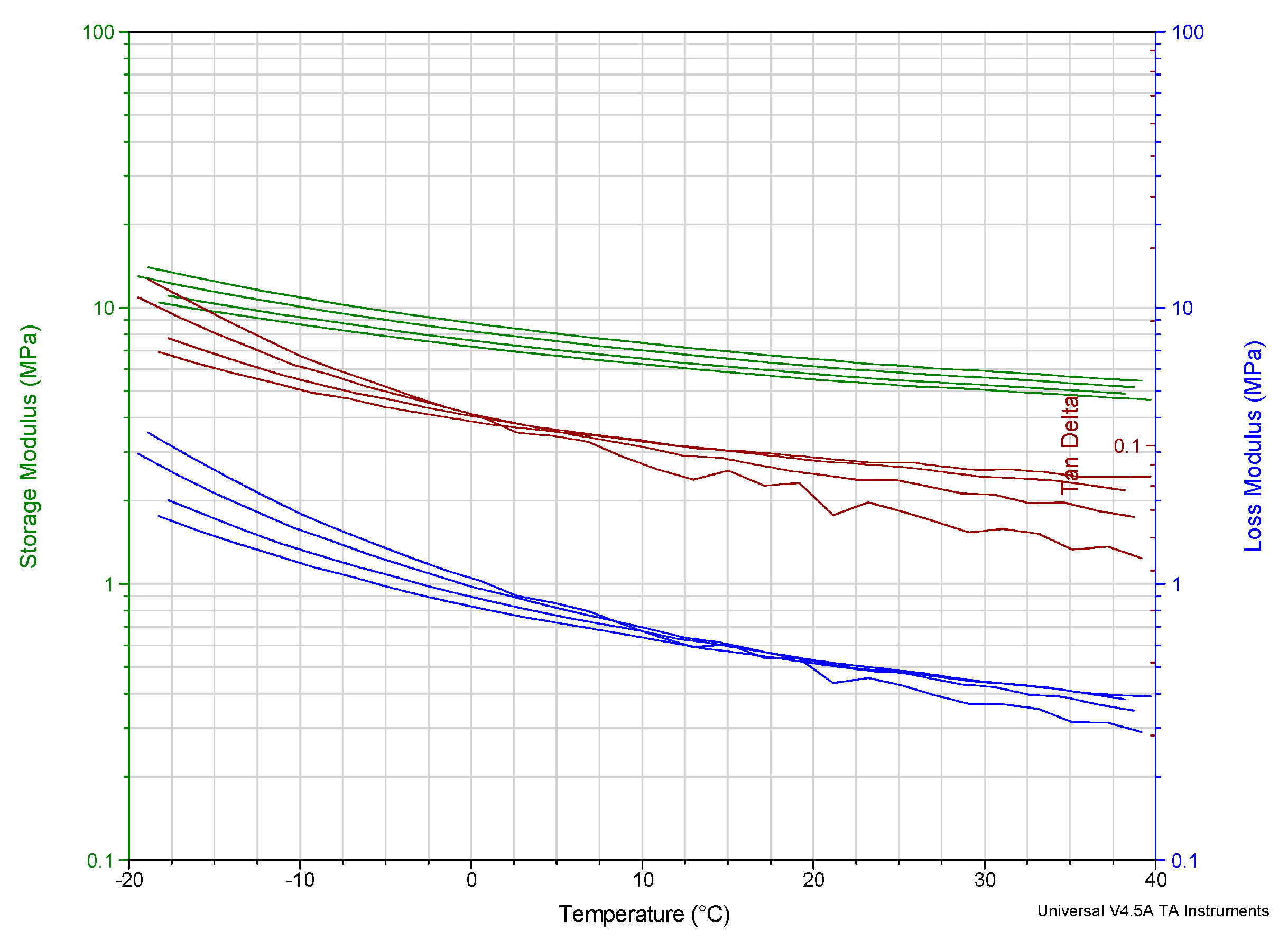
2. Material Testing
3. Testing Conditions
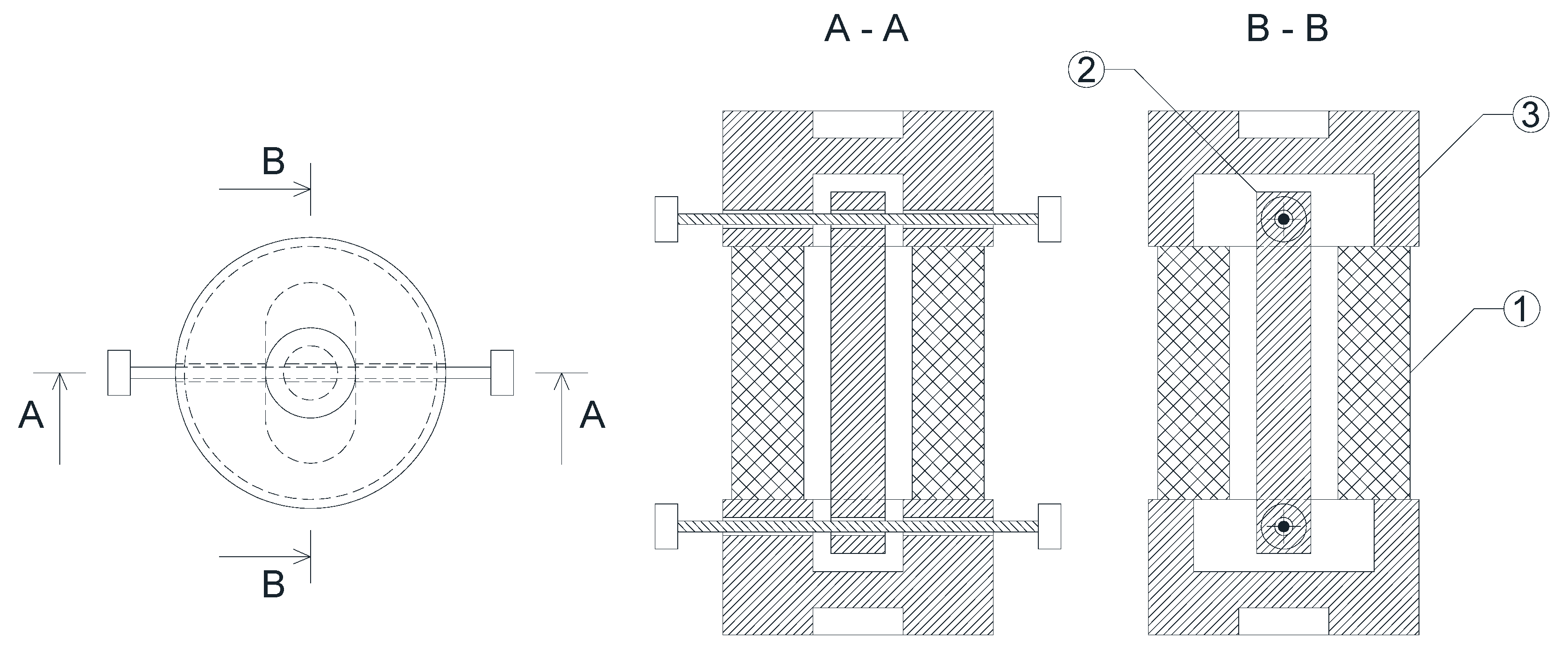
3.1. Polymeric Bearings
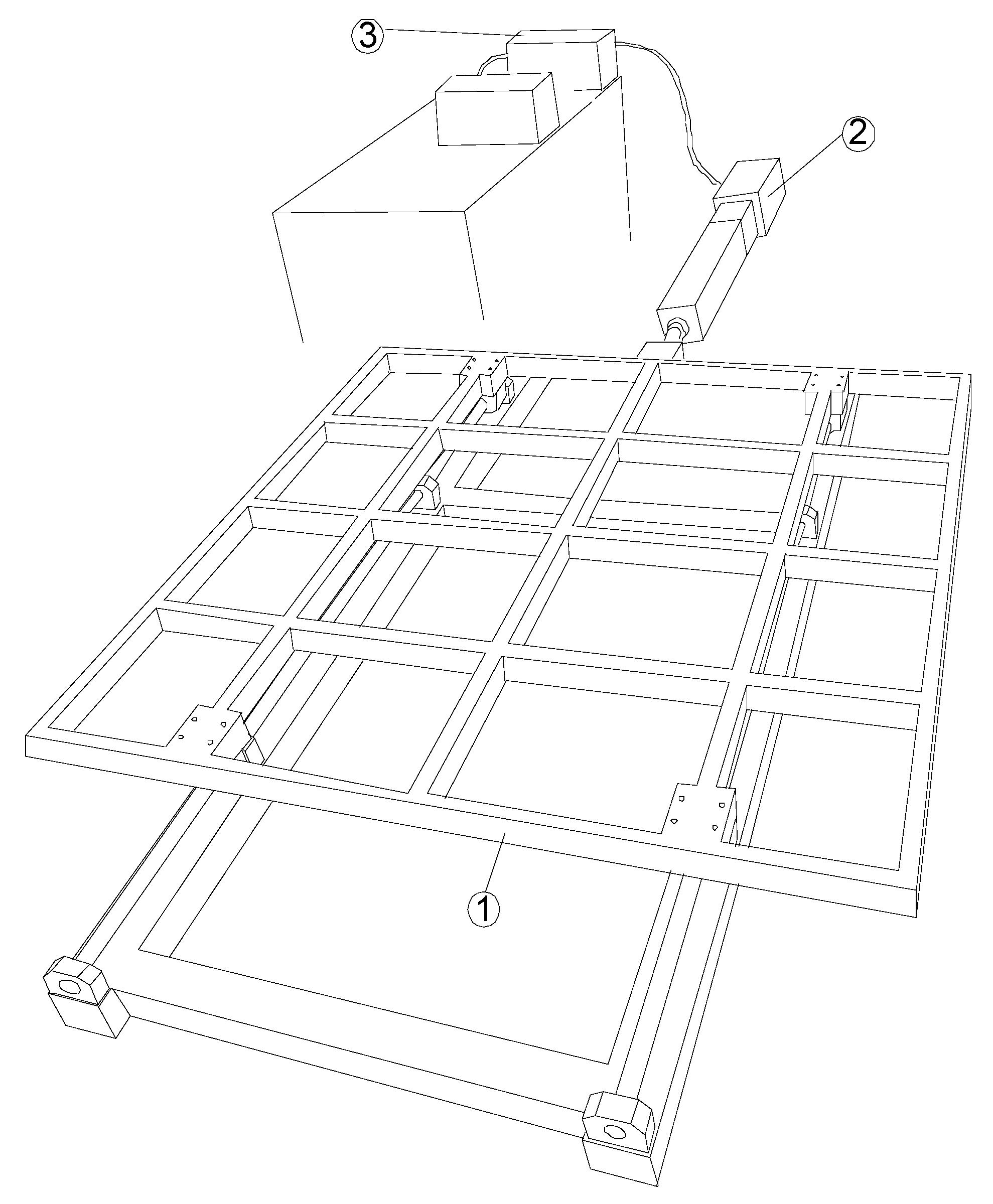
3.2. Experimental Setup
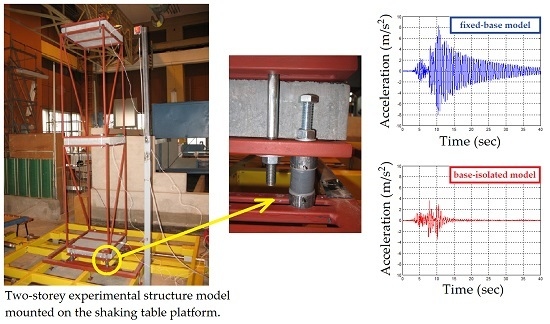
3.3. Structure Models
4. Sine Sweep Testing
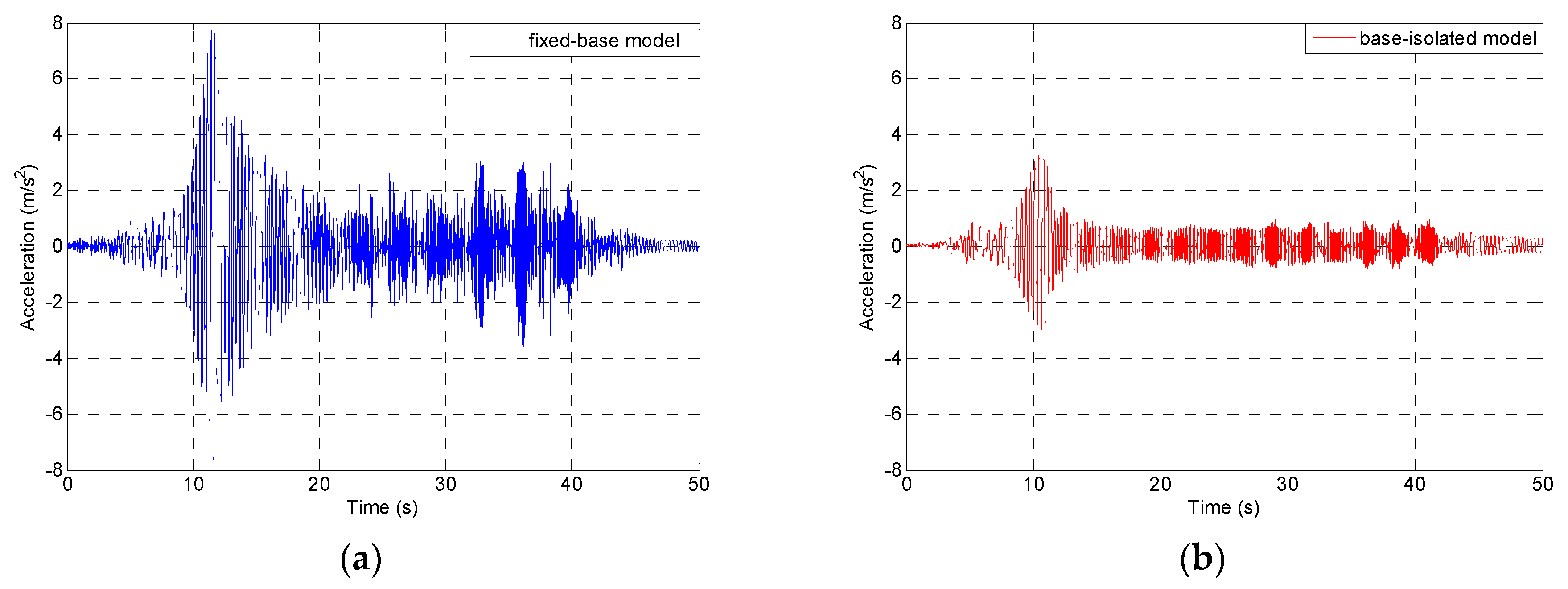
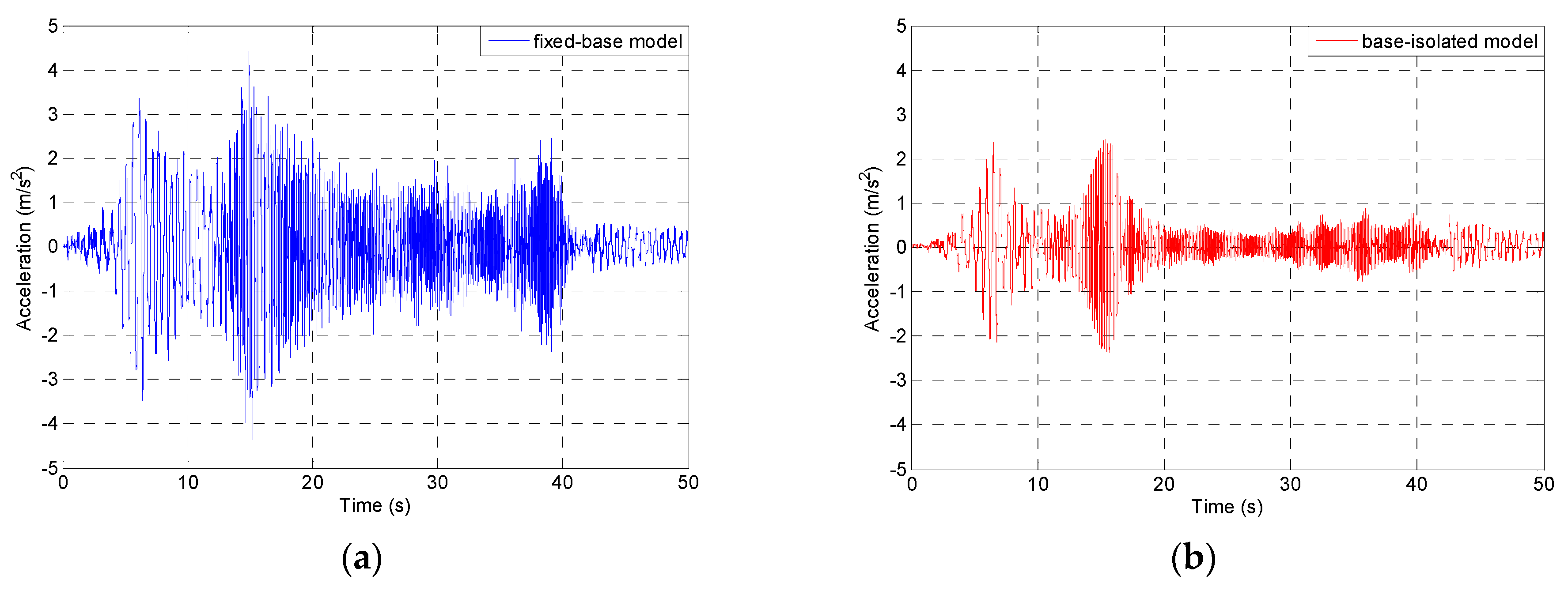
5. Shaking Table Testing
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jankowski, R.; Mahmoud, S. Earthquake-Induced Structural Pounding; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Naderpour, H.; Barros, R.C.; Khatami, S.M.; Jankowski, R. Numerical study on pounding between two adjacent buildings under earthquake excitation. Shock Vib. 2016, 1504783. [Google Scholar] [CrossRef]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Ebrahimian, M.; Todorovska, M.I.; Falborski, T. Wave Method for Structural Health Monitoring: Testing Using Full-Scale Shake Table Experiment Data. J. Struct. Eng. 2016, 143. [Google Scholar] [CrossRef]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Booth, E.; Key, D. Earthquake Design Practice for Buildings; Thomas Telford Publishing: London, UK, 2006. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2012. [Google Scholar]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Pasala, D.T.R.; Sarlis, A.A.; Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C.; Taylor, D. Adaptive negative stiffness: New structural modification approach for seismic protection. J. Struct. Eng. 2012, 193, 1112–1123. [Google Scholar] [CrossRef]
- Spencer, B.F.; Nagarajaiah, S. State of the Art of Structural Control. J. Struct. Eng. 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Wolff, E.D.; Ipek, C.; Constantinou, M.C.; Tapan, M. Effect of viscous damping devices on the response of seismically isolated structures. Earthq. Eng. Struct. Dyn. 2015, 44, 185–198. [Google Scholar] [CrossRef]
- Buckle, I.G. Passive control of structures for seismic loads. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Robinson, W.H. Passive control of structures: The New Zealand experience. J. Earthq. Technol. 1998, 35, 63–75. [Google Scholar]
- Aiken, I.D.; Nims, D.K.; Whittaker, A.S.; Kelly, J.M. Testing of passive energy dissipation systems. Earthq. Spectra 1993, 9, 335–370. [Google Scholar] [CrossRef]
- Symans, M.D.; Constantinou, M.C. Semi-active control systems for seismic protection of structures: A state-of-the-art review. Eng. Struct. 1999, 21, 469–487. [Google Scholar] [CrossRef]
- Kelly, J.M. Base isolation: Linear theory and design. Earthq. Spectra 1990, 6, 223–244. [Google Scholar] [CrossRef]
- Buckle, I.G.; Mayes, R.L. Seismic isolation: History, application, and performance: A world view. Earthq. Spectra 1990, 6, 161–201. [Google Scholar] [CrossRef]
- Skinner, R.I.; Robinson, W.H.; McVerry, G.H. An Introduction to Seismic Isolation; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Komodromos, P. Seismic Isolation of Earthquake-Resistant Structures; WIT Press: Southampton, UK, 2000. [Google Scholar]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- Mahmoud, S.; Jankowski, R. Pounding-involved response of isolated and non-isolated buildings under earthquake excitation. Earthq. Struct. 2010, 1, 231–252. [Google Scholar] [CrossRef]
- Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1993. [Google Scholar]
- Skinner, R.I.; Kelly, J.M.; Heine, A.J. Hysteretic dampers for earthquake-resistant structures. Earthq. Eng. Struct. Dyn. 1975, 3, 287–296. [Google Scholar] [CrossRef]
- Robinson, W.H.; Greenbank, L.R. An extrusion energy absorber suitable for the protection of structures during an earthquake. Earthq. Eng. Struct. Dyn. 1976, 4, 251–259. [Google Scholar] [CrossRef]
- Kumar, M.; Whittaker, A.S.; Constantinou, M.C. An advanced numerical model of elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 2014, 43, 1955–1974. [Google Scholar] [CrossRef]
- Tyler, R.G. Rubber bearings in base-isolated structures: A summary paper. Bull. N. Z. Natl. Soc. Earthq. Eng. 1991, 24, 251–274. [Google Scholar]
- Mavronicola, E.; Komodromos, P. On the response of base-isolated buildings using bilinear models for LRBs subjected to pulse-like ground motions: Sharp vs. smooth behaviour. Earthq. Struct. 2014, 7, 1223–1240. [Google Scholar] [CrossRef]
- Kumar, M.; Whittaker, A.S.; Constantinou, M.C. Characterizing friction in sliding isolation bearings. Earthq. Eng. Struct. Dyn. 2015, 44, 1409–1425. [Google Scholar] [CrossRef]
- Mokha, A.; Constantinou, M.C.; Reinhorn, A.M.; Zayas, V.A. Experimental study of friction-pendulum isolation system. J. Struct. Eng. 1991, 117, 1201–1217. [Google Scholar]
- Tsopelas, P.; Constantinou, M.C.; Kim, Y.S.; Okamoto, S. Experimental study of FPS system in bridge seismic isolation. Earthq. Eng. Struct. Dyn. 1996, 25, 65–78. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Behaviour of the double concave friction pendulum bearing. Earthq. Eng. Struct. Dyn. 2006, 35, 1403–1424. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Xiaohong, S. Seismic performance of base-isolated buildings in the 1994 Northridge earthquake. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Nagarajaiah, S.; Xiaohong, S. Response of base-isolated USC hospital building in Northridge earthquake. J. Struct. Eng. 2000, 126, 1177–1188. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488, 347–350. [Google Scholar] [CrossRef]
- Zembaty, Z. Rockburst induced ground motion-a comparative study. SDEE 2004, 24, 11–23. [Google Scholar] [CrossRef]




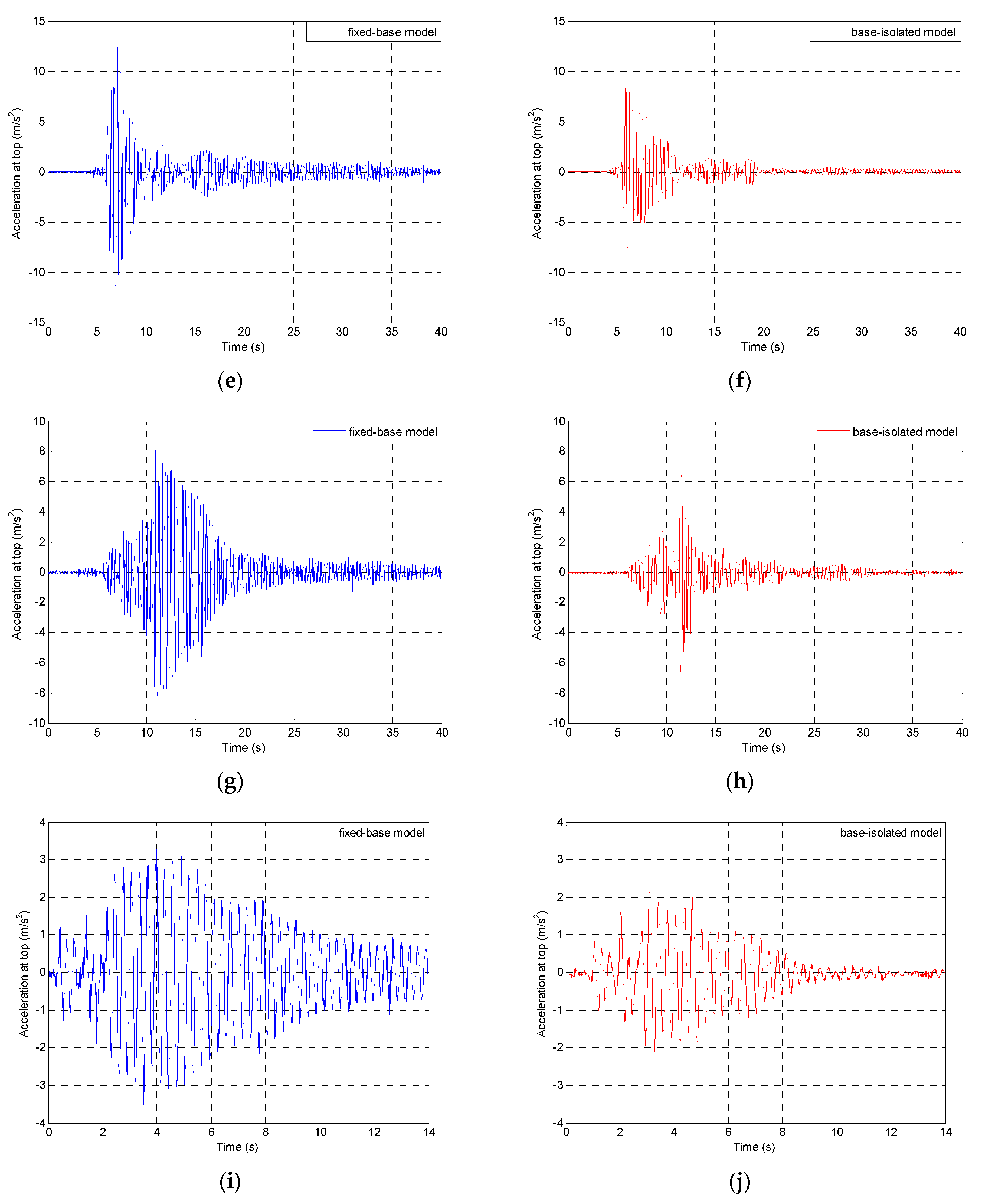
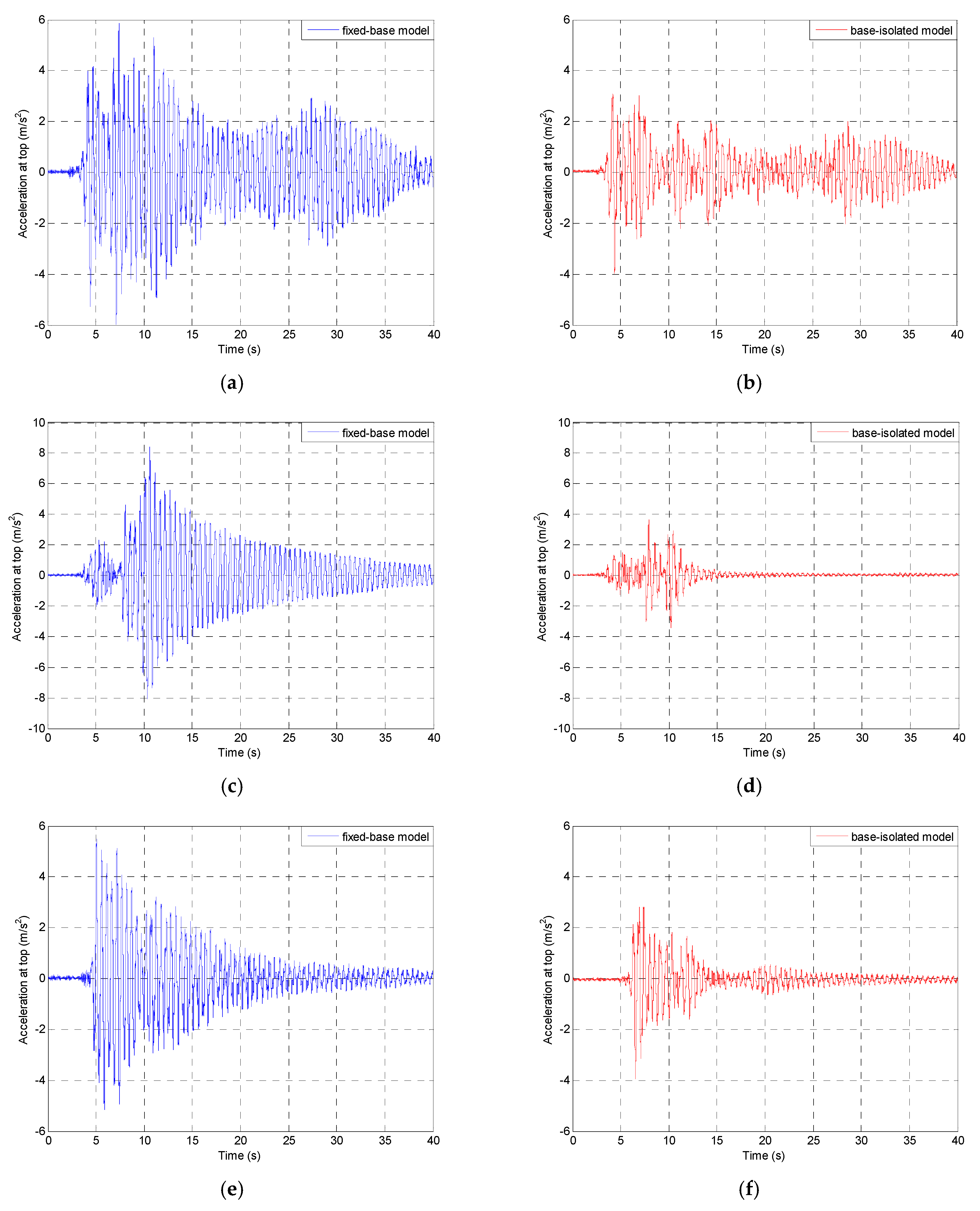
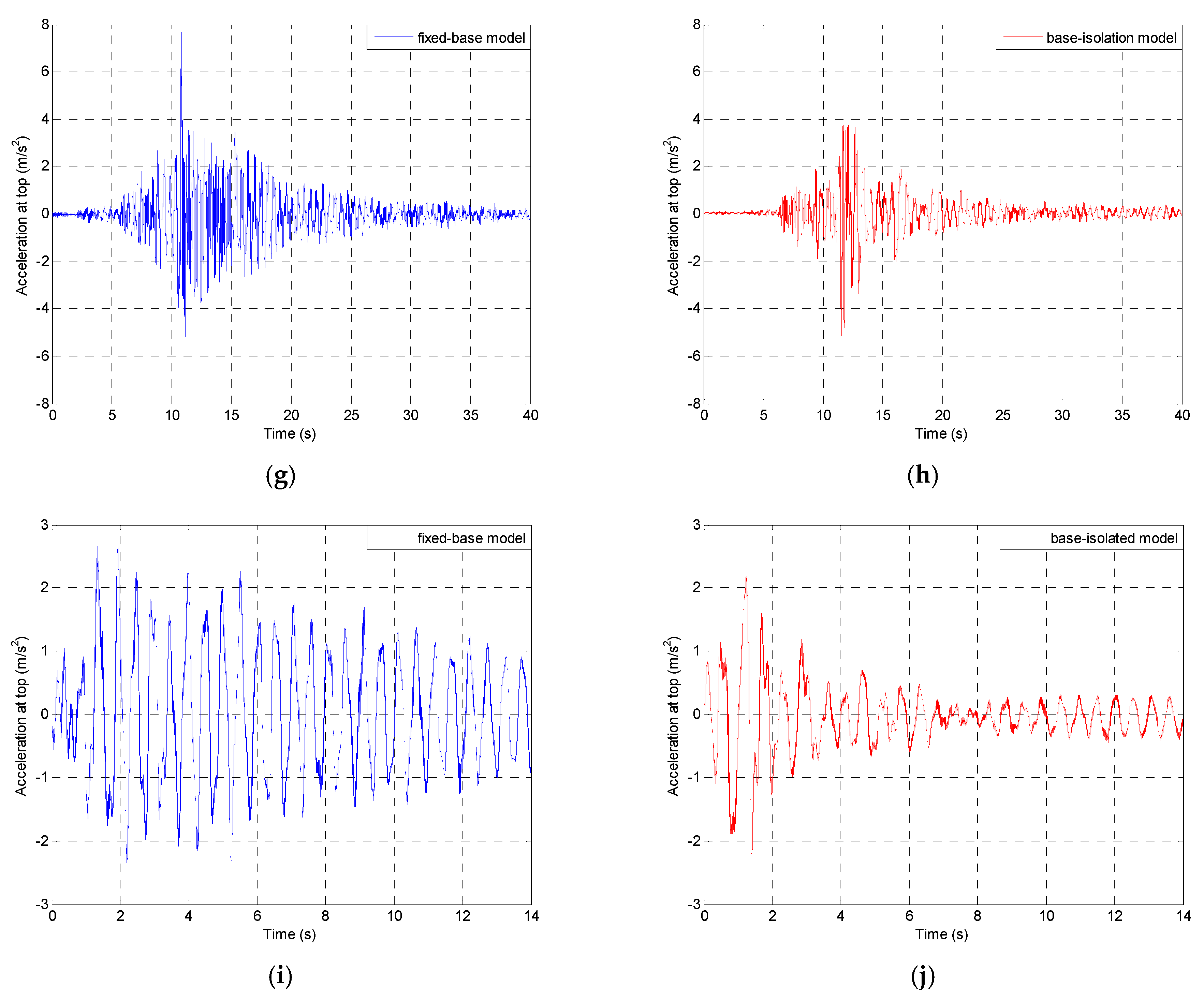
| Dynamic Excitation | Peak Acceleration at the Top of the Tested Model (m/s2) | Reduction (%) | |
|---|---|---|---|
| Fixed-Base Model | Model Isolated with PBs | ||
| 1940 El Centro earthquake NS component, original record with PGA = 3.070 m/s2 | 11.39 | 6.98 | 38.7 |
| 1971 San Fernando earthquake Pacoima Dam station, N74°E component, scaled record with PGA = 5.688 m/s2 | 15.59 | 10.47 | 32.8 |
| 1989 Loma Prieta earthquake Corralitos station, NS component, scaled record with PGA = 3.158 m/s2 | 13.82 | 8.27 | 40.2 |
| 1994 Northridge earthquake Santa Monica station, EW component, scaled record with PGA = 4.332 m/s2 | 8.73 | 7.74 | 11.3 |
| 2002 Polkowice mining tremor NS component, original record with PGA = 1.634 m/s2 | 3.53 | 2.18 | 38.2 |
| Dynamic Excitation | Peak Acceleration at the Top of the Tested Model (m/s2) | Reduction (%) | |
|---|---|---|---|
| Fixed-Base Model | Model Isolated with PBs | ||
| 1940 El Centro earthquake NS component, original record with PGA = 3.070 m/s2 | 5.98 | 3.99 | 33.3 |
| 1971 San Fernando earthquake Pacoima Dam station, N74°E component, scaled record with PGA = 5.688 m/s2 | 8.41 | 3.63 | 56.8 |
| 1989 Loma Prieta earthquake Corralitos station, NS component, scaled record with PGA = 3.158 m/s2 | 5.49 | 3.95 | 28.1 |
| 1994 Northridge earthquake Santa Monica station, EW component, scaled record with PGA = 4.332 m/s2 | 7.68 | 5.14 | 33.1 |
| 2002 Polkowice mining tremor NS component, original record with PGA = 1.634 m/s2 | 2.67 | 2.34 | 12.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falborski, T.; Jankowski, R. Experimental Study on Effectiveness of a Prototype Seismic Isolation System Made of Polymeric Bearings. Appl. Sci. 2017, 7, 808. https://doi.org/10.3390/app7080808
Falborski T, Jankowski R. Experimental Study on Effectiveness of a Prototype Seismic Isolation System Made of Polymeric Bearings. Applied Sciences. 2017; 7(8):808. https://doi.org/10.3390/app7080808
Chicago/Turabian StyleFalborski, Tomasz, and Robert Jankowski. 2017. "Experimental Study on Effectiveness of a Prototype Seismic Isolation System Made of Polymeric Bearings" Applied Sciences 7, no. 8: 808. https://doi.org/10.3390/app7080808
APA StyleFalborski, T., & Jankowski, R. (2017). Experimental Study on Effectiveness of a Prototype Seismic Isolation System Made of Polymeric Bearings. Applied Sciences, 7(8), 808. https://doi.org/10.3390/app7080808