Abstract
A three-dimensional (3D) finite element (FE) dynamic frictional rolling contact model is presented for the study of short pitch corrugation that considers direct and instantaneous coupling between the contact mechanics and the structural dynamics in a vehicle-track system. In this study, we examine the system responses in terms of vibration modes, contact forces and the resulting wear with smooth rail and corrugated rail with progressively increasing amplitude to infer the conditions for consistent corrugation initiation and growth. Wear is assumed to be the damage mechanism, and short pitch corrugation is modeled using wavelengths from field observations of a Dutch railway. The contribution of this paper is a global perspective of the consistency conditions that govern the evolution of short pitch corrugation. The main insights are as follows: (1) the longitudinal vibration modes are probably dominant for short pitch corrugation initiation; (2) during short pitch corrugation evolution, the interaction and consistency between longitudinal and vertical modes should determine the development of short pitch corrugation, and once a certain severity is reached, vertical modes become dominant; and (3) in the case simulated in this paper, corrugation does not grow probably due to not only the different resulting main frequencies of the vertical and longitudinal contact forces, but also the inconsistency between the frequencies of the vertical and longitudinal vibration modes and the resulting wear. It is inferred that in the continuous process of initiation and growth of the corrugation, there should be a consistency between them, and this could be done by the control of certain track parameters.
1. Introduction
Rail corrugations are periodic defects commonly observed in all types of railway tracks. According to the current understanding of their development mechanisms, namely the damage mechanisms and wavelength-fixing mechanisms [1], rail corrugations can be classified into six groups: heavy haul, light rail, booted sleepers, contact fatigue, rutting and short pitch corrugation. Among these groups, the development mechanisms of short pitch corrugation (hereafter corrugation) are not fully understood. Although corrugation was identified more than a century ago and despite extensive research efforts [1,2], an effective solution has not been developed to avoid the corrugation problem, which remains an enigma that has puzzled many researchers and engineers [3,4]. Grinding appears to be the only effective corrective countermeasure; however, it increases maintenance costs and reduces the availability of the railway network. Thus, the development mechanisms of this phenomenon must be elucidated, and an effective solution for its control at an early stage must be identified.
Corrugation mainly occurs on straight tracks or gentle curves where contact does not occur between the wheel flange and rail gauge corner (Figure 1), and it usually manifests as shiny ripples and dark valleys. The typical wavelength is in the range of 20–80 mm, with amplitudes up to 100 μm [1]. Corrugation is one of the most prominent problems for railway infrastructure managers because it increases the vibrations of the vehicle-track system and results in higher frequencies (more than 500 Hz) of the wheel-rail dynamic contact forces, which leads to accelerated degradation of vehicle-track system components and shortened service life [5]. In addition, the noise generated by vibrations is a nuisance to residents living near railway lines [1,6]. Because of the high level of noise, corrugation is also known as “roaring rail”. Corrugation can also generate rolling contact fatigue (RCF), such as squats [7] (Figure 1c).
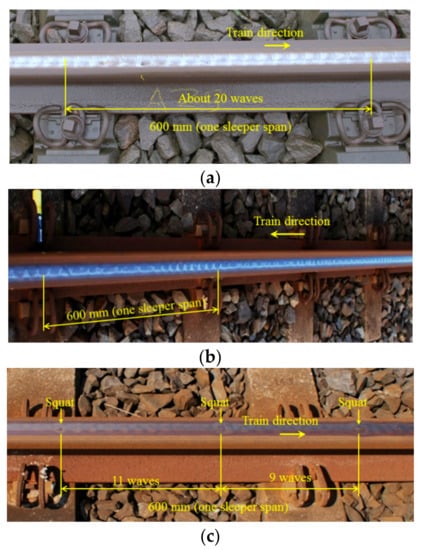
Figure 1.
Short pitch corrugation and the resulting squats in the Dutch railway network. Wavelength and periodicity are distinguished (wavelength is the distance between two adjacent shining spots of ripples, and periodicity refers to the periodic pattern that contains multiple wavelengths of non-uniform amplitude of corrugation). (a) is at a gentle curve, and (b,c) are on straight tracks. (a) Uniform corrugation with a wavelength of approximately 30 mm. Squats have not yet developed, and a ballasted track with mono-block sleepers and fastenings with a W-shaped tension clamp is shown. Photo taken near Assen, the Netherlands. (b) Non-uniform corrugation of a constant periodicity of a sleeper span. The corrugation wavelength varies largely within a period. Squats have not yet developed, and a ballasted track with duo-block sleepers and fastenings with Deenik clips is shown. Photo taken near Steenwijk, the Netherlands. (c) Non-uniform corrugation with a periodicity shorter than a sleeper span. The corrugation wavelength is approximately 30 mm. The squats were caused by corrugation, and a ballasted track with duo-block sleepers and fastenings with Deenik clips is shown. Photo taken near Steenwijk, The Netherlands.
The main damage mechanism of corrugation is commonly considered to be wear caused by longitudinal wheel slip [8,9]. Plastic deformation is another possible damage mechanism [1], and it has been investigated by a numerical approach [10] and metallurgical analyses [11]. The wear and deformation underlying corrugation are differential, i.e., they are selective processes that “consistently” occur more at certain locations than at adjacent locations, which results in the accumulation and growth of typical wave patterns [12]. In this case, “consistently” indicates that the wear and deformation caused by one-wheel passage repeats the same wavelengths and phase angle of previous wheel passages, which results in the accumulation of wear and deformations and the initiation of corrugation growth. Because damage originates in the contact patch, the contact mechanics within the contact patch must be examined to better understand the damage mechanisms. Because dynamic wheel-rail contact is difficult to measure, a numerical analysis that can accurately simulate the vehicle-track dynamic interaction must be developed to analyze corrugation under controlled conditions [13].
The Hertzian treatment of the contact problem has usually been used to solve normal contact problems [9], whereas Kalker’s theories [14] are typically employed for the tangential direction [9]. The Hertzian solution considers that contact surfaces are frictionless smooth half-spaces. However, for worn or deformed profiles, such surface approximations may not hold in the vicinity of the contact patch [15,16]. Nielsen [16] employed a two-dimensional (2D) non-Hertzian contact model and found that the shape of the normal stress distribution was not elliptic because of the geometrical asymmetry. Correspondingly, the tangential stress distribution varies along different positions of the corrugation and may be responsible for the development of corrugation. In addition, the Hertzian theory and Kalker’s theory are based on statics. However, because the contact patch is on the order of 2 cm, which is similar to the corrugation wavelength, non-steady state processes caused by dynamic interactions must be considered [17,18].
In addition to long-term damage mechanisms, a short-term dynamic process is believed to fix the wavelength through structural dynamics [1,19]. The interaction between the short- and long-term mechanisms is represented by a feedback loop [1]. Three phenomena must be defined to understand corrugation development: (1) structural dynamics excitation caused by vehicle-track interactions, (2) loading response at the wheel-rail interface involving contact mechanics and (3) feedback from the contact and damage to the structural dynamics as determined by the direct coupling between the contact mechanics and structural dynamics. In [9,20], a crucial understanding of the contact phenomena in the corrugation problem is provided. The model used in [9,20] solved the structural dynamics and contact mechanics problems separately in different models or steps. In addition to a more elaborated treatment of the contact mechanics and an accurate representation of the vehicle-track interaction, we propose a combined modeling approach that includes the coupling and interplay of both the structural dynamics and contact mechanics problems. This solution is inspired by the work of [9] and the question “why is roughness growth predicted by a simple contact model but not when complexity is increased to include non-Hertzian and non-steady contact conditions?”
The finite element method has been employed to investigate the development mechanism underlying squats in a vehicle-track system [7]. This modeling approach provides a good explanation for the development of corrugation initiated from isolated known railhead irregularities [21]. Because corrugation from isolated known railhead irregularities is of a short pitch type, this method could also be valid for investigating general types of short pitch corrugation. Corrugation that originates from railhead irregularities is caused by a dynamic force excited by known irregularities. In this case, the wavelength of the force is determined by the local track system, and the phase of the force is determined by the location of the irregularities. Thus, clear mechanisms of wavelength and phase fixing are involved. The wavelength and phase of the force at a given irregularity are always the same. Consequently, the resulting differential wear and/or plastic deformation is always in phase and damage accumulates under different wheel passages. In this way, corrugation can initiate and grow.
In the case of the general type of short pitch corrugation, a visually-identifiable initiation source is not observed. Although the wavelength might be fixed by the track structure, e.g., the “pin-pin” resonance [22] or the stick-slip process [23], the randomness of passing wheels and the track can lead to phase variations of the contact force so that the total effect of many wheel passages may cancel out or suppress the differential wear and deformation.
Regarding the latter situation, we must identify the causes of the dynamic forces that result in differential wear and differential plastic deformation, which remain in phase for the many different passing wheels such that the wear and deformation accumulate and corrugation can initiate and grow. Although the entire mechanism of the initiation and development of short pitch corrugation was not identified in this paper, we present new insights based on numerical modeling that are consistent with field observations and can contribute to a better understanding of this enigma. We expect that the new insights provided here will trigger many new research efforts in the field that will ultimately produce a more complete understanding of the enigma and a final solution.
In this paper, a 3D finite element (FE) approach is presented. This approach combines the vehicle-track interaction model of [7] with the solution for transient frictional rolling of [24]. The vehicle-track structural dynamics are directly coupled to the wheel-rail contact mechanics through the continuum treatment of the wheel and rail in the structure. The simulation of continuum mechanics has been reported to play “an important role in structural analysis” [25] and allows the instantaneous mutual influence of the contact mechanics and the structural mechanics to be simulated. This approach was presented in [26] to analyze the phase relationship between the given corrugation and the resulting periodic wear, and a similar approach was employed to study corrugation in a high-speed railway [27]. In this paper, the transient states of the rolling contact and wear are evaluated under a variety of loading conditions in relation to the dynamic forces excited by a passing wheel over a rail with and without corrugation. The damage mechanism is assumed to be limited to wear because the focus of this paper is on the conditions that may lead to the consistent initiation and growth of corrugation. To account for plasticity, the method of [28] can be readily incorporated, which will be our future research focus.
2. Model
2.1. FE Model
A schematic diagram of the 3D FE vehicle-track model is shown in Figure 2. The model is based on a symmetrical vehicle-track system assuming a straight track in which lateral movement is negligible. The wheel, rail and sleepers are modeled with solid elements. The nominal radius of the wheel is 0.46 m, and the tread coning is 1/40. The rail is a standard International Union of Railway (UIC) 54 profile with an inclination of 1/40. The contact surface of the wheel is smooth, whereas a length of corrugation is prescribed along the rail surface. The sprung mass (the weight of the car body and the bogie) is lumped into a mass element Mc supported by the primary suspension, which is represented by spring-damper elements. The sprung mass above a half wheelset is 1/8 of the sprung dynamic load of a whole vehicle, which is approximately a quarter of the sprung mass carried by a bogie. The fastening system and the ballast are also modeled as spring-damper elements. The track parameters are taken from [29] as shown in Table 1 and represent the typical Dutch railway system. In the FE model, the wheel and rail are meshed with 8-node solid elements. To achieve a solution of sufficient accuracy and an acceptable computation time, only the size of the elements in the solution zone is refined (0.8 mm × 0.8 mm in the longitudinal and lateral directions). The elements far from the solution zone are meshed at an element size up to 7.5 cm. These choices are based on [24], which concluded that the contact mechanics solution with an element size of 1.3 mm × 1.3 mm is sufficiently accurate when the FE approach used here is implemented for engineering applications. The total number of elements in the model is 1,135,384; the number of nodes is 1,297,900; and the model length is 18 m. In [30], a track length of 10 m was sufficient for problems of similar frequency and wavelength. The damage mechanism studied in this paper is wear; thus, the wheel and rail materials are assumed to be elastic. A Coulomb friction law is employed with a friction coefficient fC of 0.6 as in [31]. In the literature, the friction coefficient of dry wheel-rail contact is reported to be between 0.4 and 0.65 [32].
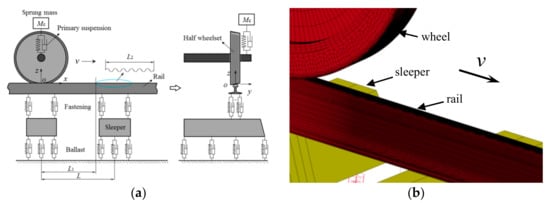
Figure 2.
Vehicle-track frictional rolling model in 3D. (a) Schematic diagram of the model. (b) FE model in 3D.

Table 1.
Vehicle parameters and track parameters.
The solution process of the simulation includes two steps: an implicit analysis (using Ansys) and an explicit analysis (using Ls-dyna). The implicit analysis is performed to identify the initial deformation in the equilibrium position of the vehicle-track system. Then, the wheel is set to roll along the rail with a constant speed v = 38.9 m/s (corresponding to the typical Dutch passenger train speed of 140 km/h). An explicit integration scheme with a central difference method is then implemented to solve the wheel-rail frictional rolling contact problems. The displacements obtained from the implicit process are used as the initial state of the explicit integration process. If the time step (4.67 × 10−8 s in this model) is smaller than the critical time step (5 × 10−8 s) determined by the Courant criterion [33], convergence is guaranteed. By keeping the time step sufficiently small, the model can include all necessary vibration modes. In the explicit analysis, the frictional rolling is modeled using a surface-to-surface algorithm with the penalty method described in [34]. Because of the nature of explicit integration, the effect of transient rolling and the high-frequency dynamic behavior of the vehicle-track system excited by the moving wheel are automatically included in the solution.
As shown in Figure 2a, a distance L1 is used during the explicit process to diminish the effect of vibration excited by imperfect initial equilibrium because of numerical errors from the implicit solution. A total of 10 waves of corrugation with length L2 are introduced after L1. The traction coefficient μ is defined as follows:
where is the normal contact force and is the resultant tangential (creep) force in the longitudinal direction caused by an applied torque. Different traction coefficients produce different adhesion-slip states, as well as damages. In the subsequent analysis, a traction load corresponding to 40% of the static normal contact force is applied via a torque about the axis of the wheel. This produces a µ of 0.4, which is usually the maximal traction coefficient of rolling stock [35,36]. Because of the dynamic nature of vehicle-track interactions, especially in the presence of corrugation, the actual contact forces are not constant. Therefore, the instantaneous traction coefficient varies with time and space along the track, and the actual value of the traction coefficient deviates from the static value. Regarding creepage, the approach of [7,24] is used in this paper, where a constant driving torque is specified. The resulting creepage fluctuates with the corrugation [27].
A few additional remarks on the model are warranted. Note that high friction and traction coefficients are used. In [37,38], high traction was reported to facilitate corrugation development. Additionally, regarding the traction coefficient, we assume that the damage mechanism is wear. Hence, a large value is chosen to ensure a high longitudinal contact force and thus obtain high wear. A large traction coefficient indicates a large slip zone. A large slip zone aids in the visualization of changes in the contact patch caused by corrugation; thus, it is easier to visualize and compare the contact solutions [24]. Finally, the model does not include brake disks or gears and will not represent torsional vibrations. Torsional wheelset vibrations have been considered as a cause of corrugation at curves [1,39,40]; however, recent research [41] has shown that torsional wheelset vibrations are not correlated with corrugation development at curves. Torsional vibration is also considered in [42] for corrugation related to vibration up to about 100 Hz. In this paper, the frequencies considered are up to 2000 Hz.
2.2. Corrugation Model
In this paper, corrugation with a sinusoidal profile is used as a test case. This choice is based on field observations, such as those shown in Figure 1a. Moreover, our work is a continuation of previous research in which corrugation was assumed to have a sinusoidal profile [3,9,43,44,45,46]. A sinusoidal corrugation with a constant wavelength is applied to the rail surface expressed by the equation:
where A is the amplitude of the corrugation, λ is the wavelength and is the phase. The second term −A guarantees that the peak of the corrugation is not higher than the initial profile of the rail surface.
The wavelength is 30 mm, which is approximately equal to one of the recorded corrugation wavelengths on the Dutch railway network shown in Figure 1a,c (see the measurement in Figure 3a). For the analysis, 10 waves are considered; thus, L2 equals 300 mm. The corrugation considered is located above a sleeper support (as shown in Figure 1b), which has been reported as a position where corrugation is more likely to develop [22]. To examine the wheel-rail contact during the growth process of the corrugation, the amplitudes of A = 0 µm for smooth rail and A = 2.5 µm, 5 µm, 10 µm and 20 µm for corrugated rail are modeled (the peak-to-trough distance is twice the amplitude). By maintaining between −π/2 and π, contact solutions can be studied at different locations within one complete corrugation wavelength, i.e., the falling edge (P1), the trough (P2), the rising edge (P3) and the peak (P4), as shown in Figure 3b. Figure 3c shows a magnified 3D configuration of the corrugation in the rail surface.
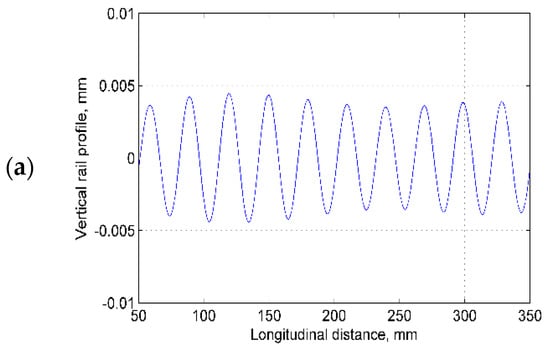
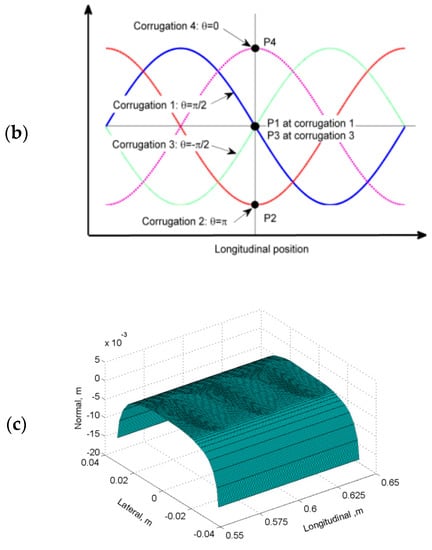
Figure 3.
Modeled corrugation: (a) field measurement of corrugation (27–33 mm bandpass filtering); (b) schematic diagram of the corrugation and 4 positions (blue line: P1, red line: P2, green line: P3 and magenta line: P4); and (c) illustration of the applied corrugation (Corrugation 2 with P2 at 0.6 m) in the rail surface with 5× magnification (only 3 complete waves are plotted).
2.3. Validity of the Model
To characterize the dynamics in the frequency range of interest as discussed in the Introduction, corrugation modeling should consider the following issues: static and dynamic contact problems should be validated; structural dynamics should be considered [47]; and coupling between the contact problem and structural dynamics should be validated.
- (1)
- With respect to the contact problems, a method similar to that of [24] is used herein. This method is suitable for resolving dynamic contact problems, and its validity has been demonstrated by the close reproduction of the evolution of squats [7,48]. Moreover, this method has been verified as suitable for resolving static contact problems based on the established solutions of Hertz, Spence, Cataneo, Mindlin and Kalker [24,49].
- (2)
- To validate the structural dynamics, (a) the approach used in this paper can reproduce the hammer test [50]; thus, the model can simulate measured track receptance based on identified track parameters. (b) Furthermore, the model can simulate axle-box acceleration (ABA) measurements [30,51]. Consequently, the model can capture the dynamics of wheels and tracks and the interaction between the vehicle and the track in the relevant frequency range.
- (3)
- With respect to assessing the validity of the model for a vehicle-track system with direct coupling between the contact problem and structural dynamics, the model exhibits a good representation of the dynamic response (spatial and frequency) of corrugation induced by squats. As noted in [21], “the model provides a good explanation for the development of corrugation initiated from isolated railhead irregularities”. Thus, in this paper, the challenge is to extend the model to the study of the more general type of corrugation that does not present clear local irregularities as the source of corrugation initiation.
As will be discussed in greater detail in Section 4.2 on the prediction of major field observations, the simulated wear in Section 4.2 is in agreement with the field observations shown in Figure 1b,c. Here, the irregular distribution of wear along one sleeper span is clear, and the observations and simulation are in agreement. In the paper, other agreements between the model results and field observations are discussed in greater detail later in the text. For example, the contact solutions that indicate that wear is the more probable damage mechanism at the corrugation trough [1,11,52] will be described in Section 3, and the occurrence of squats in agreement with the observation in Figure 1c will be explained in Section 4.2. These summaries comprehensively describe and analyze how the model in this paper was validated.
3. Contact Solutions at Corrugation
3.1. Normal Contact
The FE approach defines whether a node is within the contact patch through the node force. A node is in contact if:
where is the nodal force in the direction normal to the local surface. Because of the presence of corrugation, the stress and slip distributions will vary along a corrugation wavelength. Those differential distributions of the normal pressure, shear stress and slip are the direct factors in corrugation development.
Figure 4a shows the changes in the contact patch size at P1, P2, P3 and P4 with increasing amplitude A. Compared with A = 0 µm, an increase in size of up to 16% at P2 is observed in the case of A = 20 µm, and the increase is approximately 4% at P3. At the other two positions, the changes are minor. The maximum contact patch size is approximately 200 mm2 (A = 20 µm) at P2, i.e., the corrugation trough, whereas it is approximately 170 mm2 when the rail is smooth. Figure 4b displays the maximum contact pressure along the longitudinal axis (y = 0 mm) for different corrugation amplitudes A. As the corrugation amplitude increases from 0–20 µm, the contact pressure at P2 drops significantly to 56% of the original level, i.e., from 1320–745 MPa. This decrease is partly because of the 15% increase in the contact patch size (Figure 4a). At P1 and P3, the maximum pressure declines slightly to 78% of the original level. An increase in pressure of 6% is observed at P4 for the case of A = 20 µm.
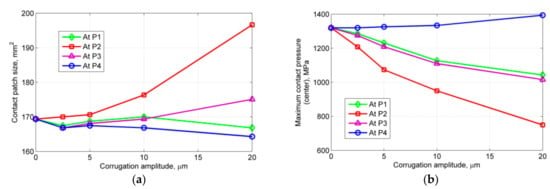
Figure 4.
Influence of corrugation amplitude on the size of the contact patch and the maximum contact pressure along the longitudinal axis y = 0 mm. (a) Contact size; (b) contact pressure.
Figure 5 shows a typical profile of the variation of the magnitude of normal force, contact size and maximum contact pressure along the longitudinal axis. In the figure, the typical normal force is the lowest at trough P2 and the highest at peak P4, with intermediate values at points P1 and P3.
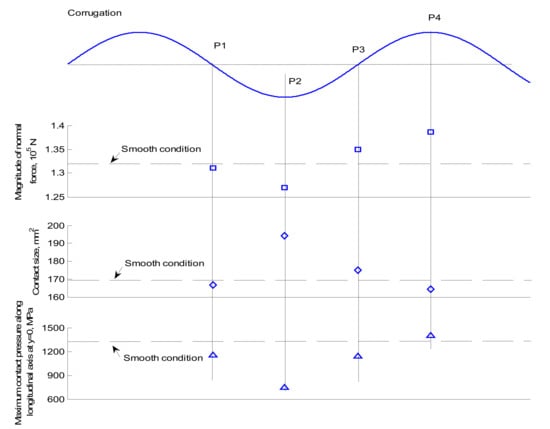
Figure 5.
Magnitude of the normal force, contact size and maximum pressure along the longitudinal axis at (y = 0 mm) at the four analyzed positions P1, P2, P3 and P4 (A = 20 μm).
As the corrugation amplitude increases, the normal contact force at P2 decreases and the area of the contact patch increases; thus, the pressure decreases. At P4, the normal contact force increases, and the area of the contact patch decreases; thus, the pressure increases. At P1 and P3, the normal contact force and the area of the contact patch are intermediate between cases P2 and P4. These patterns are further evident in Figure 4b, where the maximum contact pressure of P1 and P3 for the different corrugation amplitudes decreases, although it does not decrease as strongly as in the case of P2.
Figure 6 shows the projections of contact pressure and shear stress onto the xOy plane, the shape of the contact patch under the smooth condition and the evolution within one corrugation wavelength from P1 to P4 when A = 20 µm. Most shapes are not elliptic and thus differ from the Hertzian solution. Because of the downhill slope of the corrugation at P1, a large drop in pressure is observed at the leading edge of the contact patch and vice versa at P3. Thus, the pressure distributions at P1 and P3 take the shapes of a “waning crescent moon” and “waxing crescent moon”, respectively. At P2, the maximal pressure shifts to the field and gauge sides, thereby decreasing the contact pressure in the contact patch center to 600–800 MPa. The pressure distribution at P4 is close to the solution under the smooth rail except for a slight shrinkage of the contact patch at the leading and trailing edge centers. The maximum pressure is slightly higher than that at the other locations as shown in the pressure scaling color bar.
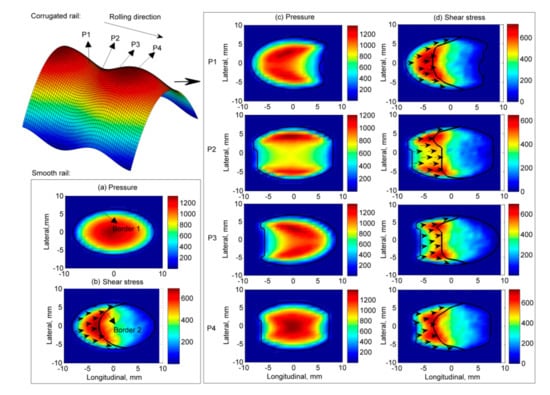
Figure 6.
Contact pressure, shear stress, contact patch, adhesion-slip distributions and vector graphs of micro-slips (vectors in Figure 6b,d) when A = 20 µm along one corrugation wavelength (P1–P4) (projection onto the xOy plane; Border 1: contact patch border; Border 2: adhesion-slip distribution border).
As also shown in Figure 5, the pressure variation within a corrugation wavelength along the longitudinal axis y = 0 mm is approximately in phase with the corrugation. Furthermore, the shapes of the contact patch differ from those under the smooth rail condition. Part of the contact patch is not present in the leading area at P1, in the trailing area at P3 and in both the leading and trailing areas at P2 and P4. Thus, the deviation from a Hertzian solution is large and further exacerbated by increases in the corrugation amplitude.
3.2. Tangential Contact
Figure 6b,d show the surface shear stress distributions when the rail is smooth and corrugated, respectively. In the presence of corrugation, especially when the amplitude is large, e.g., A = 20 µm, the distributions of the shear stress differ from those of the smooth rail case. Similar to the pressure distributions, the maximum shear stress, which occurs in the central part and at the adhesion-slip boundary within the contact patch, is cut in the middle and protrudes on the gauge and field sides, especially at P2 and P3. The development of the surface shear stress with the increase in corrugation amplitude follows a trend similar to that of the normal pressure in the slip zone of the contact patch.
When a tangential force is applied, slip arises in the contact area. In the adhesion zone, there should not be relative slip between the contacting particles of the wheel and rail where the wheel and rail surfaces stick together. There should, however, be relative slip between the contacting particles of the wheel and rail surfaces in the slip zone. The tangential contact force at a node in the slip zone equals the bound of the tangential nodal force, which is the product of the nodal force in the normal direction and the friction coefficient according to Coulomb’s law. In the adhesion zone, the tangential nodal contact force is lower than the bound. Therefore, a node is in a slip zone if:
where is the tolerance. In this paper, is 5% of the maximal tangential nodal force in the contact patch.
The adhesion-slip distribution in the presence of corrugation is shown in Figure 6d. The boundary between the adhesion and the slip zones at P2 and P3 is far from elliptic [14]. As assumed, differential wear proportional to the frictional work [9,18,22] causes the development of corrugation. Frictional work only occurs in the slip zone. Therefore, the size of the slip zone in the contact patch, as well as the magnitude of the slip might be indicators of corrugation development.
In Figure 7a, changes in the size of the slip zone with increases in corrugation amplitude at P1, P2, P3 and P4 are shown. The size fluctuates slightly at A = 0–10 µm. To study the trend of change, the corrugation amplitude is further extended to 30 µm. When the rail is smooth, the size of the slip zone is approximately 69 mm2, which is 40% of the whole contact patch (170 mm2). After the initial fluctuations at A = 2.5 µm and 5 µm, the value at P2 presents the largest change and increases up to 98 mm2 at A = 30 µm, which is 57% of the total smooth contact zone. At the other three positions, the change in the slip zone size is small. Specifically, at P3, this value remains almost at the same level, whereas at P1 and P4, a 10% decrease is observed compared with that of the smooth rail (A = 30 µm).
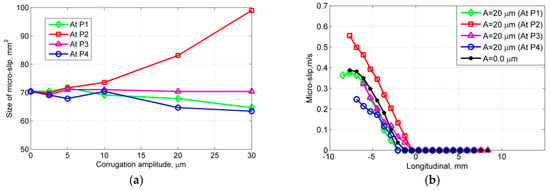
Figure 7.
Size of the slip zone as a function of the corrugation amplitude and slip distribution along the longitudinal axis y = 0 mm at the four positions. (a) Size of slip zone; (b) slip along the longitudinal axis y = 0 mm.
Figure 7b shows the change in the slip distribution along the longitudinal axis y = 0 mm. The maximum slip at P2 is much larger than that of the other cases, which is in agreement with the trend shown in Figure 7a. At P3 and P4, the magnitudes of the slip decrease compared with that of the smooth rail. The increase in the size of the slip zone and the maximum magnitude of the slip at P2 may indicate that large micro-slips in the trough could be a major driver of corrugation development. The distribution of the slip within the contact patch is shown in Figure 6b,d.
4. Wear and Corrugation Simulation
4.1. Wear Model
The contact solutions in the presence of corrugation (as previously discussed) are used to calculate the frictional work, which is considered proportional to wear [9,18,22]. This section examines whether corrugation will grow under the given conditions by comparing the phases of wear and corrugation. To consider a whole sleeper, the applied corrugation of length L2 in Figure 2a is extended along the rail to start at x = 0.87 m to cover both the middle sleeper span and sleeper support. The frictional work is calculated in the contact patch for each element for a whole wheel passage, i.e., from element entry until leaving contact. The wear of an element is as follows:
where k is the wear coefficient, Wf(x, y) is the frictional work, τi(x, y) and vi(x, y) are the local tangential stress and slip, respectively, and N is the number of time steps ∆t during which the element passes through the contact patch. The wear coefficient k is a constant that depends on the material, lubrication and temperature among other factors [8,9,53,54,55]. In this work, the calculated wear is normalized with respect to the average value of the wear under the smooth rail condition. This normalization is performed because the phase angle between wear and corrugation determines whether the corrugation will grow, which represents our main concern in this paper and is not directly affected by the wear coefficients. It is part of further research to include measurements of the wear coefficients to guide maintenance.
4.2. Prediction of Major Field Observations
In reality, the rolling of the wheel along the rail excites a range of vibrations of the structure and continua in the system. However, only a few of the vibration components are directly related to the corrugation. The corrugation wavelength observed in the field and introduced in the model is 30 mm, and the wavelength of short pitch corrugation is typically 20–80 mm, while the calculated wear is high-pass filtered to remove wear patterns shorter than 20 mm.
The wear along the longitudinal axis y = 0 mm is studied. Figure 8a shows the distribution of the simulated wear along the rail with different corrugation amplitudes for the P4 corrugation position of = 0, with 1.2 m as the corrugation peak. The results for the other corrugation positions show similar trends and are not presented. The wear is not uniform along the rail; thus, corrugation development will not be uniform under the evaluated conditions. Comparing the field observations in Figure 1 with the wear simulation results in Figure 8a reveals that the model closely reproduces the conditions in Figure 1b,c in terms of predicting the periodicity of the wear and the number of corrugation waves in the periodicity. The periodicity in Figure 1c is nine and 11 waves. The periodicity in Figure 8a is nine waves between the largest peak-to-trough wear magnitudes at 0.96 m and 1.23 m. In Figure 1c, the periodicity is counted between the squats because the squats should have been caused by the most severe corrugation, i.e., the largest wear.
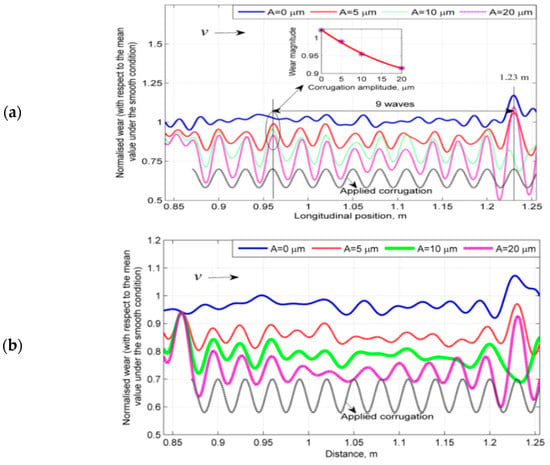
Figure 8.
Distribution of wear at different corrugation amplitudes obtained for the corrugation in Figure 3b with = 0 and P4 at 1.2 m. The middle of a sleeper is at 1.2 m, and the midpoint between two sleepers is at 0.9 m. (a) High-pass filtered at λ = 20 mm. (b) High-pass filtered at λ = 30 mm.
Furthermore, the results agree well with the field observations (Figure 1). Specifically, the model predicts that the largest wear occurs at 1.23 m above a sleeper centered at 1.2 m (Figure 8a). This is in agreement with Figure 1c, in which one of the squats was above a sleeper, and with those in Figure 1b, where the corrugation was always the most severe above the sleepers. Rails above sleepers have been reported to be more prone to corrugation [22]. The inset in Figure 8a shows that the magnitude of wear decreases as the corrugation amplitude increases. This pattern can be understood in relation to Figure 6 and Figure 7b because the wear is proportional to the product of the shear stress and the slip. The slip at A = 20 µm in Figure 7b is generally equal to or less than that at A = 0 µm, except at P2. The shear stress at A = 20 µm in Figure 6 is always less than that at A = 0 µm, and the difference is large for P2 and P3.
The wear in Figure 8a is of the same wavelength and phase as the modeled corrugation. Thus, the existing corrugation will be erased by wear and will not grow, and if the rail is smooth, no corrugation will initiate. This finding is reasonable because the simulation is based on nominal track parameters; in reality, many tracks are indeed free of corrugation. Thus, the results indicate that corrugation is sensitive to the system parameters, e.g., rail fastening [41].
4.3. Analysis of Longitudinal and Vertical Rail Modes
Figure 9 shows the power spectra of the calculated wear under different corrugation amplitudes. When A = 20 µm, a major frequency component is observed at approximately 1296 Hz, approaching the corrugation passing frequency of 1297 Hz (estimated with a wheel passing at 38.9 m/s over the corrugation with a wavelength of 30 mm). When A is reduced, this major frequency also decreases. At A = 2.5 µm, the frequency is 1290 Hz, which is 7 Hz lower. Thus, the frequency of the wear is initially (i.e., when A is small) lower than that of the modeled corrugation, and it is influenced by the corrugation.
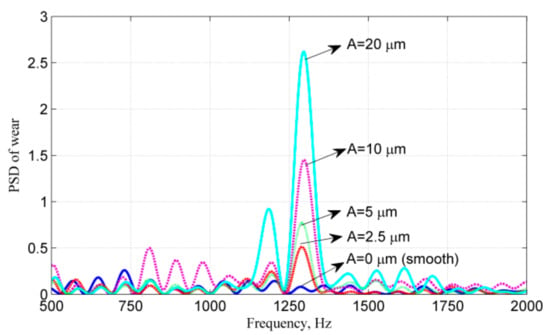
Figure 9.
Power spectral density (PSD) of wear λ = 30 mm, with a major peak at 1296 Hz and a secondary peak at 1185 Hz, when A = 20 µm.
When A is increased to 20 µm, there is a sudden PSD increase at 1185 Hz; see the second major peak in Figure 9. Modal analysis in Figure 10a,b shows that these two major frequencies of 1185 and 1296 Hz correspond to two natural frequencies of the system (1185 Hz of a vertical rail mode and 1291 Hz of a longitudinal rail mode), i.e., the two natural frequencies that are closest to and/or lower than the corrugation passing frequency of 1297 Hz (see in Figure 10 the characteristic modal shapes). The closest pin-pin resonance is at approximately 1110 Hz (Figure 10c), and it thus does not seem to have influence on the wear development in this case.
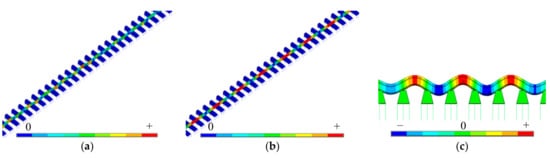
Figure 10.
Modal analysis of the two major frequencies (1185 and 1296 Hz) shown in Figure 9: (a) rail vertical mode at 1185 Hz and (b) rail longitudinal mode at 1291 Hz, in comparison with the closest vertical pin-pin mode at 1100 Hz shown in (c).
Based on Figure 9, it is reasonable to assume that the development of the observed corrugation with a wavelength of 30 mm is mainly related to these two modes. Then, the track parameters are a stronger determinant of the corresponding wavelength of the calculated wear than is the modeled corrugation because the track parameters determine the longitudinal and vertical modes.
When the corrugation amplitude is close to zero, e.g., A = 2.5 µm or less, the major frequency of the wear is approximately 1290 Hz, which is 6 Hz lower than the 1296 Hz of the wear at A = 20 µm, 1 Hz lower than the longitudinal modes, but 105 Hz higher than the vertical mode. This suggests that for the initiation of corrugation, the longitudinal mode should have played a major role compared with the vertical mode. Additionally, the periodic wear under the smooth rail condition has one peak at 1290 Hz. When the amplitude of corrugation is progressively increased, the differential wear at this frequency grows consistently. This phenomenon does not happen at the other frequencies. This implies a positive-feedback process taking place at around this frequency. Besides, in Figure 9, the series of peaks from A = 20 µm and further to the smooth rail converge asymptotically to the smooth rail situation of A = 0 µm. Based on the positive feedback and trend analysis, it is reasonable to infer that the longitudinal vibration modes are probably dominant for short pitch corrugation initiation. In the corrugation initiation, the longitudinal modes in the form of compression and rarefaction waves influence the local wheel-rail contact of forces and creepage and result in their fluctuation and thus the formation of the differential wear.
With the growth of corrugation, the vertical mode plays an increasingly important role. This behavior is confirmed by Figure 9: when A is larger than 10 µm, the PSD peak of the secondary frequency at 1185 Hz begins to make a significant contribution to the wear. This frequency corresponds to the vertical mode and is excited when the corrugation amplitude is sufficiently large. When the corrugation amplitude is further increased, it will incur wear that is of the same frequency as the corrugation. Therefore, when the corrugation amplitude is significant, the vertical modes will be dominant.
For intermediate situations, the longitudinal and vertical modes together determine whether corrugation will grow or be suppressed by wear based on whether the wear is of the same frequency and correct phase. In other words, when the vertical and longitudinal modes are inconsistent, the differential wear caused by the respective modes will suppress each other so that there will be no corrugation, no matter high or low adhesion, as long as the consistency condition is not satisfied. Certain track parameters could satisfy the required consistency requirement; thus, corrugation will appear in some places, but not in others.
In summary, the longitudinal vibration modes are probably dominant for short pitch corrugation initiation. Then, the interaction and consistency between longitudinal and vertical modes should determine the development of short pitch corrugation, and once a certain severity is reached, vertical modes become dominant. This global perspective of the consistency conditions that govern the evolution of short pitch corrugation represents a novel contribution. The literature has so far only considered the effects of the vertical, lateral and torsional modes [1,3,39,40,56,57]. In [42], the relative longitudinal vibration of the two rails of a track is considered for corrugation initiation, for which each half track is modelled as an inertia, and longitudinal vibration modes of the rail as a flexible body are not considered.
4.4. Additional Comments
Minor frequency components may also be relevant. According to the previous analysis, the wavelength of the wear changes with the corrugation amplitude A; however, Figure 8a shows a constant wear wavelength because Figure 8a was high-pass filtered at λ = 20 mm. When the same signals are high-pass filtered at λ = 30 mm, i.e., when the frequencies of 1185 Hz and 1291 Hz are given a more dominant role, the wavelength also varies (Figure 8b), and the phase of the wear changes with A. This behavior indicates that certain minor frequency components of wear shown in Figure 9 also play a relevant role in determining the wavelength and phase of the wear and thus the development of corrugation.
Studying corrugation by pre-selecting certain modes may lead to different and possibly non-physical results, thereby highlighting the subtleness of the corrugation problem. However, this also reveals one of the advantages of the proposed modeling approach, which can contain all necessary modes of the structure and continua in the system by modeling the relevant components and interfaces with realistic geometry and material properties. Several questions for further research could focus on the cut-off wavelength for filtering: what is the shortest cut-off wavelength for filtering? Could it be related to the shortest observed corrugation wavelength of 20 mm? Is the optimal cut-off frequency equal to 20 mm or should it be shorter? Is this frequency related to the concept of the contact filter [58]?
According to the above discussion, instead of increasing to 1296 Hz, the major frequency in Figure 9 should decrease from 1290 Hz at A = 2.5 µm toward the frequency of the vertical mode of 1185 Hz when the corrugation amplitude grows and the vertical mode becomes dominant. This mismatch is caused by the inconsistency between the modeled corrugation wavelength of 30 mm and the natural modes of the track, which are determined by the nominal track parameters used in the modeling. The prescribed wavelength is a field observation related to deviation from the nominal track. The nominal track parameters do not necessarily cause corrugation; otherwise, corrugation would be observed everywhere. Because of this mismatch, the calculated wear tends to erase the corrugation.
5. Relationship between Contact Forces and Wear as well as New Insights
Based on the discussion in Section 4, it may be inferred that equal longitudinal and vertical natural frequencies may represent a condition for corrugation to consistently initiate and grow; this may be achieved by properly constraining the rail by the fastening system [59]. The next question is whether corrugation occurs at certain preferred frequencies. Because the natural modes should be excited by contact forces and dynamic contact forces are caused by corrugation, the effects of the prescribed corrugation on the normal and longitudinal forces are examined below. Note that for corrugation, the difference between the vertical and normal directions of wheel-rail contact is negligible.
5.1. Normal and Longitudinal Forces Do Not Exactly Follow Corrugation in Wavelength and Phase
Figure 11 shows the normal contact force (FN) and longitudinal contact force (FL) when the rail is smooth and when corrugation is present. Although the wavelength of the modeled corrugation is constant (30 mm), the wavelengths of the resulting dynamic wheel-rail contact forces vary along the rail (Figure 11a). Specifically, FN initially lags behind the corrugation, i.e., the peak of FN appears to the left side of the corresponding corrugation peak. When approaching the sleeper, which has a width of 140 mm and is centered at 1.20 m, the force catches up and becomes in phase with the corrugation at approximately 1.1 m, i.e., near the edge of the sleeper. The force subsequently tends to lead the corrugation. A similar situation applies to FL (Figure 11b). However, FN leads FL initially, and the two forces later tend to be in phase at approximately 1.23 m, with subsequent lagging of FN. Note that the wear is also strongest at approximately 1.23 m (according to Section 4.2).
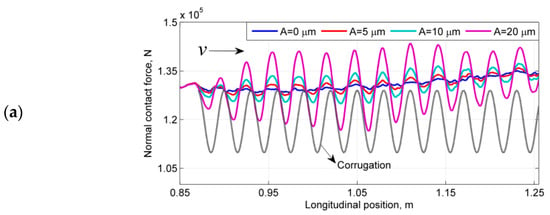
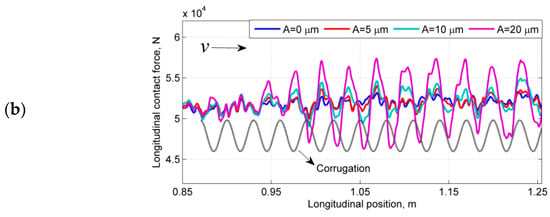
Figure 11.
Dynamic wheel-rail contact forces obtained for the corrugation in Figure 3 with = 0 and P4 at 1.2 m (1.2 m is in the middle of a sleeper and 0.9 m is at the midpoint between two sleepers.). (a) Normal contact force. (b) Longitudinal contact force.
The PSD analysis in Figure 12a reveals that the main frequency components of FN and FL are 1257 Hz and 1226 Hz, respectively. The corresponding vertical and longitudinal rail vibration modes closest to the corrugation passing frequency of 1297 Hz are 1185 and 1291 Hz, which means that the normal and longitudinal contact forces do not exactly follow the excitation and have frequencies that are different from the natural vibration modes. Previous studies have either explicitly or implicitly assumed that the frequencies of the longitudinal contact force, the normal contact force and the vertical natural mode are the same as the corrugation passing frequency; however, the longitudinal mode has not been previously considered.
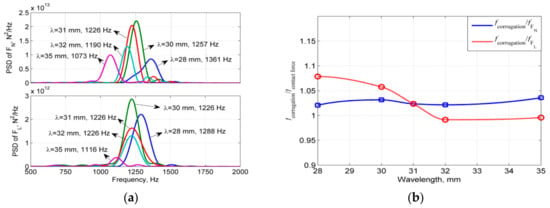
Figure 12.
Relationships between the PSD and frequencies of the contact forces and corrugation wavelength obtained for the corrugation in Figure 3b with = 0, P4 at 1.2 m and A = 20 μm. Note that in (b), fcorrugation is not constant, but changes with the corrugation wavelength. Thus, although the PSD of FL varies in a narrower band than FN in (a), the opposite pattern is observed in (b). (a) PSD of FN (upper) and FL (lower). (b) Ratio of corrugation over contact force frequency.
5.2. Preferred Frequency of Contact Forces
The dynamic normal and longitudinal contact forces are determined by the combined effects of the parameters of the structure, the excitation by the corrugation and the transient rolling contact. To investigate the contact force sensitivity to different corrugation wavelengths, the wavelength is varied at 28, 30, 31, 32 and 35 mm. Figure 12 shows the relationships between the PSD and frequencies of the contact forces and the corrugation wavelength. The following observations can be made.
- (1)
- The frequencies of the normal and longitudinal forces are different. The frequencies of the contact forces are different from that of the excitation, i.e., the passing frequency of the corrugation, and they are sensitive to and change with the corrugation wavelengths. The dynamic forces are stronger at certain wavelengths than others. With the current track parameters, both the longitudinal and vertical contact forces are strongest at λ = 30 mm. This again is in agreement with the observed corrugation wavelength of 30 mm.
- (2)
- The bandwidth of the frequency change of the longitudinal force is between 1116 Hz and 1288 Hz (Figure 12a), which is narrower than that of the normal force (between 1073 and 1361 Hz). The frequency band of the vertical force is broader because it follows the change in the corrugation wavelength, as shown in Figure 12b for the relatively constant ratio of the corrugation passing frequency to the contact force frequency. The frequency of the longitudinal contact force is lower than that of the normal contact force when the corrugation wavelength is short, i.e., between λ = 28 mm and 31 mm (Figure 12b), and vice versa when the corrugation wavelength is longer than 31 mm.
- (3)
- The frequency of the normal contact force is always lower than that of the excitation (Figure 12b). The presence of corrugation is an excitation mainly in the normal direction; thus, the response always follows the excitation. However, the frequency of the longitudinal contact force can be lower or higher than that of the excitation, which likely depends on the nearest natural frequency, as well as the complex relationship between the tangential and normal contact forces. This pattern reveals a strong dependence of the normal contact force on the excitation and a relatively weaker dependence of the longitudinal contact force on the excitation. These dependencies are in line with the narrower band of the frequency change of the longitudinal force compared with the normal force.
- (4)
- In Figure 12b, the frequency of the longitudinal contact force has the largest deviation from the corrugation passing frequency when the wavelength is shorter, i.e., at λ = 28 mm. With increasing λ, the deviation decreases. At approximately λ = 31.5 mm, the frequency of the longitudinal contact force equals the passing frequency. The longitudinal contact force subsequently follows the excitation closely.
- (5)
- The frequency curves (Figure 12b) of the normal and longitudinal contact forces cross each other at a wavelength of 31 mm, where the frequencies of the normal and longitudinal forces are equal. Is an equal frequency of the two forces a condition for the corrugation to initiate, grow and become a wavelength-fixing mechanism? As shown in Section 4.2 and Section 5.1, the wear is strongest when the normal and longitudinal forces FN and FL are in phase at 1.23 m. Because an equal frequency is a necessary condition for FN and FL to be in phase over many wavelengths, it is indeed a favorable condition for corrugation development.
These observations indicate that the system appears to have a preference for certain frequencies, which is further confirmed by Figure 12a, in which the frequency of the longitudinal contact force is 1226 Hz for λ = 30 mm, 31 mm and 32 mm. This apparent preference is also in agreement with the results of [3], which show that most models in the literature suggest a fixed frequency related to vertical resonances in the system. However, this preference appears contrary to the hypothesis of fixed wavelength [1] and is part of the enigma of the corrugation problem: is the mechanism underlying corrugation a wavelength-fixing or frequency-fixing mechanism [3]?
5.3. Frequencies Converge to Develop Uniform Corrugation
Equal longitudinal and vertical natural frequencies have been shown to represent preferred conditions under which corrugation can initiate and grow; thus, it is reasonable to infer that the frequencies of the related contact forces and the resulting wear are also equal, such that the five different frequencies converge to one frequency: the corrugation passing frequency. Therefore, the frequency appears to be fixed at a preferred resonance, whereas the wavelength is “fixed” in the sense that it can vary only in a small range. This supposition explains the observations in Section 5.2, in which the frequency converges to 1226 Hz, while the preferred wavelength varies because of the mismatch between the given corrugation wavelength and the nominal track parameters. The strongest contact forces are at λ = 30 mm; the frequencies of the longitudinal and normal forces are equal at λ = 31 mm; and the frequency of the longitudinal force and the corrugation passing frequency are equal at λ = 31.5 mm.
It is also reasonable to infer that when the track parameters that caused the observed corrugation are known and the mismatch between the model input and the prescribed corrugation is eliminated, all of the different wavelengths will converge to the observed wavelength of 30 mm if the traffic speed is 140 km/h, which implies that varying traffic speed can suppress corrugation by changing the wavelength as was shown in [60]. The problem for further research now becomes modeling degraded track to identify the track parameters at which the system converges to the preferred frequencies and wavelengths with a phase angle of wear that promotes corrugation growth at every wheel passage.
5.4. Importance of the Proposed Modeling Approach and Track Parameters
Since the foundational work of Grassie [61,62,63], modeling corrugation has generally been based on wheel and rail sub-models that consist of beams and plates, and the wheel-rail contact is solved separately via statics and then coupled to the wheel-rail system. These calculations were limited by the state of the art. For contact mechanics, “the mechanics of steady or slowly varying creep forces has been very thoroughly studied, but the behavior under transient or rapidly oscillating conditions is virtually unexplored” [63]. The longitudinal dynamics of the wheel-rail interaction were investigated experimentally in [62], and longitudinal resonances higher than 900 Hz were observed. Such resonances were not considered important and thus were ignored in further investigations, and the focus for corrugation has been on vertical, lateral and wheelset torsional dynamics [1,3,39,40,56,57]. In this paper, by analyzing the frictional rolling in the vehicle-track system under transient and rapidly oscillating conditions, the influence of both the vertical and the longitudinal vibration modes on corrugation initiation and growth was captured. However, further research should be performed that includes the influence of the track structure, especially the fastening, which plays a major role in constraining the rail and affecting its modes [59]. Studies have modelled fastenings and sleepers and identified their parameters [19,50,64,65], and these works have revealed that the alignment of the fastening system influences the frequency of normal and longitudinal dynamics and that the natural frequencies are determined by the system parameters.
Figure 1 shows different cases of corrugations under different track types, i.e., mono-block sleeper versus duo-block sleeper and W-shaped tension clamp versus Deenik clips. Among the three figures in Figure 1, Figure 1a is at a gentle curve, and the latter two figures are on straight tracks. These observations agree with the description of the short pitch corrugation [1]. Comparing the three photos reveals that the characteristics of the corrugation differ from track to track. Certain corrugations are more or less uniformly distributed along the track (Figure 1a), whereas others are more severe near the sleeper support (Figure 1b,c). The difference between Figure 1a and Figure 1b,c is the types of sleepers and fastenings. According to Figure 1b, the wavelength of the corrugation may vary significantly within a sleeper span. Moreover, Figure 1b,c is from the same track, thus having the same traffic and same types of sleeper and fastening; however, large differences in the corrugations are apparent. These observations all indicate that corrugation is sensitive to track conditions, thus highlighting directions for future work.
5.5. Additional Discussions
In this section, 2D and 3D analysis results are briefly compared. In [16], a 2D non-Hertzian contact model is developed in which the stress distribution is not symmetric at the falling and rising edges of the corrugation. The same phenomenon is observed in the present 3D numerical analysis. A clear difference between the 2D and 3D approaches is that in the 2D analysis, the contact patches at the falling and rising edges are symmetric in the longitudinal direction about the contact patch center. In the case of the 3D analysis, the contact patches are not symmetric about the contact patch center.
Wavelength fixing is also observed. In the Dutch railway network, the wavelength of the short pitch corrugation is 25–50 mm at a corresponding speed of 30–140 km/h. If the corrugation is purely determined by frequency fixing, then the wavelength should have varied in a broader range. Therefore, the numerical analyses and the field observations indicate that frequency fixing and wavelength fixing may have occurred simultaneously. One such possibility is that for a certain traffic speed, if the preferred frequency is nf0, with f0 representing the fundamental frequency, the frequency will jump to harmonics of a higher frequency (n + i)f0, i ≥ 1 when the speed is increased so that the wavelength remains at the fixed wavelength.
As shown in Figure 11a, approximately two wavelengths are required for the normal contact force to transit from the steady state before the corrugation, which starts at 0.87 m, to the new steady state controlled by the corrugation. For the tangential force, approximately 3.5 wavelengths are required. Thus, the longitudinal force lags approximately 1.5 wavelengths behind the normal force, i.e., approximately 45 mm. Because the length of the contact patch is approximately 15 mm (see Figure 6), the lag is approximately three-times the length of a contact patch. In [14], the lag for static rolling contact is one length of a contact patch, which reveals another difference between static and dynamic rolling contact. Moreover, Figure 11 shows that the tangential contact force contains considerably more harmonics than the normal force.
Metallurgical investigations on corrugated rail material show that the corrugation crest experiences high dynamic contact forces, high deformation, work hardening and, consequently, high wear resistance. The corrugation trough, instead, is reported to be developed from wear [11,52]. This is in agreement with the numerical results in the present paper, i.e., high contact pressure is found at the corrugation crest and lower pressure and high micro-slip at the corrugation trough. Additionally, the delay in corrugation growth with reduction of wear by friction modifier [66] also supports wear as a mechanism of the corrugation.
Although more research using more sophisticated models for the longitudinal support is needed, the findings of this paper have relevance for the numerical modeling of longitudinal modes. The inclusion of longitudinal support stiffness, such as in [62], results in a longitudinal mode at approximately 1298 Hz, which represents a difference of 7 Hz with respect to the model without longitudinal rail support. Hence, the more complex model does not result in a significant difference in the longitudinal dynamics. This situation should be further explored by investigating the actual parameters experimentally under Dutch conditions and verifying the dynamics.
6. Conclusions and Future Work
In this paper, the enigma of rail short pitch corrugation is examined using a novel modeling approach. Although the enigma remains unsolved, new insights on the phenomenon are described. The approach consists of simulating the vehicle-track dynamic interactions, which are directly and instantaneous coupled through frictional rolling contact. Wear is assumed to be the damage mechanism. The wheel, track and contact are treated in three dimensions so that the structural, geometric and material properties of the system and its components can be modeled sufficiently. The analysis concentrates on the transient rolling at the corrugation and the behavior of the vehicle-track system under the rapid oscillating loading of Dutch railway track and traffic in an effort to identify the preferred conditions under which corrugation can consistently initiate and grow. The findings and insights are summarized as follows.
- -
- Along the longitudinal centerline of the contact patch, increases in the contact area, maximum pressure, shear stress and micro-slips at the corrugation crest are small, and some of them even decrease with increases in the corrugation amplitude. However, changes at the trough are large. The large micro-slip and the significantly reduced contact pressure at the trough are the major contributions to the differential wear, which causes corrugation initiation and growth. The dependence of the normal contact force on corrugation excitation is strong, and the dependence of the longitudinal contact force on excitation is relatively weak.
- -
- In addition to the commonly-accepted hypothesis for corrugation studies, i.e., the vertical vibration modes of the vehicle-track system determine the development of corrugation, it is found that the longitudinal vibration modes are also important. Longitudinal modes are likely to be important for the initiation of corrugation, and when the corrugation amplitude is sufficiently large, the vertical modes will be dominant. For intermediate situations, the longitudinal and vertical modes together determine whether the corrugation will grow or be suppressed by wear depending on whether the wear is of the necessary consistent frequency and phase.
- -
- The main frequencies of the vertical and longitudinal vibration modes and contact forces, as well as the resulting wear are different. Consequently, a condition (that might not be unique) for corrugation to consistently initiate and grow should be that the longitudinal and vertical main frequencies are consistent. This consistency may be achieved by the control of certain track parameters, for instance by properly constraining the rail fastening.
The modeling and findings agree with field observations (Figure 1) of the distribution of corrugation with different severities. The proposed modeling is promising for corrugation analyses. Future work may include identifying the track parameters required for the system to converge to the preferred frequencies and wavelengths and investigating the phase-fixing mechanism of wear that promotes corrugation growth at every wheel passage. To this end, the first focus should be on rail fastening. Previous work has shown that the fastening system, including the rail pads, has a strong influence on the vertical and longitudinal dynamics.
Acknowledgments
This research is partly supported by ProRail and by NeTIRail-INFRA (Needs Tailored Interoperable Railway project focused on infrastructure), an EU Horizon 2020 program for research and innovation (Project No. 636237), as well as by an open call project of the Key Laboratory of Theory and Technology of High-Speed Railway Structures, Ministry of Education of China, Southwest Jiaotong University (Project No. 2014-HRE-03).
Author Contributions
Shaoguang Li and Zili Li conceived and designed the idea and numerical study; Shaoguang Li performed the numerical study; Shaoguang Li, Zili Li, Alfredo Núñez and Rolf Dollevoet analyzed the data and contributed in writing the paper; Rolf Dollevoet and Zili Li contributed in obtaining the funding for performing the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grassie, S.L. Rail corrugation: Characteristics, causes, and treatments. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 581–596. [Google Scholar] [CrossRef]
- Sato, Y.; Matsumoto, A.; Knothe, K.L. Review on rail corrugation studies. Wear 2002, 253, 130–139. [Google Scholar] [CrossRef]
- Afferrante, L.; Ciavarella, M. Short pitch corrugation of railway tracks with wooden or concrete sleepers: An enigma solved? Tribol. Int. 2010, 43, 610–622. [Google Scholar] [CrossRef]
- Meehan, P.A.; Bellette, P.A.; Horwood, R.J. “Does god play dice with corrugations?”: Environmental effects on growth. Wear 2014, 314, 254–260. [Google Scholar] [CrossRef]
- Giannakos, K. Modeling the influence of short wavelength defects in a railway track on the dynamic behavior of the non-suspended masses. Mech. Syst. Signal Process. 2016, 68, 68–83. [Google Scholar] [CrossRef]
- Tavares de Freitas, R.; Kaewunruen, S. Life Cycle Cost Evaluation of Noise and Vibration Control Methods at Urban Railway Turnouts. Environments 2016, 3, 34. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, X.; Esveld, C.; Dollevoet, R.; Molodova, M. An investigation into the causes of squats-correlation analysis and numerical modelling. Wear 2008, 265, 1349–1355. [Google Scholar] [CrossRef]
- Nielsen, J.C.O. Numerical prediction of rail roughness growth on tangent railway tracks. J. Sound Vib. 2003, 267, 537–548. [Google Scholar] [CrossRef]
- Xie, G.; Iwnicki, S.D. Calculation of wear on a corrugated rail using a three-dimensional contact model. Wear 2008, 265, 1238–1248. [Google Scholar] [CrossRef]
- Böhmer, A.; Klimpel, T. Plastic deformation of corrugated rails—A numerical approach using material data of rail steel. Wear 2002, 253, 150–161. [Google Scholar] [CrossRef]
- Baumann, G.; Fecht, H.J.; Liebelt, S. Formation of white-etching layers on rail treads. Wear 1996, 191, 133–140. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, X.; Dollevoet, R.; Molodova, M. Differential wear and plastic deformation as causes of squat at track local stiffness change combined with other track short defects. Veh. Syst. Dyn. 2008, 46, 237–246. [Google Scholar] [CrossRef]
- Saulot, A.; Descartes, S.; Berthier, Y. Sharp curved track corrugation: From corrugation observed on-site, to corrugation reproduced on simulators. Tribol. Int. 2009, 42, 1691–1705. [Google Scholar] [CrossRef]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Li, Z. Wheel-Rail Rolling Contact and Its Application to Wear Simulation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Nielsen, J.B. Evolution of rail corrugation predicted with a nonlinear wear model. J. Sound Vib. 1999, 227, 915–933. [Google Scholar] [CrossRef]
- Shen, Z.; Li, Z. A fast non-steady state creep force model based on the simplified theory. Wear 1996, 191, 242–244. [Google Scholar] [CrossRef]
- Knothe, K.; Groß-Thebing, A. Short wavelength rail corrugation and non-steady-state contact mechanics. Veh. Syst. Dyn. 2008, 46, 49–66. [Google Scholar] [CrossRef]
- Ilias, H. The influence of railpad stiffness on wheelset/track interaction and corrugation growth. J. Sound Vib. 1999, 227, 935–948. [Google Scholar] [CrossRef]
- Jin, X.; Wen, Z. Effect of discrete track support by sleepers on rail corrugation at a curved track. J. Sound Vib. 2008, 315, 279–300. [Google Scholar] [CrossRef]
- Grassie, S.L. Squats and squat-type defects in rails: The understanding to date. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 235–242. [Google Scholar] [CrossRef]
- Hempelmann, K.; Knothe, K. An extended linear model for the prediction of short pitch corrugation. Wear 1996, 191, 161–169. [Google Scholar] [CrossRef]
- Saulot, A.; Baillet, L. Dynamic finite element simulations for understanding wheel-rail contact oscillatory states occurring under sliding conditions. J. Tribol. ASME 2006, 128, 761–770. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z. The solution of frictional wheel-rail rolling contact with a 3D transient finite element model: Validation and error analysis. Wear 2011, 271, 444–452. [Google Scholar] [CrossRef]
- Nishiura, D.; Sakaguchi, H.; Aikawa, A. Development of Viscoelastic Multi-Body Simulation and Impact Response Analysis of a Ballasted Railway Track under Cyclic Loading. Materials 2017, 10, 615. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, Z.; Dollevoet, R. Wear study of short pitch corrugation using an integrated 3D FE train-track interaction model. In Proceedings of the 9th International Conference on Contact Mechanics and Wear of Rail/Wheel Systems, Chengdu, China, 27–30 August 2012; pp. 216–222. [Google Scholar]
- Zhao, X.; Wen, Z.; Wang, H.; Jin, X.; Zhu, M. Modeling of high-speed wheel-rail rolling contact on a corrugated rail and corrugation development. J. Zhejiang Univ. Sci. A 2014, 15, 946–963. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z. A three-dimensional finite element solution of frictional wheel-rail rolling contact in elasto-plasticity. Proc. Inst. Mech. Eng. Part F J. Eng. Tribol. 2015, 229, 86–100. [Google Scholar] [CrossRef]
- Hiensch, M.; Nielson, J.C.O.; Verherjen, E. Rail corrugation in The Netherlands—Measurements and simulations. Wear 2002, 253, 140–149. [Google Scholar] [CrossRef]
- Molodova, M.; Li, Z.; Núñez, A.; Dollevoet, R. Validation of a finite element model for axle box acceleration at squats in the high frequency range. Comput. Struct. 2014, 141, 84–93. [Google Scholar] [CrossRef]
- Arias-Cuevas, O.; Li, Z.; Lewis, R. Investigating the lubricity and electrical insulation caused by sanding in dry wheel-rail contacts. Tribol. Lett. 2010, 37, 623–635. [Google Scholar] [CrossRef]
- Cann, P.M. The ‘‘leaves on the line’’ problem—A study of leaf residue film formation and lubricity under laboratory test conditions. Tribol. Lett. 2006, 24, 151–158. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.O.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Benson, D.J.; Hallquist, J.O. A single surface contact algorithm for the post buckling analysis of shell structures. Comput. Methods Appl. Mater Eng. 1990, 78, 141–163. [Google Scholar] [CrossRef]
- Popovici, R. Friction in Wheel-Rail Contacts. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar]
- Bhushan, B. Modern Tribology Handbook: Principles of Tribology; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Oostermeijer, K.H. Review on short pitch rail corrugation studies. Wear 2008, 265, 1231–1237. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, B.; Zhou, Z. An experimental study of rail corrugation. Wear 2003, 255, 1121–1126. [Google Scholar] [CrossRef]
- Collette, C.; Horodinca, M.; Preumont, A. Rotational vibration absorber for the mitigation of rail rutting corrugation. Veh. Syst. Dyn. 2009, 47, 641–659. [Google Scholar] [CrossRef]
- Tassilly, E.; Vincent, N. A linear model for the corrugation of rails. J. Sound Vib. 1991, 150, 25–45. [Google Scholar] [CrossRef]
- Li, W.; Wang, H.; Wen, Z.; Du, X.; Wu, L.; Li, X.; Jin, X. An investigation into the mechanism of metro rail corrugation using experimental and theoretical methods. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1025–1039. [Google Scholar] [CrossRef]
- Hayes, W.F.; Tucker, H.G. Wheelset-track resonance as a possible source of corrugation wear. Wear 1991, 144, 211–226. [Google Scholar] [CrossRef]
- Suda, Y.; Komine, H.; Iwasa, T.; Terumichi, Y. Experimental study on mechanism of rail corrugation using corrugation simulator. Wear 2002, 253, 162–171. [Google Scholar] [CrossRef]
- Jin, X.; Xiao, X.; Wen, Z.; Zhou, Z. Effect of sleeper pitch on rail corrugation at a tangent track in vehicle hunting. Wear 2008, 265, 1163–1175. [Google Scholar] [CrossRef]
- Grassie, S.L.; Johnson, K.L. Periodic microslip between a rolling wheel and a corrugated rail. Wear 1985, 101, 291–309. [Google Scholar] [CrossRef]
- Bellette, P.A.; Meehan, P.A.; Daniel, W.J.T. Effects of variable pass speed on wear-type corrugation growth. J. Sound Vib. 2008, 314, 616–634. [Google Scholar] [CrossRef]
- Knothe, K.L.; Grassie, S.L. Modelling of railway track and vehicle/track interaction at high frequencies. Veh. Syst. Dyn. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Li, Z.; Dollevoet, R.; Molodova, M.; Zhao, X. Squat growth—Some observations and the validation of numerical predictions. Wear 2011, 271, 148–157. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Z.; Qian, Z.; Chen, R.; Dollevoet, R. 3D FE modelling and validation of frictional contact with partial slip in compression-shift-rolling evolution. Int. J. Rail Transp. 2015, 4, 20–36. [Google Scholar] [CrossRef]
- Oregui, M.; Li, Z.; Dollevoet, R. An investigation into the vertical dynamics of tracks with monoblock sleepers with a 3D finite-element model. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 891–908. [Google Scholar] [CrossRef]
- Molodova, M. Detection of Early Squats by Axle Box Acceleration. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Feller, H.G.; Waif, K. Surface analysis of corrugated rail treads. Wear 1991, 144, 153–161. [Google Scholar] [CrossRef]
- Jin, X.; Wen, Z.; Wang, K.; Zhang, W. Effect of a scratch on curved rail on initiation and evolution of rail corrugation. Tribol. Int. 2004, 37, 385–394. [Google Scholar] [CrossRef]
- Igeland, A. Railhead corrugation growth explained by dynamic interaction between track and bogie wheelsets. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1996, 210, 11–20. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of at surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Tassilly, E.; Vincent, N. Rail corrugation: Analytical model and field tests. Wear 1991, 144, 163–178. [Google Scholar] [CrossRef]
- Ahlbeck, D.R.; Daniels, L.E. Investigation of rail corrugations on the Baltimore metro. Wear 1991, 144, 197–210. [Google Scholar] [CrossRef]
- Remington, P.J. Wheel/rail noise-part IV: Rolling noise. J. Sound Vib. 1976, 46, 419–436. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Dollevoet, R. Influence of the fastening modeling on the vehicle-track interaction at singular rail surface defects. J. Comput. Nonliner Dyn. 2014, 9, 031002. [Google Scholar] [CrossRef]
- Meehan, P.A.; Batten, R.D.; Bellette, P.A. The effect of non-uniform train speed distribution on rail corrugation growth in curves/corners. Wear 2016, 366, 27–37. [Google Scholar] [CrossRef]
- Grassie, S.L.; Gregory, R.W.; Harrison, D.; Johnson, K.L. The dynamic response of railway track to high frequency vertical excitation. J. Mech. Eng. Sci. 1982, 24, 77–90. [Google Scholar] [CrossRef]
- Grassie, S.L.; Gregory, R.W.; Johnson, K.L. The dynamic response of railway track to high frequency longitudinal excitation. J. Mech. Eng. Sci. 1982, 24, 97–102. [Google Scholar] [CrossRef]
- Grassie, S.L.; Gregory, R.W.; Johnson, K.L. The behaviour of railway wheelsets and track at high frequencies of excitation. J. Mech. Eng. Sci. 1982, 24, 103–111. [Google Scholar] [CrossRef]
- Egana, J.I.; Vinolas, J.; Seco, M. Investigation of the influence of rail pad stiffness on rail corrugation on a transit system. Wear 2006, 261, 216–224. [Google Scholar] [CrossRef]
- Oregui, M.; Núñez, A.; Dollevoet, R.; Li, Z. Sensitivity analysis of railpad parameters on vertical railway track dynamics. J. Eng. Mech. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Egana, J.I.; Vinolas, J.; Gil-Negrete, N. Effect of liquid high positive friction (HPF) modifier on wheel-rail contact and rail corrugation. Tribol. Int. 2005, 38, 769–774. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).