Auditory Distance Control Using a Variable-Directivity Loudspeaker †
Abstract
:1. Introduction
2. Experiment I: Directivity-Controlled Auditory Distance in Auralized Rooms
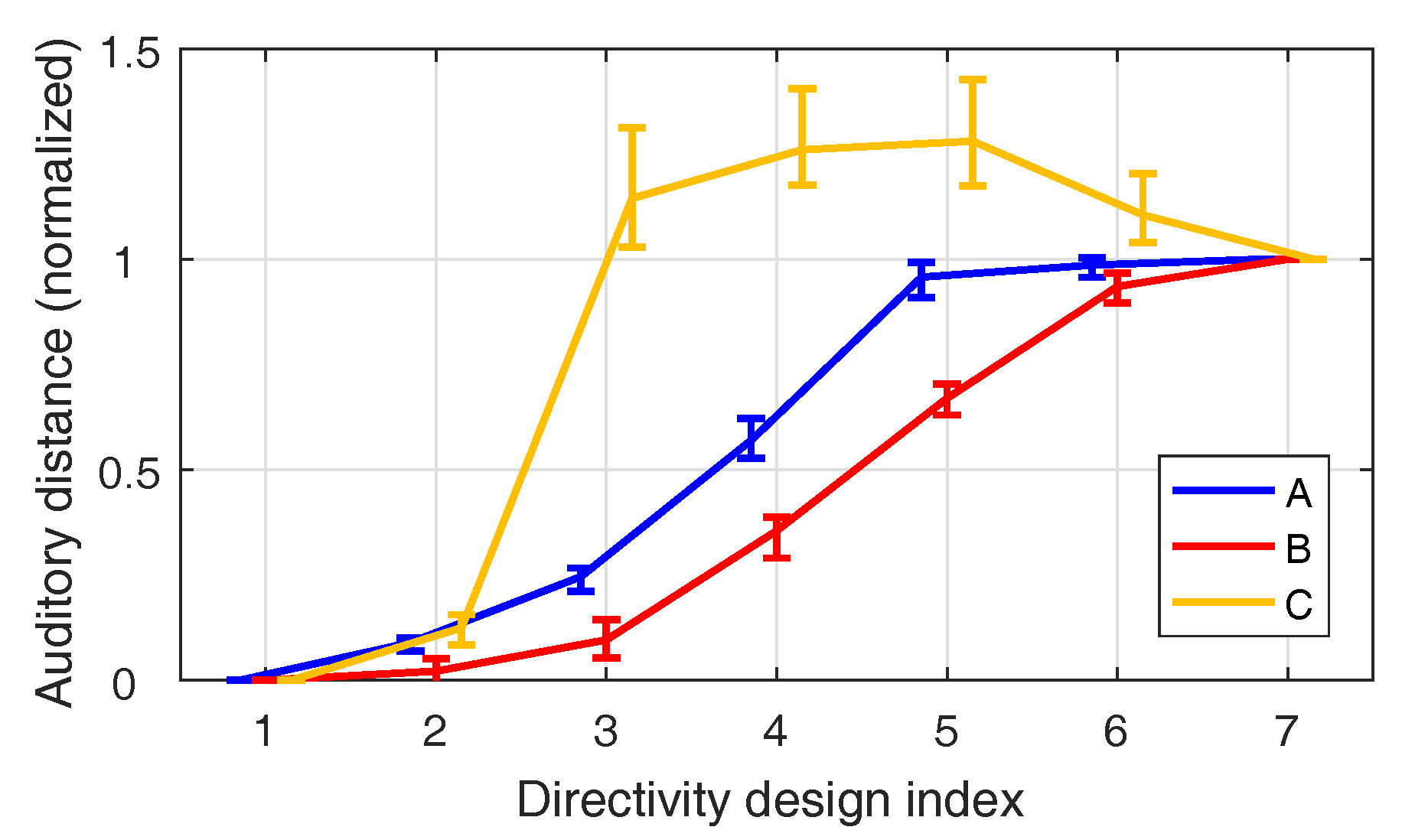
- A
- the beam order i from three to zero for and ;
- B
- the ratio of two opposing beams: ;
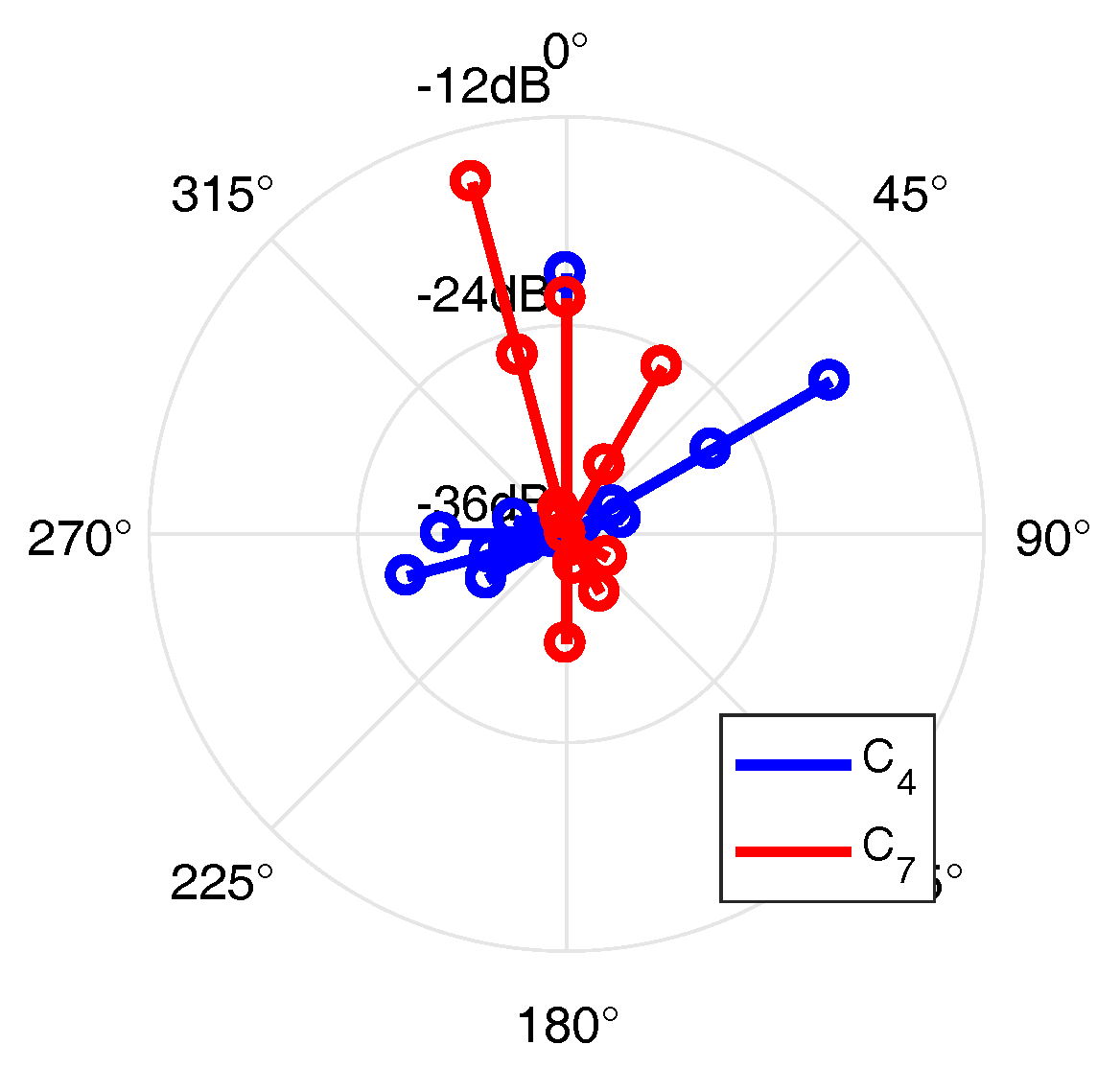
- C
- the angle of a beam pair: .
2.1. Experimental Setup
2.2. Influence of Beampattern Design
2.3. Influence of the Signal
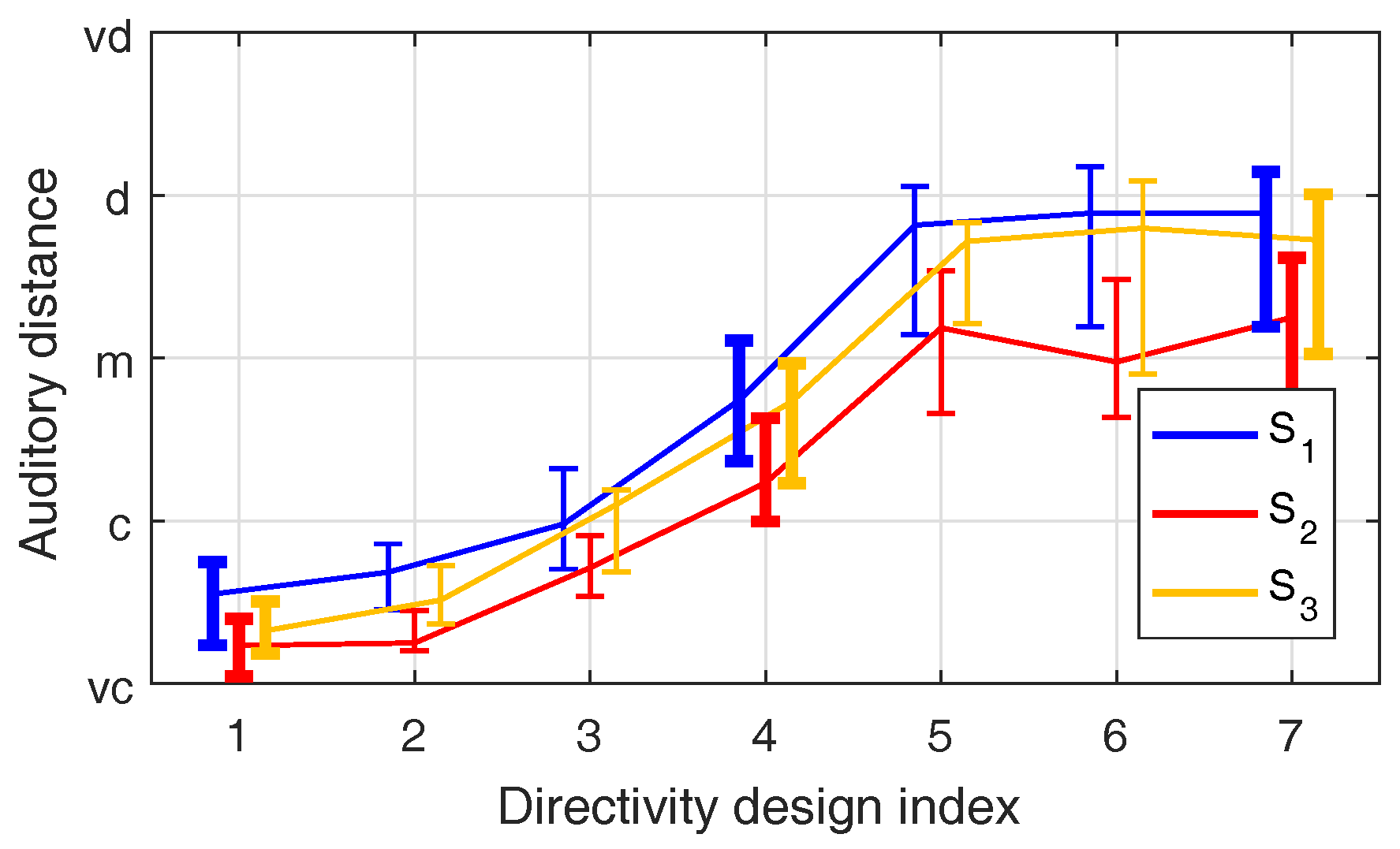
2.4. Influence of the Room
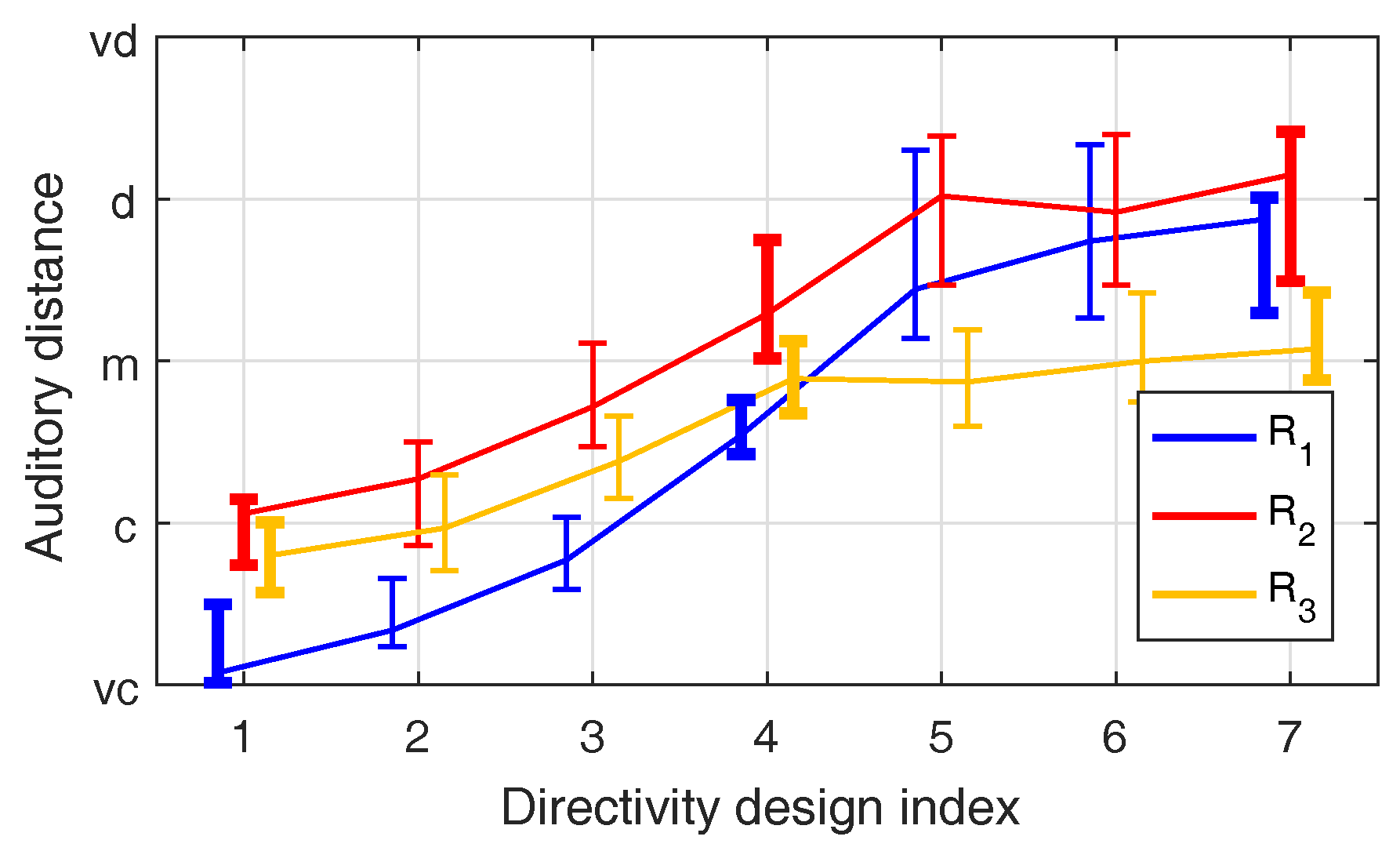
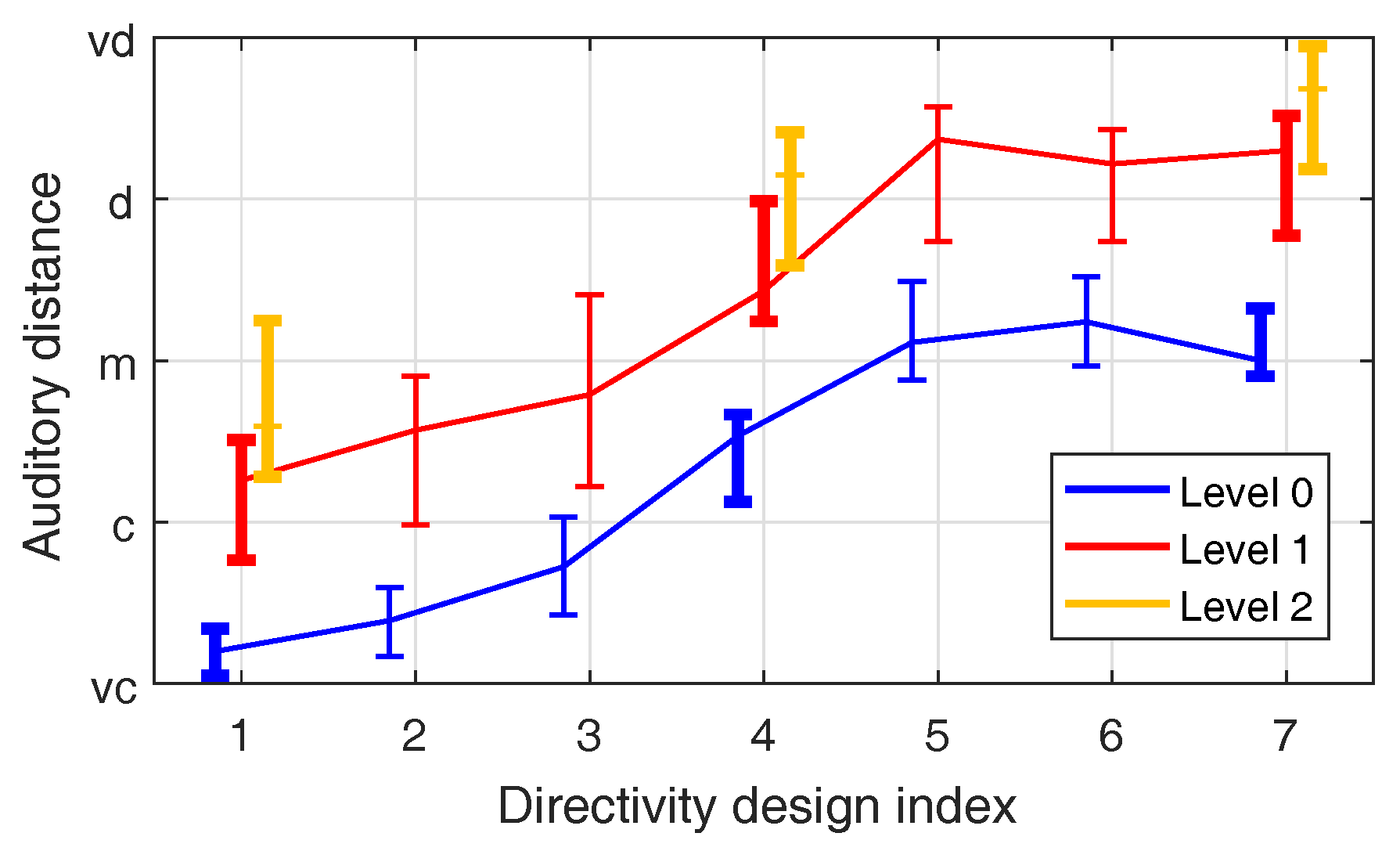
2.5. Influence of Single-Channel Reverberation
3. Modeling the Auditory Distance
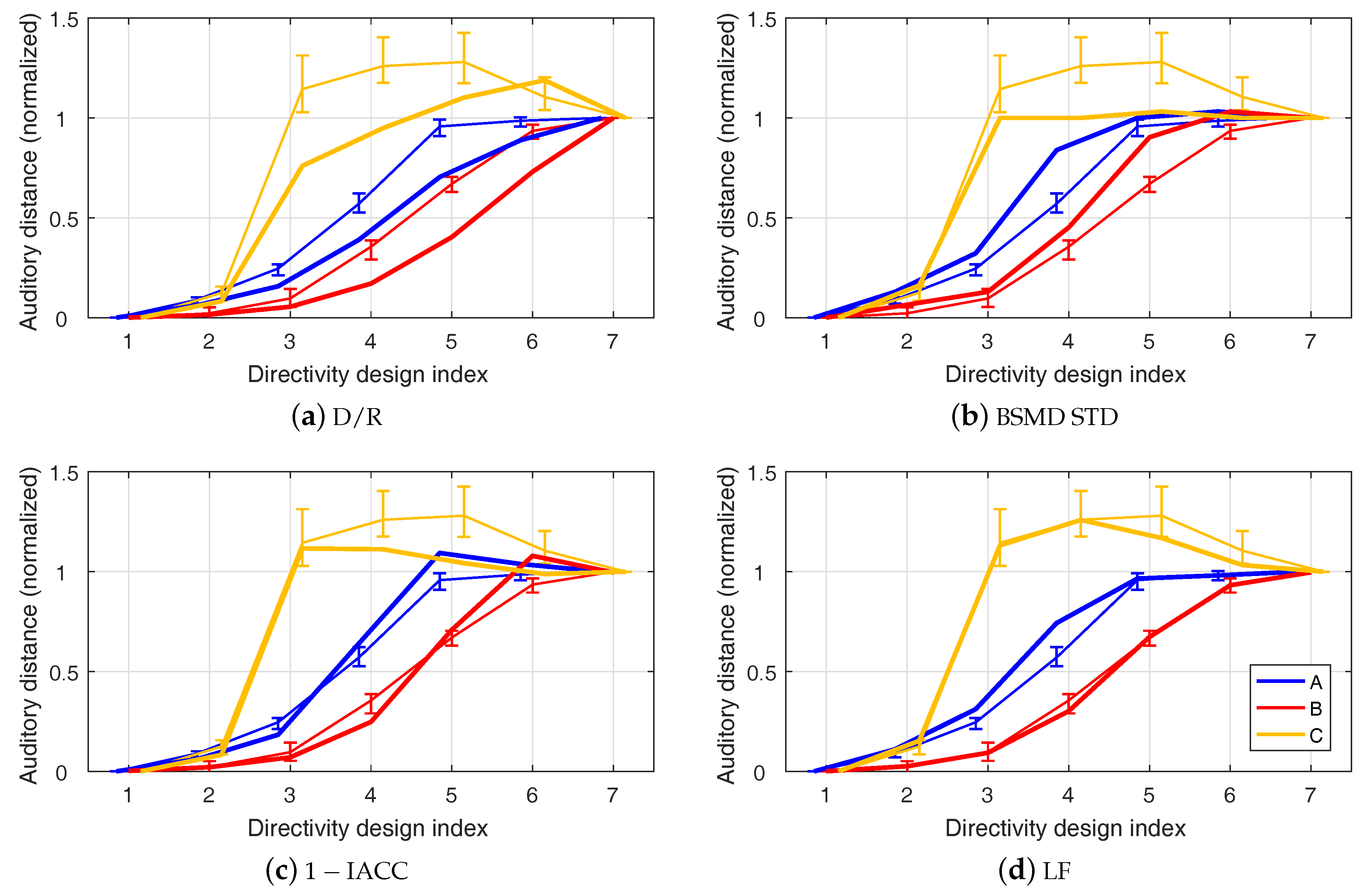
3.1. Direct-To-Reverberant Energy Ratio
3.2. Binaural Spectral Magnitude Difference Standard Deviation
3.3. Inter-Aural Cross Correlation Coefficient
3.4. Lateral Energy Fraction
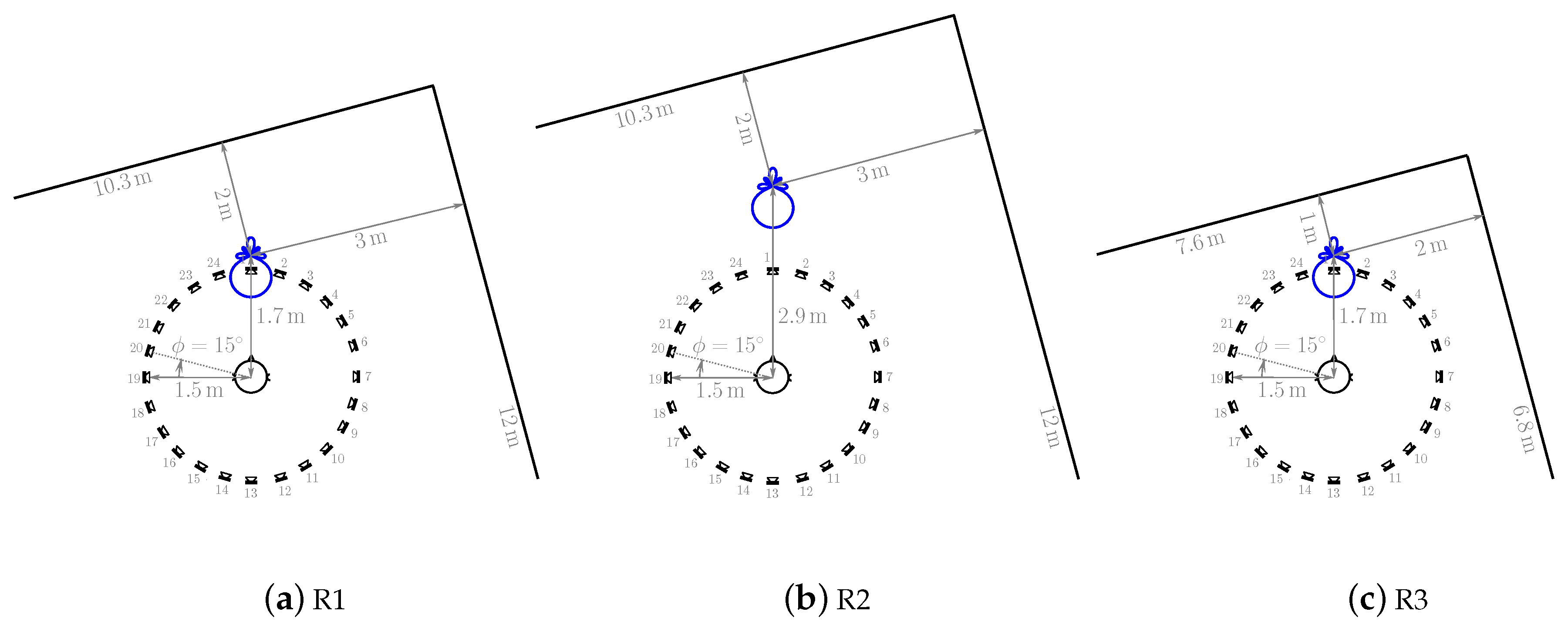
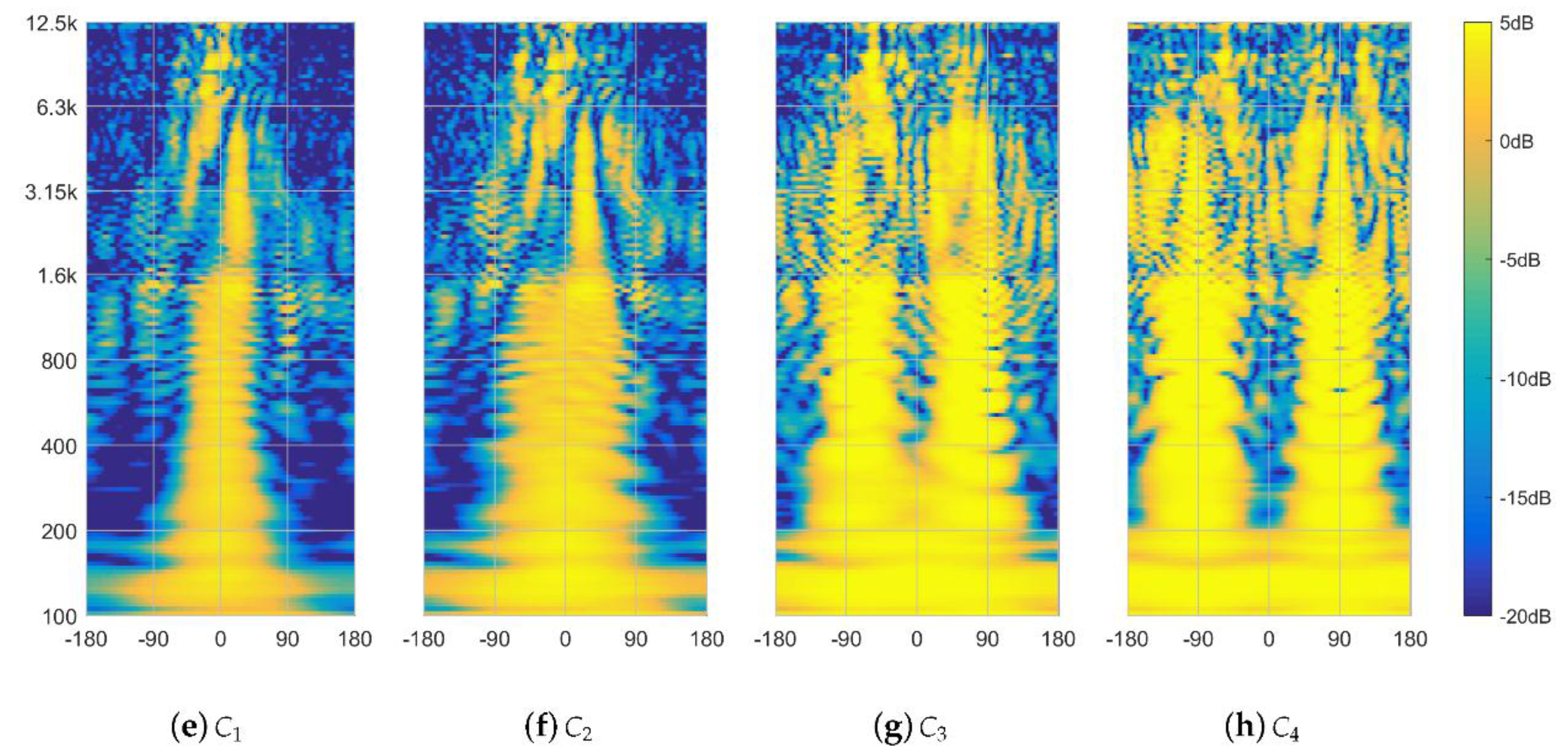
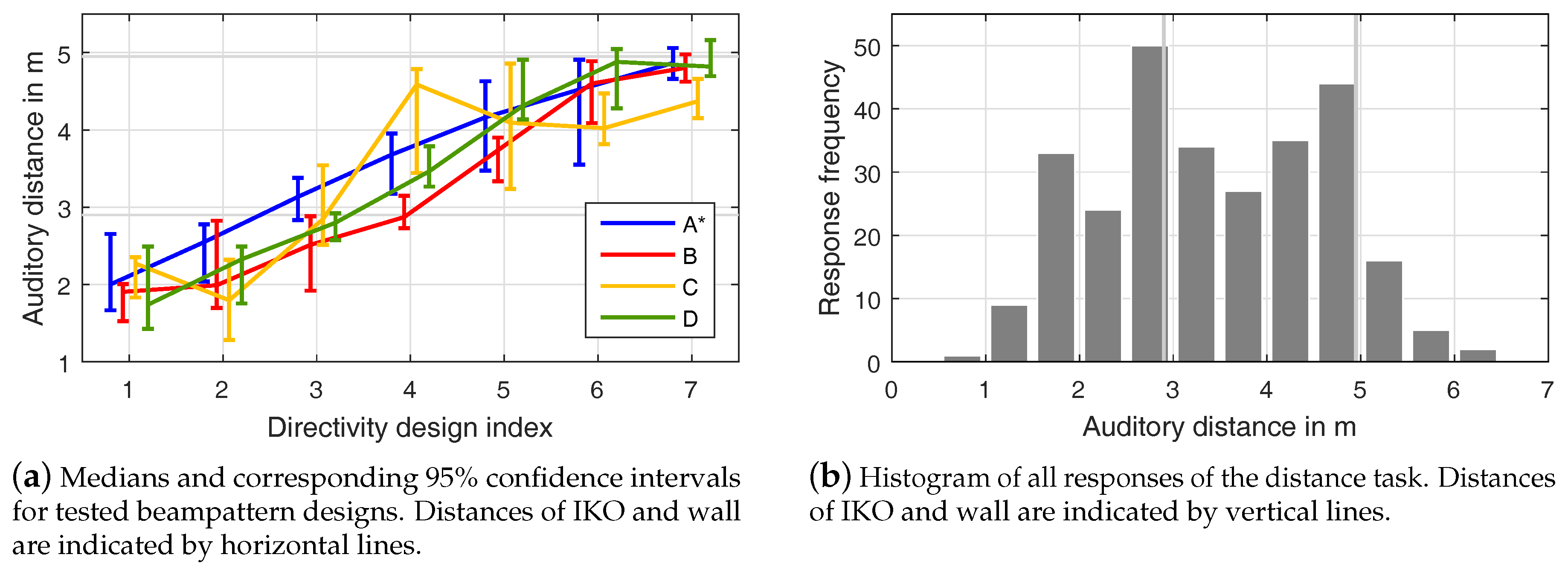
4. Experiment II: Directivity-Controlled Auditory Distance in a Real Room
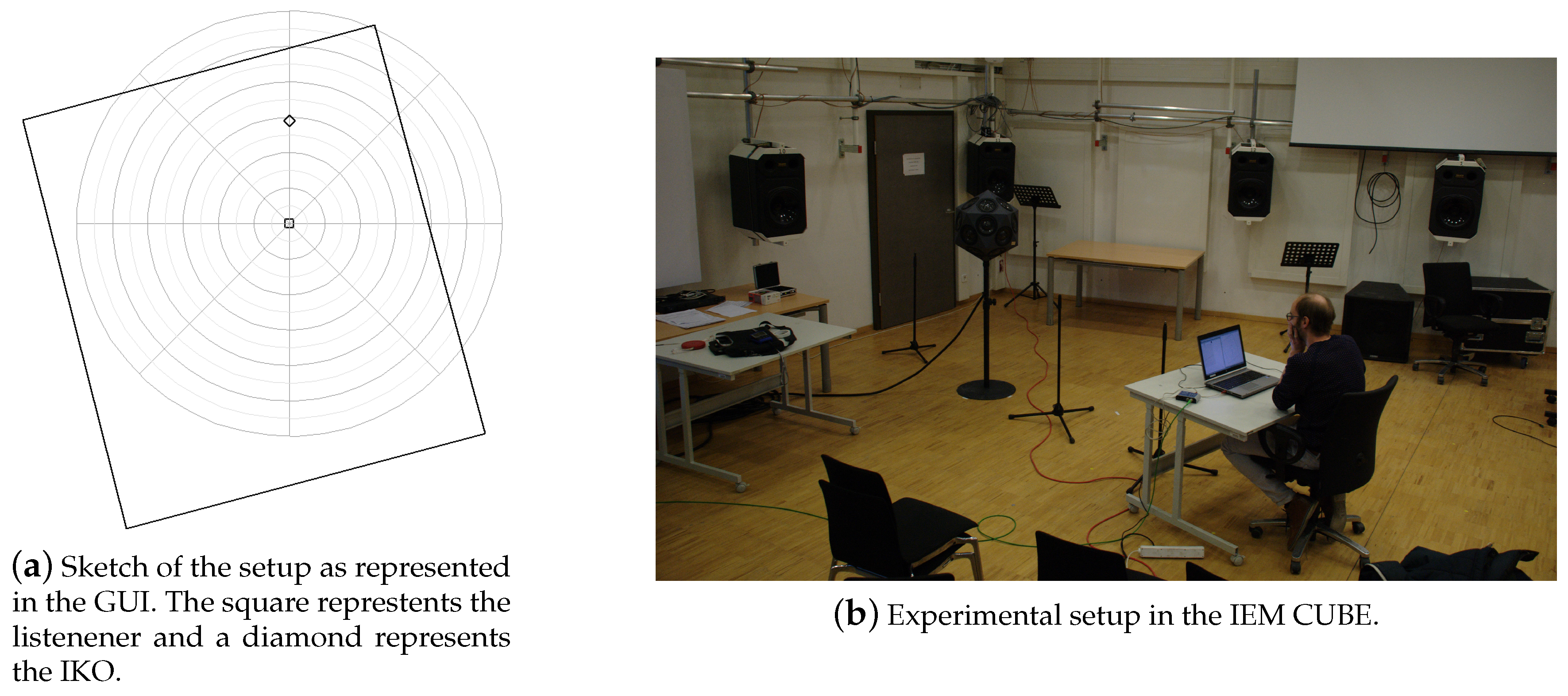
4.1. Experimental Setup
4.2. Auditory Distance
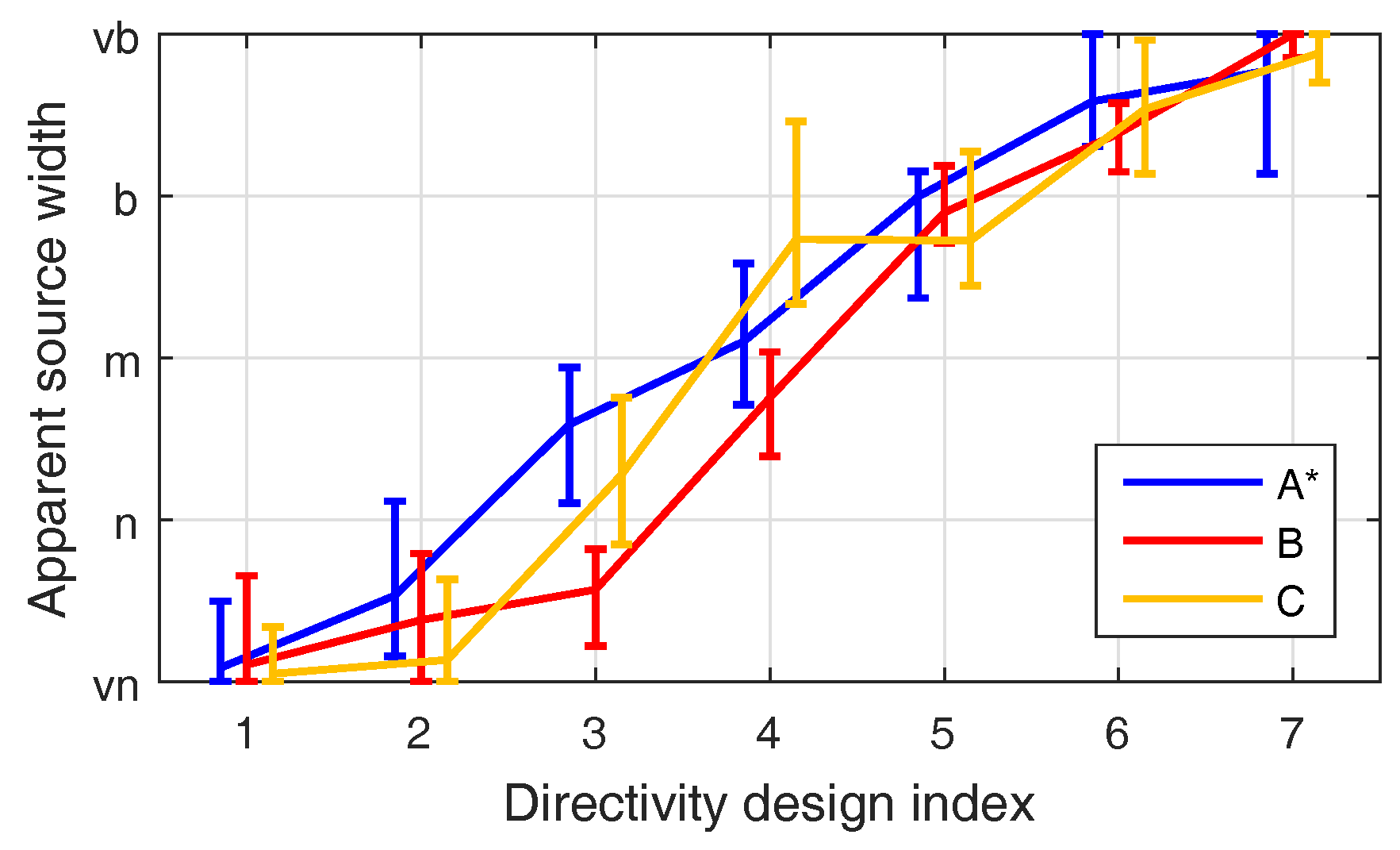
4.3. Apparent Source Width
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mason, R. How Important Is Accurate Localization in Reproduced Sound? In Proceedings of the 142th Convention of the Audio Engineering Society, Berlin, Germany, 20–23 May 2017. [Google Scholar]
- Zahorik, P.; Brungart, D.S.; Bronkhorst, A.W. Auditory distance perception in humans: A summary of past and present research. Acta Acust. United Acust. 2005, 91, 409–420. [Google Scholar]
- Kolarik, A.J.; Moore, B.C.J.; Zahorik, P.; Cirstea, S.; Pardhan, S. Auditory distance perception in humans: A review of cues, development, neuronal bases, and effects of sensory loss. Atten. Percept. Psychophys. 2016, 78, 373–395. [Google Scholar] [CrossRef] [PubMed]
- Mershon, D.H.; King, L.E. Intensity and reverberation as factors in the auditory perception of egocentric distance. Percept. Psychophys. 1975, 18, 409–415. [Google Scholar] [CrossRef]
- Zahorik, P. Assessing auditory distance perception using virtual acoustics. J. Acoust. Soc. Am. 2002, 111, 1832–1846. [Google Scholar] [CrossRef] [PubMed]
- Larsen, E.; Iyer, N.; Lansing, C.R.; Feng, A.S. On the minimum audible difference in direct-to-reverberant energy ratio. J. Acoust. Soc. Am. 2008, 124, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Kolarik, A.; Cirstea, S.; Pardhan, S. Discrimination of virtual auditory distance using level and direct-to-reverberant ratio cues. J. Acoust. Soc. Am. 2013, 134, 3395–3398. [Google Scholar] [CrossRef] [PubMed]
- Laitinen, M.V.; Politis, A.; Huhtakallio, I.; Pulkki, V. Controlling the perceived distance of an auditory object by manipulation of loudspeaker directivity. J. Acoust. Soc. Am. 2015, 137, EL462–EL468. [Google Scholar] [CrossRef] [PubMed]
- Wendt, F.; Frank, M.; Zotter, F.; Höldrich, R. Directivity patterns controlling the auditory source distance. In Proceedings of the 19th International Conference on Digital Audio Effects (DAFx-16), Brno, Czech Republic, 5–9 September 2016; pp. 295–300. [Google Scholar]
- Zotter, F.; Zaunschirm, M.; Frank, M.; Kronlachner, M. A Beamformer to Play with Wall Reflections: The Icosahedral Loudspeaker. Comput. Music J. (Accept. Publ.) 2017, 41. [Google Scholar]
- Daniel, J. Représentation de Champs Acoustiques, Application à la Transmission et à la Reproduction de Scènes Sonores Complexes Dans un Contexte Multimédia. Ph.D. Thesis, Université Paris 6, Paris, France, 2001. [Google Scholar]
- Zotter, F.; Frank, M. All-round ambisonic panning and decoding. AES J. Audio Eng. Soc. 2012, 60, 807–820. [Google Scholar]
- Allen, J.B.; Berkley, D.A. Image Method for Efficiently Simulating Small-room Acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Wabnitz, A.; Epain, N.; Jin, C.T.; Van Schaik, A. Room acoustics simulation for multichannel microphone arrays. In Proceedings of the International Symposium on Room Acoustics, Melbourne, Australia, 29–31 August 2010. [Google Scholar]
- Tervo, S.; Pätynen, J.; Kuusinen, A.; Lokki, T. Spatial decomposition method for room impulse responses. J. Audio Eng. Soc. 2013, 61, 17–28. [Google Scholar]
- Guski, R. Auditory localization: Effects of reflecting surfaces. Perception 1990, 19, 819–830. [Google Scholar] [CrossRef] [PubMed]
- Wendt, F.; Sharma, G.K.; Frank, M.; Zotter, F.; Höldrich, R. Perception of Spatial Sound Phenomena Created by the Icosahedral Loudspeaker. Comput. Music J. 2017, 41, 76–88. [Google Scholar] [CrossRef]
- Zaunschirm, M.; Frank, M.; Zotter, F. An Interactive Virtual Icosahedral Loudspeaker Array. Fortschritte der Akusitk 2016, 1331–1334. [Google Scholar]
- Kohlrausch, A.; Kortekaas, R.; van der Heijden, M.; van de Par, S.; Oxenham, A.J.; Püschel, D. Detection of Tones in Low-noise Noise: Further Evidence for the Role of Envelope Fluctuations. Acta Acust. United Acust. 1997, 83, 659–669. [Google Scholar]
- Coleman, P. Dual Role of Frequency Spectrum in Determination of Auditory Distance. J. Acoust. Soc. Am. 1968, 44, 631–632. [Google Scholar] [CrossRef] [PubMed]
- Little, A.D.; Mershon, D.H.; Cox, P.H. Spectral content as a cue to perceived auditory distance. Perception 1992, 21, 405–416. [Google Scholar] [CrossRef] [PubMed]
- Georganti, E.; May, T.; Van De Par, S.; Mourjopoulos, J. Sound source distance estimation in rooms based on statistical properties of binaural signals. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1727–1741. [Google Scholar] [CrossRef]
- Marshall, A.H. A note on the importance of room cross-section in concert halls. J. Sound Vib. 1967, 5, 100–112. [Google Scholar] [CrossRef]
- Barron, M.; Marshall, A.H. Spatial impression due to early lateral reflections in concert halls: The derivation of a physical measure. J. Sound Vib. 1981, 77, 211–232. [Google Scholar] [CrossRef]
- Lösler, S. MIMO-Rekursivfilter für Kugelarrays. Master’s Thesis, University of Music and Performing Arts Graz, Graz, Austria, 2014. [Google Scholar]
- Zotter, F. Analysis and Synthesis of Sound-Radiation with Spherical Arrays. Ph.D. Thesis, University of Music and Performing Arts Graz, Graz, Austria, 2009. [Google Scholar]
- Kronlachner, M. Plug-in Suite for Mastering the Production and Playback in Surround Sound and Ambisonics. In Proceedings of the 136th Convention of the Audio Engineering Society, Berlin, Germany, 26–29 April 2014. [Google Scholar]
- Anderson, P.W.; Zahorik, P. Auditory/visual distance estimation: Accuracy and variability. Front. Psychol. 2014, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ernst, M.O.; Banks, M.S. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 2002, 415, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, C.; Mandelli, P.; Pulkki, V. Modeling the Perception of Audiovisual Distance: Bayesian Causal Inference and Other Models. PLoS ONE 2016, 11, e0165391. [Google Scholar]
- Lee, H. Apparent Source Width and Listener Envelopment in Relation to Source-Listener Distance. In Proceedings of the 52nd Audio Engineering Society Conference, Guildford, UK, 2–4 September 2013. [Google Scholar]
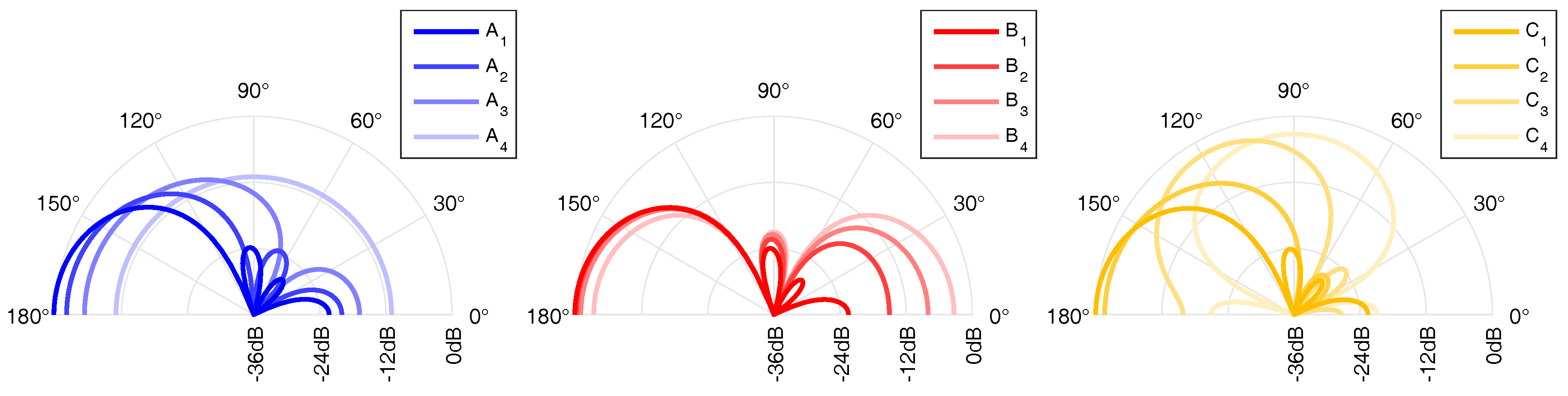

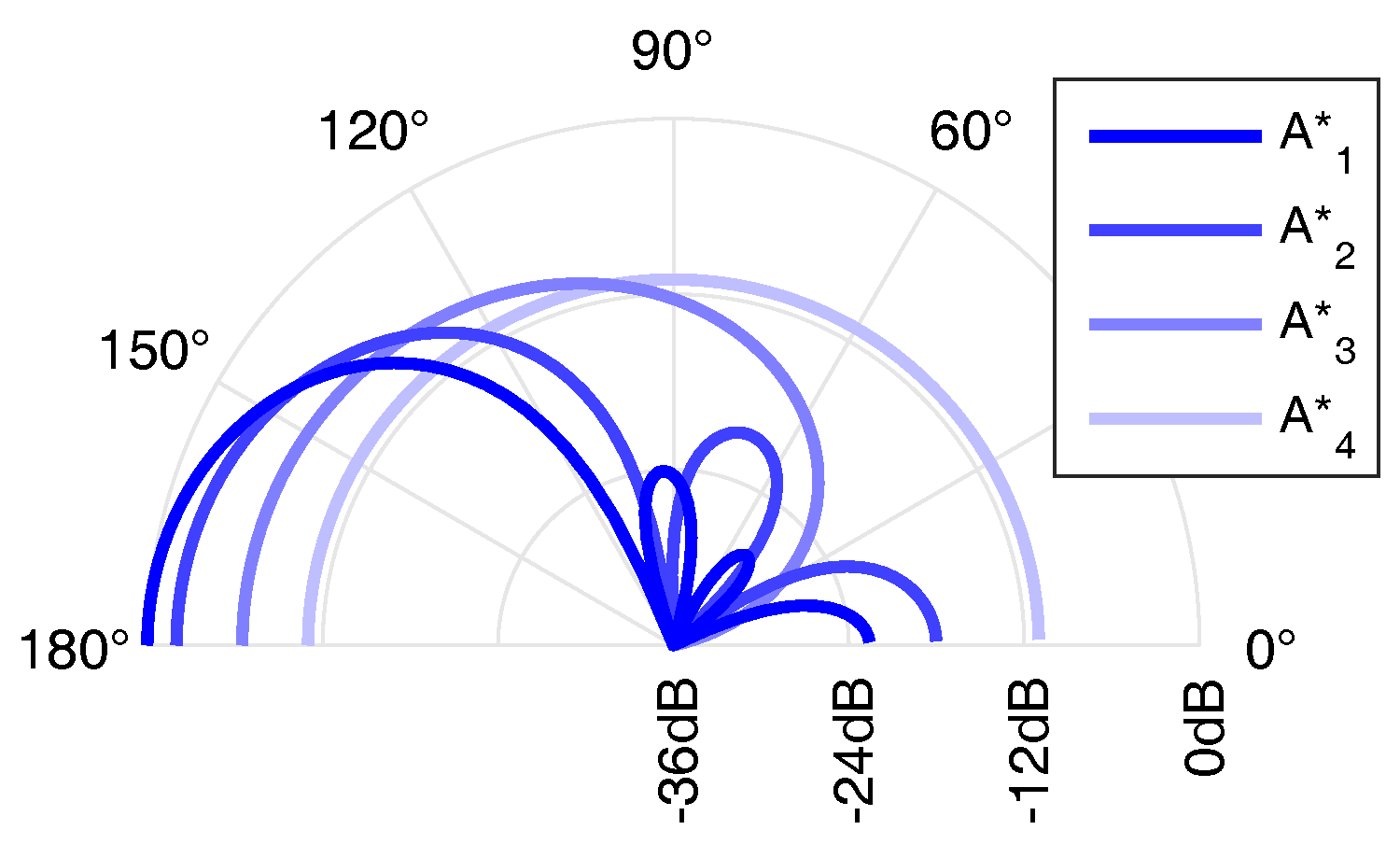
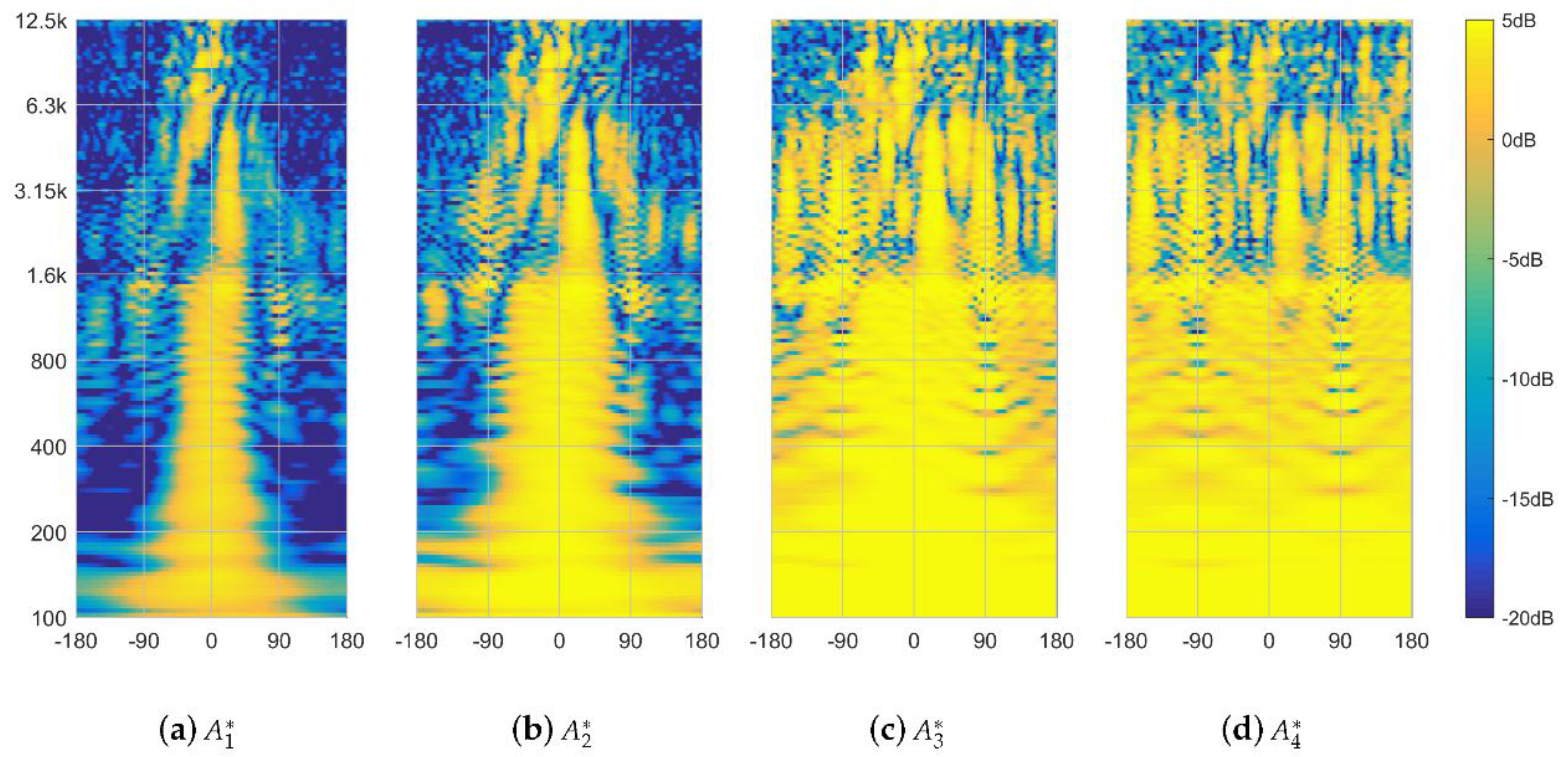
| A | 3rd-order max- beam to/off listener | |
| 2nd-order max- beam to/off listener | ||
| 1st-order max- beam to/off listener | ||
| omnidirectional beampattern | ||
| B | 3rd-order max- beams to and off listener linearly | |
| blended at dB | ||
| C | two 3rd-order max- beams horizontally arranged | |
| at with respect to the listener |
| room | IEM CUBE, | , | , | ||
| IEM CUBE, | , | , | |||
| IEM Lecture Room, | , | , | |||
| signal | female speech taken from Music for Archimedes, CD Bang and Olufsen 101 (1992) | ||||
| sequence of irregular artificial bursts | |||||
| speech-spectrum noise with increased kurtosis | |||||
| Set No. | Design | Index | Signal | Room | Reverb. Level |
|---|---|---|---|---|---|
| 1 | A | 0 | |||
| 2 | A | 0 | |||
| 3 | A | 0 | |||
| 4 | B | 0 | |||
| 5 | B | 0 | |||
| 6 | B | 0 | |||
| 7 | C | 0 | |||
| 8 | C | 0 | |||
| 9 | C | 0 | |||
| 10 | A | 0 | |||
| 11 | A | 0 | |||
| 12 | A | 1 | |||
| 13 | A | 0 | |||
| 14 | A | 0 | |||
| 15 | A |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wendt, F.; Zotter, F.; Frank, M.; Höldrich, R. Auditory Distance Control Using a Variable-Directivity Loudspeaker. Appl. Sci. 2017, 7, 666. https://doi.org/10.3390/app7070666
Wendt F, Zotter F, Frank M, Höldrich R. Auditory Distance Control Using a Variable-Directivity Loudspeaker. Applied Sciences. 2017; 7(7):666. https://doi.org/10.3390/app7070666
Chicago/Turabian StyleWendt, Florian, Franz Zotter, Matthias Frank, and Robert Höldrich. 2017. "Auditory Distance Control Using a Variable-Directivity Loudspeaker" Applied Sciences 7, no. 7: 666. https://doi.org/10.3390/app7070666
APA StyleWendt, F., Zotter, F., Frank, M., & Höldrich, R. (2017). Auditory Distance Control Using a Variable-Directivity Loudspeaker. Applied Sciences, 7(7), 666. https://doi.org/10.3390/app7070666






