Abstract
Relative wavelet energy entropy (RWEE) is proposed to detect and quantify damage to hysteretic dampers used for the passive seismic control of building structures. Hysteretic dampers have the role of dissipating most of the energy input of an earthquake. Minor or moderate earthquakes do not exhaust the energy dissipation capacity of the dampers, yet they damage them. For this reason, continuous or periodic damper-health evaluation is required to decide if they need to be replaced. Such evaluation calls for the application of efficient structural health monitoring techniques (SHM). This paper focuses on the well-known vibration technique, which is applied to a particular type of hysteretic damper called Web Plastifying Damper (WPD), patented by the University of Granada. Vibration signals, properly recorded by piezoelectric sensors attached around the damaged area of the dampers, are decomposed by means of wavelet packet analysis. Then, the relative wavelet energy entropy of these decompositions is used to calculate the proposed index. Validation of RWEE for this particular application involved dampers installed in two different specimens of reinforced concrete structures subjected to earthquake sequences of increasing intensity. When compared with a well-established mechanical energy-based damage index, results demonstrate that RWEE is a successful and low-cost technique for reliable in-situ monitoring of dampers.
1. Introduction
The passive control of structures subjected to seismic actions through the use of energy dissipating devices (EDD) is a common solution in earthquake-prone areas. A typical building structure with passive control systems consists of a main frame that works in conjunction with special elements called EDDs or simply dampers, whose main role is to dissipate most of the energy input from an earthquake. Among the different types of EDDs available, the so-called hysteretic dampers are probably the most widely used due to their advantages in terms of robustness, reliability and cost. The source of energy dissipation through hysteretic dampers is the plastic deformation of metals (typically steel). In deciding whether or not to replace the EDDs by new ones, a key factor is the non-destructive evaluation of the level of damage to the dampers after a seismic event. This decision has important economic and safety-related consequences, thus making periodic inspection a very relevant issue. Hysteretic dampers do not necessarily need to be replaced after minor/moderate damage, or even after a large earthquake, because they have a high energy dissipation capacity. Hence, the development of reliable Non-Destructive Testing (NDT) techniques for inspection is essential for determining the remaining life of the dampers.
Visual inspection is not applicable in such cases, because damage is not visible until the element is on the brim of failure. Past research has shown that the level of damage and the proximity to failure of hysteretic dampers subjected to arbitrarily cyclic loading can be reliably estimated by decomposing the force-displacement curves endured by the damper into the so-called skeleton and Bauschinger parts [1]. This decomposition is the basis of a mechanical damage index called ID that has been extensively validated with static and dynamic tests. However, measuring the force and the displacement of dampers during operation involves very expensive and sophisticated instrumentation, which is hardly justified when the probability of an earthquake occurring is very low.
A cheaper and more practical alternative is to conduct simple vibration tests on the dampers by means of low-cost piezoceramic sensors permanently attached to the damper [2,3,4,5]. Damage due to plastic deformations induces changes in the vibration response (resonance frequencies, modes, damping coefficients, etc.) that can be evaluated via proper processing of the signals captured by piezoceramic sensors. Although many papers in the literature deal with time vibration series analysis for damage detection in structures and materials [6,7,8,9,10,11,12,13], the suggestion of its application to hysteretic dampers is an original contribution by our research group.
More concretely, this paper proposes the use of Relative Wavelet Energy Entropy (RWEE) to evaluate damage to hysteretic dampers subjected to seismic events. This index combines wavelet transform with information entropy, taking the advantages of both techniques to obtain a reliable quantification of the damage level of the dampers. Firstly, the wavelet package decomposition of the vibration signals is carried out. Wavelet transform of vibration signals has been widely used for structural damage detection [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Basically, by means of the wavelet decomposition of the time-domain signal on the time-frequency domain, it is possible to observe dominant modes of variability of the signal (frequencies) and how these modes vary over time. Previous results have proven that the energy of the decomposed wavelet vibrational signals using the wavelet packet (wavelet energy) shows higher sensitivity to minor damage [31,32,33,34]. Secondly, Shannon entropy [35,36,37,38] is applied to calculate the wavelet entropy of the vibration signals [33,39,40,41,42,43,44,45].
Wavelet entropy (WE) represents the degree of order/disorder of the vibration signals, hence providing very useful information about the underlying mechanical process associated with them. The level of damage can be derived by quantifying changes in the wavelet entropy of the vibration signals before (baseline phase) and after (inspection phase) damage. The relative wavelet entropy (RWE) provides a measure of the degree of similarity between two probability distributions. If the relative wavelet energy distributions are almost the same during the baseline and inspection phases, the RWE will be close to zero, and a non-damage state will be assigned to the damper. If the damper is damaged, the distribution of vibration responses during the baseline and inspection phases will be changed, and RWE will be not zero. This idea is the foundation for the formulation of the damage index RWEE.
The RWEE index was validated experimentally with dynamic shaking table tests conducted on several Web Plastifying Dampers (WPDs). The results presented here show a very good correlation between the RWEE index and the established mechanical damage index ID. In other words, we demonstrate that the RWEE index can reliably evaluate the level of damage on dampers without the need to know the load-displacement relationship endured by the damper, and thus without resorting to the cumbersome and expensive instrumentation required to obtain the ID.
2. Web Plastifying Dampers (WPD)
The WPD is a particular type of hysteretic damper developed and patented by the authors [46]. It is based on the properties of deformation and hysteresis of steel (Figure 1a). Basically, it consists of several short segments of double-T structural shapes (I or H-profiles, hereafter referred to as I-sections) that are assembled on two auxiliary bars also made of steel. The I-sections are the dissipative part of the damper, while the bars work as auxiliary elements that connect the I-section steel segments with the main frame. Energy dissipation on the damper occurs when the web of the I-section undergoes out-of-plane plastic deformation under imposed relative displacements between the flanges, as shown in Figure 2.
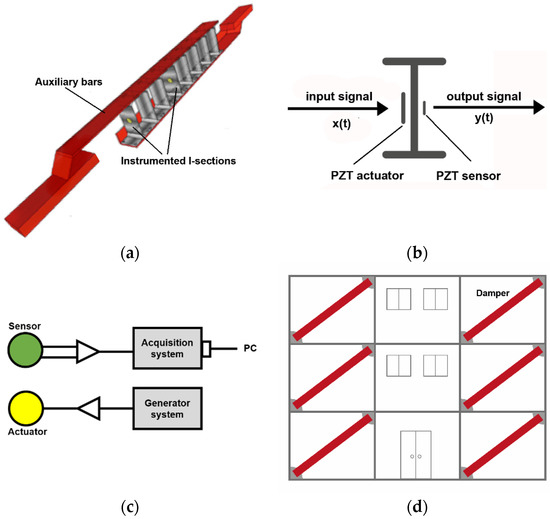
Figure 1.
(a) Instrumented I-sections in a particular Web Plastifying Damper (WPD) damper; (b) I-section instrumented with two piezoelectric transducers (PZT), one acting as actuator (input signal) and one acting as sensor (output signal); (c) Connection of the PZT transducers to the electronic system; (d) Installation of the dampers in the building.
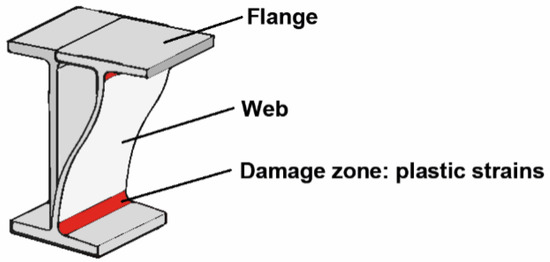
Figure 2.
Deformation of an I-section segment of a WPD.
3. Description of the Vibration Test on the Dampers
This section provides precise information on how the signals used for health monitoring the dampers were obtained. With this information the vibration test can be replicated. Vibration tests consisted of induced vibrations, x(t), conducted on each instrumented I-section by means of the piezoelectric transducer (PZT) actuator attached to the center of the web, and measuring the signal response, y(t), through the PZT sensor adhered on the opposite side of the I-section web as shown in Figure 1. It also shows a general scheme of a building with dampers installed in it and a particular WPD damper with several I-sections instrumented with PZT transducers connected to the electronic equipment for online and real-time inspection (Structural Health Monitoring of the Dampers). The I-sections were excited with random white noise generated by CoCo80 equipment (CRYSTAL Instruments, Santa Clara, CA, USA) and an EPA104 piezoelectric amplifier (Piezo Systems, Woburn, MA, USA) that provided a gain of 20. The level of deformation induced by the vibration tests in the web of the damper was very low: strains were less than 2 µmm/mm. Each vibration test was carried out four times with different white noise trials. The duration of each test was 20 s and the sampling rate of signals was 65,536 Hz. The response signal of the I-sections was recorded by two PULSE 3560-B Brüel & Kjær systems (Nærum, Denmark). Figure 3 shows a typical response signal obtained from the vibration tests. All electronic devices were properly connected to the grounding system; connections were made so that the measurement system would achieve a good performance against the electrical and environmental noises. In this way, a robust measurement system was obtained, with controlled noise conditions and high quality vibration signals. Analysis of the output signal shows that it is affected by the level of damage in the damper, as shown in the following sections.
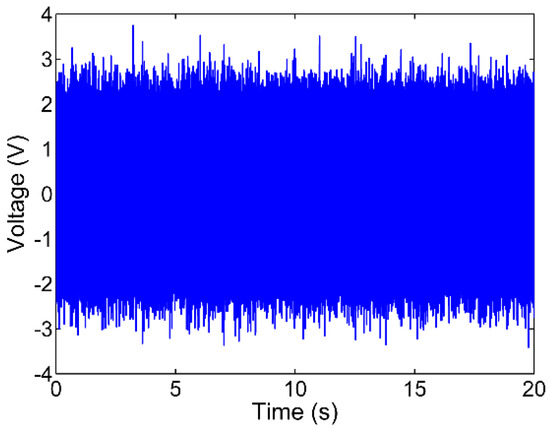
Figure 3.
Response signal obtained from the vibration tests.
4. Vibration Data Analysis: Definition of the RWEE Damage Index
4.1. Wavelet Packet Decomposition and Wavelet Energy
Wavelet Packet Transform (WPT) is one extension of the Wavelet Transform (WT) to decompose a signal repeatedly into successive low and high frequency components [47,48]. A wavelet packet is a family of scaling functions and wavelet functions constructed by following a binary tree of dilations/translations. The wavelet packet, , is a function of three indices, where i, j and k are integers representing the modulation, the scale and the translation parameters, respectively. It can be written as
where the wavelets are obtained from the following recursive relationships
h(k) and g(k) being quadrative mirror filters associated with the scaling function and the mother wavelet function, respectively [49,50]. In the two above equations, is the mother wavelet function. There are quite a few mother wavelets reported in the literature, developed to satisfy some important properties such as invertibility or orthogonality [51,52]. Daubechies [50] developed a family of mother wavelets based on the solution of a dilation equation. In the present work, among several alternatives, Daubechies functions of the order 5 (db5) were selected as mother wavelets on the basis of trial and error tests.
The analytical procedure starts by computing the wavelet packet decomposition of the monitored vibration signal at level N using a given wavelet. This means there are 2N components at the Nth level, providing flexibility for choosing the way to encode the original signal, so that the reconstruction error is minimal. A schematic representation of the WPT of a time-domain signal f(t) up to the 3rd level of decomposition is presented in Figure 4; it can be obtained, for instance, by summing the signal components , , and . The approximations correspond to the low scale (low frequency components) of the signal, while the details correspond to the high scale (high frequency components) of the signal.
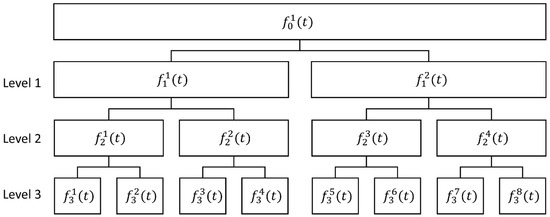
Figure 4.
Schematic representation of three Wavelet Packet Transform (WPT) levels of a signal.
The wavelet packet component signal can be expressed by a linear combination of wavelet packet functions as follows
and the wavelet packet coefficients can be obtained from
Each component in the WPT tree can be viewed as the output of a filter tuned to a particular basis function, so that the whole tree can be regarded as a filter bank. At the top of the WPT tree (lower level), the WPT yields good resolution in the time domain but poor resolution in the frequency domain. At the bottom of the WPT tree (higher level), the WPT results are in good resolution in the frequency domain but in poor resolution in the time domain.
The RWEE index is based on the energy evaluation of the WPT. The energy of each sub-signal is calculated according to the following equation
where i is the number of the node and j is the level of decomposition.
4.2. Wavelet Entropy (WE)
Wavelet entropy is a combination of wavelet decomposition and entropy statistics theories. This concept presents the advantages of multi-resolution analysis and complexity evaluation for time-varying signals, which means that the macro and micro aspects of some special signals could be researched in the time-frequency domain [48]. For this reason, wavelet entropy has gradually been adopted for a great variety of applications in medicine, machinery vibration detection, and system fault diagnosis [35,36,40,41].
Damage is shown as a disorder at the structural response signal. One natural approximation to quantify the order level of a complex signal is through spectral entropy or Shannon entropy, defined from the Fourier power spectrum [37].
Shannon entropy can be calculated using the formula
where is the probability that a system is in the state i and N is the total number of states.
Wavelet entropy is used to characterize the degree of order/disorder associated with a signal of multifrequency response. Wavelet energy entropy is based on the relationship between the concept of entropy and the energy obtained from each frequency band of the wavelet decomposition, as
where is the energy of each node and is the sum of the energy of all considered nodes.
4.3. Relative Wavelet Entropy (RWE): RWEE Damage Index Definition
Results show that entropy based on the wavelet transform is a good candidate to characterize damage because of its sensitivity to local structural damage [37]. That is, the wavelet entropy changes when the structure is damaged. The RWE is known to be associated with different frequency bands of signals obtained from the baseline or inspection phases, thereby allowing for detection of changes in the level of damage of the I-section. The relative wavelet energy entropy (RWEE) is based on this concept together with entropy, i.e.,
where and are the vectors that relate the wavelet energy of each node with respect to the total energy of the considered nodes of the vibration signals recorded in the inspection phase and baseline phase, respectively. The vectors and are defined as
If the evaluated I-section is undamaged or has a very low level of damage, the value of RWEE will be close to zero. If damage is substantial, the RWEE value will be farther from null.
In order to calculate the RWEE damage index, the following steps are taken:
- Firstly, normalization and scaling must be applied to counteract different excitation levels and environmental conditions and to compensate the off-set and amplitude variability among signals. This normalization is carried out as follows:where is the normalized signal, is the recorded signal and and are the mean value and the standard deviation of the , respectively.
- The normalized signal is decomposed into multiple sub-signals in various frequency bands using the WPT. Let denote the normalized response signal shown in the first step. Through trial and error tests, it was found that the optimum level of decomposition is 7; thus, 27 (128 nodes) is the number of sub-signals to be obtained in the proposed procedure.
- The energy of each sub-signal is calculated according to the following equationproviding the energy for the undamaged I-section and energy for the inspected I-section, where i is the number of the node and j is the level of decomposition.Steps 1, 2 and 3 must be carried out in both baseline and inspection phases.
- Finally, the RWEE index is calculated using Equation (14), where is the energy of each sub-signal on the level of decomposition j, and is the sum of the energy of the all sub-signals of level j, both calculated for the inspection phase. The same parameters calculated for the baseline inspection are and , respectively. N is the total number of sub-signals, in the present study 128.The RWEE index is obtained for the whole signal, i.e., considering all frequencies of the signals.
5. Specimen and Experiment Descriptions
Two reinforced concrete (RC) prototype structures having three stories and 3 × 3 bays were designed to sustain the gravity loads established under current codes in Spain. One prototype consisted of a frame structure and the other a flat-slab structure. Each prototype was equipped with WPDs designed to sustain the seismic loads prescribed by the Spanish Seismic Code [53]. From each prototype, a test model that represented a portion of the prototype structure was defined and constructed by applying a scaling factor of 2/5 to the geometry. The test model that represented the frame structure is called specimen FD and it is shown in Figure 5a. The test model that represents the flat-slab structure is named specimen SD and is shown in Figure 5b. Each test model has two levels; the lowest level will be referred to as ground floor and the highest one as first floor herein. A detailed description of the test structures can be found in [54,55]. Specimen FD was equipped with four WPDs, two on the ground floor and two on the first floor. Specimen SD was equipped with two WPDs, one on each floor.

Figure 5.
Overview of test models and set-up on the shaking table. (a) Frame with dampers (FD) specimen; (b) Flat-slab with dampers (SD) specimen.
Both test models were mounted on the uniaxial 3 × 3 m2 shaking table of the University of Granada, as shown in Figure 5, and subjected to successive seismic simulations of increasing amplitude. Each specimen underwent one-dimensional dynamic shaking table tests. The acceleration was applied to the table in a horizontal direction, parallel to a plane containing the axis of the dampers and the axis of one (in the case of specimen SD) or two (for specimen FD) columns. Before the test, steel blocks were attached at the top of the RC slab and at the top of the columns of the second story to represent the gravity loads that act on the floors and also to satisfy similitude requirements between prototype and specimen. Pin joint connections were used at the top of the half-columns in the second story, and at the ends of the half-beams of the first floor. The vertical movements of the ends of the half-beams of the first floor were prevented using pin-ended steel bars that connected the ends of the beams with the steel plates on the top of the specimen. The total mass of the specimen (including the additional masses) was 12,450 kg. The tests were conducted controlling the table by a real-time, uniaxial, digital controller able to provide three-variable closed loop control along with adaptive control. Moreover, the tests were conducted in the acceleration control mode in order to accurately reproduce the desired acceleration record in the table. The lateral displacements induced in the test model during each simulation imposed forced axial deformations on the dampers that damaged the I-section steel segments. In each seismic simulation, the shaking table reproduced the ground motion acceleration recorded at Calitri during the Campano Lucano earthquake (1980), scaled in amplitude to different levels. The scaling factors applied to the test model FD were 100%, 200%, 300% and 350% times the acceleration of the original record, and the corresponding peak ground accelerations were 0.16 g, 0.31 g, 0.47 g and 0.54 g (here, g is the acceleration of gravity). The respective levels of damage to the WPDs at the end of each seismic simulation will hereafter be identified as d0, d1, d2 and d3. The scaling factors applied to test model SD were 100%, 200%, 300%, 400%, 500% and 600% times the acceleration of the original record, and the corresponding levels of damage will be identified as d0, d1, d2, d3, d4 and d5 hereafter. The test models and the dampers were instrumented with displacement transducers, strain gauges and accelerometers. For illustrative purposes, Figure 6 shows the histories of acceleration applied to specimens FD and SD.
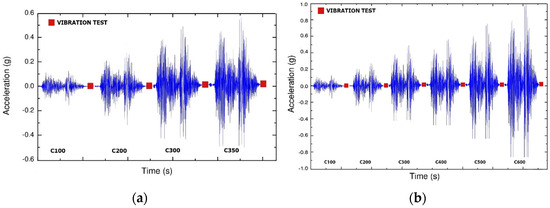
Figure 6.
Accelerations of the seismic simulations applied to the structures FD (a) and SD (b).
Four dampers were installed on the FD specimen, which consisted of two frames, each having two dampers, on the ground and first floors. Dampers on the ground floor had 10 I-sections, while dampers on the first floor had eight sections. To save time and cost, only six I-sections were instrumented with piezoelectric sensors. Four of them corresponded to the dampers of one frame (two on each floor) and the other two corresponded to the dampers of the other frame (one on each floor).
Specimen SD had only two dampers, one on the ground floor (with 20 I-sections) and one on the first floor (with 15 I-sections). Four I-sections of each damper were instrumented with piezoelectric transducers, two around the center and two around the ends of the dampers.
In this paper, for the sake of brevity, we present only the results corresponding to two I-sections on each floor for both specimens, i.e., four I-sections for each specimen (FD and SD). The values of the mechanical damage index at the end of each seismic simulation are shown in Table 1. They were calculated following [46]. The index ID measures the level of damage between 0 (no damage) and 1 (imminent failure) and its accuracy has been verified experimentally through dynamic real-time shaking table tests [46]. To calculate ID, first the curve that relates the axial force N endured by the damper with the axial relative displacement of its ends ∆ measured during the tests is split into the so-called “skeleton part” and “Bauschinger part”. To construct the skeleton part in each domain of loading, the segments of the N-∆ curve that exceed the load level attained by the preceding cycle of deformation in the same domain of loading are connected sequentially. The segments of the N-∆ curves that do not satisfy the above condition are classified as segments of the Bauschinger part. Next, the index ID is obtained from the energy dissipated by the damper in each part and in each loading domain. A more detailed explanation of this decomposition and the precise equations to obtain ID can be found in reference [46]. Note that although the ID index will be the same for all the I-sections of one particular damper (it evaluates damage of the whole damper), the RWEE index will be different, because vibration tests are carried out for each I-section and its particular level of damage. For statistical reasons, each vibration test—conducted before and after seismic simulations—was repeated four times and the average data were used.

Table 1.
Values of index at different levels of damage to the WPDs.
6. Results
Figure 7 and Figure 8 show the wavelet energy as a function of frequency for one I-section of the ground floor of specimens FD and SD, respectively. The baseline values for calculation of the RWEE were considered to be the C100 values, after seismic simulation applied 100% times the acceleration of the original earthquake. Peaks of this plot correspond with the natural frequencies of the I-sections. Few differences are visually observed as the level of damage of the damper increases, although some changes are perceived around the resonance at 25 kHz, approximately. For a better view, the Figure also shows a zoomed in version of Figure 7 and Figure 8 around this resonance. Evident in this case is a clear increase of the wavelet energy magnitude as the damage level increases. Damage to the I-sections produces a change in their mechanical properties, in turn producing a change in the vibrational response. It is very well known that as the order of the resonance frequency increases, the change in the vibrational response becomes greater. This is why the differences are more evident around 25 kHz.
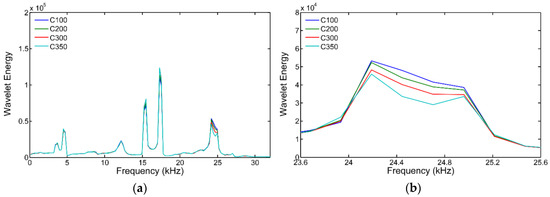
Figure 7.
Wavelet energy of one I-section of the ground floor of specimen FD. (a) Complete frequency range; (b) Zoom around the 25 kHz natural frequency.
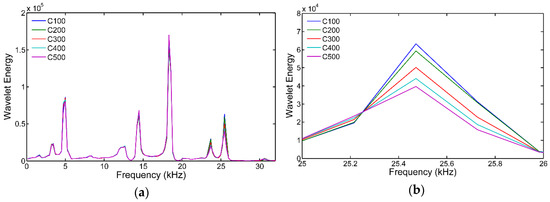
Figure 8.
Wavelet energy of one I-section of the ground floor of specimen SD. (a) Complete frequency range; (b) Zoom around the 25 kHz natural frequency.
Given the wavelet energy, the WE and the damage index RWEE were calculated as explained in Section 4. In order to establish the reliability of the proposed index, a comparison with the mechanical damage index ID was carried out [3,4]. Firstly, a comparison was made for each repetition of the vibration test (T1, T2, T3, T4) at each level of damage of the I-section steel segments of specimen FD, and for T1, T2 and T3 of the I-section steel segment of specimen SD. Results are shown in Figure 9 and Figure 10. It can be seen that the RWEE index follows the behavior of the ID index as the level of damage increases. No important differences exist between the repetitions of the vibration tests.
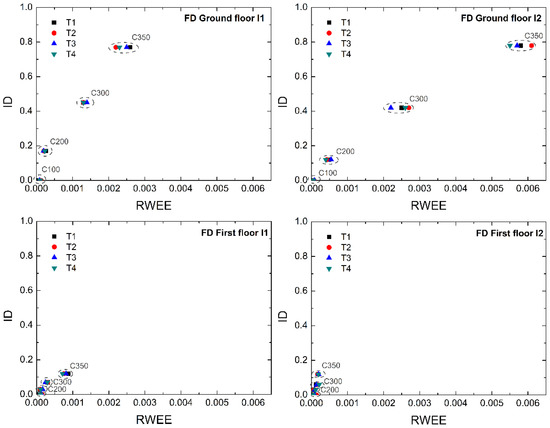
Figure 9.
The relative wavelet energy entropy index (RWEE) vs. mechanical damage index (ID) for each I-section of the dampers of FD.
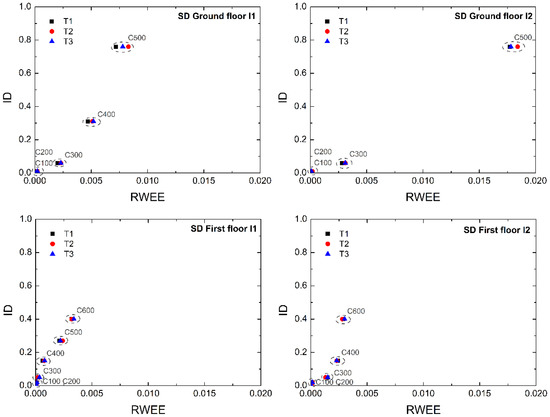
Figure 10.
RWEE vs. ID for each I-section of the dampers of SD.
Figure 11 presents the RWEE versus ID plots grouping the four I-sections of each specimen. Each point in this plot is an average of the repetitions of the vibration test. Linear fitting and correlation coefficients are given in each case. Results are generally very satisfactory. In view of the good correlation between the ID and RWEE indices, ID can be indirectly obtained from the RWEE index, thus providing a quantification of damage to the I-section. This affords two important advantages: (i) no real-time data recordings during the earthquake are required; and (ii) the instrumentation needed is simpler and cheaper.
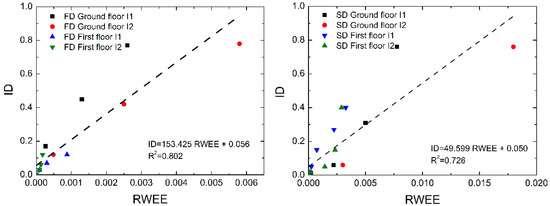
Figure 11.
RWEE vs. ID for dampers of specimens FD and SD.
7. Discussion and Conclusions
The relative wavelet energy entropy (RWEE) is introduced as an index to quantify the damage of hysteretic dampers subjected to random seismic-type dynamic loadings using the correlation between RWEE and ID indices. It is based on the wavelet package decomposition of output signals obtained from simple vibration tests conducted with low-cost piezoelectric transducers placed on the I-section of the damper. The validity of the RWEE index was assessed experimentally by testing a particular type of hysteretic damper called Web Plastifying Damper (WPD), installed in two different reinforced concrete structures (a frame structure and a flat-plate structure). Both sub-structures were subjected to several seismic simulations of increasing magnitude by means of a 3 × 3m2 shaking table. The damage accumulated in the I-section of the dampers at the end of each seismic simulation was quantified twice, once with the mechanical damage index ID proposed in past research and extensively calibrated with the results of static and dynamic tests. The main drawback of the ID index is that its calculation requires knowledge of the load-displacement curve endured by the hysteretic damper during the seismic event. The other quantification was provided by the RWEE index, which entails low-cost instrumentation and low computational requirements. Results demonstrate that the RWEE index correlates very well with the ID index. This enables one to assess the damage on hysteretic dampers without resorting to the cumbersome and expensive instrumentation required for in-situ continuous monitoring of dampers.
Author Contributions
A. Gallego and A. Benavent-Climent conceived and designed the test models with WPDs and the seismic simulations carried out on the shaking table; A. Gallego carried out the vibration tests on the hysteretic dampers and the acquisition of data; E. Suarez carried out the calculations and data analysis; A. Benavent-Climent calculated the mechanical damage index; A. Roldán developed the electronic measurement systems; all authors contributed to write the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Benavent-Climent, A. An energy-based damage model for seismic response of steel structures. Earthq. Eng. Struct. Dyn. 2007, 36, 1049–1064. [Google Scholar] [CrossRef]
- Gallego, A.; Benavent-Climent, A.; Romo-Melo, L. Piezoelectric sensing and non-parametric statistical signal processing for health monitoring of hysteretic dampers used in seismic-resistant structures. Mech. Syst. Signal Process. 2015, 60–61, 90–105. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Gallego, A.; Romo-Melo, L.; Morillas, L. Health Monitoring of web plastifying dampers subjected to cyclic loading through vibration tests. Struct. Health Monit. 2014, 13, 33–49. [Google Scholar] [CrossRef]
- Romo, L.; Benavent-Climent, A.; Morillas, L.; Escolano, D.; Gallego, A. Health monitoring of a new hysteretic damper subjected to earthquakes on a shaking table. Earthq. Struct. 2015, 8, 485–509. [Google Scholar] [CrossRef]
- Romo, L. Diagnóstico de Daño en Disipadores de Energía Histeréticos Usados Como Sistema de Control Pasivo en Estructuras Sismorresistentes, Mediante Técnicas de Procesamiento Digital de Señales de Vibraciones. Ph.D. Thesis, University of Granada, Granada, Spain, 2012. [Google Scholar]
- Worden, K.; Manson, G. Experimental validation of a structural health monitoring methodology. Part I. Novelty detection on a laboratory structure. J. Sound Vib. 2003, 259, 323–343. [Google Scholar] [CrossRef]
- Fassois, S.; Sakellariou, J. Time series methods for fault detection and identification in vibrating structures. R. Soc. Philos. Trans.: Math. Phys. Eng. Sci. 2007, 365, 411–448. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Geoffrey Chase, J.; Rodgers, G.W. Nonlinear Regression Based Health Monitoring of Hysteretic Structures under Seismic Excitation. Shock Vib. 2015, 2015, 193136:1–193136:12. [Google Scholar] [CrossRef]
- Hearn, G.; Testa, R.B. Modal analysis for damage detection in structures. J. Struct. Eng. 1991, 117, 3042–3063. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Peeters, B.; Maeck, J.; De Roeck, G. Vibration-based damage detection in civil engineering: Excitation sources and temperature effects. Smart Mater. Struct. 2001, 10. article 518. [Google Scholar] [CrossRef]
- Ko, J.M.; Ni, Y.Q. Technology developments in structural health monitoring of large-scale bridges. Eng. Struct. 2005, 27, 1715–1725. [Google Scholar] [CrossRef]
- Chang, P.C.; Flatau, A.; Liu, S.C. Review paper: Health monitoring of civil infrastructure. Struct. Health Monit. 2003, 2, 257–267. [Google Scholar] [CrossRef]
- Law, S.S.; Li, X.Y.; Zhu, X.Q.; Chan, S.L. Structural damage detection from wavelet packet sensitivity. Eng. Struct. 2005, 27, 1339–1348. [Google Scholar] [CrossRef]
- Chiariotti, P.; Martarelli, M.; Revel, G.M. Delamination detection by Multi-Level Wavelet Processing of Continuous Scanning Laser Doppler Vibrometry data. Opt. Lasers Eng. 2017, in press. [Google Scholar] [CrossRef]
- Nikolaou, N.G.; Antoniadis, I.A. Rolling element bearing fault diagnosis using wavelet packets. NDT&E Int. 2002, 35, 197–205. [Google Scholar]
- Han, L.; Li, C.W.; Guo, S.L.; Su, X.W. Feature extraction method of bearing AE signal based on improved FAST-ICA and wavelet packet energy. Mech. Syst. Signal Process. 2015, 62–63, 91–99. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. Application of fast Fourier and wavelet transforms towards actuator leakage diagnosis: A comparative study. Int. J. Fluid Power 2014, 14, 39–51. [Google Scholar] [CrossRef]
- Peng, X.-L.; Hao, H.; Li, Z.-X. Application of wavelet packet transform in subsea pipeline bedding condition assessment. Eng. Struct. 2012, 39, 50–65. [Google Scholar] [CrossRef]
- Noh, H.Y.; Nair, K.K.; Lignos, D.G.; Kiremidjan, A.S. Use of wavelet-based damage-sensitive features for structural diagnosis using strong motion data. Am. Soc. Civ. Eng. 2011, 137, 1215–1228. [Google Scholar]
- Yan, Y.J.; Yam, L.H. Detection of delamination damage in composite plates using energy spectrum of structural dynamic responses decomposed by wavelet analysis. Comput. Struct. 2004, 82, 347–358. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Ju, Y.-F.; Duan, C.-D.; Zhao, X.-F. Structure damage diagnosis using neural network and feature fusion. Eng. Appl. Artif. Intell. 2011, 24, 87–92. [Google Scholar] [CrossRef]
- Feng, Y.; Schlindwein, F.S. Normalized wavelet packets quantifiers for condition monitoring. Mech. Syst. Signal Process. 2009, 23, 712–723. [Google Scholar] [CrossRef]
- Jian-Gang, H.; Wei-Xin, R.; Zeng-Shou, S. Wavelet packet based damage identification of beam structures. Int. J. Solids Struct. 2005, 42, 6610–6627. [Google Scholar]
- Yan, Y.J.; Hao, H.N.; Yam, L.H. Vibration-based construction and extraction of structural damage feature index. Int. J. Solids Struct. 2004, 41, 6661–6676. [Google Scholar] [CrossRef]
- Hou, Z.; Noori, M.; Amand, R., St. Wavelet-based approach for structural damage detection. J. Eng. Mech. 2000, 26, 677–683. [Google Scholar] [CrossRef]
- Reda Taha, M.M.; Noureldin, A.; Lucero, J.L.; Baca, T.J. Wavelet Transform for Structural Health Monitoring: A compendium of Uses and Features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Kim, H.; Melhem, H. Damage detection of structures by wavelet analysis. Eng. Struct. 2004, 26, 347–362. [Google Scholar] [CrossRef]
- Perez-Ramirez, C.A.; Jaen-Cuellar, A.Y.; Valtierra-Rodriguez, M.; Dominguez-Gonzalez, A.; Osornio-Rios, R.A.; Romero-Troncoso, R.J.; Amezquita-Sanchez, J.P. A two-step strategy for system identification of civil structures for Structural Health Monitoring using wavelet transform and genetic algorithms. Appl. Sci. 2017, 7, 111. [Google Scholar] [CrossRef]
- Bayissa, W.L.; Haritos, N.; Thelandersson, S. Vibration-based structural damage identification using wavelet transform. Mech. Syst. Signal Process. 2008, 22, 1194–1215. [Google Scholar] [CrossRef]
- Asgarian, B.; Aghaeidoost, V.; Shokrgozar, H.R. Damage detection of jacket type offshore platforms using rate of signal energy using wavelet packet transform. Mar. Struct. 2016, 45, 1–21. [Google Scholar] [CrossRef]
- Guosheng, Z.; Jiang, L.; Kui, Z. Structural safety criteria for blasting vibration based on wavelet packet energy spectra. Min. Sci. Technol. 2011, 21, 35–40. [Google Scholar] [CrossRef]
- Ekici, S.; Yildirim, S.; Poyraz, M. Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition. Expert Syst. Appl. 2008, 34, 2937–2944. [Google Scholar] [CrossRef]
- Junsheng, C.; Dejie, Y.; Yu, Y. Time-energy analysis based on wavelet transform. NDT&E Int. 2005, 38, 569–572. [Google Scholar]
- Castro, E.; Moreno-Garcia, P.; Gallego, A. Damage detection in CFRP plates using spectral entropy. Shock Vib. 2014, 2014, 693593:1–693593:8. [Google Scholar] [CrossRef]
- Morgaz, J.; Granados, M.; Dominguez, J.; Navarrete, R.; Fernandez, A.; Galan, A.; Munoz, P.; Gomez-Villamandos, R. Evaluation of spectral entropy to measure anesthetic depth and antinociception in sevoflurance-anaesthetised Beagle dogs. Vet. J. 2011, 188, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Powell, G.; Percival, I. A spectral entropy method for distinguishing regular and irregular motion of Hamiltonian systems. J. Phys. Chem. A 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Beenamol, M.; Prabavathy, S.; Mohanalin, J. Wavelet based seismic signal de-noising using Shannon and Tsallis entropy. Comput. Math. Appl. 2012, 64, 3580–3593. [Google Scholar] [CrossRef]
- Chen, J.; Li, G. Tsallis Wavelet Entropy and Its Application in Power Signal Analysis. Entropy 2014, 16, 3009–3025. [Google Scholar] [CrossRef]
- Quiroga, R.; Rosso, O.; Basar, E.; Schurmann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEg oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- AlNashash, H.; Thakor, N. Monitoring of global cerebral ischemia using wavelet entropy rate of change. IEEE Trans. Biome. Eng. 2005, 52, 2119–2122. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Rosso, O.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schurmann, M.; Basar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Basu, B. Identification of stiffness degradation in structures using wavelet analysis. Constr. Build. Mater. 2005, 19, 713–721. [Google Scholar] [CrossRef]
- Nair, K.K.; Kiremidjian, A.S.; Law, K.H. Time series-based damage detection and localization algorithm with application to the ASCE benchmark structure. J. Sound Vib. 2006, 291, 349–368. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Morillas, L.; Vico, J.M. A study on using wide-flange section web under out-of-plane flexure for passive energy dissipation. Earthq. Eng. Struct. Dyn. 2011, 40, 473–490. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: London, UK, 1999. [Google Scholar]
- Sun, Z.; Chang, C.C. Structural damage assessment based on wavelet packet transform. ASCE J. Struct. Eng. 2002, 128, 1354–1361. [Google Scholar] [CrossRef]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Chui, C.K. Wavelets: A Mathematical Tool for Signal Processing; SIAM Monographs on Mathematical Modeling and Computation: Philadelphia, PA, USA, 1997. [Google Scholar]
- Burrus, C.S.; Gopinath, R.A.; Guo, H. Introduction to Wavelets and Wavelet Transforms: A Primer; Pearson: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- NCSE-02. Norma de Construcción Sismorresistente: Parte General y Edificación; Ministerio de Fomento, Gobierno de España, 2002; [RD 997/2002 de 27 de Septiembre].
- Benavent-Climent, A.; Morillas, L.; Escolano-Margarit, D. Seismic performance and damage evaluation of a reinforced concrete frame with hysteretic dampers through shake-table tests. Earthq. Eng. Struct. Dyn. 2014, 43, 2399–2417. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Donaire-Avila, J.; Oliver-Saiz, E. Shaking table tests of a reinforced concrete waffle-flat plate structure designed following modern codes: Seismic performance and damage evaluation. Earthq. Eng. Struct. Dyn. 2016, 45, 315–336. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).