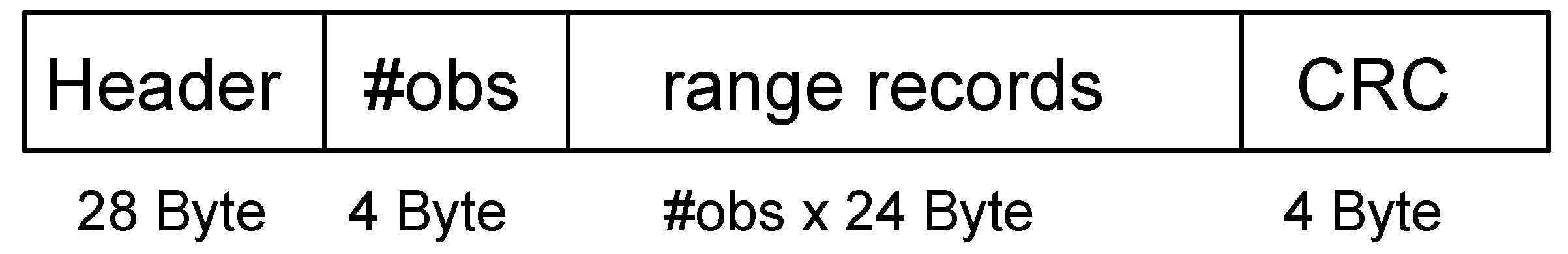1. Introduction
Structural health monitoring (SHM) of bridges can provide important information about structural performance and may help to detect anomalies or threats originating from damages or deteriorations at early stages. SHM can also be used to estimate remaining lifetime, to assist in bridge maintenance planning, to verify construction designs and to deliver important data in the case of disasters or extreme events [
1,
2]. There exist three different techniques of SHM for bridges that can be classified into in situ, on-site and remote monitoring techniques. In situ monitoring techniques use sensors that are installed directly at a structure. On-site monitoring techniques are based on more complex sensors that are brought to a bridge during the monitoring campaign. Remote monitoring is done from a greater distance, for example by analyzing photographs of the structure taken from satellites or airplanes [
3]. Especially in situ monitoring systems are often realized with the help of wireless sensor networks (WSNs), as they are inexpensive and easy to install on existing structures. Wireless sensor networks consist of sensor nodes, which are self- or battery-powered small units and communicate wirelessly with each other.
Several wireless sensor network systems have been introduced during the last few years and decades for structural health monitoring of bridges. O’Connor gives in [
4] a comprehensive overview of installations for short-term monitoring and long-term monitoring. Short-term installations like [
5,
6,
7,
8,
9,
10,
11] mostly measure accelerations, but some also include sensors for strain, temperature and velocity. Limitations arise mostly from the high power demands of the sensor nodes or base stations.
Hu et al. [
11], for example, presents a wireless sensor network to monitor the Zhengdian Highway Bridge based on wireless sensor nodes, which use an MSP430 microcontroller and a CC2420 radio. The nodes are running TinyOS, which uses MintRout to send data over multi-hops to a base station. Including an energy storage of 7500 mAh, a node is able to monitor strain or acceleration continuously for around 168 h, or when choosing a sampling period of 1 h/day, the lifetime can be extended to 168 days. The base station is connected via a USB connector to a powerful host computer.
Amongst the wireless monitoring systems reviewed in [
4], there are also three long-term monitoring installations, one on the Jindo Bridge [
12], one on the Stork Bridge [
13] and one on the New Carquinez Bridge [
14]. The work in [
4] summarizes the challenges arising in long-term installations originating from power supplies, communication reliability, sensor reliability and challenging environmental conditions.
As Casciati and Chen point out in [
15], large and dense sensor network deployments are often affected by large transmission delays as sensors cannot transmit their data concurrently. To increase communication reliability and to balance communication range, power consumption, data rate and link quality, Casciati and Chen [
15] introduce a wireless sensor node that uses frequency-division multiplexing to transmit data simultaneously using different frequencies. Furthermore, in [
16], Chen introduces a wireless sensor platform for SHM applications. The wireless sensor platform includes a power management unit to reduce the platform’s energy consumption and can be equipped with several types of sensors ranging from low power to energy-hungry devices. Chen also proposes an adaptive radio transmission power control algorithm along with a single-hop communication strategy. The power control algorithm adjusts the radio transmission energy to the link quality to save energy during the wireless data acquisition [
16].
With respect to structural health monitoring, one other important measurement is the three-dimensional displacement of a structure or of parts of it. These measurements can be done by using on-site sensors [
17] or by using in situ measurements provided by Global Communication System (GPS) receivers [
18,
19,
20,
21,
22]. Here, GPS-based monitoring systems provide several advantages, such as weather independence, absolute displacement measurements, autonomous operation and no need for a line-of-sight connection between different measurement points. Additionally, GPS provides both static and dynamic structural response information, and the position information is free from any measurement drifts and error accumulation [
23].
By applying differential data processing of two or more concurrently logging GPS receivers, displacements in the range of 5 mm or below can be detected, as well as oscillation frequencies of up to and above 4 Hz. The authors of [
19,
20,
22], for example, recorded the dynamical response of the Wilford Bridge in Nottingham, using GPS receivers in combination with accelerometers to validate the data and to improve the monitoring system’s performance. More recently, Kaloop et al. [
24] presented GPS-based positioning data taken at the Mansoura railway bridge using Trimble-5700 dual-frequency GPS receivers logging at a rate of 1 Hz. The authors also present data taken from the long-term SHM system installed on the two towers of the Yonghe Bridge. Here, the GPS receivers are logging with a sampling frequency of 20 Hz. Reported standard deviations are in the mm range. However, these systems were all either tethered installations or short-term measurement campaigns.
Although there are several existing wireless sensor networks that support the use of GNSS (global navigation satellite system) receivers [
25,
26,
27,
28,
29,
30,
31], to the author’s knowledge, there is no such system available to monitor the dynamical behavior of bridges. Difficulties are in the high power demands of GNSS receivers and in the large amounts of data that need to be transmitted wirelessly.
In this article, we present a wireless sensor node that can be equipped with an OEM615 GNSS receiver from NovAtel. The nodes provide sampling rates up to 20 Hz. To transmit the large amount of data resulting from this high sampling rate, we use a wake-up receiver-based cross-layer routing protocol that is able to transfer large data packets without many overhead data [
32].
The rest of the article is structured as follows. In
Section 2, we present the wireless sensor network and the wireless sensor nodes. We analyze power requirements, as well as the amounts of data to be transmitted and the routing protocol. Based on these, we find a resulting sensor node lifetime in the range of 20 to 200 days dependent on the GNSS sensor logging period. In
Section 3, we introduce the differential GNSS measurement technique as it is the key to achieving sub-centimeter accuracy in GNSS measurements. In
Section 4, we present and discuss the measurements taken with the GNSS sensors and analyze the results. Furthermore, we compare the GNSS results to the measurements taken with the accelerometer in
Section 4 and, finally, conclude our article in
Section 5.
2. Wireless Sensor Network
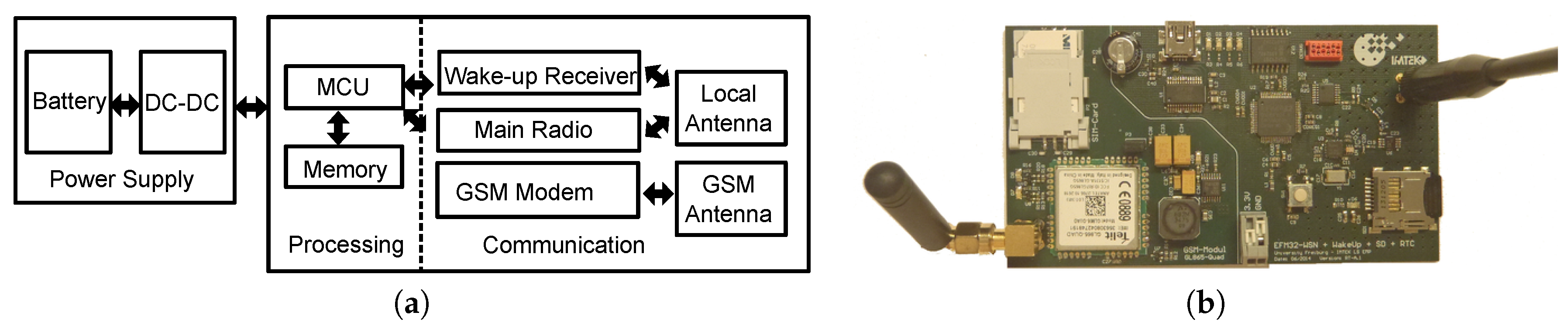
Generally, a wireless sensor node consists of four basic components: power supply, sensing, processing and communication.
Figure 1 visualizes the main blocks of a wireless sensor node schematically. The figure is taken from [
33], but enhanced by the wake-up receiver.
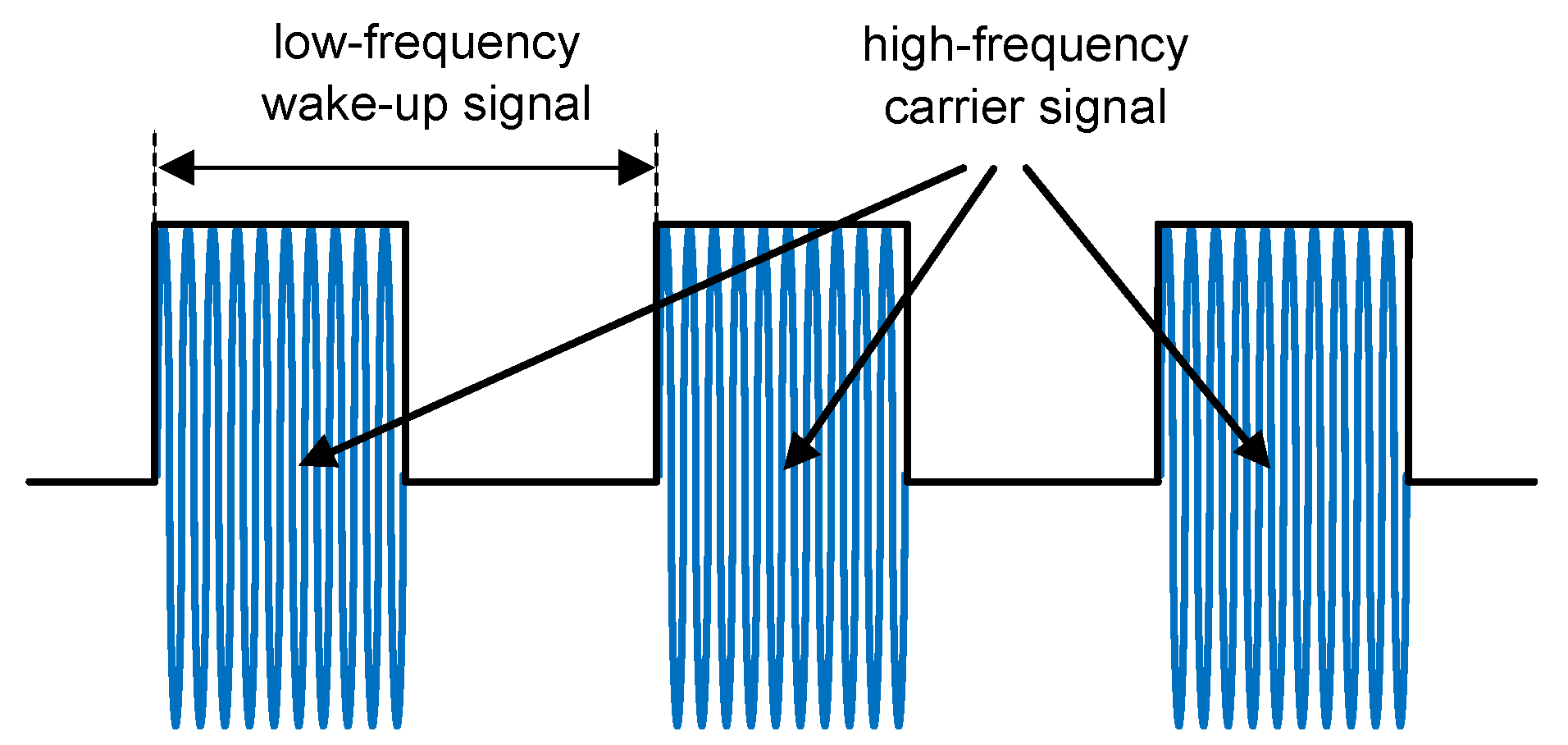
The wake-up receiver is an additional radio receiver that listens permanently to the wireless channel in the kilohertz range having a constant, but marginal power requirement in the area of
W. The low-frequency wake-up signal is modulated onto the high-frequency carrier signal and demodulated passively by the envelope detector.
Figure 2 schematically shows a wake-up signal generated by means of on-off-keying modulation of the high-frequency carrier signal [
34]. In the case of ultra-low power wake-up receivers, the envelope detector often merely consists of diodes and capacitors to ensure its energy efficiency [
35,
36,
37]. As the signal is transmitted on the high-frequency carrier, the antenna receives the wake-up message with high efficiency. Signal losses happen mainly during the passive demodulation (envelope detection) of the wake-up signal.
Blanckenstein et al. present in [
38] an overview of current low-power transceivers. With respect to energy consumption, the range goes from highly integrated concepts that require 0.1
W to several solutions between 10 and 1000
W.
The wireless nodes used in this work are based on the sensor nodes introduced in [
34,
39,
40]. The microcontroller utilized on the boards is a 32-bit EFM32G222F128 manufactured by SiliconLabs running at 14 MHz. It provides several low power states to reduce energy consumption. In run mode, it draws around 2.5 mA and 0.9
A in deep sleep mode. Including all peripherals, the sensor node requires around 4.0 mA in run mode. The communication radio is a CC1101 from Texas Instruments. It has a current consumption of 34.2 mA when transmitting at +12 dBm output power at 868 MHz and around 16.4 mA when transmitting at 0 dBm. Its sensitivity is approximately in between −95 dBm and −104 dBm, depending on the data rate. The 125-kHz low-frequency receiver (AS3932) from AMS has a current consumption of around 3
A in listening mode. It correlates the incoming signal to a pre-configured address and creates an interrupt if send and stored addresses match. In combination with the matching network and envelope detector, the wake-up receiver has a sensitivity around −51 dBm [
34,
39]. Transmitting at 12 dBm, the wake-up range of this wake-up receiver could be determined by [
39] as around 45 m.
Using wake-up receivers can save energy as a wireless sensor node does not have to be active if no tasks need to be done. Furthermore, wake-up receivers provide a fully asynchronous communication, which means synchronization messages are obsolete. Due to this, wireless sensor nodes with wake-up receivers can communicate as soon as they have a message that needs to be delivered, but they can also accumulate sensor data to large data packets and stay in a very-low-power listening state during times when no tasks need to be done.
2.1. GNSS Sensor Node
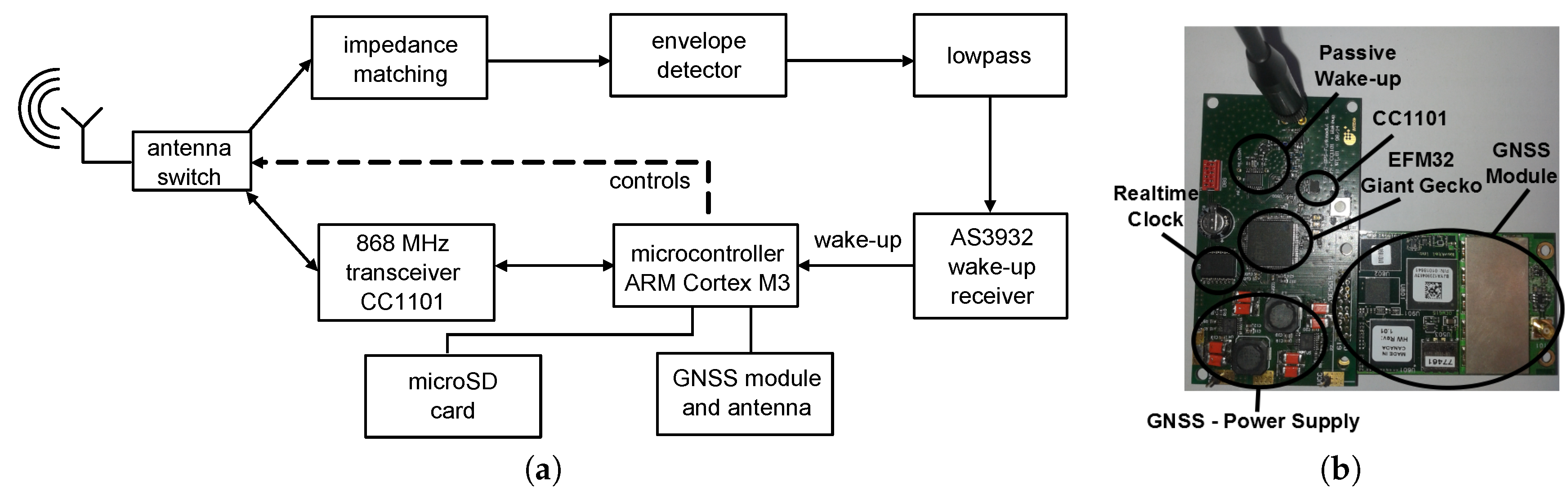
Figure 3a schematically shows the GNSS (global navigation satellite system) receiver node including its hardware blocks, which we also introduced in [
41]. The node basically consists of the same hardware components as the sensor nodes introduced above in
Figure 1, but is additionally equipped with a GNSS receiver. The NovAtel OEM615 GNSS receiver module supports GPS, GLONASS, Galileo and Compass frequencies and sampling rates up to 20 Hz. In active mode, the GNSS receiver draws constantly around 400 mA. To reduce the average power consumption, the module is activated only periodically and can be switched off completely during times when it is inactive.
Figure 3b shows a photo of the GNSS receiver node. The GNSS receiver module is connected to the wireless sensor node by a 20-pin connector. The satellite antenna is a GPS-701-GG antenna from NovAtel. A UART interface is used to configure the GNSS module and to read out the GNSS data periodically.
A GNSS range message generally consists of four fields as depicted in
Figure 4. The first 28 bytes are the header that includes information like message type, time, length, etc. The next four bytes’ large field gives the number of valid observations; the third 24 bytes’ large field includes all valid observations; and the last field is a 32-bit cyclic redundancy check. Altogether, a range message varies in its size from 50 bytes in the case of one valid observation to 516 bytes for 20 valid observation. At a sampling frequency of 4 Hz, this sums up to 200 bytes per second for one valid observation and 2064 bytes per second for 20 valid observations. At a sampling frequency of 20 Hz, the observation of one satellite results in 1000 bytes per second, and the observation of 20 valid satellites results in 10,320 bytes per second.
We use a baud rate of 230 kBit per second (equal to 23 kByte per second for an 8N1 transmission) to transmit data from the NovAtel board to the sensor node. The GNSS data are firstly stored in an internal 14-kByte memory buffer and then transferred periodically onto a 4-GB Micro SD Card. To increase the speed, the MCU is running at 28 MHz during this process. By assuming a sampling rate of 4 Hz and 15 valid observations per message (396 bytes), a 4-Hz logging frequency (1584 bytes per second) for a duration of 30 min (1800 s) adds up to 2851.2 kByte, which have to be transferred wirelessly. At 20-Hz logging, we expect around 14,256 kByte data sampled during a 30-min logging period in the case of 15 valid satellites.
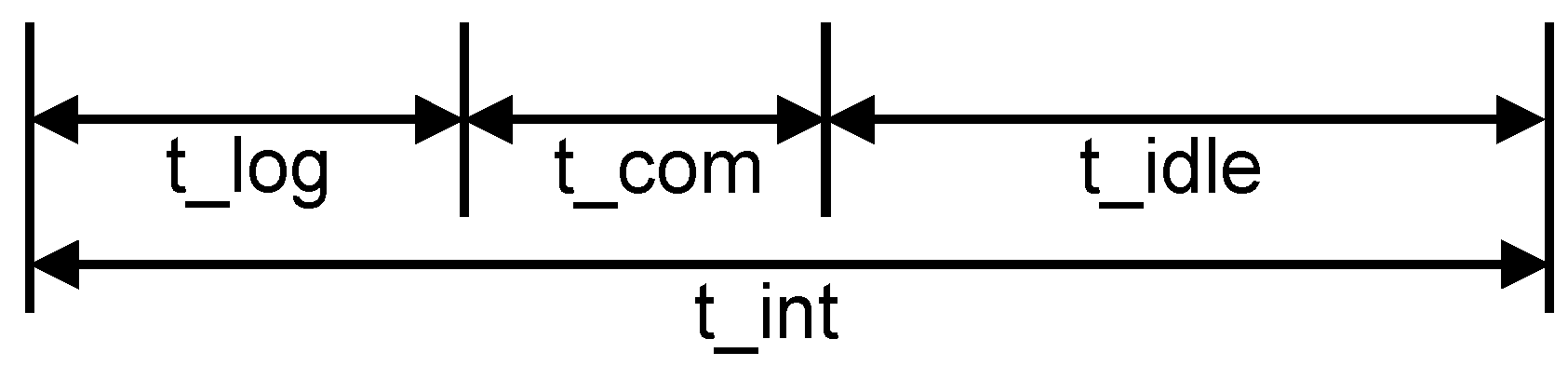
An important parameter to consider is the lifetime of the GNSS sensor node, that is the time the node can autonomously operate before it dies due to low energy. As presented in [
34], the lifetime is connected to the node’s battery capacity and to the times where the node is actively logging (
) or communicating (
) as the sensor node requires most energy during these periods. During idle times (
), the node requires only marginal power in comparison to active times.
Figure 5 depicts
,
and
during a certain time interval
.
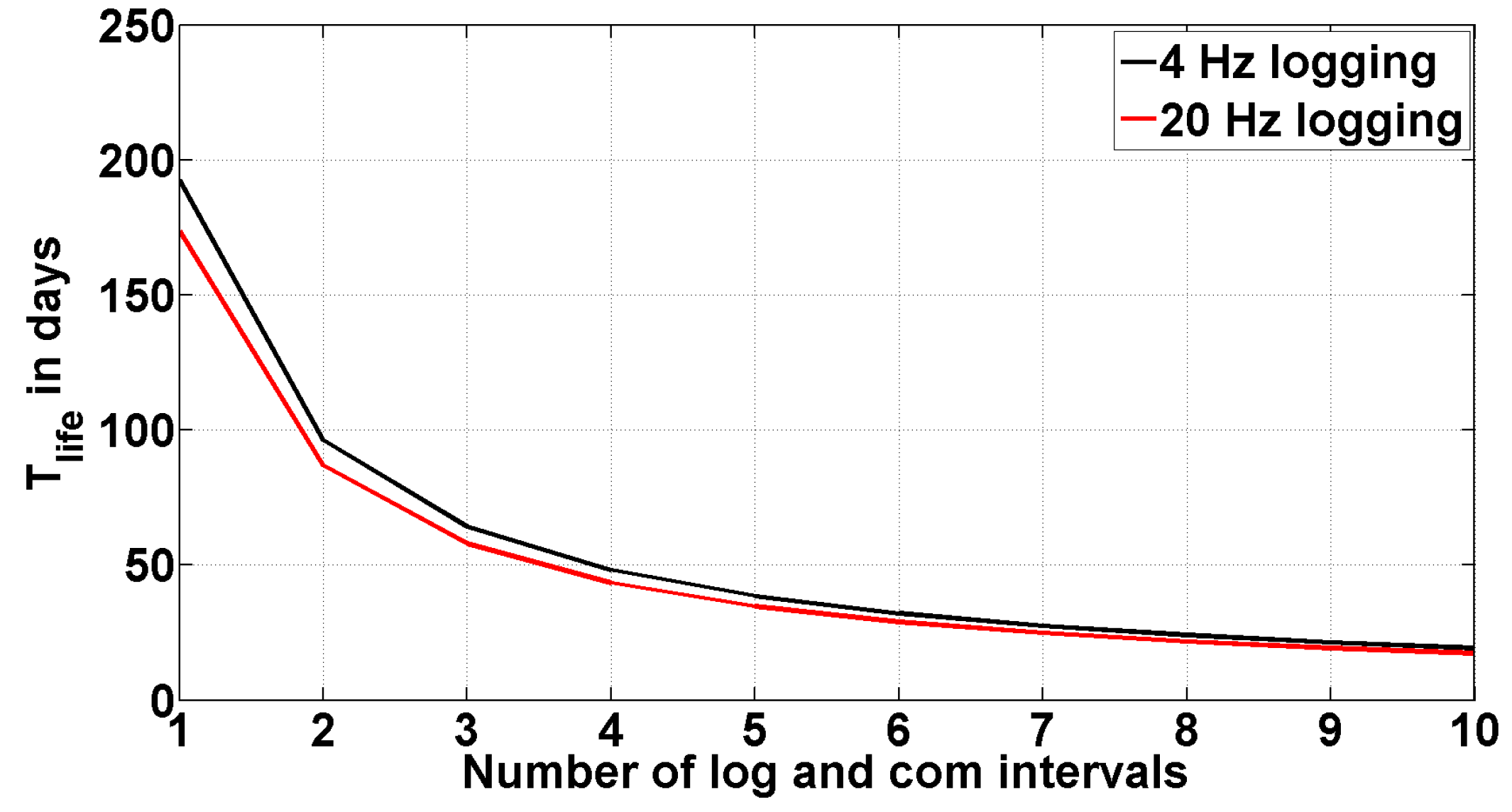
To calculate a certain lifetime, we considered one logging interval (
) to be 1800 s and the corresponding communication interval (
) to be 900 s for a 4-Hz logging frequency and 3600 s in case of a 20-Hz logging. The interval (
) is 24 h. This means if the sensor node does one logging in 24 h, it is in idle state for 83,700 s ((
).
Figure 6 shows the lifetime of our GNSS sensor node plotted over an increasing number of logging and communication intervals in 24 h assuming a battery capacity of 40 Ah and no energy harvesting.
2.2. GSM Base Station and Remote Server
The GSM (global system for mobile communications) node acts as a gateway between the local wireless sensor network and the remote server. As such, it has two communication modules, as depicted in
Figure 7a.
Figure 7b shows a photo of the gateway with its two antennas. The node has an internal memory buffer to transmit several data packets at once to the server via GSM.
The remote server was a Raspberry Pi located at the Laboratory for Electrical Instrumentation, Department of Microsystems Engineering, University of Freiburg, Building 106 running a MySQL database. The main purpose of the database, was to store the data received from the wireless sensor network. However, another purpose was to reassemble the previously separated GNSS messages using their measurement timestamps as unique IDs, as will be introduced in following
Section 2.3.
2.3. Cross-Layer Routing Protocol
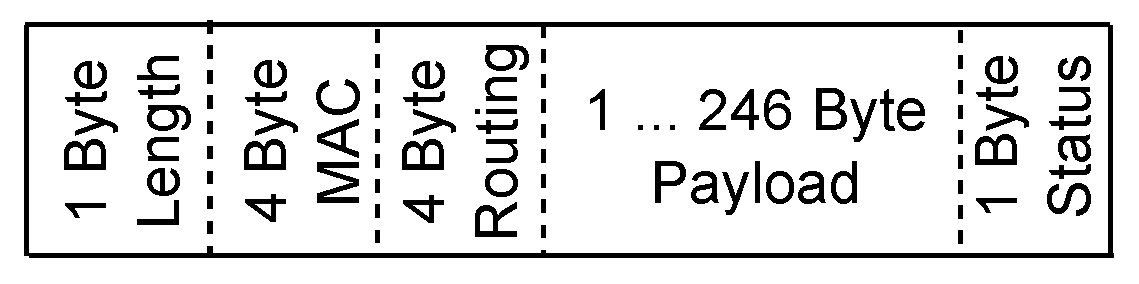
The communication radio utilized in this work supports messages up to a size of 256 bytes. This means GNSS messages that usually consist of several kilobytes had to be split into smaller packets before sending. Additionally, the expected total amount of data received from the GNSS receiver is quite high. For this reasons, we used a cross-layer routing protocol [
32,
42] that is able to transmit large data packets with only a few control bytes, as depicted in
Figure 8, which shows a data packet consisting of eight control bytes and one to 246 data bytes.
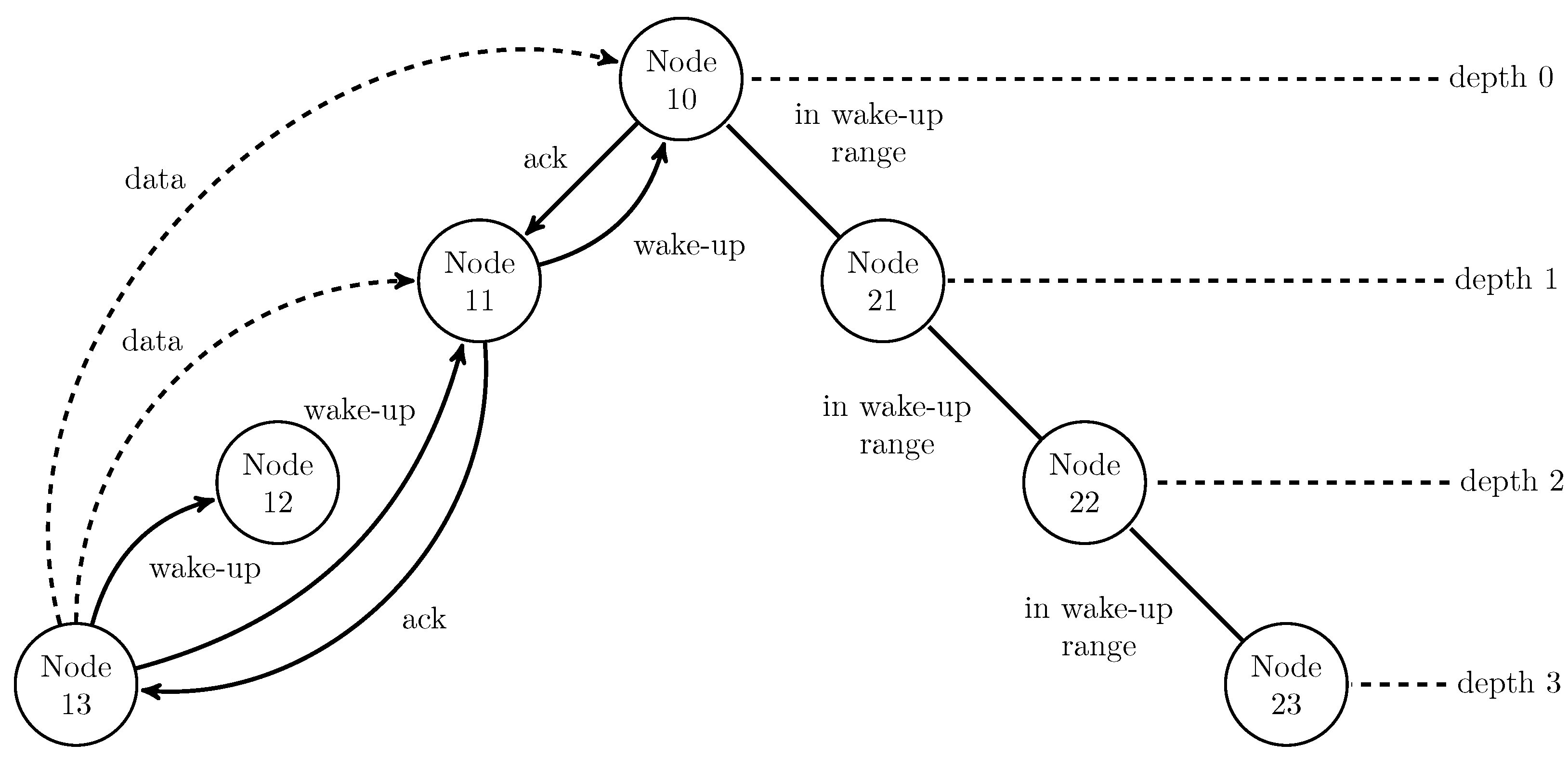
As the range of communication messages is larger than the range of wake-up messages, the routing protocol supports the use of wake-up relay nodes as visualized in
Figure 9 from [
42]. In this routing protocol, neighboring nodes (child and parent nodes) are able to wake-up themselves, which means nodes of depth
i can wake-up nodes of depth
.
Furthermore, it is possible to wake-up several nodes in a row to communicate data across several levels from depth
i to depth
with
limited by the root node and communication range. In
Figure 9 Node 13 sends for example a wake-up signal to Node 12, which forwards the wake-up to Node 11, and so on, until a defined maximum number
n of forwards or the destination is reached. Then, data can be sent directly from Node 13 to one of the woken Nodes 10, 11 or 12.
In case a connecting relay node fails due to the temporary or permanent outage, nodes of depth i are also able to wake-up nodes of depth with , if they are in wake-up range. If, for example, Node 12 is unreachable due to changes in the link or due to low energy, Node 13 is also able to wake-up one of the parent nodes of Node 12.
Once the communication link to a node is established, up to 64 data packets (with up to 246 bytes of payload each) can be transmitted subsequently. After transmission, the link is closed, and the participating nodes go back to sleep again.
To be able to split large GNSS messages into several smaller radio packets and to be able to reassemble them later, every GNSS measurement had a unique ID based on its measurement time. Additionally, each packet number was related to the total number of packets of which a complete GNSS message consisted.
Figure 10 depicts a payload packet to visualize this.
From
Figure 8 and
Figure 10, it becomes obvious that the routing protocol is able to transmit up to 238 bytes of GNSS data per packet. As the expected number of bytes to be transmitted is in the order of several kilobytes, this is still challenging. As the routing algorithm is able to transmit up to 64 data packets along an existing link, this adds up to 15,232 bytes of payload. The data rate could be changed between 38.4, 100 and 250 kBit per second. At a data rate of 38 kBit per second (equal to 4.75 kByte per second), a transmission of 64 data packets takes roughly 4 s. The transmission of a 30-min period of 15 observations logged at 4 Hz (2852 kByte) takes around 10 min. However, due to the need for additionally required control messages before each sending of 64 packets, the required time is even longer. The transmission of a 30-min logging period at 20 Hz (14,256 kByte) takes around 50 min at a baud rate of 38.4 kBit per second. Using higher data rates, the transmission times can be decreased obviously, but the possibility of bit errors increases.
3. Differential GNSS
A single GNSS (global navigation satellite system) receiver can achieve an accuracy in the meter range. If a higher accuracy is required, a differential GNSS (DGNSS) can be used. DGNSS are based either on code- or on phase-range measurements. The accuracy of code-range-based differential techniques will improve compared to that of single receiver accuracy, but this is usually not as accurate as the carrier-phase differential measurement. Generally, differential GNSS measurements determine the position of a rover station related to a base station whose position is accurately known.
To determine the phase-range, the receiver mixes the incoming satellite signal with a locally-generated signal [
43]. Then, the calculation of the phase-range
can be achieved by [
43]:
with
c = 299,792,458 m s
in vacuum and time
being the time when the signal was received. Time
resembles the time when the signal was transmitted by the satellite.
includes additionally a time offset
originating from the clock offset of the receiver. By assuming
t to be the true system time,
can be expressed as
. Likewise,
includes
, which represents the clock offset of the satellite from the system time, that is
. The subscripts
etc., indicate receiver-specific quantities, and the superscripts
etc., indicate satellite-specific quantities and with
[
43]. Here,
is the wavelength of the carrier signal;
is the initial phase of the receiver local oscillator; and
is the initial phase of the transmitted satellite signal at initial time
.
is called carrier-phase integer ambiguity [
44].
is not an integer, but includes unknown phase offsets of the receiver and satellite [
43].
The first term of Equation (
1) is the pseudorange
from satellite
j to receiver
A. Accordingly, including clock biases and atmospheric error terms, Equation (
1) can be written as [
43]:
with
being the message delay due to the troposphere,
being the delay due to the ionosphere and
, which incorporates measurement errors related to receiver hardware and multipath effects. Now, as the goal is to achieve the precise position information, Equation (
2) includes still several uncertainties (clock biases, ionospheric delay and tropospheric delay) that need to be taken care of. The differencing techniques introduced in the following paragraphs can be used to mitigate these effects.
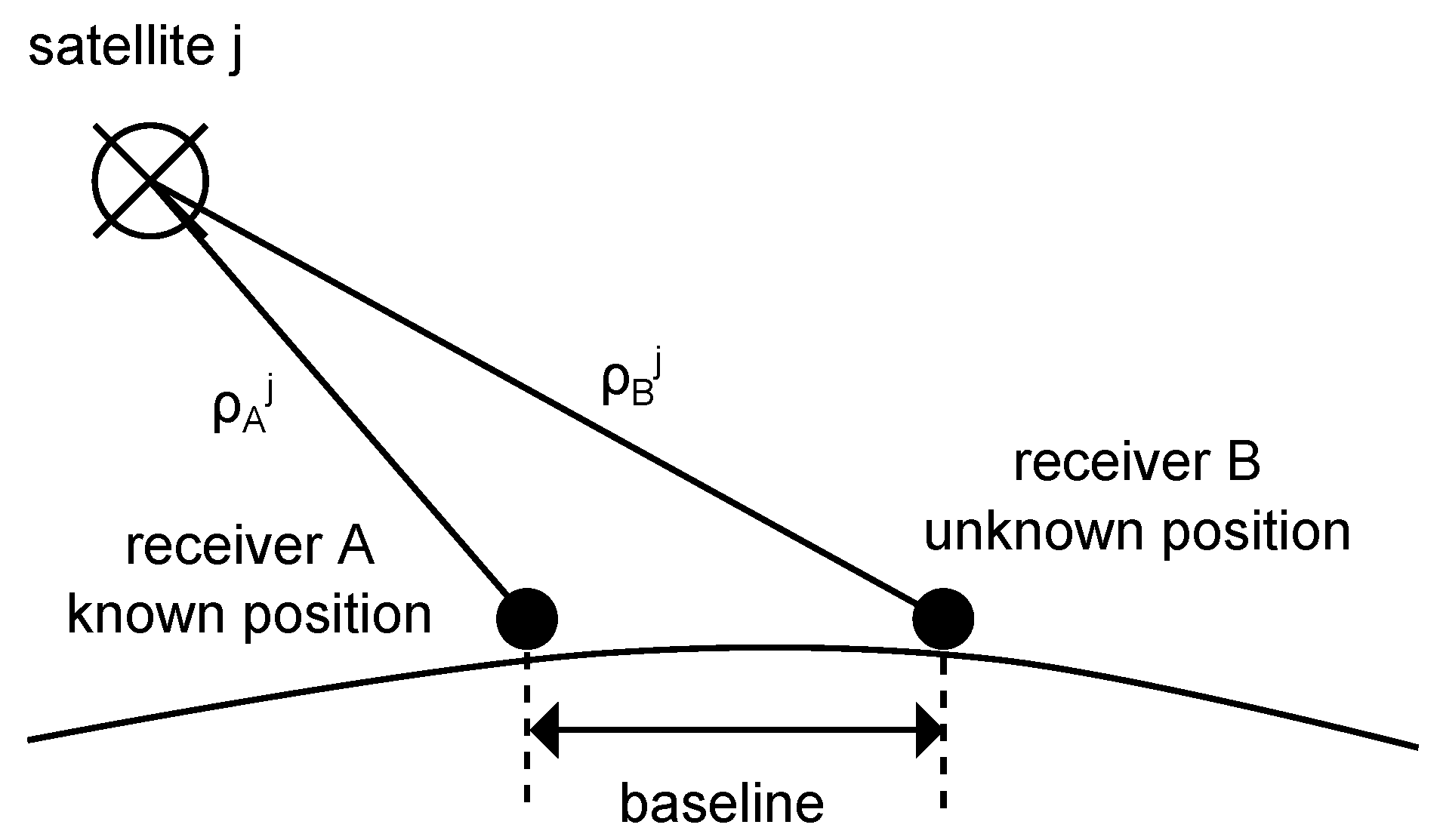
3.1. Single Differencing
Figure 11 illustrates the geometry of single differencing that is based on calculating the difference
between range
(distance from receiver
A to satellite
j) and
(distance from receiver
B to satellite
j) according to Equation (
2). That is [
43]:
First, it can be observed in Equation (
3) that the satellite clock bias
is removed by calculating the range differences. Furthermore, in the case of short (<10 km) baselines (distance from receiver
A to receiver
B), the ionospheric and tropospheric effects are nearly the same, that is
and
, so that Equation (
3) can be further simplified to
[
44]. Although many uncertainties can be removed by single differencing, the receiver clock biases
are not removed. This can be achieved by using double differencing.
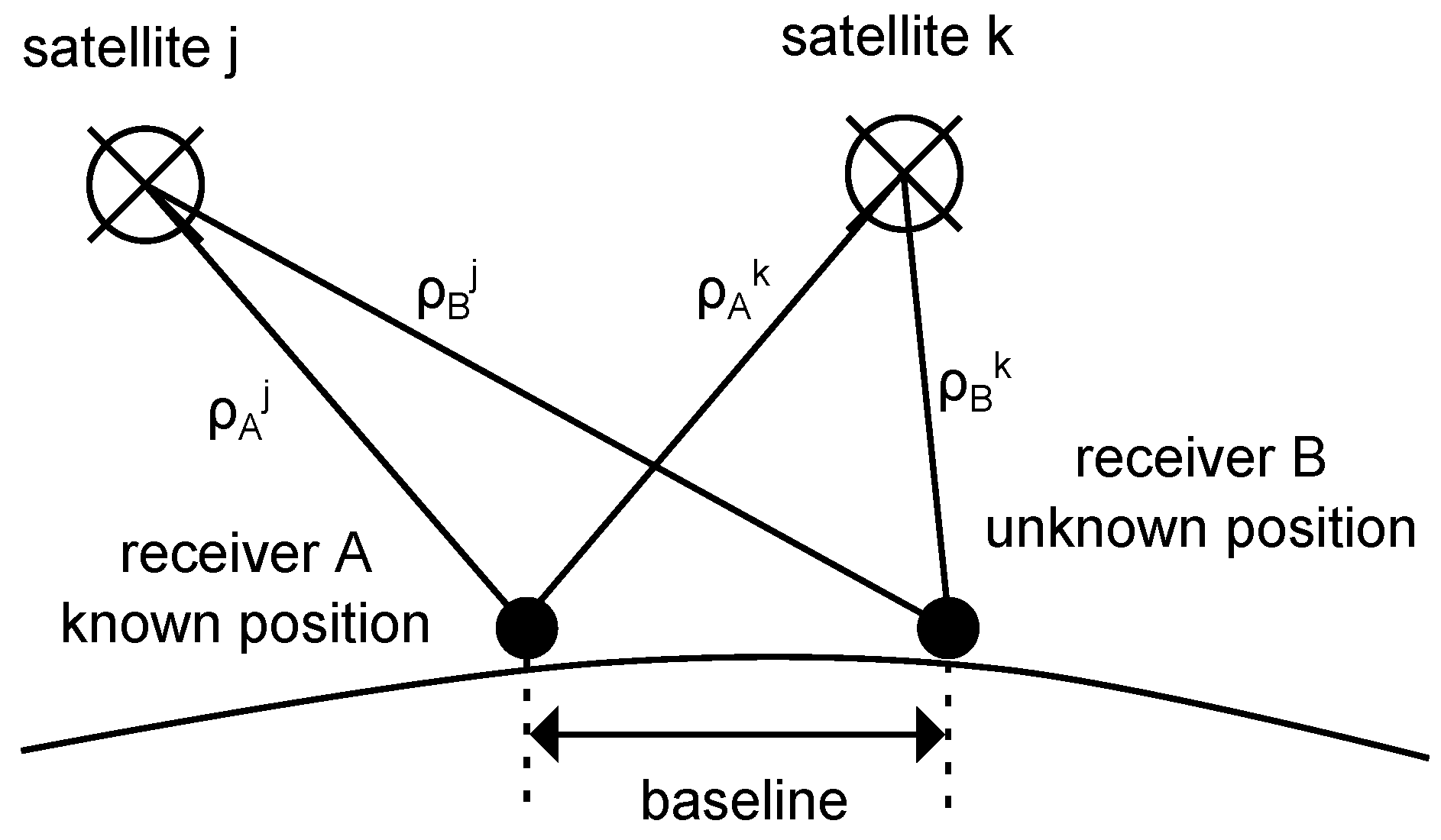
3.2. Double Differencing
Figure 12 illustrates the geometry of double differencing. Here, both receivers
A and
B track simultaneously two satellites
j and
k. The single differences
and
can be calculated as shown in
Section 3.1 by using Equation (
3). The double difference
is the difference between the single differences
and
. The upside-down triangular symbol ∇ is a mnemonic device to emphasizes that the calculated differences are between two points in the sky. Finally, the double difference is [
43]:
Equation (
4) includes the phase-range ambiguity
.
is reduced in single differencing to
. Now, in double differencing, the ambiguity reduces to
as it is assumed that each receiver logs all incoming satellite signals at exactly the same time. Doing so, it becomes obvious that the range-phase ambiguity becomes an integer, which is another advantage of the double differencing technique. Finally, estimating and validating the integer ambiguity can be achieved by using the pseudorange solution and then constraining the estimations to an integer solution [
45]. The detailed steps of resolving the integer ambiguity can be found for example in [
44,
45]. When the integer ambiguity is fixed, the carrier phase range measurements result in precise positioning results in the mm-range.
4. Experimental Results
Figure 13 shows a photo of the Weitinger Neckartal Bridge on Highway 81 from Stuttgart to Singen. The bridge is 900 m long and around 127 m above ground at its highest point. The bridge is made of five spans, and its two end spans consist of inverted cable stay towers that support massive beam spans of 263 m on the southern side and 234 m on the northern side. The bridge has four lanes, two for each driving direction. The total width of the bridge deck is 31.5 m.
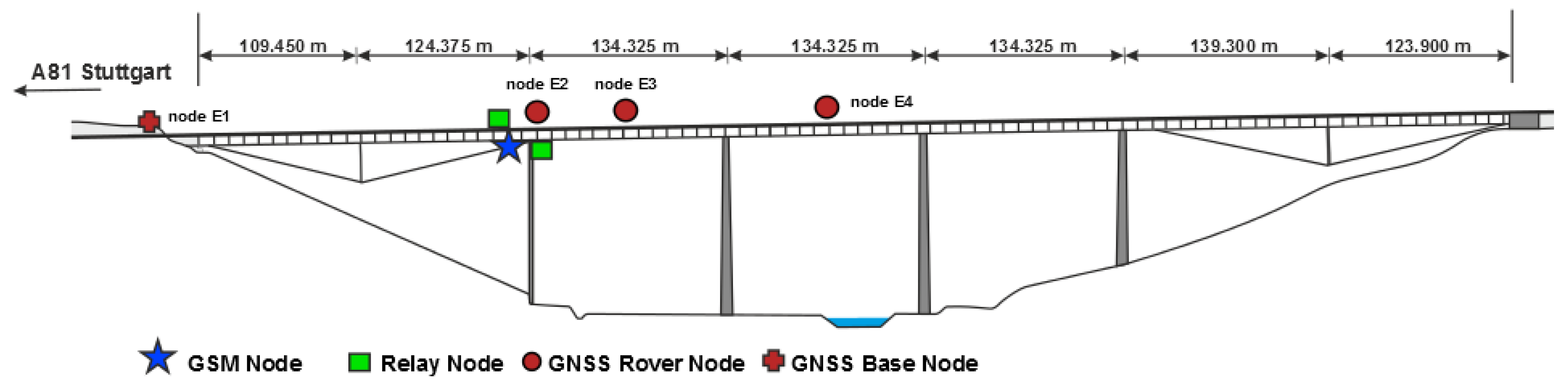
Figure 14 shows the schematic of the Neckartal Bridge indicating the deployed GNSS receiver nodes together with the two relay nodes and the GSM base station. Three GNSS receivers were placed on the deck of the bridge, one above the first pillar (Node E2), one just in the middle of the span between Pillars 1 and 2 (Node E3) and one in the middle of the bridge (Node E4). A GNSS reference node (E1) was placed on the ground before the bridge. As the distances from E1 and E4 to the base station were quite large, they only logged the data. Due to the strong attenuation of the radio waves by the steel girder box, the data could not be sent directly from the bridge deck to the GSM node located inside the steel girder box. Therefore, the data were sent from the GNSS sensor node to a relay node located below the deck on top of one pillar, as shown in
Figure 15b.
Figure 15a exemplary shows a GNSS receiver antenna attached to the bridge by magnets. It can be seen that the antennas have a unobstructed view of the horizon.
The above-described points E1, E2, E3 and E4 have been installed with GNSS equipment and measured for a period of 40 min. Then positions E2 and E3 were logging and sending data for four consecutive days applying a logging period of three times 30 min per day. For reasons of clarity, the following processing examples are showing selected samples of 10 min for each of the mentioned points taken from the first 40 min interval.
At first, the GNSS raw data are processed by applying the software RTKLib [
44] developed by T. Takasu and A. Yasuda at the Laboratory of Satellite Navigation, Tokyo University of Marine Science and Technology, Japan. The RTKLib offers a sophisticated post-processing module, RTKPOST, that applies ambiguity fixing strategies, to achieve the required accuracy for structural monitoring. Depending on the distance between the GNSS base station and the rover point, accuracies in the region of one to five millimeters are possible. To eliminate the main error sources of GNSS position, this package applies double differencing as introduced above in
Section 3.2 within an extended Kalman filter. A detailed description of the applied algorithms may be found in [
44].
The resulting point positions from GNSS processing are usually represented as Earth-centered Earth-fixed coordinates, referring to the WGS84 ellipsoid. As these coordinates have no direct relation to the observed structure, the resulting coordinates have been rotated, in a manner that the
x- and
y-coordinates are representing the longitudinal and transversal axes of the Neckartal bridge, respectively, and the
z-component represents the vertical axis.
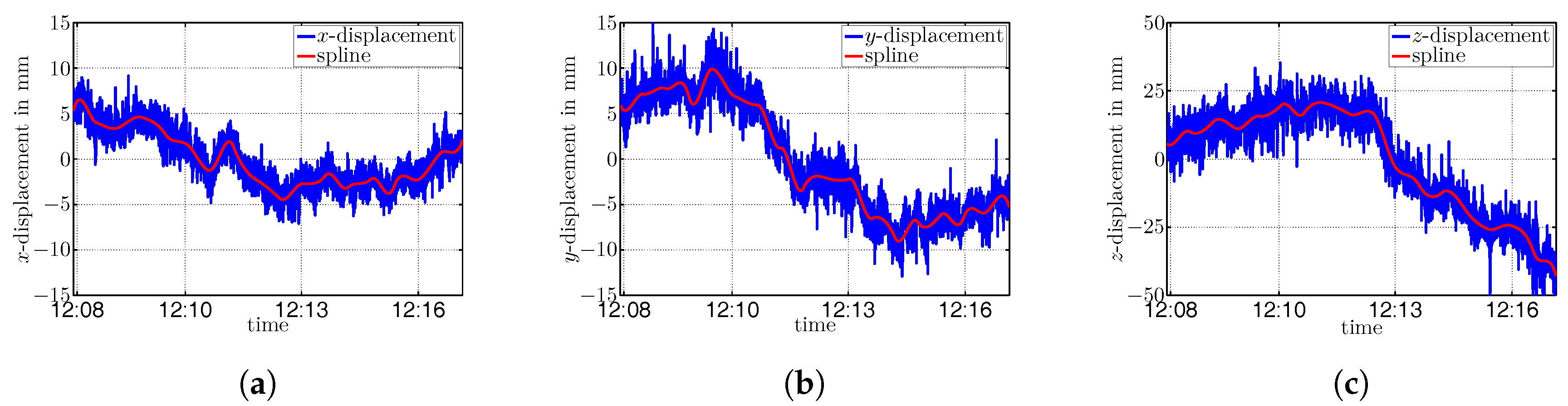
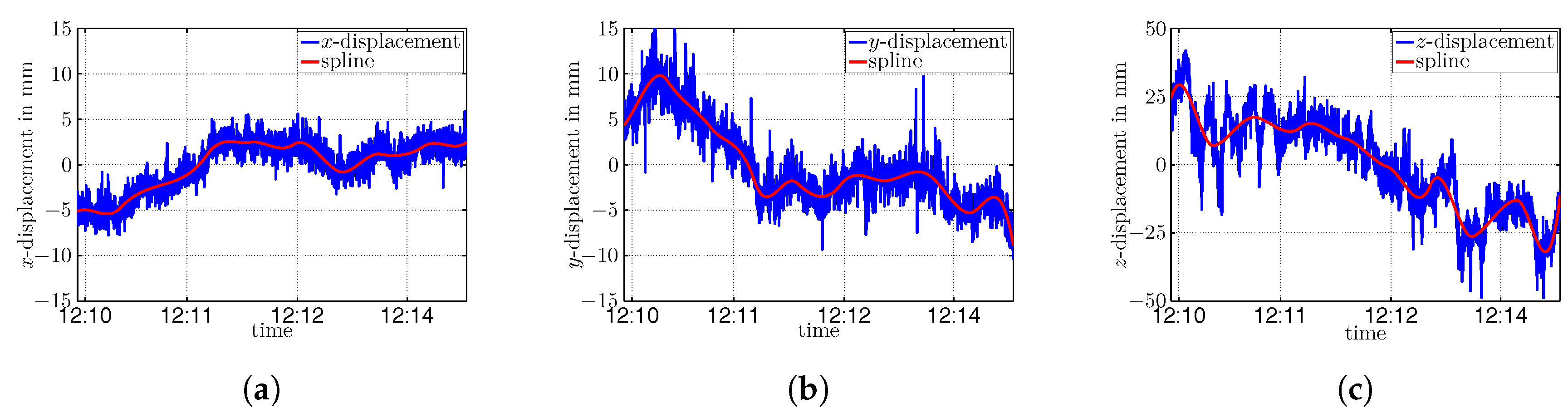
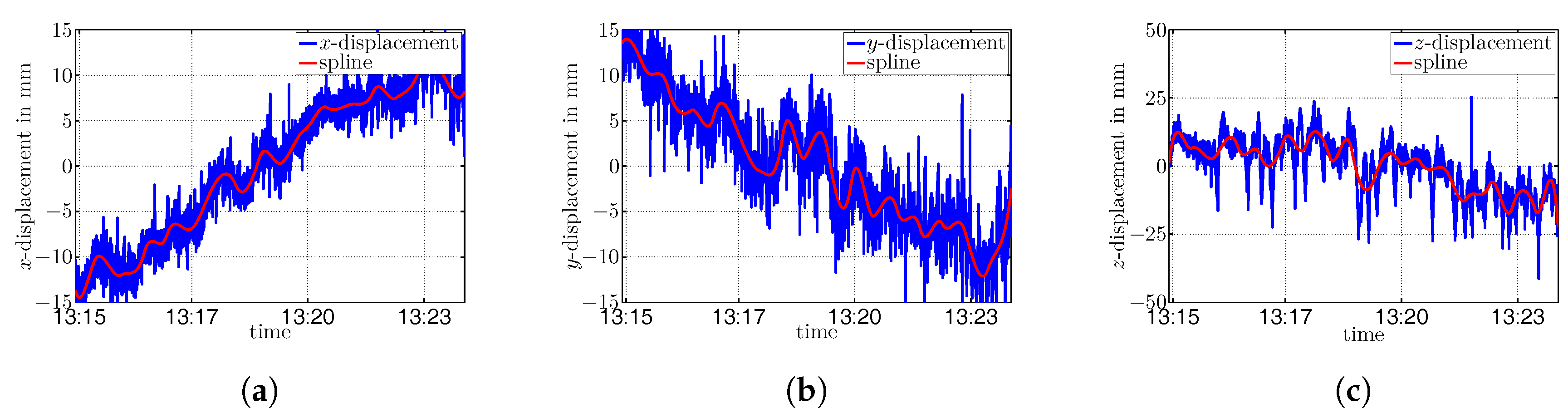
Figure 16,
Figure 17 and
Figure 18 show the resulting time series of the transformed point positions
x,
y and
z for E2, E3 and E4.
As can be seen in
Figure 16,
Figure 17 and
Figure 18, besides several short wave vibrations, there are also superposed significant low-frequency oscillations resulting from unknown sources, but that could be caused by a varying dilution of precision as indicated by Casciati and Fuggini in [
46]. Furthermore, the wind forces the bridge to swing, and temperature effects cause strains in the load-carrying concrete pillars. Oscillations induced by the heavy traffic on the Autobahn A81 and multipath effects could be further sources of these long wave signals. For example, Ni et al. compare in [
47] displacements detected by a GPS system to the displacements detected by a vision-based system. Both systems correlate well with each other, but Ni et al. observed additional low-frequency oscillations in the GPS measurements that were not present in the vision-based measurements.
Keeping this in mind, it becomes obvious that for professional and efficient vibration monitoring, samples are best taken during nighttime, when there is almost no traffic on the bridge, or the bridge should be closed during this measurement campaign. However, to demonstrate the usability of the developed GNSS sensor network for dynamic structural monitoring, these long-wave effects are simply eliminated from the data samples before applying frequency analysis.
In order to eliminate the long-wave signals from the time series of each coordinate component of the point positions
x,
y and
z, we introduced a cubic spline approximation [
48] as also shown in
Figure 16,
Figure 17 and
Figure 18. The spline is generated by
n cubic polynomials
that partially approximate the point position
x,
y and
z over time as shown in Equation (
5):
where vector
comprises the
n sets of polynomial parameters
,
,
and
. These parameters are determined within a least squares adjustment of the coordinates of the point position at the respective point of time,
,
and
. For the y-coordinate component, for example, the system of observation equations reads as Equation (
6):
With . The index i denotes the respective cubic polynomial depending on the point of time. The length of each of the n polynomials can be predefined by using a time interval that determines the length of each polynomial. In the following example, was set to 30 s. Therefore, each of the n-polynomials in the generated spline represents the point position during this period. Furthermore, the quantity denotes the estimated residual for the introduced observation y. For the residual, impliesthat its expected value is equal to zero, that is .
With , we introduce a set of C-continuity conditions between two neighboring polynomials and . For the data presented in the following, we applied , and continuity at the transition of each polynomial to the polynomial . continuity hereby forces identical value of the polynomial representation, that is . continuity forces the identical value of the first derivative in time, that is , and continuity forces the same value for the second derivative in time as .
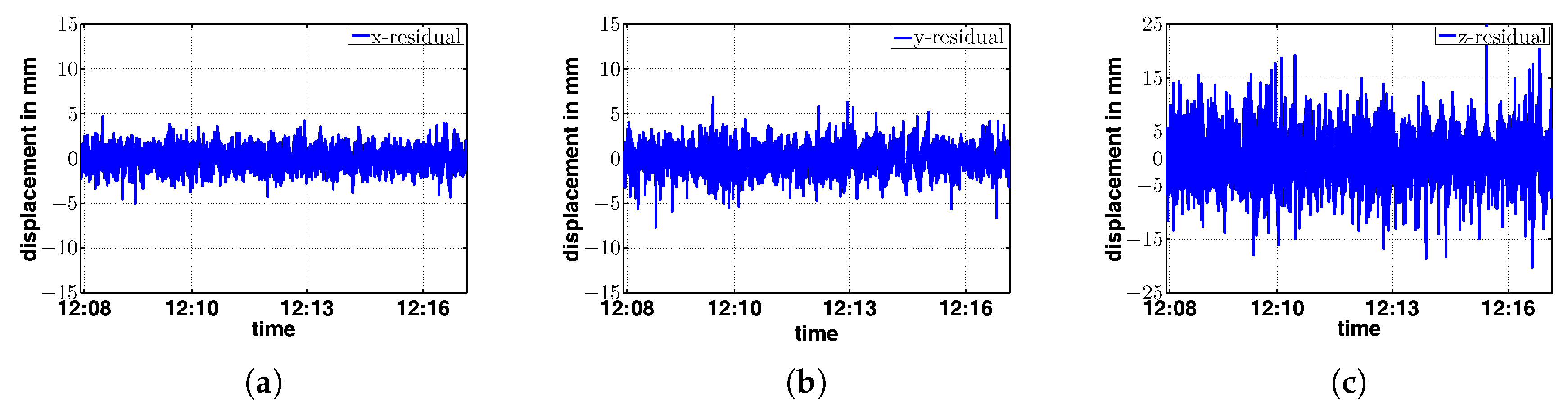
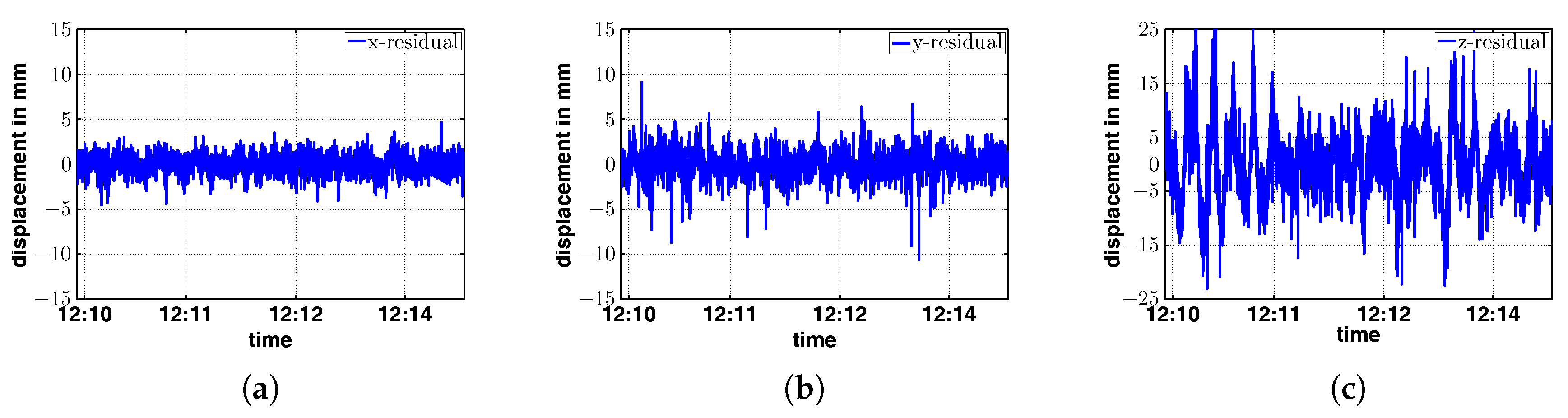
Applying spline approximation of the time series of the point positions leads to a smooth representation over time. The estimated spline parameters
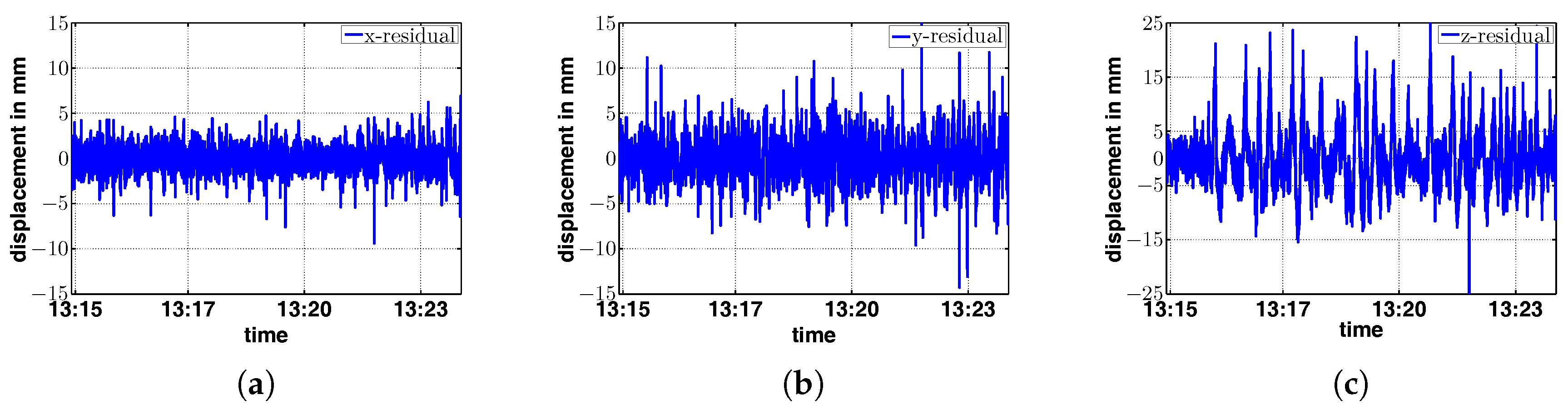
p are carrying the long-wave components of the recorded signals. The remaining residuals, resulting from the least squares adjustment, are now free of average, as can be seen in
Figure 19,
Figure 20 and
Figure 21, which show the remaining residuals for the measurement points E1, E2 and E4.
The residuals can now be further analyzed, for example by performing a discrete time frequency analysis by applying Equation (
7):
Here, the quantity
denotes the residual for the coordinate component
y, resulting from the above-described least squares adjustment. The quantity
denotes the amplitude of the investigated frequency
, and
gives the respective phase offset. In
Figure 22,
Figure 23 and
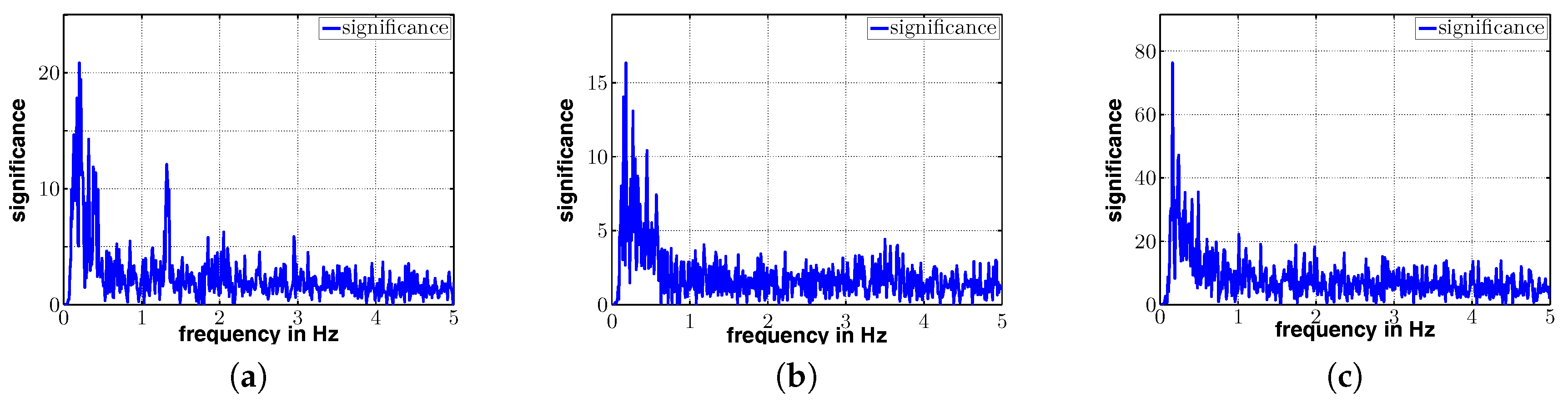
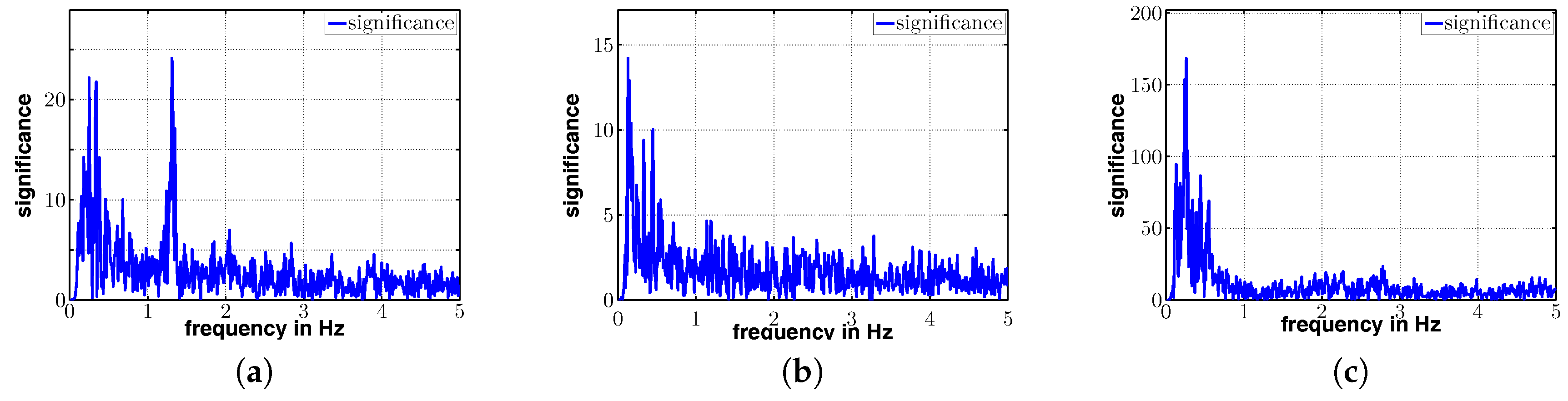
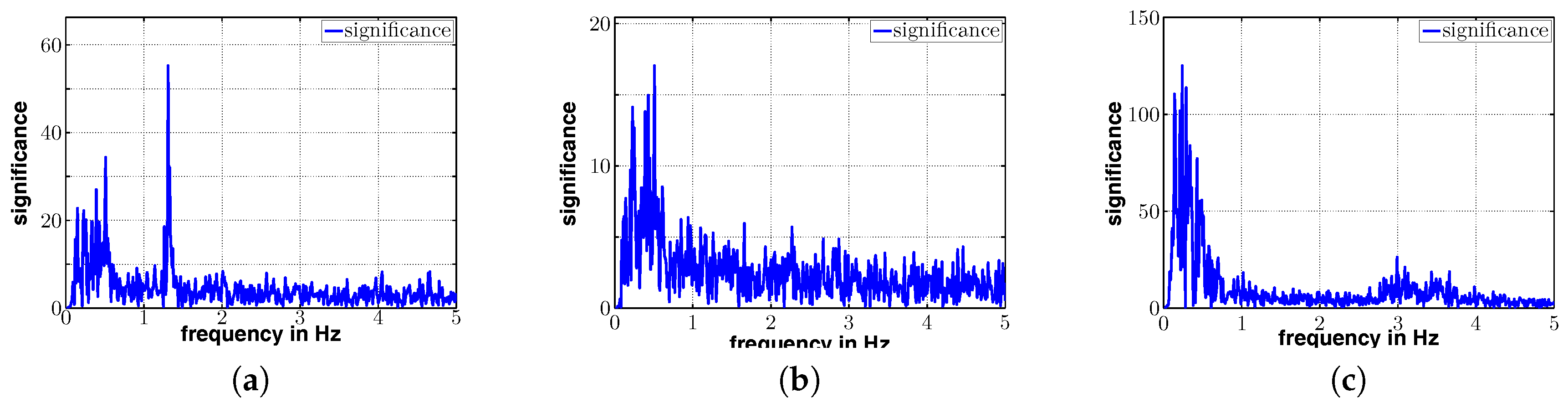
Figure 24, the results from the analysis of frequencies up to 5 Hz are shown for the GNSS points E2, E3 and E4.
Our analysis reveals a frequency response in the
x-direction at 1.31 Hz, visible in
Figure 22a,
Figure 23a and
Figure 24a. The significance/amplitude at position E2 is lower compared to the amplitudes at positions E3 and E4. This reflects the fact that E2 is above a pillar and as such is expected to make fewer movements, whereas nodes E3 and E4 were placed between two pillars. The biggest movements were expected at position E4, which also has the greatest amplitude compared to the others.
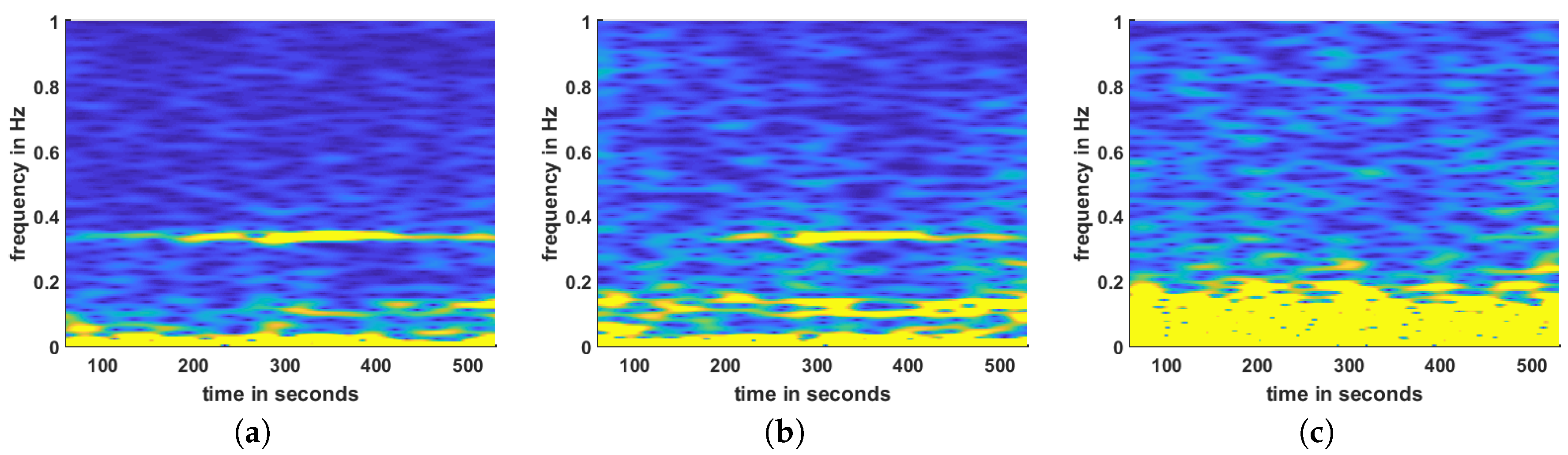
By further analyzing the GNSS spectrograms achieved by using a short-time Fourier transform on the measurement data at position E4, an additional peak is visible at 0.33 Hz mainly in the lateral movement of the bridge, but also in longitudinal movement.
Figure 25 visualizes the spectrograms for the
x-,
y- and
z-direction at Position E4 from 0 to 1 Hz.
Figure 25c also clearly shows the GNSS inherent additional noise in the
z-direction (up/down) compared to the
x- and
y-direction.
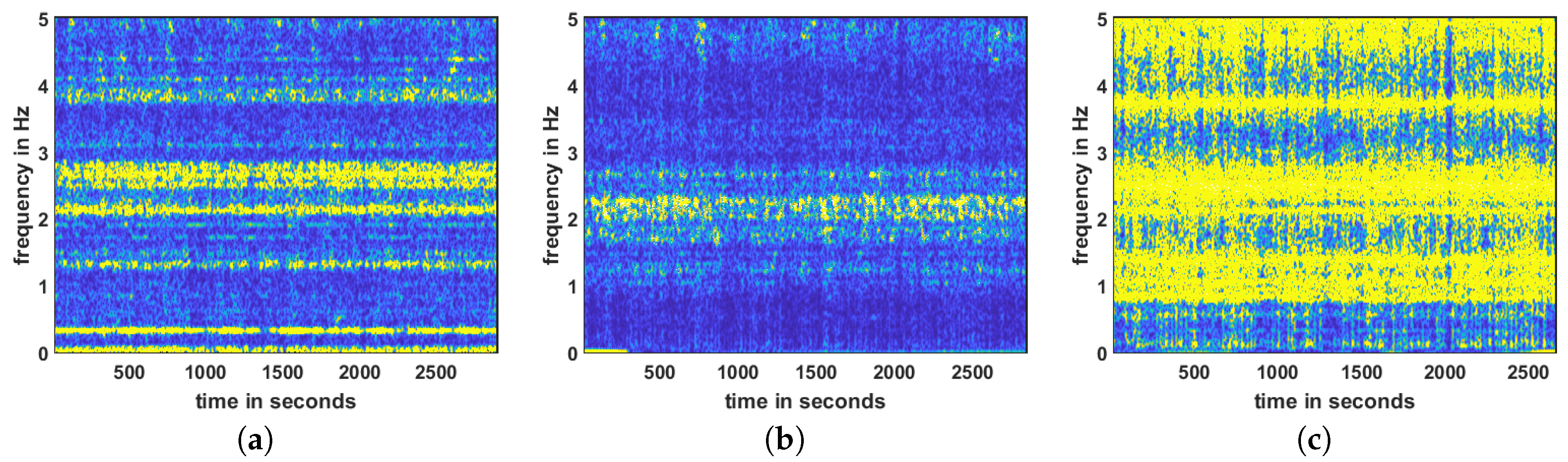
Comparing GNSS and Acceleration Measurements
As there are no structural response data available for this bridge, we placed an accelerometer at Position E4, to measure its movements in the
x-,
y- and
z-directions, to verify the GNSS measurement data. The following
Figure 26a–c show the frequency responses over time from 0 to 5 Hz as measured by the accelerometer. In the
x-direction (
Figure 26a), the sensor clearly shows the 1.3-Hz response that was also detected by the GNSS sensor, as can be seen for example in
Figure 24a. Furthermore, the
x-direction acceleration data show a significant frequency at 0.33 Hz, as well as several frequencies above 2 Hz. The 0.33-Hz resonance is also visible in the GNSS dataset as for example visualized in
Figure 25a,b, but the frequencies above 2 Hz could not be detected by the GNSS sensors.
In the
y-direction, the accelerometer measurements indicate a resonance frequency around 2 Hz, and in the
z-direction, there appears to be several frequencies in the range from 1 to 5 Hz. Although the acceleration measurements in the
z-direction are generally noisier, four frequencies can be seen, the first at around 1.3 Hz, the second around 2.5 Hz, the third at 3.7 Hz and the fourth around 5 Hz. The GNSS data show in the
z-direction some response in the area between 2.7 Hz and 4 Hz (
Figure 24c), but clearly not as significant as the measurements taken with the accelerometer.
In summary, the data presented here clearly demonstrate the feasibility of the GNSS measurements to detect low frequencies and underpins the assumption that the detected frequencies are real structural resonance frequencies of the bridge. The comparison of the accelerometer and GNSS sensor measurements shows that the GNSS sensor has a better sensitivity for lower frequencies than the acceleration sensor, but is limited in its response to higher frequency signals probably due to their lower amplitudes.