A Novel Dual–Parallelogram Passive Rocking Vibration Isolator: A Theoretical Investigation and Experiment
Abstract
:1. Introduction
2. Kinematic Analysis of a Dual–Parallelogram Passive Rocking Vibration Isolator
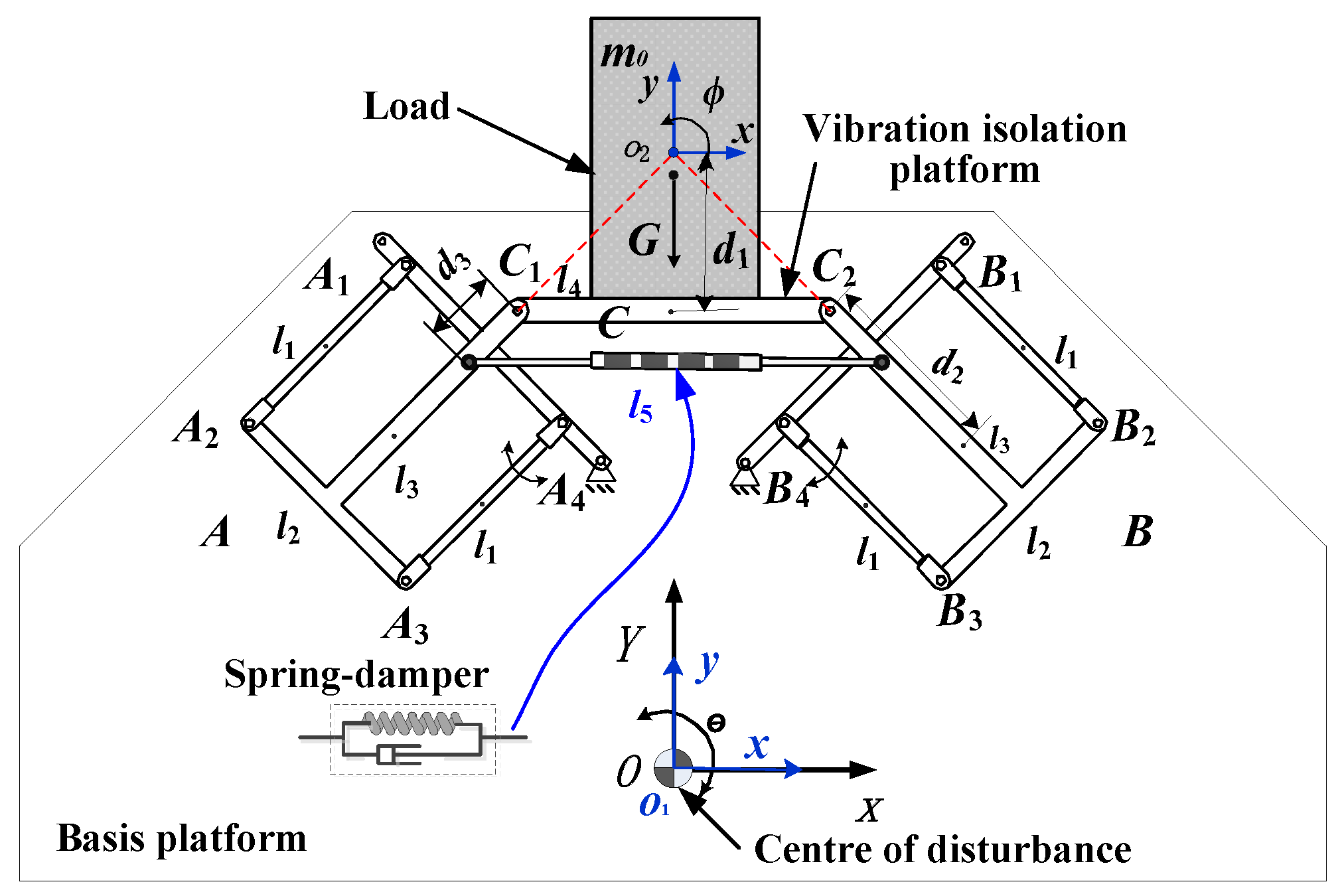
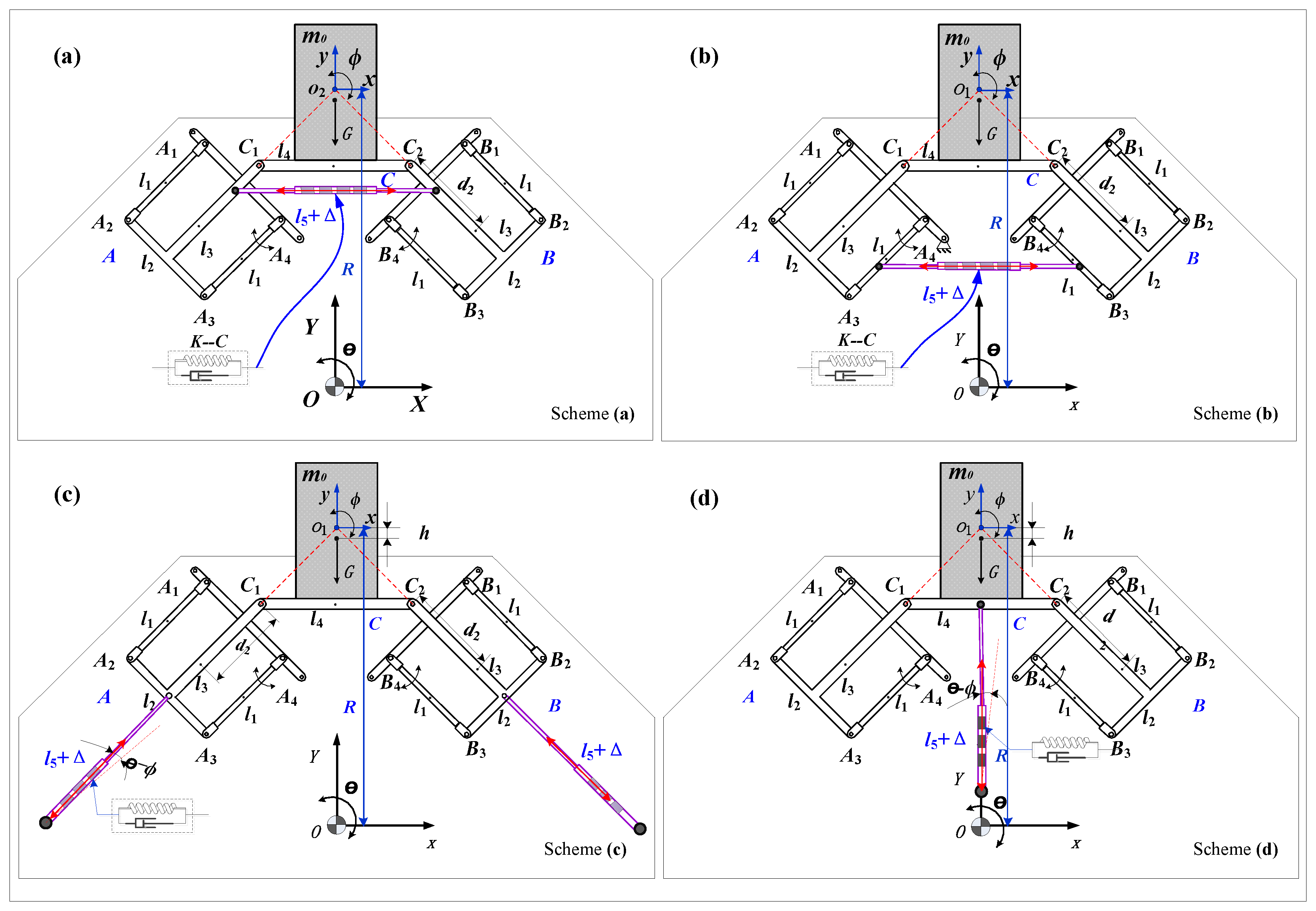
2.1. Description of Mechanism
2.2. Kinematic Analysis
3. QZS Analysis
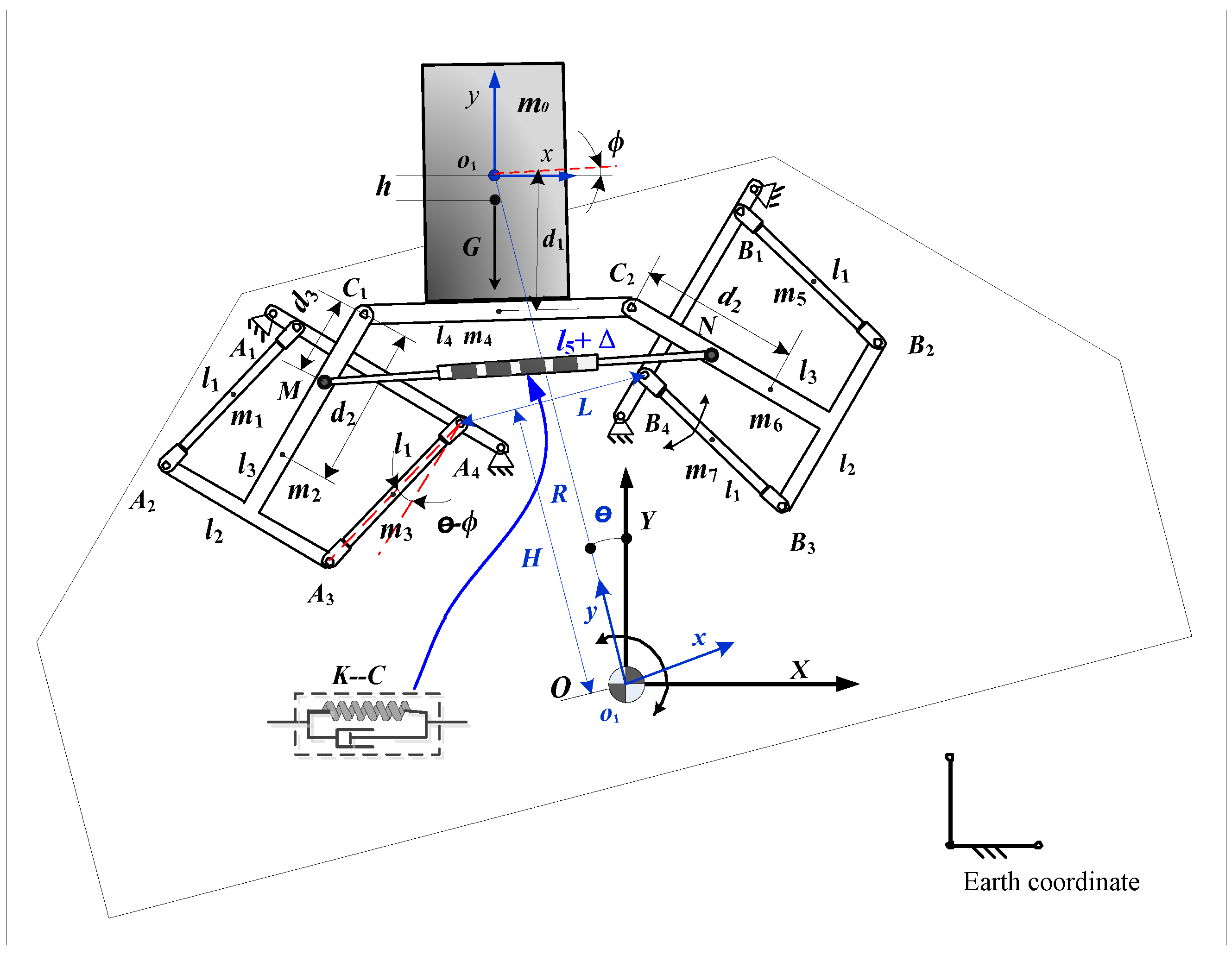
3.1. Modeling of the QZS System
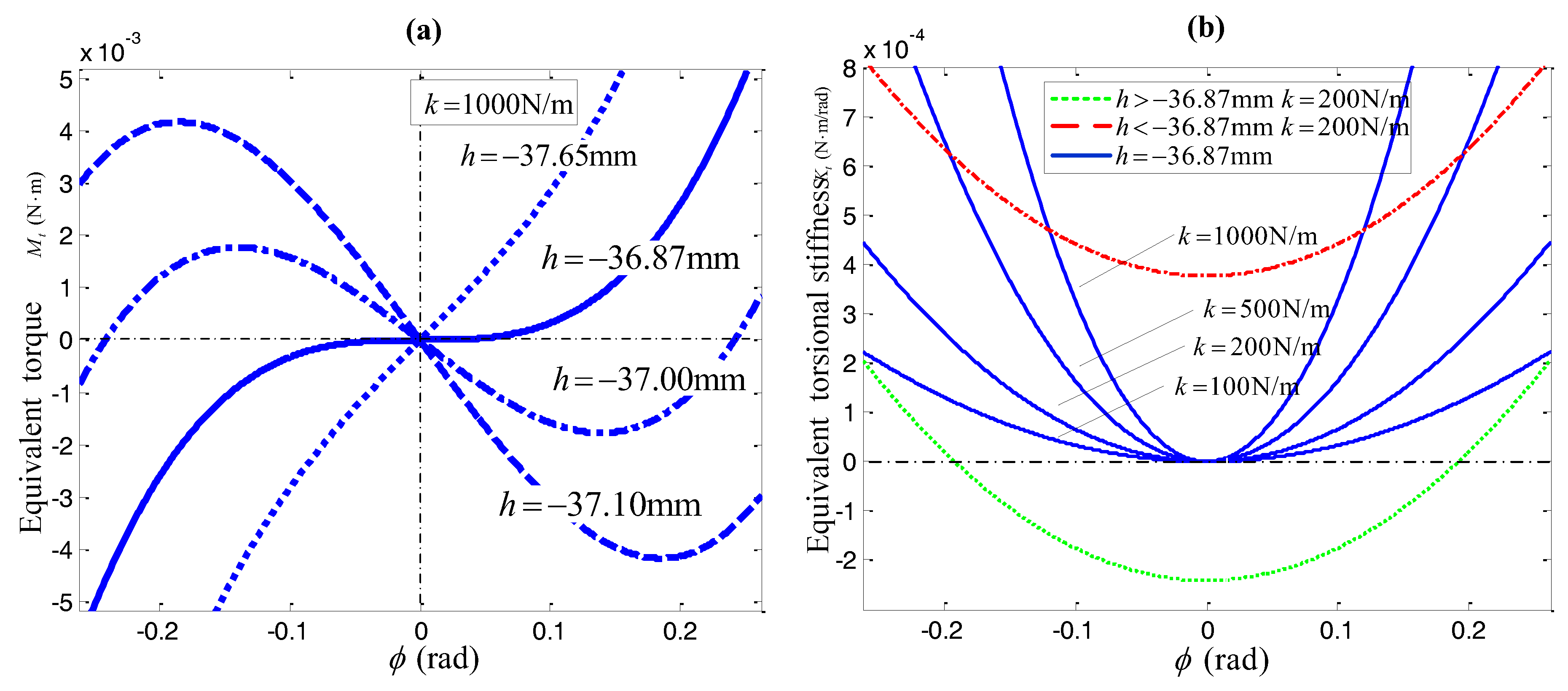
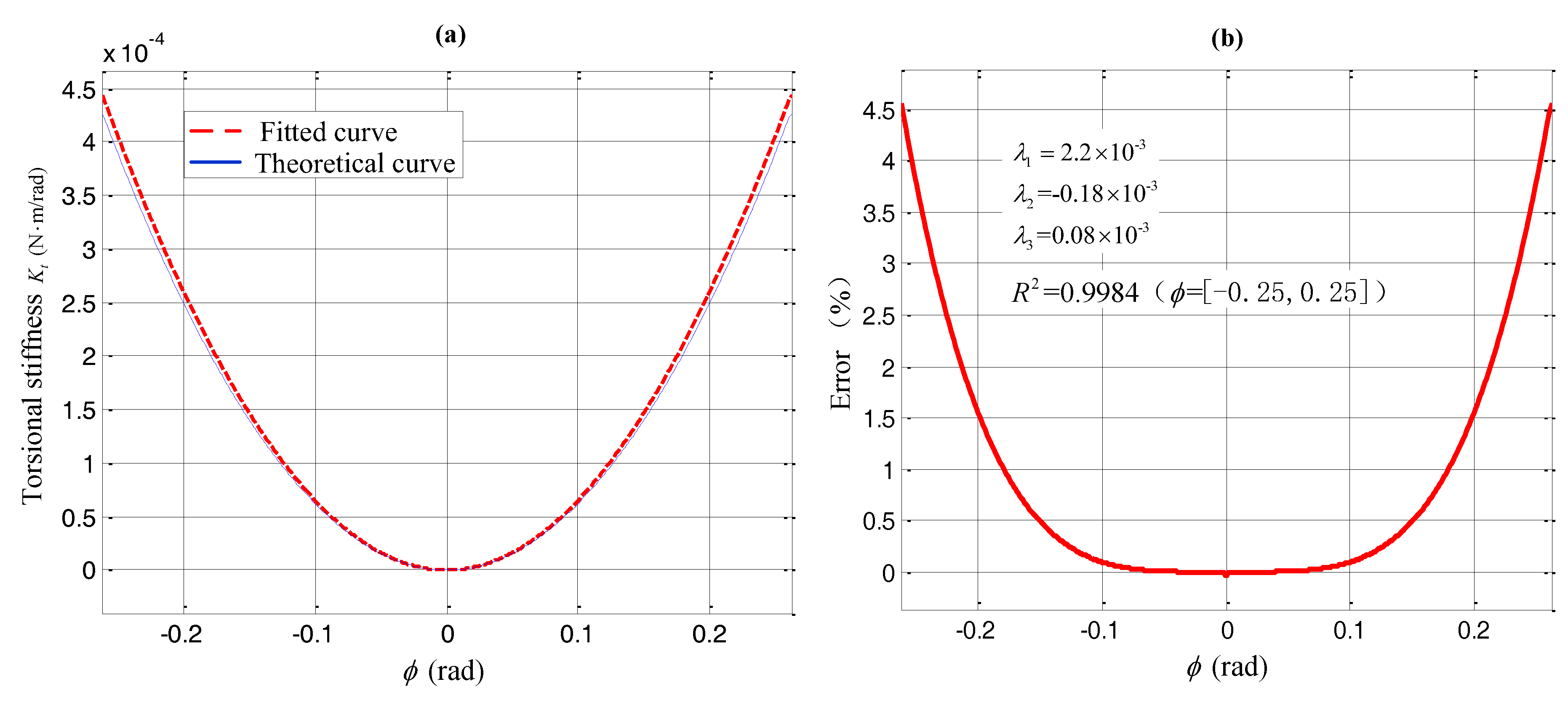
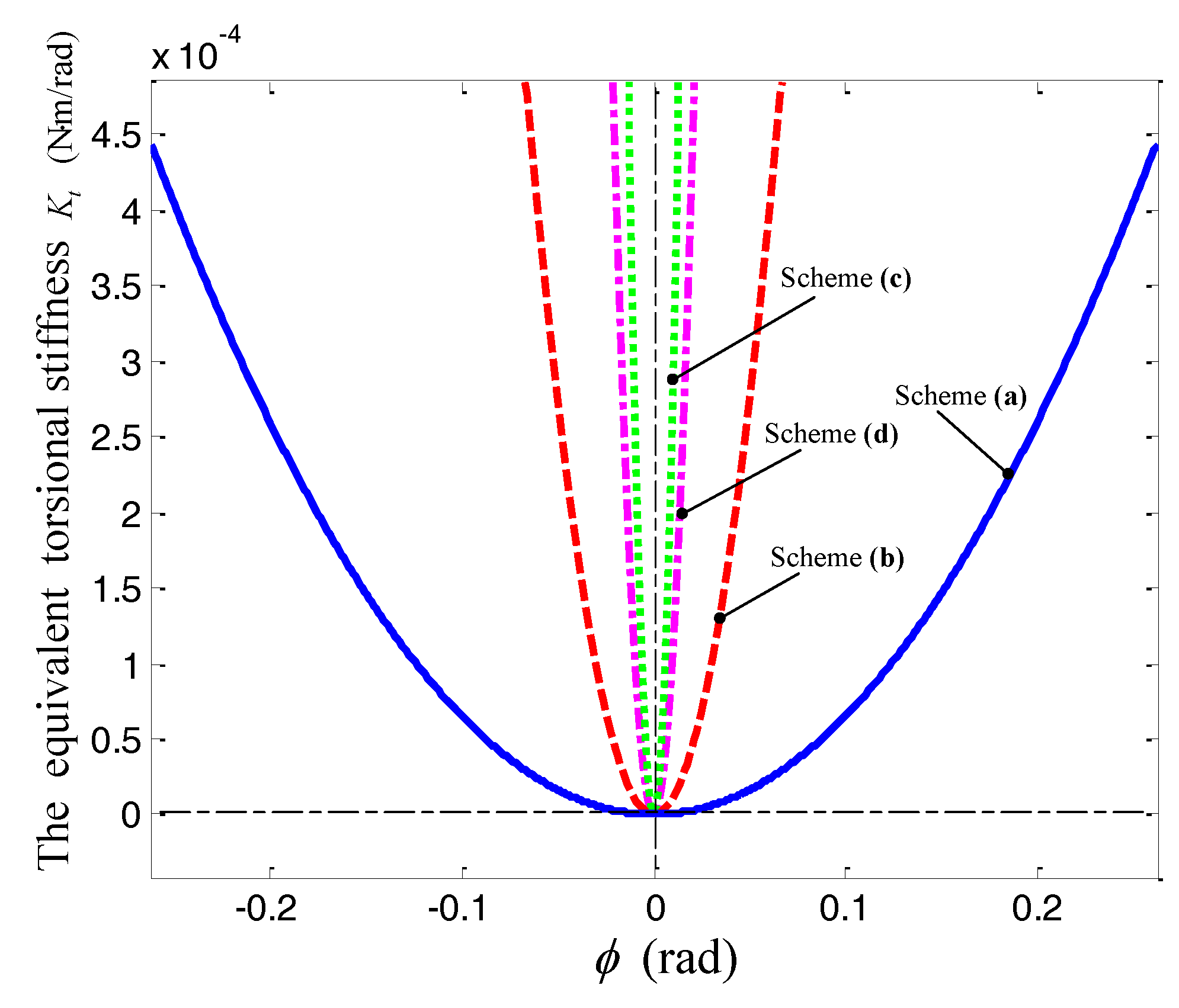
3.2. Comparative Analysis of Four Linear Spring Configuration Schemes to Achieve QZS
4. Dynamic Modeling of the Vibration Isolator
4.1. Dynamic Model Based on a Lagrangian Equation
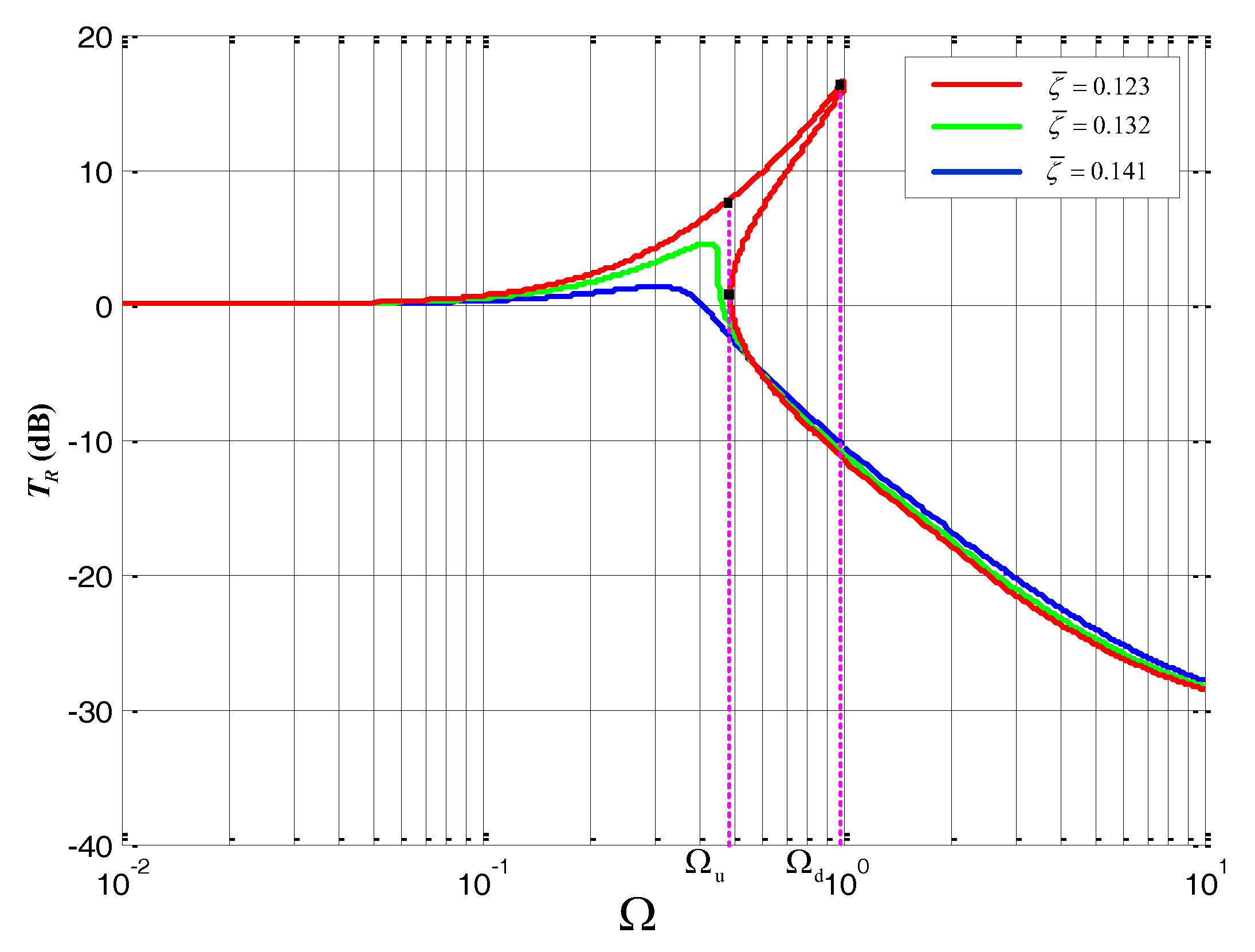
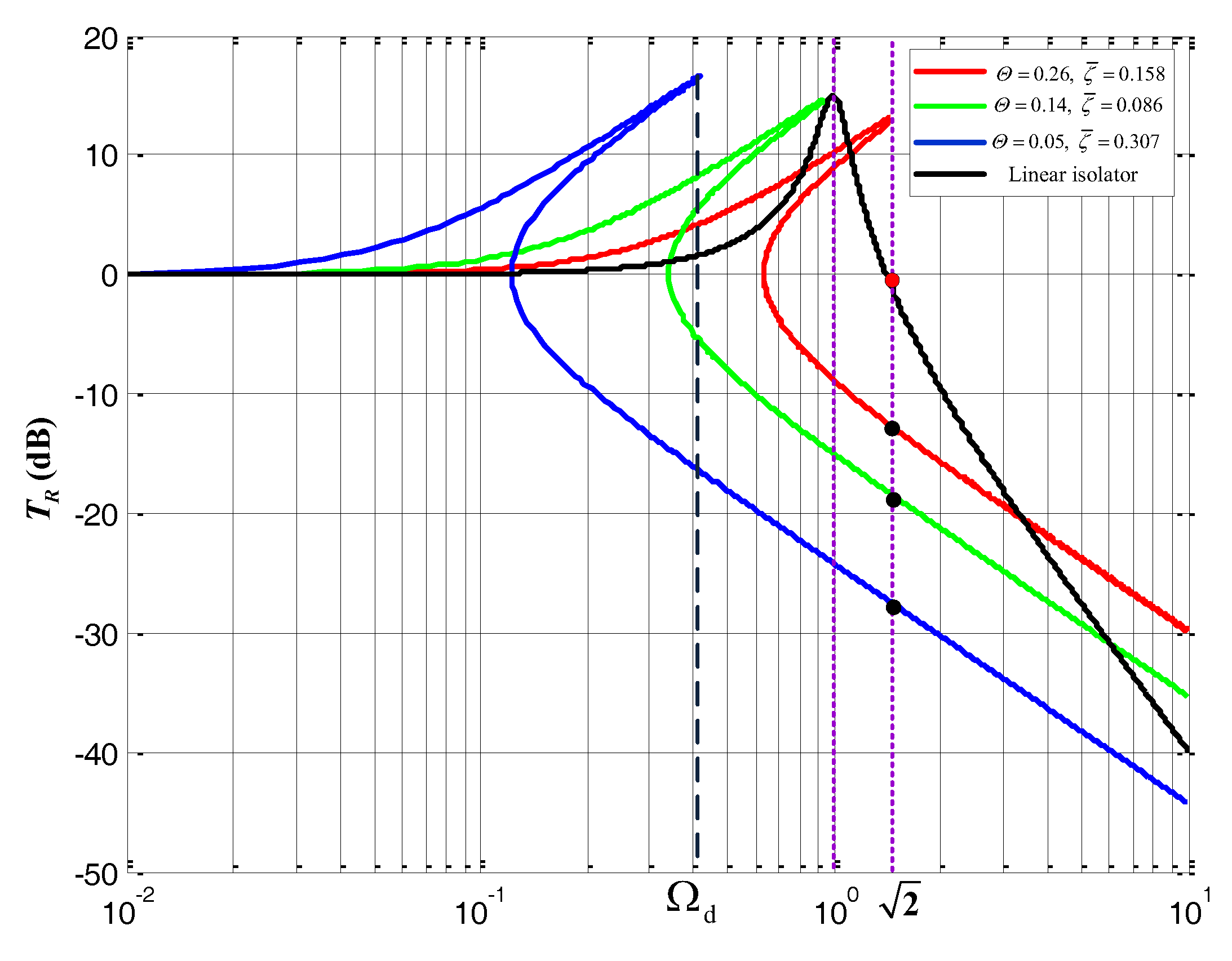
4.2. Analysis of Transmissibility
5. Simulation and Experiment
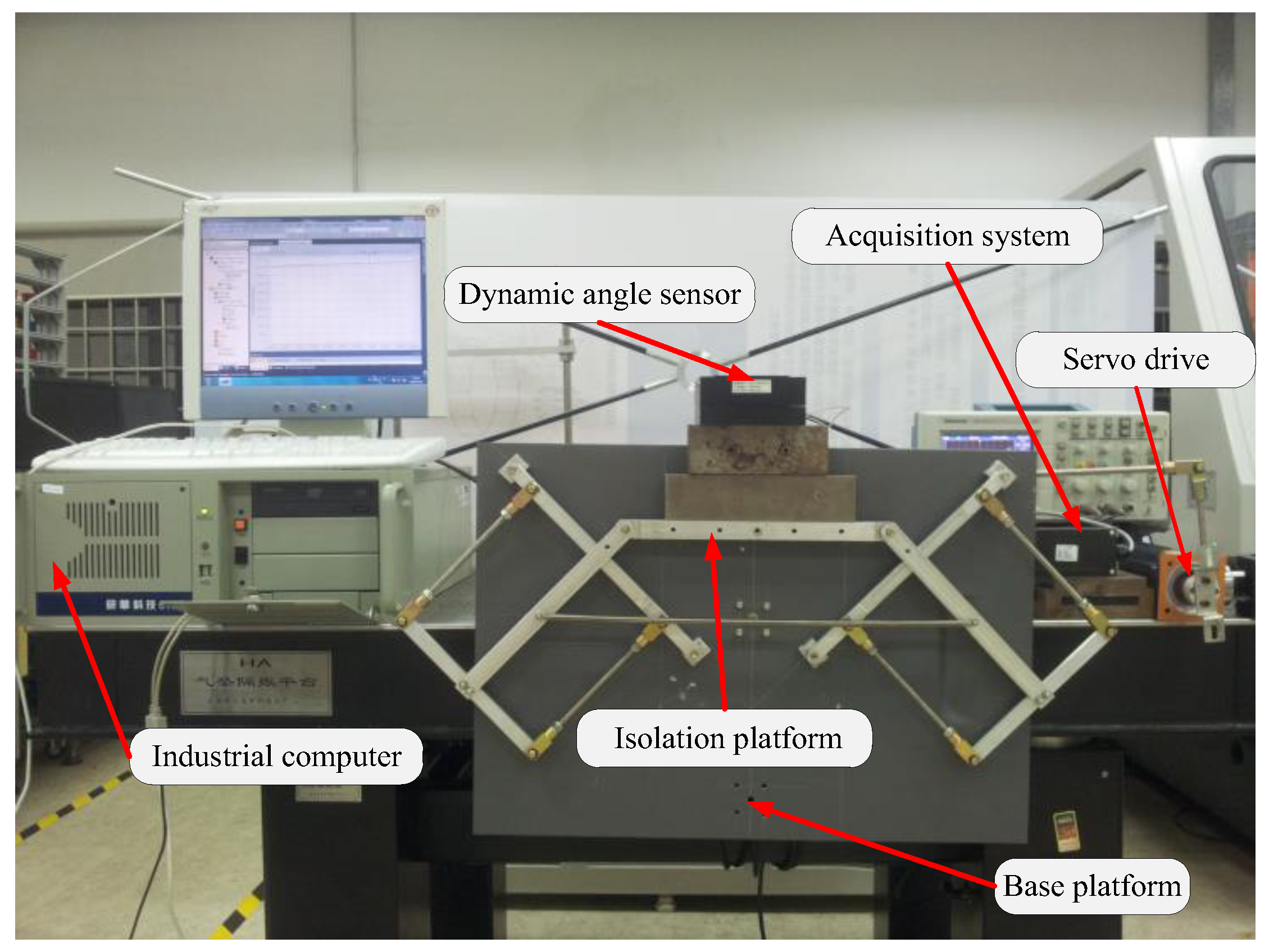
5.1. Experimental Design
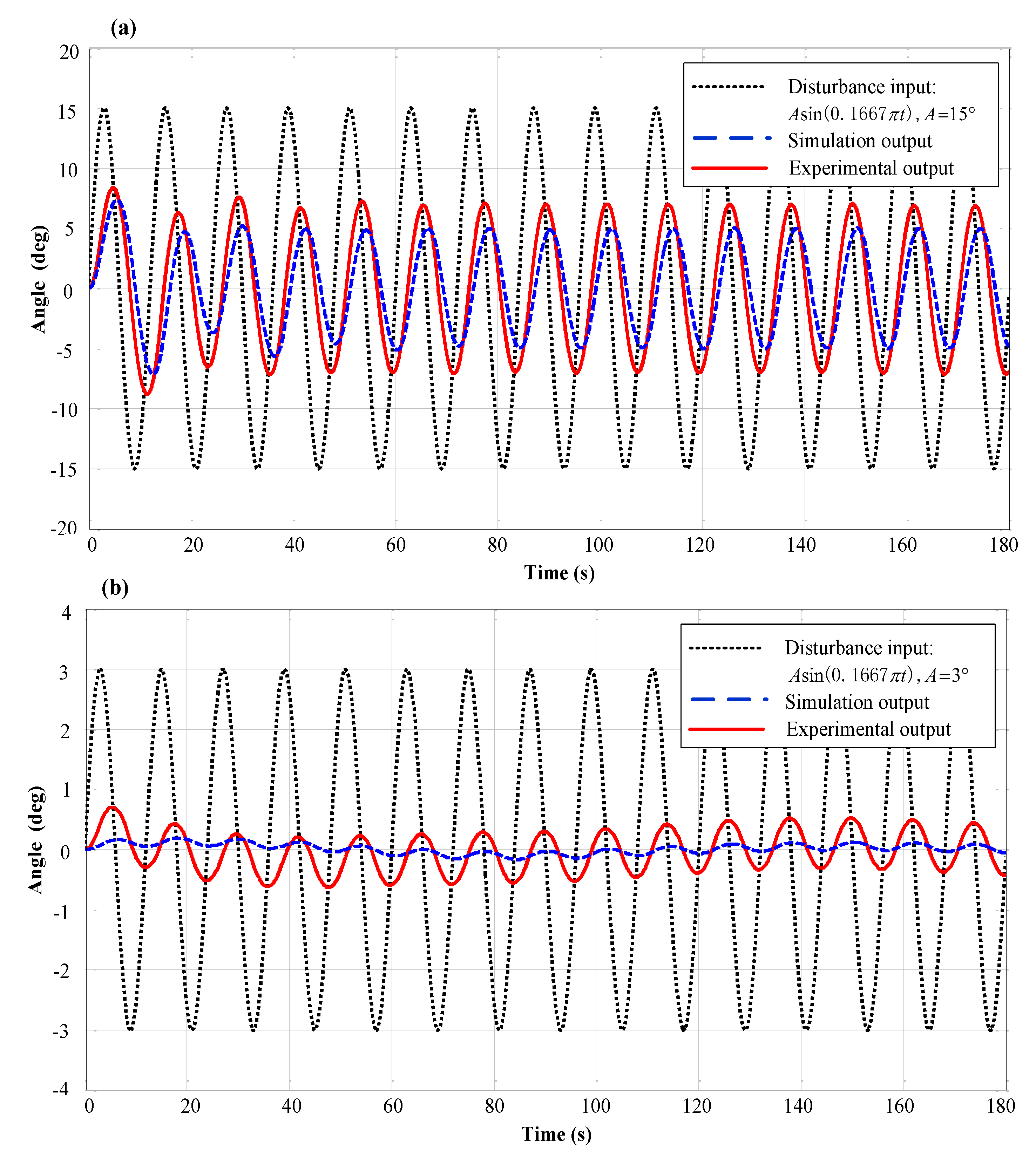
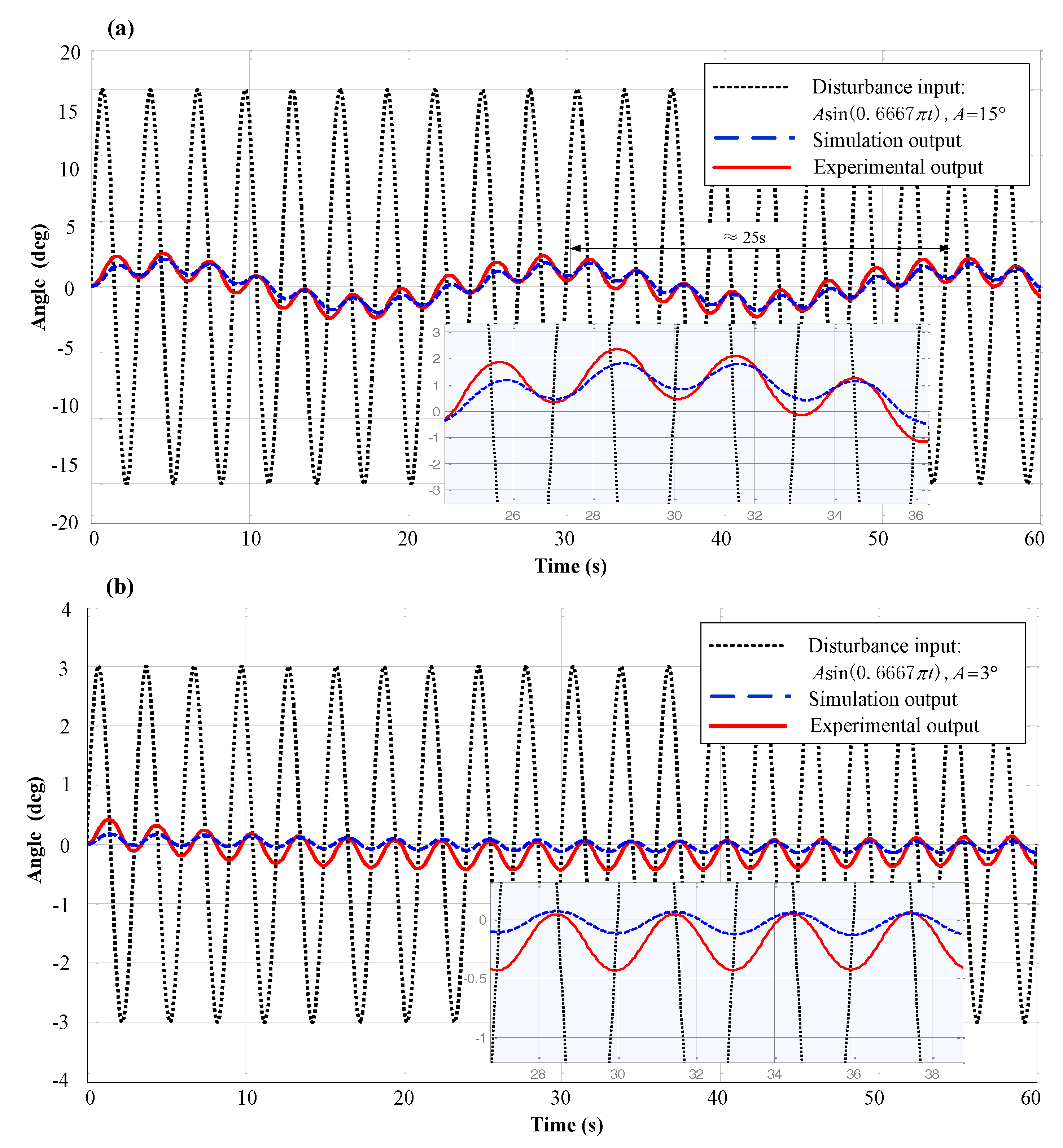
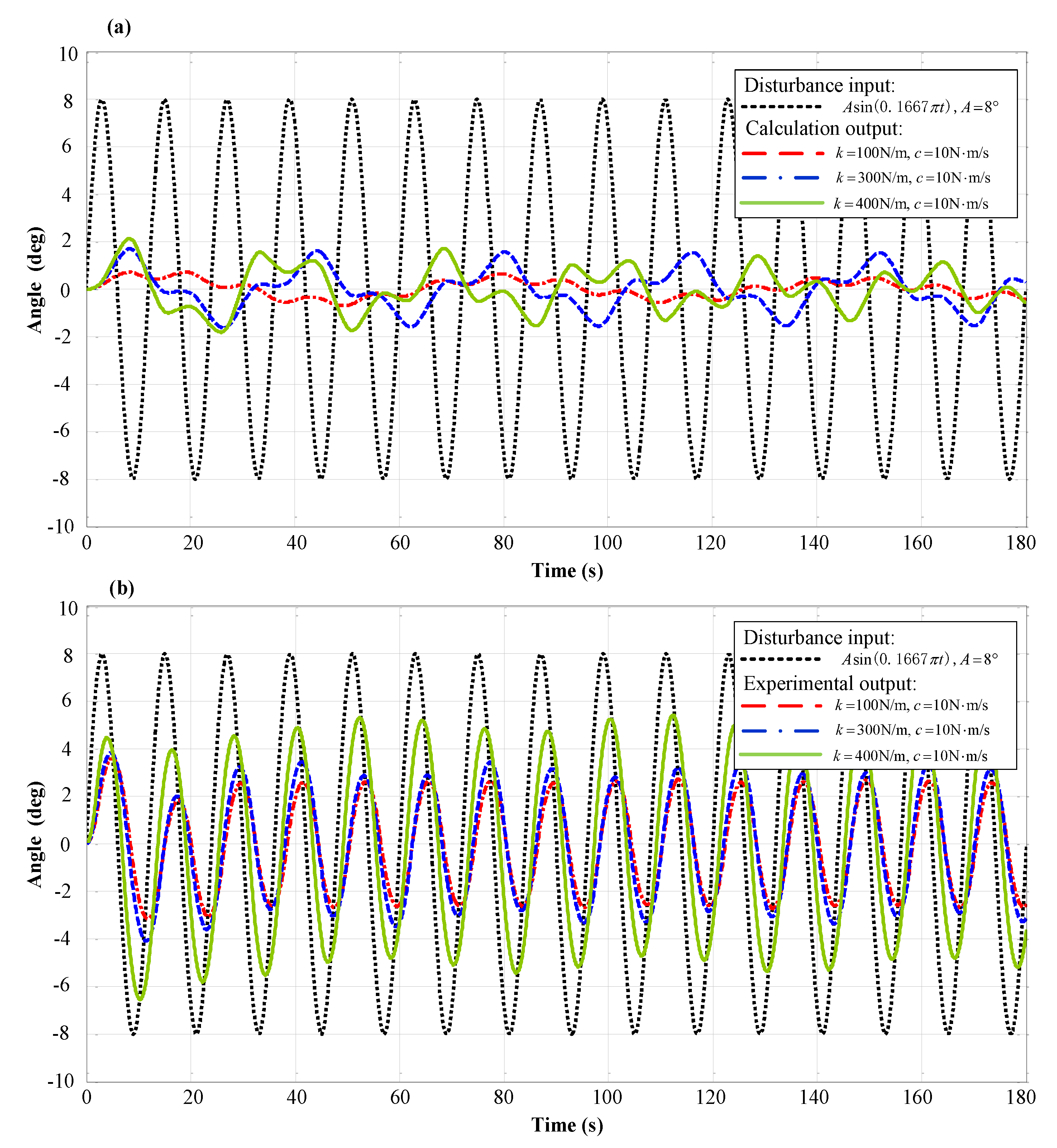
5.2. Simulation and Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rivin, E.I. Passive Vibration Isolation; ASME Press: New York, NY, USA, 2001. [Google Scholar]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Ahn, H.J.; Lim, S.H.; Park, C. An integrated design of quasi-zero stiffness mechanism. J. Mech. Sci. Technol. 2016, 30, 1071–1075. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Shin, K. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets. J. Sound Vib. 2008, 315, 712–720. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Q.; Xu, D.; Hu, C.; Zhang, M. Modeling and analysis of a negative stiffness magnetic suspension vibration isolator with experimental investigations. Rev. Sci. Instrum. 2012, 83, 095108. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Chen, X.; Shan, Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J. Sound Vib. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Hua, H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 2013, 332, 3359–3376. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study. J. Sound Vib. 2014, 333, 1132–1148. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Xu, D.; Bishop, S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar] [CrossRef]
- Winterflood, J.; Barber, T.; Blair, D.G. Using Euler buckling springs for vibration isolation. Class. Ouant. Grav. 2002, 19, 1639. [Google Scholar] [CrossRef]
- Hosain, M.A.; Sirr, A.; Ju, L.; Blair, D.G. Novel Euler-LaCoste linkage as a very low frequency vertical vibration isolator. Rev. Sci. Instrum. 2012, 83, 085108. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Hu, H.; Wu, K.; Wang, G.; Wang, L.J. Ultra-low frequency vertical vibration isolator based on LaCoste spring linkage. Rev. Sci. Instrum. 2014, 85, 104502. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhu, Y.; Xu, D.; Hu, J.; Min, W.; Pang, L. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J. Mech. Sci. Technol. 2013, 27, 813–824. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, L.; Yu, Y.; Shi, M.; Zhou, J. The Stiffness and Damping Characteristics of a Dual-Chamber Air Spring Device Applied to Motion Suppression of Marine Structures. Appl. Sci. 2016, 6, 74. [Google Scholar] [CrossRef]
- Liu, J.; Ju, L.; Blair, D.G. Vibration isolation performance of an ultra-low frequency folded pendulum resonator. Phys. Lett. A 1997, 228, 243–249. [Google Scholar] [CrossRef]
- Barone, F.; Giordano, G.; Acernese, F.; Romano, R. Large band high sensitivity motion measurement and control of spacecrafts and satellites. Proc. SPIE 2016, 9803, 98034G. [Google Scholar]
- Losurdo, G.; Bernardini, M.; Braccini, S.; Bradaschia, C.; Casciano, C.; Dattilo, V.; Gennai, A. An inverted pendulum preisolator stage for the VIRGO suspension system. Rev. Sci. Instrum. 1999, 70, 2507–2515. [Google Scholar] [CrossRef]
- Takamori, A.; Raffai, P.; Márka, S.; DeSalvo, R.; Sannibale, V.; Tariq, H.; Takahashi, R. Inverted pendulum as low-frequency pre-isolation for advanced gravitational wave detectors. Nuclear Instrum. Methods Phys. Res. Sect. A 2007, 582, 683–692. [Google Scholar] [CrossRef]
- Bosetti, P.; Biral, F.; Bortoluzzi, D. Design, manufacturing, and performance verification of a Roberts linkage for inertial isolation. Precis. Eng. 2014, 38, 138–147. [Google Scholar] [CrossRef]
- Winterflood, J.; Blair, D.G. A long-period conical pendulum for vibration isolation. Phys. Lett. A 1996, 222, 141–147. [Google Scholar] [CrossRef]
- Wu, X.W.; Cheng, Y.J.; Chen, Y.J.; Wang, W. A research of conical pendulum low-frequency horizontal displacement apparatus. Mach. Design Manuf. 2007, 10, 053. [Google Scholar]
- Matta, E.; De Stefano, A.; Spencer, B.F. A new passive rolling-pendulum vibration absorber using a non-axial-symmetrical guide to achieve bidirectional tuning. Earthq. Eng. Struct. D 2009, 38, 1729–1750. [Google Scholar] [CrossRef]
- Shaw, A.D.; Neild, S.A.; Wagg, D.J. Dynamic analysis of high static low dynamic stiffness vibration isolation mounts. J. Sound Vib. 2013, 332, 1437–1455. [Google Scholar] [CrossRef]
- Harvey, P.S., Jr.; Wiebe, R.; Gavin, H.P. On the chaotic response of a nonlinear rolling isolation system. Phys. D Nonlinear Phenom. 2013, 256, 36–42. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D.; Ouyang, H.; Duan, Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017, 87, 633–646. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.E.; Bab, S.; Friswell, M.I. Vibration control of a rotor supported by journal bearings and an asymmetric high-static low-dynamic stiffness suspension. Nonlinear Dyn. 2016, 85, 525–545. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Bishop, S. A torsion quasi-zero stiffness vibration isolator. J. Sound Vib. 2015, 338, 121–133. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.E.; Bab, S. Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. J. Vib. Control 2016. [Google Scholar] [CrossRef]
- Xue, S.D.; Ko, J.M.; Xu, Y.L. Optimum parameters of tuned liquid column damper for suppressing pitching vibration of an undamped structure. J. Sound Vib. 2000, 235, 639–653. [Google Scholar] [CrossRef]
- Wei, S.; Hua, L.L.; Hong, Z. Influence of sway motion on passive anti-rolling tank. J. Mar. Sci. Appl. 2006, 5, 17–22. [Google Scholar] [CrossRef]
- Lewis, E.V. The motion of ships in waves. In Principles of Naval Architecture; The Society of Naval Architect and Marin Engineers: New York, NY, USA, 1967; pp. 628–634. [Google Scholar]
| Geometrical Parameters (mm) | Mass Parameters (kg) | Moment of Inertia (kg·m2) |
|---|---|---|
| - | - | |
| - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Gao, P.; Hu, Y.; Li, B. A Novel Dual–Parallelogram Passive Rocking Vibration Isolator: A Theoretical Investigation and Experiment. Appl. Sci. 2017, 7, 367. https://doi.org/10.3390/app7040367
Wang S, Gao P, Hu Y, Li B. A Novel Dual–Parallelogram Passive Rocking Vibration Isolator: A Theoretical Investigation and Experiment. Applied Sciences. 2017; 7(4):367. https://doi.org/10.3390/app7040367
Chicago/Turabian StyleWang, Shuai, Peng Gao, Ying Hu, and Bing Li. 2017. "A Novel Dual–Parallelogram Passive Rocking Vibration Isolator: A Theoretical Investigation and Experiment" Applied Sciences 7, no. 4: 367. https://doi.org/10.3390/app7040367
APA StyleWang, S., Gao, P., Hu, Y., & Li, B. (2017). A Novel Dual–Parallelogram Passive Rocking Vibration Isolator: A Theoretical Investigation and Experiment. Applied Sciences, 7(4), 367. https://doi.org/10.3390/app7040367





