Seismic Damage Evaluation of Concrete-Encased Steel Frame-Reinforced Concrete Core Tube Buildings Based on Dynamic Characteristics
Abstract
:1. Introduction
2. Experimental Program
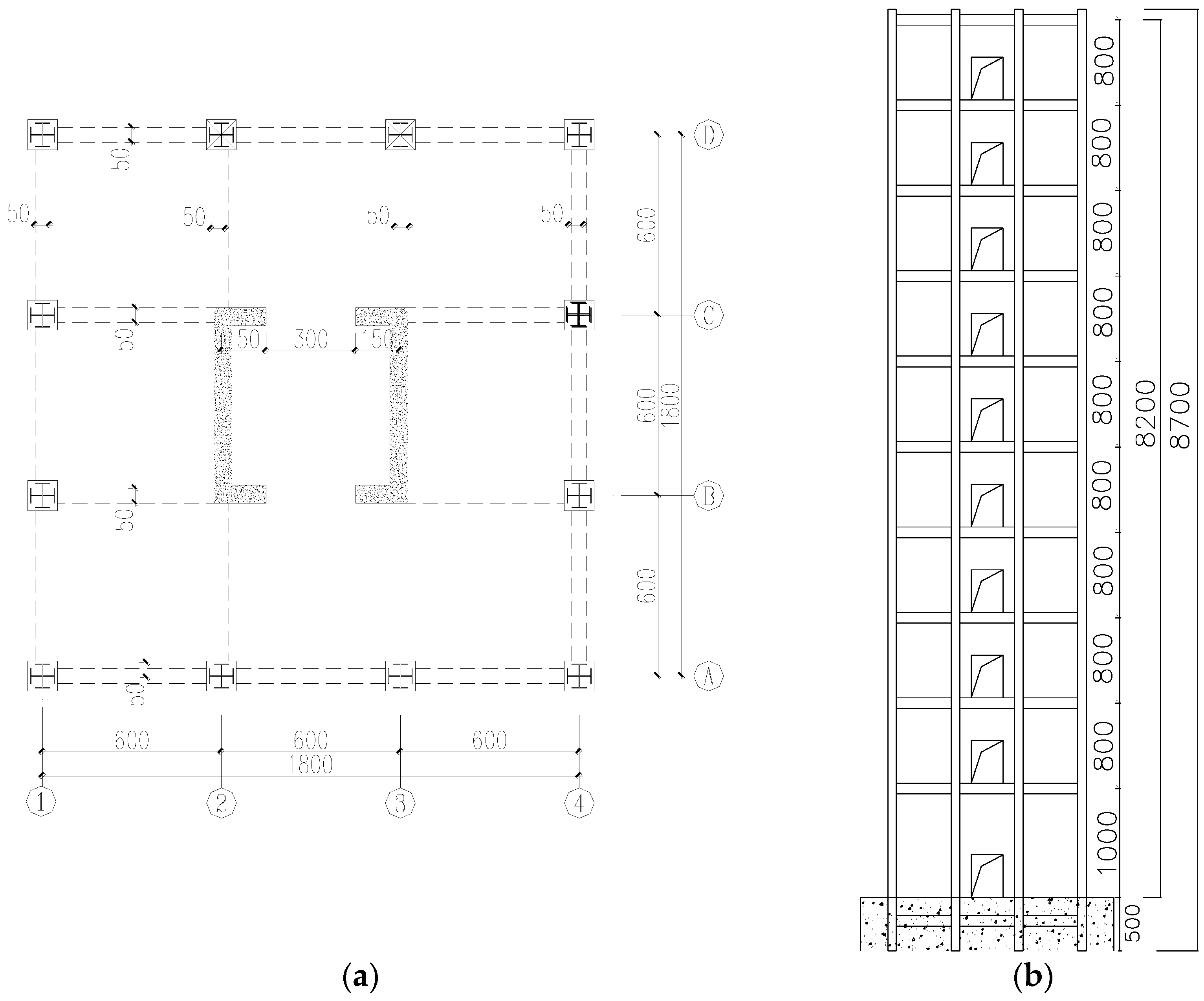
2.1. Details of Specimen
2.2. Test Setup and Procedure
3. Finite Element Analysis
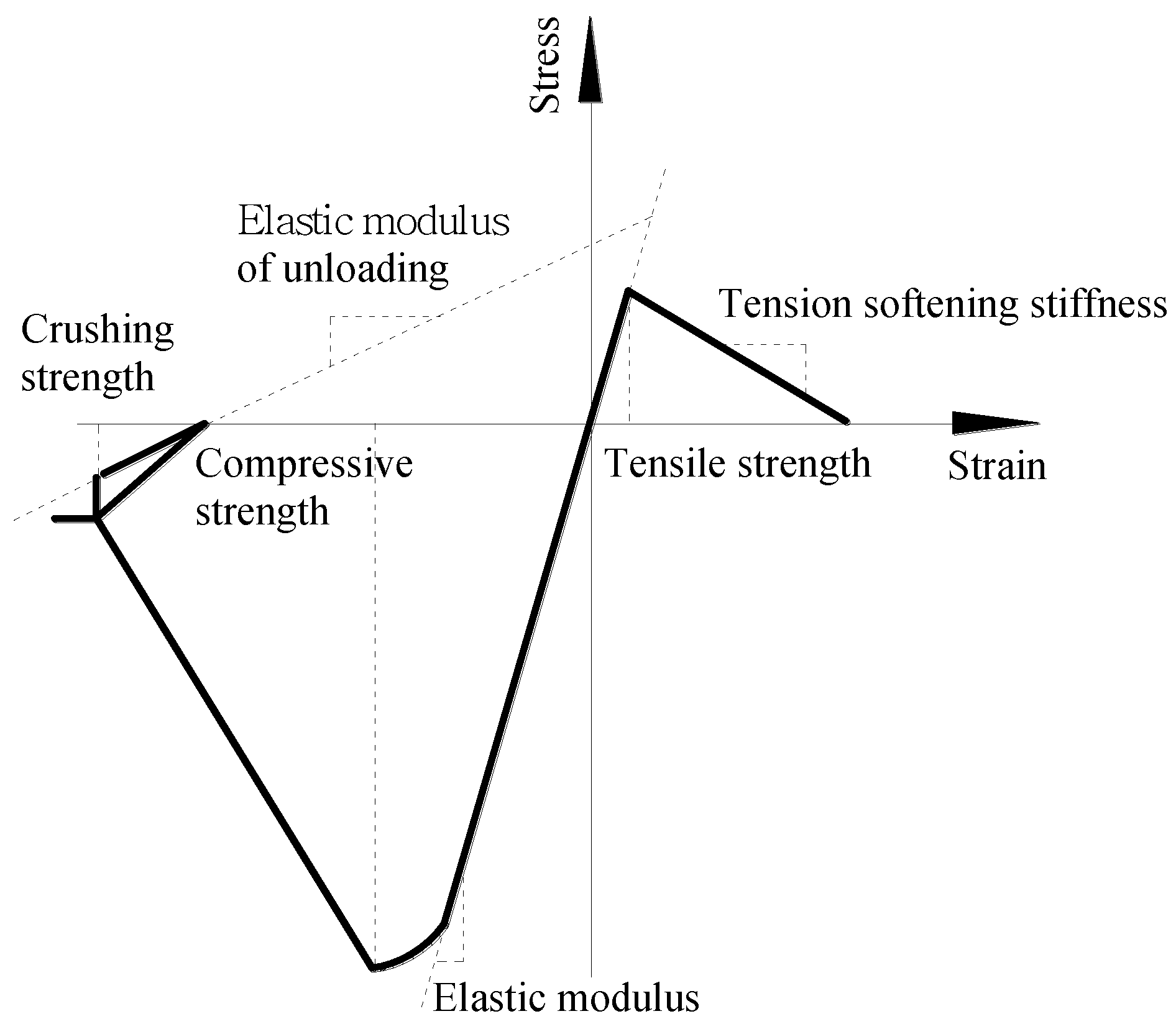
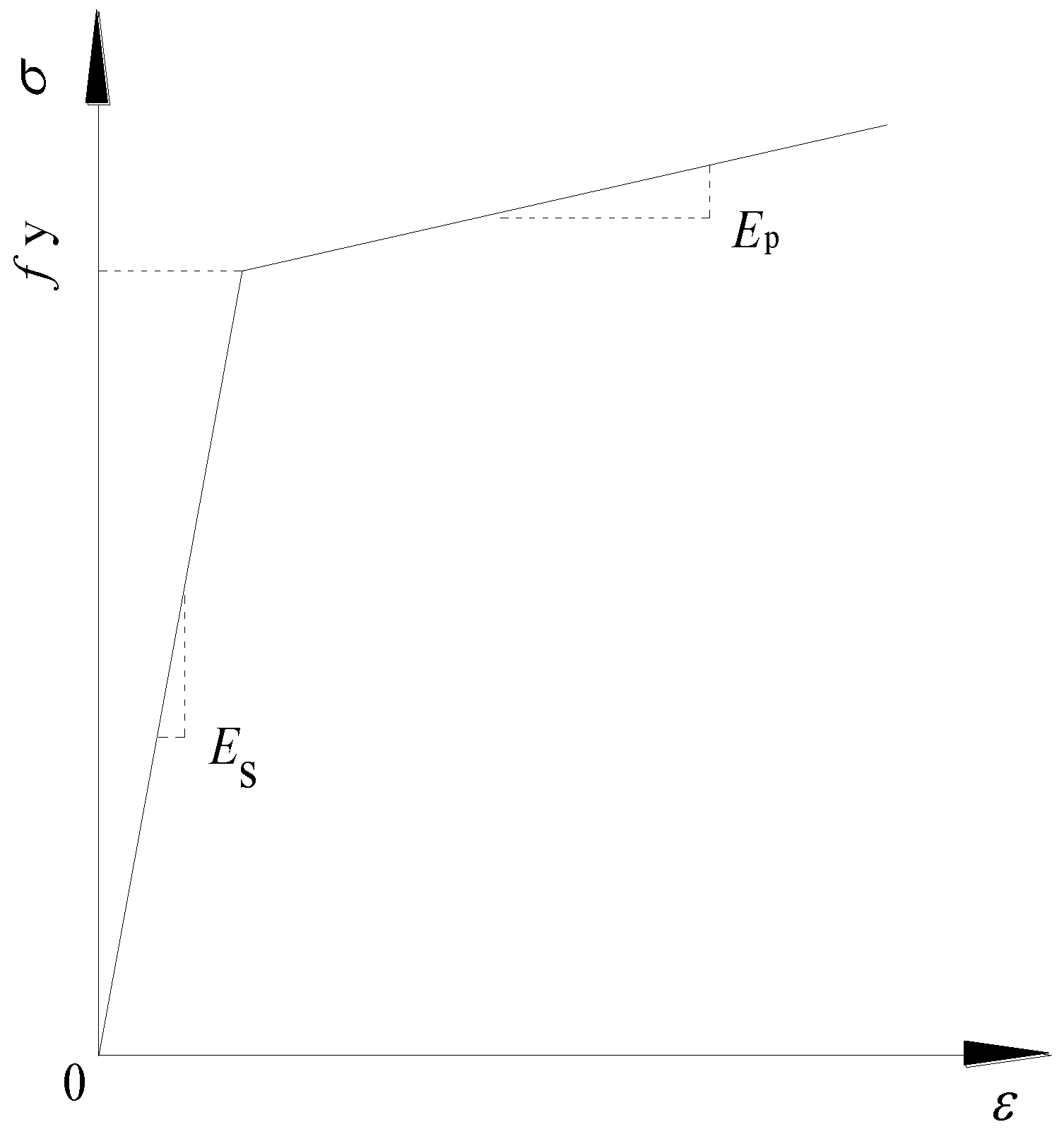
3.1. Material Modeling
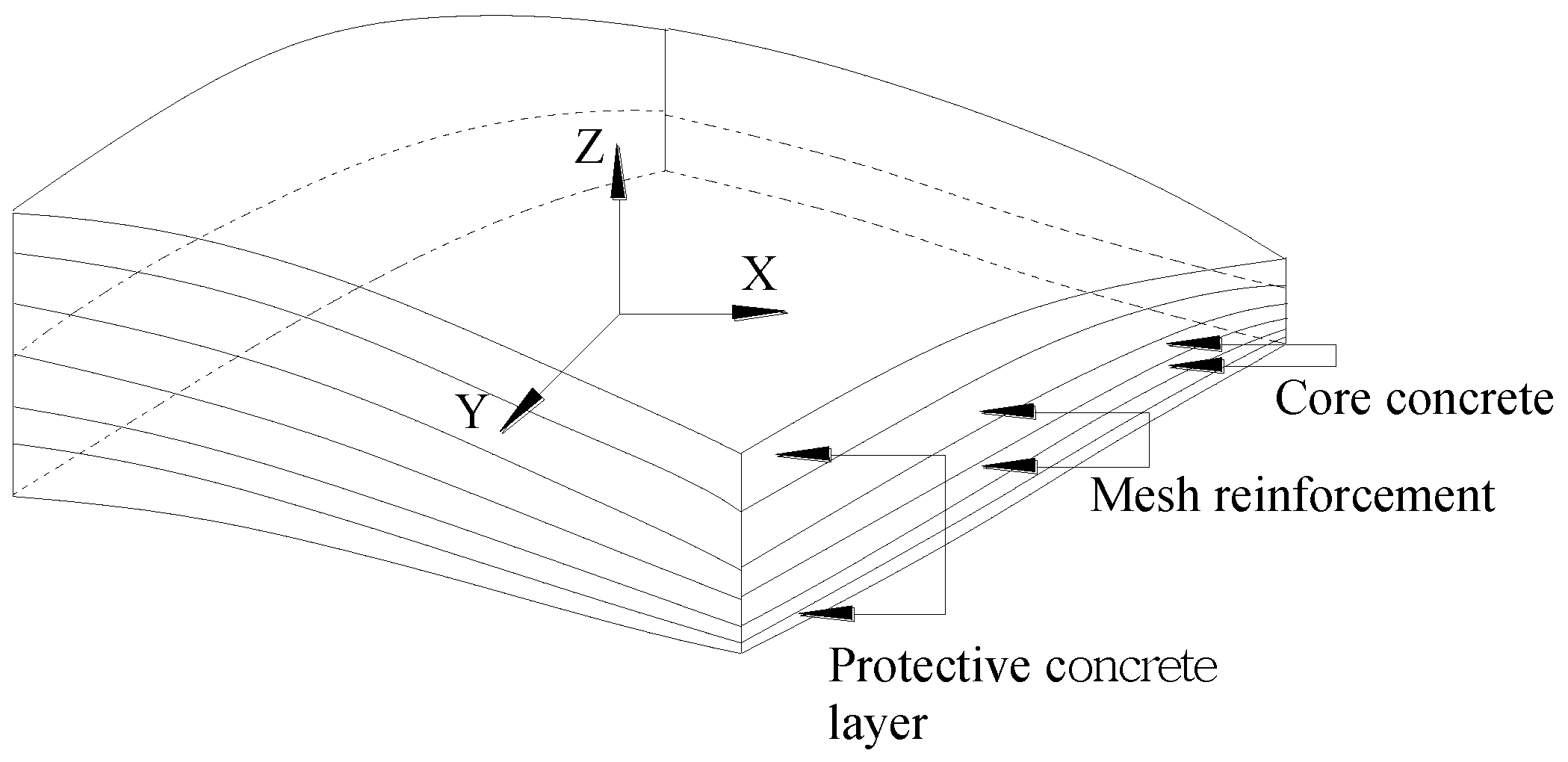
3.2. Elements of Component
3.3. Comparison between Experimental Investigations and FEA
4. Seismic Damage Evaluation
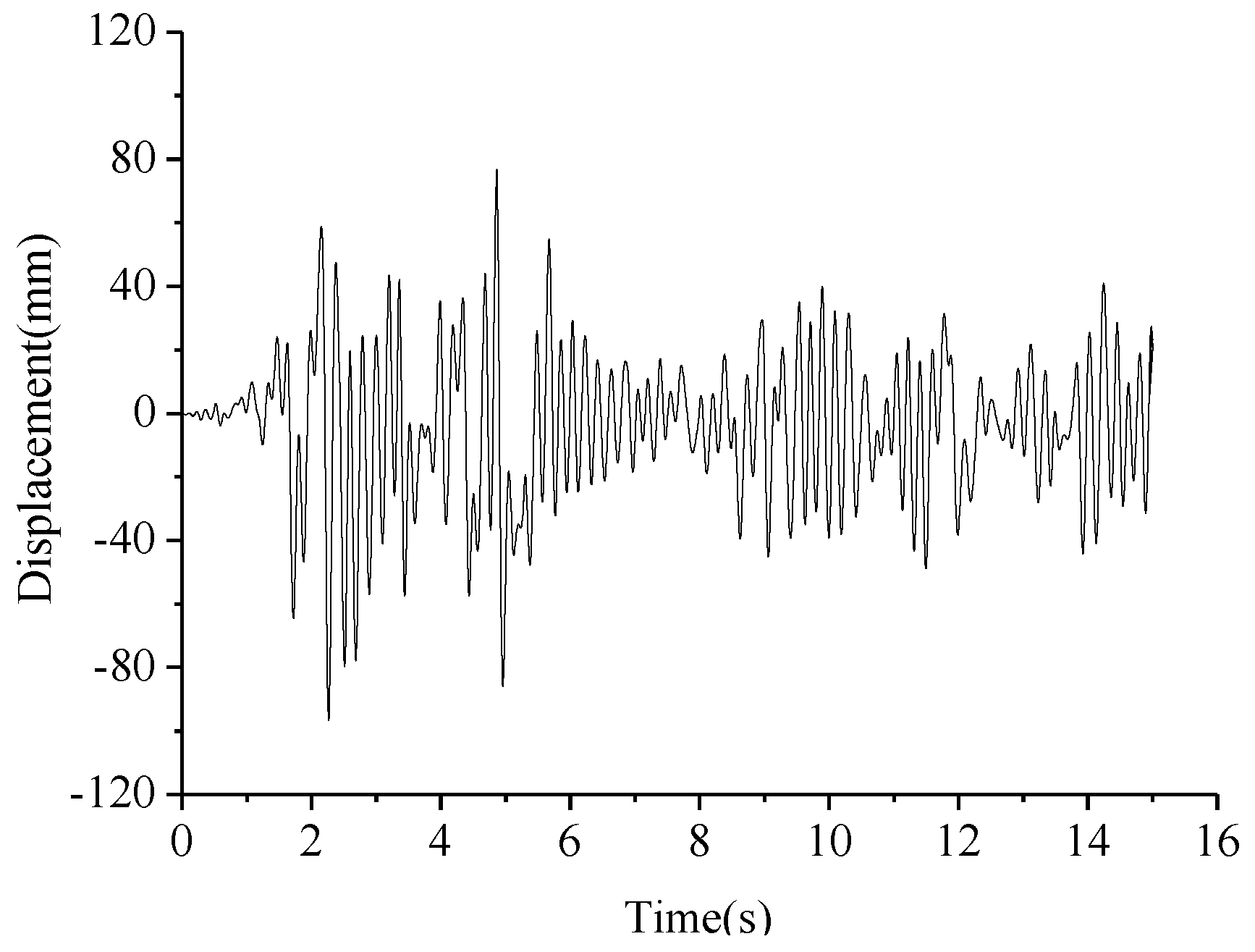
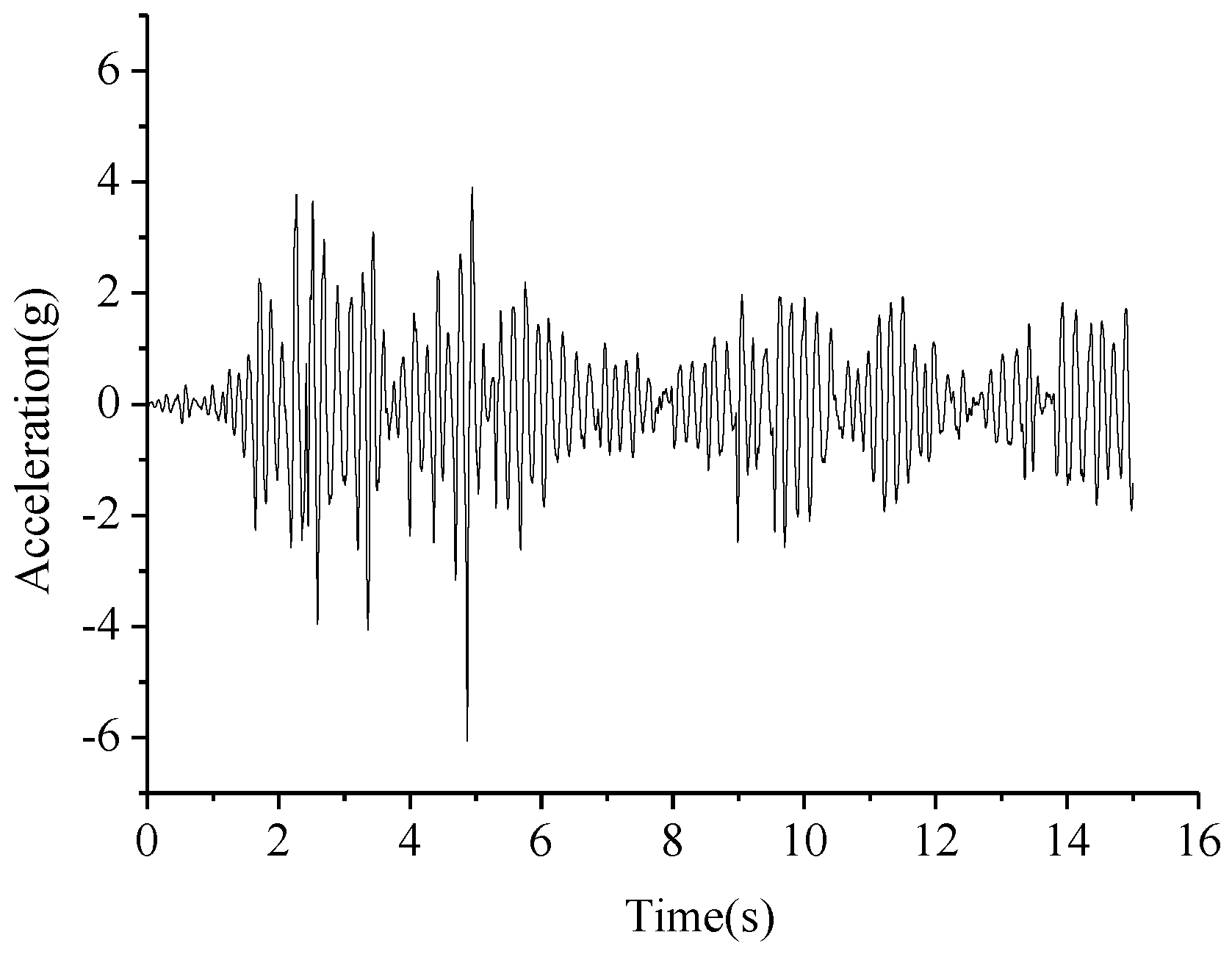
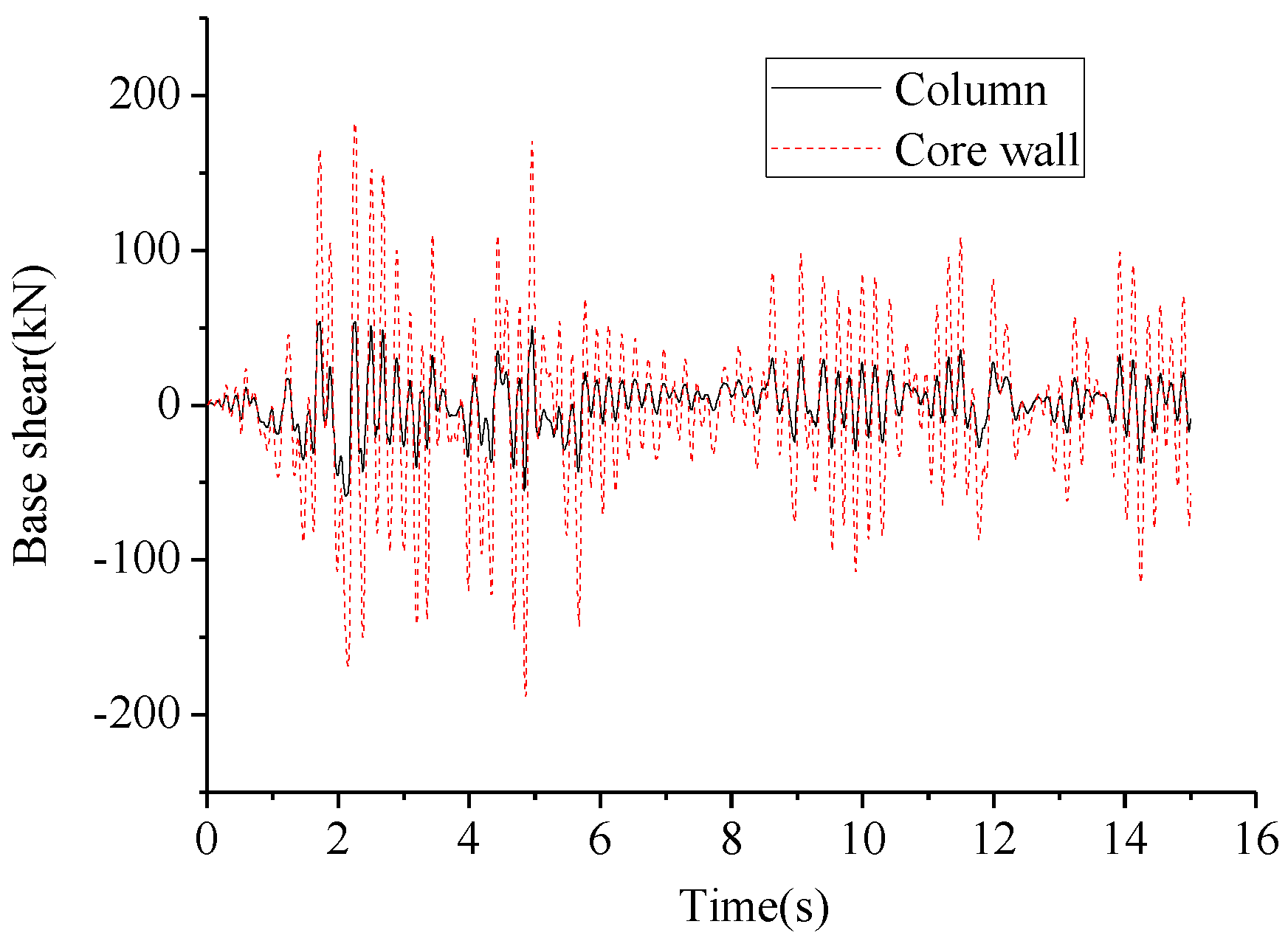
4.1. Structural Damage Analysis under Earthquake Action
4.2. Criterion of Seismic Damage Assessment
5. Seismic Damage Analysis
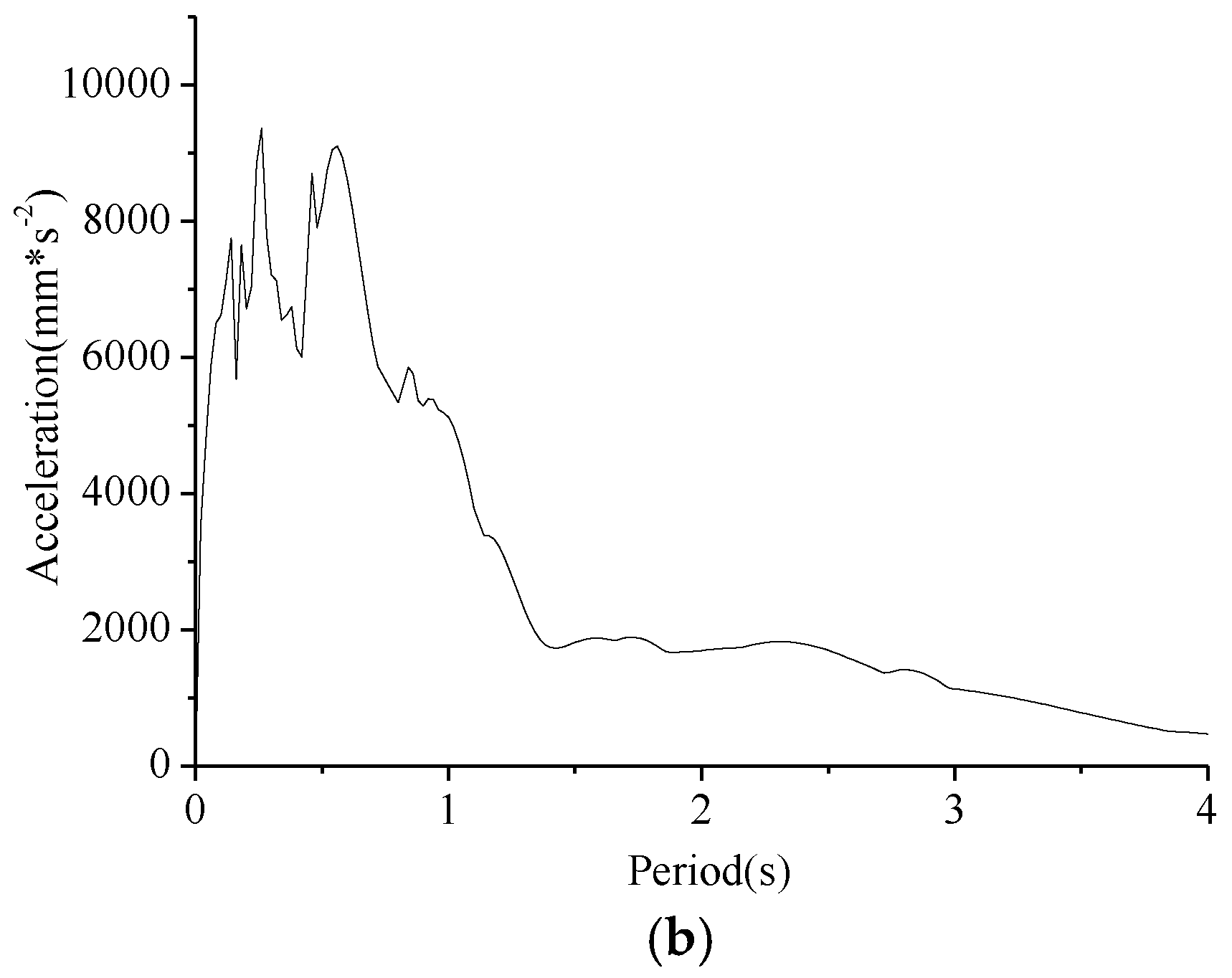
5.1. Influence of Earthquake Intensity
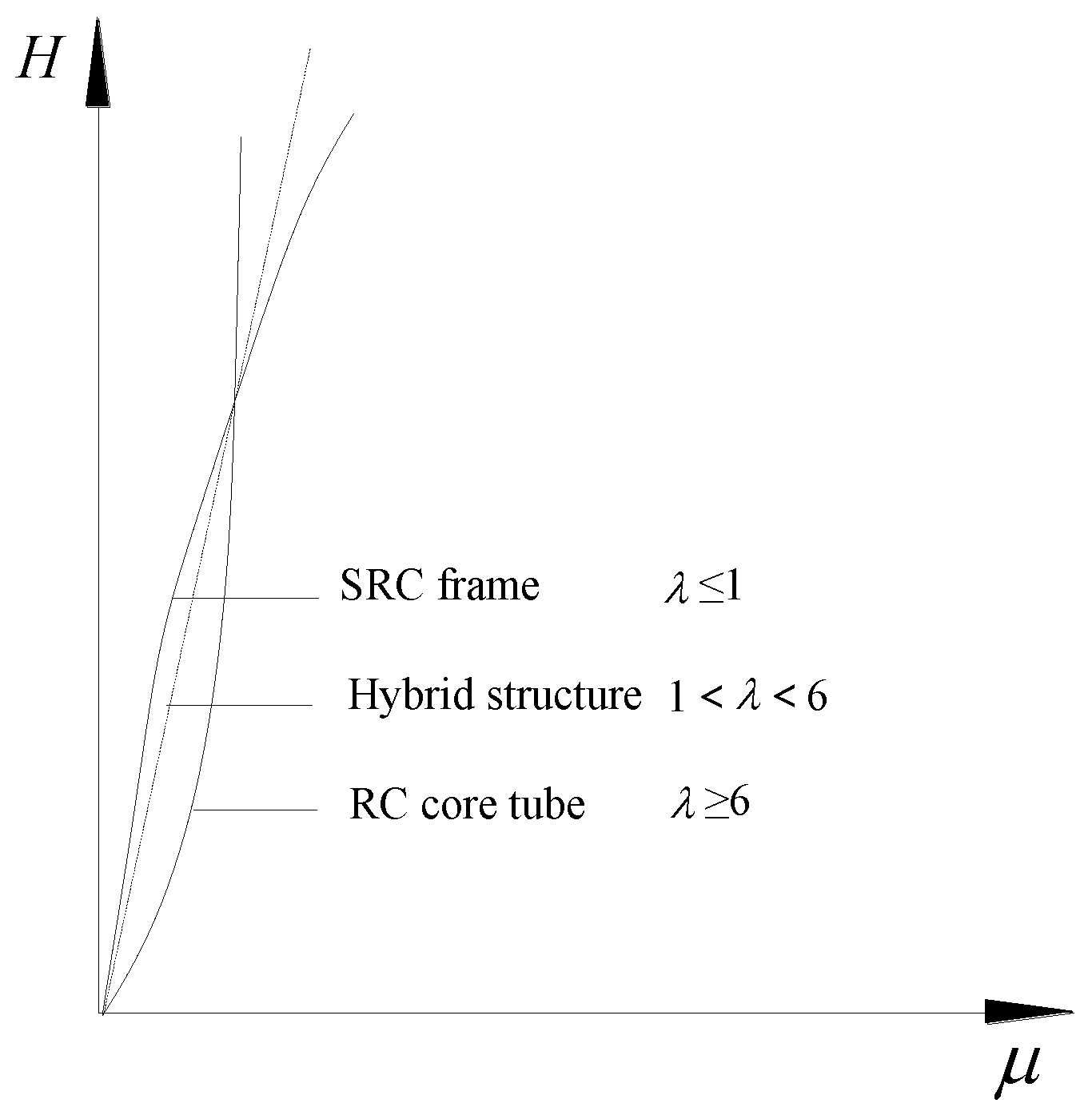
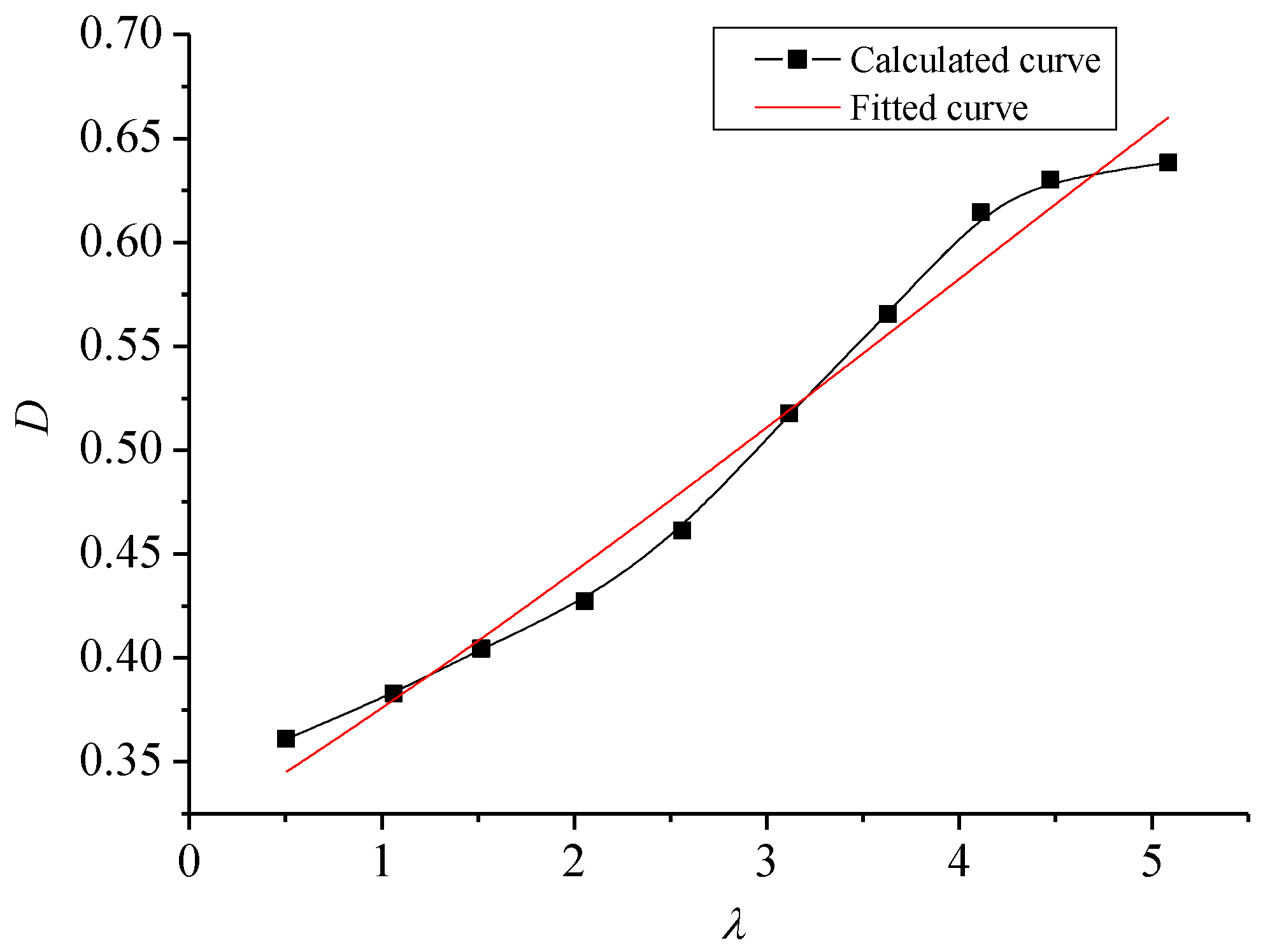
5.2. Structural Stiffness Ratio
6. Conclusions
- (1)
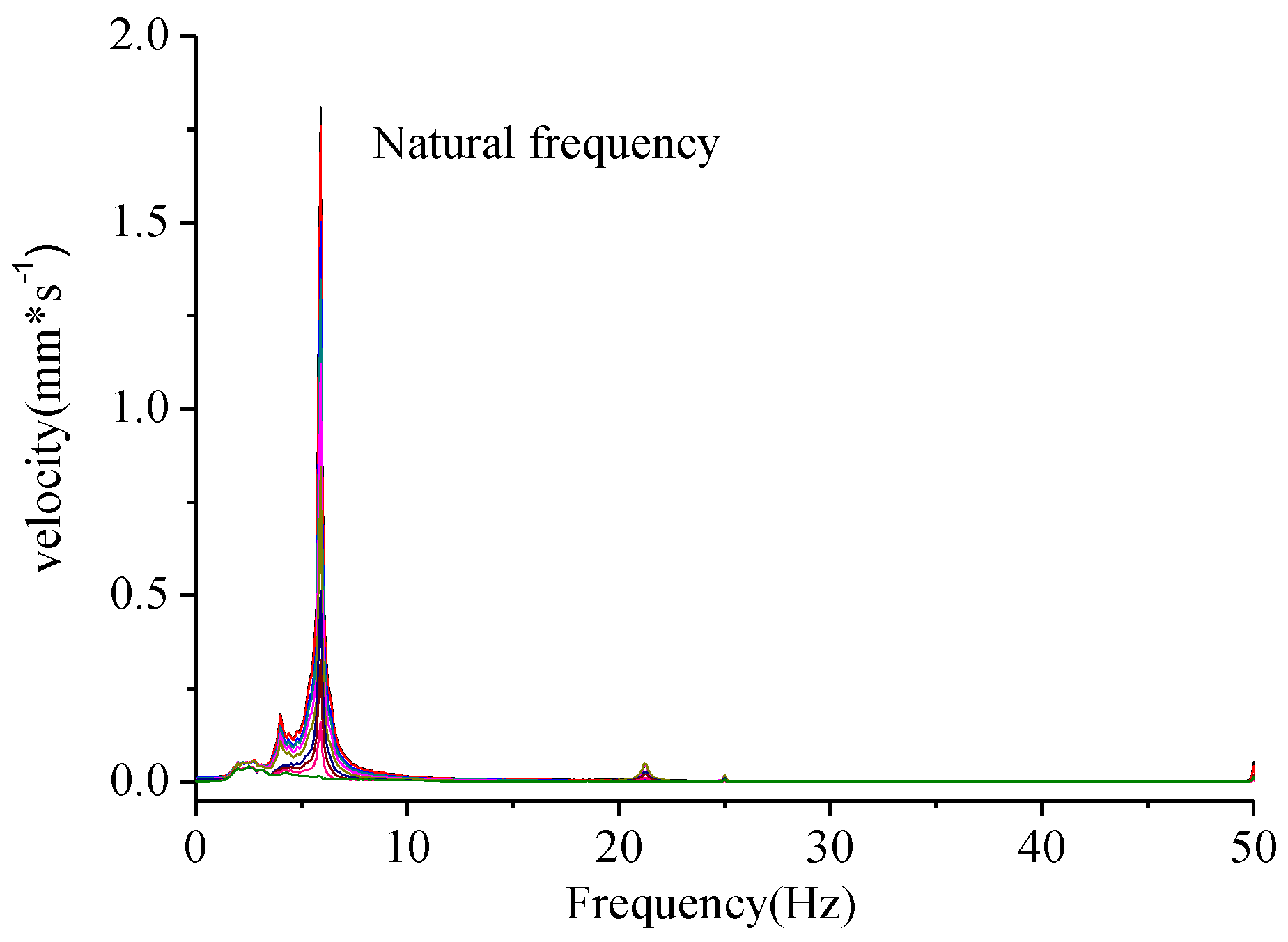
- A dynamic characteristics test was conducted on a 1/5 scale and 10-storey concrete-encased steel frame-reinforced concrete core tube building model. The natural frequency was measured by the high precision USB (Universal Serial Bus) acquisition instrument, and higher order frequencies through modal analysis were obtained. As a result, first five order frequencies were obtained according to experimental data.
- (2)
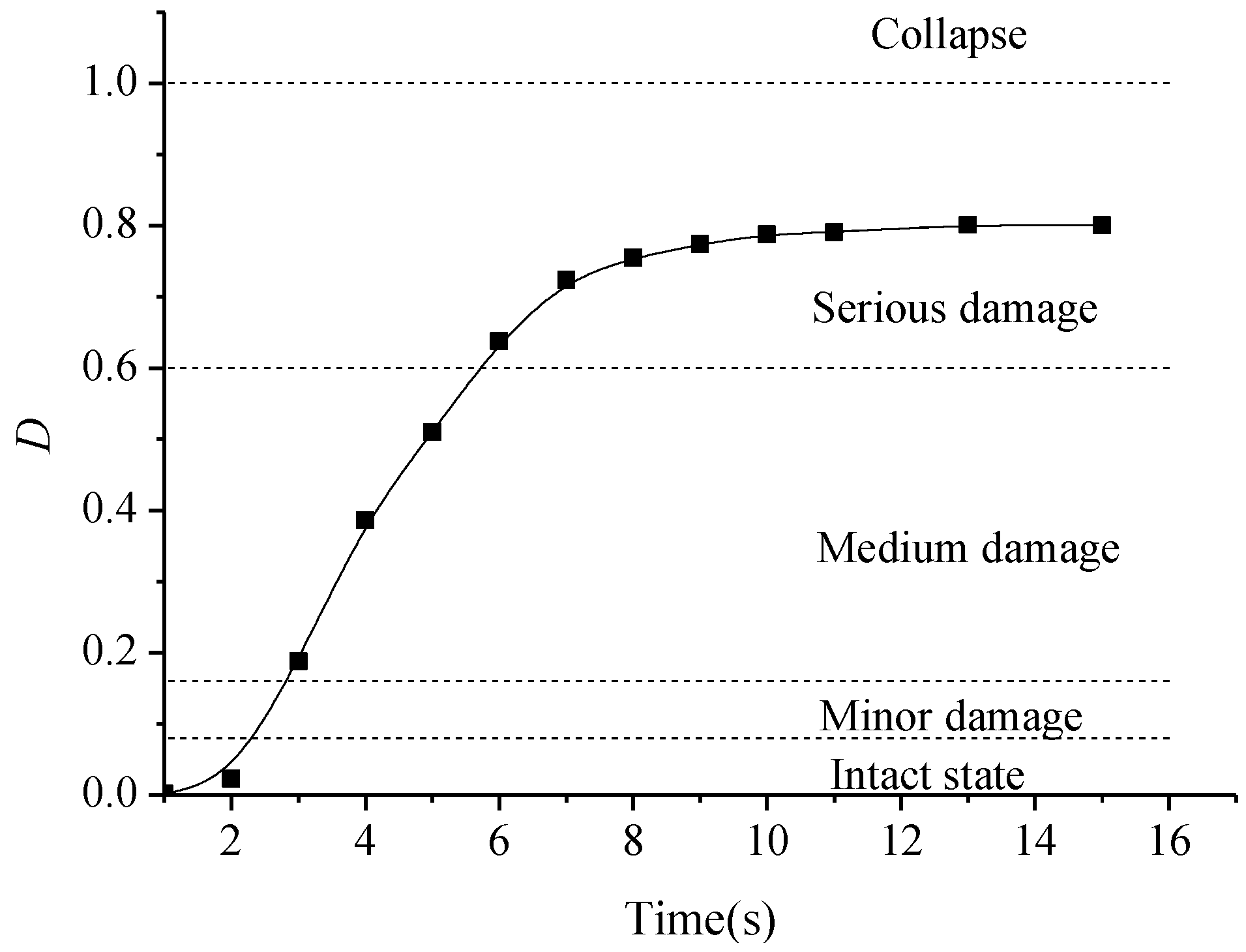
- Modal analysis was carried out using a nonlinear finite element program based on the fiber model. The simulation results agreed well with those of experiments. The damage process under El-Centro wave was analyzed. Compared with the intact state, the first two frequencies of the ultimate state had an obvious degradation of about 56.16%, and the higher frequencies had an obvious degradation of about 21.87%. The max story drift angle increased from 0.819% to 4.062%, and the proportion of the total shear in the core tube increased from 53.37% to 77.36%.
- (3)
- The max story drift angle was chosen to reflect the damage state and to quantify the damage degree on five levels. A criterion of seismic damage assessment was proposed with the consideration of higher-order vibration modes and its validity was confirmed by finite element analysis. The influence of earthquake intensity and structural stiffness ratio on dynamic characteristics were discussed. This work is hoped to provide references for structural health monitoring and quantifying the degree of post-earthquake restoration.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shanmugam, N.E.; Lakshmi, B. State of the art report on steel-concrete composite columns. J. Constr. Steel Res. 2001, 57, 1041–1080. [Google Scholar] [CrossRef]
- Nie, J.; Tao, M.; Huang, Y.; Tian, S.; Chen, G. Research advances of steel-concrete composite structural systems. J. Build. Struct. 2010, 31, 71–80. [Google Scholar]
- Deierlein, G.G.; Noguchi, H. Overview of US-Japan research on the seismic design of composite reinforced concrete and steel moment frame structures. J. Struct. Eng. 2004, 130, 361–367. [Google Scholar] [CrossRef]
- Goel, S.C. United States-Japan cooperative earthquake engineering research program on composite and hybrid structures. J. Struct. Eng. 2004, 130, 157–158. [Google Scholar] [CrossRef]
- Zeng, L.; Cui, Z.K.; Xiao, Y.F.; Jin, S.Q.; Wu, Y.Y. Cyclical Behavior of Concrete-Encased Composite Frame Joints with High Strength Concrete. Adv. Mater. Sci. Eng. 2015, 2015, 873162. [Google Scholar]
- Zheng, S.S.; Zeng, L. Experimental research on seismic behavior of steel reinforced high strength and high performance concrete frame joints. J. Build. Struct. 2008, 29, 74–81. [Google Scholar]
- Zhou, X.; Li, G. Shaking table model test of a steel-concrete composite high-rise building. J. Earthq. Eng. 2010, 14, 601–625. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, P.; Wang, J.; Jin, X. Seismic analysis of the hung curtain wall structure in Shanghai Center Tower. Struct. Des. Tall Spec. Build. 2013, 22, 847–861. [Google Scholar] [CrossRef]
- Lu, X.L.; Yin, X.W.; Jiang, H.J. Shaking table scaled model test on a high-rise building with CFT frame and composite core wall. Eur. J. Environ. Civ. Eng. 2013, 17, 616–634. [Google Scholar] [CrossRef]
- Gong, Z.G.; Li, X.L.; Lu, W.S.; Li, P.Z.; Yang, S.; Zhao, B. Shaking table model test of a hybrid high-rise building structure. Earthq. Eng. Eng. Vib. 2004, 24, 99–105. [Google Scholar]
- Zhou, F.; Mosalam, K.M.; Nakashima, M. Finite-element analysis of a composite frame under large lateral cyclic loading. J. Struct. Eng. 2007, 133, 1018–1026. [Google Scholar] [CrossRef]
- Zona, A.; Ranzi, G. Finite element models for nonlinear analysis of steel–concrete composite beams with partial interaction in combined bending and shear. Finite Elem. Anal. Des. 2011, 47, 98–118. [Google Scholar] [CrossRef]
- Sebastian, W.M.; McConnel, R.E. Nonlinear FE analysis of steel-concrete composite structures. J. Struct. Eng. 2000, 126, 662–674. [Google Scholar] [CrossRef]
- Miao, Z.; Ye, L.; Guan, H.; Lu, X. Evaluation of modal and traditional pushover analyses in frame-shear-wall structures. Adv. Struct. Eng. 2011, 14, 815–836. [Google Scholar] [CrossRef]
- Lu, X.; Lu, X.; Guan, H.; Ye, L. Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes. Earthq. Eng. Struct. Dyn. 2013, 42, 705–723. [Google Scholar] [CrossRef]
- Shahrooz, B.M.; Gong, B.; Tunc, G.; Deason, J.T. An overview of reinforced concrete core wall–steel frame hybrid structures. Prog. Struct. Eng. Mater. 2001, 3, 149–158. [Google Scholar] [CrossRef]
- Králik, J. Seismic analysis of reinforced concrete frame-wall systems considering ductility effects in accordance to Eurocode. Eng. Struct. 2010, 31, 2865–2872. [Google Scholar] [CrossRef]
- Darwin, D.; Nmai, C.K. Energy dissipation in RC beams under cyclic load. J. Struct. Eng. 1986, 112, 1829–1846. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.S.; Wen, Y.K. Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. 1985, 111, 740–757. [Google Scholar] [CrossRef]
- Lu, X.; Lu, X.; Guan, H.; Ye, L. Earthquake-induced collapse simulation of a super-tall mega-braced frame-core tube building. J. Constr. Steel Res. 2013, 82, 59–71. [Google Scholar] [CrossRef]
- Zeng, L.; Parvasi, S.M.; Kong, Q.; Huo, L.; Lim, I.; Li, M.; Song, G. Bond slip detection of concrete-encased composite structure using shear wave based active sensing approach. Smart Mater. Struct. 2015, 24, 125026. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, T.; Song, G.; Gu, H. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Signal Process. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Xu, B.; Li, B.; Song, G. Active Debonding Detection for Large Rectangular CFSTs Based on Wavelet Packet Energy Spectrum with Piezoceramics. ASCE J. Struct. Eng. 2013, 139, 1435–1443. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, B.; Li, B.; Song, G.; Teng, J. Monitoring for large cross-section CFSTs of a super high-rise building with piezoceramic actuators and sensors. Adv. Mater. Res. 2011, 163–167, 2553–2559. [Google Scholar] [CrossRef]
- Gu, H.; Moslehy, Y.; Sanders, D.; Song, G.; Mo, Y.L. Multi-functional smart aggregate-based structural health monitoring of circular reinforced concrete columns subjected to seismic excitations. Smart Mater. Struct. 2010, 19, 322–328. [Google Scholar] [CrossRef]
- Qin, F.; Kong, Q.; Li, M.; Mo, Y.; Song, G.; Fan, F. Bond slip detection of steel plate and concrete beams using smart aggregates. Smart Mater. Struct. 2015, 24, 115039. [Google Scholar] [CrossRef]
- Laskar, A.; Gu, H.; Mo, Y.L.; Song, G. Progressive collapse of a two-story reinforced concrete frame with embedded smart aggregates. Smart Mater. Struct. 2009, 18, 5844–5877. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.H.; Silva, P.; Mo, Y.L. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Yin, H.; Wang, T.; Yang, D.; Liu, S.; Shao, J.; Li, Y. A smart washer for bolt looseness monitoring based on piezoelectric active sensing method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Zhu, W.D.; Liu, J.M.; Xu, Y.F.; Yin, H.Q. A modal test method using sound pressure transducers based on vibro-acoustic reciprocity. J. Sound Vib. 2014, 333, 2728–2742. [Google Scholar] [CrossRef]
- Kang, H.J.; Zhao, Y.Y.; Zhu, H.P. Analytical and experimental dynamic behavior of a new type of cable-arch bridge. J. Constr. Steel Res. 2014, 101, 385–394. [Google Scholar] [CrossRef]
- Jiang, B.C.; He, Z.; Zhu, S. OpenSees-based master-slave modeling technique in progressive collapse analysis of concrete structures. J. Disaster Prev. Mitig. Eng. 2014, 34, 632–636. [Google Scholar]
- Fanaie, N.; Ezzatshoar, S. Studying the seismic behavior of gate braced frames by incremental dynamic analysis (IDA). J. Constr. Steel Res. 2014, 99, 111–120. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar]
- Wu, Y.T.; Kang, D.Y.; Yang, Y.B. Seismic performance of steel and concrete composite shear walls with embedded steel truss for use in high-rise buildings. Eng. Struct. 2016, 125, 39–53. [Google Scholar] [CrossRef]
- Chen, X.W.; Lin, Z. Structural Nonlinear Analysis Program Opensees Theory and Tutorial; China Architecture & Building Press: Beijing, China, 2014; pp. 87–89. [Google Scholar]
- Kamaris, G.S.; Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Seismic damage estimation of in-plane regular steel/concrete composite moment resisting frames. Eng. Struct. 2016, 115, 67–77. [Google Scholar] [CrossRef]
- Spacone, E.; Eltawil, S. Nonlinear Analysis of Steel-Concrete Composite Structures: State of the Art. J. Struct. Eng. 2004, 130, 159–168. [Google Scholar] [CrossRef]
- Arshian, A.H.; Morgenthal, G.; Narayanan, S. Influence of modelling strategies on uncertainty propagation in the alternate path mechanism of reinforced concrete framed structures. Science 2016, 802, 241–245. [Google Scholar] [CrossRef]
- Vigh, L.G.; Deierlein, G.G.; Miranda, E.; Liel, A.B.; Tipping, S. Seismic performance assessment of steel corrugated shear wall system using non-linear analysis. J. Constr. Steel Res. 2013, 85, 48–59. [Google Scholar]
- Tirca, L.; Chen, L.; Tremblay, R. Assessing collapse safety of CBF buildings subjected to crustal and subduction earthquakes. J. Constr. Steel Res. 2015, 115, 47–61. [Google Scholar] [CrossRef]
- Pucinotti, R.; Bursi, O.S.; Demonceau, J.F. Post-earthquake fire and seismic performance of welded steel–concrete composite beam-to-column joints. J. Constr. Steel Res. 2011, 67, 1358–1375. [Google Scholar] [CrossRef]
- Shen, W.H. Structural Damage Detection Based on Experimental Modal Analysis. Master’s Thesis, Jinan University, Guangzhou, China, 2006. [Google Scholar]
- Shi, W.X.; Wang, Y.; Liu, C.Q. Damage analysis of high-rise building under seismic load based on frequency measurement. J. Southwest Jiaotong Univ. 2007, 42, 389–394. [Google Scholar]
- Tao, Q.L. Research on the Damage Model of SRC Frame-RC Core Wall Hybrid Structure under Seismic Excitation. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2011. [Google Scholar]
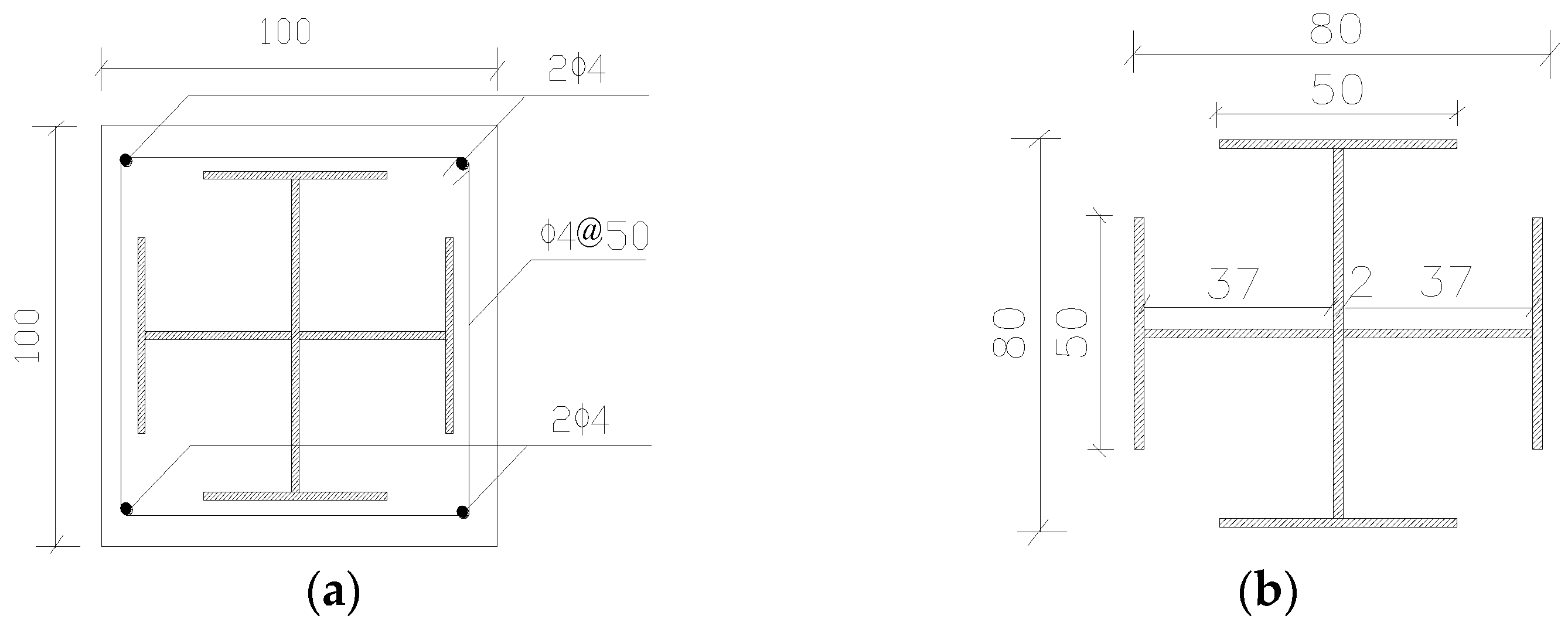




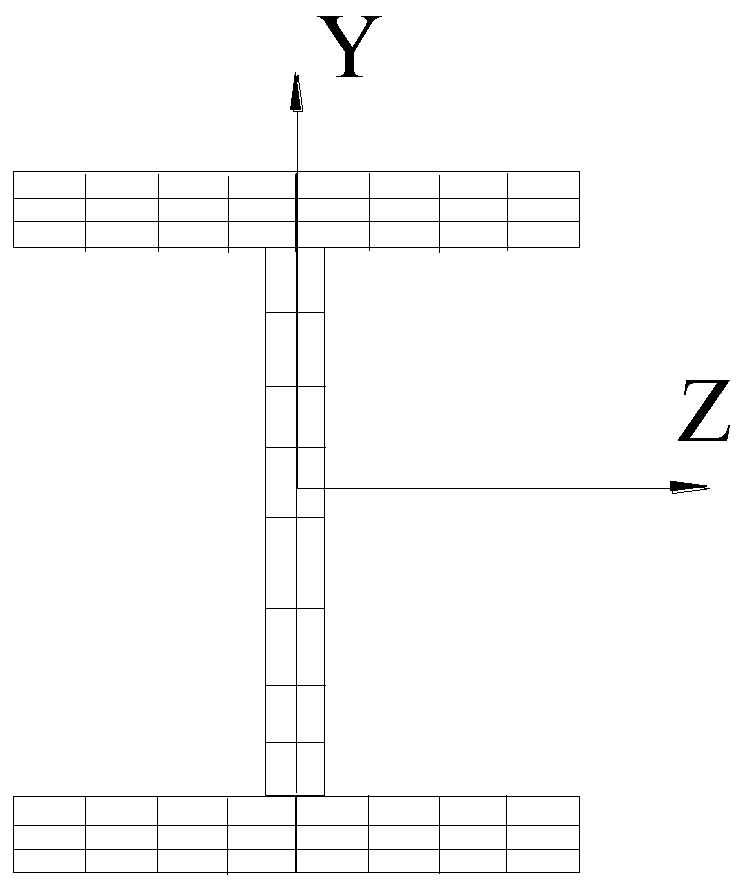


| Material | Yield Strength fy (N/mm2) | Ultimate Strength fu (N/mm2) | Elastic Modulus Es (N/mm2) |
|---|---|---|---|
| Φ4 bars | 305 | 424 | 2.1 × 105 |
| Steel plate | 327 | 463 | 2.0 × 105 |
| Vibration Mode | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| f (Hz) | 5.942 | 18.981 | 25.130 | 37.935 | 50.034 |
| Item | Quantity |
|---|---|
| Node | 340 |
| “dispBeamColumn” element | 420 |
| “ShellMITC4” element | 220 |
| Order | Frequencies of Specimen (Hz) | Frequencies of FEA (Hz) | Absolute Error (%) |
|---|---|---|---|
| 1 | 5.942 | 5.864 | 1.312 |
| 2 | 18.981 | 18.126 | 4.504 |
| 3 | 25.130 | 23.974 | 4.601 |
| 4 | 37.935 | 36.469 | 3.865 |
| 5 | 50.034 | 48.433 | 3.199 |
| Intact State | Minor Damage | Medium Damage | Serious Damage | Collapse |
|---|---|---|---|---|
| D ≤ 0.08 | 0.08 < D ≤ 0.16 | 0.16 < D ≤ 0.60 | 0.60 < D ≤ 1.0 | D > 1 |
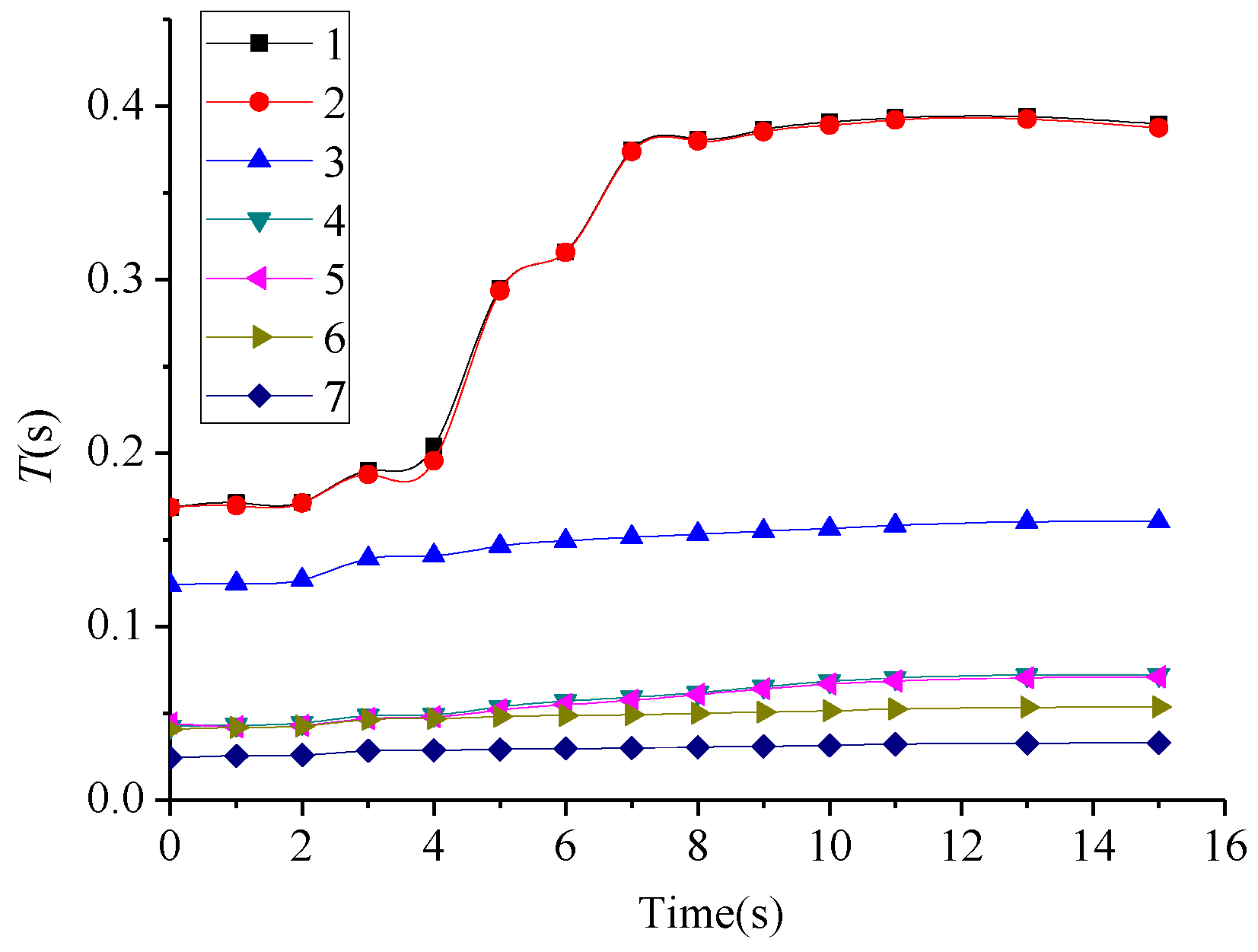
| Time | Frequencies of Vibration Modes (Hz) | Dθ | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 s | 5.833 | 5.888 | 7.999 | 22.957 | 23.691 | 23.895 | 39.124 | 0.00145 |
| 2 s | 5.819 | 5.834 | 7.865 | 22.553 | 23.326 | 23.425 | 38.402 | 0.0227 |
| 3 s | 5.266 | 5.328 | 7.184 | 20.534 | 21.277 | 21.459 | 35.088 | 0.18822 |
| 4 s | 4.902 | 5.112 | 7.097 | 20.284 | 20.877 | 21.231 | 34.843 | 0.38641 |
| 5 s | 3.392 | 3.407 | 6.826 | 18.622 | 19.231 | 20.704 | 34.130 | 0.50969 |
| 6 s | 3.164 | 3.167 | 6.680 | 17.513 | 18.149 | 20.492 | 33.670 | 0.63802 |
| 7 s | 2.670 | 2.675 | 6.592 | 16.835 | 17.361 | 20.284 | 33.223 | 0.72402 |
| 8 s | 2.624 | 2.632 | 6.519 | 16.129 | 16.393 | 20.000 | 32.680 | 0.75483 |
| 9 s | 2.587 | 2.595 | 6.447 | 15.267 | 15.576 | 19.724 | 32.154 | 0.77435 |
| 10 s | 2.558 | 2.569 | 6.382 | 14.620 | 14.925 | 19.380 | 31.646 | 0.78807 |
| 11 s | 2.542 | 2.550 | 6.310 | 14.162 | 14.548 | 19.048 | 31.027 | 0.79134 |
| 13 s | 2.538 | 2.546 | 6.229 | 13.866 | 14.162 | 18.671 | 30.358 | 0.80114 |
| 15 s | 2.565 | 2.580 | 6.221 | 13.856 | 14.077 | 18.574 | 30.184 | 0.80065 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Xiao, Y.; Chen, Y.; Jin, S.; Xie, W.; Li, X. Seismic Damage Evaluation of Concrete-Encased Steel Frame-Reinforced Concrete Core Tube Buildings Based on Dynamic Characteristics. Appl. Sci. 2017, 7, 314. https://doi.org/10.3390/app7040314
Zeng L, Xiao Y, Chen Y, Jin S, Xie W, Li X. Seismic Damage Evaluation of Concrete-Encased Steel Frame-Reinforced Concrete Core Tube Buildings Based on Dynamic Characteristics. Applied Sciences. 2017; 7(4):314. https://doi.org/10.3390/app7040314
Chicago/Turabian StyleZeng, Lei, Yunfeng Xiao, Yiguang Chen, Siqian Jin, Wei Xie, and Xianjie Li. 2017. "Seismic Damage Evaluation of Concrete-Encased Steel Frame-Reinforced Concrete Core Tube Buildings Based on Dynamic Characteristics" Applied Sciences 7, no. 4: 314. https://doi.org/10.3390/app7040314
APA StyleZeng, L., Xiao, Y., Chen, Y., Jin, S., Xie, W., & Li, X. (2017). Seismic Damage Evaluation of Concrete-Encased Steel Frame-Reinforced Concrete Core Tube Buildings Based on Dynamic Characteristics. Applied Sciences, 7(4), 314. https://doi.org/10.3390/app7040314





