Universal Voltage Conveyor and its Novel Dual-Output Fully-Cascadable VM APF Application
Abstract
:1. Introduction
- (i)
- (ii)
- (iii)
- All passive components are grounded, which is advantageous for monolithic integration [9],
- (iv)
- (v)
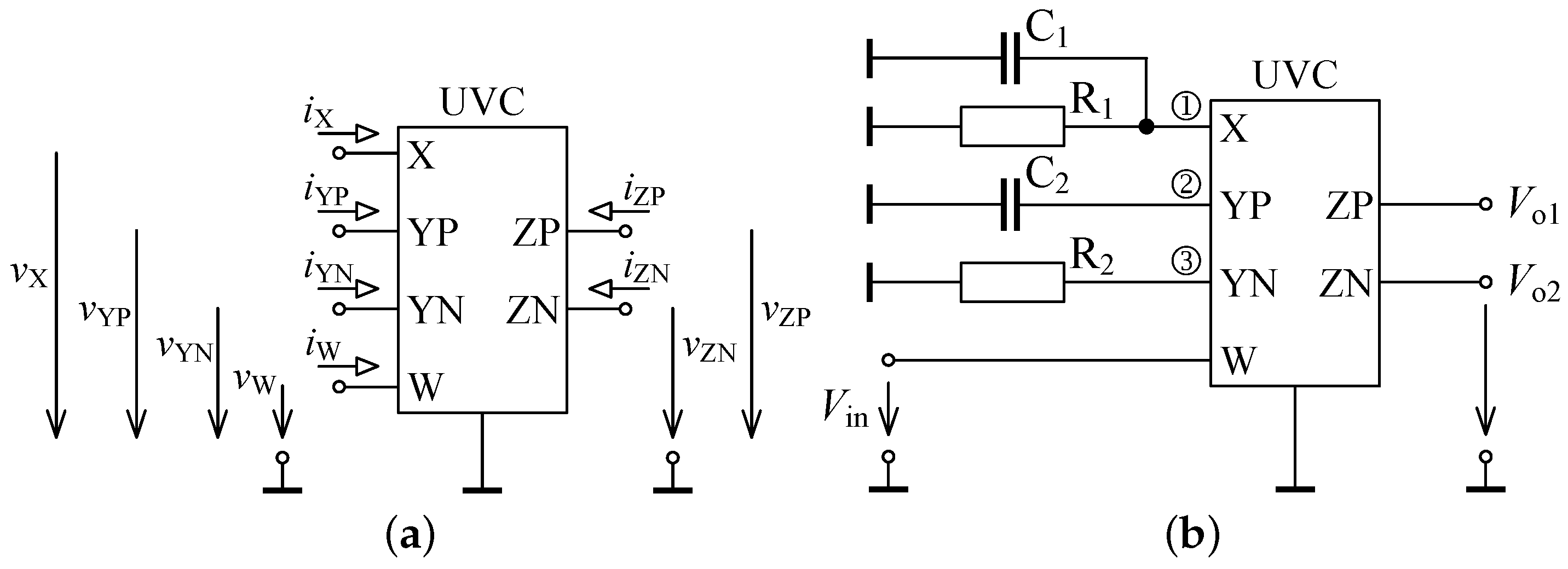
2. Circuit Description
3. Non-Ideal Analysis
- the parasitic resistance and parasitic capacitance appear between the high-impedance terminal X of the UVC and ground and their values computed in SPICE software are k pF, respectively,
- the non-zero parasitic resistance and at two difference current inputs YP and YN have values Ω and Ω, respectively,
- the parasitic resistance and parasitic capacitance appear between the auxiliary terminal W of the UVC and ground and their values are M pF, respectively,
- the non-zero parasitic resistance and at mutually inverse voltage outputs ZP and ZN have values Ω and Ω, respectively.
- at the node ①, a parasitic impedance can be seen. Note that the capacitance and resistance can be absorbed into external capacitor and resistor , respectively, as they appear in parallel. Hence, in further analysis the total capacitance and resistance at this node will be considered and ,
- the node ② at low-impedance terminal YP is characterized by a parasitic impedance , which is in series with external capacitor , and by assuming it as an impedance , the total impedance at this node can be described as ,
- finally, the node ③ can be characterized by a parasitic impedance , which appears in series with external resistor . Hence, the total impedance at this node can be labeled as .
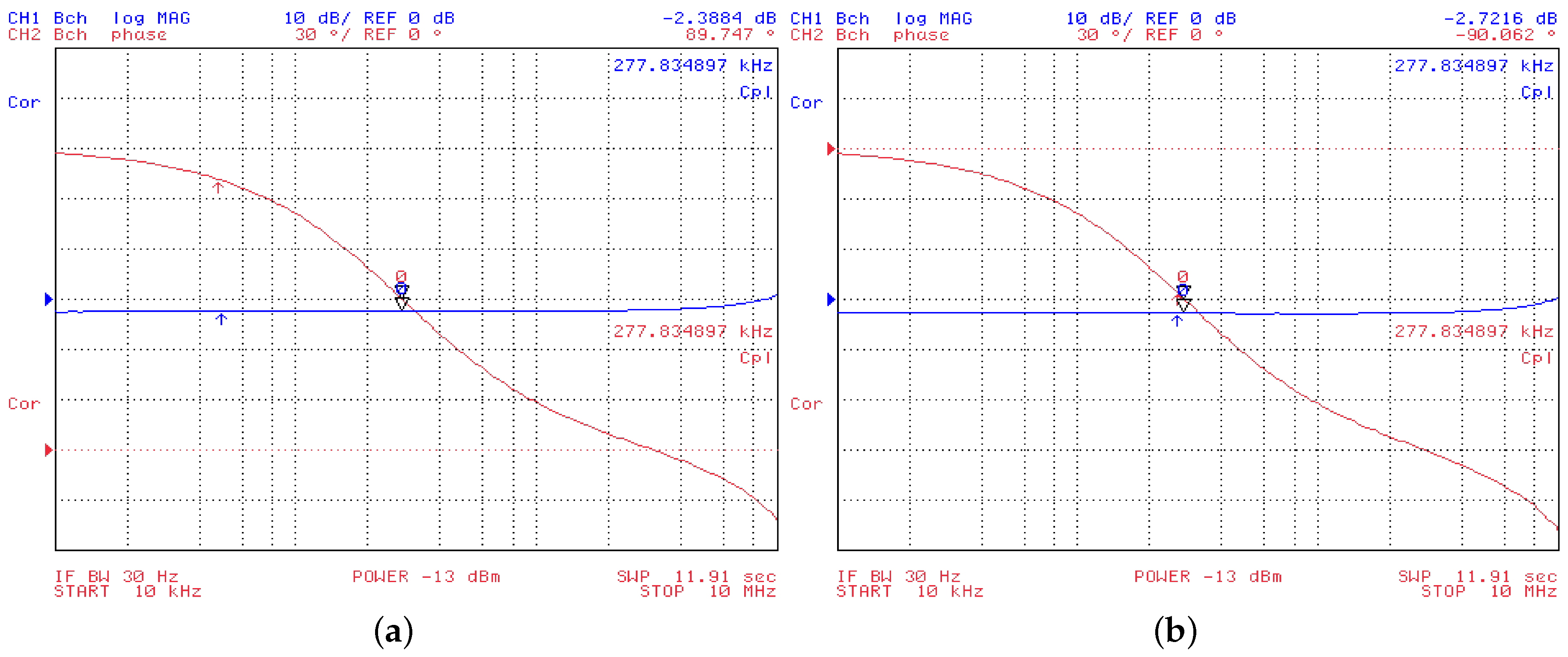
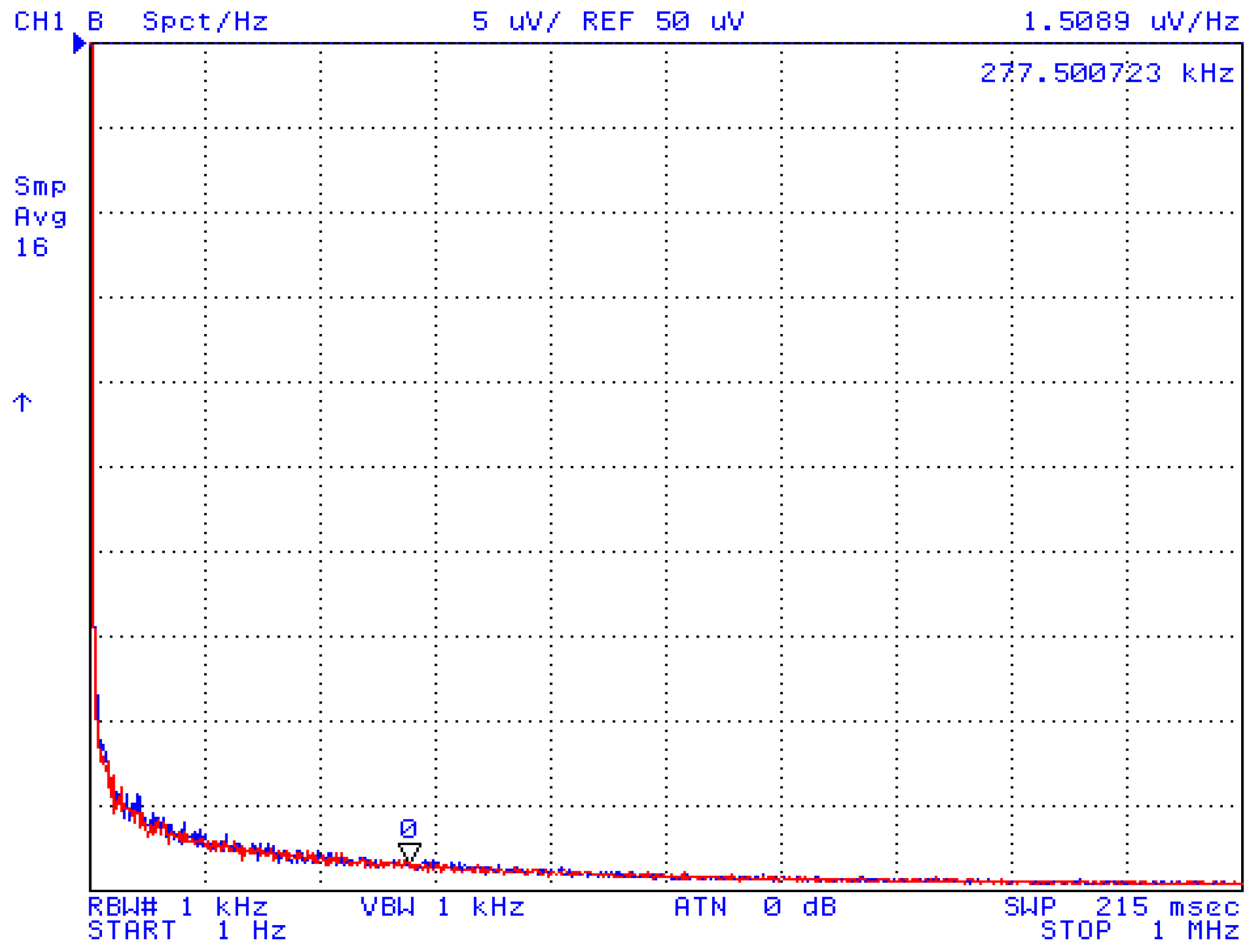
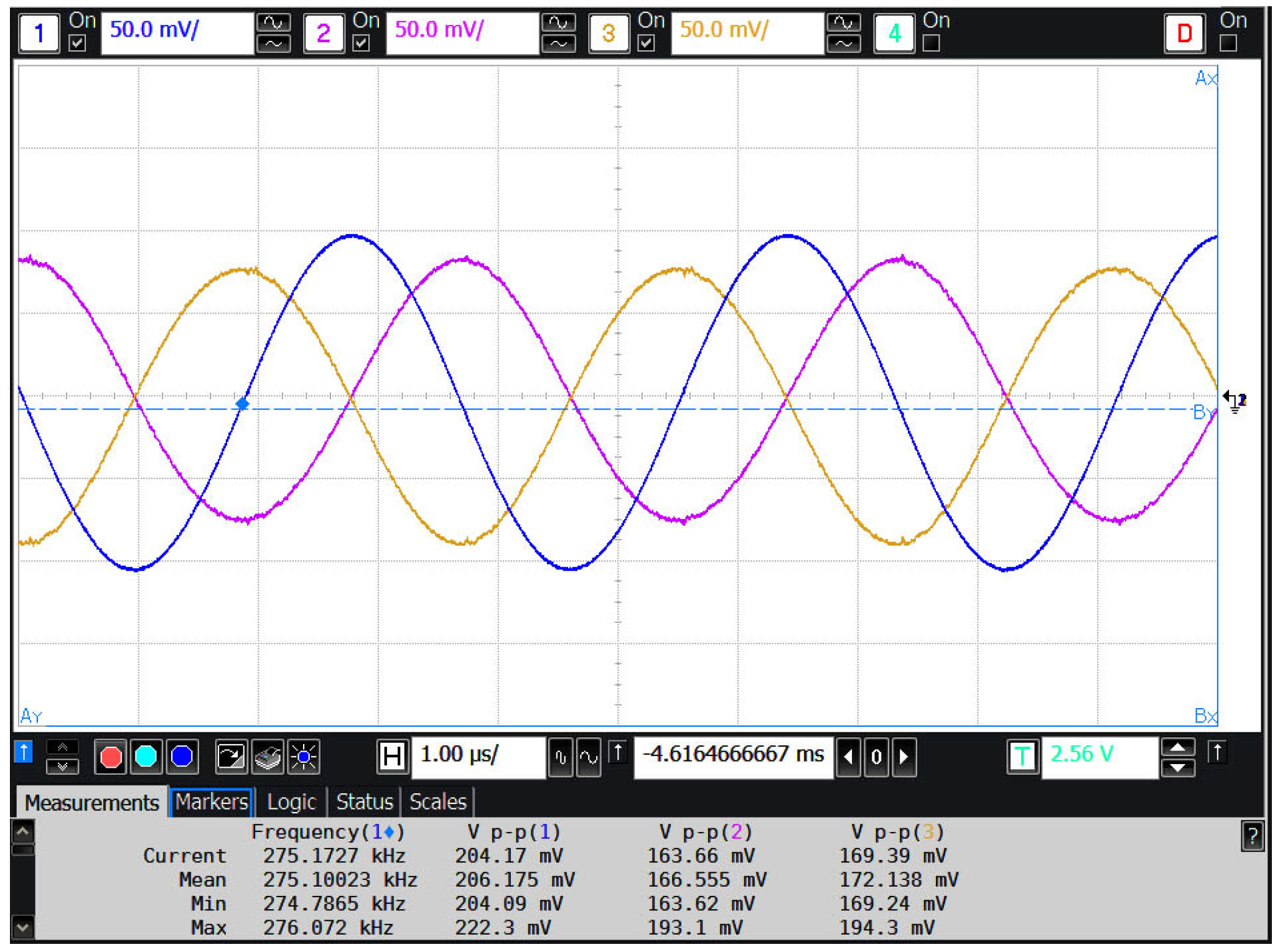
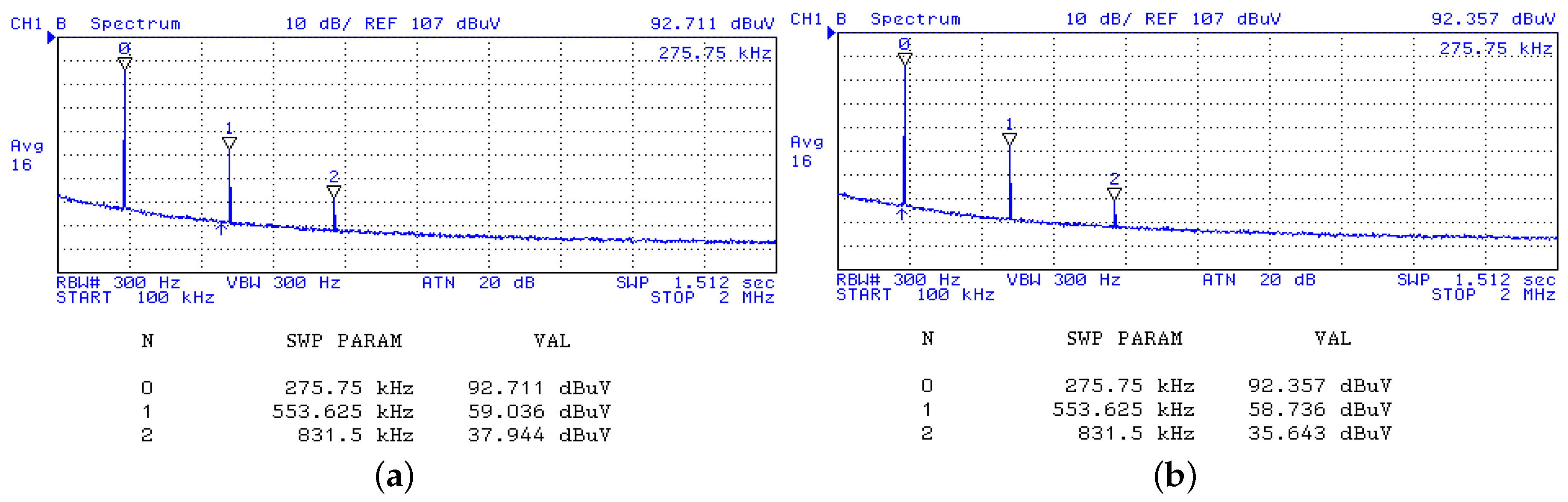
4. Experimental Verification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maheshwari, S. Analogue signal processing applications using a new circuit topology. IET Circ. Device Syst. 2009, 3, 106–115. [Google Scholar] [CrossRef]
- Chen, H.P.; Wu, K.H. Grounded-capacitor first-order filter using minimum components. IEICE Trans. Fundam. 2006, E89-A, 3730–3731. [Google Scholar] [CrossRef]
- Tran, H.-D.; Wang, H.-Y.; Lin, M.-C.; Nguyen, Q.-M. Synthesis of cascadable DDCC-based universal filter using NAM. Appl. Sci. 2015, 5, 320–343. [Google Scholar] [CrossRef]
- Kartci, A.; Sotner, R.; Jerabek, J.; Herencsar, N.; Petrzela, J. Phase shift keying modulator design employing electronically controllable all-pass sections. Analog Integr. Circ. Signal Process. 2016, 89, 781–800. [Google Scholar] [CrossRef]
- Biolek, D.; Biolkova, V. All-Pass Filters Employing Differential Op-Amps. Electron. World 2010, 116, 44–45. [Google Scholar]
- Biolkova, V.; Kolka, Z.; Biolek, D. Dual-output all-pass filter employing fully-differential operational amplifier and current-controlled current conveyor. In Proceedings of the 2011 7th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 1–4 December 2011; pp. 340–344.
- Chen, H.-P.; Lin, M.-T.; Yang, W.-S. Novel first-order non-inverting and inverting output of all-pass filter at the same configuration using ICCII. IEICE Trans. Electron. 2006, 89-C, 865–867. [Google Scholar] [CrossRef]
- Mohan, J.; Maheshwari, S.; Chauhan, D.S. Minimum component based first-order inverting and non-inverting outputs of all-pass filter at the same circuit. ACEEE Int. J. Electr. Power Eng. 2010, 1, 32–35. [Google Scholar]
- Chaturvedi, B.; Mohan, J. Single DV-DXCCII based voltage controlled first order all-pass filter with inverting and non-inverting responses. Iran. J. Electr. Electron. Eng. 2015, 11, 301–309. [Google Scholar]
- Herencsar, N.; Minaei, S.; Koton, J.; Yuce, E.; Vrba, K. New resistorless and electronically tunable realization of dual-output VM all-pass filter using VDIBA. Analog Integr. Circ. Signal Process. 2013, 74, 141–154. [Google Scholar] [CrossRef]
- Herencsar, N.; Koton, J.; Vrba, K. A new electronically tunable voltage-mode active-C phase shifter using UVC and OTA. IEICE Electron. Express 2009, 6, 1212–1218. [Google Scholar] [CrossRef]
- Herencsar, N.; Koton, J.; Vrba, K.; Cicekoglu, O. High-input and low-output impedance voltage-mode all-pass filter using single universal voltage conveyor. In Proceedings of the International Conference on Telecommunications and Signal Processing TSP 2010, Baden near Vienna, Austria, 17–20 August 2010; pp. 42–46.
- Herencsar, N.; Koton, J.; Jerabek, J.; Vrba, K.; Cicekoglu, O. Voltage-mode all-pass filters using universal voltage conveyor and MOSFET-based electronic resistors. Radioengineering 2011, 20, 10–18. [Google Scholar]
- Metin, B.; Herencsar, N.; Koton, J. Cascadable all-pass filter using a single universal voltage conveyor. In Proceedings of the 2012 22nd International Conference Radioelektronika (RADIOELEKTRONIKA), Brno, Czech Republic, 17–18 April 2012; pp. 97–100.
- Filanovsky, I.M.; Stromsmoe, K.A. Current-voltage conveyor. Electron. Lett. 1981, 17, 129–130. [Google Scholar] [CrossRef]
- Salama, K.; Soliman, A. Novel MOS-C quadrature oscillator using the differential current voltage conveyor. In Proceedings of the 42nd Midwest Symposium on Circuits and Systems, Las Cruces, NM, USA, 8–11 August 1999; pp. 279–282.
- Acar, C.; Ozoguz, S. A new versatile building block: Current differencing buffered amplifier suitable for analog signal processing filters. Microelectron. J. 1999, 30, 157–160. [Google Scholar] [CrossRef]
- Pathak, J.K.; Singh, A.K.; Senani, R. New canonic lossy inductor using a single CDBA and its application. Int. J. Electron. 2016, 103, 1–13. [Google Scholar] [CrossRef]
- Minarcik, M.; Vrba, K. Single-input six-output voltage-mode filter using universal voltage conveyors. IEICE Trans. Fundam. 2008, E91-A, 2035–2037. [Google Scholar] [CrossRef]
- Koton, J.; Vrba, K.; Herencsar, N. Tuneable filter using voltage conveyors and current active elements. Int. J. Electron. 2009, 96, 787–794. [Google Scholar] [CrossRef]
- Koton, J.; Herencsar, N.; Vrba, K. Minimal configuration precision full-wave rectifier using current and voltage conveyors. IEICE Electron. Express 2010, 7, 844–849. [Google Scholar] [CrossRef]
- Koton, J.; Herencsar, N.; Vrba, K. KHN-equivalent voltage-mode filters using universal voltage conveyors. AEU Int. J. Electron. Commun. 2011, 65, 154–160. [Google Scholar] [CrossRef]
- Sponar, R.; Vrba, K. Measurements and behavioral modelling of modern conveyors. Int. J. Comput. Sci. Netw. Secur. 2006, 6, 57–65. [Google Scholar]
- UVC-N1C 0520 Datasheet; Universal Voltage Conveyor: ON Semiconductor & Brno University of Technology, Czech Republic. 2010. Available online: www.utko.feec.vutbr.cz/∼herencsar/UVC_N1C_0520.pdf (accessed on 10 February 2017).


| Reference | ABB Type | Grounded R/C | Floating R/C | Simul./Meas. | (Hz) | Supply (V) |
|---|---|---|---|---|---|---|
| Figure 4b in [5] | FD-OPA & CCII | 0/0 | 1/1 | Meas. | 29.6 k | ±5 |
| Figure 1 in [6] | FD-OPA | 0/0 | 0/1 | Simul. | 92 k | ±1.5 |
| Figure 2 in [7] | ICCII+ | 0/0 | 1/1 | Simul. | 1.59 M | ±1.25 |
| Figure 2 in [8] | FDCCII | 0/1 | 1/0 | Simul. | 159.2 k | ±3 |
| Figure 2 in [9] | DV-DXCCII & 1 NMOS | 0/1 | 0/0 | Simul. | 27 M | ±0.9 |
| Figure 3 in [10] | VDIBA | 0/0 | 0/1 | Both | S: 9.44 M; M: 1 M | ±0.9; ±5 |
| Figure 1 in [11] | UVC & OTA | 0/0 | 0/1 | Simul. | 3 M | ±2 |
| Figure 3 in [12] | UVC | 2/0 | 1.I | Both | S: 3.5 M; M: 160.4 k | ±2.5; ±1.65 |
| Figure 2a in [13] | UVC | 2/0 | 0/1 | Simul. | 1.17 M | ±2.5 |
| Figure 2b in [13] | UVC | 2/0 | 0/1 | Both | S: 1.17 M; M: 746.4 k | ±2.5; ±1.65 |
| Figure 2 in [14] | UVC | 0/1 | 2/0 | Simul. | 390 k | ±2.5 |
| This work | UVC | 2/2 | 0/0 | Meas. | 277.8 k | ±1.65 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herencsar, N.; Koton, J.; Hanak, P. Universal Voltage Conveyor and its Novel Dual-Output Fully-Cascadable VM APF Application. Appl. Sci. 2017, 7, 307. https://doi.org/10.3390/app7030307
Herencsar N, Koton J, Hanak P. Universal Voltage Conveyor and its Novel Dual-Output Fully-Cascadable VM APF Application. Applied Sciences. 2017; 7(3):307. https://doi.org/10.3390/app7030307
Chicago/Turabian StyleHerencsar, Norbert, Jaroslav Koton, and Pavel Hanak. 2017. "Universal Voltage Conveyor and its Novel Dual-Output Fully-Cascadable VM APF Application" Applied Sciences 7, no. 3: 307. https://doi.org/10.3390/app7030307
APA StyleHerencsar, N., Koton, J., & Hanak, P. (2017). Universal Voltage Conveyor and its Novel Dual-Output Fully-Cascadable VM APF Application. Applied Sciences, 7(3), 307. https://doi.org/10.3390/app7030307







