1. Introduction
During the last decade, the advent of new light sources, capable of delivering intense and/or ultrashort, coherent radiation in the soft- and hard-X-ray regime, either directly by free-electron lasers (FEL) or indirectly by high-harmonic generation techniques, has renewed interest in experimental and theoretical photoionization studies of multiply charged ions. The excitation of atoms/molecules involving inner-shell electrons with such light sources offers the possibility of investigating processes at their natural time-scale, such as Auger processes and its variations [
1], double core-hole creation and ionization [
2], resonant enhanced photoionization, etc. Beyond the viewpoint of accessing the dynamics of these processes, the availability of extremely high flux has made it feasible to experimentally create the required conditions and observe for the first time new processes, for example the two-photon single- and double-(direct) photoionization of helium, the complete stripping of neon [
3] and multiphoton inner-shell ionization in noble gases [
4] and solid targets [
5]. Since a number of recent reviews elaborate on experimental and theoretical studies as well as on their numerous applications in this short wavelength regime [
6,
7,
8,
9], we will only mention here that typical fluxes of FELs to date range between 5 × 10
11 Wcm
-2 to 5 × 10
18 Wcm
-2, photon energies range in (0.02–15) KeV, while average full width at half maximum (FWHM) durations vary from 10 fs to 85 fs. It is also worth noting that three new FELs are under development and set to start user operations soon (E-XFEL, Swiss FEL, PAL) with extra pulse parameter specifications compared to the current ones. Notably, the Swiss FEL will provide pulses as short as 2 fs while E-XFEL as long as 100 fs with a repetition rate between 50–100 times higher than any other existing FEL.
From the above discussion, it appears that, nowadays, in these wavelength regimes, excitation/ionization processes involving more than one photon are routinely feasible. Accordingly, their quantitative description requires theoretical approaches capable of coping with the non-linear features of the interaction between X-ray radiation with atomic and molecular systems. Amongst the various theoretical approaches, one is based on a perturbation expansion of the interaction potential with respect to the electric field, known as lowest-order (non-vanishing) perturbation theory (LOPT) [
10]. In the case of X-ray quasi-monochromatic radiation, the use of LOPT is well justified for the current available peak intensities. The main requirements are for (a) the ponderomotive potential,
, and (b) the bandwidth,
, to be much smaller than the mean central photon frequency,
ω, of the radiation. For our case, for example, if we choose a peak intensity at the higher end,
W/cm
2, and a mean photon energy at the lowest limit of soft X-ray spectrum, say
270 eV, then
. Since for current FEL sources the bandwidth,
, ranges in (
–
, LOPT is very well suited to provide reliable quantitative information about various quantities of experimental interest, for example, ion and fluorescence yields.
The validity of LOPT to calculate few X-ray photon processes allows the development of an alternative theoretical framework in place of the direct, but much more demanding, integration of a multielectron time-dependent Schrödinger equation. In the present work, we have chosen to apply LOPT to three elements of high experimental interest, namely Li, Ne and Ar. As it is known, these three atomic elements have been the subject of numerous experiments and theoretical studies since the inception of quantum mechanics. Excitation and ionization of the valence shells of the neutral species of these elements have been extensively studied and experimental reports and theoretical calculations about their photoionization cross sections are available in literature. In contrast to this plethora of data, the availability of analogous studies of their ionized species are scarce, especially when few-photon ionization is involved. To provide one example illustrating the need for such data, we mention the case of neon’s multiple ionization in the pioneering experiment of Young et al. [
3] at LCLS with a FEL pulse at a photon energy circa 1110 eV (pulse peak intensity and FWHM duration were estimated to be 10
17 W/cm
2 and 100 fs, respectively). In this experiment, the ionization of Ne
8+, following the sequential one-photon stripping of the lower charged neon ions, proceeds mainly through a two-photon absorption (the ionization potential of Ne
8+ is circa 1362 eV). It is needless to say that the same two-photon ionization channel would have been the dominant ionization channel for any photon in the energy range between 681 eV
eV; thus, the need for two-photon ionization cross sections for a range of photon energies. Of course, similar considerations can be carried over to any atomic system and of any degree of charge in the presence of X-ray radiation.
In the simplest case of the one-electron charged ions, multiphoton cross sections can be straightforwardly calculated by scaling the corresponding hydrogen cross sections according to the relation
[
11], where
is the
N-photon cross section of hydrogen and
Z is the atomic number of the element. Throughout the years, a number of reports have appeared in literature with multiphoton cross sections of hydrogen involving quite a high number of photons as, for example, the calculations by Karule [
12] and by Potvliege and Shakeshaft (
N = 20) [
13]. Next in line are charged ions with only their K-shell electrons remaining, making them helium-like (two-electron) systems. For helium, systematic studies exist where two, three- and four-photon LOPT ionization cross sections are calculated [
14]; it appears, despite the significance of Li, Ne and Ar as experimental and theoretical targets, that no similar detailed study has been extended to these systems. To the best of our knowledge, we are aware of the two- and three-photon total ionization cross sections that have been calculated on Li
+ with the use of single-channel quantum-defect theory (SQDT) [
15], the work of Novikov and Hopersky in neon ions [
16], the more recent work by the group of R. Santra [
17] (Ne
8+) and the two-photon total cross sections on Ne
8+ and Ar
16+, obtained through a Greens-function method calculation [
18].
More specifically, in the present study, we apply an ab initio configuration interaction (CI) approach and make use of LOPT to calculate the two- and three-photon partial photoionization cross sections for Li
+, Ne
8+ and Ar
16+. In addition to this, we have calculated details of their electronic structure. The structure of the text is as follows: in
Section 2, we present the theoretical method in sufficient detail for a self-contained formulation of the present study; in
Section 3, we present and discuss our results about the calculated energies and the LOPT two- and three-photon ionization partial cross sections. Finally, we conclude with a summary of our findings and a brief discussion of possible further investigations within the present context. In the presentation of the theoretical formulas, we use the atomic-Gaussian unit system (
). In the figures, the cross sections and the energies are presented in more traditional units, namely, eV for the energies, and
and
for the two- and three-photon cross sections, respectively.
3. Results and Discussion
In
Table 1, we give information related to the CI basis used for the various symmetries
1S,
1P,
1D and
1F. The configuration states,
, have been constructed according to Equation (
5) by one-electron orbitals with angular momenta given in
Table 1 and energies sufficiently high to ensure convergence of the results. The order of B-splines was
with the total number of B-spline polynomials set at
for Li
+ and
for Ne
9+ and Ar
16+. The box radius varied between
a.u. for Li
+,
a.u. for Ne
8+ and
a.u. for Ar
16+. The knot sequence of the spatial grid for the B-spline basis was linear. The two-electron wavefunctions,
, have been constructed from the zero-order configurations by one-electron orbitals with angular momenta given in the mentioned table and energies determined by the indices
in the following ranges:
and
. The relationship of the indices
to the energies of the zero-order wavefunctions depends on the basis size parameters such as the maximum value of the box radius as well as the number of B-spline basis functions used. In summary, the whole basis, for each symmetry, resulted in the inclusion of the following number of functions for each ion: 1650–1940 for Li
+, 1600 for Ne
8+ and 2040 for Ar
16+.
In
Table 2, we show the calculated energies for a few lower bound states of the hydrogenic ions Li
2+, Ne
9+ and Ar
17+. The degree of the agreement with those reported in the National Institute of Standards and Technology (NIST) atomic spectra database [
28] is given in the last row of the table. In all cases, the percentage discrepancies of the ground state energies (between the calculated and those of the NIST database) are of the order 0.1% while the excited states are of similar or even smaller order.
In
Table 3, we show the energy differences of the few lowest states of Li
+, Ne
8+ and Ar
16+ ions with respect to the respective ground state (
) energy of each ion. In all cases, the percentage discrepancies of the ground state energies (between the calculated and those of the NIST) are of the order 0.1% while the excited states are of similar or even of smaller order. This is not surprising as the role of correlation is more important in the lower energy states, where the electrons are on average closer relative to the higher-energy states.
Having examined the reliability of the calculated electronic structure, within the available theoretical and experimental data to compare, we proceed to the main subject of this work: the presentation of ionization cross sections for a range of photon frequencies. In all the following, the horizontal axis in the figures represents the photon energy, given in eV. The cross sections are given in SI units, cm, where N is the order of the process (here equivalent with the number of the photons absorbed). The final angular momenta, following two-photon absorption are the 1S, 1D continua, while in the case of three-photon absorption are the 1P, 1F continua. The cross sections have been evaluated using both the length and the velocity forms of the dipole operator. They generally have excellent agreement throughout all the spectral regions considered, especially for the non-resonant ones. Relative agreement between the length and the velocity forms is important since it provides strong evidence that the dipole matrix elements, contributing in the multiphoton transition amplitude, have been converged.
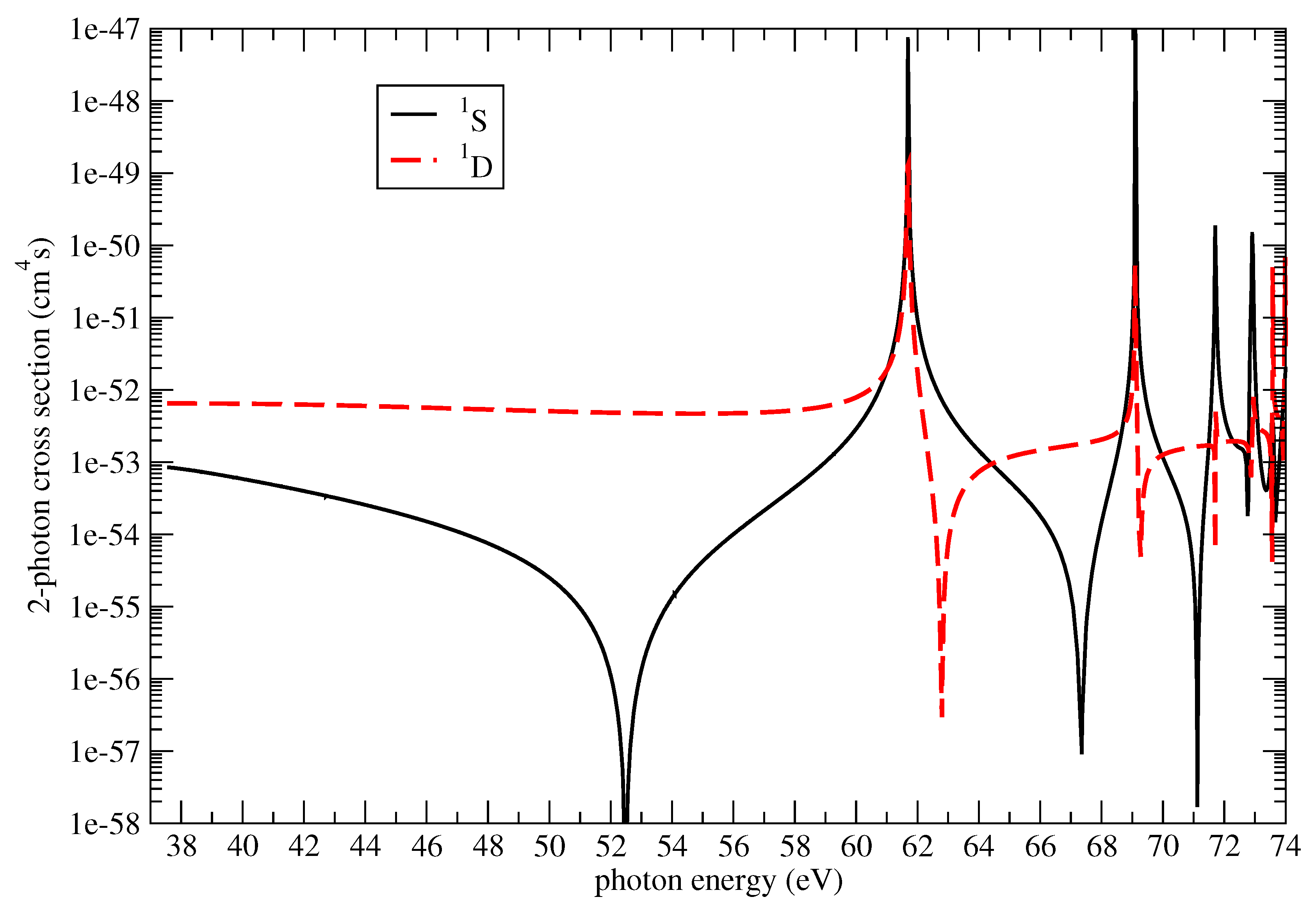
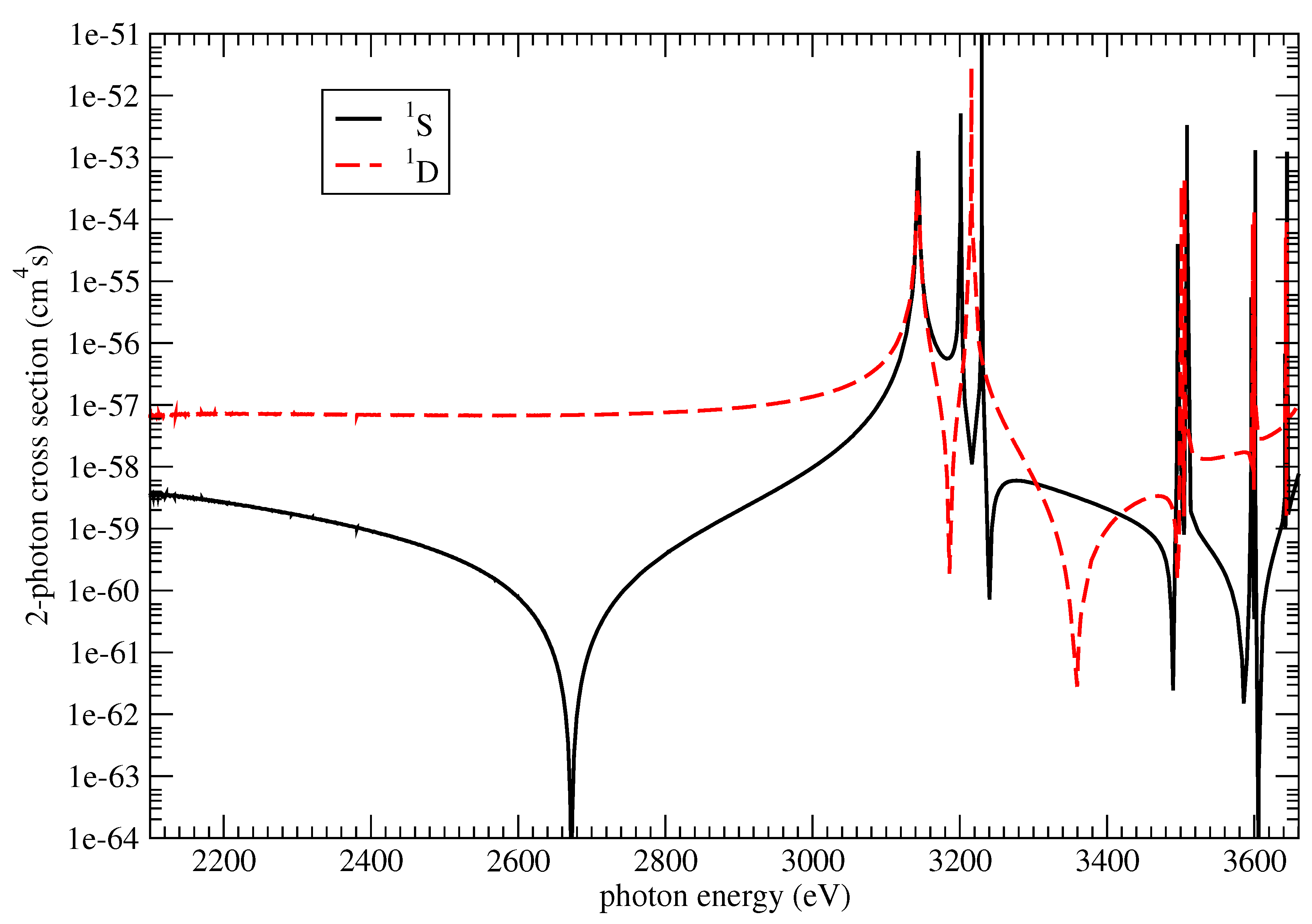
In
Figure 1,
Figure 2 and
Figure 3, we show the photon energy dependence of the calculated two photon partial-ionization cross sections,
, of Li
+, Ne
8+ and Ar
16+, respectively, from the ground state,
, to final states of symmetry
1S,
1D. Summing the latter, we obtain the corresponding total two-photon ionization cross sections,
. For clarity, we have plotted only the length-form results. Generally, for all three ions, the dominant two-photon ionization channel is the
1D symmetry. The cross sections exhibit strong peak structures, which appear in both the
1S and
1D final symmetries, due to one-photon resonance with the intermediate states
. Apart from these intermediate-resonance peaks, there are further peaks due to strong configuration mixing of the type
, associated with the
continua.
The configuration-mixing peaks are absent for two-photon ionization of Li
+ ionization since these would occur at higher photon energy, past about 75 eV, as the lowest post-ionization energy levels are about 150 eV and half that value (two photons) is about 75 eV. When we add the
1S and
1D cross sections to obtain the total cross section, we find a relatively good agreement with that of Ref. [
15], which models two-photon ionization of Li
+ employing a less elaborate approach, namely, single-channel quantum defect theory; when our shift is accounted for, our peaks occur close to that work (62.2 eV
, 69.7 eV
, 72.3 eV
and 73.5 eV
), and our (partial-wave sum) cross section baseline between 50–55 eV is within the same order of magnitude as in Ref. [
15] (both between
–
cm
4·s); however, our shape is slightly different here, being slightly convex (downward) in this region.
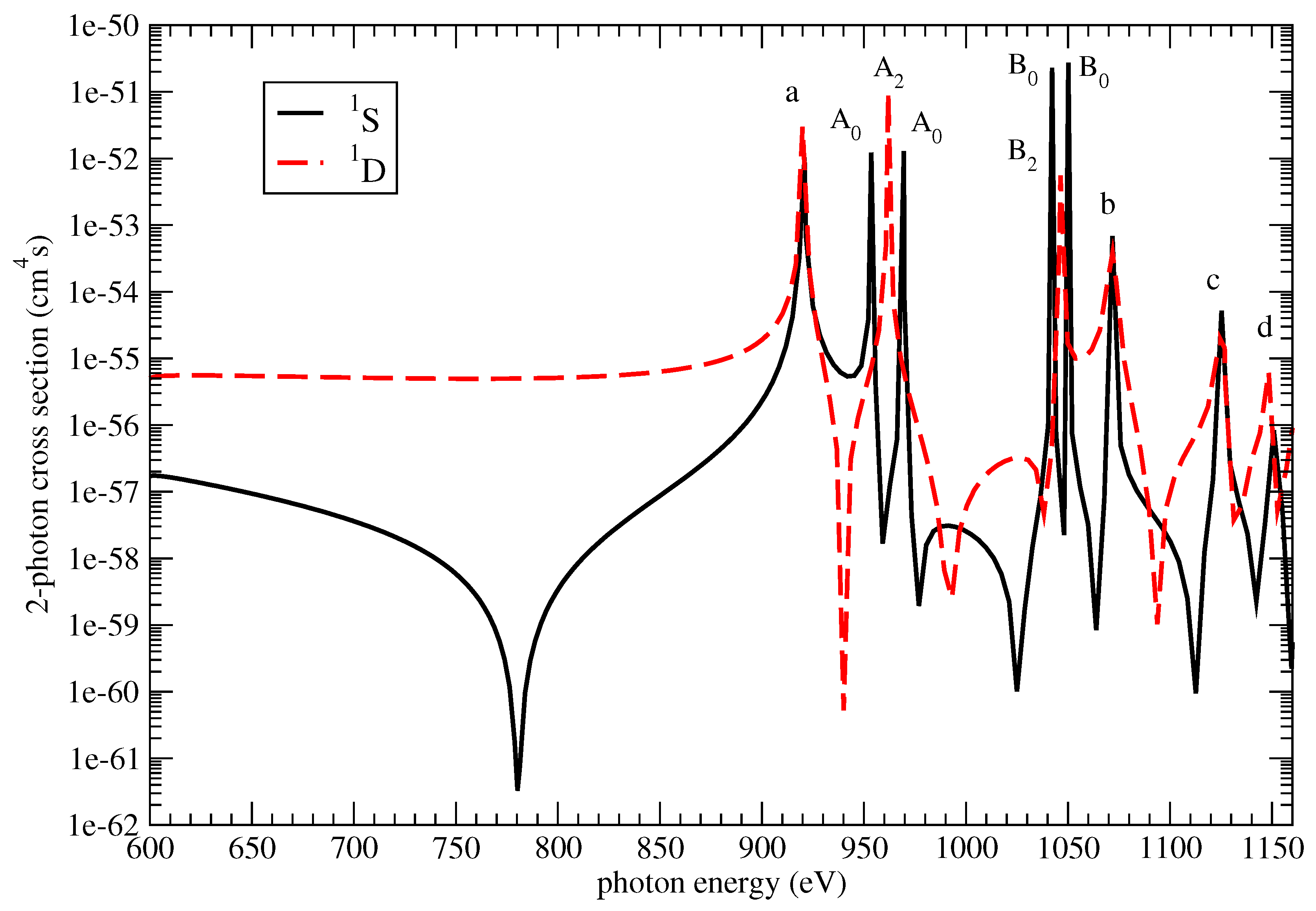
For Ne
8+ and Ar
16+, our values are also in good agreement with the Green-function calculations in Ref. [
18]. In addition, for Ne
8+, we have also compared our values with the second-order perturbation theory calculation of Novikov and Hopersky [
16]; their
and
one-photon resonance peaks (these are their only peaks) are comparable to ours occurring at around 920 eV and 1070 eV, respectively. Their cross section base-line (non-resonant part) circa 600–800 eV is also close to ours, i.e., within the same order of magnitude (both between
–
cm
4·s).
In relation to the intermediate resonance peaks in
Table 3, we show the energy differences of the few lowest states of Li
+, Ne
8+ and Ar
16+ ions from their respective ground state (
) energy,
, namely,
, (i.e., corresponding to peaks (a–d) in
Figure 2). Their importance is derived from the fact that these energy differences appear in the denominator of the two-photon cross section expression, Equation (
7), i.e.,
. It is then immediately evident that the photon energy detuning from these energy differences generates a series of characteristic features in the cross section. A word of caution is necessary at this point: within the current formulation, the height of these peaks becomes infinite in the exact on-resonance case,
. The first point to note is that we have ignored the inherent spontaneous decay width of the intermediate bound states. This would have served only to remove the unphysical singularities that occur at the resonances positions. However, most importantly, the LOPT cross sections fail to provide the correct ionization yields. In other words, in the resonant case, the LOPT relation for the ionization yield,
(
F is the pulse’s flux) becomes invalid. It is well established that, for resonant and near-resonant processes, while perturbation theory is still valid, an alternative formulation is required for the calculation of the expected ionization yields. This formulation, in addition to the ionization of the system directly from the ground state, takes into account the stepwise formation and the subsequent ionization of the intermediate states. Without going into the details, we shall only mention that in such cases the formulation should be developed in terms of a density matrix representation in combination with a proper representation of the spatiotemporal profile of the laser field. At this point, it is worth noting the pulse properties for which the LOPT cross sections presented here are valid. Equation (
10) is only just marginally applicable for a pulse with its detuning from a resonance of the same order as its bandwidth,
∼
, where
is the bandwidth. If we take as a rough rule that the bandwidth of the pulse is, say, a 1/100-th of its average photon energy (
∼
), that would mean that the cross section values within the range
eV (first peak in the two-photon cross section for Li
+) cannot be safely used in combination with Equation (
10). Similar considerations should be assumed for the higher peaks. For completeness, for Ne
8+ and Ar
16+, if based again on the appearance of the first peaks in the two-photon cross section (see the first row for the
state in
Table 3), the corresponding intervals are scaled upwards to
eV (∼920/100) and
eV (∼3126/100), respectively. A case that such a discrepancy between the LOPT two-photon ionization cross section [
16] and the experimental value [
29] is attributed to the bandwidth of the X-ray pulse can be found in Ref. [
17]. More specifically, for an X-ray photon energy of 1110 eV (in between (b) and (c) peaks in
Figure 2), the reported experimental value was
cm
4·s [
29] while the theoretical cross section based on a Hartree–Fock–Slater (HFS) model was found to be equal to 4.0 × 10
−57 cm
4s. Our calculated value for this photon energy is about 4.6 × 10
−57 cm
4s for the
1D wave while the
1S value makes a negligible contribution to the total cross section.
For Ne
8+ and Ar
16+, the ’twin’ peaks (see
peaks in
Figure 2), exclusive to the
1S symmetry, are due to the strong coupling between the
and
configurations in the expansion Equation (
4). Since in the
1D symmetry the
configuration is missing, we observe only one peak (
in
Figure 2), in between the
ones. To confirm this, we have performed some further tests where, for example, we excluded the
,
zero-order states (separately each time) from the CI wavefunction, Equation (
4). By doing this, we obtain a cross section with only one
peak at the same position where the
peak appears. This suggests that the observed (two)
peaks are the result of strong-mixing of the
and
configurations, mainly due to their proximity in energy.
Similar considerations hold for the peaks
at higher photon energies. The
twin peaks are due to the mixing of the
,
configurations in the
1S symmetry, while the
peak is due to the
state exclusively. We mention here that these doubly excited (highly correlated) states are also known as autoionizing states as they are associated with a temporal trap of the two excited electrons in the core’s region, eventually leading to the ejection of one of them and the residual (higher-charged ion) to its ground state. In the present (static) context of the CI calculation, these doubly excited states are degenerate with the
or
continua, which eventually cause their radiationless (auto)-ionization [
30].
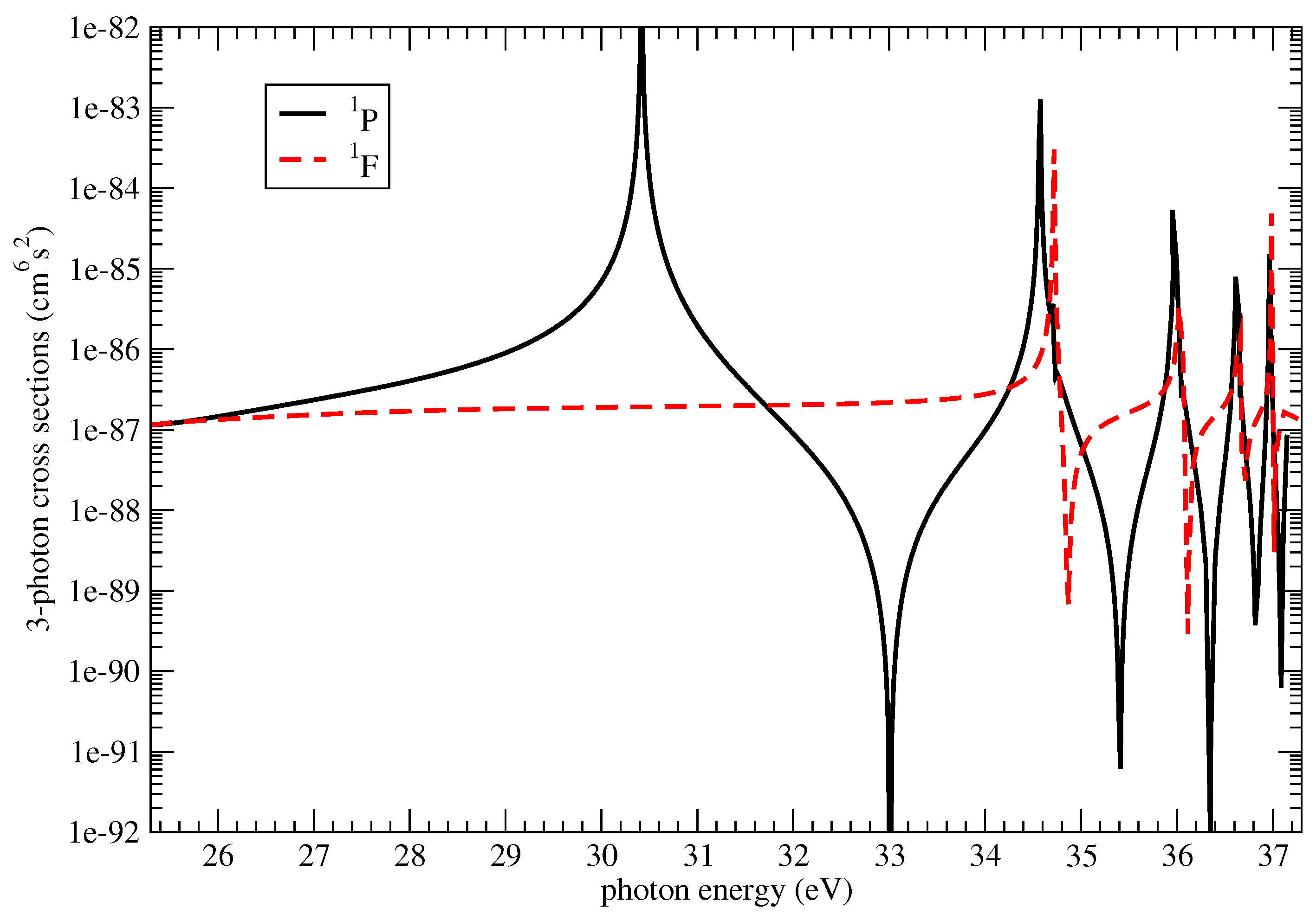
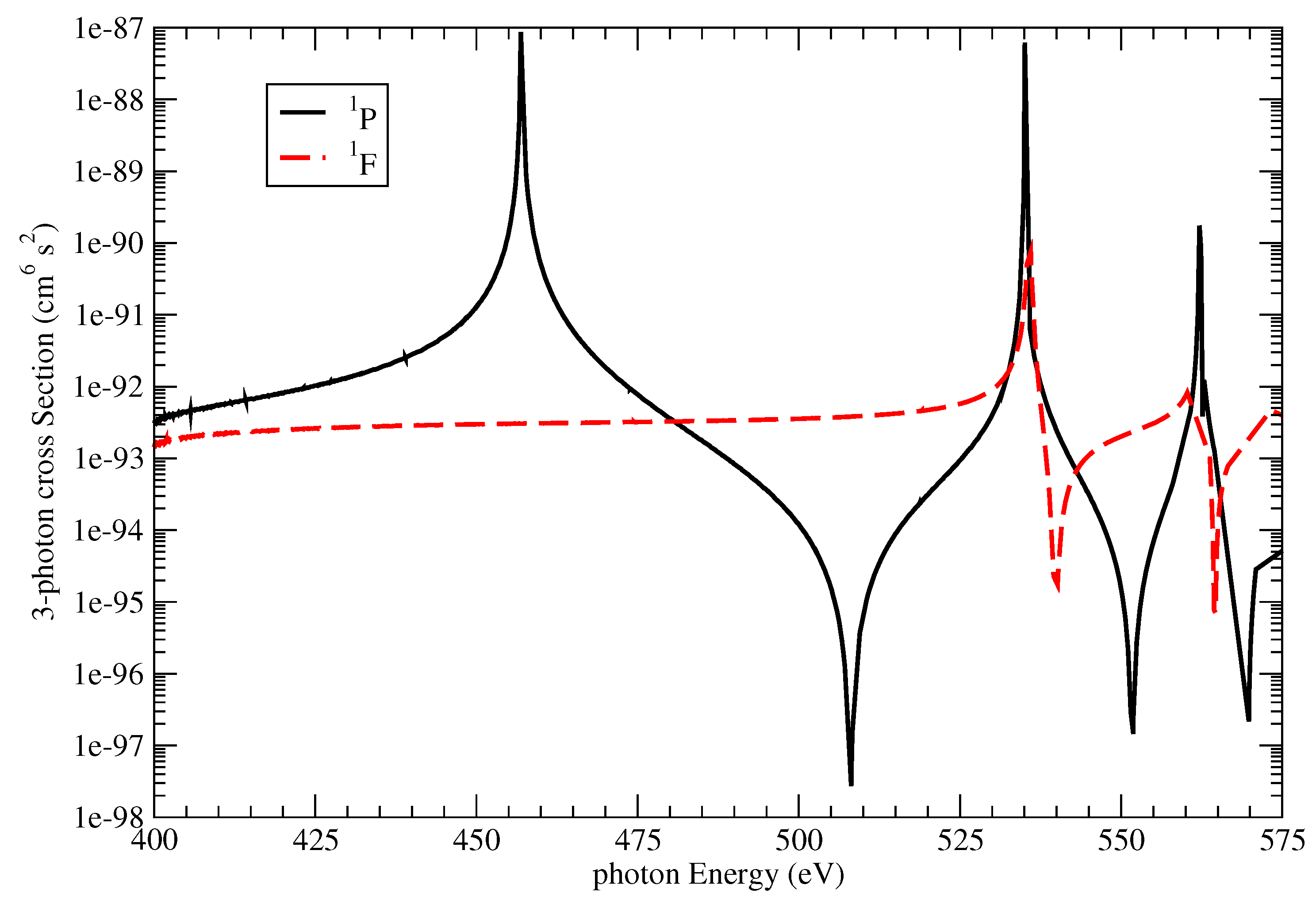
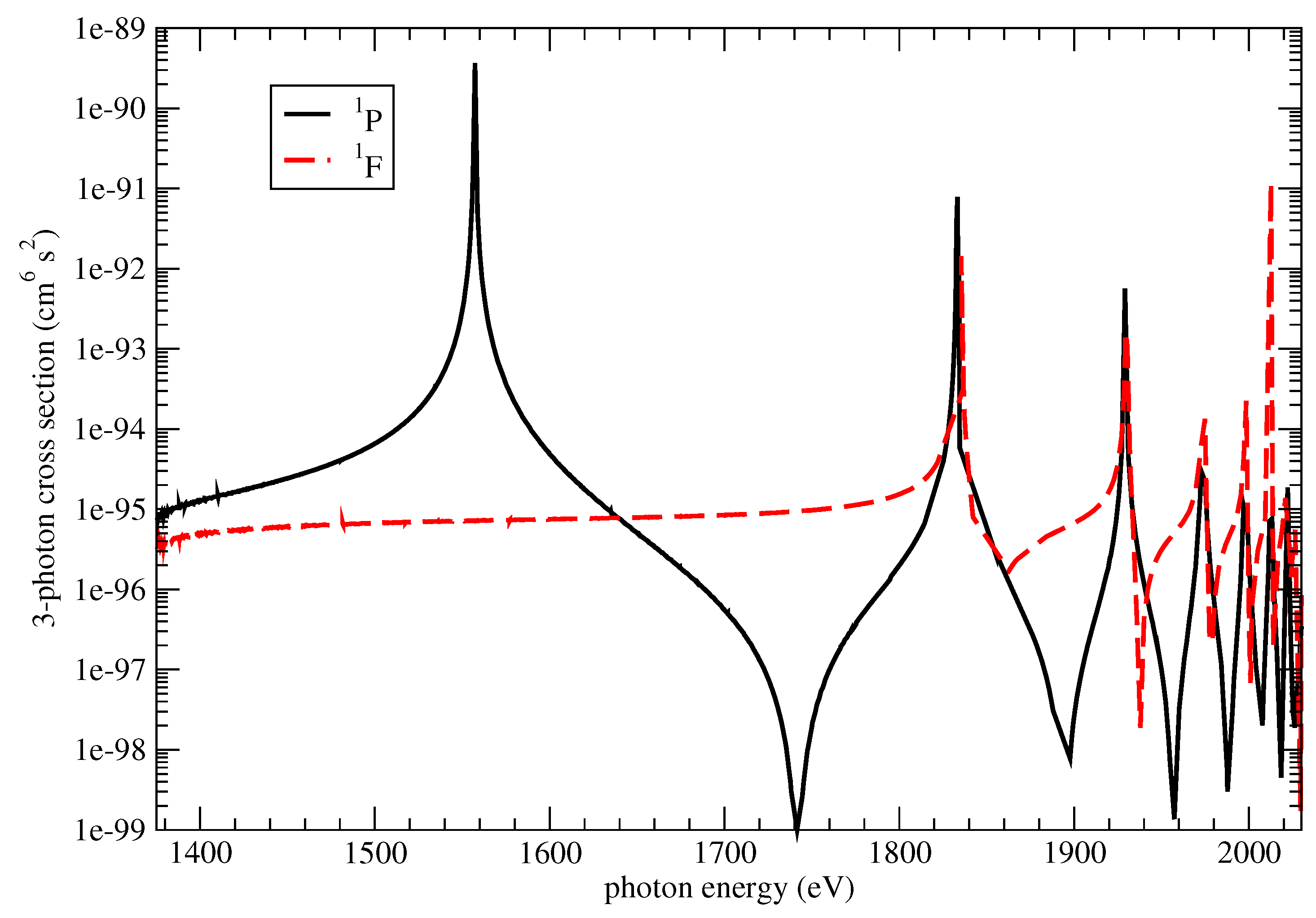
In
Figure 4,
Figure 5 and
Figure 6, we present our calculated three photon partial-ionization cross sections of Li
+, Ne
8+ and Ar
16+, respectively, from the ground state
. The final angular momentum of the ions, following three-photon absorption, are the
continua, all being of singlet symmetry. Similarly, as in the two-photon case, the total three-photon ionization cross section is obtained by the addition of the
1P and
1F partial-wave cross sections. Again, the final state is dominated by configurations with the residual ion in its ground state and the ejected electron with angular momentum
for the
1P and
for the
1F symmetry. The three-photon cross sections exhibit strong peak structures, which appear in both
1P and
1F final symmetries, due to two-photon resonances with the intermediate states
(see denominators (
) in Equations (
8) and (
9)). In the
1P symmetry, there are additional peaks due to two-photon resonance states of the type
. Because the
and
states have slightly different energy positions, the intermediate resonance peaks for the
1P and
1F (for example circa 34.4 eV for Li
+) do not generally coincide. Note that the
1P final states are reached by the coherent superposition of two ionization absorption channels:
and
. In contrast, the
1F states are reached only via one ionization channel, namely:
.
At this point, it might be worth comparing the cross sections among the three investigated ions. It is clearly visible from the figures that generally the ionization cross section decreases from Li
+ towards Ar
16+. This observation is rather consistent with the (exact) scaling,
, of the
N-photon cross section for hydrogenic systems [
11]. A second point worth mentioning is that the cross sections ending on the higher symmetry,
1D for two-photon and
1F for three-photon ionization, are proportional to the cross sections for circularly polarized light. To be more specific, due to the dipole selection rules, ionization by circularly polarized light will proceed through intermediate states where
will change either by
or by
monotonously. For example, let us assume circularly polarized light which causes a change of the magnetic quantum number by
. This means that if we start from the ground state, where
and
, then the first ionization step will involve only states with
. Similarly, the next ionization step will involve states that differ by
from the previous step, meaning that only states with
will be accessed in this step. In this case, these states will necessarily have
. Accordingly, if further ionization occurs (three-photon ionization), for the same reason, only states with
will be reached, thus ending necessarily with an
total orbital angular momentum. Similar considerations hold had we started by circularly polarized light with opposite helicity, leading to a change of
. In short, for two-photon ionization, only the ionization path
is allowed. Accordingly, for three-photon ionization, only the
ionization channel will occur. Now the crucial observation is that the transition amplitudes by circularly and linearly polarized light for these ionization paths differ only by the total magnetic quantum number,
. For linearly polarized light, it is
while for circularly polarized light, it is
. Straightforward angular momentum algebra for these transition amplitudes (
for circular(linear)-polarized light) of two-electron states shows that they differ only by a proportional factor; namely,
for two-photon ionization and
, for three-photon ionization, where
D and
F denote the final angular momentum channel for two-photon and three-photon ionization, respectively [
31]. Nevertheless, note that circularly polarized light does not guarantee that the total ionization cross section will provide higher rates relative to the ionization by linearly polarized light; the final rate depends on the number of available ionization paths available and the electric field intensity and, in fact, high
N-photon ionization by linearly polarized light is more effective.