Fuzzy Synthetic Evaluation of the Long-Term Health of Tunnel Structures
Abstract
:1. Introduction
2. Determination of the Evaluation Methods and Ideas for the Tunnel Structural Health
2.1. Selection of Evaluation Method for Tunnel Structural Health
2.2. Evaluation Idea for Tunnel Structural Health
3. Application of the Fuzzy Synthetic Evaluation Method to Cang Ling Tunnel Structural Health Evaluation
3.1. General Situation of Application Engineering
3.2. Choice and Implementation of Long-Term Health Monitoring Project
3.3. The Classification of Health Levels for a Tunnel Structure
3.4. Application of Fuzzy Synthetic Evaluation of Long-Term Structural Health in Cang Ling Tunnel
3.4.1. Establishment of the Evaluation Model
- (1)
- When the eccentricity , where “h” is the thickness of the secondary lining, the section of the concrete is an axial compression member or a compression member with a small eccentricity. The bearing capacity is controlled by the compressive strength. The safety factor is calculated as follows:where: Ra: The ultimate compressive strength of the concrete, which is applied according to the Code for Design of Highway Tunnel [30]. K: The safety factor. N: The axial force of the section (KN). B: The width of the secondary lining. Take b = 1 m. h: The thickness of the secondary lining (m). : The longitudinal bending coefficient of the member, can be taken as = 1. : The eccentric influencing coefficient of the axial force that is applied according to the Code for Design of Highway Tunnels [30].
- (2)
- When the eccentricity , the section of the concrete is a compression member with a large eccentricity. The bearing capacity is controlled by the tensile strength. The safety factor is calculated as follows:where Rl is the ultimate tensile strength of the concrete, which is applied according to the Code for Design of Highway Tunnels [30]. Other symbols are the same as in Equation (1).
3.4.2. The Determination of Criteria and Weight of Each Index in the Evaluation Model
- (1)
- In order to keep the plane strain state and reduce the friction between the test tank and the simulated surrounding rock, the upper and lower steel plate and the distribution beam are buttered. Then the film is pasted on the upper and the lower steel plate to isolate the surrounding rock and the butter;
- (2)
- According to the different factors of surrounding rock, wires are pulled around the test tank to control the feeding quantity. After artificial leveling, a compaction rammer is used. Compacted density is controlled by the cutting ring method. The upper steel plate is lifted after compaction, then the vertical jack is installed to restrain the vertical displacement;
- (3)
- According to the initial geostress field of each section in the similarity comparison tests, the specimen is loaded with the initial geostress before the excavation of the tunnel. Then the tunnel is excavated in the middle of the surrounding rock under the initial geostress field. Rock bolts are inserted and a steel arch is installed when necessary;
- (4)
- The primary support is constructed and the pressure cells are fixed to it with cross buckles. Then, the secondary lining with strain gauges is placed in the excavated model tunnel to simulate the construction process of the tunnel;
- (5)
- The wires of the pressure cells and the strain gauges are connected to the strain acquisition instrument and the displacement meters are displayed. When the strength of the primary support reaches the design strength, the specimen is loaded with the initial geostress fields of different sections, from small to large, until the main structure of the tunnel is destroyed (lateral pressure coefficient is fixed during the loading process). When the structure is stable after the loading of each level of initial geostress field, corresponding strain, pressure, and displacement are measured by the data acquisition instrument controlled by a computer;
- (6)
- The behavior of the secondary lining from the first crack appearing to the final complete failure is recorded in detail. The structural failure characteristics, damage location, crack width, depth, etc. are paid attention to. After the secondary lining is completely destroyed, the specimen is unloaded and the test is finished;
- (7)
- The data are arranged and analyzed. Based on the data, a study of the mechanical behavior of the main structure of the tunnel under different initial geostress fields during construction and operation can be carried out.
3.4.3. Determination of the Membership Function
4. Evaluation of Structural Health Status of Cang Ling Tunnel Based on Filed Data
5. Conclusions
- (1)
- A tunnel is a coupled system of the surrounding rock and the supporting structure. The safety status of the tunnel structure is a complex system that is influenced by various factors. In addition, these factors are coupled and interact with each other, which calls for a linguistic description of the tunnel safety level. Therefore, the fuzzy synthetic method should be adopted;
- (2)
- According to the investigation and analysis of the safety status classification of tunnels at home and abroad, and combined with the present situation of safety status classification of tunnel structures in China, the health status of a highway tunnel structure is divided into four levels: safe, basically safe, potentially unsafe, and unsafe. In this research, the fuzzy synthetic method is proposed to evaluate the tunnel safety level;
- (3)
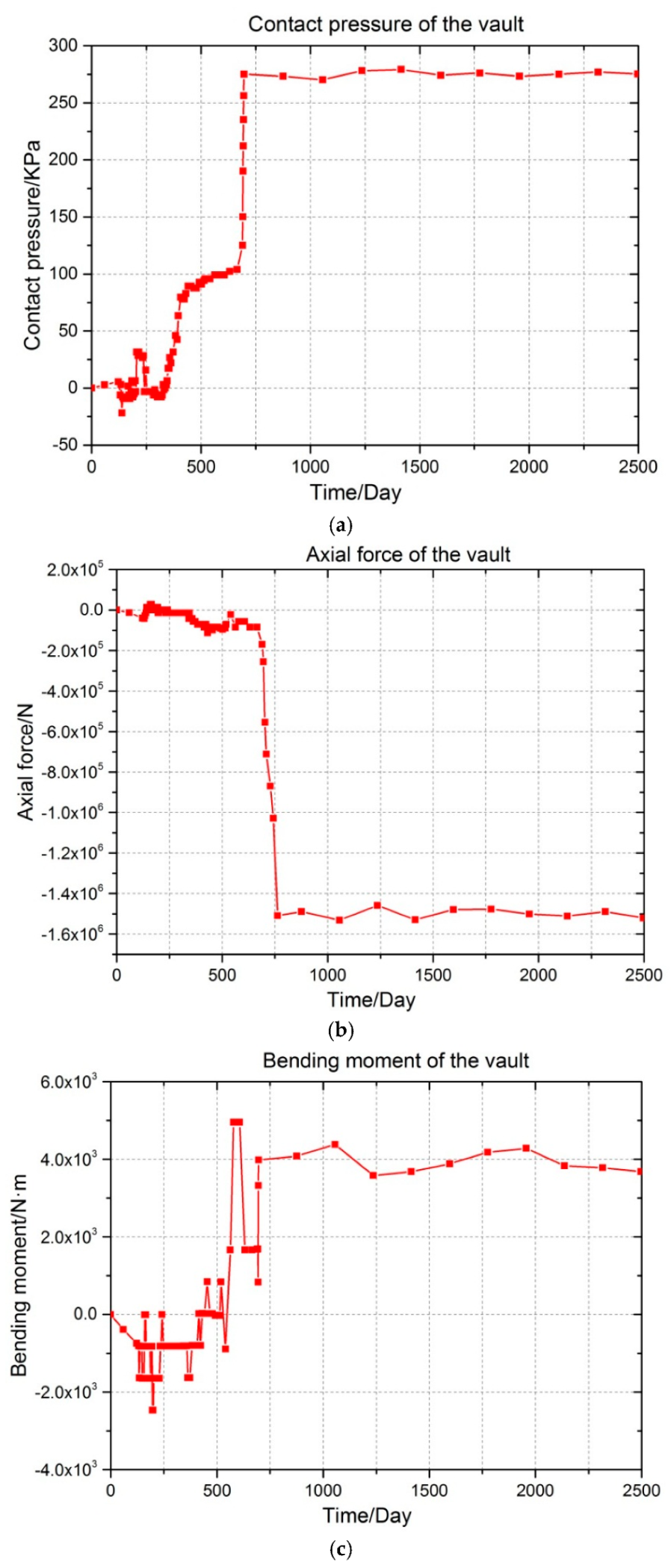
- With the increase of service time of the tunnel, the primary support gradually deteriorates. The safety of the tunnel structure will be reflected in the safety of the secondary lining. Therefore, the stress of the secondary lining and the contact pressure between the primary support and the secondary lining are selected as a long-term monitoring project. Long-term monitoring sensors are embedded to acquire structural stress characteristics, providing data for structural safety evaluation. The sensors that monitor the stress of the secondary lining and the contact pressure are embedded in the lining of the Cang Ling Tunnel. From these sensors, the stress data for the safety evaluation of the tunnel structure are obtained;
- (4)
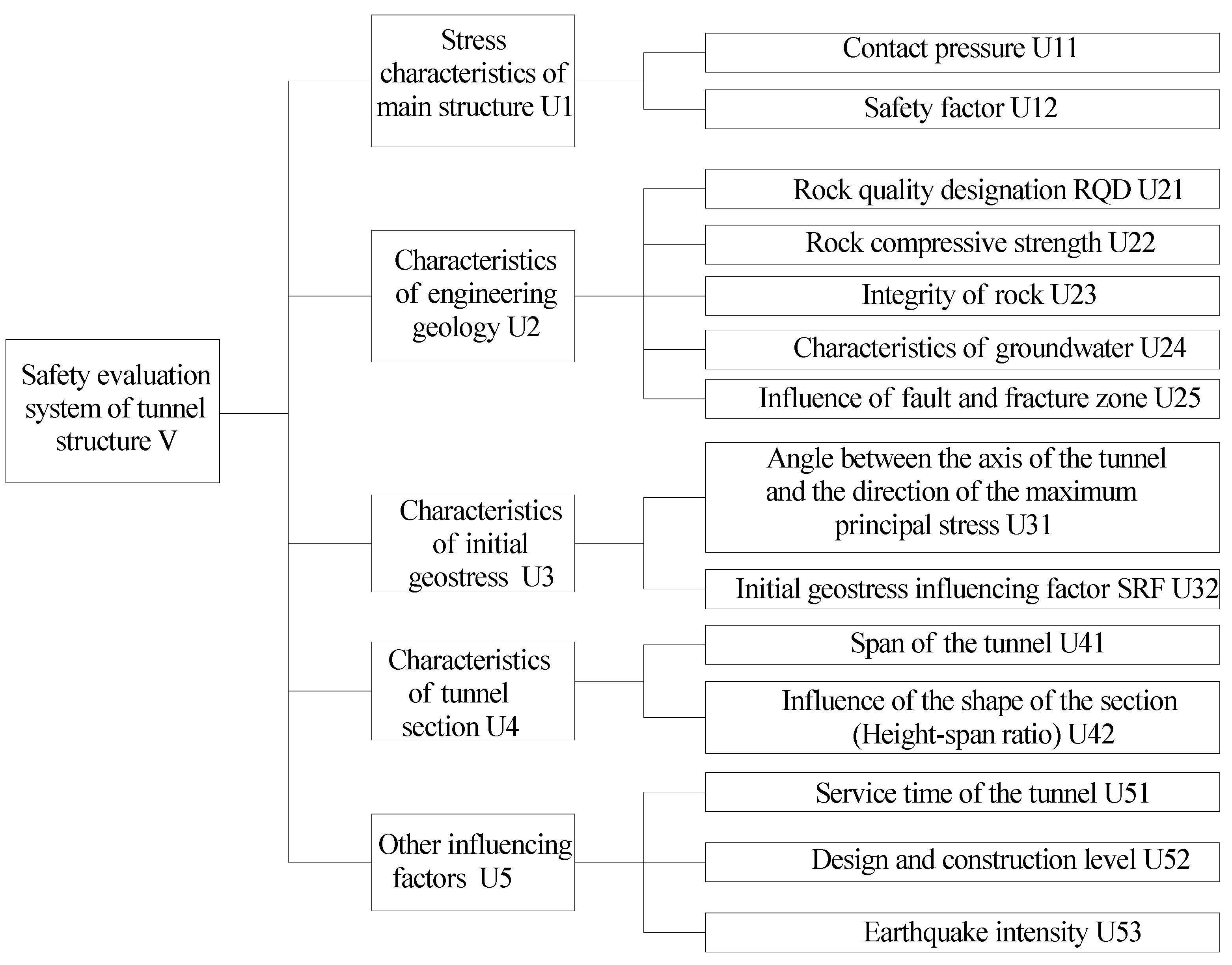
- Through analysis of the various factors affecting the health status of the tunnel structure, coupled with the long-term monitoring project carried out in the Cang Ling Tunnel, the two-level fuzzy synthetic evaluation model of the structural health status for the Cang Ling Tunnel is established. The fuzzy synthetic evaluation model mainly includes the stress characteristics of the tunnel structure, the engineering geological characteristics, the characteristics of the initial geostress, and the characteristics of the tunnel section. Moreover, the factors are refined into 14 specific indices;
- (5)
- As for the tunnel structural health, through the analysis of the distribution characteristics of the influencing indices, the membership functions of indices in the fuzzy synthetic evaluation model are established. The types of membership functions are mainly normal distribution and trapezoidal distribution. The corresponding relationship between each index in the fuzzy synthetic evaluation model and the health level of the tunnel structure and the determination criteria are established using model tests, field tests, and other methods. By using the AHP, the weight of each index in the safety evaluation system of tunnel structure is obtained. According to the membership functions, the determination criteria, and the weight values of the evaluation model, the subordinate degree is obtained using the method of fuzzy mathematics;
- (6)
- According to the principle of maximum membership degree, based on the contact pressure and the stress of the secondary lining acquired by the long-term health monitoring sensors of Cang Ling Tunnel, the health status of the main structure of Cang Ling Tunnel is evaluated using the proposed fuzzy synthetic evaluation. The results show that the current health status of most of Cang Ling Tunnel is at level I safety status. Only a small number of segments are at the basic safety status, which is level II.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, S.; Lin, C.; Zhang, Z.; Li, Z. Application of structural health monitoring in Hangzhou Qiantang River Tunnel. In Proceedings of the International Conference on Electric Technology and Civil Engineering, Lushan, China, 22–24 April 2011; pp. 2004–2007.
- Ke, S.; Zhang, W.; Ding, P.L. The structural health monitoring system for Nanjing Yangtze River Tunnels. In Proceedings of the Second International Conference on Electric Information and Control Engineering, Lushan, China, 6–8 April 2012; pp. 1562–1566.
- Wang, B.; He, C.; Wu, D.X. Ideas of tunnel structure health monitoring system and its technology application. J. Railw. Eng. Soc. 2012, 1, 67–72. [Google Scholar]
- Li, X.; He, C.; Wang, S.M.; Wang, B. Design and Application of Long-term Safety Monitoring System of Highway Tunnel under Complex Geological Conditions. China Saf. Sci. J. 2013, 23, 89–95. [Google Scholar] [CrossRef]
- Zheng, Z.; Lei, Y. Structural monitoring techniques for the largest excavation section subsea tunnel: Xiamen Xiang’an Subsea Tunnel. J. Aerosp. Eng. 2016, B4016002. [Google Scholar] [CrossRef]
- Schotte, K.; Nuttens, T.; Wulf, A.D.; Bogaert, P.V.; Backer, H.D. Monitoring the structural response of the Liefkenshoek Rail Tunnel to tidal level fluctuations. J. Perform. Constr. Facil. 2016, 30, 04016007. [Google Scholar] [CrossRef]
- Su, J.; Zhang, D.; Niu, X.; Fang, Q. Research on design of subsea tunnel structural health monitoring. Chin. J. Rock Mech. Eng. 2007, 26, 3785–3792. [Google Scholar]
- Soga, K.; Amatya, B.; Wright, P.; Bennett, P.J.; Kobayashi, Y.; Cheung, L.L.K. Optical fibre strain measurement for tunnel lining monitoring. Geotech. Eng. 2010, 163, 119–130. [Google Scholar]
- Bursi, O.S.; Tondini, N.; Fassin, M.; Bonelli, A. Structural monitoring for the cyclic behaviour of concrete tunnel lining sections using FBG sensors. Struct. Control Health Monit. 2015, 23, 749–763. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Qi, D.; Liu, Y. Automatic crack detection and classification method for subway tunnel safety monitoring. Sensors 2014, 14, 19307–19328. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.W.; Ni, Y.Q.; Yin, J.H. Safety monitoring of railway tunnel construction using FBG sensing technology. Adv. Struct. Eng. 2013, 16, 1401–1410. [Google Scholar] [CrossRef]
- Lindenbergh, R.; Bucksch, A.; Uchanski, L.; Gosliga, R.V. Structural monitoring of tunnels using terrestrial laser scanning. Rep. Geod. 2009, z. 2/87, 231–238. [Google Scholar]
- Lopes, V.; Park, G.; Cudney, H.H.; Inman, D.J. Impedance-based structural health monitoring with artificial neural networks. J. Intell. Mater. Syst. Struct. 2000, 11, 206–214. [Google Scholar]
- Wang, H.; Song, G.B. Innovative NARX recurrent neural network model for ultra-thin shape memory alloy wire. Neurocomputing 2014, 134, 289–295. [Google Scholar] [CrossRef]
- Canelon, J.I.; Shieh, L.S.; Song, G.B. A new neural network-based approach for self-tuning control of nonlinear SISO discrete-time systems. Int. J. Syst. Sci. 2010, 41, 1421–1435. [Google Scholar] [CrossRef]
- Guo, H.Y.; Zhang, L.L.; Zhou, J.X. Optimal placement of sensor for structural health monitoring using improved genetic algorithms. Smart Mater. Struct. 2004, 13, 528. [Google Scholar] [CrossRef]
- Li, L.; Song, G.B.; Ou, J. A genetic algorithm-based two-phase design for optimal placement of semiactive dampers for nonlinear benchmark structure. J. Vib. Control 2010, 16, 1379–1392. [Google Scholar] [CrossRef]
- Li, L.; Song, G.B.; Ou, J. Hybrid active mass damper (AMD) vibration suppression of nonlinear high-rise structure using fuzzy logic control algorithm under earthquake excitations. Struct. Control Health Monit. 2011, 18, 698–709. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.B.; Malki, H. Chattering-free fuzzy adaptive robust sliding-mode vibration control of a smart flexible beam. Smart Mater. Struct. 2008, 17, 4006–4032. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, K.; Lei, C.; Zhang, Y.; Li, H.; Spencer, B.F. Fuzzy analytic hierarchy process synthetic evaluation models for the health monitoring of shield tunnels. Comput. Aided Civil Infrastruct. Eng. 2014, 29, 676–688. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, X.; Yuan, C. The research of optimal monitoring point placement for health monitoring of dredger based on analytic hierarchy process. In Proceedings of the Prognostics and Health Management Conference, Macau, China, 12–14 January 2010; pp. 1–5.
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Shang, L.; Tan, L.; Yu, C.; Liu, Y. Bridge Structural Health Evaluation Based on Multi-Level Fuzzy Comprehensive Evaluation; Springer: Berlin/Heidelberg, Germany, 2011; pp. 661–668. [Google Scholar]
- Liu, Y.; Hui, X. Extended multi-level fuzzy comprehensive evaluation model of bridges maintenance based on fuzzy set. Int. J. Adv. Comput. Technol. 2012, 4, 158–166. [Google Scholar]
- Wu, L.M.; Wang, Z.J. Fuzzy comprehensive evaluation method and application of slope stability. Adv. Mater. Res. 2011, 243, 4969–4974. [Google Scholar] [CrossRef]
- Feng, S.J.; Yao, A.M.; Dong, Y.F. Fuzzy comprehensive evaluation of open-pit slope stability. Adv. Mater. Res. 2014, 962, 1029–1033. [Google Scholar] [CrossRef]
- Onkal-Engin, G.; Demir, I.; Hiz, H. Assessment of urban air quality in istanbul using fuzzy synthetic evaluation. Atmos. Environ. 2004, 38, 3809–3815. [Google Scholar] [CrossRef]
- Rajani, B.; Kleiner, Y.; Sadiq, R. Translation of pipe inspection results into condition ratings using the fuzzy synthetic evaluation technique. J. Water Supply Res. Technol. AQUA 2006, 55, 11–24. [Google Scholar] [CrossRef]
- Sadiq, R.; Husain, T.; Veitch, B.; Bose, N. Risk-based decision-making for drilling waste discharges using a fuzzy synthetic evaluation technique. Ocean Eng. 2004, 31, 1929–1953. [Google Scholar] [CrossRef]
- Code for Design of Highway Tunnel; China Communications Press: Beijing, China, 2004.
- Code for Design of Railway Tunnel; China Railway Press: Beijing, China, 2005.
- Wu, C.G.; He, C.; Li, X.; Zhang, F. Model test research on structure mechanics of tunnel in high geostress. Mod. Tunn. Technol. 2008, S1, 250–255. [Google Scholar]
- Wang, B. Study on Safety Monitoring Technique for Expressway Tunnel during Period of Construction and Operation; Southwest Jiaotong University: Chengdu, China, 2008. [Google Scholar]
- Vallejo, L.I.G.D. SRC rock mass classification of tunnels under high tectonic stress excavated in weak rocks. Eng. Geol. 2003, 69, 273–285. [Google Scholar] [CrossRef]
- Habibagahi, G.; Katebi, S. Rock mass classification using fuzzy sets. Iran. J. Sci. Technol. Trans. B Eng. 1996, 20, 273–284. [Google Scholar]
- Jing, S.T.; Zhu, Y.Q.; Song, Y.X. Reliability of Tunnel Structure; China Railway Press: Beijing, China, 2002. [Google Scholar]

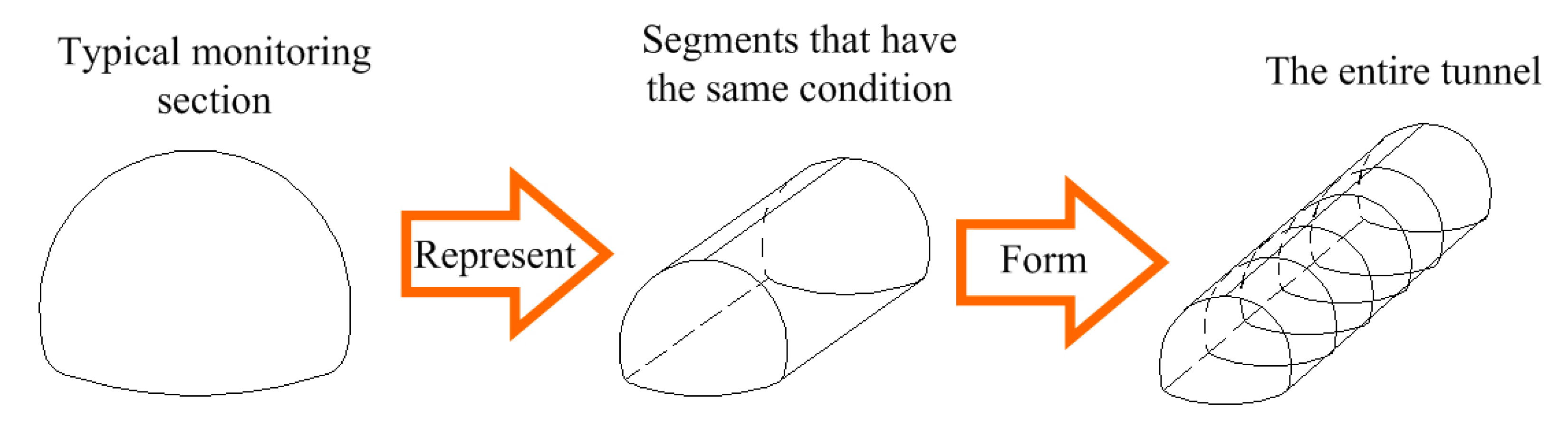
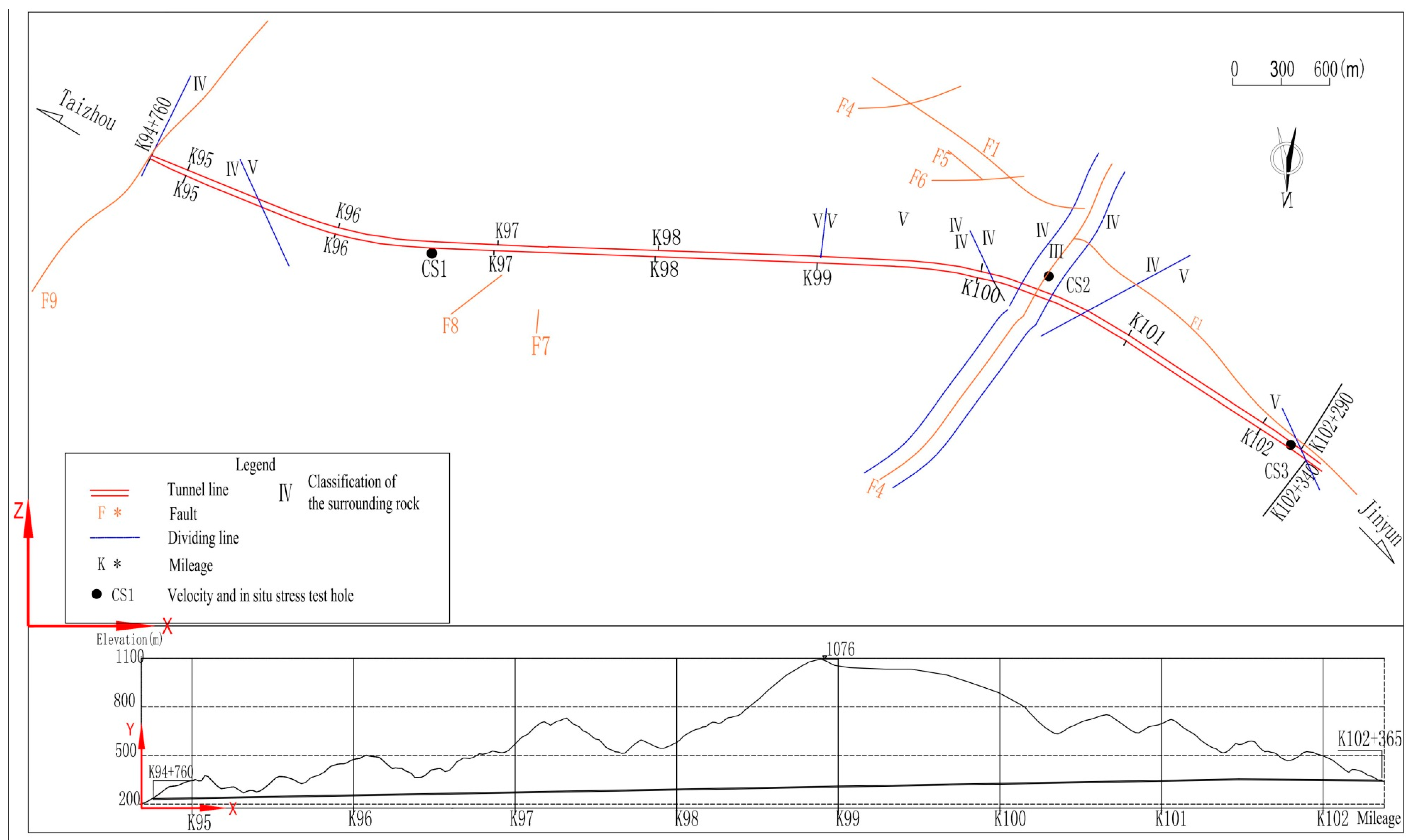
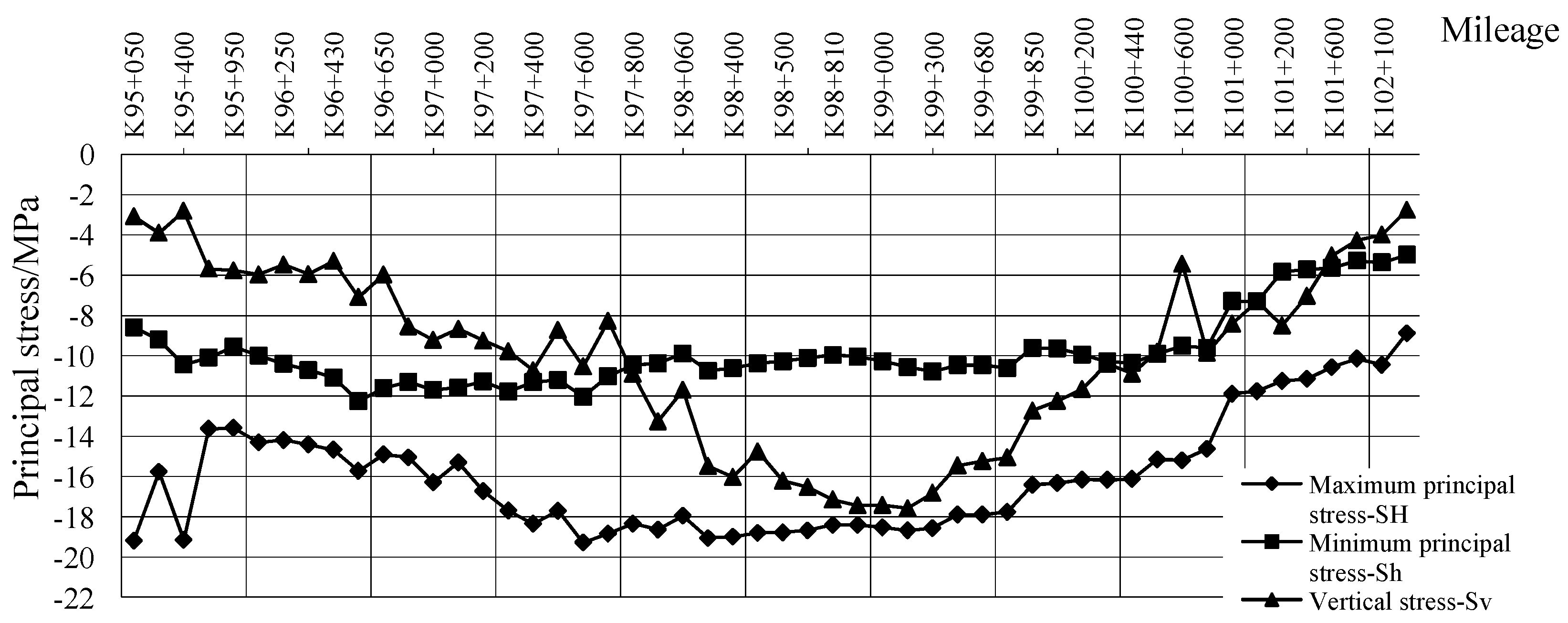
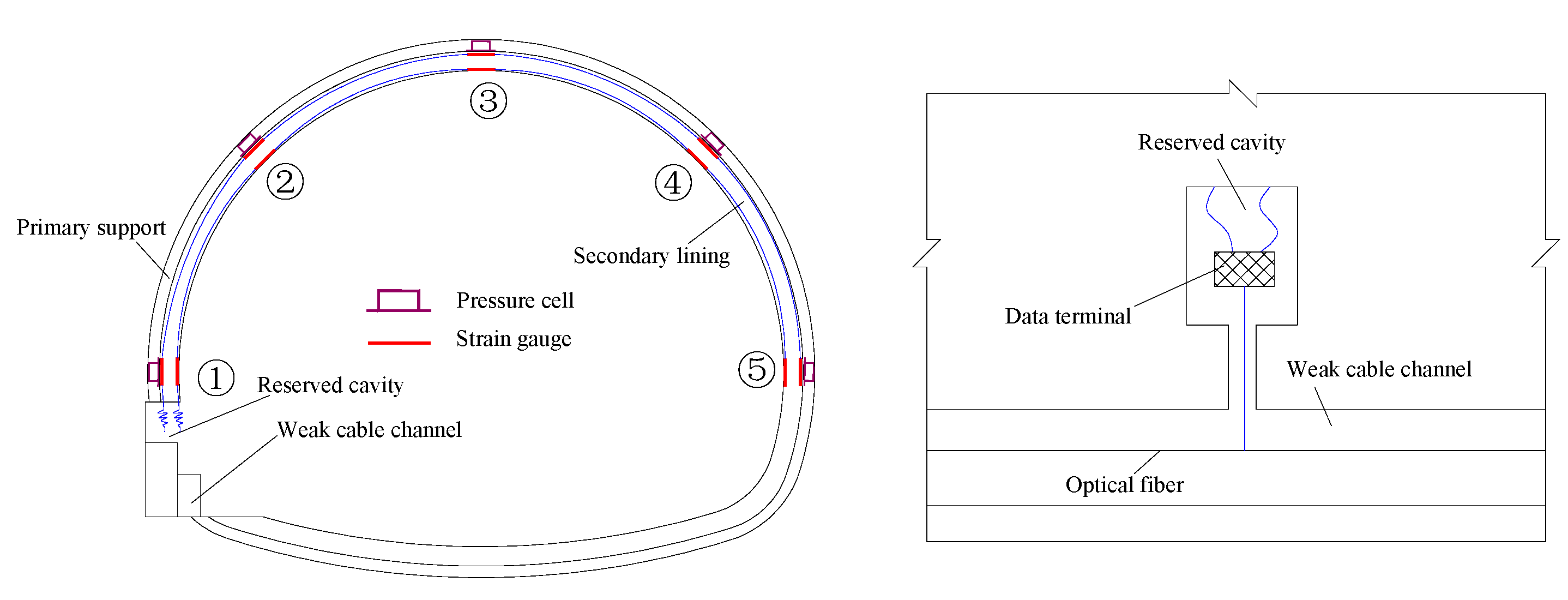



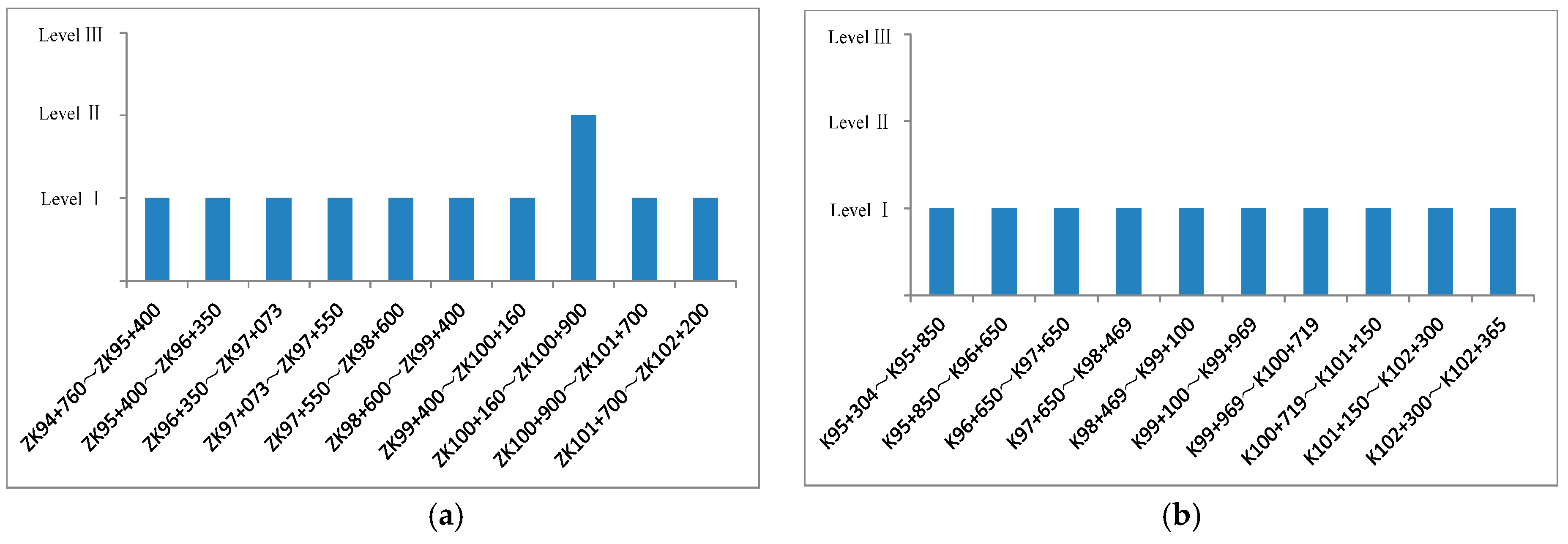
| Serial Number | Mileage of the Segment | Typical Monitoring Section | Serial Number | Mileage of the Segment | Typical Monitoring Section |
|---|---|---|---|---|---|
| 1 | ZK94+760~ZK95+400 | ZK94+900 | 11 | K95+304~K95+850 | K95+350 |
| 2 | ZK95+400~ZK96+350 | ZK95+609 | 12 | K95+850~K96+650 | K96+000 |
| 3 | ZK96+350~ZK97+073 | ZK96+370 | 13 | K96+650~K97+650 | K96+790 |
| 4 | ZK97+073~ZK97+550 | ZK97+093 | 14 | K97+650~K98+469 | K98+000 |
| 5 | ZK97+550~ZK98+600 | ZK97+655 | 15 | K98+469~K99+100 | K98+490 |
| 6 | ZK98+600~ZK99+400 | ZK98+895 | 16 | K99+100~K99+969 | K99+240 |
| 7 | ZK99+400~ZK100+160 | ZK99+521 | 17 | K99+969~K100+719 | K100+000 |
| 8 | ZK100+160~ZK100+900 | ZK100+220 | 18 | K100+719~K101+150 | K100+740 |
| 9 | ZK100+900~ZK101+700 | ZK101+050 | 19 | K101+150~K102+300 | K101+535 |
| 10 | ZK101+700~ZK102+200 | ZK101+900 | 20 | K102+300~K102+365 | K102+340 |
| Health Levels | Evaluation |
|---|---|
| Level I (Safe) | The structure is safe. The structure is intact or has tiny cracks. In this stage, pedestrians and traffic safety will not be affected. Maintaining daily monitoring is enough |
| Level II (Basically Safe) | The structure is basically safe. The structure is slightly damaged or has tiny cracks. In this stage, pedestrians and traffic safety will not be affected. Maintaining daily monitoring is enough. Whether the structural stress will develop further or not should be determined by the combined judgment of the long-term monitoring project. Strengthening the monitoring frequency and daily maintenance are suggested |
| Level III (Potentially Unsafe) | The structure is potentially unsafe. The structure is seriously damaged or has cracks. In this stage, pedestrians and traffic safety will be affected sooner or later. Further development will lead to the decrease of the structure function or even the failure of the structure. Increasing the monitoring frequency and taking strengthening measures as soon as possible are suggested |
| Level IV (Unsafe) | The structure is unsafe. The structure is seriously damaged and the damage continues to develop. In this stage, pedestrians and traffic are endangered. Immediately increasing the monitoring frequency and taking reinforcement measures are suggested |
| Section Type | Classification | The Thickness of the Lining (cm) | Influencing Factor | Health Level | |||
|---|---|---|---|---|---|---|---|
| Level I | Level II | Level III | Level IV | ||||
| Standard section | Surrounding rock of grade IV | 45 | Contact pressure (kPa) | <540 | 540~1012 | 1013~1263 | >1263 |
| Safety factor | >4.49 | 4.49~2.54 | 2.55~1.01 | <1.01 | |||
| 35 | Contact pressure (kPa) | <420 | 420~720 | 721~878 | >878 | ||
| Safety factor | >4.23 | 4.23~2.16 | 2.17~1.12 | <1.12 | |||
| Surrounding rock of grade III | 30 | Contact pressure (kPa) | <390 | 390~640 | 641~814 | >814 | |
| Safety factor | >4.46 | 4.46~2.37 | 2.38~0.99 | <0.99 | |||
| Surrounding rock of grade II | 30 | Contact pressure (kPa) | <482 | 482~709 | 710~810 | >810 | |
| Safety factor | >4.215 | 4.22~1.95 | 1.96~1.15 | <1.15 | |||
| Enlarged section | Emergency parking area | 40 | Contact pressure (kPa) | <395 | 395~590 | 591~781 | >781 |
| Safety factor | >3.71 | 3.71~1.82 | 1.83~0.96 | <0.96 | |||
| Vehicle cross channel | 50 | Contact pressure (kPa) | <443 | 443~626 | 627~874 | >874 | |
| Safety factor | >3.91 | 3.91~2.15 | 2.16~1.02 | <1.02 | |||
| Health Level Influencing Factor | Level I | Level II | Level III | Level IV | |
|---|---|---|---|---|---|
| Engineering geological characteristics | Rock quality designation RQD/% | 100~91 | 90~76 | 75~51 | 50~0 |
| Rock compressive strength/MPa | 200~121 | 120~61 | 60~31 | 30~0 | |
| Rock integrity | 1.0~0.76 | 0.75~0.56 | 0.55~0.36 | 0.35~0 | |
| Groundwater conditions/ | 0~10 | 11~25 | 26~125 | 126~300 | |
| Influence of the fault fracture zone | No fault or fracture zone nearby | Small fault nearby or the fracture zone is far away | Tunnel is near to the small fault or passes through small fracture zone | Large fault has a certain effect, or the tunnel is near to the large fault or the fracture zone or passes through them | |
| Stress field characteristics | Angle between the axis of the tunnel and the direction of the maximum principal stress | Very favorable (0~) | Favorable (~) | Generally favorable (~) | Disadvantage(>) |
| Initial geostress influencing factor, SRF | <5 | 5–10 | 11–20 | >20 | |
| Cavity characteristics | Span of the tunnel/m | 0~5 | 6~15 | 16~20 | >20 |
| Influence of the shape of the tunnel (height-span ratio) | Very favorable | Favorable | Generally favorable | Disadvantage | |
| Other influencing factors | Service time of the tunnel/year | 0~10 | 11~20 | 21~40 | >40 |
| Design and construction level | High | Relatively high | Normal | Low | |
| Seismic intensity | 1~3 | 4~5 | 6~7 | 8~12 | |
| Control Layer | Weight of the Control Layer | Index Layer | Weight of the Index Layer |
|---|---|---|---|
| Stress characteristics of the main structure | 0.524 | Contact pressure between layers | 0.5 |
| Conventional safety evaluation | 0.5 | ||
| Engineering geological characteristics | 0.244 | Rock quality designation RQD | 0.206 |
| Rock compressive strength | 0.367 | ||
| Rock integrity coefficient | 0.206 | ||
| Situation of the underground water | 0.125 | ||
| Influence of the fault and the fracture zone | 0.096 | ||
| Stress field characteristics | 0.107 | Angle between the axis of the tunnel and the direction of the maximum principal stress | 0.667 |
| Initial geostress influencing factor, SRF | 0.333 | ||
| Cavity characteristics | 0.063 | Span of the tunnel | 0.5 |
| Influence of the shape of the tunnel (height-span ratio) | 0.5 | ||
| Other influencing factors | 0.063 | Service time of the tunnel | 0.320 |
| Design and construction level | 0.558 | ||
| Seismic intensity | 0.122 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Mo, C.; He, C.; Yan, Q. Fuzzy Synthetic Evaluation of the Long-Term Health of Tunnel Structures. Appl. Sci. 2017, 7, 203. https://doi.org/10.3390/app7020203
Wang B, Mo C, He C, Yan Q. Fuzzy Synthetic Evaluation of the Long-Term Health of Tunnel Structures. Applied Sciences. 2017; 7(2):203. https://doi.org/10.3390/app7020203
Chicago/Turabian StyleWang, Bo, Chencong Mo, Chuan He, and Qixiang Yan. 2017. "Fuzzy Synthetic Evaluation of the Long-Term Health of Tunnel Structures" Applied Sciences 7, no. 2: 203. https://doi.org/10.3390/app7020203
APA StyleWang, B., Mo, C., He, C., & Yan, Q. (2017). Fuzzy Synthetic Evaluation of the Long-Term Health of Tunnel Structures. Applied Sciences, 7(2), 203. https://doi.org/10.3390/app7020203




