Voltage-Mode and Current-Mode Resistorless Third-Order Quadrature Oscillator

Abstract

This paper presents the realization of a resistorless third-order quadrature oscillator using two multiple-output current controlled current conveyor transconductance amplifiers (MO-CCCCTAs) and three grounded capacitors. The proposed circuit provides two quadrature voltage outputs, two high-impedance quadrature current outputs, and one high-impedance amplitude-controllable current output. The proposed oscillator satisfies the industrial requirement for amplifier and modulation signals and phase shift keying signals, when the input bias current of the second MO-CCCCTA is used as a modulating signal. Its oscillation condition and oscillation frequency can be adjusted independently by two different bias currents of MO-CCCCTAs. The structure of resistorless and only grounded capacitors suggests that the proposed oscillator can be easily implemented in an integrated circuit.

1. Introduction

A quadrature sinusoidal oscillator is a very important active element for communication, instrumentation, and measurement systems, and can be employed in a quadrature mixer and a single-sideband modulator of telecommunications [1,2]. In communication systems, a sinusoidal oscillator can generate an amplitude-controllable sinusoidal signal, which can be used to apply the carrier signal for amplitude modulation (AM) and amplitude shift keying (ASK) signal systems [3]. Recently, current conveyors are receiving considerable attention due to their potential advantages, such as inherently wide bandwidth, high slew-rate, good linearity, wide dynamic range, simple circuitry, and low power consumption [4]. This interesting active element, based on second-generation current conveyor transconductance amplifiers (CCIITA) [5], has been introduced to provide new possibilities in the realization of a class of analog signal processing circuits. This CCIITA can provide flexibility in operating both current and voltage modes, and can enable a variety of circuit designs and provides electronic tuning ability through its transconductance gain, g_m. However, the CCIITA cannot control the parasitic resistance, R_X, at X port. Hence, when the CCIITA is used in some circuits, it must unavoidably require some external passive components, especially with the resistors. In contrast, the introduced current-controlled current conveyor transconductance amplifier (CCCCTA) [5,6] has two electronically adjustable ports, whereas the CCIITA has only one electronically adjustable port. The parasitic resistance, R_X, at current input port of the CCCCTA can be adjusted by an input bias current, which does not require a resistor in practical applications. Intuitively, the CCCCTA is a versatile active building block, which provides the possibility of utilizing its transconductance gain, g_m, and its equivalent input resistance, namely parasitic resistance, R_X, to create a resistorless oscillator scheme. The multiple current output terminals of the CCCCTA can be easily obtained by adding additional current mirrors at these output terminals.

Electronically tunable active components are receiving more attention as traditional electronic components may have deviations in fine-tuning the tolerances of the electronic components [7]. The electronically tunable active components of the previous second-order oscillators include second generation current controlled conveyors (CCCIIs) [8,9]; operational transconductance amplifiers (OTAs) [10]; current differencing buffered amplifiers (CDBAs) [11,12]; the CCIITA [13]; current differencing transconductance amplifiers (CDTAs) [14,15,16,17,18,19]; multiple-output current controlled current conveyor transconductance amplifiers (MO-CCCCTAs) [20]; and voltage differencing transconductance amplifiers (VDTAs) [21]. These circuits were used to design the second-order quadrature current outputs, quadrature voltage outputs, or both quadrature current and voltage outputs. In addition to all of the above second-order quadrature oscillators, several third-order quadrature oscillators have also been proposed [22,23,24,25,26,27,28,29,30,31,32].

The third-order oscillators have higher accuracy, higher quality factor, and lower harmonic distortion than the second-order oscillators [22,23]. However, the third-order oscillator in Figure 7 of Reference [22] uses three OTAs and three grounded capacitors. The third-order oscillator in Reference [23] uses four multiple-output second-generation current-controlled conveyors (MO-CCCIIs) and three grounded capacitors. The third-order oscillator in Figure 1 of Reference [24] uses three second-generation current conveyors (CCIIs), five grounded resistors and three capacitors. The third-order oscillator in Reference [25] uses two MO-CCCCTAs and three grounded capacitors. The third-order oscillator in Figure 3 of Reference [26] uses three voltage controlled differential voltage current conveyors (VC-DVCCs) and three grounded capacitors. The third-order oscillator in Reference [27] uses three MO-CCCIIs and three grounded capacitors. The third-order oscillator in Reference [28] uses three multiple-output current differencing transconductance amplifiers (MO-CDTAs) and three grounded capacitors. Although the third-order oscillator in Reference [29] uses two multiple-output second-generation current conveyors (MO-CCIIs), three resistors, and three grounded capacitors, one of the resistors is a floating connection. The third-order oscillator in Reference [30] uses three multiple-output differential voltage current conveyors (MO-DVCCs), three resistors, and three grounded capacitors; however, one of the resistors is also a floating connection. The oscillator in Figure 2 of Reference [31] uses three operational transresistance amplifiers (OTRAs), four resistors and three capacitors; however, not all of the resistors and capacitors are grounded.

In 2015, two new third-order quadrature oscillators were proposed [32], which employed two multiple-output differential voltage current conveyor transconductance amplifiers (MO-DVCCTAs), one/two resistors, and three grounded capacitors. However, these circuits [22,23,24,25,26,27,28,29,30,31,32] suffered from one or more of the following drawbacks: (i) the inclusion of three/four active components [22,23,24,26,27,28,30,31]; (ii) the lack of both a voltage-mode and current-mode quadrature oscillator in one circuit topology [22,23,24,25,31]; (iii) the lack of a resistorless oscillator [24,29,30,31,32]; (iv) the lack of an independently electronically tunable for the oscillation condition and frequency [22,24,30,32]; (v) the lack of amplitude-controllable for output current signal [22,23,24,25,26,27,28,29,30,31,32]; and (vi) the lack of quadrature voltage outputs, quadrature current outputs, and a high-impedance amplitude-controllable current output in one circuit topology [22,23,24,25,26,27,28,29,30,31,32], especially, the electronically controllable amplitude of the sinusoidal current output signal that can be easily used in AM/ASK systems.

In this paper, a new approach to realize third-order quadrature oscillators using a lossy integrator and two lossless integrators is proposed. The proposed third-order quadrature resistorless oscillator employs two MO-CCCCTAs and three grounded capacitors. The proposed third-order quadrature oscillator has the following seven advantages simultaneously: (i) it contains only two active components and three grounded capacitors; (ii) it has both voltage-mode and current-mode third-order sinusoidal quadrature oscillator in the same topology; (iii) it achieves quadrature voltage outputs, quadrature current outputs, and a high-impedance amplitude-controllable current output in one circuit topology; (iv) it has independent electronically tunable characteristics for the condition of oscillation (CO) and the frequency of oscillation (FO); (v) it provides a high-impedance current output of adjustable magnitude, without effecting the CO and FO and is suitable for AM/ASK modulations; (vi) it uses only grounded capacitors; and (vii) it holds low active and passive sensitivity performances.

Table 1. Number of component and number of output signal comparisons with previous third-order oscillators.

Reference	No. of Components Used		No. of Output Signals Used
	Active Elements	C/R/Resistorless Structure	Voltage	Current
[22] Figure 7	3 OTAs	3/0/yes	1	0
[23]	4 MO-CCCIIs	3/0/yes	0	4
[24] Figure 1	3 CCIIs	3/5/no	2	0
[25]	2 MO-CCCCTAs	3/0/yes	0	2
[26] Figure 2	3 MO-DVCCs	3/3/no	5	2
[26] Figure 3	3 VC-DVCCs	3/0/yes	3	2
[27]	3 MO-CCCIIs	3/0/yes	2	4
[28]	3 MO-CDTAs	3/0/yes	2	2
[29]	2 MO-CCIIs	3/3/no	2	2
[30]	3 MO-DVCCs	3/3/no	2	4
[31] Figure 3	3 OTRAs	3/5/no	2	0
[32] Figure 4a	2 MO-DVCCTAs	3/1/no	3	3
[32] Figure 4b	2 MO-DVCCTAs	3/2/no	3	3
This work	2 MO-CCCCTAs	3/0/yes	2	3

and

Table 2. Characteristic comparisons with previous third-order oscillators.

Reference	Electronic Tuning FO without Disturbing CO	Independent Control of CO and FO	Controllable Amplitude of AM/ASK
[22] Figure 7	no	no	no
[23]	yes	yes	no
[24] Figure 1	no	no	no
[25]	yes	yes	no
[26] Figure 2	no	yes	no
[26] Figure 3	yes	yes	no
[27]	yes	yes	no
[28]	yes	yes	no
[29]	no	yes	no
[30]	no	no	no
[31] Figure 3	no	yes	no
[32] Figure 4a	no	yes	no
[32] Figure 4b	no	no	no
This work	yes	yes	yes

compare the main features of the proposed circuit with previous third-order sinusoidal oscillators [22,23,24,25,26,27,28,29,30,31,32].

2. Proposed Method

The proposed realization of a third-order quadrature oscillator is shown in Figure 1, and consists of a current-mode lossy integrator and two current-mode lossless integrators. The system can be analyzed as:

$$\frac{I_2}{I_1}=\frac{-a}{s+a},\frac{I_3}{I_2}=\frac{b}{s},\frac{I_1}{I_4}=\frac{c}{s}$$

(1)

$$I_4=I_2+I_3=(1+\frac{b}{s})I_2$$

(2)

Equation (1) shows the functions of one current-mode inverting lossy integrator and two current-mode non-inverting lossless integrators in the functional block diagram. Substitute Equation (1) into Equation (2), and obtain the relationship between I₁ and I₄ currents as:

$$\frac{I_1}{I_4}=\frac{I_1}{(1+\frac{b}{s})I_2}=\frac{c}{s}$$

(3)

Rearrange Equation (3), and yield the transfer function between I₁ and I₂ currents as follows:

$$\frac{I_1}{I_2}=(1+\frac{b}{s})(\frac{c}{s})=(\frac{s+b}{s})(\frac{c}{s})$$

(4)

Then, the characteristic equation of the functional block diagram in Figure 1 can be expressed as:

$$s^3+a{s}^2+acs+abc=0$$

(5)

From Equation (5), the CO and the FO are obtained as follows:

CO: a = b

(6)

$$\mathrm{FO}: {\omega }_o=\sqrt{bc}$$

(7)

3. Circuit Descriptions

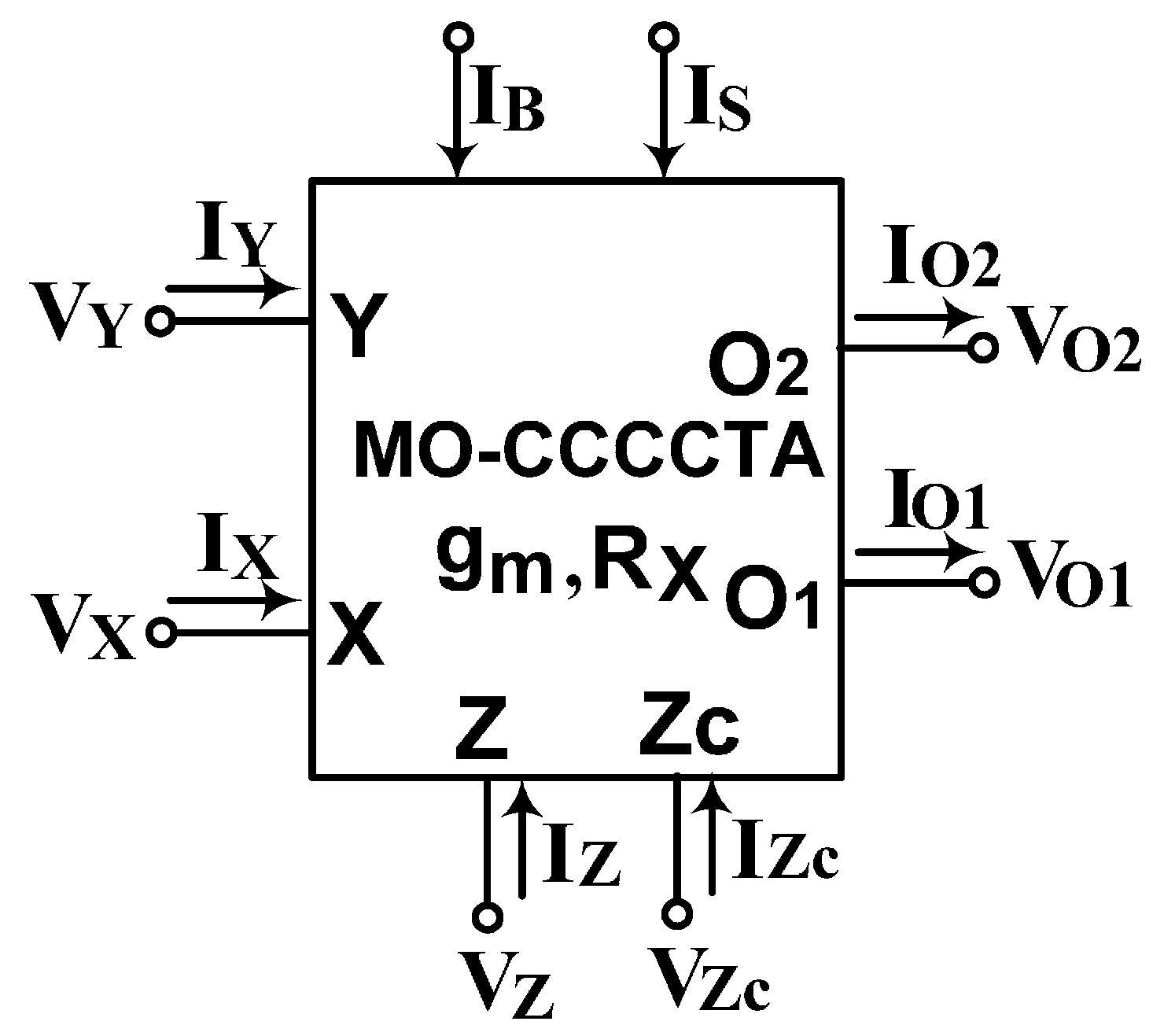
The CCCCTA is an active building block, which is useful in simplifying the circuit design. The CCCCTA device integrates a CCCII and an OTA into a versatile component to facilitate the implementation of analog signal-processing circuits. The CCCCTA does not need a resistor in practical applications, as its transconductance gain, g_m, and parasitic resistance, R_X, are electronic adjustable. Figure 2 shows the symbol of a multiple-output CCCCTA (MO-CCCCTA) [33]. The MO-CCCCTA properties can be expressed as V_X = V_Y + I_XR_X, I_Z = I_ZC1 = I_ZC2 = I_X and I_O1 = I_O2 = g_mV_Z, where R_X is the parasitic resistance of the X-terminal, and g_m is the transconductance gain of the MO-CCCCTA. The bias currents, I_S and I_B, of MO-CCCCTA can control the parasitic resistance, R_X, and the transconductance gain, g_m, respectively [33,34]. 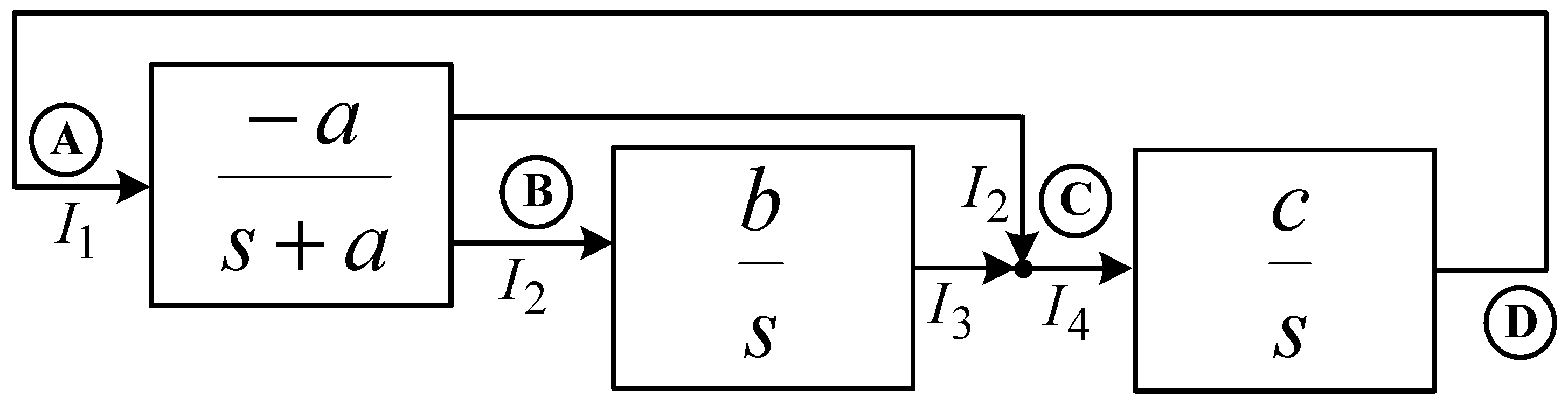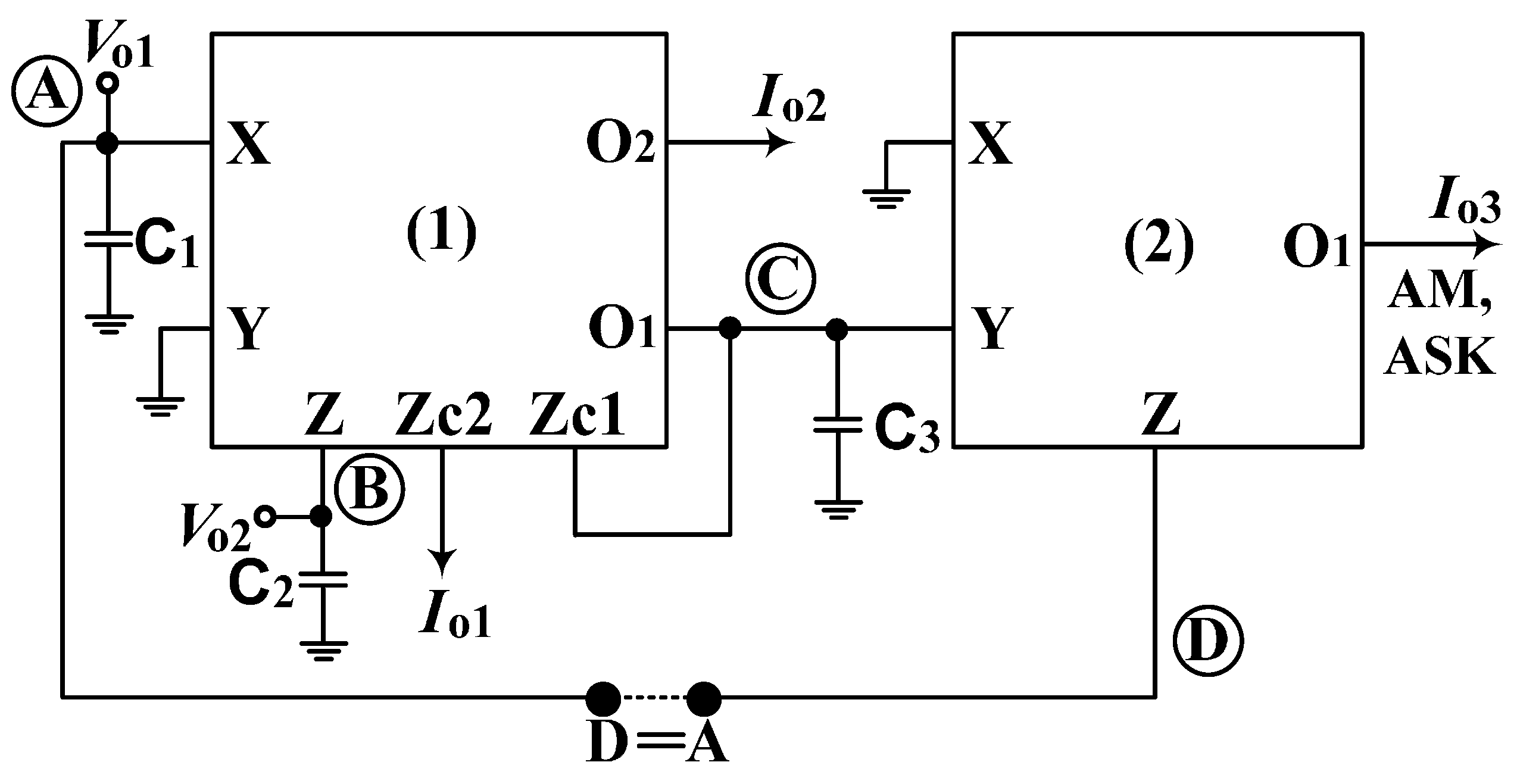Figure 3 shows the proposed schematic of the resistorless third-order quadrature oscillator, which consists of two MO-CCCCTAs and three grounded capacitors. The only grounded capacitors without a resistor structure in the proposed circuit are easily integrated into a single chip. In Figure 3, the transfer function, B/A, realizes a current-mode lossy integrator, and the transfer functions, C/B and D/C, realize two current-mode lossless integrators.

Let D = A, and the close-loop circuit analysis provides the following system characteristic equation.

$$s^3{C}_1{C}_2{C}_3{R}_{X1}{R}_{X2}+s^2{C}_2{C}_3{R}_{X2}+s{C}_2+g_{m1}=0$$

(8)

and the CO and FO can be obtained as:

$$\mathrm{CO}: g_{m1}{R}_{X1}=\frac{C_2}{C_1}$$

(9)

$$\mathrm{FO}: {\omega }_o=\sqrt{\frac{g_{m1}}{R_{X2}{C}_2{C}_3}}$$

(10)

As indicated by Equations (9) and (10), the CO can be adjusted by R_X1 without disturbing the FO, and the FO can be controlled by R_X2 without affecting the CO. In other words, the CO and FO are controlled independently by the bias currents, I_S1 and I_S2, respectively. As the parasitic resistances, R_X1 and R_X2, of the MO-CCCCTA can be electronically controlled by I_S1 and I_S2, respectively, both the CO and FO are independently and electronically controllable. In a steady state, the two voltage outputs and two current outputs in Figure 3 are:

$$V_{o1}=-j{k}_1{V}_{o2}, I_{o1}=j{k}_2{I}_{o2}$$

(11)

where $k_1={\omega }_o{C}_2{R}_{X1}$, and $k_2=\frac{{\omega }_o{C}_2}{g_{m1}}$.

Equation (11) shows that the proposed circuit can obtain the quadrature voltage outputs and the quadrature current outputs simultaneously. The magnitude ratios of the quadrature voltage outputs and the quadrature current outputs are the function of the operating frequency. Thus, the value of R_X2 will affect the oscillation frequency and the magnitude ratios of the generated quadrature signals. However, this problem can be solved by using C₁ = C₂ = C₃, R_X1 = R_X2, and letting the product g_m1R_X1 = 1. Subsequently, the amplitude of voltages and currents in Equation (11) are equal and ensure k₁ = k₂ = 1.

The output current, I_o3, can be given as follows:

$$I_{o3}=g_{m2}{V}_{o1}$$

(12)

where the g_m2 of the second MO-CCCCTA can be independently tuned by the bias current, I_B2. This means that the g_m2-value can be tuned by I_B2, without disturbing the CO and FO. Thus, if a modulating signal is applied to I_B2, then the AM/ASK signals can be obtained from I_o3.

From Equation (11), the magnitude of V_o2 and V_o1 or I_o2 and I_o1 is dependent on the factor k₁ or k₂. Therefore, the mechanism of amplitude limitation will depend on the factors k₁ and k₂. For complementary metal oxide semiconductor (CMOS) implementation of CCCCTA [34], the R_X and g_m are written as:

$$R_X=\frac{1}{\sqrt{8k_{RX}{I}_S}} \mathrm{and} g_m=\sqrt{k_{gm}{I}_B}$$

(13)

where $k_{RX}={\mu }_n{C}_{OX}{(\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$L$}\right.)}_{1,2}={\mu }_p{C}_{OX}{(\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$L$}\right.)}_{3,4}$, $k_{gm}={\mu }_n{C}_{OX}{(\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$L$}\right.)}_{20,21}$. R_X is the parasitic resistance of the X-terminal and g_m is the transconductance gain of the CCCCTA. Here k is the physical transconductance parameter of the MOS transistor. I_S and I_B are the bias current used to control the parasitic resistance and transconductance gain, respectively. In other words, the variation of CCCCTA bias current range will limit the stability of the output amplitude.

4. Phase Noise and Phase Error Analysis

The phase noise, which are the important performance parameters of an oscillator, can be calculated by the method outlined in Reference [35] and can be represented in the block diagram of Figure 4. The spectral density of the phase noise is defined in Reference [35].

$${\left|\frac{Y}{X}[j({\omega }_o+\Delta \omega ]\right|}^2=\frac{1}{{(\Delta \omega )}^2{\left|\frac{dH}{d\omega }\right|}^2}$$

(14)

where ω_o is oscillation frequency and ω = ω_o + Δω is carrier frequency approximation.

If $H(j\omega )=A(\omega )\exp [j\phi (\omega )]$, then:

$$\frac{dH}{d\omega }=(\frac{dA}{d\omega }+jA\frac{d\phi }{d\omega })\exp [j\phi (\omega )]$$

(15)

Substitute Equation (15) into Equation (14) and get:

$${\left|\frac{Y}{X}[j({\omega }_o+\Delta \omega ]\right|}^2=\frac{1}{{(\Delta \omega )}^2[{(\frac{dA}{d\omega })}^2+{(\frac{d\phi }{d\omega })}^2]} \mathrm{for} \omega \approx {\omega }_o, A \approx 1$$

(16)

The phase noise of the proposed circuit can be obtained by Equations (14)–(16).

Quadrature oscillators are widely used in communication systems due to its in-phase and quadrature phase signals, which deviate from 90°. Therefore, the quadrature phase accuracy between the two output signals should be reasonable. Generally, the in-phase and quadrature phase expressions of the quadrature oscillator signals can be written as:

$$V_I(t)=V_m(I)\cos (\omega t+\theta (I))$$

(17)

$$V_Q(t)=V_m(Q)\cos (\omega t+\theta (Q))$$

(18)

$$\theta (Q)-\theta (I)=\frac{\pi }{2}+\varphi$$

(19)

where ω is the oscillation frequency and ϕ is the phase deviation from the quadrature signal. V_I(t) is the in-phase signal and V_Q(t) is the quadrature phase signal. The phase error of the proposed circuit can be obtained by Equations (17)–(19).

5. Non-Ideal Discussion

The terminal voltage and current relationships of the non-ideal i^th MO-CCCCTA can be rewritten as V_Xi = β_iV_Yi + I_XiR_Xi, I_Zi = α_iI_X, I_ZC1i = η_iI_Xi, I_O1i = γ_ig_miV_Zi and I_O2i = λ_ig_miV_Zi for i = 1, 2, where β_i, α_i. γ_i, η_i and λ_i represent the tracking errors of the MO-CCCCTA voltage and current, respectively [20]. The characteristic equation of the proposed circuit in Figure 3 can be rewritten as:

$$s^3{C}_1{C}_2{C}_3{R}_{X1}{R}_{X2}+s^2{C}_2{C}_3{R}_{X2}+{\alpha }_2{\beta }_2{\eta }_{1}s{C}_2+{\alpha }_1{\alpha }_2{\beta }_2{\gamma }_1{g}_{m1}=0$$

(20)

In this case, the CO and FO of the non-ideal oscillator can be expressed as:

$$\mathrm{CO}: g_{m1}{R}_{X1}=\frac{{\eta }_1{C}_2}{{\alpha }_1{\gamma }_1{C}_1}$$

(21)

$$\mathrm{FO}: {\omega }_o=\sqrt{\frac{{\alpha }_1{\alpha }_2{\beta }_2{\gamma }_1{g}_{m1}}{R_{X2}{C}_2{C}_3}}$$

(22)

The active and passive sensitivities of the non-ideal oscillator parameters are shown as:

$$S_{{\alpha }_1,{\alpha }_2,{\beta }_2,{\gamma }_1}^{{\omega }_0}=S_{g_{m1}}^{{\omega }_0}=-S_{R_{X2},C_2,C_3}^{{\omega }_0}=\frac{1}{2}$$

(23)

From Equation (23), the active and passive sensitivities are equal to 0.5, which satisfy the sensitivity performance of the circuit.

The parasitic terminal impedances of the i^th non-ideal MO-CCCCTA are (R_Yi//C_Yi) of terminal Y_i, (R_Zi//C_Zi) of terminal Z_i, (R_ZC1i//C_ZC1i) of terminal Z_C1i, (R_ZC2i//C_ZC2i) of terminal Z_C2i, (R_O1i//C_O1i) of terminal O_1i, and (R_O2i//C_O2i) of terminal O_2i [20,33]. The X, Z, and O₁ of the first MO-CCCCTA terminals connect to the external C₁, C₂ and C₃ capacitors in parallel, respectively, as shown in Figure 3. If C₁ >> C_Z2, C₂ >> C_Z1 and C₃ >> (C_O11 + C_Y2 + C_ZC11), the effects of the parasitic capacitances, C_Z2, C_Z1 and C_O11, can be ignored. Hence, to minimize the effects of the MO-CCCCTA parasitic terminal impedances, the external capacitor values should be restricted by

$$\frac{1}{s(C_1+C_{Z2})}<<R_{Z2}$$

(24)

$$\frac{1}{s(C_2+C_{Z1})}<<R_{Z1}$$

(25)

$$\frac{1}{s(C_3+C_{O11}+C_{Y2}+C_{ZC11})}<<R_{O11}//R_{Y2}//R_{ZC11}$$

(26)

6. Simulation Results

To verify the theoretical analysis of the proposed circuit, an H-Spice simulation with Taiwan Semiconductor Manufacturing Company (TSMC) 0.18 µm process was performed. Figure 5 shows the CMOS schematic of a MO-CCCCTA [34], where the multiple outputs are multiple current mirrors. The aspect ratios (W/L) of the MOS transistors of Figure 5 are given in

Table 3. The aspect ratios of the CMOS transistors in MO-CCCCTA implementation.

Transistors	L (µm)	W (µm)
M1–M2	0.35	7
M3–M4	0.35	14
M5–M10	0.5	20
M11–M17, M20, M21	0.5	10
M18, M19, M27	0.8	8
M22–M26	0.8	25

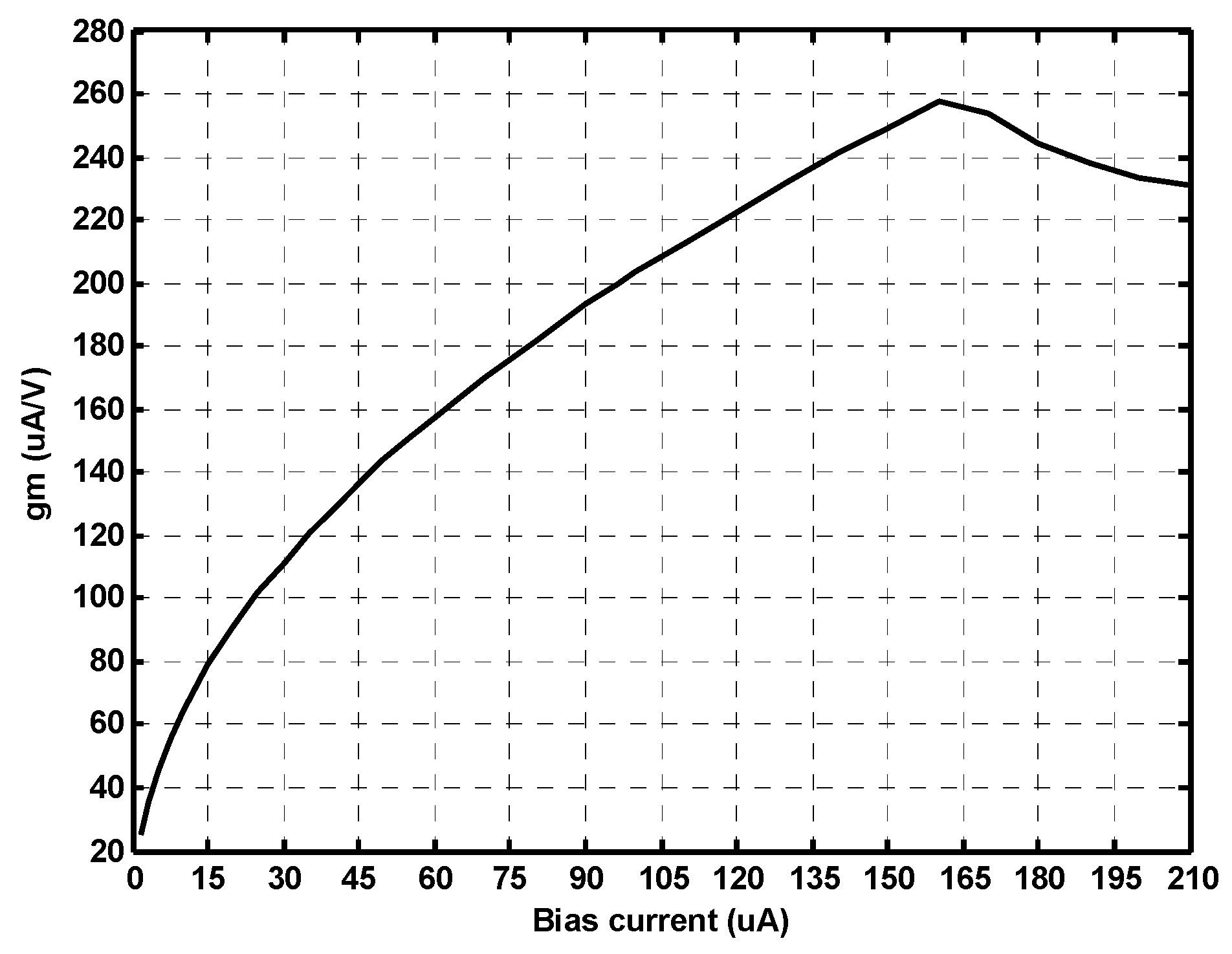
. The supply voltages are V_DD = −V_SS = 0.9 V. In order to get the f_o ≅ 2.12 MHz oscillation frequency of the sinusoidal output waveforms, the values of the active and passive components have been chosen as g_m1 = g_m2 = 133.33 µA/V (I_B = 42.9 µA); R_X1 = R_X2 = 7.5 kΩ (I_S = 3.96 µA); C₁ = 10.1 pF; and C₂ = C₃ = 10 pF. The variation of the transconductance value changes I_B from 1.5 μA to 210 μA as depicted in Figure 6. When the bias current is larger than 160 μA, the transconductance gain is decreased as the transistors (M20, M21) enter the linear region from a saturation region. The maximum transconductance gain is approximately 256 µA/V. In other words, when the bias current is larger than 160 μA, the internal construction transistors of the MO-CCCCTA operates in the linear region, which will result in the distortion of the output swing. The steady state output waveforms of the quadrature voltages are shown in Figure 7 and the quadrature currents are shown in Figure 8. The oscillation frequency, f_o, of the simulation results is equal to 2.11 MHz, which is consistent with the theoretical analysis. The total harmonic distortion (THD) analysis of the V_o1, V_o2, I_o1 and I_o2 are summarized in

Table 4. Total harmonic distortion analysis of V_o1 in Figure 3.

Harmonic Number	Frequency (MHz)	Fourier Component	Phase (degree)
1	2.122	131.6570 m	152.1558
2	4.244	1.7963 m	−145.6957
3	6.366	1.3875 m	−16.7744
4	8.488	280.3543 u	−35.0773
5	10.610	59.7176 u	−158.4953
6	12.732	139.7939 u	−8.9033
7	14.854	117.2583 u	−9.5498
8	16.976	100.4933 u	2.8933
9	19.098	101.7488 u	8.4091
DC component = 3.419 × 10−3
Total harmonic distortion = 1.7465%

,

Table 5. Total harmonic distortion analysis of V_o2 in Figure 3.

Harmonic Number	Frequency (MHz)	Fourier Component	Phase (degree)
1	2.122	131.7010 m	117.7808
2	4.244	557.7167 u	107.6894
3	6.366	591.5883 u	51.9561
4	8.488	195.7997 u	27.5504
5	10.610	71.6988 u	2.9989
6	12.732	64.9872 u	16.6679
7	14.854	67.4512 u	7.9859
8	16.976	60.2372 u	11.2194
9	19.098	51.7097 u	15.5339
DC component = −4.142 × 10−4
Total harmonic distortion = 644.0952 m%

,

Table 6. Total harmonic distortion analysis of I_o1 in Figure 3.

Harmonic Number	Frequency (MHz)	Fourier Component	Phase (degree)
1	2.122	17.5810 u	−27.9532
2	4.244	175.7963 n	−143.2494
3	6.366	204.1361 n	155.1108
4	8.488	57.0393 n	145.0789
5	10.610	12.1911 n	−93.1991
6	12.732	16.2208 n	−141.3161
7	14.854	6.6238 n	157.6872
8	16.976	10.0840 n	161.5075
9	19.098	13.2706 n	−179.8498
DC component = −2.993 × 10−8
Total harmonic distortion = 1.5739%

and

Table 7. Total harmonic distortion analysis of I_o2 in Figure 3.

Harmonic Number	Frequency (MHz)	Fourier Component	Phase (degree)
1	2.122	17.2823 u	−117.8809
2	4.244	72.1321 n	106.2341
3	6.366	156.5673 n	26.8057
4	8.488	24.1643 n	25.9664
5	10.610	8.2084 n	1.3462
6	12.732	7.7736 n	16.4662
7	14.854	8.5334 n	8.0360
8	16.976	7.7471 n	11.0721
9	19.098	6.5087 n	14.8607
DC component = −5.366 × 10−8
Total harmonic distortion = 1.0122%

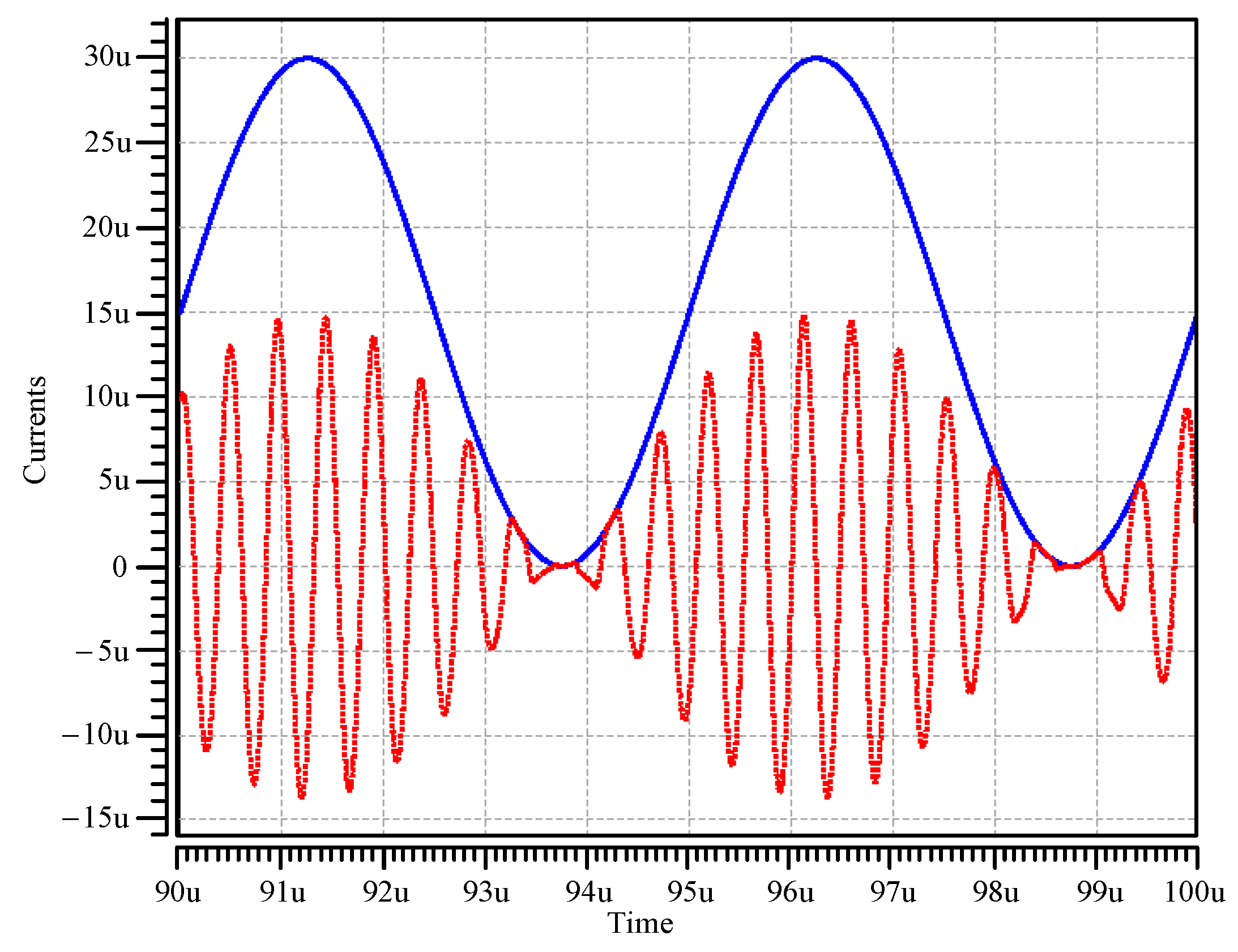
, respectively. Furthermore, the output current, I_o3, can be used as an AM or ASK signal generator, when the amplitude of the input bias current, I_B2, is applied to a sinusoidal signal, a triangular signal, or a pulse signal. Thus, the proposed oscillator can generate either AM or ASK signals without additional elements. Figure 9 and Figure 10 show the simulated results of the proposed circuit serving as an AM signal generator, when the input bias current, I_B2, is applied to a sinusoidal signal or a triangular signal with a 200-kHz frequency. 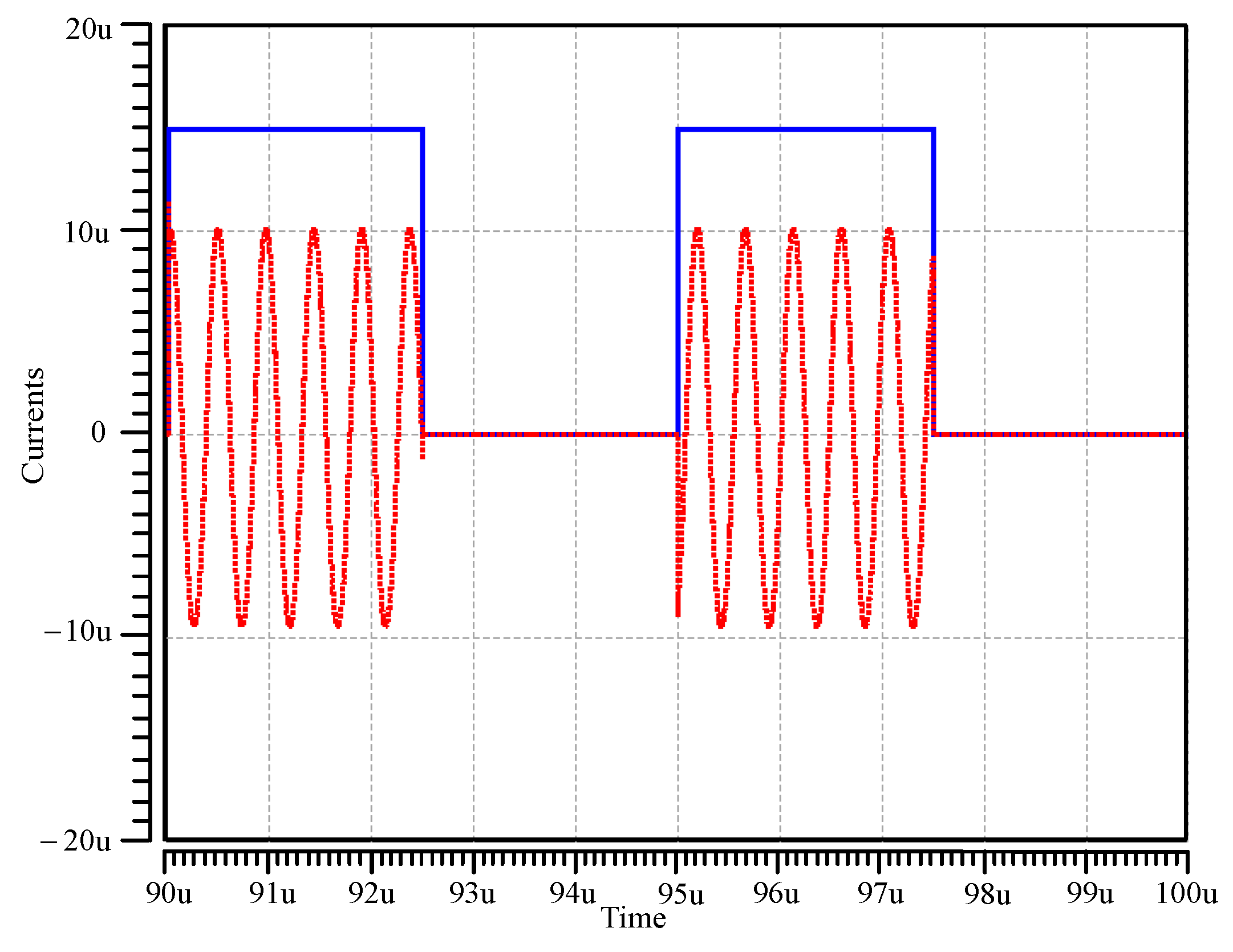Figure 11 shows the simulated results of the proposed circuit serving as an ASK signal generator when the input bias current, I_B2, is applied to a pulse signal with a 200-kHz frequency.

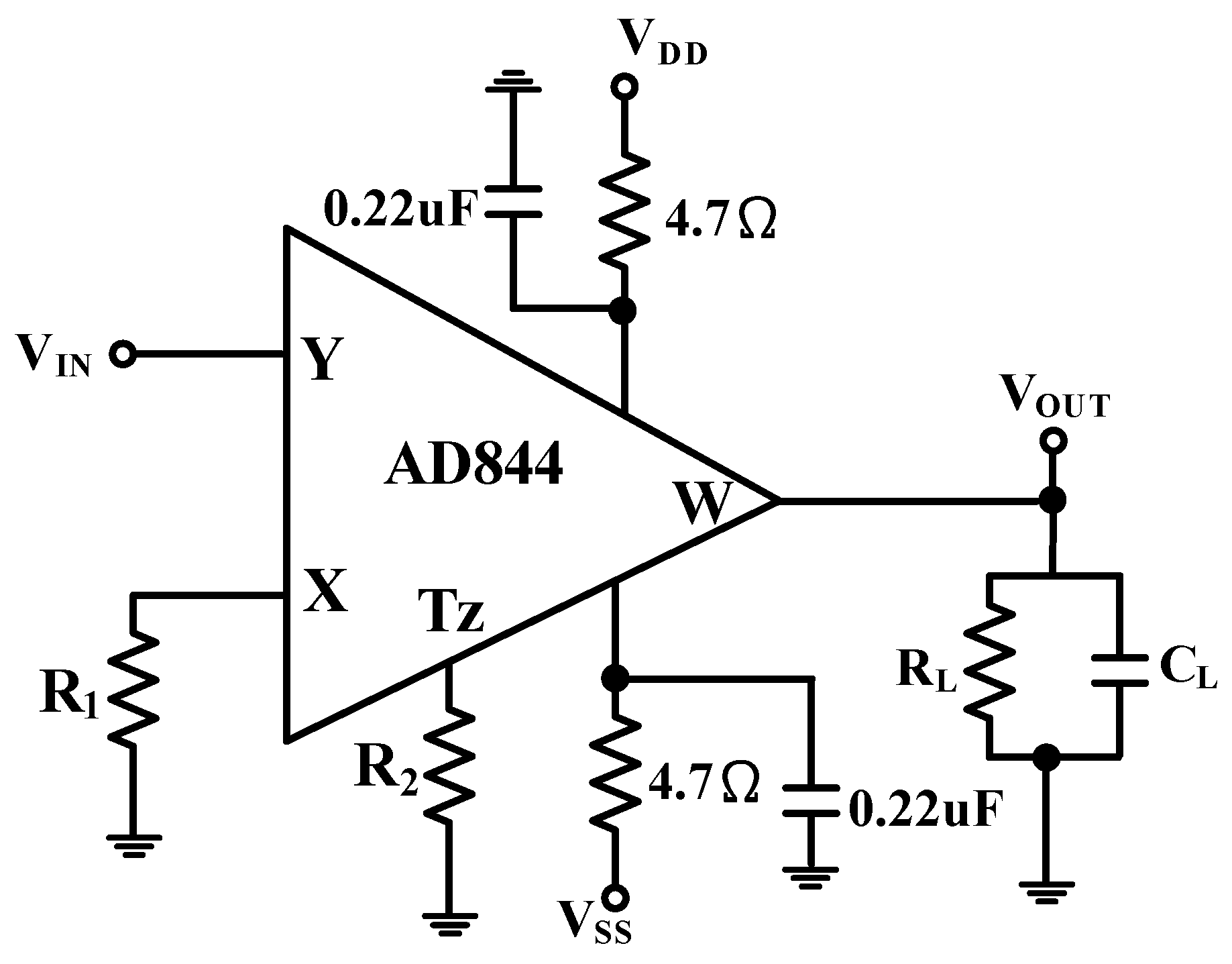
The MO-CCCCTA is not an off-the-shelf component but can be built by commercially available integrated circuits (ICs). For testing the proposed oscillator, Figure 12 shows an equivalent method similar to Figure 3 by using ready-to-use ICs, which include the operational amplifiers of AD844s and the operational transconductance amplifiers of MAX435 and CA3080. The DC power supply voltages are ±5 V. The g_m-value of the MAX435 is equal to 4/R_g, where R_g is an external resistor [36]. In general, the applicability of such current-feedback operational amplifier (CFOA)-based oscillators is usually limited to a few hundred kilohertz [37,38]. Figure 13 shows the experimental result of the frequency range of a commercially available AD844 with ±5 V DC supply. In Figure 13, the values of the resistors were chosen as R₁ = R₂ = 1 kΩ (5 kΩ, 10 kΩ), R_L = 500 Ω, C_L = 10 pF, and the input power was 0 dBm. Figure 14 is the measured result of a spectrum analyzer, which shows that the measured result of the frequency range of AD844 was limited to 2 MHz. The passive component values of the circuit in Figure 12 were set as g_m1 = 1.428 mS (i.e., R_g = 2.8 kΩ), R_X1 = 0.73 kΩ, R_X2 = 0.7 kΩ, R = 1 kΩ and C₁ = C₂ = C₃ = 750 pF, where R_X1 was designed to be larger than the theoretical value to ensure that the oscillator will start, before the centre frequency was obtained as f_o = 303.15 kHz. 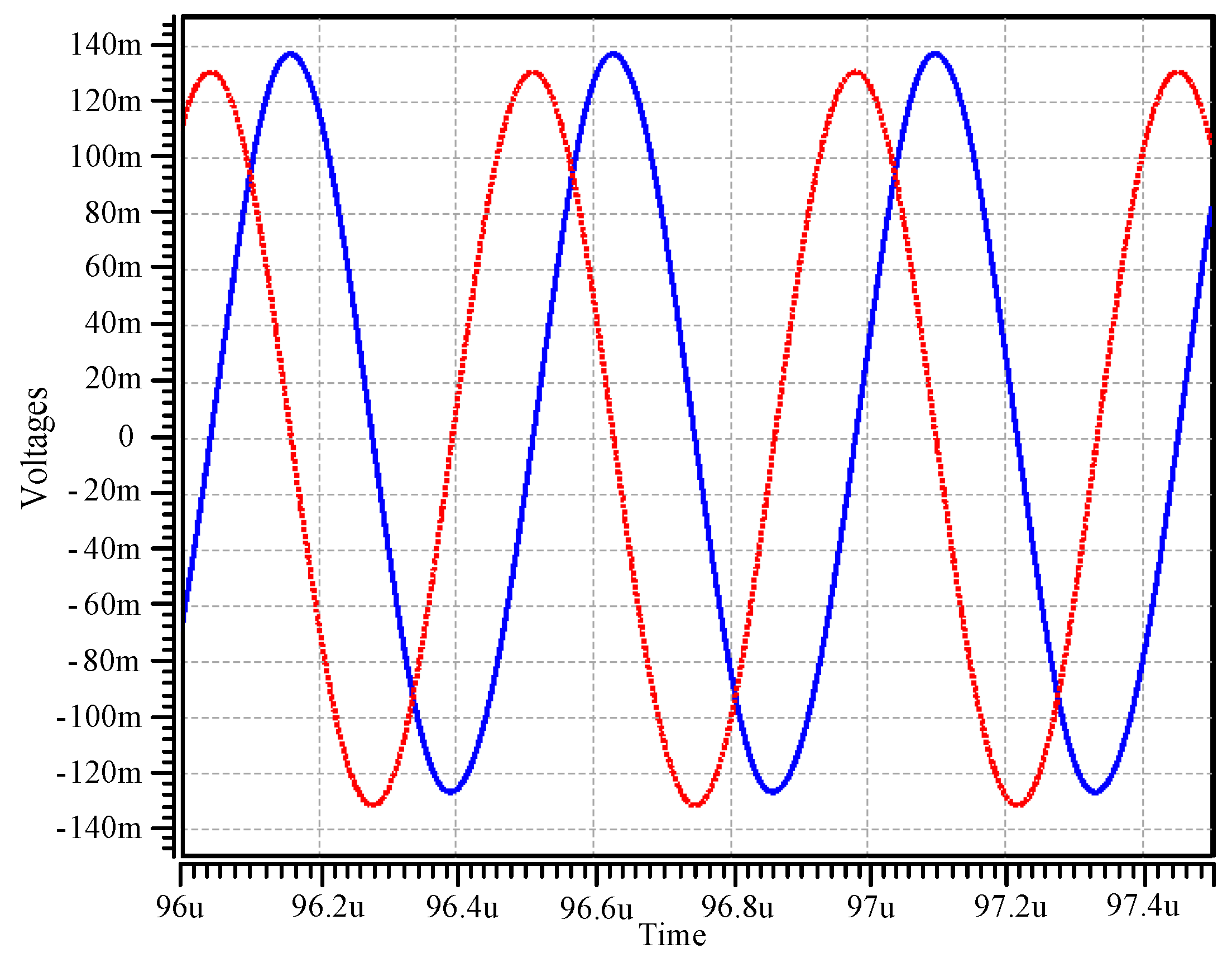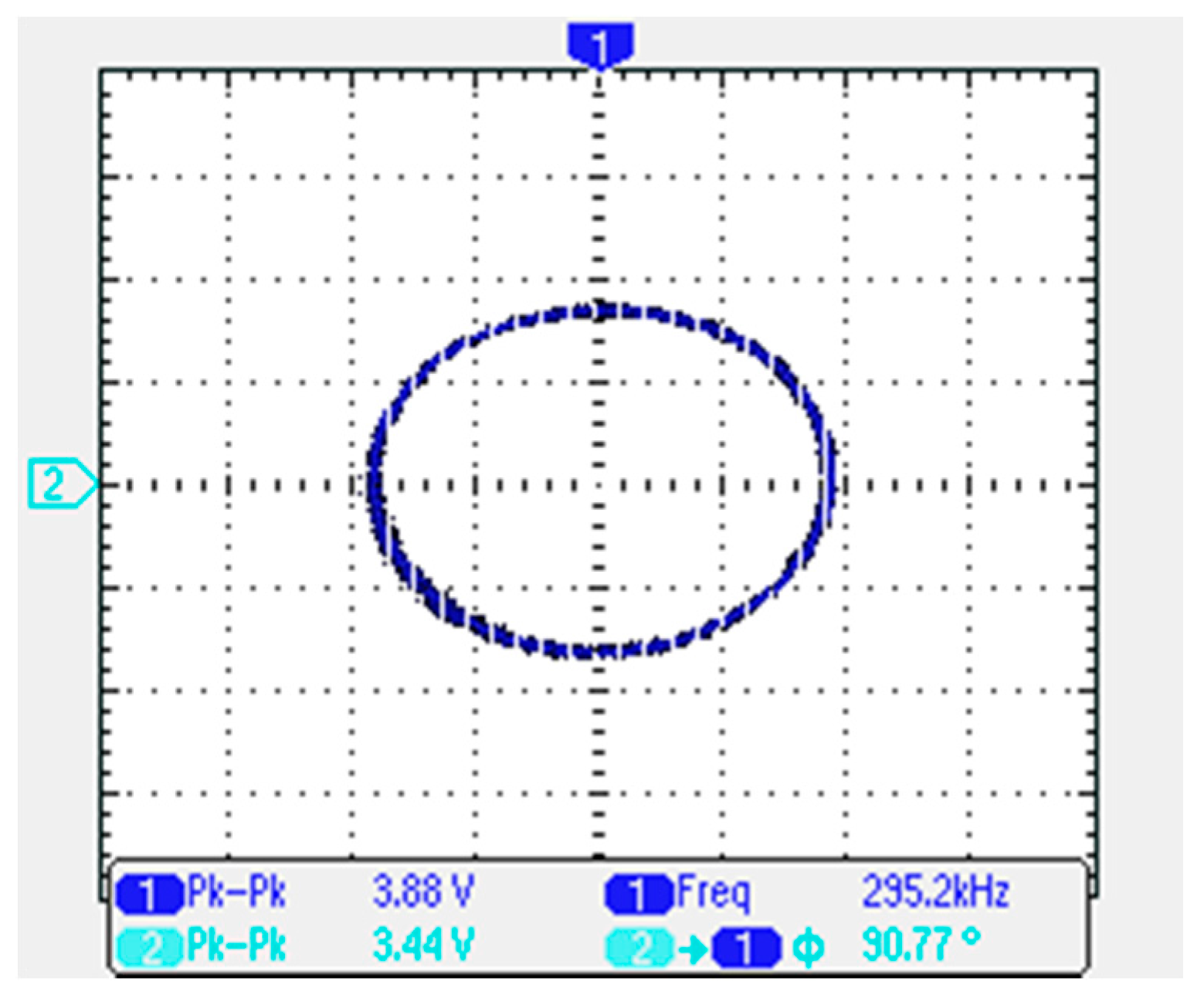The oscilloscope output waveforms, V_o1 and V_o2, of the proposed oscillator are shown in Figure 15, and the X–Y plot of V_o1 and V_o2 output voltages are shown in Figure 16. The experimental oscillation frequency in Figure 15 is 295.2 kHz, which is close to the theoretical value of 303.15 kHz with a 2.62% error rate. 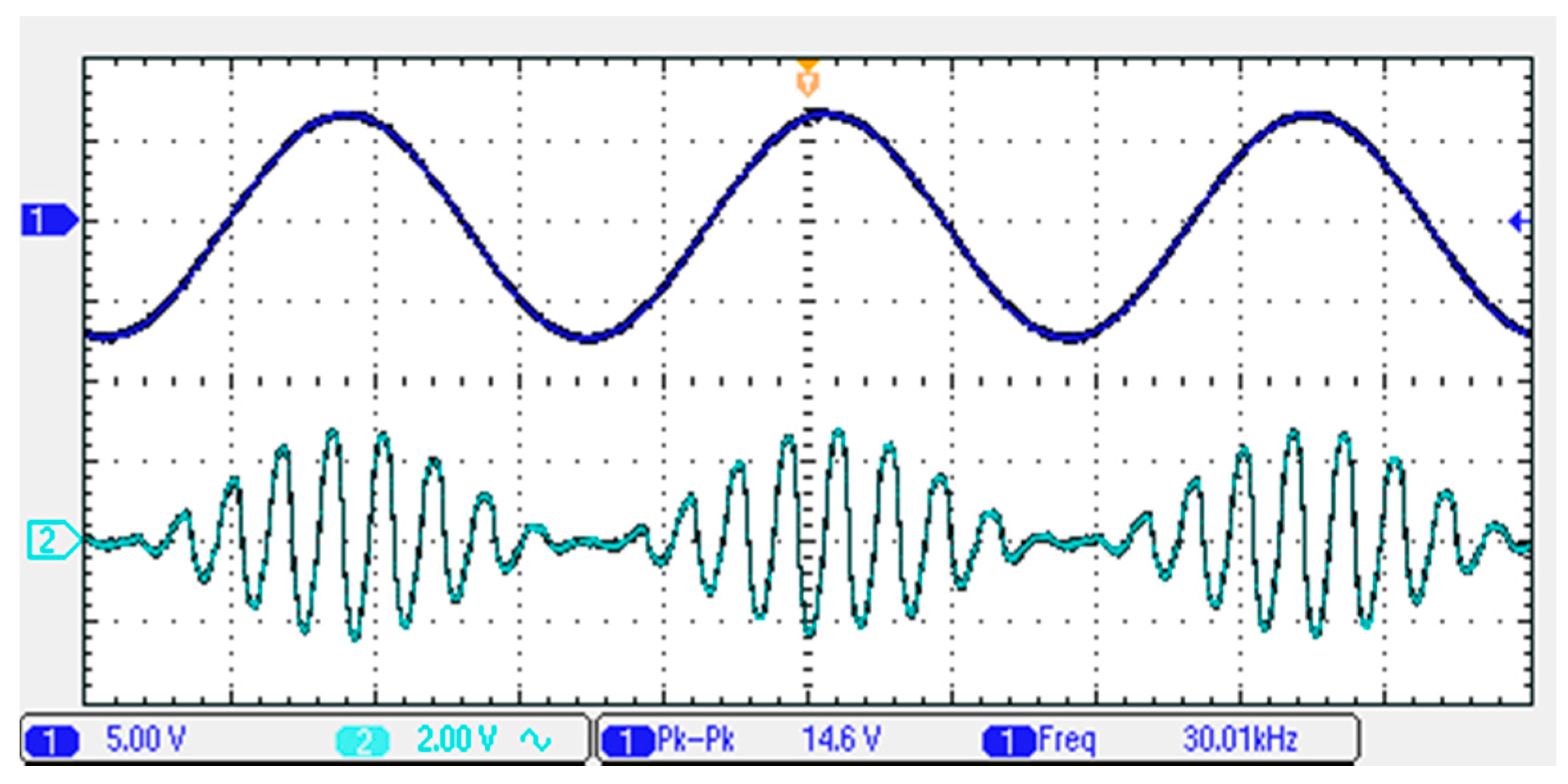Figure 17, Figure 18 and Figure 19 show the AM and the ASK signal outputs of the quadrature oscillator, where the modulation signal, I_B2, applied a sinusoidal signal, a triangular signal, or a pulse signal with a 30-kHz frequency. The experimental results are close to the theoretical analysis of Equation (12).

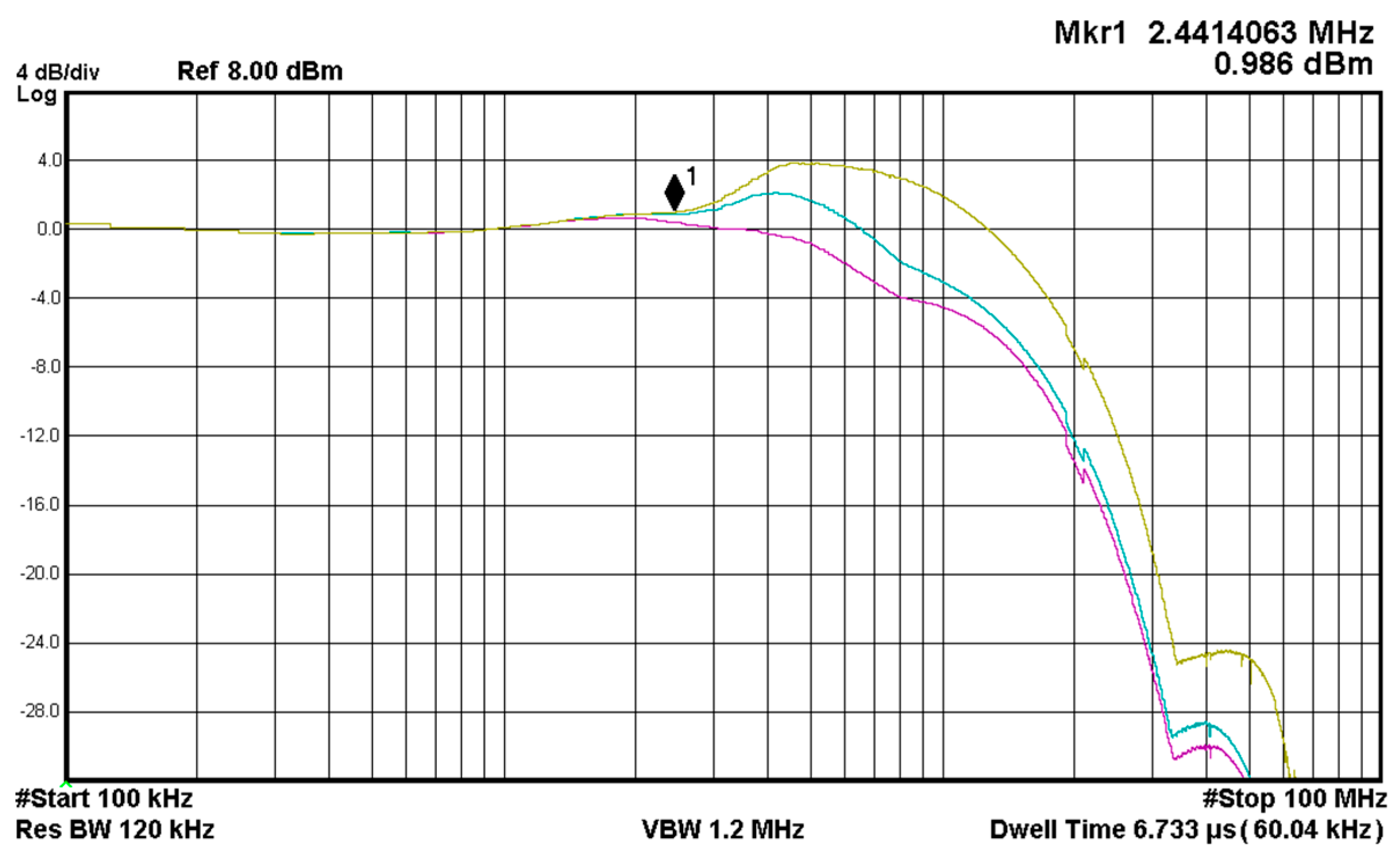
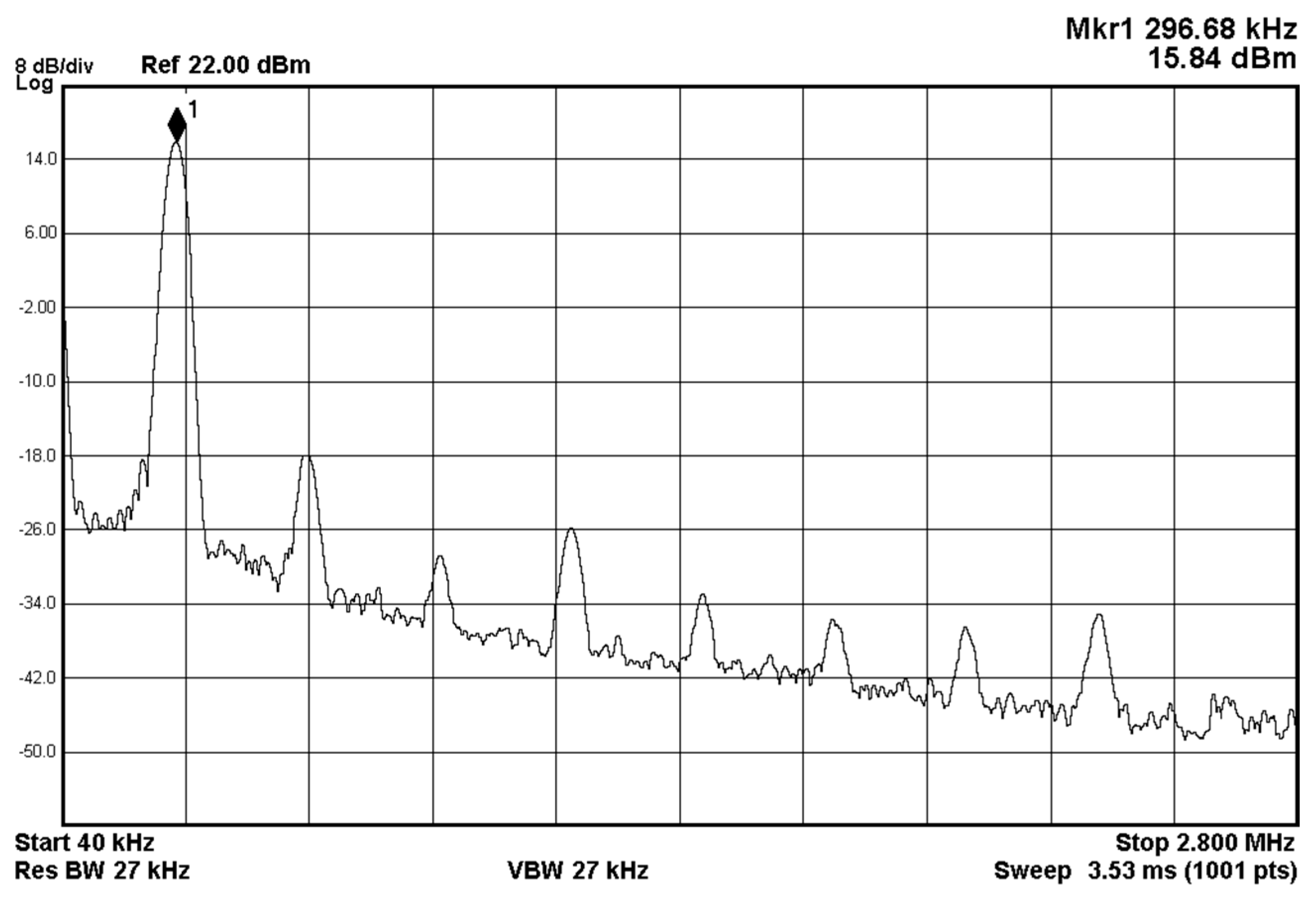
The frequency spectrum of the oscillator output voltage, V_o1, is shown in Figure 20. The measured oscillation frequency was 296.68 kHz, which is close to the theoretical value of 303.15 kHz with a 2.13% error rate. The THD, including the first harmonic through to the ninth harmonic components, is approximately 2.35%. The experimental results are consistent with the theoretical values. For oscillators, noise is a major concern where even a small noise in an oscillator will cause dramatic changes in its frequency spectrum and timing properties. Figure 21 shows the phase noise using the Agilent phase noise measurement solution. The phase noise of the proposed oscillator is less than −88.2 dBc/Hz at 10 kHz offset. Figure 22 shows the root mean square (RMS) jitter of the proposed oscillator, which is 6 ns at an operating frequency of 295.2 kHz.

7. Conclusions

A new resistorless third-order electronically tunable quadrature oscillator was proposed in this paper, which uses two MO-CCCCTAs and three grounded capacitors. The proposed oscillator provided two quadrature voltage output signals with a 90^o phase difference; two high-impedance quadrature current output signals with a 90^o phase difference; and one high-impedance current output signal with an electronically controlled amplitude of the sinusoidal signal, all simultaneously. The proposed oscillator can generate either AM or ASK signals for communication systems. Furthermore, the oscillation condition and oscillation frequency are independently adjustable by two different input bias currents of the MO-CCCCTAs. Since the proposed oscillator does not require external resistors and uses only grounded capacitors, it is suitable for integrated circuit implementation. The simulation and experimental results validate the feasibility of the proposed theory.