1. Introduction
Concrete is a heterogeneous cementitious material and the second most consumed material in the world. Concrete has long been used for all types of civil structures worldwide. In China, abundant megaprojects use cement concrete as basic building blocks, or as precast beam components in civil structures. According to the Chinese National Bureau of Statistics, China’s commodity concrete production was 1.64 billion cubic meters (BCMs) in 2015, and when compared to the value of 0.74 BCMs in 2011, it has increased by 222% [
1]. This value indicates that China is the largest producer and consumer of concrete in the world, and its production roughly occupies about 15% of global production. The concrete which is mixed and cast to conform to the Chinese standard is termed the Guo Biao (GB) concrete [
2,
3]. There are many similarities between the Chinese standard concrete (JGJ55) and the European one (EN206-1). For example, the compressive strengths are both classified as C30, C35, C40, and so on, indicating that the minimum values of the corresponding compressive strengths are 30 MPa, 35 MPa, 40 MPa, and so on. However, the use of superplasticizer is recommended by the EN206-1, whereas the Chinese concrete does not strictly require this in JGJ55. The main differences among the worldwide standards are the physical properties (e.g., density) of the raw materials used, such as cement, sand, and coarse aggregate.
Ordinary cement concrete behaves like a brittle material, where cracks occur in the course of its long-term use. Such cracks are inevitable due to a variety of natural or man-made factors, and cause the compressive strength to decline, leading to structure deformation, and thus affecting the performance of structural integrity. Numerous nondestructive testing or evaluation (NDT/E) methods have been developed for the prediction of compressive strength, development monitoring, and the evaluation of standard concretes [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. Conventional NDT/E techniques, such as visual inspection, rebound hammers, the pull-off resistance correlation method [
4,
5], and the maturity test [
6], etc., often suffer from inaccuracy, being cost-intensive and time-consuming. Recently, state-of-the-art NDT techniques were developed for the monitoring, prediction, and evaluation of the mechanical deformation of concrete structures [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. In particular, the piezoceramic-based smart aggregates play a significant role in concrete structural health monitoring (SHM) [
7,
8,
9,
10], wherein the determination of concrete properties was performed by using the travel time of longitudinal waves over a known distance, between smart aggregates. Electrical resistance and resistivity measurements were employed as a relation to the microstructure development of concrete mix, such as pore structure, porosity, and pore-size distribution, etc., and hence, for compressive strength prediction and evaluation [
11,
12,
13,
14,
15]. Electrical conductance at microwave frequency has also been used in [
16], as a function of the mobility and concentration of the ions in the pore solution of cementitious composites. More recently, novel methods were proposed, based on the communication of electromagnetic waves at low (stress wave) [
17,
18], highly nonlinear solitary wave [
19], and high (microwave) [
20] frequencies, used for concrete characterization, concrete surface moisture detection, and strength estimation, respectively. Their ultimate purpose was to detect damages, evaluate health conditions, alleviate hazards, and extend the working life of civil structures.
All of the described DNT techniques have their relative pros and cons, and no unique technique has been identified as perfect in all aspects, including the reduction of the life-cycle cost (LCC) [
21]. The LCC comprises the initial cost, maintenance or repair cost, and cost of failure, power efficiency, and effectiveness. With the increasingly international widespread use of GB concrete, the demand for novel NDT/E techniques and those combining multiple techniques [
22] for concrete-based structures, in terms of compressive strength prediction, evaluation, and other mechanical properties, is highly expected. Thus, this topic is of importance in the areas of cross-disciplinary research. One of the most important physical properties that governs electromagnetic wave propagation, is the relative dielectric constant (
εr′) of the concrete. Thus far, studies on the dielectric properties of cementitious materials have received great attention in civil engineering [
23,
24,
25,
26,
27,
28,
29,
30,
31]. The use of real-time dielectric constant measurements to evaluate the corresponding variation in the compressive strength of concrete, is a technique that will be well suited for SHM.
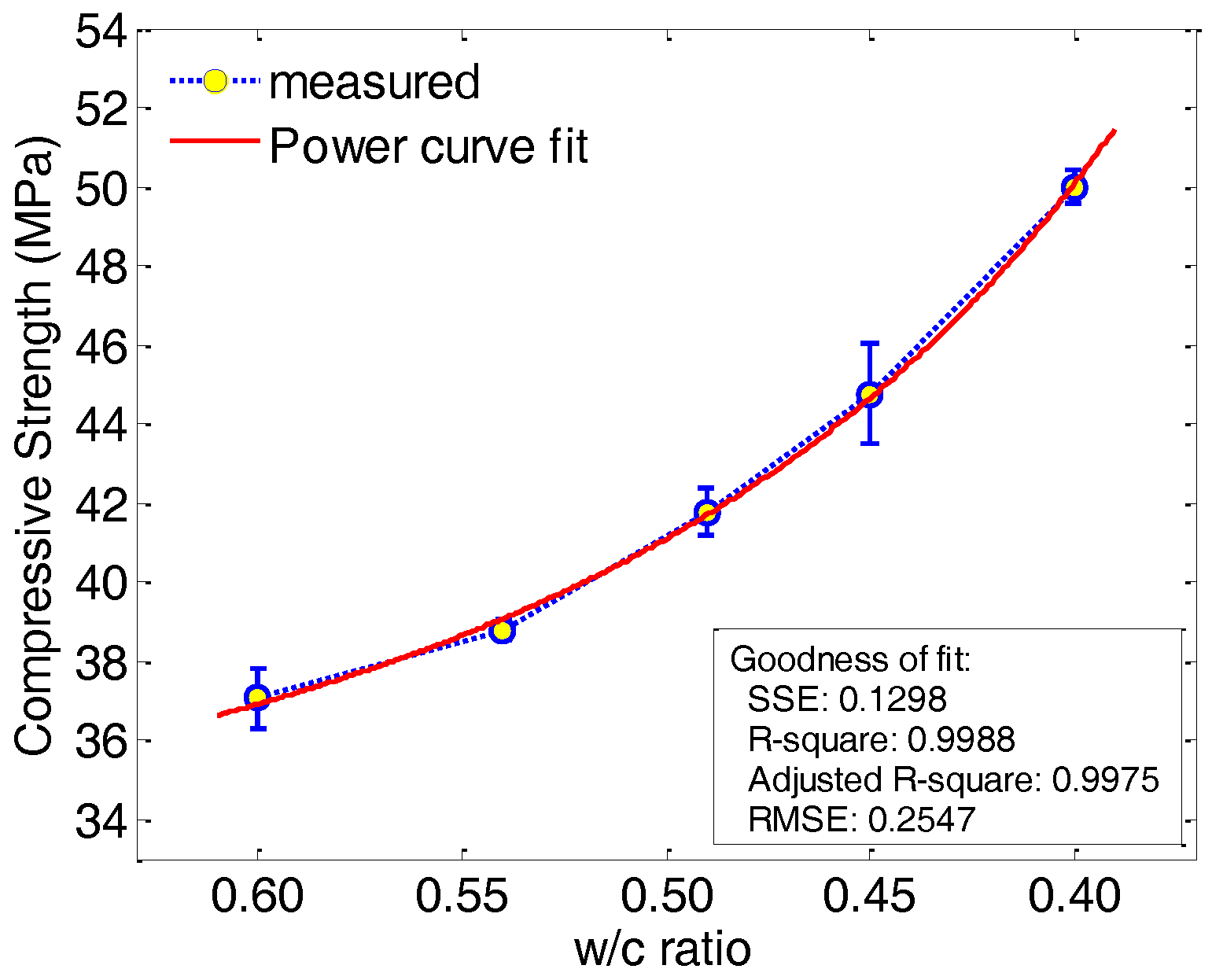
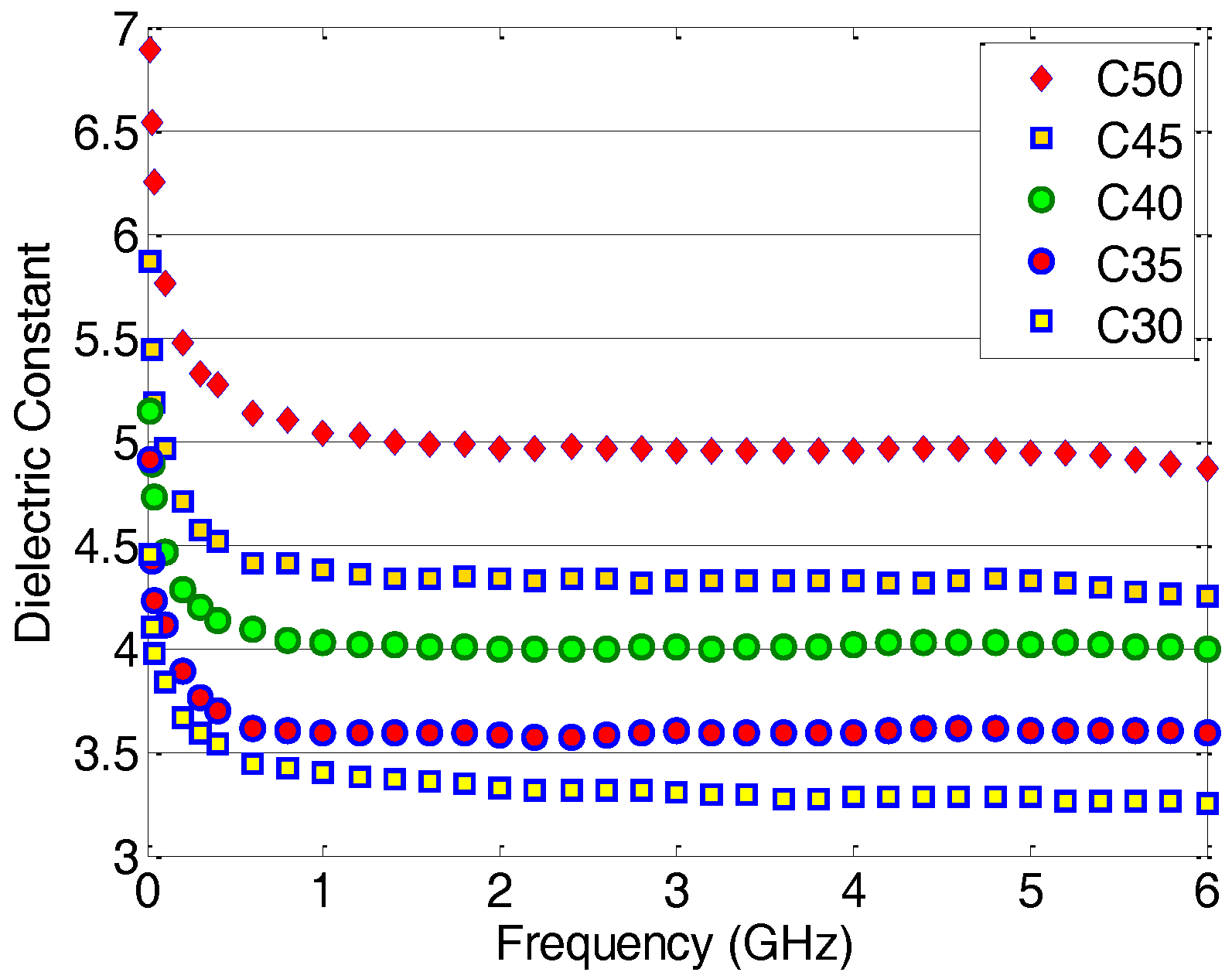
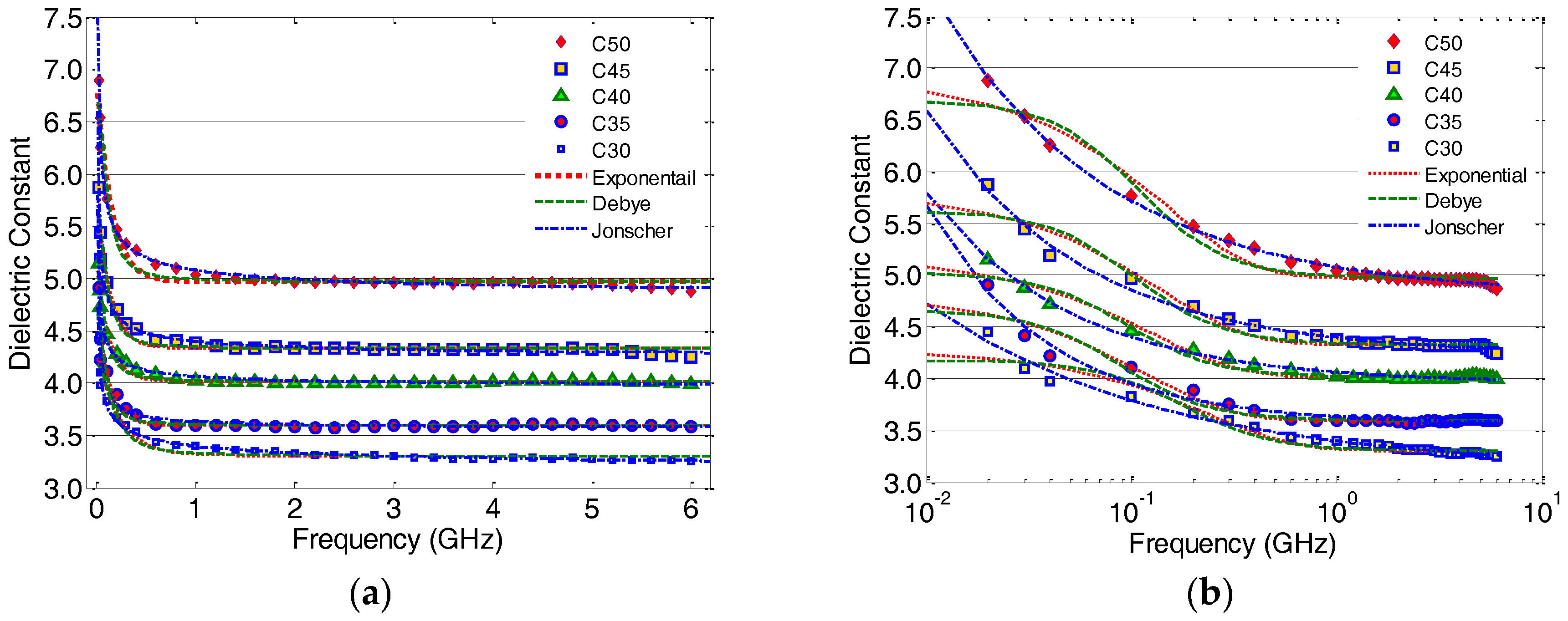
In this paper, the authors present experimental results on the dielectric characterization of standard concrete. Regression modeling of the measured values and analysis, against the water-to-cement ratio of the 28-day concrete, will be considered.
Figure 1 illustrates a big picture of the dual-disciplinary experimental work on the dielectric constant and compressive strength of standard concrete. The objective of this study is to develop a data set of nominal values of the dielectric constant for the GB concrete, in accordance with the Chinese standard JGJ55-2011 [
2]. Correlations between the dielectric constants and compressive strengths will be considered. Ordinary concrete is a heterogeneous porous material. When the maximum size of the coarse aggregates (31.5 mm used in this study) are comparable to the signal’s wavelength, extreme heterogeneous dielectric characteristics may arise. Therefore, a signal frequency of 10 GHz is the highest frequency of interest in this study.
4. Correlation between Compressive Strength and Dielectric Constant
Using the results of the Jonscher model of GB concrete, the dielectric constant values at 0.5 GHz, 2.45 GHz, 5.0 GHz, and 10 GHz were computed and compared, as summarized in
Table 7. It is known that the compressive strength of concrete is a decreasing function of increasing
w/
c, whereas the dielectric constant is a function of frequency and the initial values of
w/
c. Therefore, the computed dielectric constant at various frequencies can be further described by a double power law, as a function of
w/
c and
f, given by:
where
p and
q are the regression coefficients for the
w/
c and
f, respectively.
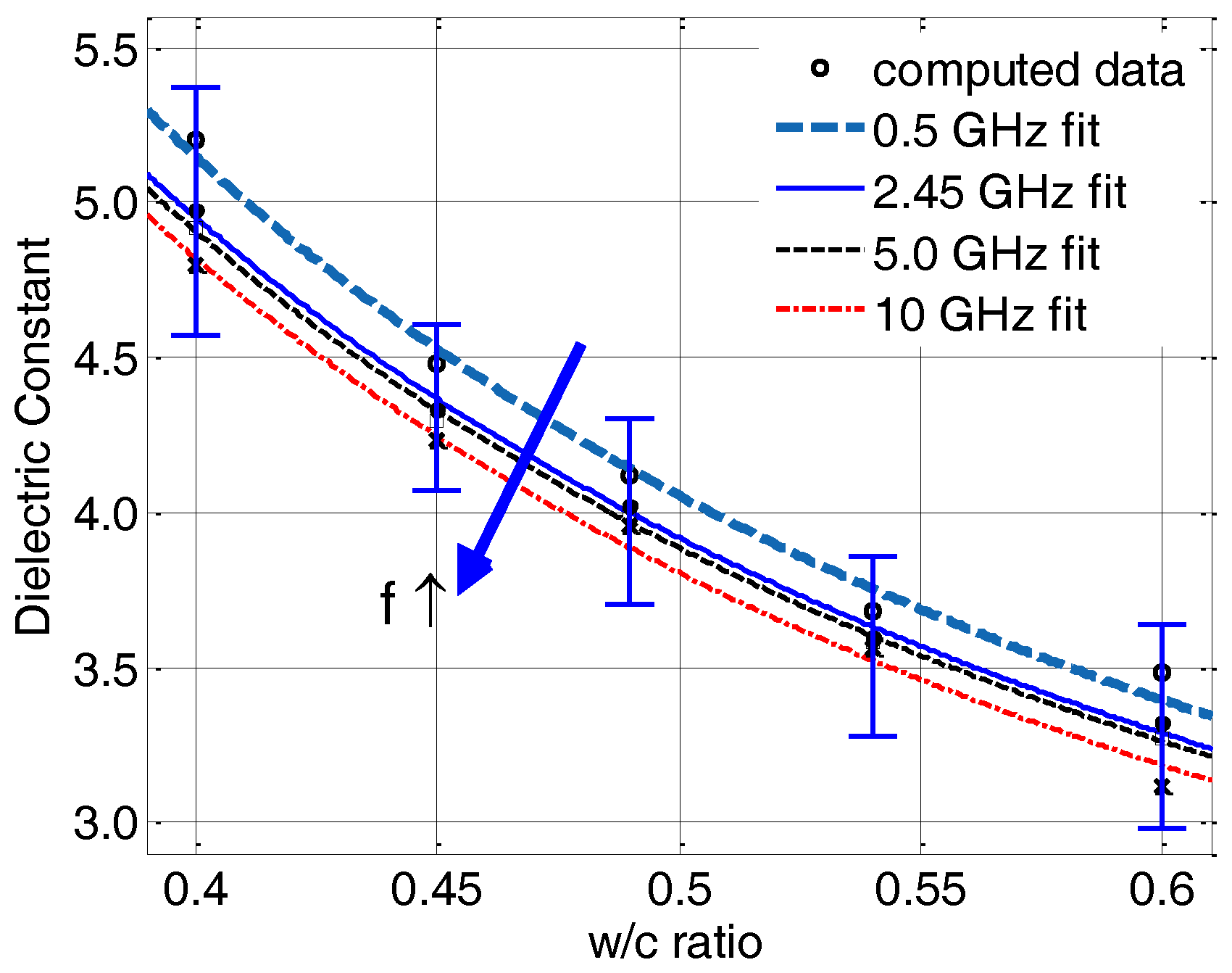
Figure 7 shows the regression curves of the computed dielectric constant versus the water-to-cement ratio, whereas the regression coefficients and the goodness-of-fits are listed in
Table 8. As can be seen, all curves are virtually consistent, presenting decreasing trends with an increasing
w/
c ratio. A small dispersion with a frequency increasing beyond 0.5 GHz is observed. It is worth noting that, apart from the limiting case of 0.5 GHz, the difference between the pair of power curves, e.g., 2.45 GHz and 5.0 GHz, is sufficiently small, particularly within the standard deviations of the measured data at 2.45 GHz. Therefore, the frequency dispersion has a minimal effect on the computed values of the dielectric constant, as shown in
Figure 7.
By combining Equations (3) and (11), one can establish the correlation between the compressive strength and the dielectric constant of GB concrete, via the common variable of
w/
c, as given by:
where
r and
A are the regression coefficients, whose values and the goodness-of-fits are summarized in
Table 9.
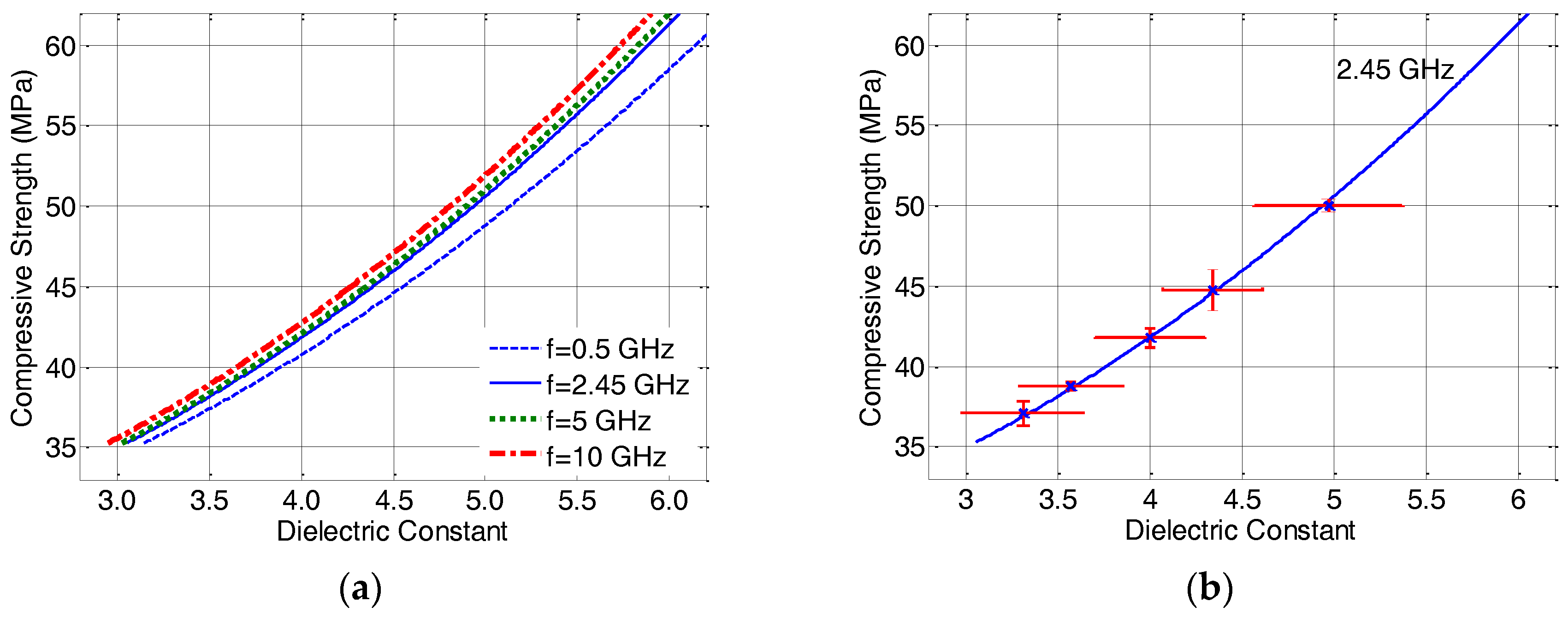
Figure 8a shows the correlations between the compressive strength and dielectric constant of GB concrete, at various frequencies. The correlation has been described by the power law function expressed in (12). By further considering the standard deviations of both of the measured data,
Figure 8b illustrates the correlation at a frequency of 2.45 GHz. It is noteworthy to describe that the frequency dispersion has a minimal effect on the dielectric constants, where the discrepancies are far less than the standard deviations from the measurement. The relatively high standard deviation from the dielectric constant is attributed to the high heterogeneity of the GB concrete, where the maximum size of the coarse aggregates used in the fabrication was 31.5 mm.