Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study
Abstract
:1. Introduction
2. Field Monitoring Project
2.1. General Situation
2.2. Tunnel Structure
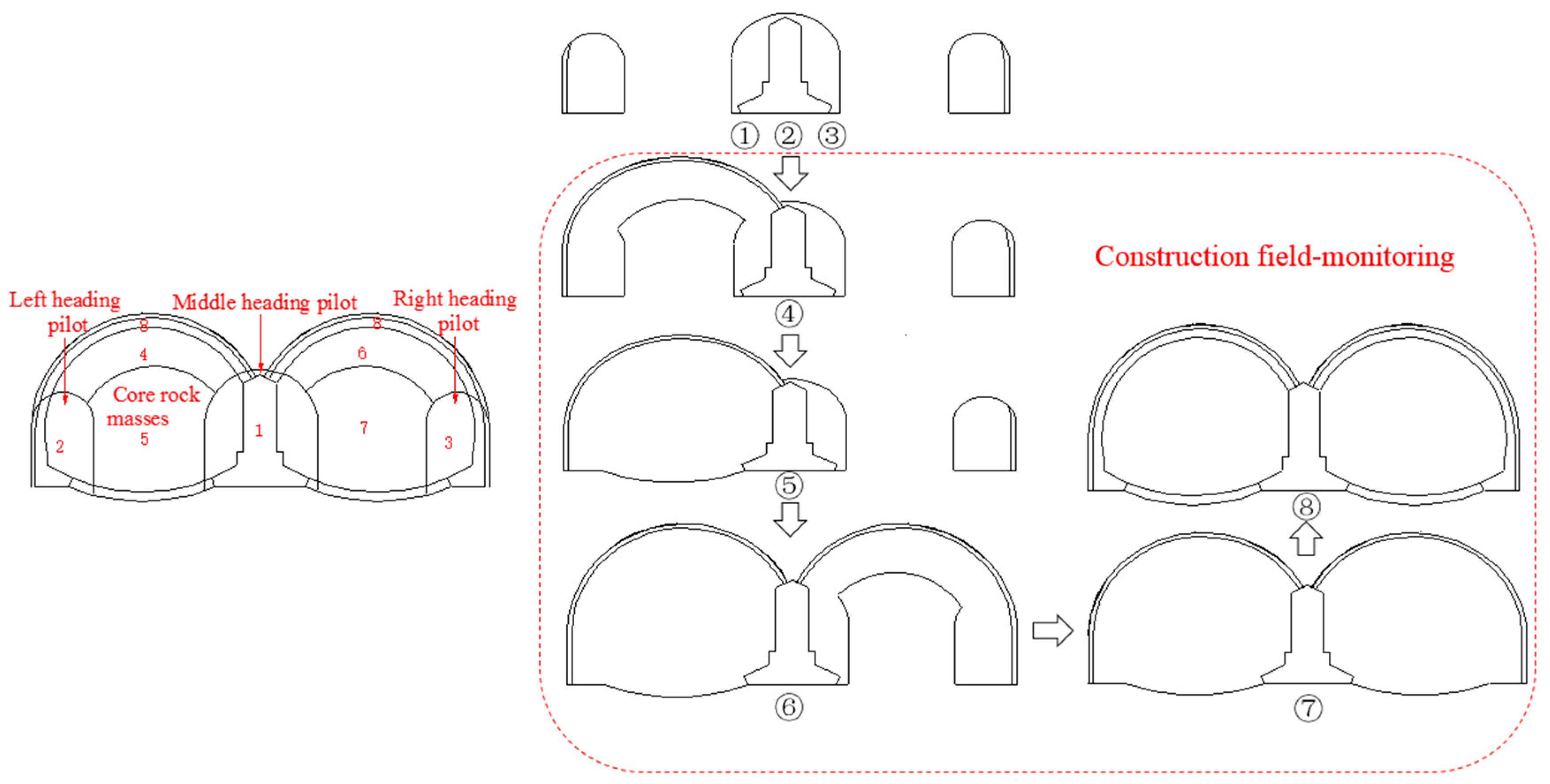
2.3. Tunnel Construction
2.4. Monitoring Parameters and Methods
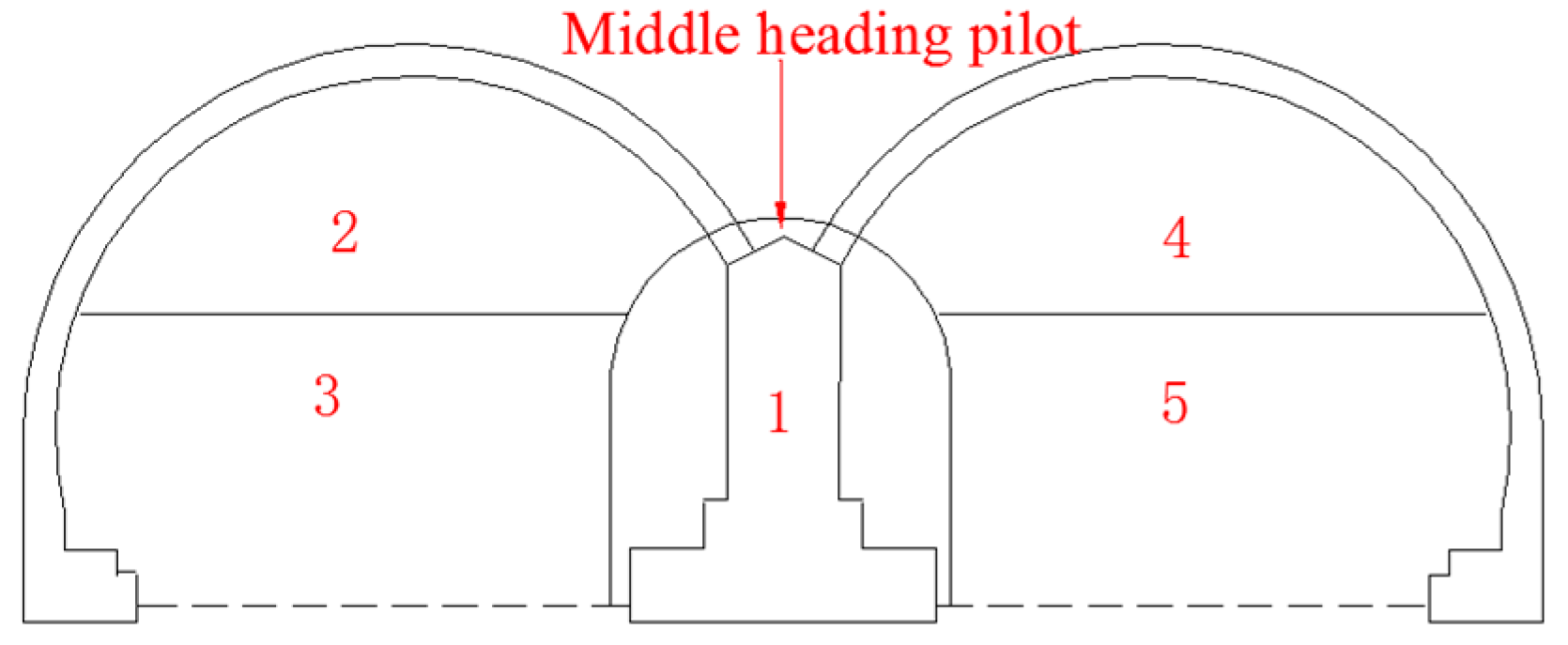
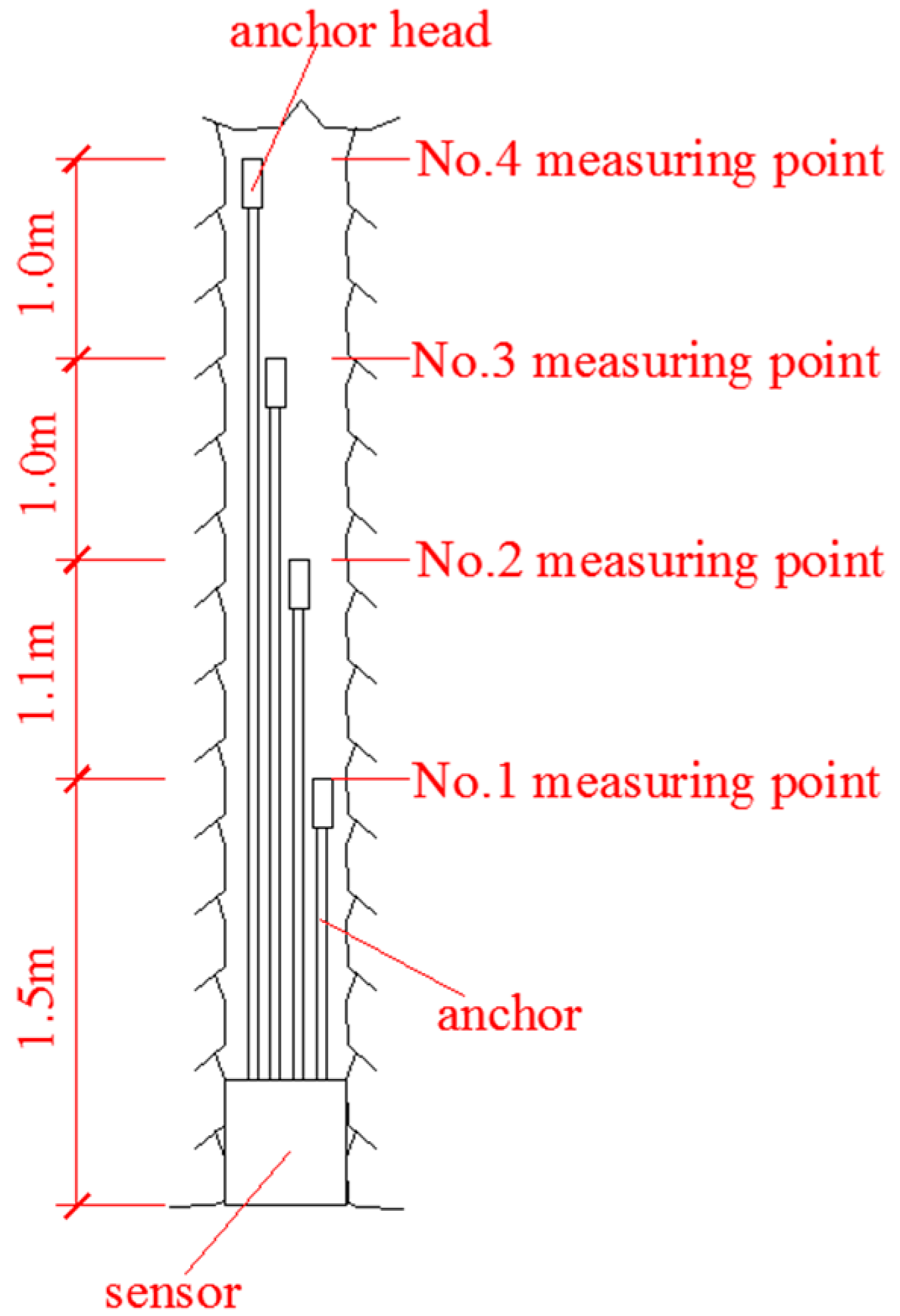
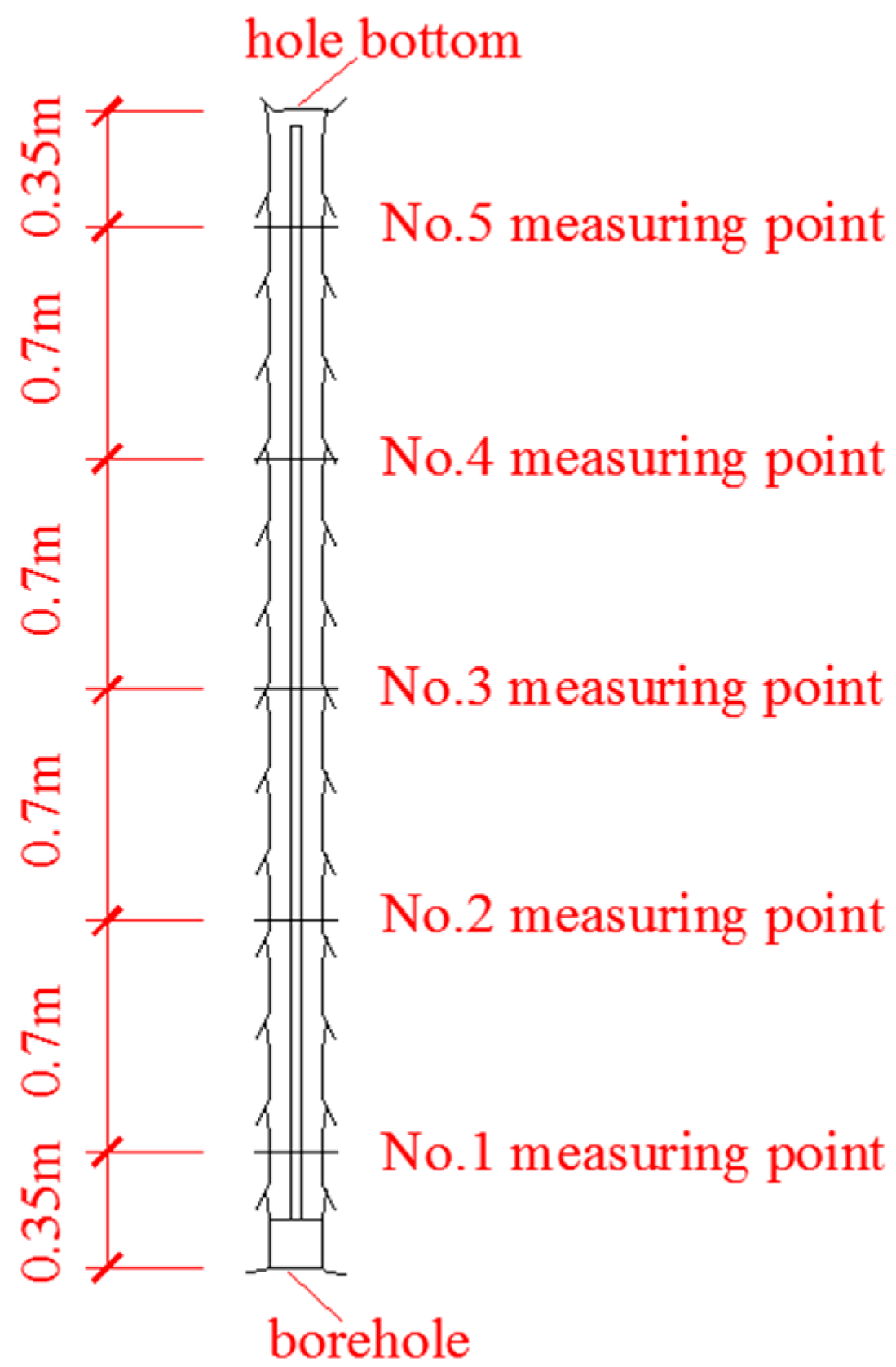
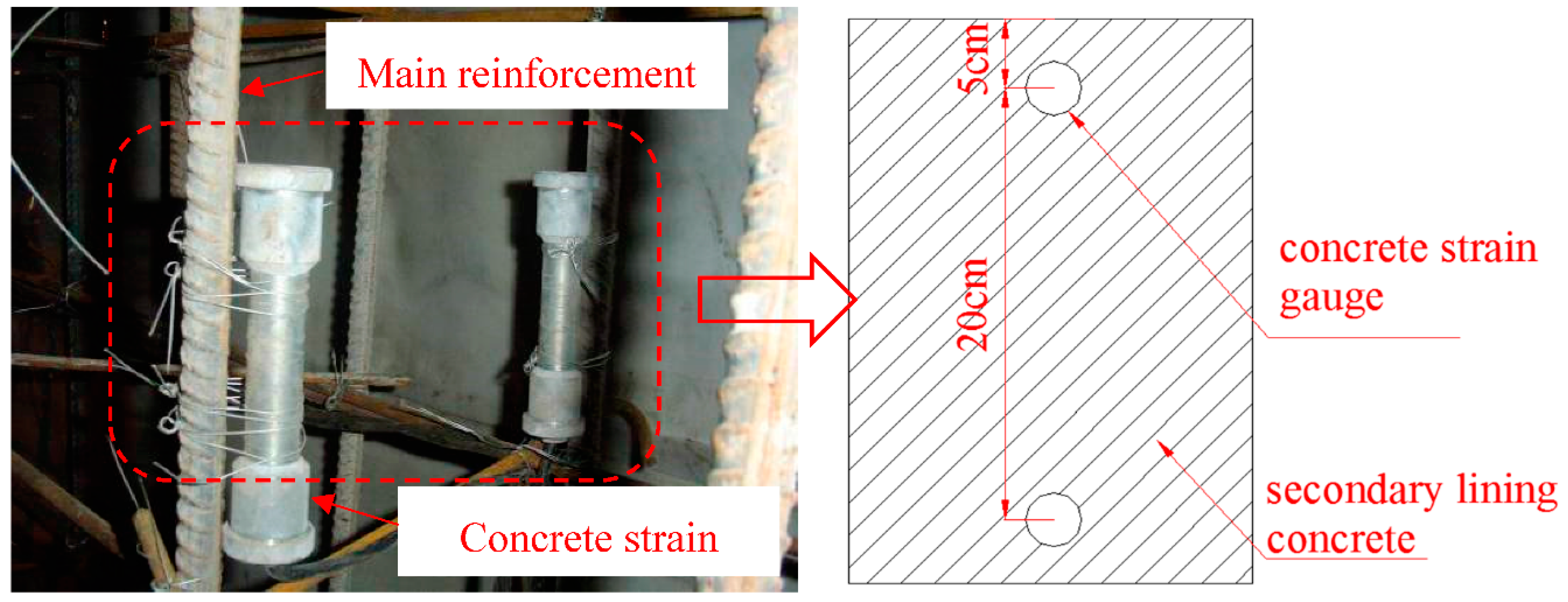
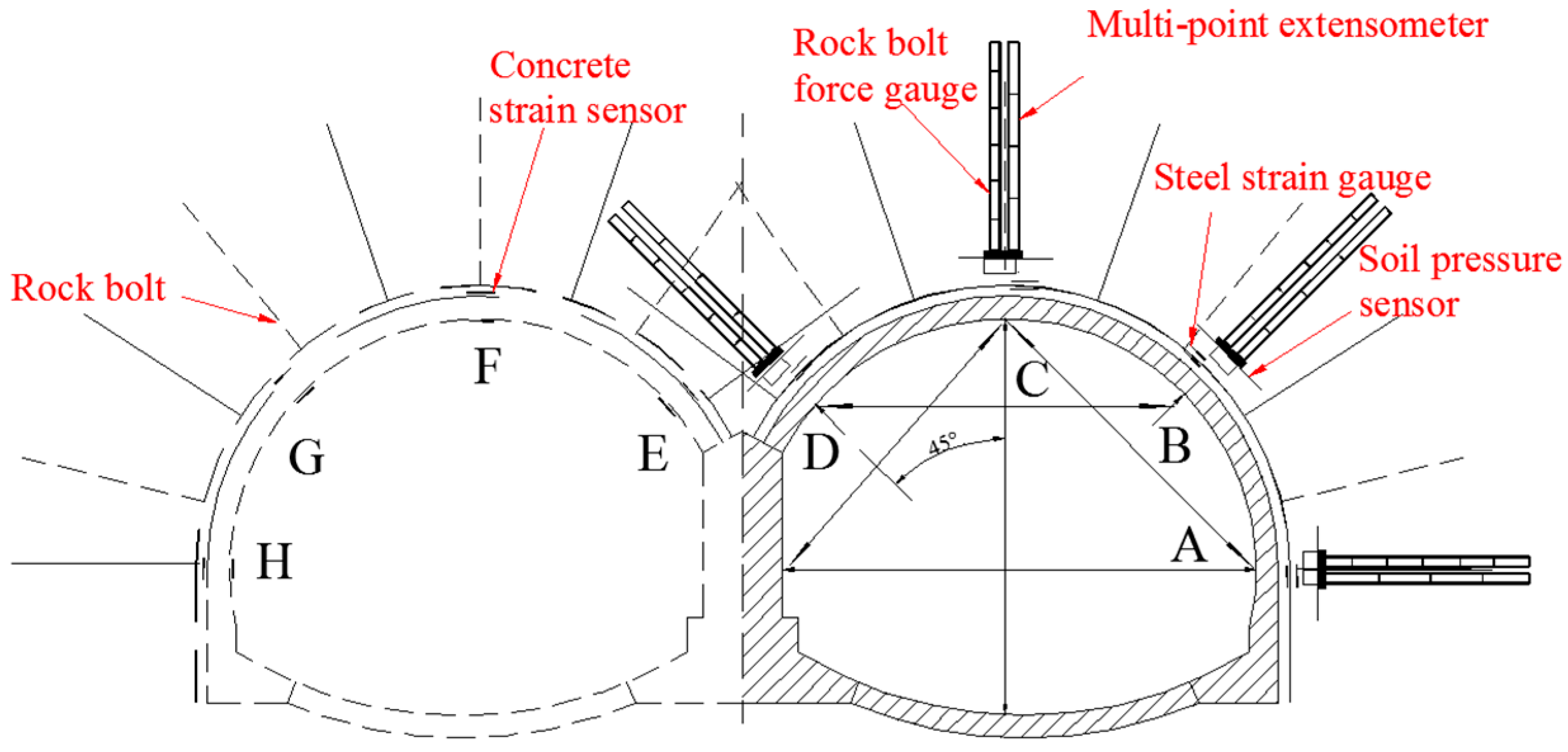
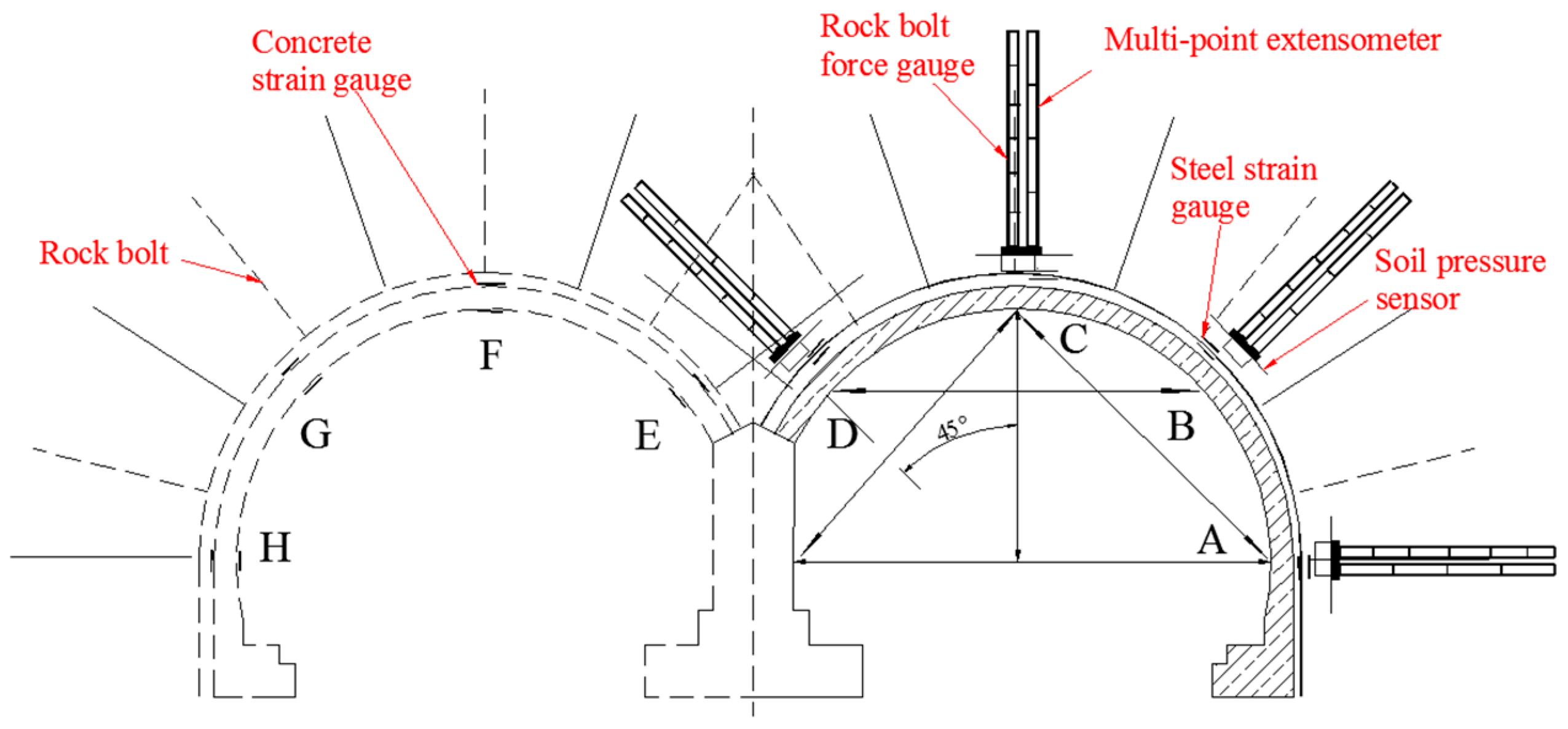
2.5. Monitoring Sections and Measuring Points Layouts
3. Monitoring Results and Analysis
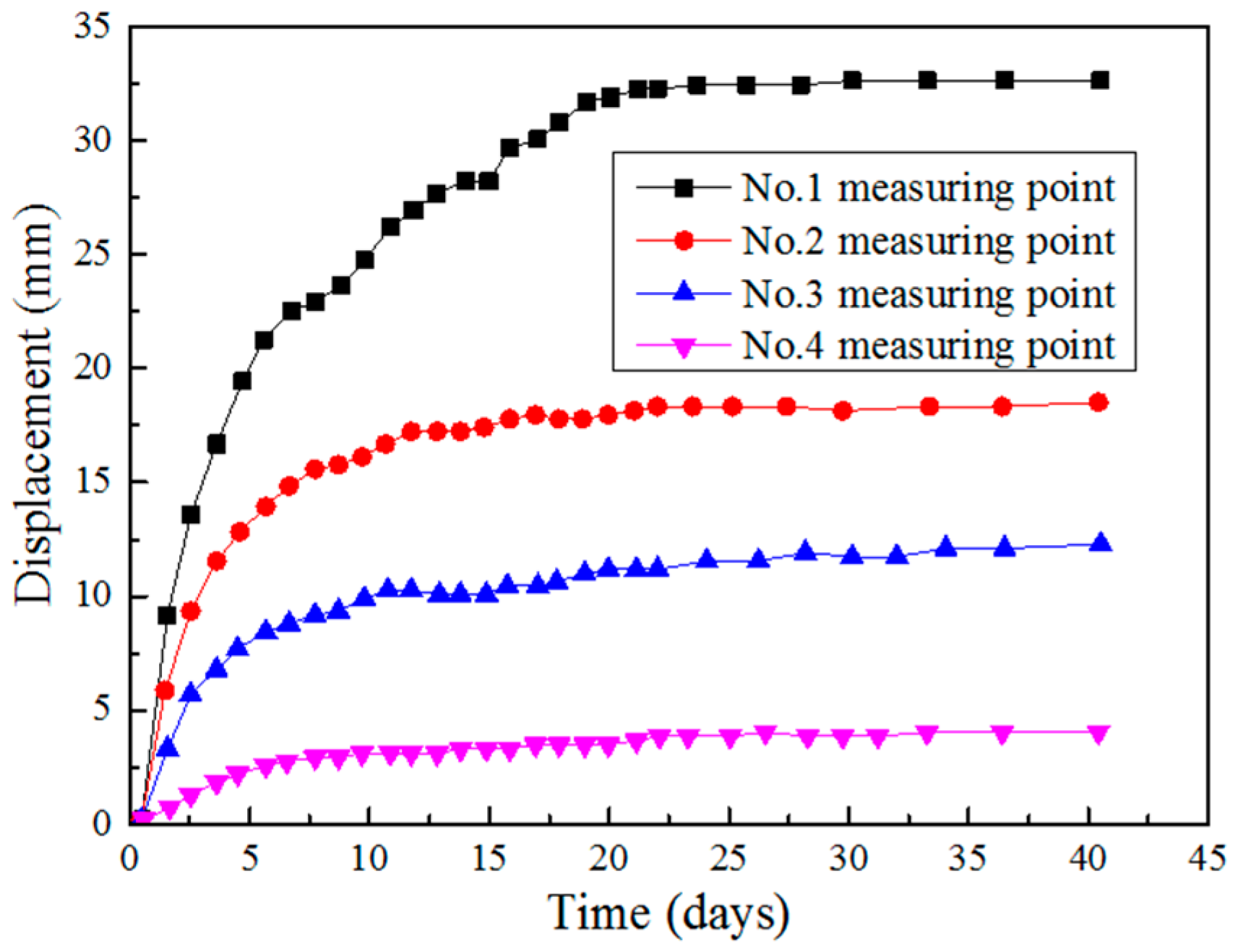
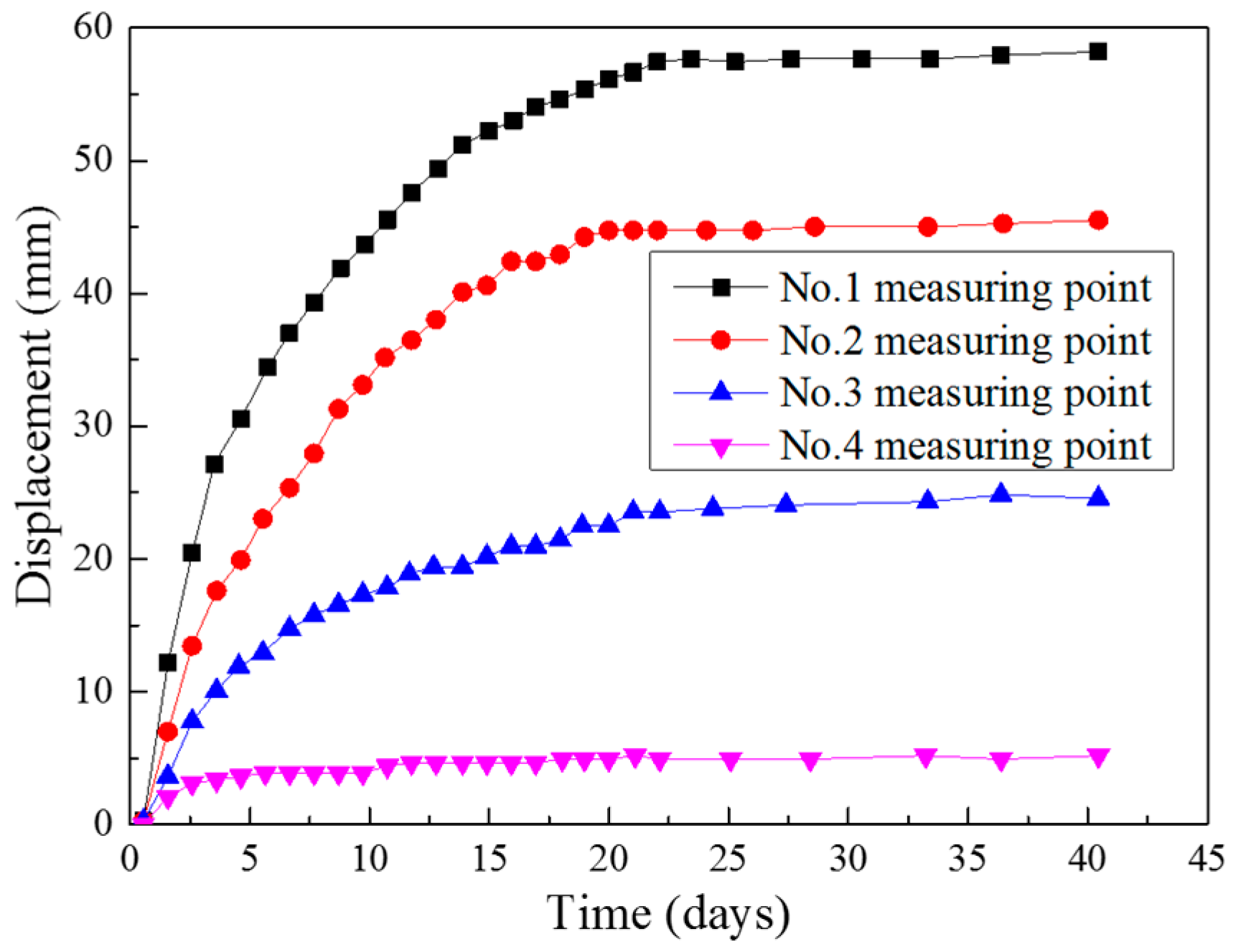
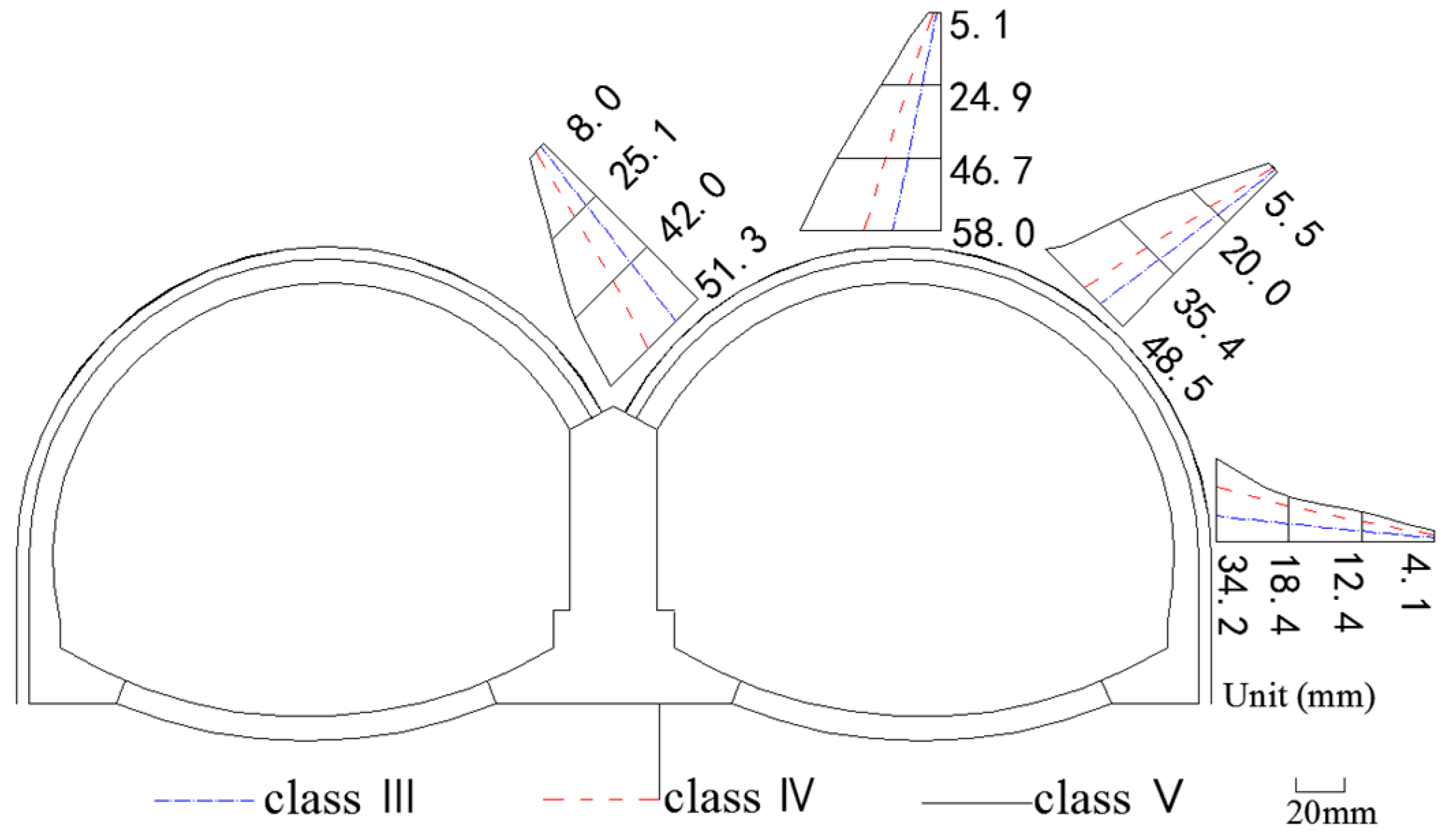
3.1. Internal Displacements of Surrounding Rocks
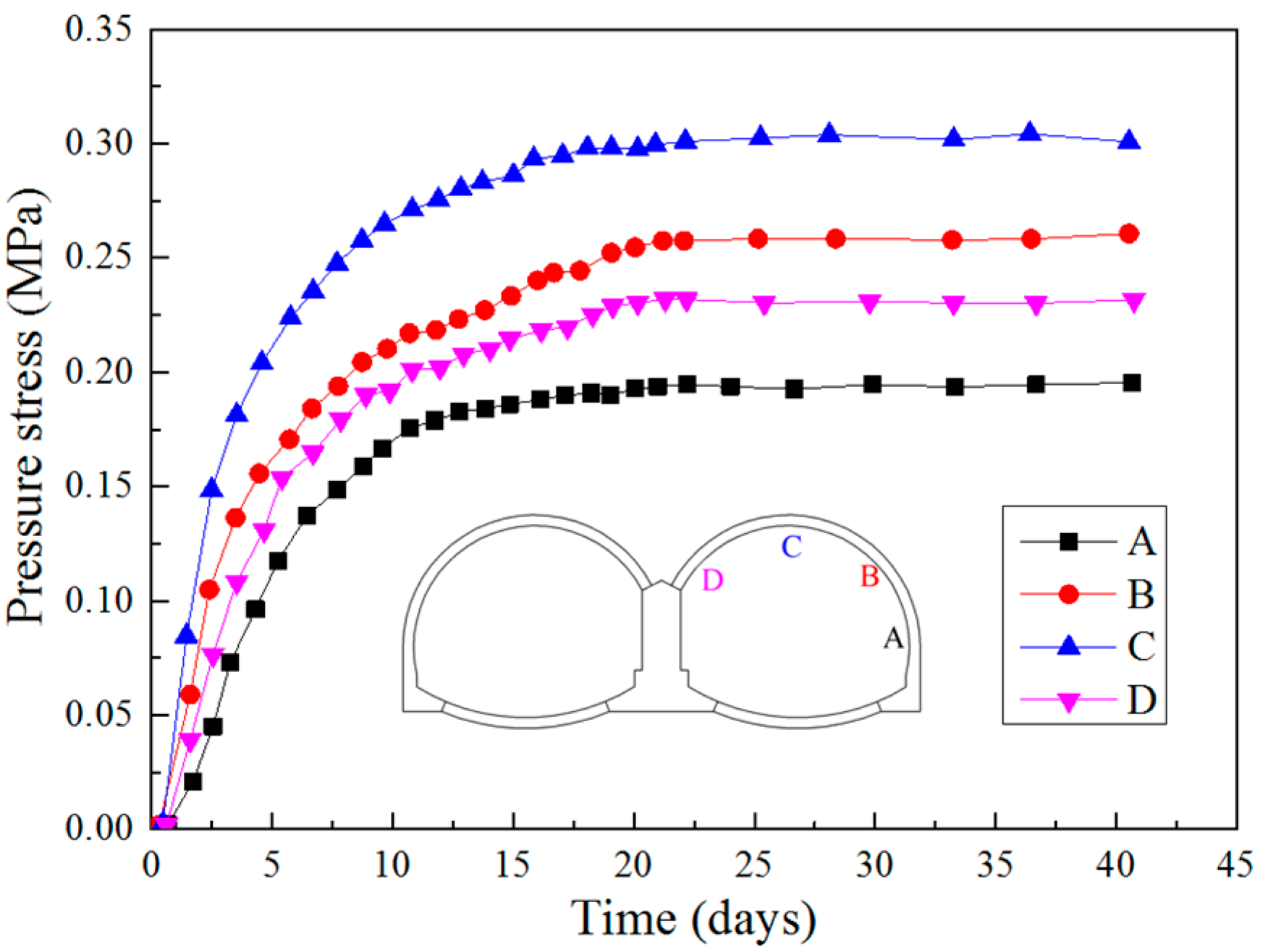
3.2. Contact Pressures between Surrounding Rocks and Primary Linings
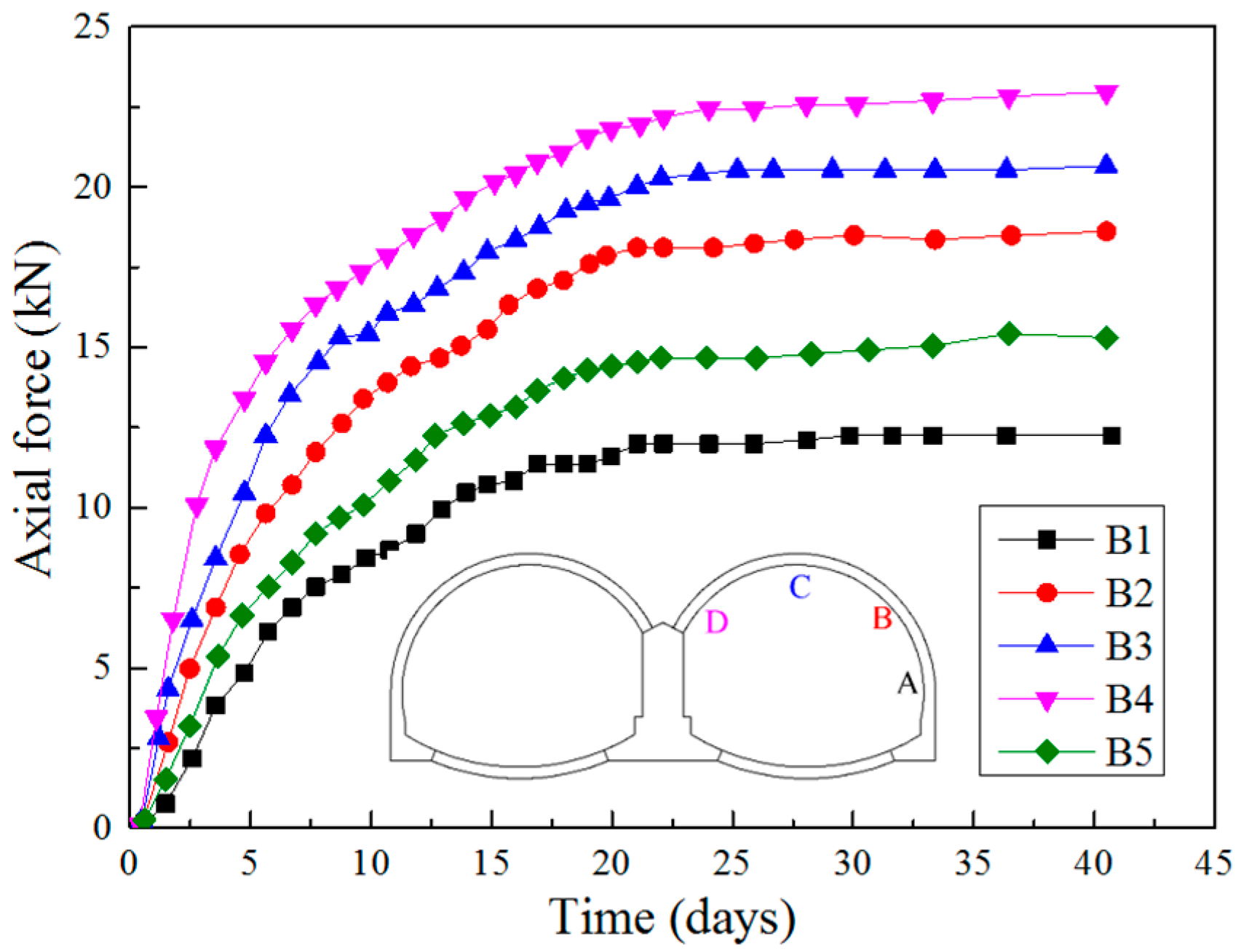
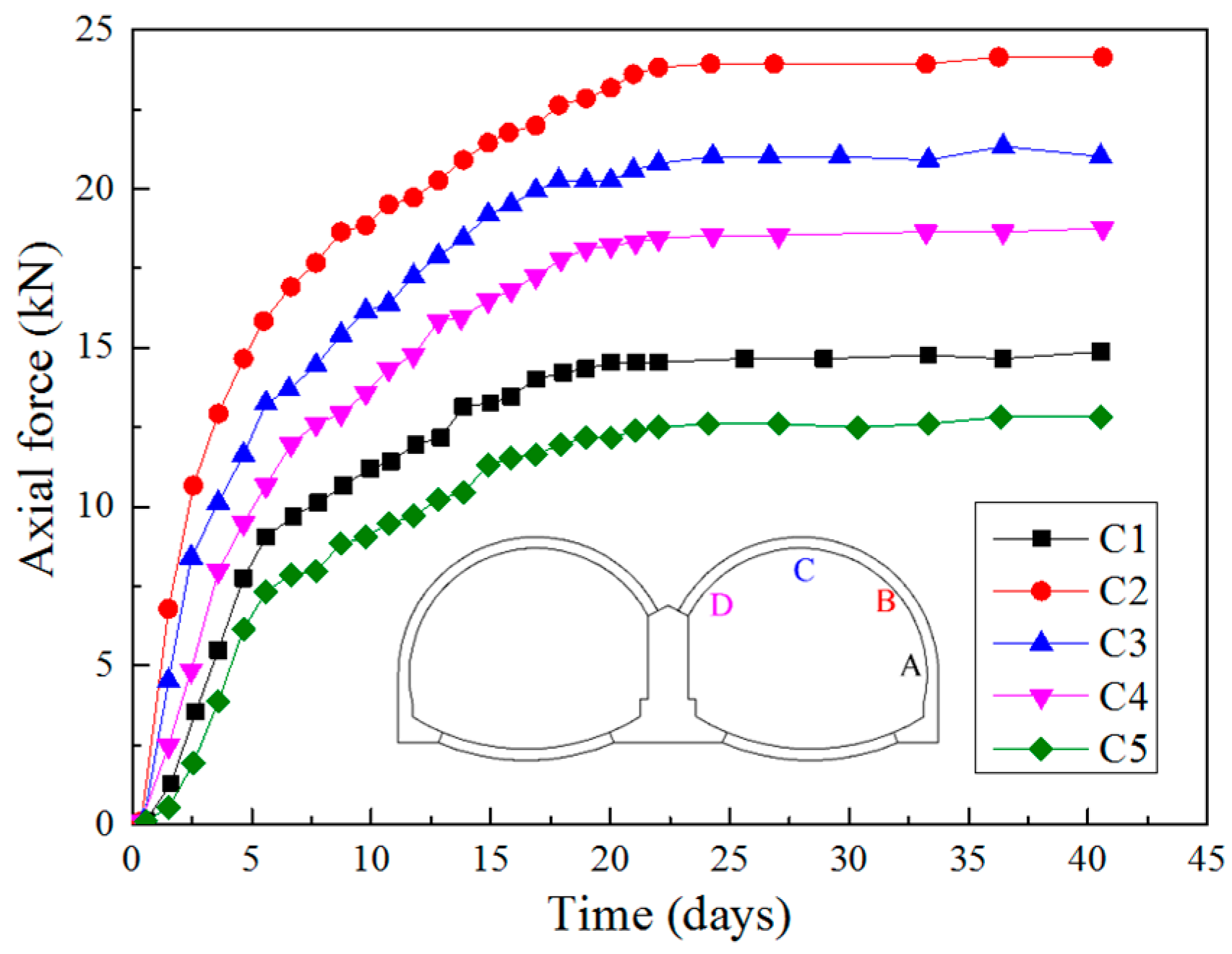
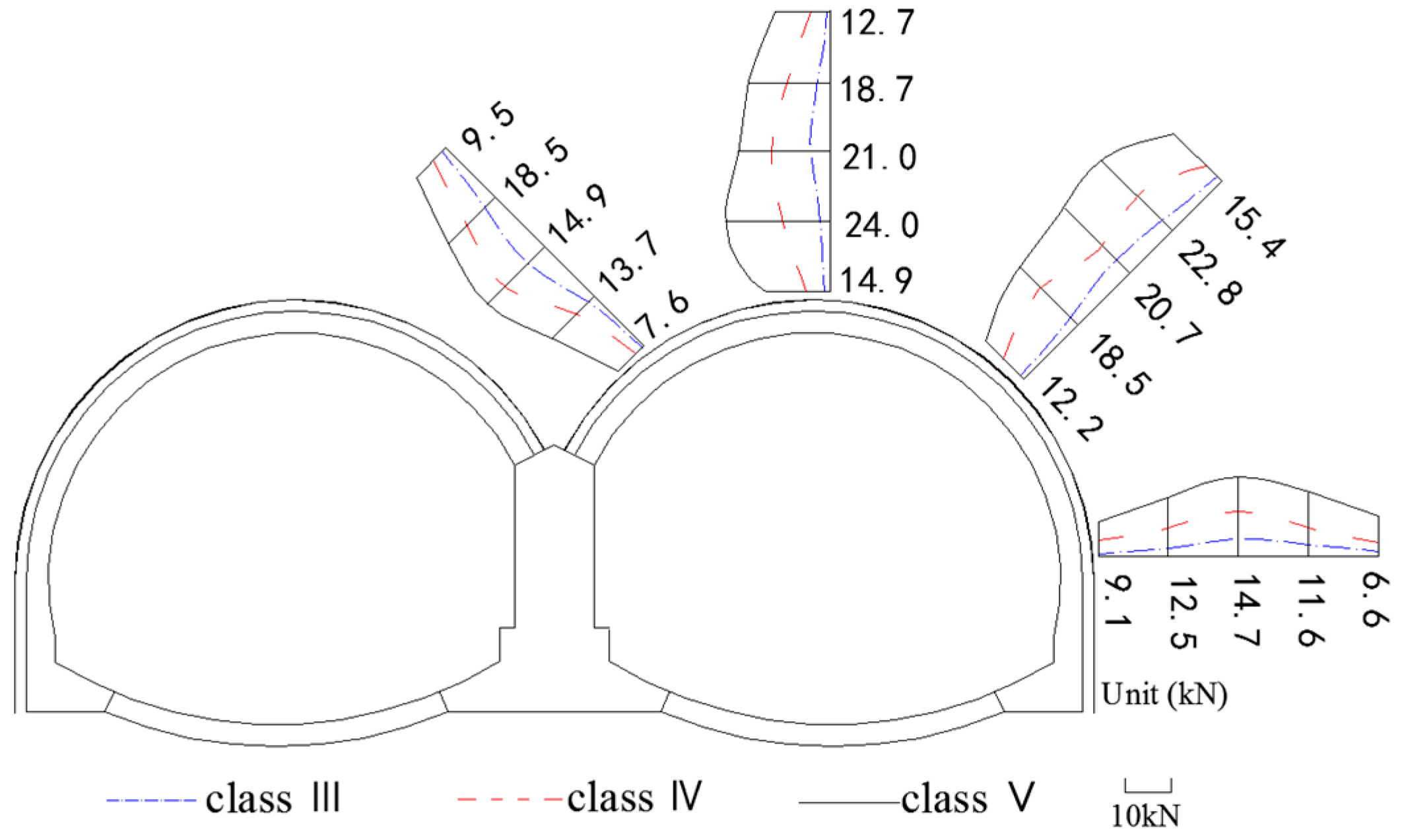
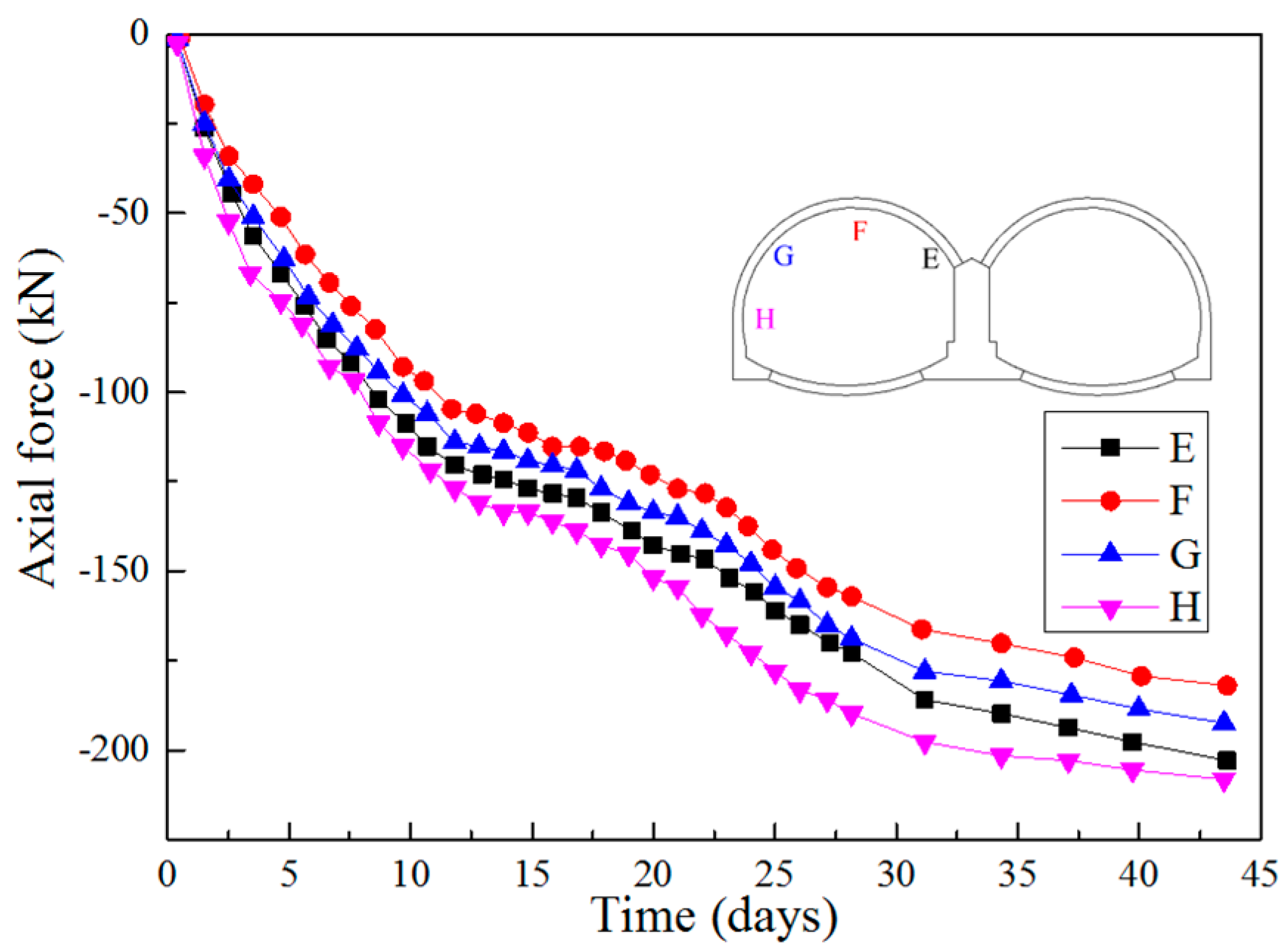
3.3. Axial Forces in Rock Bolts
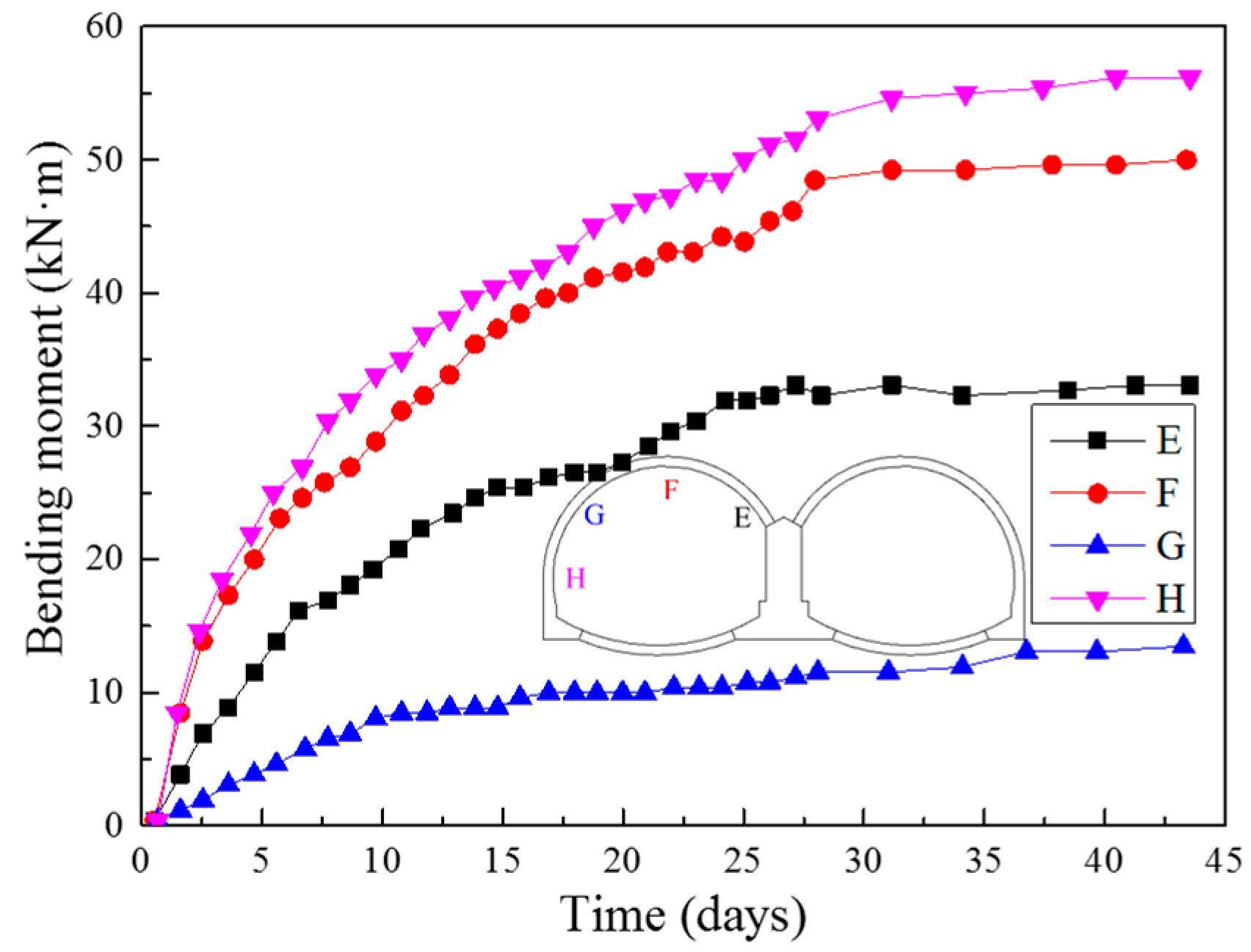
3.4. Internal Forces in Steel Arches
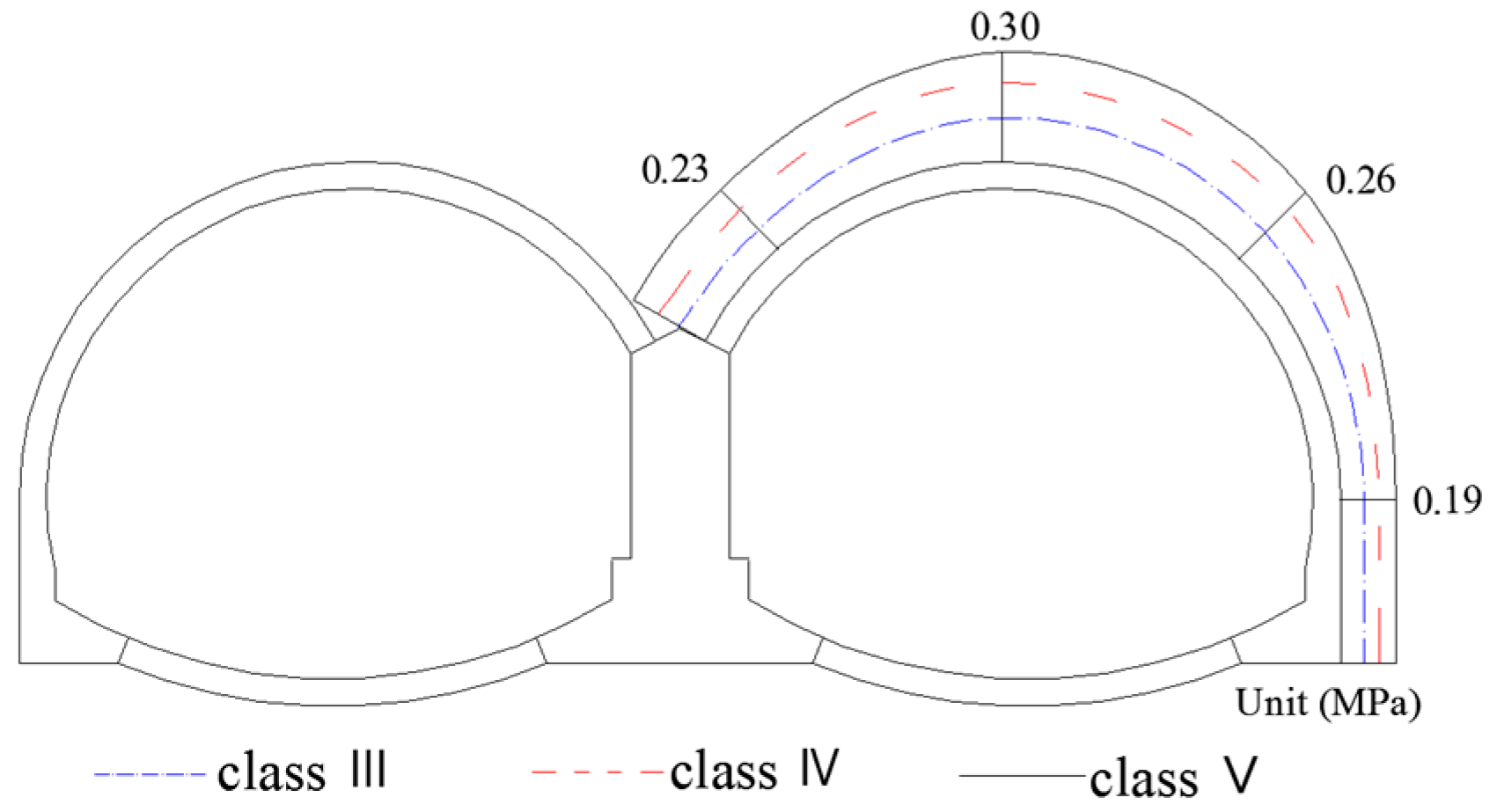
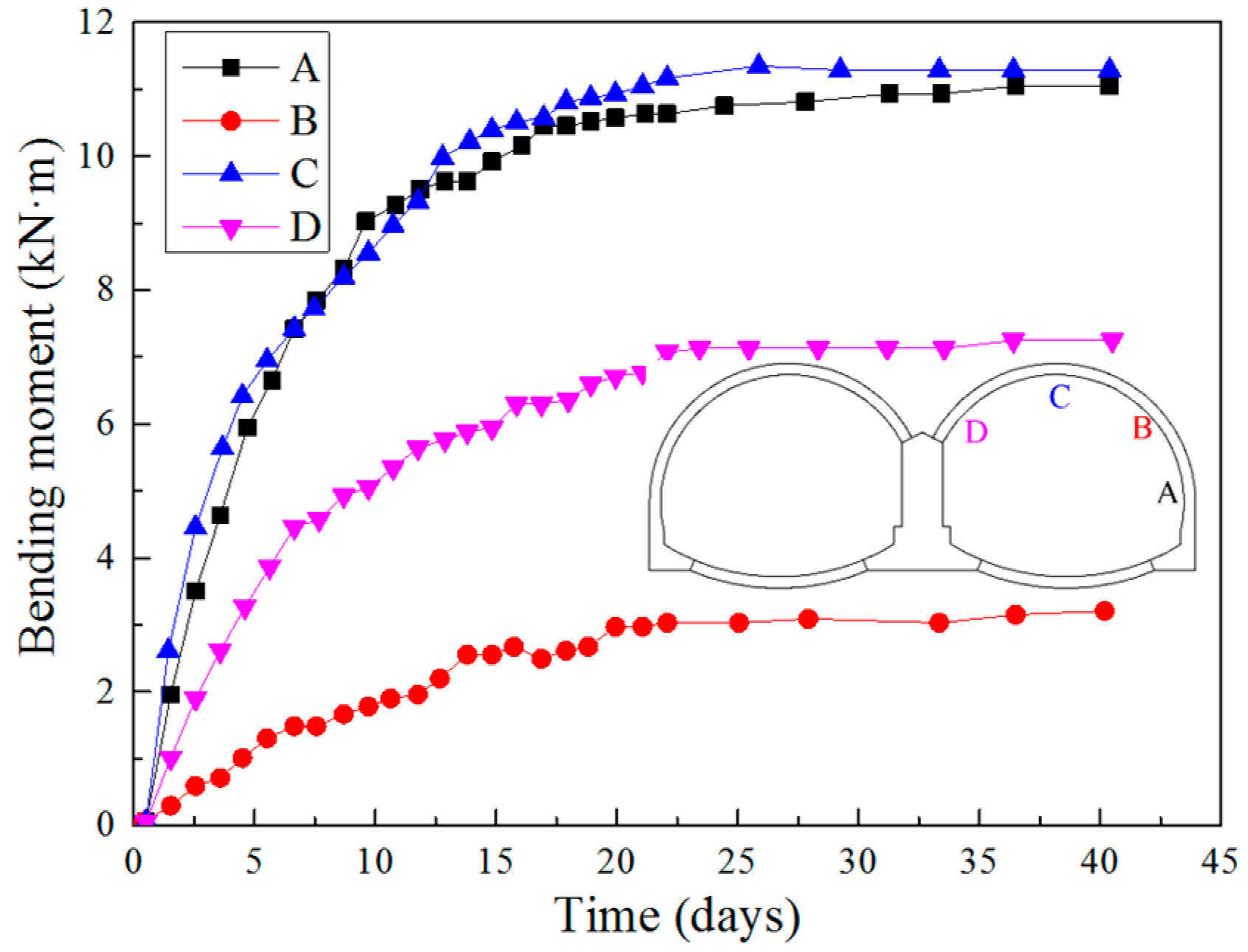
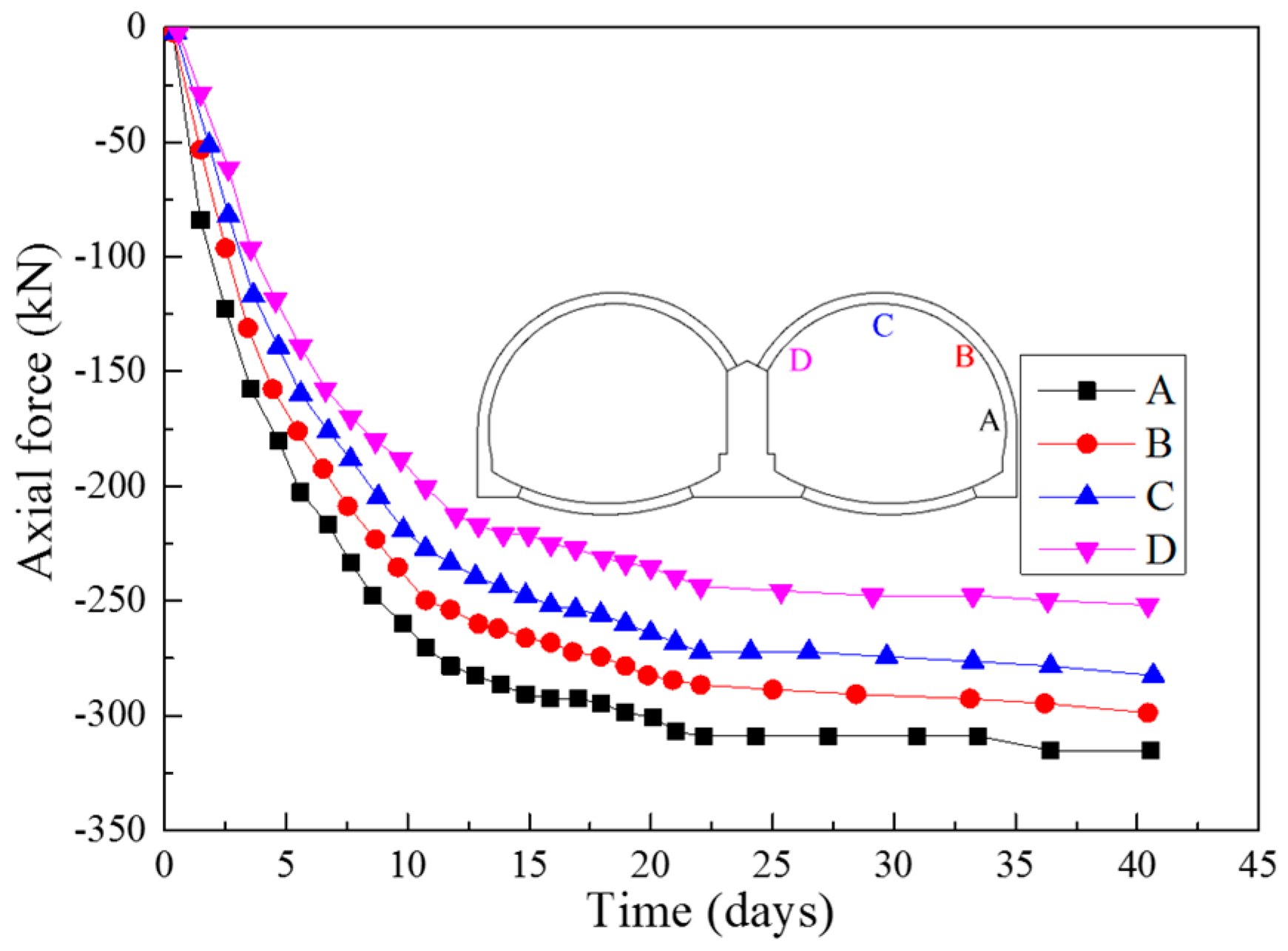
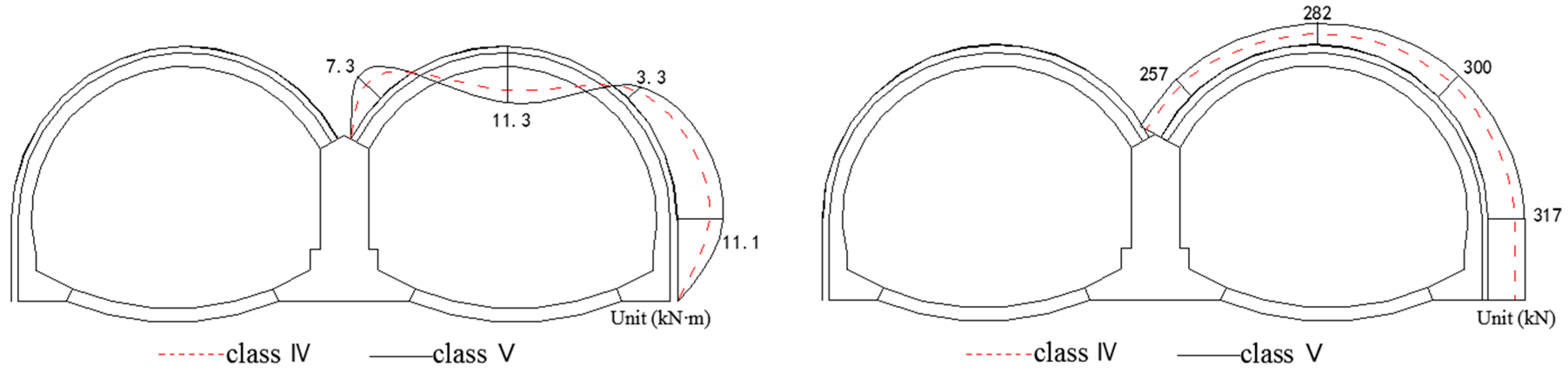
3.5. Internal Forces in Secondary Linings
4. Conclusions
- (1)
- The dynamic evolution of the internal displacements of surrounding rocks is closely related to the tunnel construction procedures. The internal displacements of surrounding rocks did not reach the stable state until the completion of the secondary linings. At different locations in the monitoring section, the internal displacements of surrounding rocks at the tunnel vault are greater than that at the tunnel spandrel, which are even greater than that at the side wall of the tunnel. The internal deformations of surrounding rocks are larger in the cross section with lower-level surrounding rock masses.
- (2)
- The contact pressure between surrounding rocks and primary linings converged rapidly and it generally reached its stable state within 5 days after the construction of primary linings. The monitoring results show that the existence of the middle wall is able to effectively transfer the surrounding rock pressures on the primary linings near the middle wall, resulting in the decreasing of the contact pressures at that side. The contact pressures between surrounding rocks and primary linings are greater in the cross section with lower-level surrounding rocks. In addition, based on Protodyakonov’s theory, a simplified method was proposed to estimate the surrounding rock pressures of the double-arched tunnel and the calculated values are in better agreement with the measured values.
- (3)
- Single rock bolt bears pure tensile stresses which are relatively larger in the middle of the rock bolt and lower at the two ends. At different positions in the same cross section, the axial forces in rock bolts at the tunnel vault are higher than that at the spandrel, which are even higher than that at the side wall of the tunnel. Through calculation, the tensile stress of a single bolt is far less than its ultimate tensile stress, which shows that the rock bolt does not play its role to the full potential and it is necessary to take appropriate measures to strengthen the anchoring forces.
- (4)
- The internal forces in steel arches increased greatly at the very beginning. As the excavation proceeded, the growth rate gradually slowed down and eventually the forces tended to stabilize after the construction of secondary linings. By analysis of the internal forces at different positions in steel arches, it is found that the steel arch vault is the most disadvantaged loading position.
- (5)
- The secondary linings not only serve as a structure for sufficient safety margin but also bear certain loadings in the construction and long-term operation periods of the Gangkou tunnel. The lower the rock mass classification, the larger the internal forces in secondary linings. The internal forces in secondary linings are larger in the cross section with lower class of rock masses.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hwang, J.H.; Kikumoto, M.; Kishida, K.; Kimura, M. Dynamic stability of multi-arch culvert tunnel using 3-D FEM. Tunn. Undergr. Space Technol. 2005, 21, 384. [Google Scholar] [CrossRef]
- Wang, J.; Xia, C.; Zhu, H.; Li, Y.; Lin, Z.; Chen, X. Site monitoring and analysis of non-symmetrical muti-arch highway tunnel. Chin. J. Rock Mech. Eng. 2004, 23, 267–271. (In Chinese) [Google Scholar]
- Tao, L.; Shen, M.; Tao, L.; He, Z.; Yuan, Y. Model test and 3D numerical simulation study on excavation of double-arch tunnel. Chin. J. Rock Mech. Eng. 2006, 25, 1802–1808. (In Chinese) [Google Scholar]
- Lei, M.; Omer, J. Study on train vibration response and cumulative deformation of double arch tunnel in Kast foundation. Geotech. Geol. Eng. 2015, 33, 549–558. [Google Scholar] [CrossRef]
- Wang, S.; Li, C.; Wang, Y.; Zou, Z. Evolution characteristics analysis of pressure-arch in a double-arch tunnel. Tehnicki Vjesnik 2016, 23, 181–189. [Google Scholar]
- Huang, R.; Xiao, H. Deformation mechanism of a shallow double-arch tunnel in a sloping rock mass. Bull. Eng. Geol. Environ. 2010, 69, 89–97. [Google Scholar]
- Li, D.; Li, X.; Li, C.C.; Huang, B.; Gong, F.; Zhang, W. Case studies of groundwater flow into tunnels and an innovative water-gathering system for water drainage. Tunn. Undergr. Space Technol. 2009, 24, 260–268. [Google Scholar] [CrossRef]
- Rabcewicz, L. The New Austrian Tunneling Method. Water Power 1964, 16, 453–457. [Google Scholar]
- Hellmich, C.; Ulm, F.J.; Mang, H.A. Multisurface Chemoplasticity. II: Numerical Studies on NATM Tunneling. J. Eng. Mech. 1999, 125, 702–713. [Google Scholar] [CrossRef]
- Sauer, G.; Gold, H. NATM ground support concepts and their effects on contracting practices. In Proceedings of the 9th Rapid Excavation and Tunneling Conference (RETC), Los Angeles, CA, USA, 11–14 June 1989.
- Jenkins, J.D.; Sander, H.J. Principles of the NATM and Other Uses of the Geologic Monitoring Techniques. In High Level Radioactive Waste Management; American Society of Civil Engineers (ASCE): Las Vegas, NE, USA, 1991. [Google Scholar]
- Muller, L. Removing misconceptions on the New Austrian Tunneling Method. Tunn. Tunn. Int. 1978, 10, 29–32. [Google Scholar]
- Bieniawski, Z.T. 22-Classification of Rock Masses for Engineering: The RMR System and Future Trends. Rock Test. Site Charact. 1993, 3, 553–573. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Aydin, A.; Ozbek, A.; Acar, A. Geomechanical characterization, 3-D optical monitoring and numerical modeling in Kirkgecit-1 tunnel, Turkey. Eng. Geol. 2014, 181, 38–47. [Google Scholar] [CrossRef]
- Yoshimura, H.; Yuki, T.; Yamada, Y.; Kobubun, N. Analysis and monitoring of the Miyana railway tunnel constructed using the New Austrian tunneling method. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 67–75. [Google Scholar] [CrossRef]
- Lefas, I.D.; Georgiannou, V.N.; Boronkay, K.A. Monitoring of tunnel behaviour through cataclastic rocks. Geotech. Eng. 2006, 159, 113–123. [Google Scholar]
- Ariznavarreta-Fernández, F.; González-Palacio, C.; Menéndez-Díaz, A.; Ordoñez, C. Measurement system with angular encoders for continuous monitoring of tunnel convergence. Tunn. Undergr. Space Technol. 2016, 56, 176–185. [Google Scholar] [CrossRef]
- Hellmich, C.; Ulm, F.J.; Mang, H. Modeling of Early-Age Creep of Shotcrete. I: Model and Model Parameters. J. Eng. Mech. 2000, 126, 284–291. [Google Scholar] [CrossRef]
- Hellmich, C.; Mang, H.A.; Ulm, F.J. Hybrid method for quantification of stress states in shotcrete tunnel shells: Combination of 3D in situ displacement measurements and thermochemoplastic material law. Comput. Struct. 2001, 79, 2103–2115. [Google Scholar] [CrossRef]
- Ullah, S.; Pichler, B.; Scheiner, S.; Hellmich, C. Shell-specific interpolation of measured 3D displacements, for micromechanics-based rapid safety assessment of shotcrete tunnels. Comput. Model. Eng. Sci. 2010, 57, 279–314. [Google Scholar]
- Ullah, S.; Pichler, B.; Hellmich, C. Modeling Ground-Shell Contact Forces in NATM Tunneling, Based on 3D Displacement Measurements. J. Geotech. Geoenviron. Eng. 2013, 139, 444–457. [Google Scholar] [CrossRef]
- Fuentes, R. Internal forces of underground structures from observed displacements. Tunn. Undergr. Space Technol. 2015, 49, 50–66. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, S.H.; Guo-Ping, D.U.; Dan, L.I. In-situ testing study on lining system of double-arched tunnel. Chin. J. Rock Mech. Eng. 2005, 24, 480–484. (In Chinese) [Google Scholar]
- Erbing, L.I.; Wang, D.; Wang, Y.; Tan, Y.; Zhang, L. Monitoring and control of construction deformation of urban shallow-buried large-span double-arch tunnel under complex condition. Chin. J. Rock Mech. Eng. 2007, 26, 833–839. (In Chinese) [Google Scholar]
- JTG D70-2004, Code for Design of Road Tunnel; China Communication Press: Beijing, China, 2004. (In Chinese)



| Rock Mass Classification | Cohesion (MPa) | Internal Friction Angle (°) | Elastic Modulus (GPa) | Unit Weight (kN/m3) |
|---|---|---|---|---|
| III | 1.3–1.4 | 36°–38° | 7–10 | 33.0–35.0 |
| IV | 0.5–0.7 | 32°–34° | 4–6 | 31.5–33.0 |
| V | 0.07–0.10 | 27°–29° | 0.8–1.9 | 27.5–31.5 |
| class IV surrounding rocks | Rock bolt | Steel arch | Sprayed concrete | Secondary lining |
| Diameter: 2.5 cm; Length: 300 cm; Longitudinal and circumferential spacing: 120, 50 cm Material: HRB 335 round steel. | No. 14 hot rolled joist steel with a cross-sectional area of 21.5 cm2; Longitudinal spacing: 200 cm. | Thickness of sprayed concrete: 20 cm. | Thickness of formworking concrete: 40 cm; Diameter of main reinforcement: 2.2 cm; Spacing of main reinforcement: 20 cm. |
| class V surrounding rocks | Rock bolt | Steel arch | Sprayed concrete | Secondary lining |
| Diameter: 2.5 cm; Length: 350 cm; Longitudinal and circumferential spacing: 120, 50 cm Material: HRB 335 round steel. | No.14 hot rolled joist steel with a cross-sectional area of 21.5 cm2; Longitudinal spacing: 150 cm. | Thickness of sprayed concrete: 25 cm. | Thickness of formworking concrete: 50 cm; Diameter of main reinforcement: 2.2 cm; Spacing of main reinforcement: 20 cm. |
| No. | Parameters | Sensors and Sensing Devices | Range | Accuracy | Frequency |
|---|---|---|---|---|---|
| 1 | internal displacements of surrounding rocks | multi-point extensometer, dial indicator | 100 mm | 0.1 mm | 2–4 times/day (displacement velocity > 10 mm/day); once/day (5–10 mm/day); once/2 days (1–5 mm/day); once/week (<1 mm/day). |
| 2 | contact pressures between surrounding rocks and primary linings | vibrating-wire pressure cell, cymometer | 0.6 MPa | ±1.5% F.S | 2–4 times/day (construction time 1–15 days); once/day (16–30 days); once/week (30–90 days); once/month (>90 days). |
| 3 | axial forces in rock bolts | vibrating-wire bolt force gauge, cymometer | 2000 kN | ±1.0% F.S | |
| 4 | internal forces in steel arches | vibrating-wire steel strain gauge, cymometer | 3000 με | ±1.0% F.S | |
| 5 | internal forces in secondary linings | embedded concrete strain gauge, cymometer | 3000 με | ±1.0% F.S |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Zhang, C.; Lin, G.; Wang, B. Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study. Appl. Sci. 2017, 7, 169. https://doi.org/10.3390/app7020169
Yan Q, Zhang C, Lin G, Wang B. Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study. Applied Sciences. 2017; 7(2):169. https://doi.org/10.3390/app7020169
Chicago/Turabian StyleYan, Qixiang, Chuan Zhang, Gang Lin, and Bo Wang. 2017. "Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study" Applied Sciences 7, no. 2: 169. https://doi.org/10.3390/app7020169
APA StyleYan, Q., Zhang, C., Lin, G., & Wang, B. (2017). Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study. Applied Sciences, 7(2), 169. https://doi.org/10.3390/app7020169







