CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish
Abstract
:1. Introduction
2. Physical Problems of Carangiform Fish
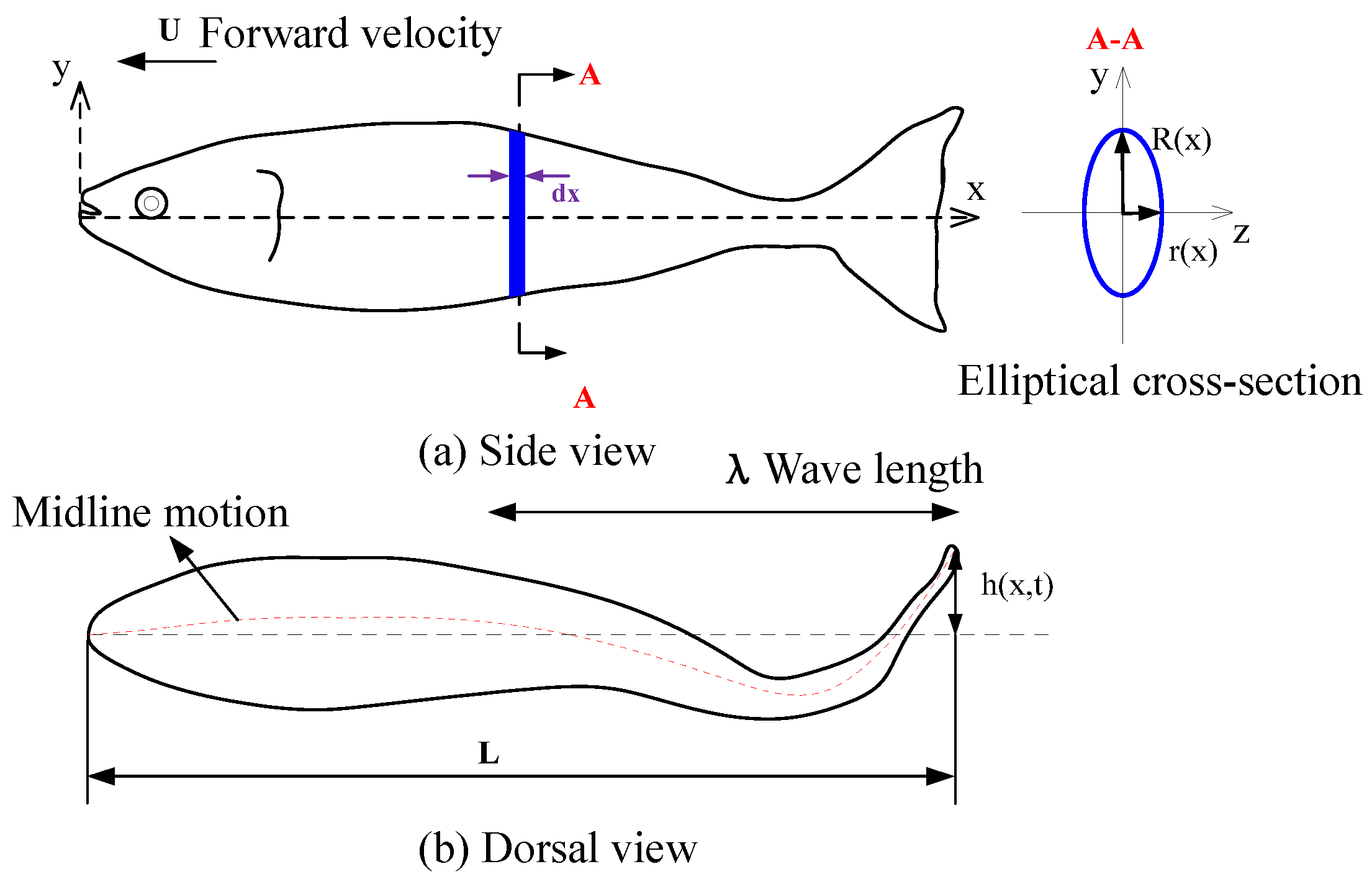
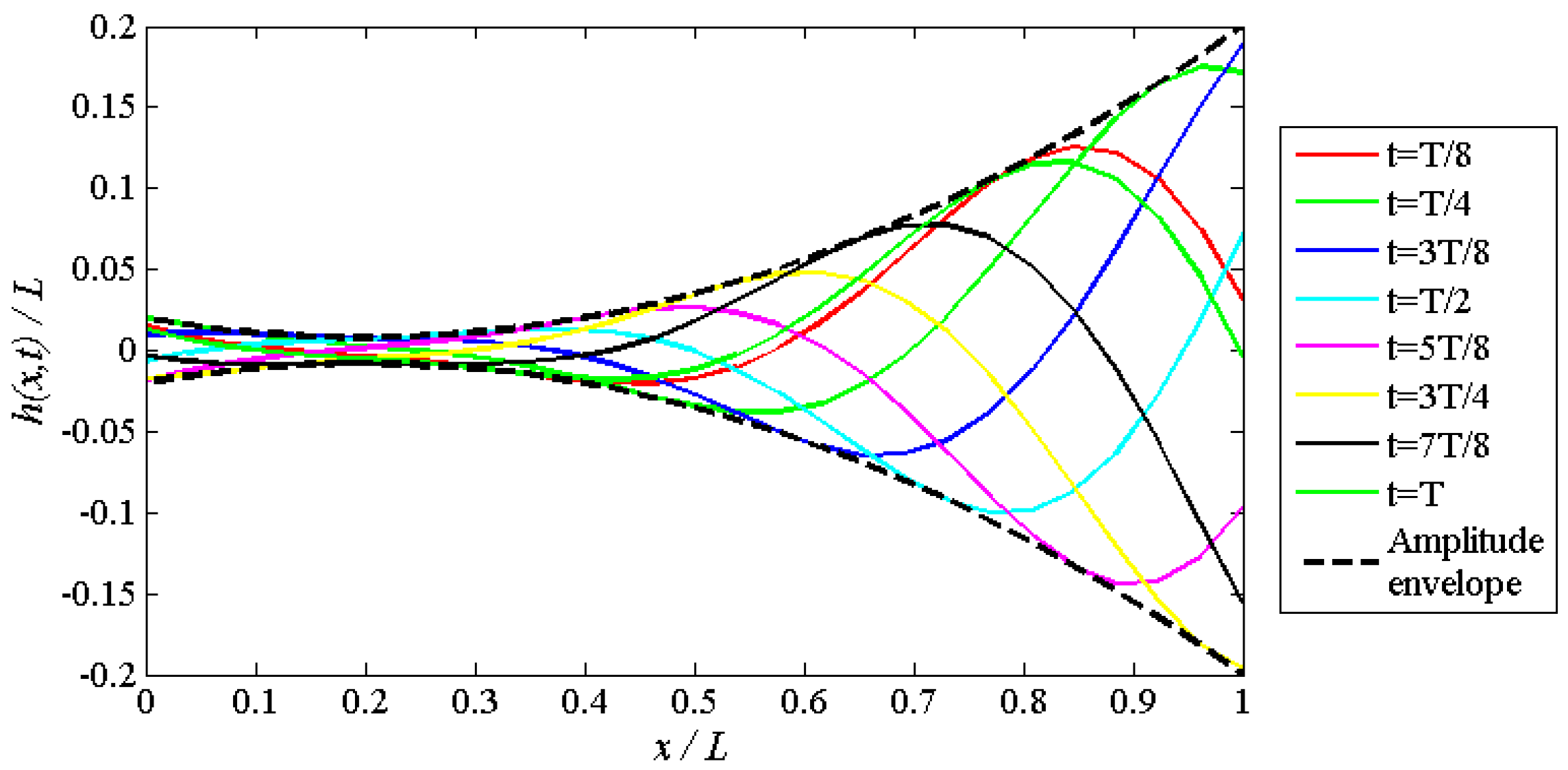
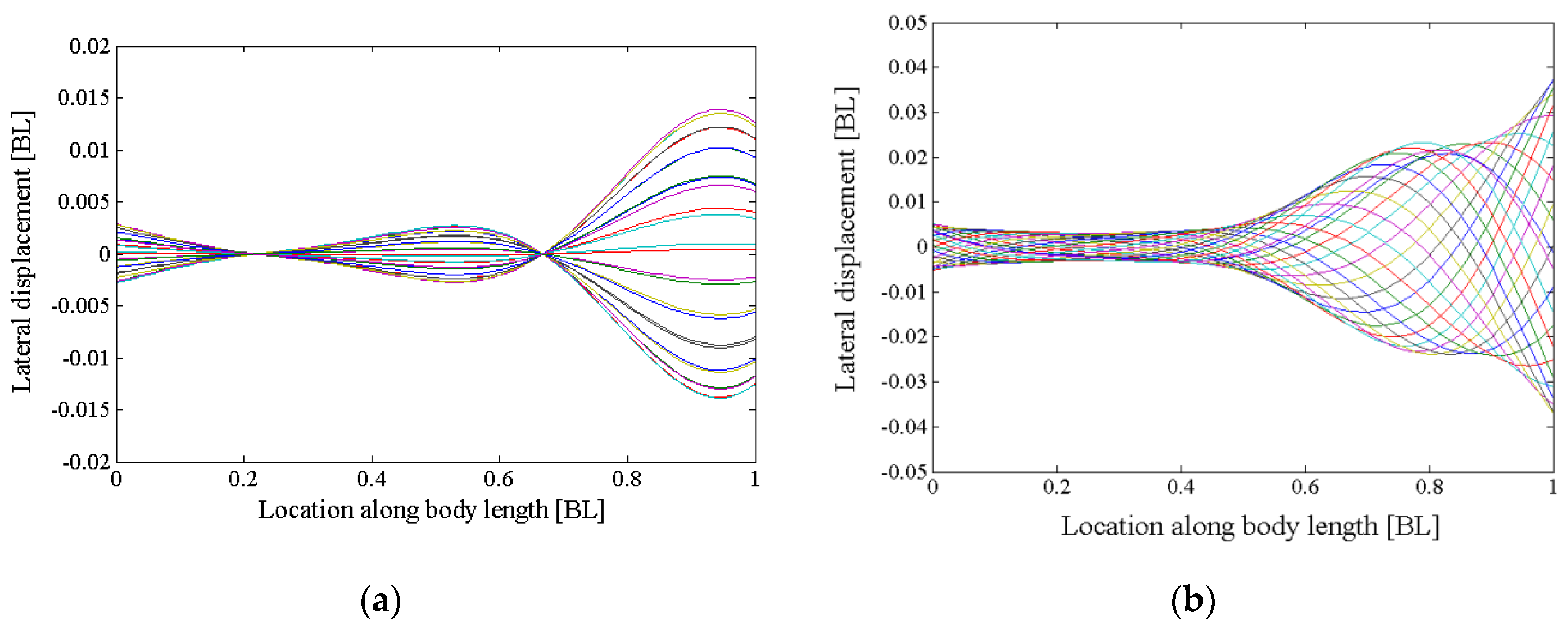
2.1. Shape and Kinematic Parametrization
2.2. Self-Propelled Fish Model
2.3. Evaluations of Swimming Performance
3. Numerical Methods
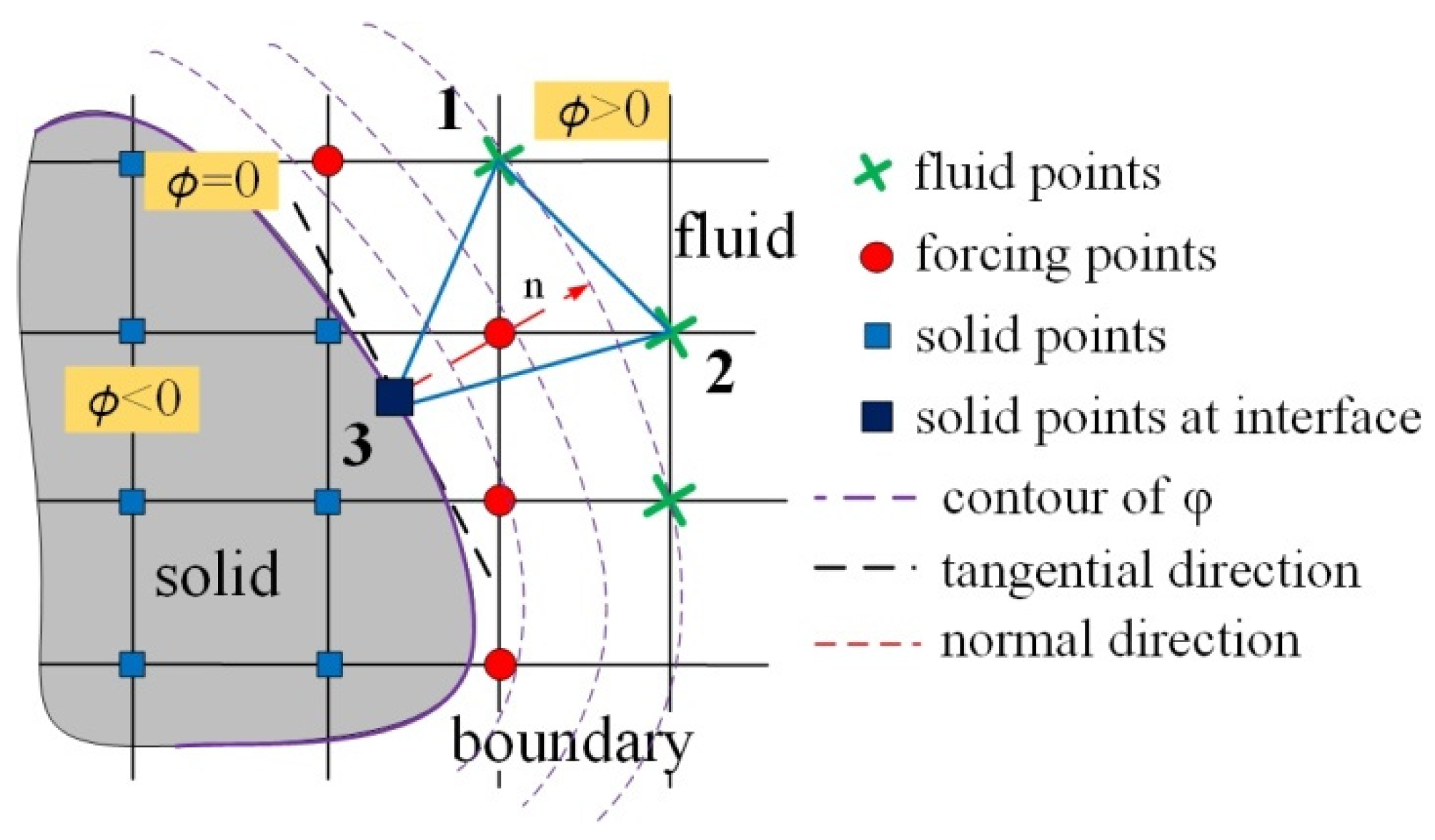
3.1. Level Set Function
3.2. Immersed Boundary Method
3.3. Validation Cases
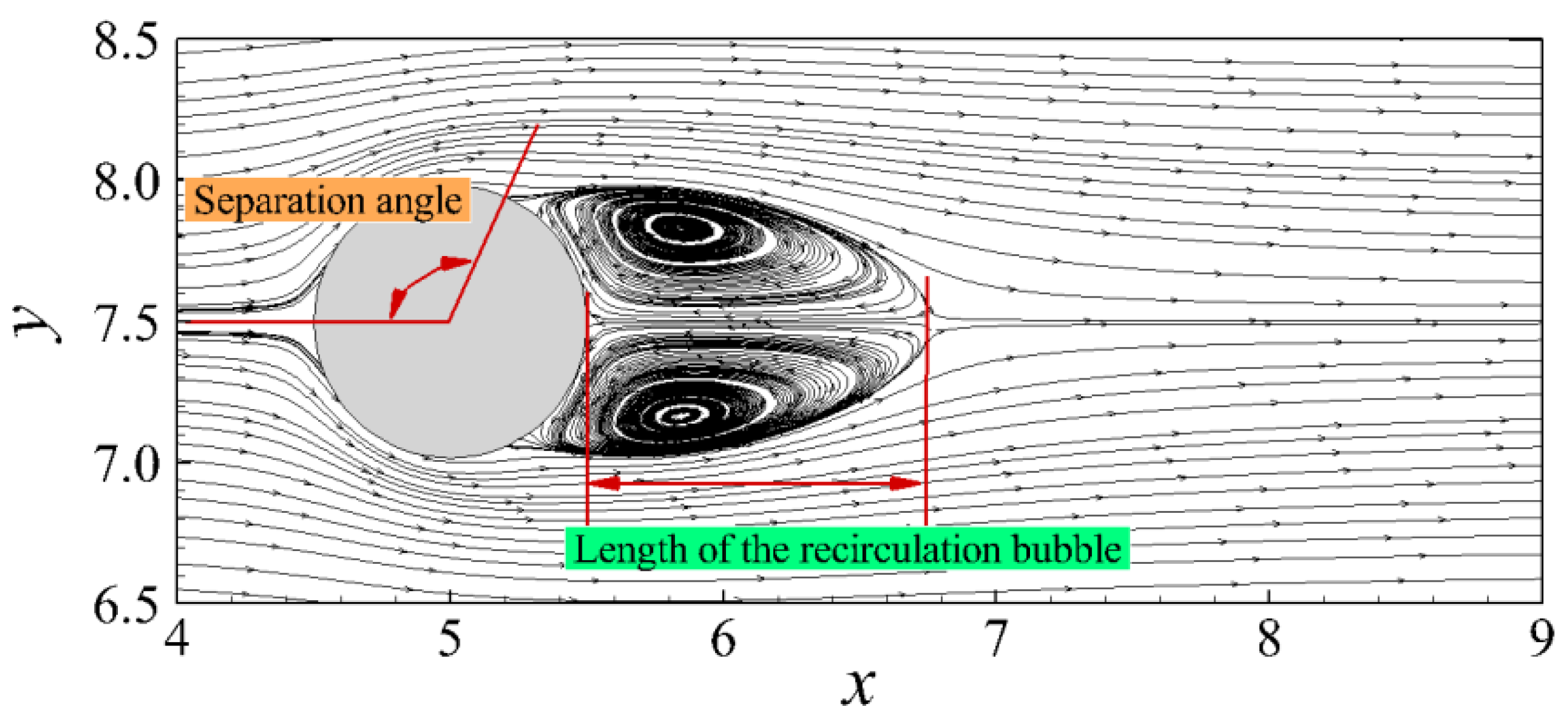
3.3.1. Flow Past a Sphere
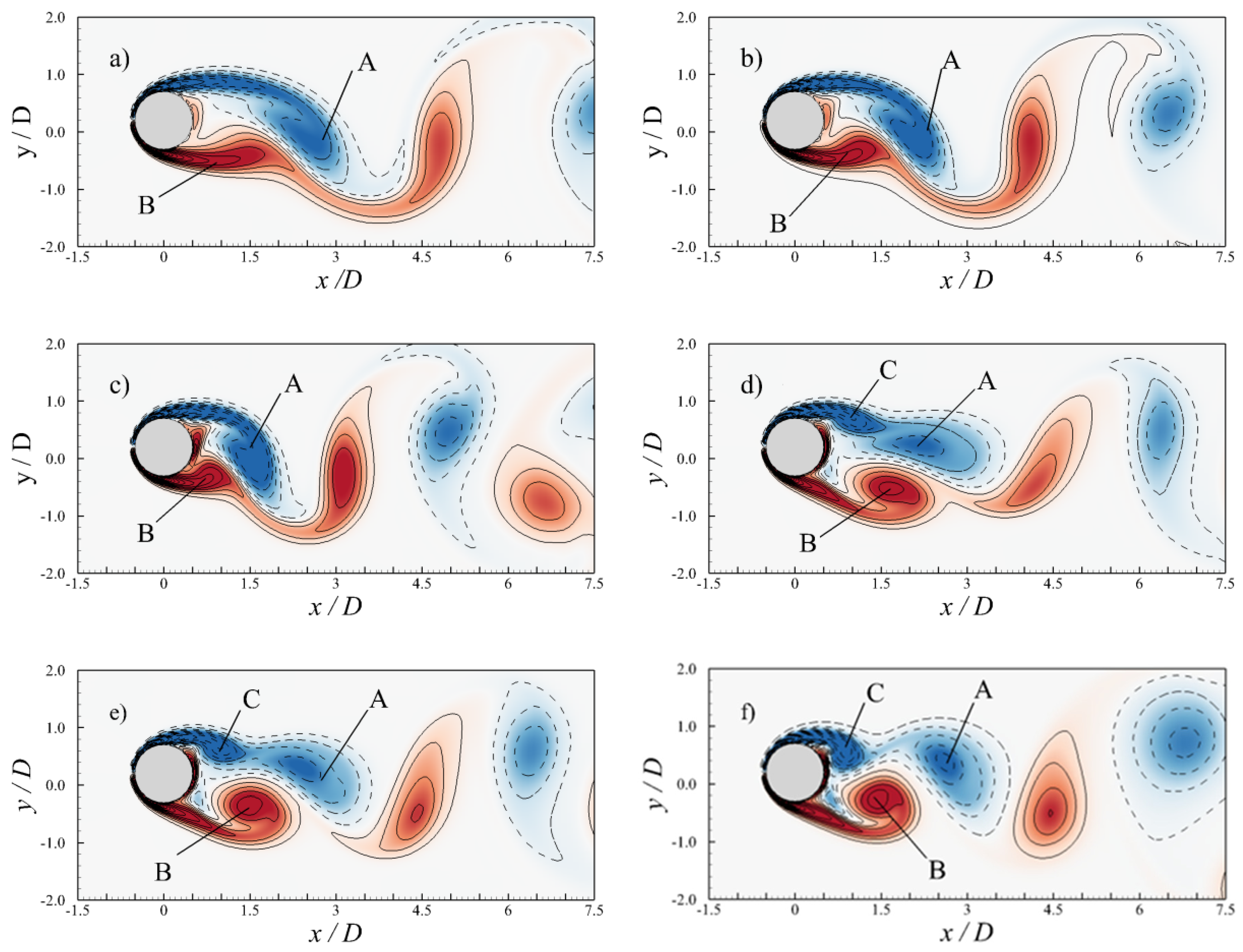
3.3.2. Flow Past a Transversely Oscillating Cylinder
4. Results
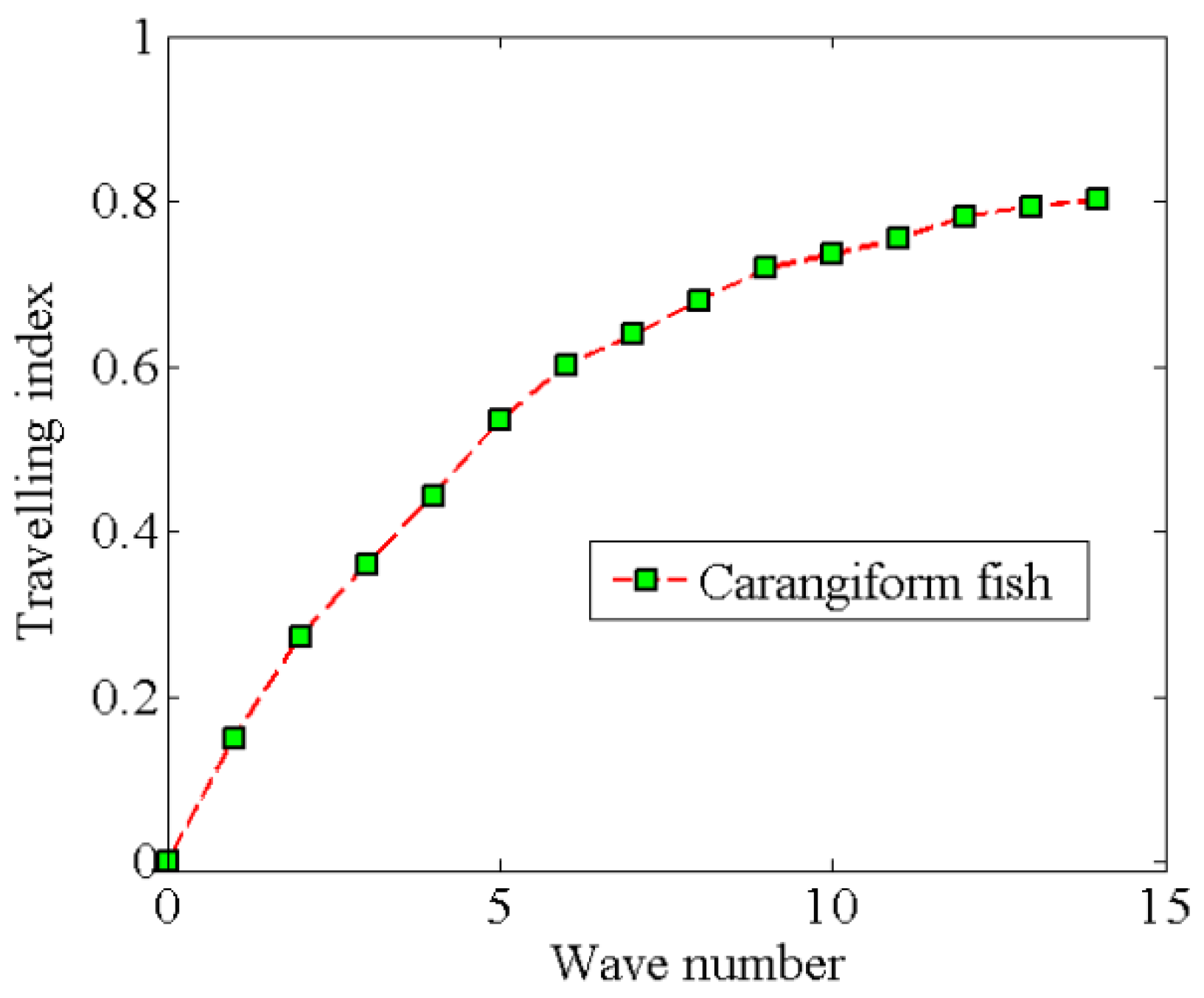
4.1. Relation between Travelling Index and Wave Number
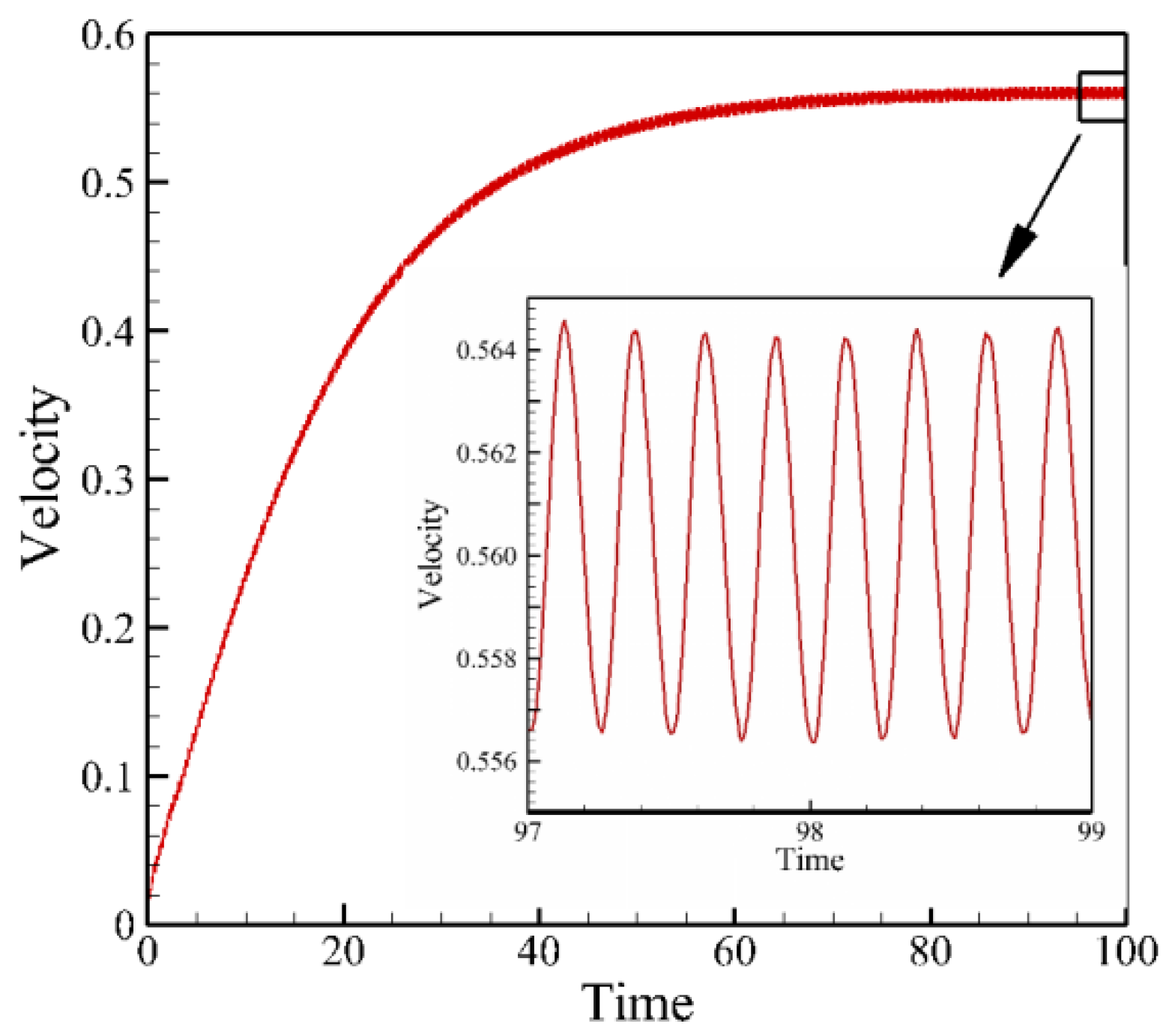
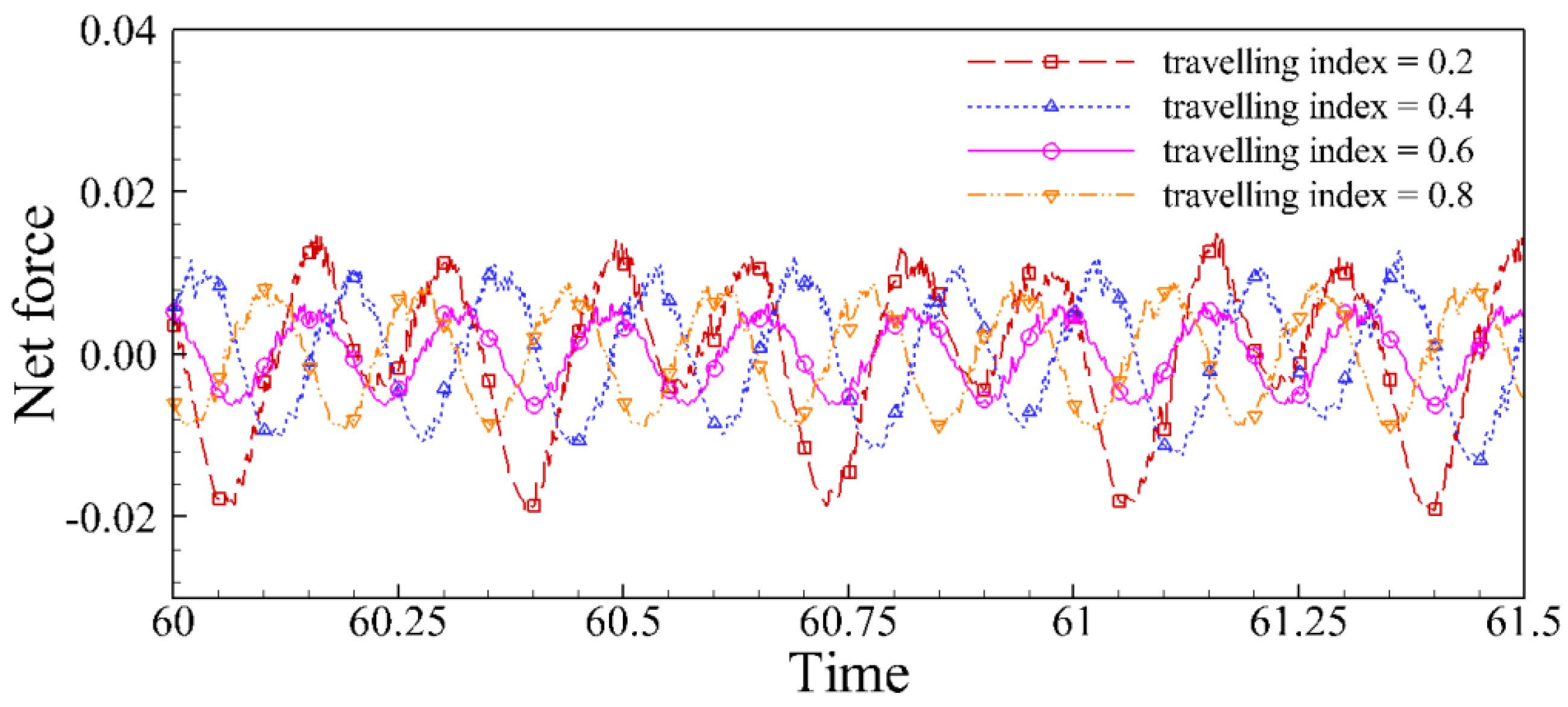
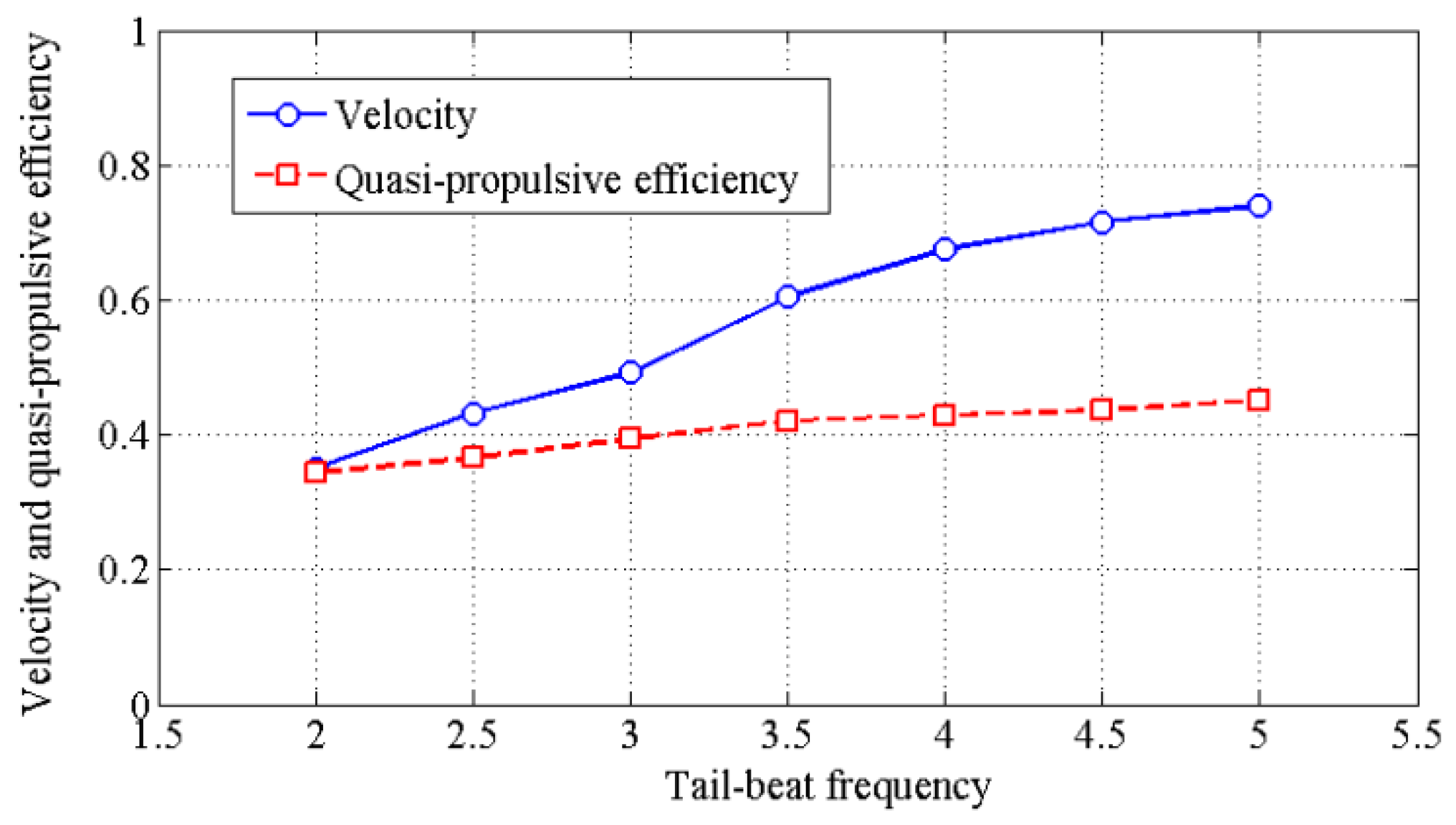
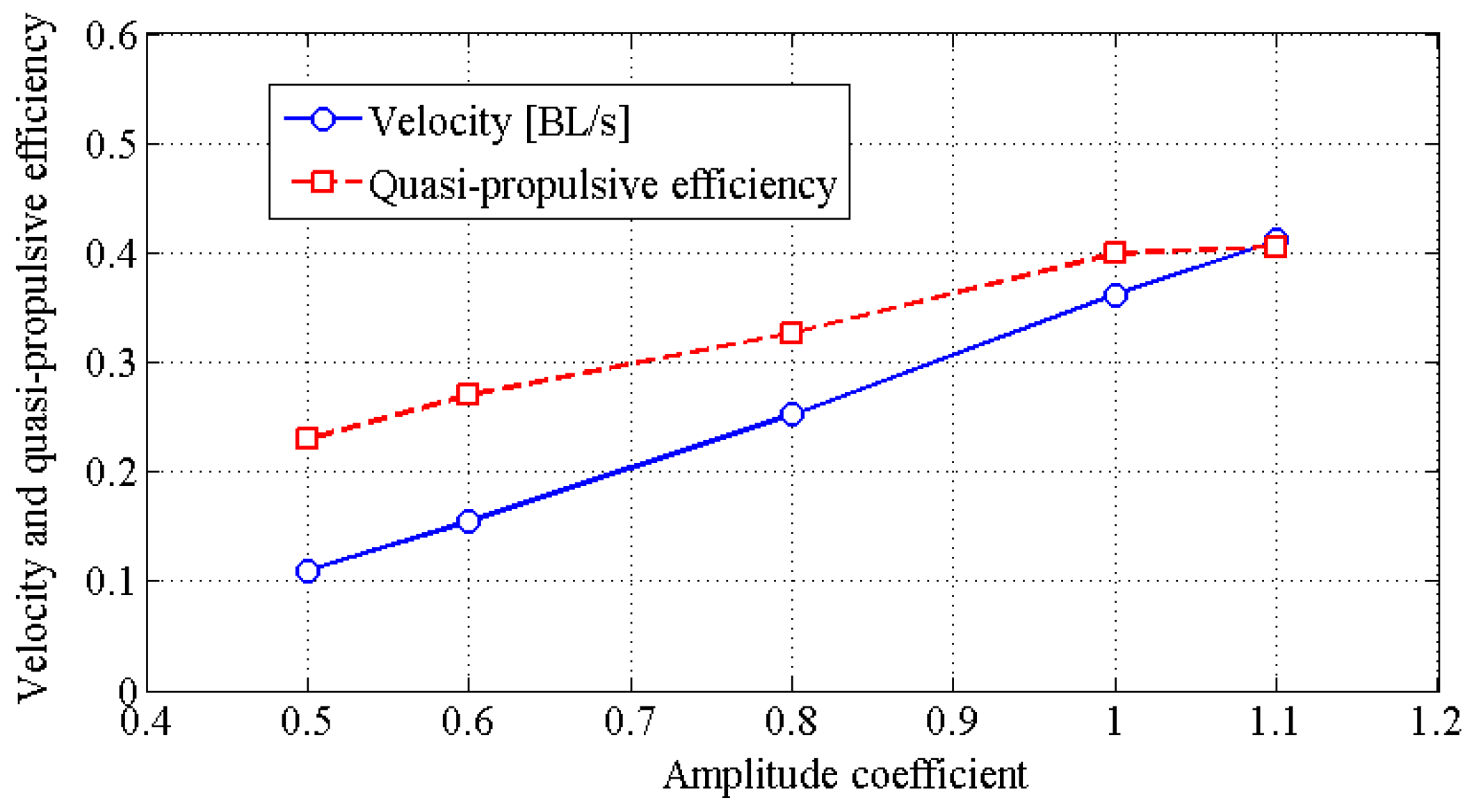
4.2. Effects of Travelling Index on Forward Speed
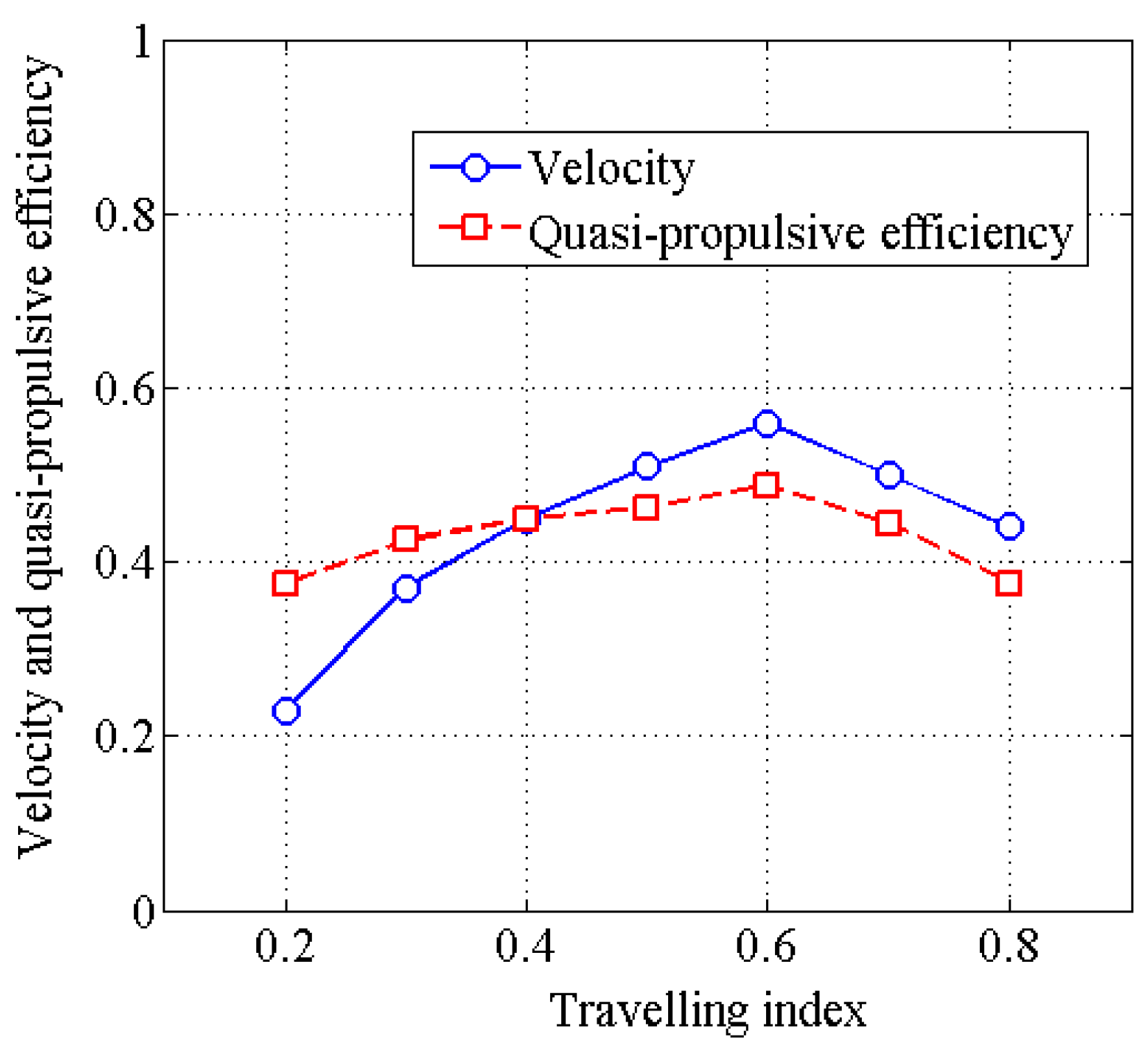
4.3. Effects of Travelling Index on Swimming Efficiency
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sfakiotakis, M.; Lane, D.M.; Davies, J.B.C. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef]
- Videler, J.J. Fish Swimming; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Barrett, D.S.; Triantafyllou, M.S.; Yue, D.K.P. Drag reduction in fish-like locomotion. J. Fluid Mech. 1999, 392, 183–212. [Google Scholar] [CrossRef]
- Lighthill, M.J. Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 1971, 179, 125–138. [Google Scholar] [CrossRef]
- Anderson, E.J.; McGillis, W.R.; Grosenbaugh, M.A. The boundary layer of swimming fish. J. Exp. Biol. 2001, 201, 81–102. [Google Scholar]
- Feeny, B.F. A complex orthogonal decomposition for wave motion analysis. J. Sound Vib. 2008, 310, 77–90. [Google Scholar] [CrossRef]
- Feeny, B.F.; Feeny, A.K. Complex modal analysis of the swimming motion of a whiting. J. Vib. Acoust. 2013, 135, 021004. [Google Scholar] [CrossRef]
- Carling, J.; Williams, T.L.; Bowtell, G. Self-propelled anguilliform swimming: Simultaneous solution of the two-dimensional Navier-Stokes equations and Newton's laws of motion. J. Exp. Biol. 1998, 201, 3143–3166. [Google Scholar] [PubMed]
- Borazjani, I.; Sotiropoulos, F. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 2010, 213, 89–107. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.B.; Xu, Y.Q.; Tang, X.Y.; Deng, Y.L. Study on a self-propelled fish swimming in viscous fluid by a finite element method. J. Mech. Med. Biol. 2013, 13, 1340012. [Google Scholar] [CrossRef]
- Tian, F.B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid-structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.M.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Dai, H.; Ferreira de Sousa, P.; Yin, B. On numerical oscillation of the direct-forcing immersed-boundary method for moving boundaries. Comput. Fluids 2012, 56, 61–76. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.; Choi, H. An immersed boundary finite volume method for simulations of flow in complex geometries. J. Comput. Phys. 2001, 171, 132–150. [Google Scholar] [CrossRef]
- Cheny, Y.; Botella, O. The LS-STAG method: A new immersed boundary/level-set method for the computation of incompressible viscous flows in complex moving geometries with good conservation properties. J. Comput. Phys. 2010, 229, 1043–1076. [Google Scholar] [CrossRef]
- Meyer, M.; Devesa, A.; Hickel, S.; Hu, X.; Adams, N. A conservative immersed interface method for Large-Eddy Simulation of incompressible flows. J. Comput. Phys. 2010, 229, 6300–6317. [Google Scholar] [CrossRef]
- Shrivastava, M.; Agrawal, A.; Sharma, A. A novel level set-based immersed-boundary method for CFD simulation of moving-boundary problems. Numer. Heat. Transf. B 2013, 63, 304–326. [Google Scholar] [CrossRef]
- Alvarado, P.V.Y. Design of Biomimetic Compliant Devices for Locomotion in Liquid Environments; Massachusetts Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Maertens, A.P.; Triantafyllou, M.S.; Yue, D.K.P. Efficiency of fish propulsion. Bioinspir. Biomim. 2015, 10, 46013–46023. [Google Scholar] [CrossRef] [PubMed]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P. Application of a fractional-step method to incompressible Navier-Stokes equations. J. Comput. Phys. 1985, 59, 308–323. [Google Scholar] [CrossRef]
- Liu, Y. Numerical Study of Strong Free Surface Flow and Breaking Waves; The Johns Hopkins University: Baltimore, MD, USA, 2013. [Google Scholar]
- Le, D.V.; Khoo, B.C.; Peraire, J. An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries. J. Comput. Phys. 2006, 220, 109–138. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Courier Corporation: North Chelmsford, MA, USA, 2005. [Google Scholar]
- Yang, J.M. An Embedded Boundary Formulation for Large-Eddy Simulation of Turbulent Flows Interacting with Moving Boundaries; University of Maryland: Baltimore, MD, USA, 2005. [Google Scholar]
- Johnson, T.A.; Patel, V.C. Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 1999, 378, 19–70. [Google Scholar] [CrossRef]
- Tomboulides, A.G.; Orszag, S.A. Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 2000, 416, 45–73. [Google Scholar] [CrossRef]
- Constantinescu, G.S.; Squires, K.D. LES and DES investigations of turbulent flow over a sphere. AIAA Pap. 2000, 2000–0540. [Google Scholar] [CrossRef]
- Ploumhans, P.; Winckelmans, G.S.; Salmon, J.K.; Leonard, A.; Warren, M.S. Vortex methods for direct numerical simulation of three-dimensional bluff body flows: Applications to the sphere at Re = 300, 500 and 1000. J. Comput. Phys. 2002, 178, 427–463. [Google Scholar] [CrossRef]
- Guilmineau, E.; Queutey, P. A numerical simulation of vortex shedding from an oscillating circular cylinder. J. Fluid Struct. 2002, 16, 773–794. [Google Scholar] [CrossRef]
- Yang, J.; Balaras, E. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. J. Comput. Phys. 2006, 215, 12–40. [Google Scholar] [CrossRef]
- Videler, J.J.; Hess, F. Fast continuous swimming of two pelagic predators, saithe (Pollachius virens) and mackerel (Scomber scombrus)—A kinematic analysis. J. Exp. Biol. 1984, 109, 209–228. [Google Scholar]
- Gray, J. Studies in animal locomotion III: The propulsive mechanism of the whiting (Gadus merlangus). J. Exp. Biol. 1933, 10, 391–402. [Google Scholar]
- Müller, U.K.; Smit, J.; Stamhuis, E.J.; Videler, J.J. How the body contributes to the wave in undulatory fish swimming. J. Exp. Biol. 2001, 204, 2751–2762. [Google Scholar] [PubMed]
- Shen, L.; Zhang, X.; Yue, D.K.P.; Triantafyllou, M.S. Turbulent flow over a flexible wall undergoing a streamwise travelling wave motion. J. Fluid Mech. 2003, 484, 197–221. [Google Scholar] [CrossRef]
- Tian, F.B.; Lu, X.Y.; Luo, H. Propulsive performance of a body with a traveling wave surface. Phys. Rev. E 2012, 86, 016304. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Yu, Y.L.; Tong, B.G. Flow control by means of a traveling curvature wave in fishlike escape responses. Phys. Rev. E 2011, 84, 056312. [Google Scholar] [CrossRef] [PubMed]
- Bainbridge, R. The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J. Exp. Biol. 1958, 35, 109–133. [Google Scholar]

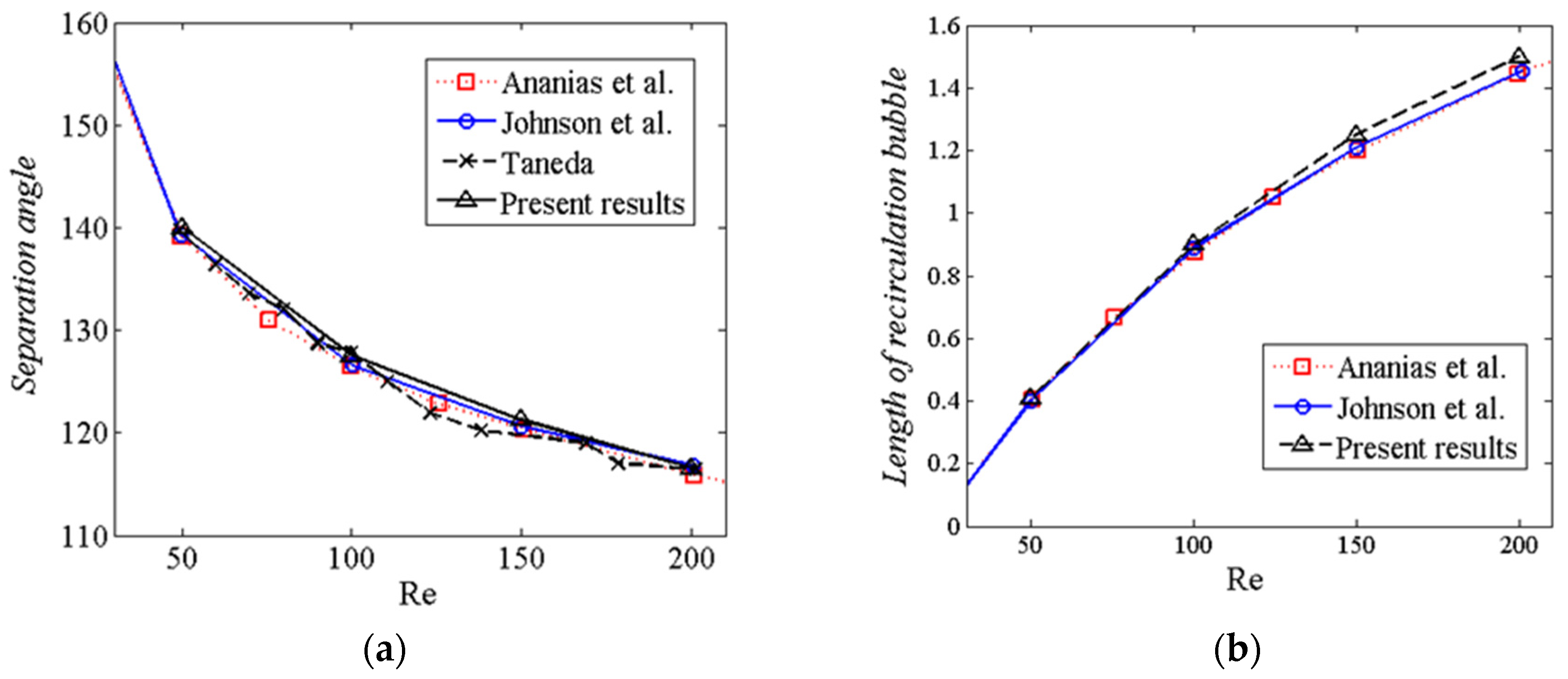
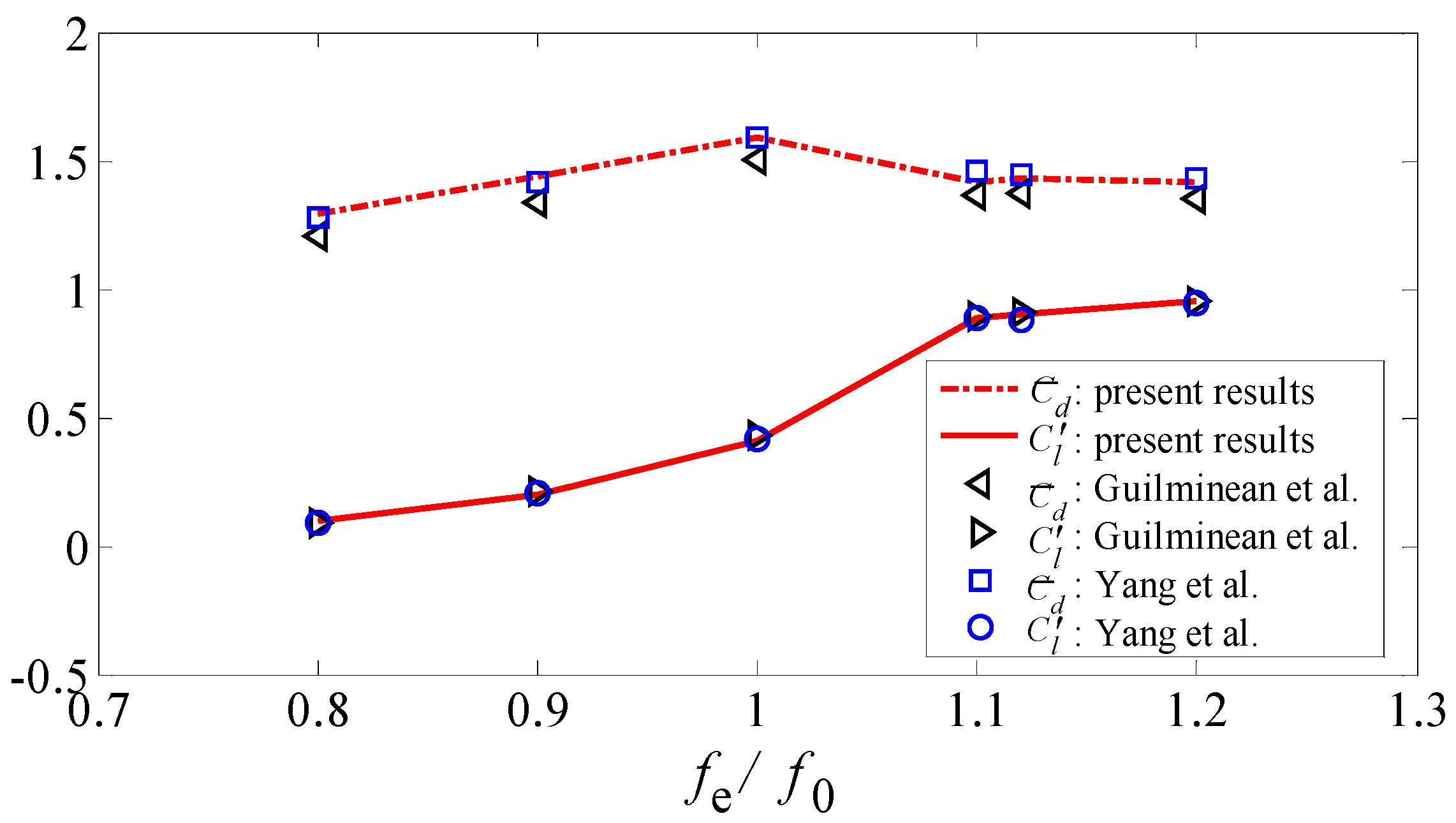
| Results from | Re = 50 | Re = 100 | Re = 150 | Re = 200 |
|---|---|---|---|---|
| Experiment [27] | 1.574 | 1.087 | 0.889 | 0.776 |
| Yang [28] | 1.610 | 1.118 | 0.920 | 0.807 |
| Johnson and Pater [29] | 1.575 | 1.100 | 0.900 | 0.775 |
| Present method | 1.610 | 1.120 | 0.921 | 0.804 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Gu, X.; Li, K.; Jiang, H. CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish. Appl. Sci. 2017, 7, 149. https://doi.org/10.3390/app7020149
Cui Z, Gu X, Li K, Jiang H. CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish. Applied Sciences. 2017; 7(2):149. https://doi.org/10.3390/app7020149
Chicago/Turabian StyleCui, Zuo, Xingshi Gu, Kangkang Li, and Hongzhou Jiang. 2017. "CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish" Applied Sciences 7, no. 2: 149. https://doi.org/10.3390/app7020149
APA StyleCui, Z., Gu, X., Li, K., & Jiang, H. (2017). CFD Studies of the Effects of Waveform on Swimming Performance of Carangiform Fish. Applied Sciences, 7(2), 149. https://doi.org/10.3390/app7020149





